Characterization of Viscoelastic Poisson’s Ratio of Engineering Elastomers via DIC-Based Creep Testing
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ernst, L.J.; Zhang, G.Q.; Jansen, K.M.B.; Bressers, H.J.L. Time- and Temperature-Dependent Thermo-Mechanical Modeling of a Packaging Molding Compound and its Effect on Packaging Process Stresses. J. Electron. Packag. 2003, 125, 539–548. [Google Scholar] [CrossRef]
- Świeszkowski, W.; Ku, D.N.; Bersee, H.E.; Kurzydlowski, K.J. An elastic material for cartilage replacement in an arthritic shoulder joint. Biomaterials 2006, 27, 1534–1541. [Google Scholar] [CrossRef] [PubMed]
- Al-Hiddabi, S.A.; Pervez, T.; Qamar, S.; Al-Jahwari, F.; Marketz, F.; Al-Houqani, S.; van de Velden, M. Analytical model of elastomer seal performance in oil wells. Appl. Math. Model. 2015, 39, 2836–2848. [Google Scholar] [CrossRef]
- Kugler, H.P.; Stacer, R.G.; Steimle, C. Direct Measurement of Poisson’s Ratio in Elastomers. Rubber Chem. Technol. 1990, 63, 473–487. [Google Scholar] [CrossRef]
- Saseendran, S.; Wysocki, M.; Varna, J. Cure-state dependent viscoelastic Poisson’s ratio of LY5052 epoxy resin. Adv. Manuf. Polym. Compos. Sci. 2017, 3, 92–100. [Google Scholar] [CrossRef]
- Pandini, S.; Pegoretti, A. Time, temperature, and strain effects on viscoelastic Poisson’s ratio of epoxy resins. Polym. Eng. Sci. 2008, 48, 1434–1441. [Google Scholar] [CrossRef]
- Cui, H.; Ma, W.; Lv, X.; Li, C.; Ding, Y. Investigation on Viscoelastic Poisson’s Ratio of Composite Materials considering the Effects of Dewetting. Int. J. Aerosp. Eng. 2022, 2022, 3696330. [Google Scholar] [CrossRef]
- Cui, H.-R.; Shen, Z.-B. An investigation on a new creep constitutive model and its implementation with the effects of time- and temperature-dependent Poisson’s ratio. Acta Mech. 2018, 229, 4605–4621. [Google Scholar] [CrossRef]
- Tschoegl, N.W.; Knauss, W.G.; Emri, I. Poisson’s Ratio in Linear Viscoelasticity—A Critical Review. Mech. Time-Depend. Mater. 2002, 6, 3–51. [Google Scholar] [CrossRef]
- Van Der Varst, P.G.T.; Kortsmit, W.W. Notes on the lateral contraction of linear isotropic visco-elastic materials. Arch. Appl. Mech. 1992, 62, 338–346. [Google Scholar] [CrossRef][Green Version]
- Ashrafi, H.; Shariyat, M. A mathematical approach for describing the time-dependent Poisson’s ratio of viscoelastic ligaments mechanical characteristics of biological tissues. In Proceedings of the 17th Iranian Conference of Biomedical Engineering (ICBME), Isfahan, Iran, 3–4 November 2010. [Google Scholar] [CrossRef]
- O’Brien, D.J.; Sottos, N.R.; White, S.R. Cure-dependent Viscoelastic Poisson’s Ratio of Epoxy. Exp. Mech. 2007, 47, 237–249. [Google Scholar] [CrossRef]
- Farfan-Cabrera, L.I.; Pascual-Francisco, J.B. An Experimental Methodological Approach for Obtaining Viscoelastic Poisson’s Ratio of Elastomers from Creep Strain DIC-Based Measurements. Exp. Mech. 2022, 62, 287–297. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Pascual-Francisco, J.B.; Barragán-Pérez, O.; Susarrey-Huerta, O.; Michtchenko, A.; Martínez-García, A.; Farfán-Cabrera, L.I. The effectiveness of shearography and digital image correlation for the study of creep in elastomers. Mater. Res. Express 2017, 4, 115301. [Google Scholar] [CrossRef]
- Sahu, R.; Patra, K.; Szpunar, J. Experimental Study and Numerical Modelling of Creep and Stress Relaxation of Dielectric Elastomers. Strain 2014, 51, 43–54. [Google Scholar] [CrossRef]
- Degrange, J.-M.; Thomine, M.; Kapsa, P.; Pelletier, J.M.; Chazeau, L.; Vigier, G.; Dudragne, G.; Guerbé, L. Influence of viscoelasticity on the tribological behaviour of carbon black filled nitrile rubber (NBR) for lip seal application. Wear 2005, 259, 684–692. [Google Scholar] [CrossRef]
- Herbert, E.G.; Phani, P.S.; Johanns, K.E. Nanoindentation of viscoelastic solids: A critical assessment of experimental methods. Curr. Opin. Solid State Mater. Sci. 2015, 19, 334–339. [Google Scholar] [CrossRef]
- Tweedie, C.A.; Van Vliet, K.J. Contact creep compliance of viscoelastic materials via nanoindentation. J. Mater. Res. 2006, 21, 1576–1589. [Google Scholar] [CrossRef]
- Yoneyama, S.; Takashi, M.; Gotoh, J. Photoviscoelastic Stress Analysis near Contact Regions under Complex Loads. Mech. Time-Depend. Mater. 1997, 1, 51–65. [Google Scholar] [CrossRef]
- Darlix, B.; Montmitonnet, P.; Monasse, B. Creep of polymers under ball indentation: A theoretical and experimental study. Polym. Test. 1986, 6, 189–203. [Google Scholar] [CrossRef]
- Oyen, M.L. Spherical Indentation Creep Following Ramp Loading. J. Mater. Res. 2005, 20, 2094–2100. [Google Scholar] [CrossRef]
- Rubin, A.; Favier, D.; Danieau, P.; Giraudel, M.; Chambard, J.-P.; Gauthier, C. Direct observation of contact on non transparent viscoelastic polymers surfaces: A new way to study creep and recovery. Prog. Org. Coat. 2016, 99, 134–139. [Google Scholar] [CrossRef]
- Pascual-Francisco, J.B.; Farfan-Cabrera, L.I.; Susarrey-Huerta, O. Characterization of tension set behavior of a silicone rubber at different loads and temperatures via digital image correlation. Polym. Test. 2020, 81, 106226. [Google Scholar] [CrossRef]
- Stoček, R.; Stěnička, M.; Maloch, J. Determining Parametrical Functions Defining the Deformations of a Plane Strain Tensile Rubber Sample. In Fatigue Crack Growth in Rubber Materials. Advances in Polymer Science; Heinrich, G., Kipscholl, R., Stoček, R., Eds.; Springer: Cham, Germany, 2020; Volume 286, pp. 19–38. [Google Scholar] [CrossRef]
- Stoček, R.; Heinrich, G.; Gehde, M.; Kipscholl, R. A new testing concept for determination of dynamic crack propagation in rubber materials. KGK Rubberpoint 2012, 65, 49–53. [Google Scholar]
- Stoček, R.; Heinrich, G.; Gehde, M.; Kipscholl, R. Analysis of dynamic crack propagation in elastomers by simultaneous tensile- and pure-shear-mode testing. In Fracture Mechanics and Statistical Mechanics of Reinforced Elastomeric Blends (Lecture Notes in Applied and Computational Mechanics); Grellmann, W., Heinrich, G., Kaliske, M., Klüppel, M., Schneider, K., Vilgis, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 70, pp. 269–301. [Google Scholar] [CrossRef]
- Robertson, C.G.; Hardman, N.J. Nature of Carbon Black Reinforcement of Rubber: Perspective on the Original Polymer Nanocomposite. Polymers 2021, 13, 538. [Google Scholar] [CrossRef] [PubMed]
- Findley, W.N.; Lai, J.S.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Materials; Dover Publications: New York, NY, USA, 1976; pp. 50–70. [Google Scholar]
- Cui, H.R.; Tang, G.J.; Shen, Z.B. Study on the Viscoelastic Poisson’s Ratio of Solid Propellants Using Digital Image Correlation Method. Propellants Explos. Pyrotech. 2016, 41, 835. [Google Scholar] [CrossRef]
- Grassia, L.; D’Amore, A.; Simon, S.L. On the viscoelastic Poisson’s ratio in amorphous polymers. J. Rheol. 2010, 54, 1009–1022. [Google Scholar] [CrossRef]
- Aili, A.; Vandamme, M.; Torrenti, J.-M.; Masson, B. Theoretical and practical differences between creep and relaxation Poisson’s ratios in linear viscoelasticity. Mech. Time-Depend. Mater. 2015, 19, 537–555. [Google Scholar] [CrossRef]
- Charpin, L.; Sanahuja, J. Creep and relaxation Poisson’s ratio: Back to the foundations of linear viscoelasticity. Application to concrete. Int. J. Solids Struct. 2017, 110, 2–14. [Google Scholar] [CrossRef]
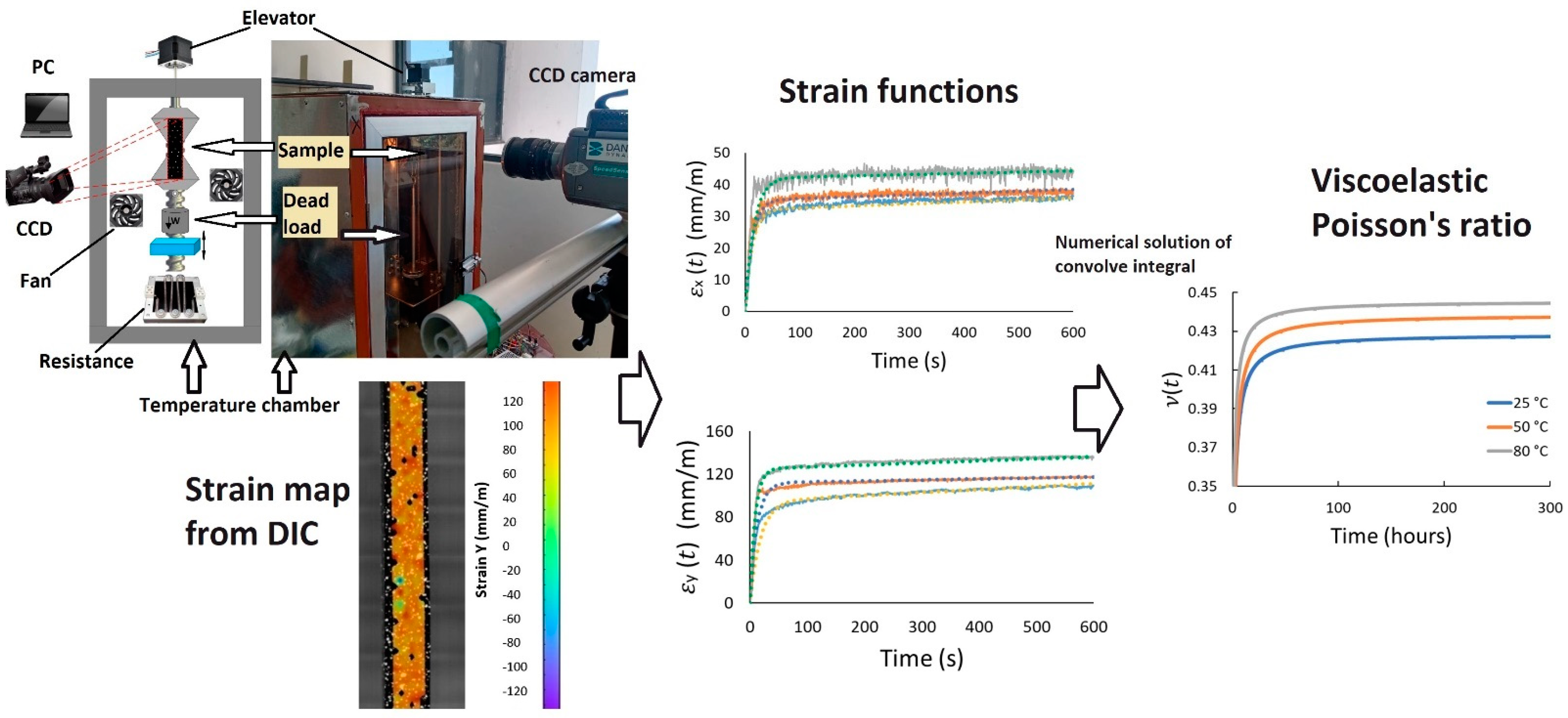
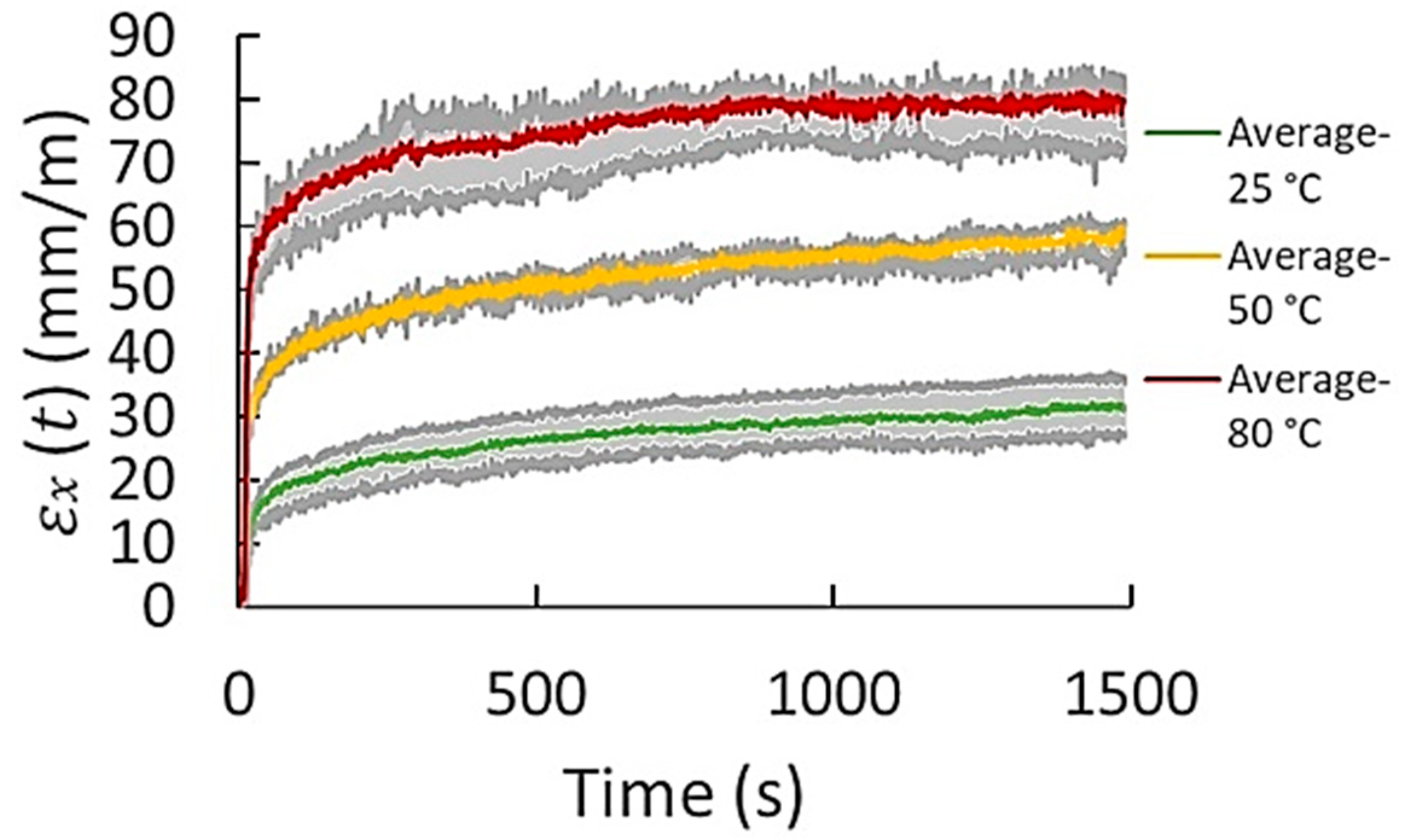
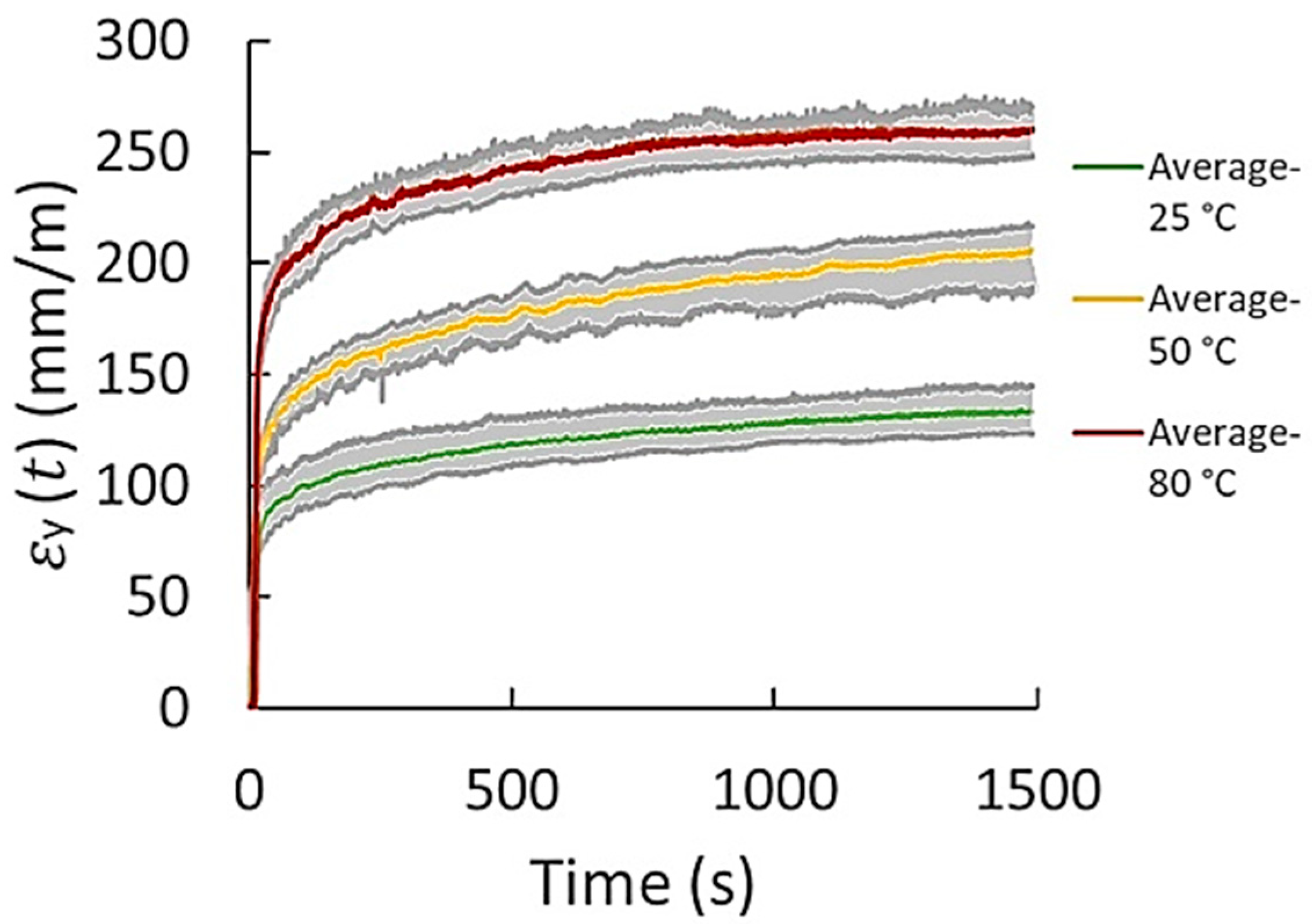
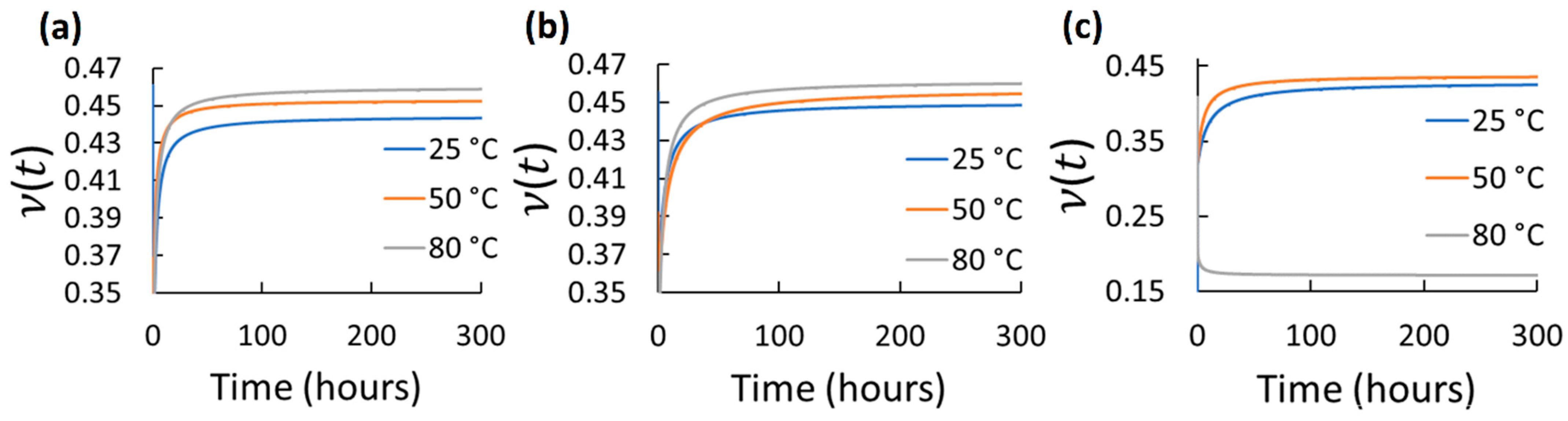
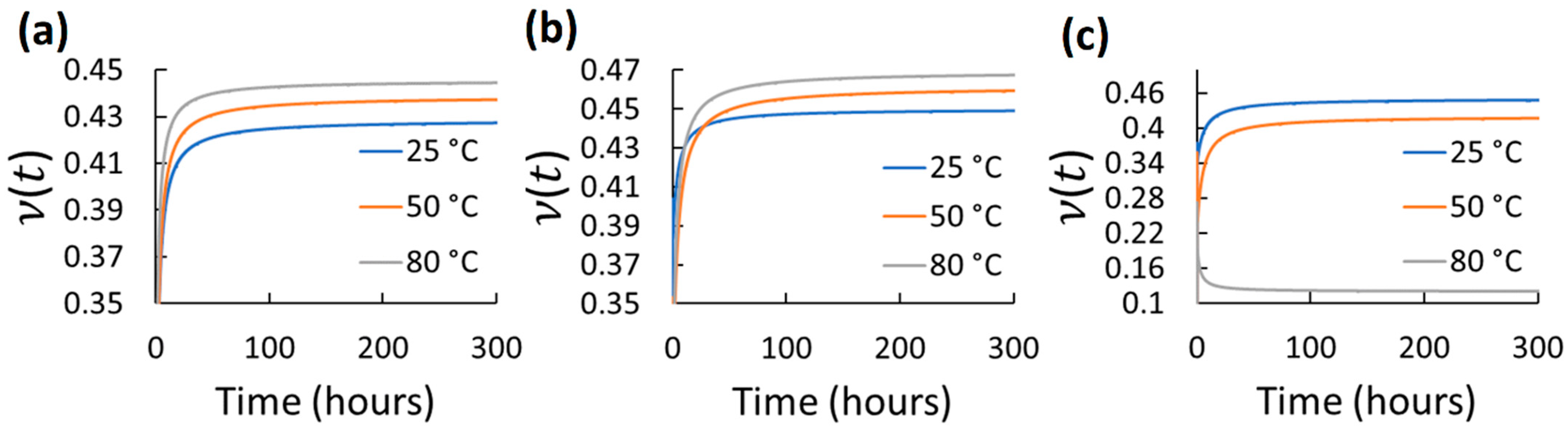
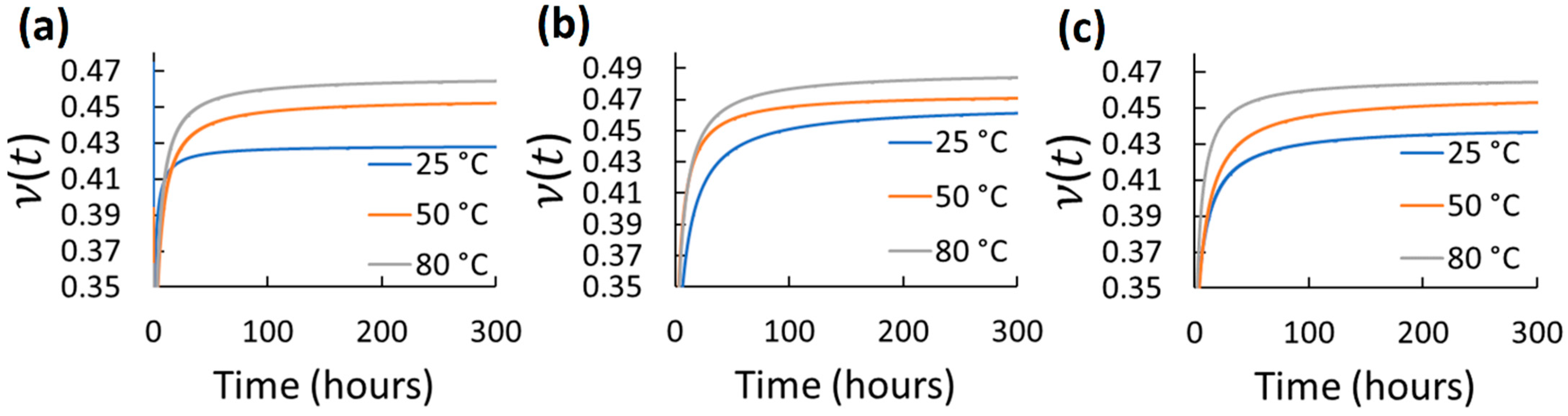
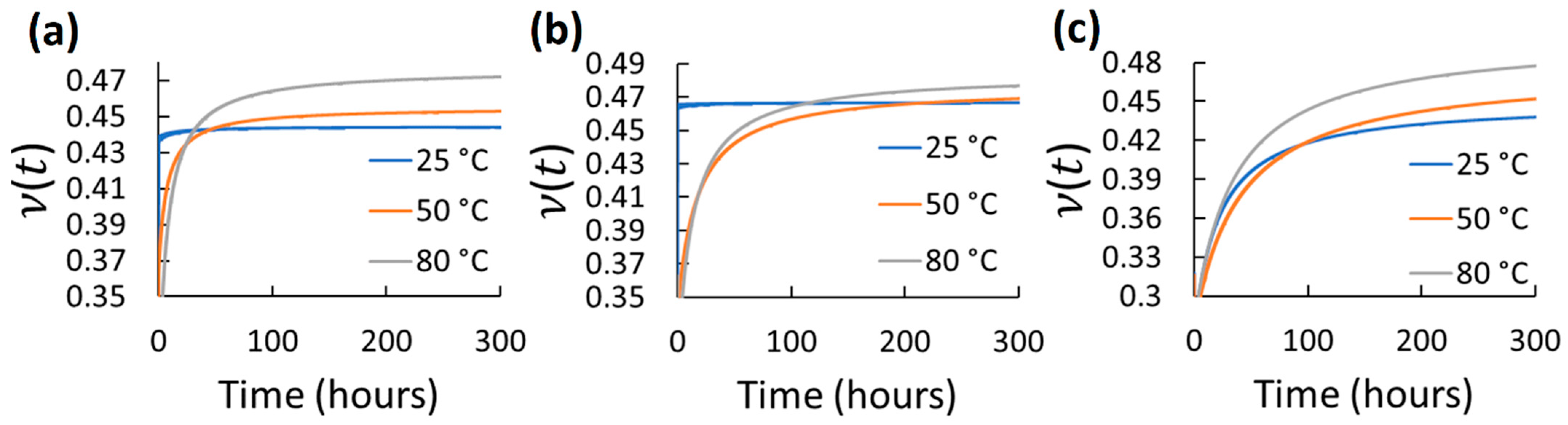

| Material/Test | Property/Parameter | Value |
|---|---|---|
| Ethylene-Propylene-Diene Monomer (EPDM) (Manufacturer: Rodillos BMR®, Guadalajara, Jalisco, México) | Hardness, ASTM-D2240 (Shore A) | 68.5 ± 2 |
| Tensile breaking strength, ASTM-D412 (MPa) | 14 ± 0.6 | |
| Flouroelastomer, Viton® (FKM) (Manufacturer: Rodillos BMR®, Guadalajara, Jalisco, México) | Hardness, ASTM-D2240 (Shore A) | 77.5 ± 2 |
| Tensile breaking strength, ASTM-D412 (MPa) | 11 ± 0.7 | |
| Nitrile Butadiene Rubber (NBR) (Manufacturer: Rodillos BMR®, Guadalajara, Jalisco, México) | Hardness, ASTM-D2240 (Shore A) | 73 ± 2 |
| Tensile breaking strength, ASTM-D412 (MPa) | 6.9 ± 0.5 | |
| Silicone rubber/Vinyl-Methyl silicone (VMQ) (Manufacturer: Rodillos BMR®, Guadalajara, Jalisco, México) | Hardness, ASTM-D2240 (Shore A) | 47.5 ± 1.5 |
| Tensile breaking strength, ASTM-D412 (MPa) | 5 ± 0.8 | |
| Neoprene/Chloroprene Rubber (CR) (Manufacturer: Rodillos BMR®, Guadalajara, Jalisco, México) | Hardness, ASTM-D2240 (Shore A) | 69 ± 2 |
| Tensile breaking strength, ASTM-D412 (MPa) | 3.5 ± 0.5 | |
| Strain measurement/DIC parameters | Subset (pixels) | 17 |
| Step (pixels) | 3 | |
| Field of view (mm × mm) | 55 × 36 | |
| Measurement points (points) | 425 | |
| Temporal resolution (fps) | 1 | |
| Camera distance (mm) | 200 | |
| Image resolution (pixels × pixels) | 1280 × 800 | |
| Spatial resolution (mm) | 0.1 | |
| Strain resolution (mm/m) | 0.25 | |
| Frame amount | 1800 | |
| Measurement time (minutes) | 30 | |
| Creep test | Tensile load (N) | 2, 4, 6 |
| Stress (kPa) | 200, 400, 600 | |
| Temperature (°C) | 25 ± 1, 50 ± 2 and 80 ± 2 | |
| Test time (minutes) | 30 |
| Material | Stress (kPa) | Temperature (°C) | Error (%) | Error (%) | ||
|---|---|---|---|---|---|---|
| EPDM | 200 | 25 | 3.7 | 9.5 | ||
| 50 | 5.5 | 4.4 | ||||
| 80 | 1.8 | 3.1 | ||||
| 400 | 25 | 1.6 | 3.5 | |||
| 50 | 2.0 | 2.7 | ||||
| 80 | 3.6 | 3.6 | ||||
| 600 | 25 | 3.0 | 2.0 | |||
| 50 | 4.0 | 3.3 | ||||
| 80 | 4.8 | 2.5 | ||||
| CR | 200 | 25 | 3.1 | 6.3 | ||
| 50 | 1.4 | 3.4 | ||||
| 80 | 2.4 | 4.1 | ||||
| 400 | 25 | 1.9 | 4.8 | |||
| 50 | 3.0 | 3.8 | ||||
| 80 | 2.3 | 3.2 | ||||
| 600 | 25 | 2.3 | 4.6 | |||
| 50 | 2.2 | 4.5 | ||||
| 80 | 3.1 | 4.2 | ||||
| NBR | 200 | 25 | 2.0 | 11 | ||
| 50 | 3.0 | 11 | ||||
| 80 | 1.6 | 4.6 | ||||
| 400 | 25 | 1.0 | 3.1 | |||
| 50 | 3.0 | 5.5 | ||||
| 80 | 2.3 | 3.6 | ||||
| 600 | 25 | 2.0 | 2.4 | |||
| 50 | 2.7 | 2.6 | ||||
| 80 | 2.0 | 3.9 | ||||
| VMQ | 200 | 25 | 3.2 | 4.2 | ||
| 50 | 1.9 | 3.6 | ||||
| 80 | 1.3 | 5.5 | ||||
| 400 | 25 | 2.6 | 3.3 | |||
| 50 | 1.7 | 2.4 | ||||
| 80 | 1.5 | 2.0 | ||||
| 600 | 25 | 2.0 | 3.0 | |||
| 50 | 1.1 | 2.3 | ||||
| 80 | 2.2 | 2.2 | ||||
| FKM | 200 | 25 | 4.3 | 22 | ||
| 50 | 2.4 | 5.5 | ||||
| 80 | 1.4 | 5.6 | ||||
| 400 | 25 | 2.4 | 3.6 | |||
| 50 | 3.8 | 3.7 | ||||
| 80 | 2.3 | 2.8 | ||||
| 600 | 25 | 3.2 | 3.9 | |||
| 50 | 2.7 | 2.9 | ||||
| 80 | 3.3 | 3.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sotomayor-del-Moral, J.A.; Pascual-Francisco, J.B.; Susarrey-Huerta, O.; Resendiz-Calderon, C.D.; Gallardo-Hernández, E.A.; Farfan-Cabrera, L.I. Characterization of Viscoelastic Poisson’s Ratio of Engineering Elastomers via DIC-Based Creep Testing. Polymers 2022, 14, 1837. https://doi.org/10.3390/polym14091837
Sotomayor-del-Moral JA, Pascual-Francisco JB, Susarrey-Huerta O, Resendiz-Calderon CD, Gallardo-Hernández EA, Farfan-Cabrera LI. Characterization of Viscoelastic Poisson’s Ratio of Engineering Elastomers via DIC-Based Creep Testing. Polymers. 2022; 14(9):1837. https://doi.org/10.3390/polym14091837
Chicago/Turabian StyleSotomayor-del-Moral, Jonathan A., Juan B. Pascual-Francisco, Orlando Susarrey-Huerta, Cesar D. Resendiz-Calderon, Ezequiel A. Gallardo-Hernández, and Leonardo I. Farfan-Cabrera. 2022. "Characterization of Viscoelastic Poisson’s Ratio of Engineering Elastomers via DIC-Based Creep Testing" Polymers 14, no. 9: 1837. https://doi.org/10.3390/polym14091837
APA StyleSotomayor-del-Moral, J. A., Pascual-Francisco, J. B., Susarrey-Huerta, O., Resendiz-Calderon, C. D., Gallardo-Hernández, E. A., & Farfan-Cabrera, L. I. (2022). Characterization of Viscoelastic Poisson’s Ratio of Engineering Elastomers via DIC-Based Creep Testing. Polymers, 14(9), 1837. https://doi.org/10.3390/polym14091837






