Novel Diffusion Mechanism of Polymers Pinned to an Attractive Impurity
Abstract
1. Introduction
2. Model and Theory
3. Monte Carlo Simulations
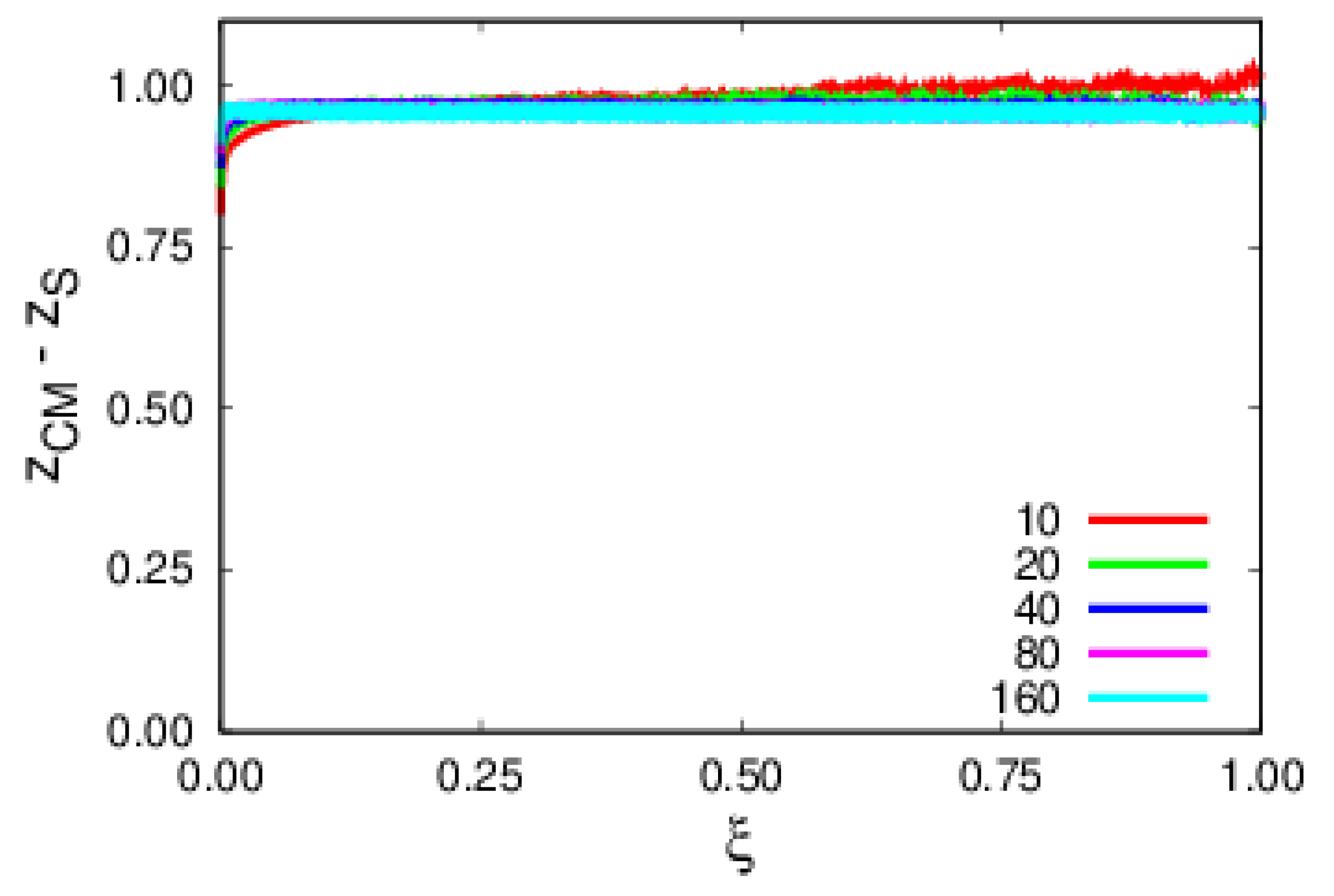
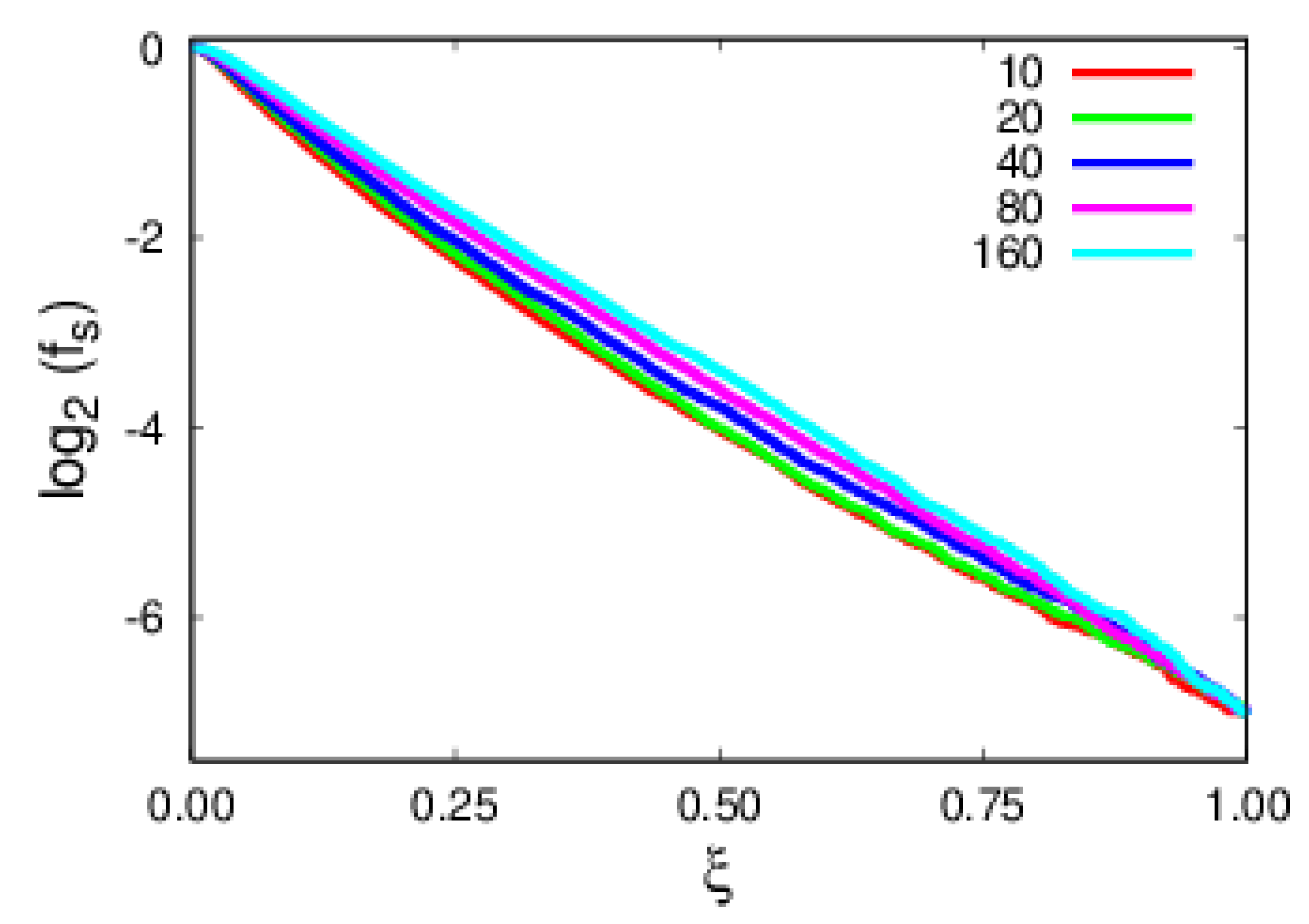
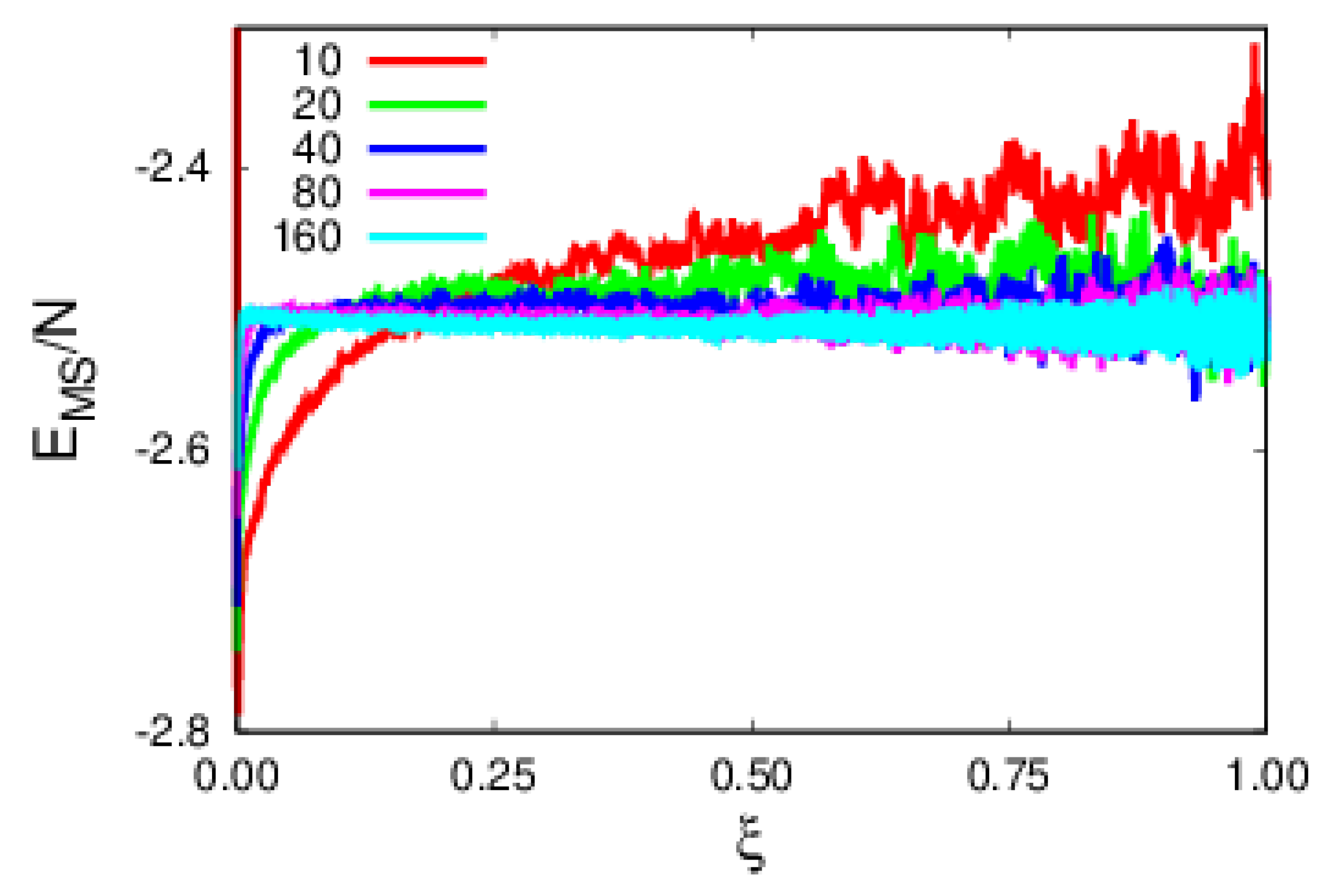
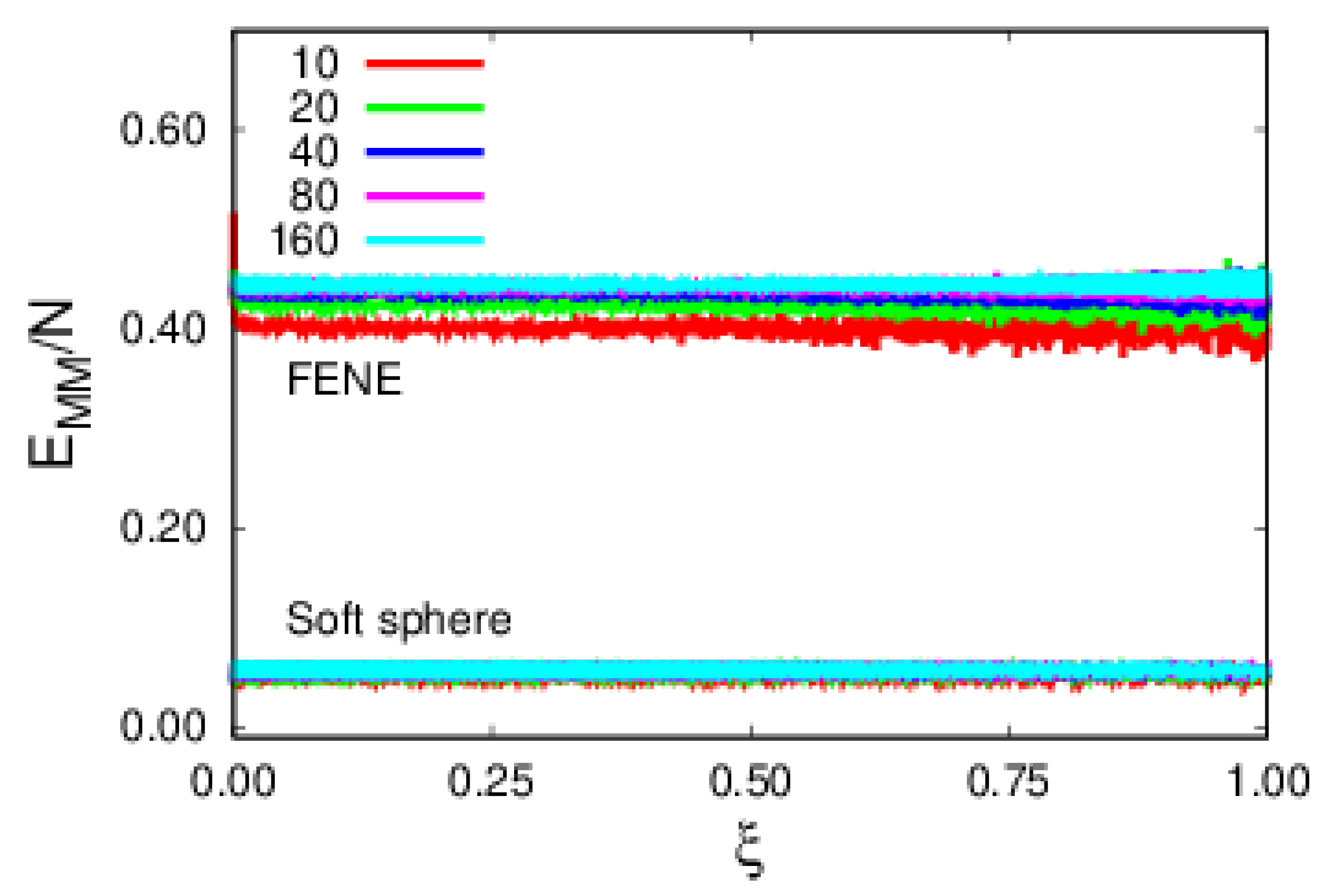
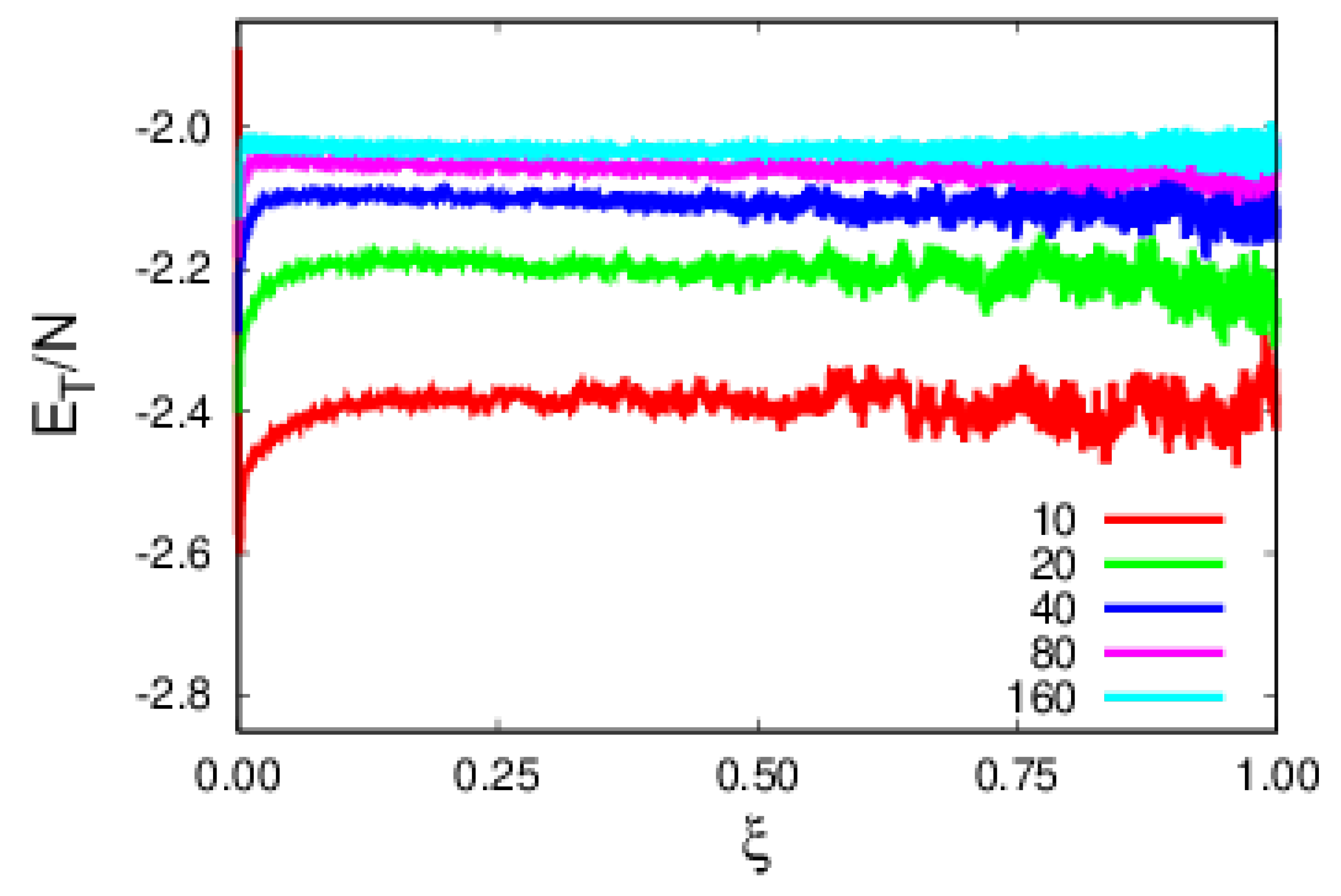
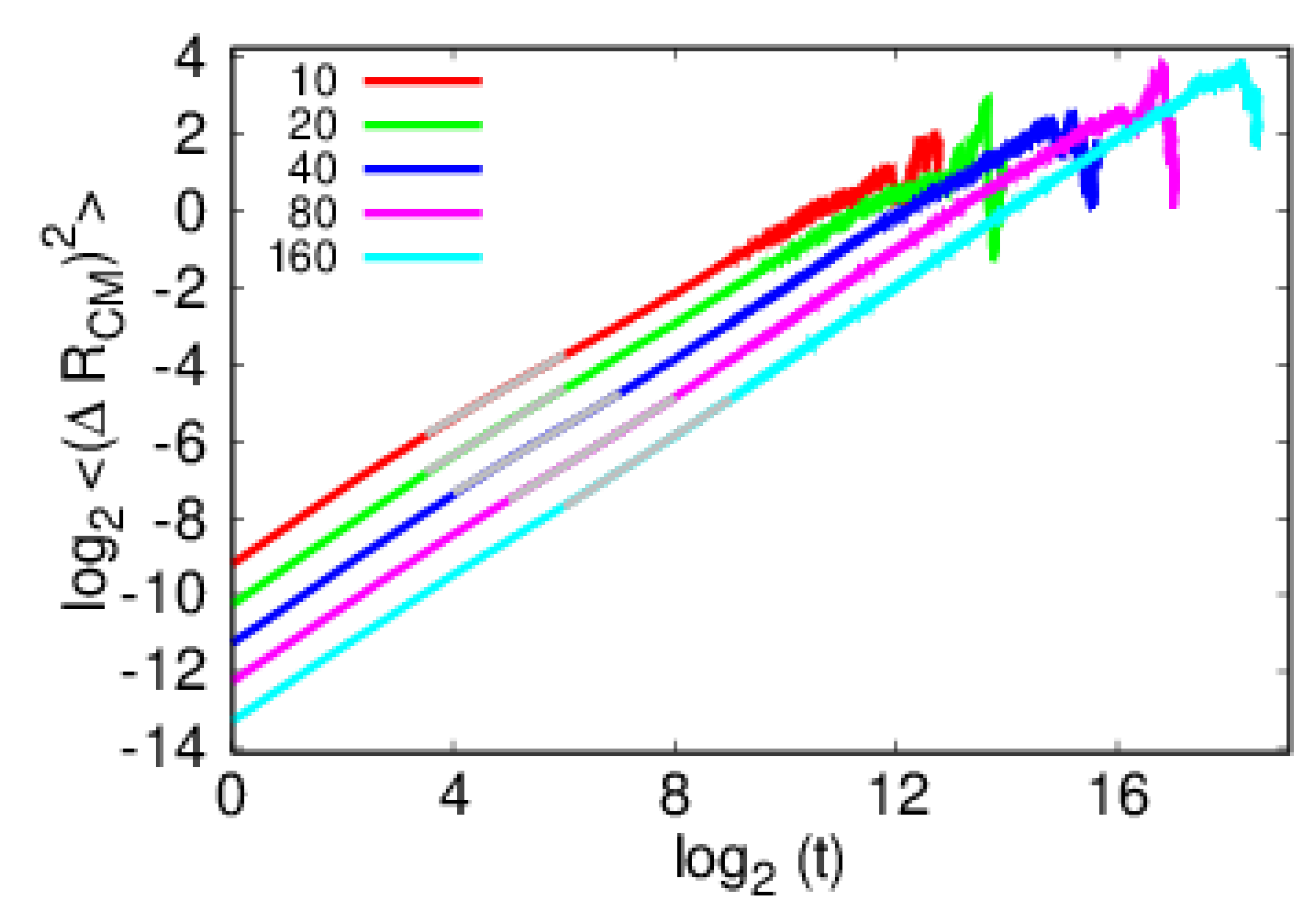
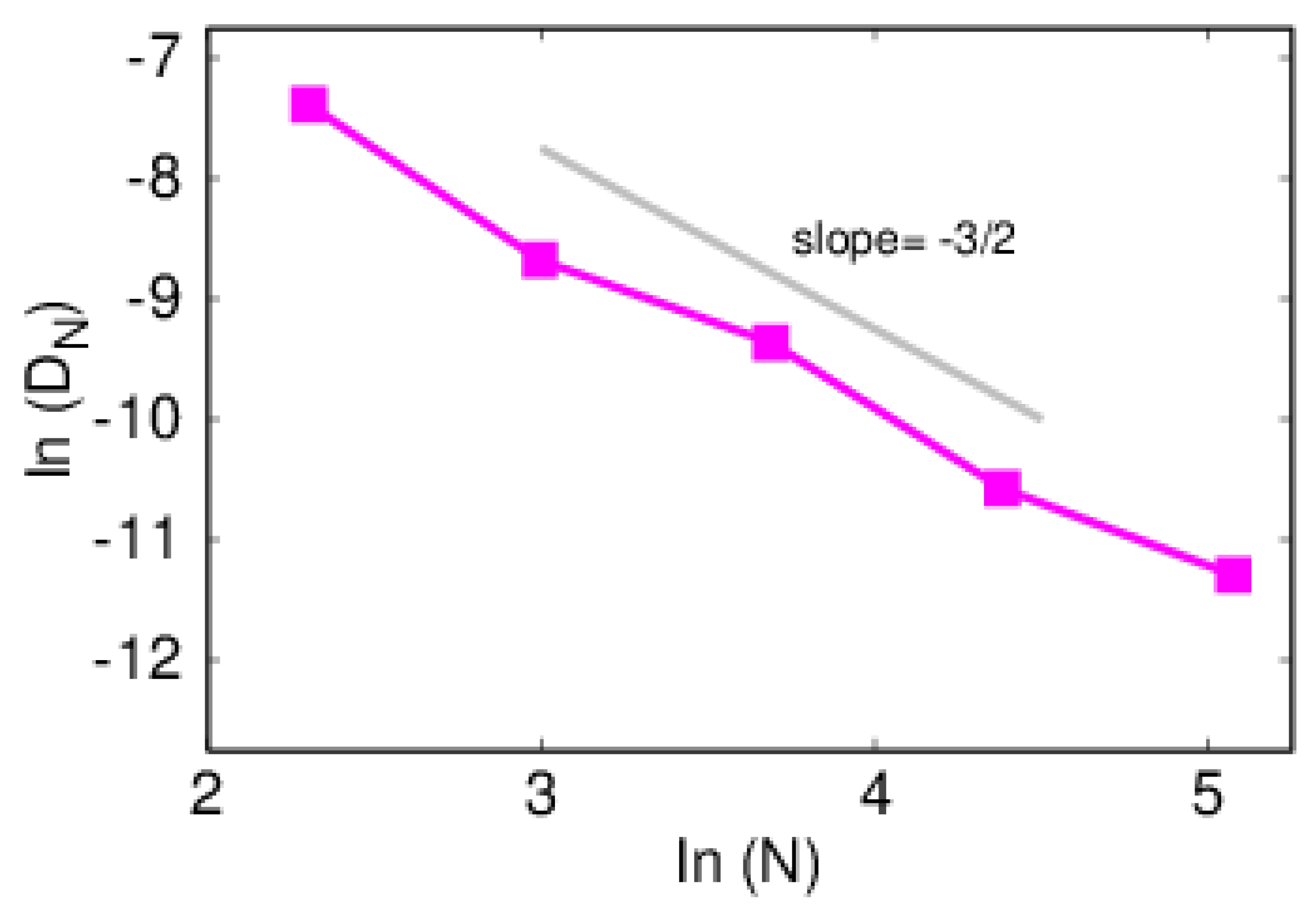
4. Results and Discussion
5. Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University: Ithaca, NY, USA, 1979. [Google Scholar]
- De Gennes, P.G. Dynamics of Entangled Polymer Solutions. I. The Rouse Model. Macromolecules 1976, 9, 587–593. [Google Scholar] [CrossRef]
- Azuma, R.; Takayama, H. Diffusion of Single Long Polymers in Fixed and Low Density Matrix of Obstacles Confined to Two Dimensions. J. Chem. Phys. 1999, 111, 8666. [Google Scholar] [CrossRef][Green Version]
- Binder, K.; Milchev, A.; Baschnagel, J. Simulation Studies on the Dynamics of Polymers at Interfaces. Annu. Rev. Mater. Sci. 1996, 26, 107–134. [Google Scholar] [CrossRef]
- Binder, K.; Paul, W. Recent Developments in Monte Carlo Simulations of Lattice Models for Polymer Systems. Macromolecules 2008, 41, 4537–4550. [Google Scholar] [CrossRef]
- Desai, T.G.; Keblinski, P.; Kumar, S.K.; Granick, S. Modeling Diffusion of Adsorbed Polymer with Explicit Solvent. Phys. Rev. Lett. 2007, 98, 218301. [Google Scholar] [CrossRef] [PubMed]
- Desai, T.; Keblinski, P.; Kumar, S.K. Molecular Dynamics Simulations of Polymer Transport in Nanocomposites. J. Chem. Phys. 2005, 122, 134910. [Google Scholar] [CrossRef]
- Eisenriegler, E.; Kremer, K.; Binder, K. Adsorption of Polymer Chains at Surfaces: Scaling and Monte Carlo Analyses. J. Chem. Phys. 1982, 77, 6296–6320. [Google Scholar] [CrossRef]
- Falck, E.; Punkkinen, O.; Vattulainen, I.; Ala-Nissila, T. Dynamics and Scaling of Two-Dimensional Polymers in a Dilute Solution. Phys. Rev. E 2003, 68, 50102. [Google Scholar] [CrossRef] [PubMed]
- Lai, P.-Y. Statics and Dynamics of a Polymer Chain Adsorbed on a Surface: Monte Carlo Simulation Using the Bond-Fluctuation Model. Phys. Rev. E 1994, 49, 5420–5430. [Google Scholar] [CrossRef]
- Liao, Q.; Carrillo, J.-M.Y.; Dobrynin, A.V.; Rubinstein, M. Rouse Dynamics of Polyelectrolyte Solutions: Molecular Dynamics Study. Macromolecules 2007, 40, 7671–7679. [Google Scholar] [CrossRef]
- Maier, B.; Rädler, J.O. Conformation and Self-Diffusion of Single DNA Molecules Confined to Two Dimensions. Phys. Rev. Lett. 1999, 82, 1911–1914. [Google Scholar] [CrossRef]
- Milchev, A.; Binder, K. Dewetting of Thin Polymer Films Adsorbed on Solid Substrates: A Monte Carlo Simulation of the Early Stages. J. Chem. Phys. 1997, 106, 1978–1989. [Google Scholar] [CrossRef]
- Mukherji, D.; Bartels, G.; Müser, M.H. Scaling Laws of Single Polymer Dynamics Near Attractive Surfaces. Phys. Rev. Lett. 2008, 100, 068301. [Google Scholar] [CrossRef] [PubMed]
- Paul, W.; Binder, K.; Heermann, D.W.; Kremer, K. Dynamics of Polymer Solutions and Melts. Reptation Predictions and Scaling of Relaxation Times. J. Chem. Phys. 1991, 95, 7726–7740. [Google Scholar] [CrossRef]
- Sukhishvili, S.A.; Chen, Y.; Müller, J.D.; Gratton, E.; Schweizer, K.S.; Granick, S. Diffusion of a Polymer ‘Pancake’. Nature 2000, 406, 146. [Google Scholar] [CrossRef]
- Qian, H.-J.; Chen, L.-J.; Lu, Z.-Y.; Li, Z.-S. Surface Diffusion Dynamics of a Single Polymer Chain in Dilute Solution. Phys. Rev. Lett. 2007, 99, 068301. [Google Scholar] [CrossRef] [PubMed]
- Savovic, S.; Djordjevich, A. Investigation of Mode Coupling in Graded Index Plastic Optical Fibers Using the Langevin Equation. J. Light. Technol. 2020, 38, 6644–6647. [Google Scholar] [CrossRef]
- Oliveira, M.G.; Francisco, M.F.F.; de Lima, S.R.; Guarany, C.A.; Gonçalves, A.A.; Andrade, A.A.; Messias, D.N.M.; Pilla, V. Optical Characterization of X-Ray Irradiated CdSe/ZnS Quantum Dots Embedded in Polymeric Resins for Dosimetry Applications. Opt. Mater. 2021, 122, 111687. [Google Scholar] [CrossRef]
- Li, J.; Zhang, R.; Ding, M.; Shi, T. Unusual Self-Diffusion Behaviors of Polymer Adsorbed on Rough Surfaces. J. Chem. Phys. 2019, 150, 064902. [Google Scholar] [CrossRef]
- Raut, J.S.; Fichthorn, K.A. Diffusion Mechanisms of Short-Chain Alkanes on Metal Substrates: Unique Molecular Features. J. Chem. Phys. 1998, 108, 1626–1635. [Google Scholar] [CrossRef]
- Sassi, A.S.; Assenza, S.; De Los Rios, P. Shape of a Stretched Polymer. Phys. Rev. Lett. 2017, 119, 037801. [Google Scholar] [CrossRef]
- Wang, D.; He, C.; Stoykovich, M.P.; Schwartz, D.K. Nanoscale Topography Influences Polymer Surface Diffusion. ACS Nano 2015, 9, 1656–1664. [Google Scholar] [CrossRef]
- Zhang, B.; Cao, X.; Zhou, G.; Zhao, N. Anomalous Diffusion of Polystyrene from an Attractive Substrate Based on All-Atom Simulation. Phys. Chem. Chem. Phys. 2018, 20, 25304–25313. [Google Scholar] [CrossRef] [PubMed]
- Rouse, P.E. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amesterdam, The Netherlands, 1992. [Google Scholar]
- Choi, J.; Clarke, N.; Winey, K.I.; Composto, R.J. Polymer Diffusion from Attractive and Athermal Substrates. Macromolecules 2017, 50, 3038–3042. [Google Scholar] [CrossRef]
- Evangelopoulos, A.E.A.S.; Rissanou, A.N.; Glynos, E.; Bitsanis, I.A.; Anastasiadis, S.H.; Koutos, V. Wetting Behavior of Polymer Droplets: Effects of Droplet Size and Chain Length. Macromolecules 2018, 51, 2805–2816. [Google Scholar] [CrossRef]
- Wei, H.-H.; Li, Y.-C. Conformational Transitions of Single Polymer Adsorption in Poor Solvent: Wetting Transition Due to Molecular Confinement Induced Line Tension. Phys. Rev. E 2016, 94, 012501. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys. 1943, 15, 1–89. [Google Scholar] [CrossRef]
- Kramers, H.A. Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions. Physica 1940, VII, 284–304. [Google Scholar] [CrossRef]
- Vineyard, G.H. Frequency Factors and Isotope Effects in Solid State Rate Processes. J. Phys. Chem. Solids 1957, 3, 121–127. [Google Scholar] [CrossRef]
- Hänggi, P.; Talkner, P.; Borkovec, M. Reaction-Rate Theory: Fifty Years After Kramers. Rev. Mod. Phys. 1990, 62, 251–341. [Google Scholar] [CrossRef]
- Talkner, P.; Łuczka, J. Rate Description of Fokker-Planck Processes with Time-Dependent Parameters. Phys. Rev. E 2004, 69, 046109. [Google Scholar] [CrossRef]
- Voter, A.F.; Doll, J.D. Transition State Theory Description of Surface Self-Diffusion: Comparison with Classical Trajectory Results. J. Chem. Phys. 1984, 80, 5832–5838. [Google Scholar] [CrossRef]
- Voter, A.F. Parallel Replica Method for Dynamics of Infrequent Events. Phys. Rev. B 1998, 57, R13985–R13988. [Google Scholar] [CrossRef]
- Perez, D.; Uberuaga, B.P.; Voter, A.F. The Parallel Replica Dynamics Method—Coming of Age. Comp. Mater. Sci. 2015, 100, 90–103. [Google Scholar] [CrossRef]
- Risken, H. The Fokker-Planck Equation; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Cadilhe, A.; Coura, P.; Costa, B. Effects of Monomer Size on Polymer Mass Transport at a Crystalline Interface. J. Stat. Mech. 2017, 2017, 123301. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Kröger, M. Simple Models for Complex Nonequilibrium Fluids. Phys. Rep. 2004, 390, 453–551. [Google Scholar] [CrossRef]
- Milchev, A.; Binder, K. Static and Dynamic Properties of Adsorbed Chains at Surfaces: Monte Carlo Simulation of a Bead-Spring Model. Macromolecules 1996, 29, 343–354. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerra, J.C.O.; Cadilhe, A. Novel Diffusion Mechanism of Polymers Pinned to an Attractive Impurity. Polymers 2022, 14, 1459. https://doi.org/10.3390/polym14071459
Guerra JCO, Cadilhe A. Novel Diffusion Mechanism of Polymers Pinned to an Attractive Impurity. Polymers. 2022; 14(7):1459. https://doi.org/10.3390/polym14071459
Chicago/Turabian StyleGuerra, João C. O., and Antonio Cadilhe. 2022. "Novel Diffusion Mechanism of Polymers Pinned to an Attractive Impurity" Polymers 14, no. 7: 1459. https://doi.org/10.3390/polym14071459
APA StyleGuerra, J. C. O., & Cadilhe, A. (2022). Novel Diffusion Mechanism of Polymers Pinned to an Attractive Impurity. Polymers, 14(7), 1459. https://doi.org/10.3390/polym14071459





