Interdependencies between Dynamic Response and Crack Growth in a 3D-Printed Acrylonitrile Butadiene Styrene (ABS) Cantilever Beam under Thermo-Mechanical Loads
Abstract
1. Introduction
2. Analytical Modelling
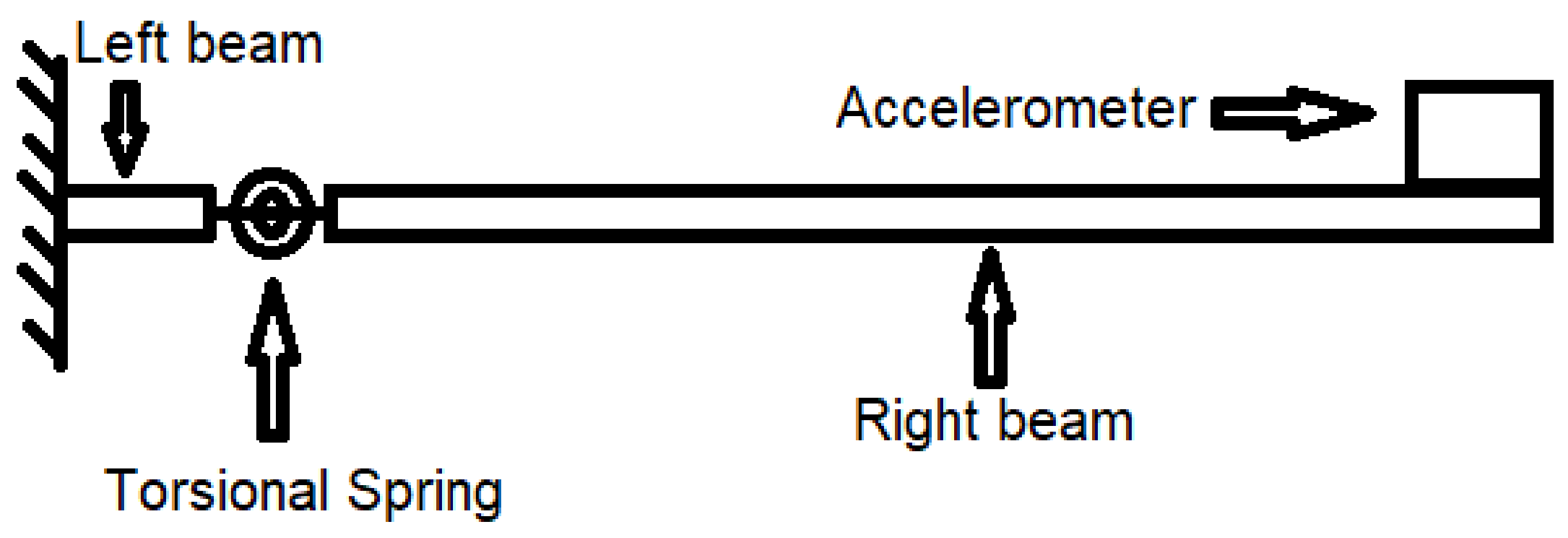
2.1. Problem Description
2.2. Cantilever Beam Geometry
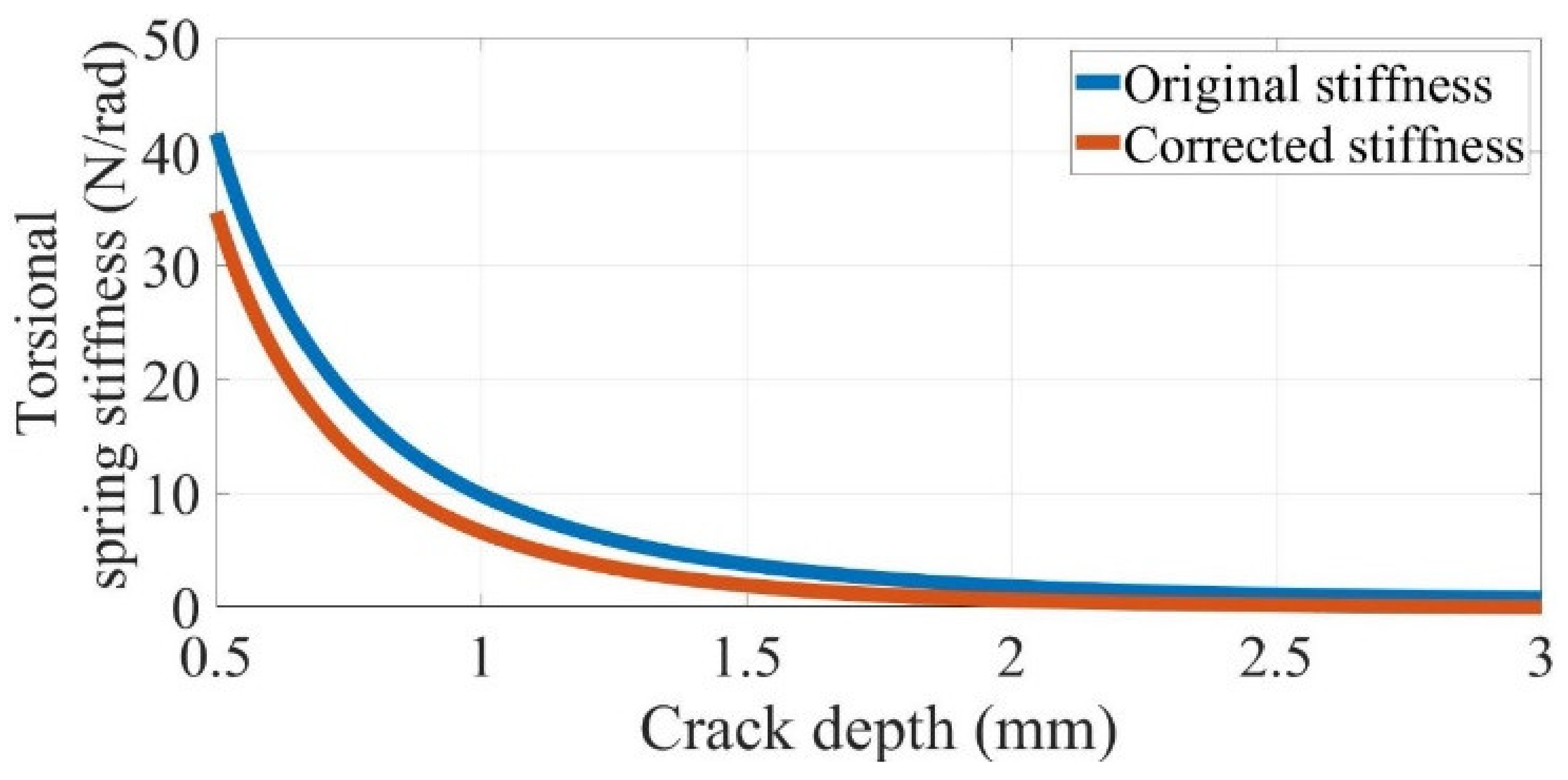
2.3. Crack Size Modelling
2.4. Natural Frequency of the System
2.5. Displacement Response of the System under Forced Vibration
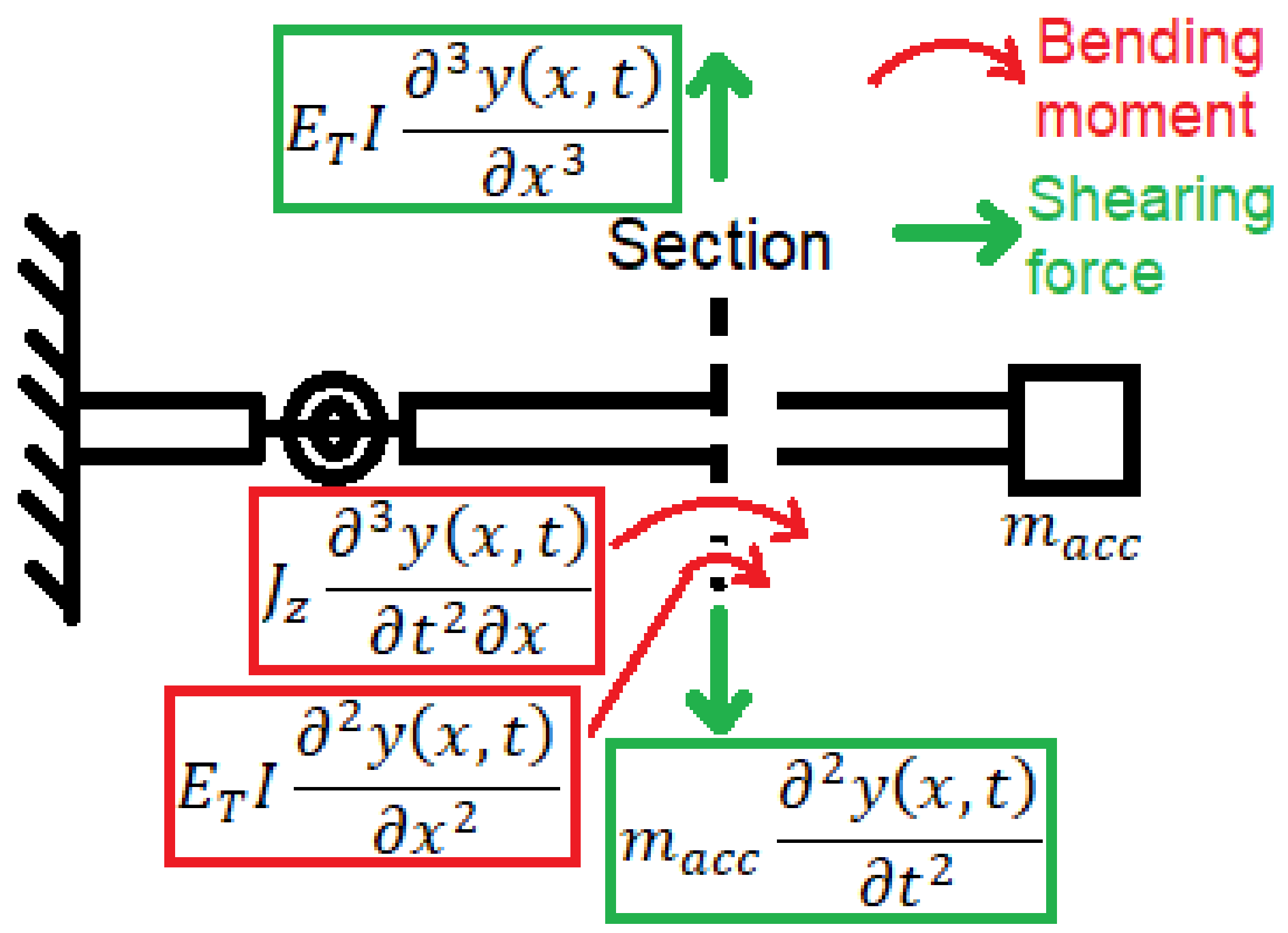
2.5.1. Equation of Motion
2.5.2. Orthogonality of the Mode Shapes for the System
2.5.3. Displacement Response and Amplitude under the First Mode Natural Frequency
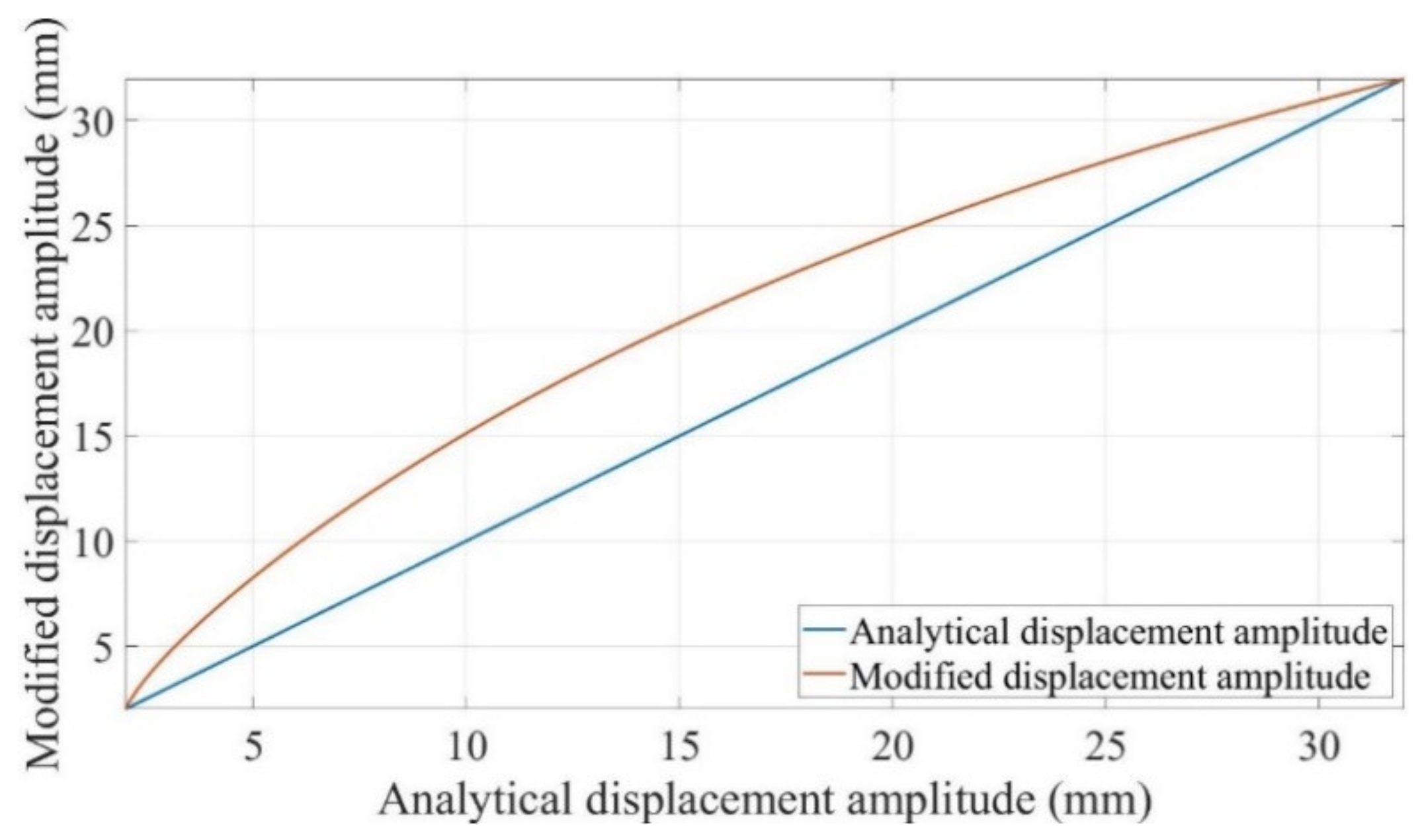
2.5.4. Mathematical Approximation of the Displacement Amplitude
3. Experimental Methodology
3.1. Specimen Preparation
3.2. Experiment Scheme
3.3. Experimental Setup and Procedure
3.3.1. Dynamic Response Measurement
3.3.2. DMA Test Procedure
4. Results and Discussion
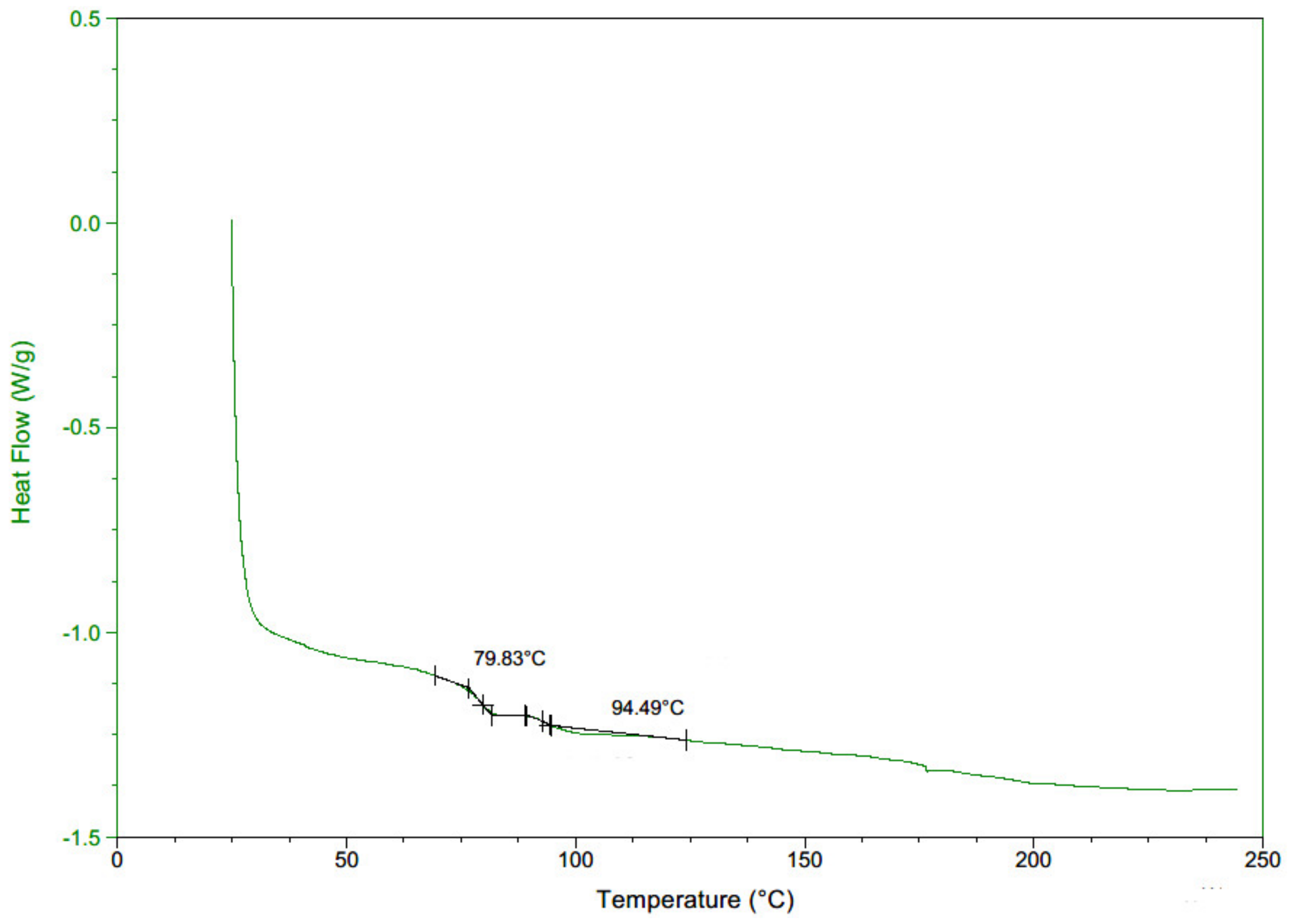
4.1. Results and Analysis for the DMA Test
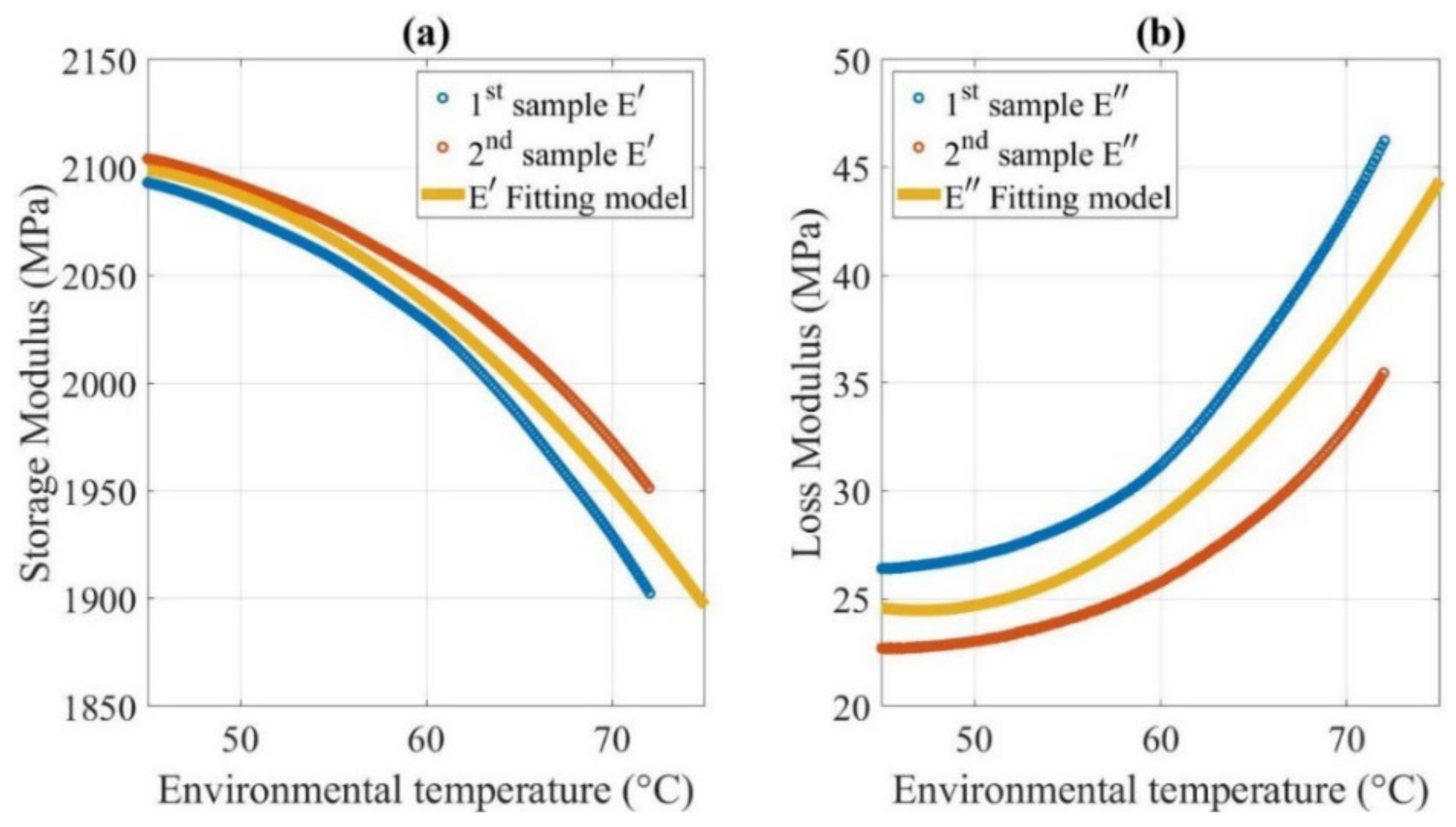
4.1.1. Tensile Modulus of FDM ABS
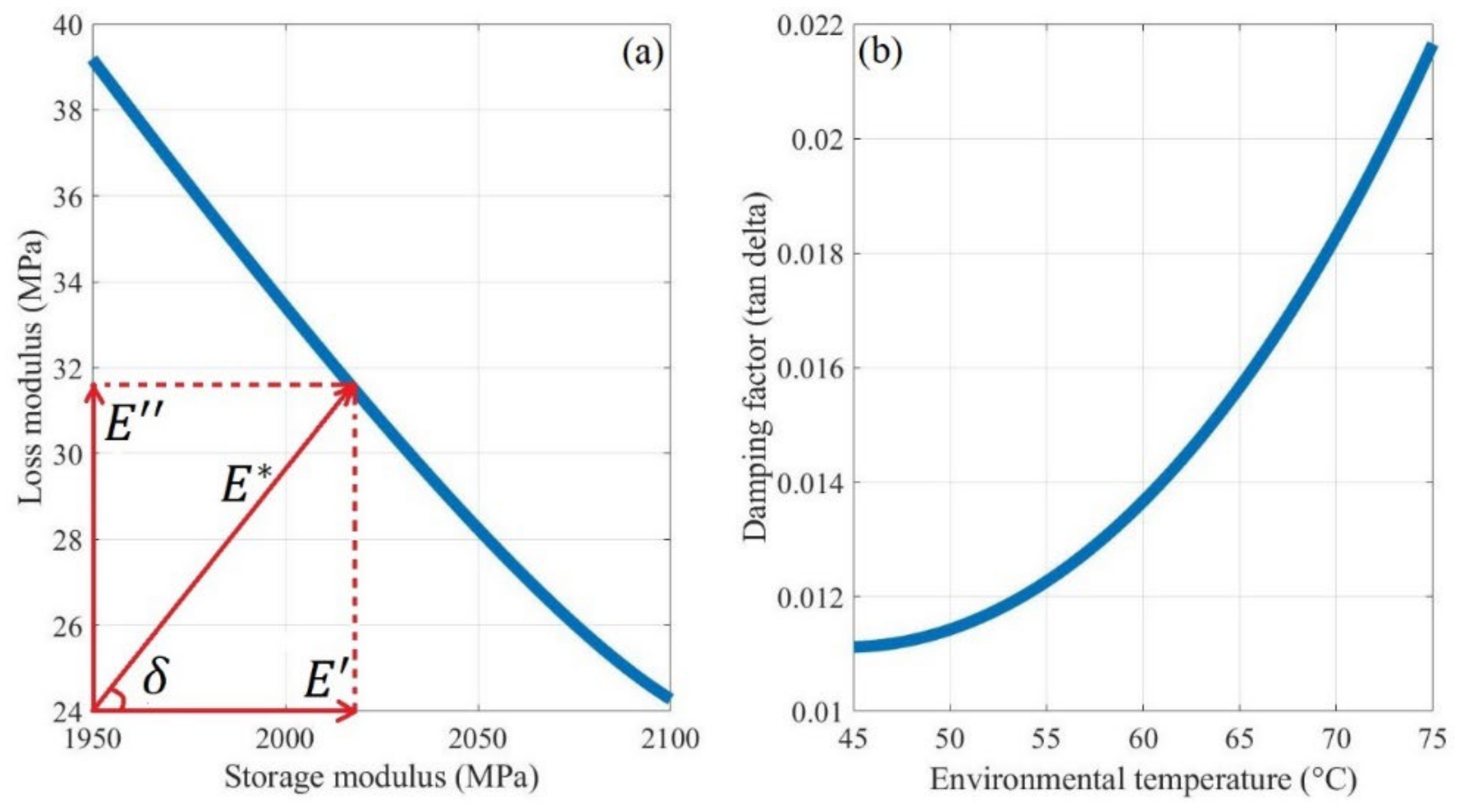
4.1.2. Damping of the FDM ABS Cantilever Beam
4.2. Dynamic Response of the Cantilever Beam–End Mass System
4.2.1. Comparison of Analytical Models with Differently Modelled Torsional Spring Stiffness Values
4.2.1.1. Comparison and Analysis of Differences in the Fundamental Frequency
4.2.1.2. Comparison and Analysis of the Differences in the Displacement Amplitude
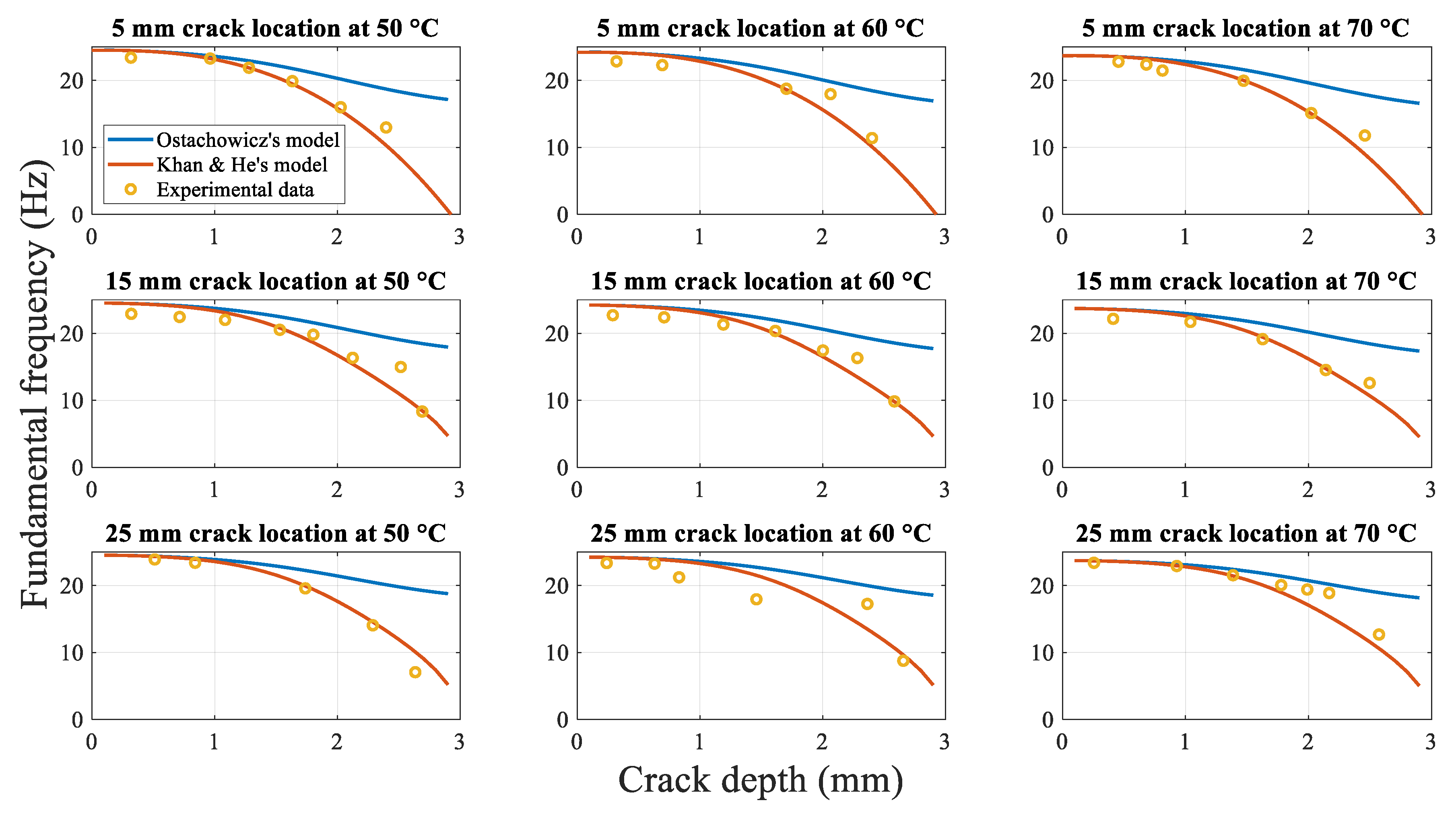
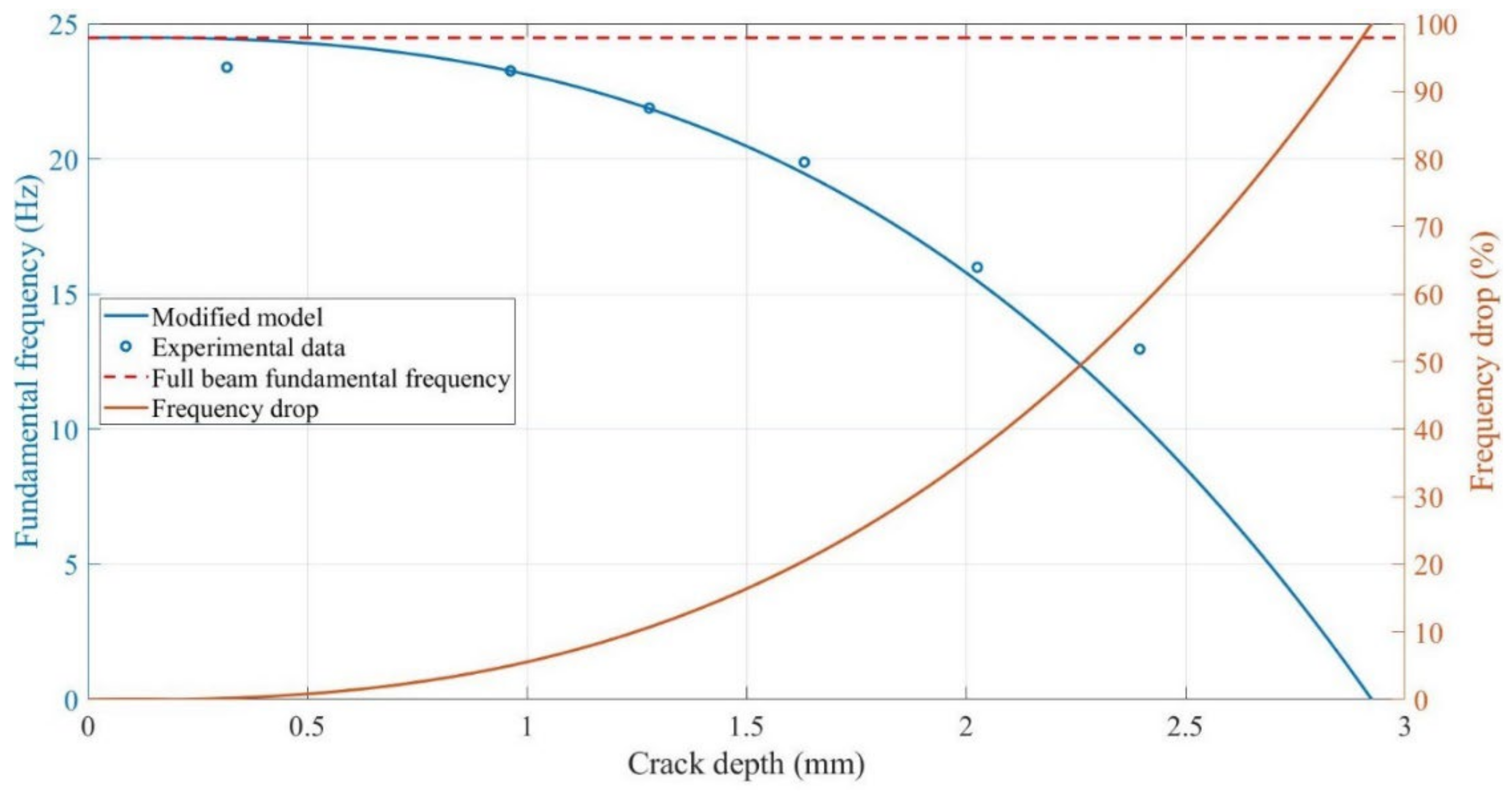
4.2.2. Fundamental Frequency for the Cracked Beam
4.2.2.1. Influence of the Crack Depth on Natural Frequencies
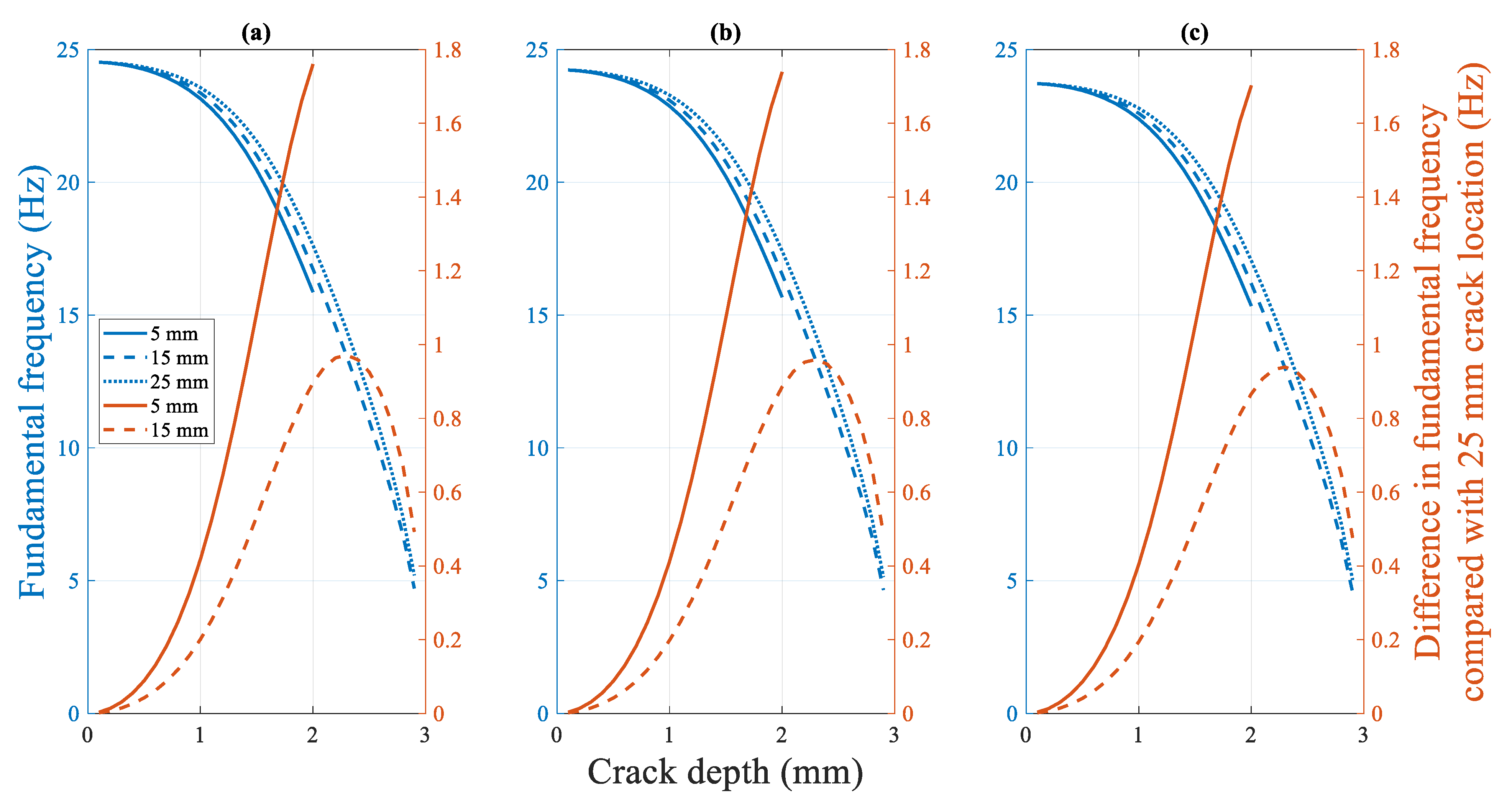
4.2.2.2. Influence of the Crack Location on the Fundamental Frequency
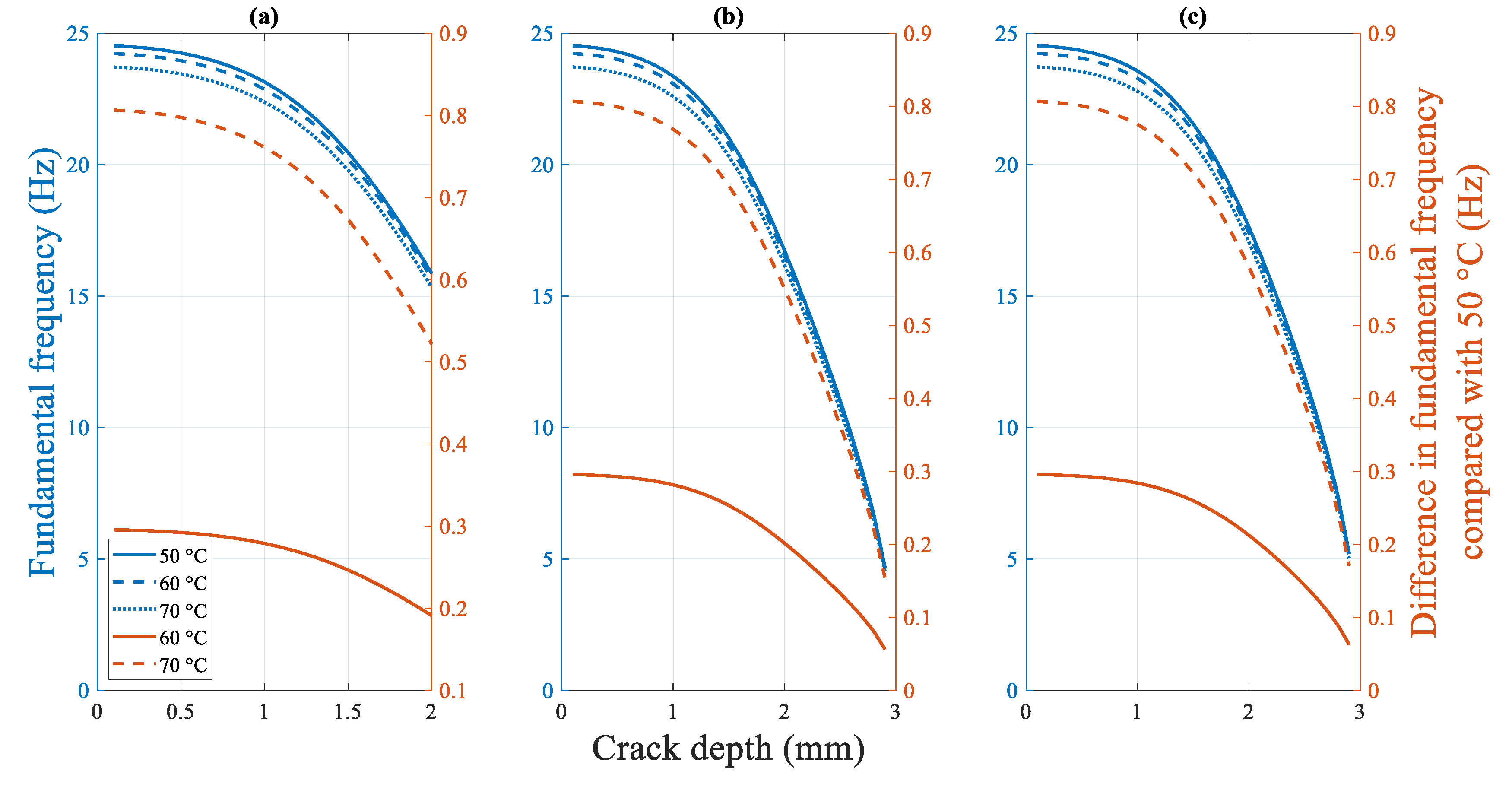
4.2.2.3. Influence of the Temperature on the Fundamental Frequency
4.2.3. Displacement Amplitude for the Cracked Beam under Resonance
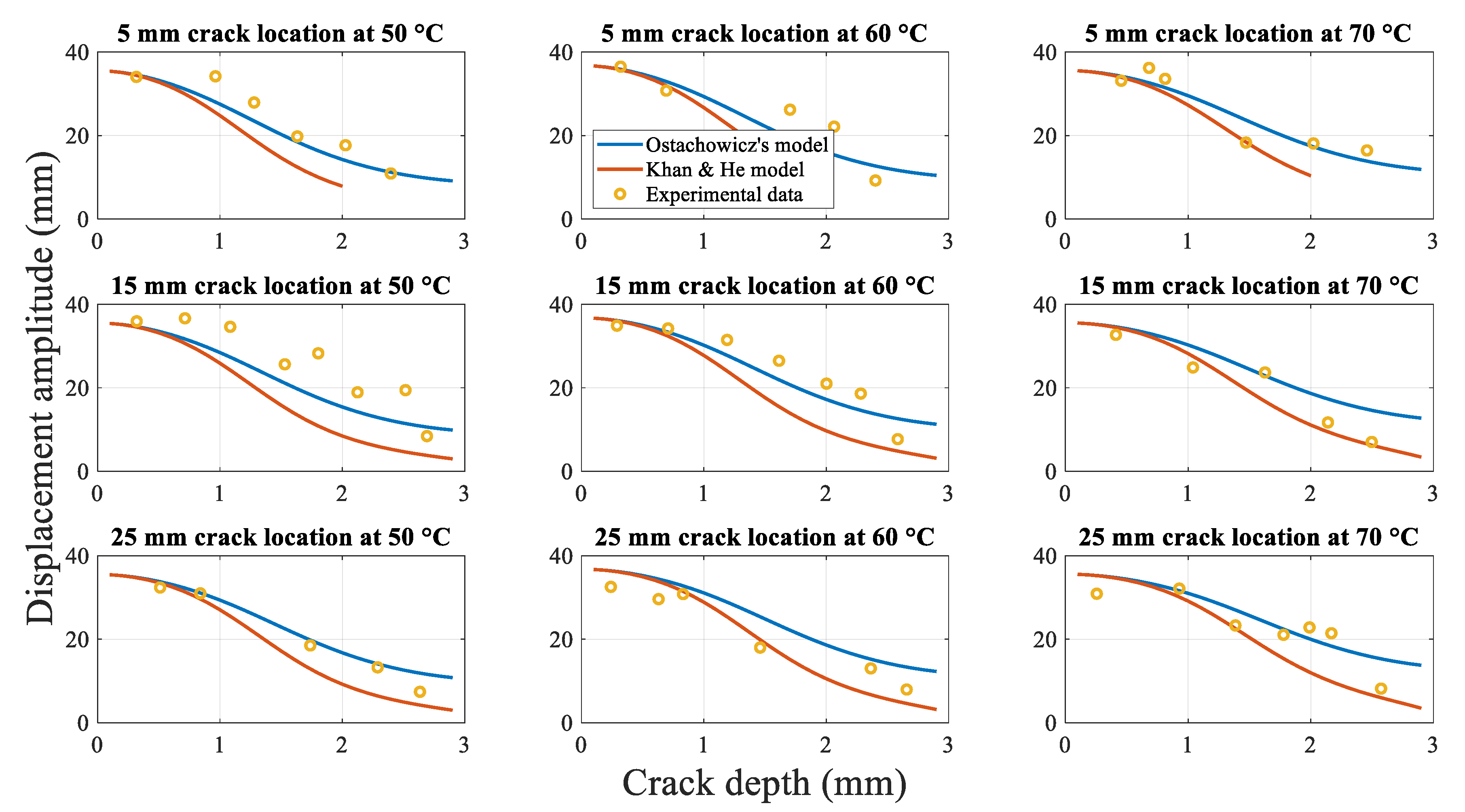
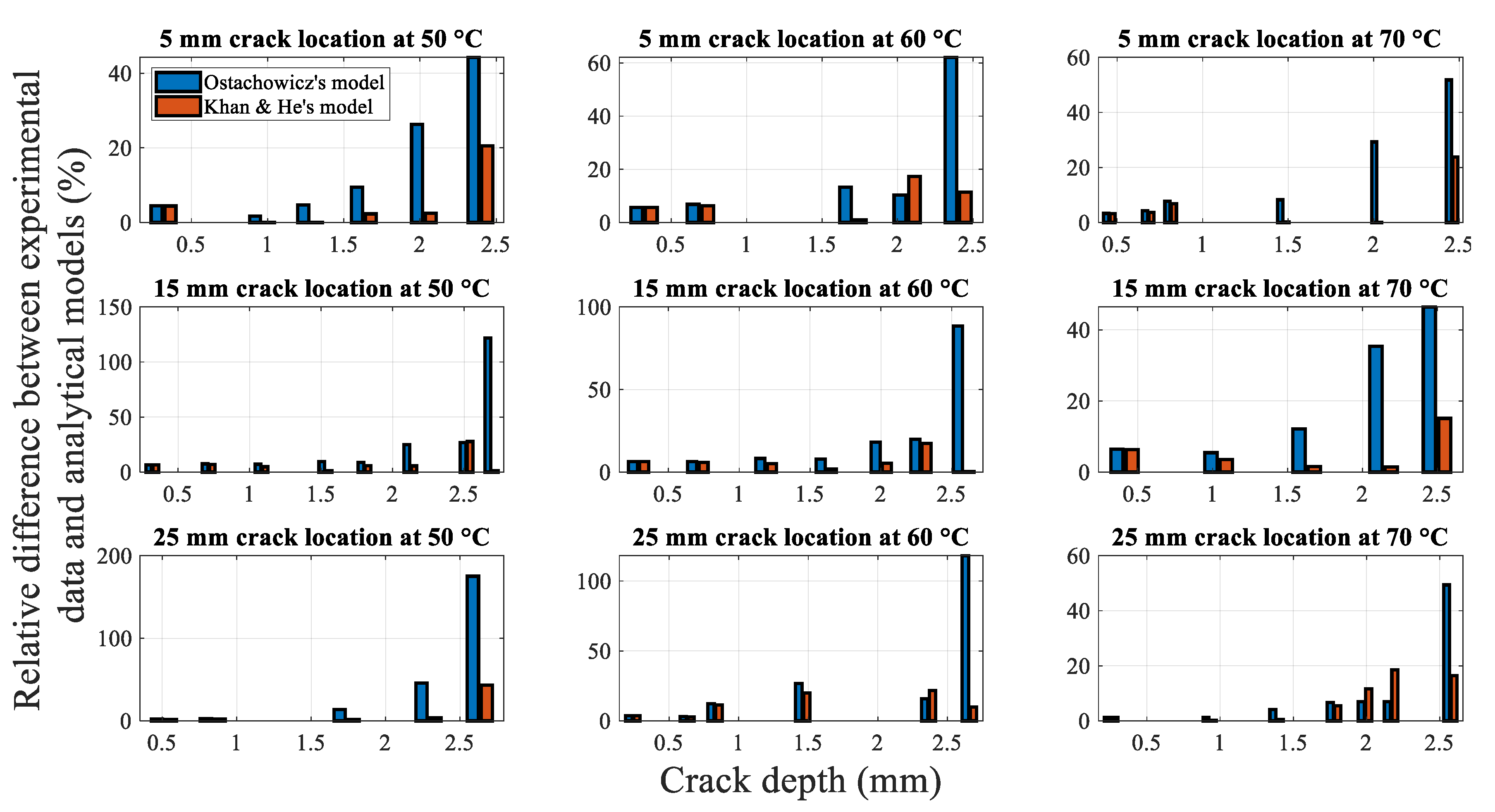
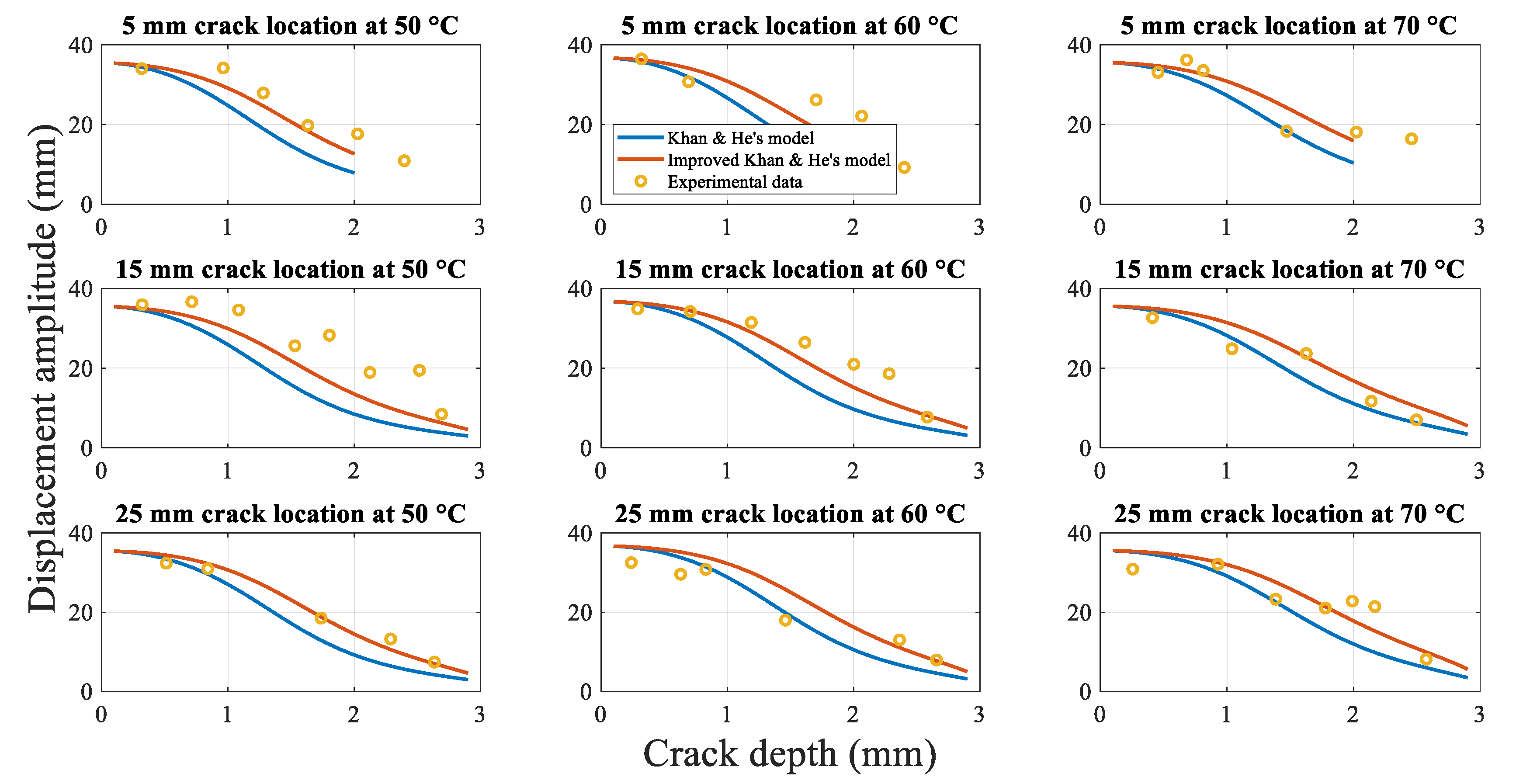
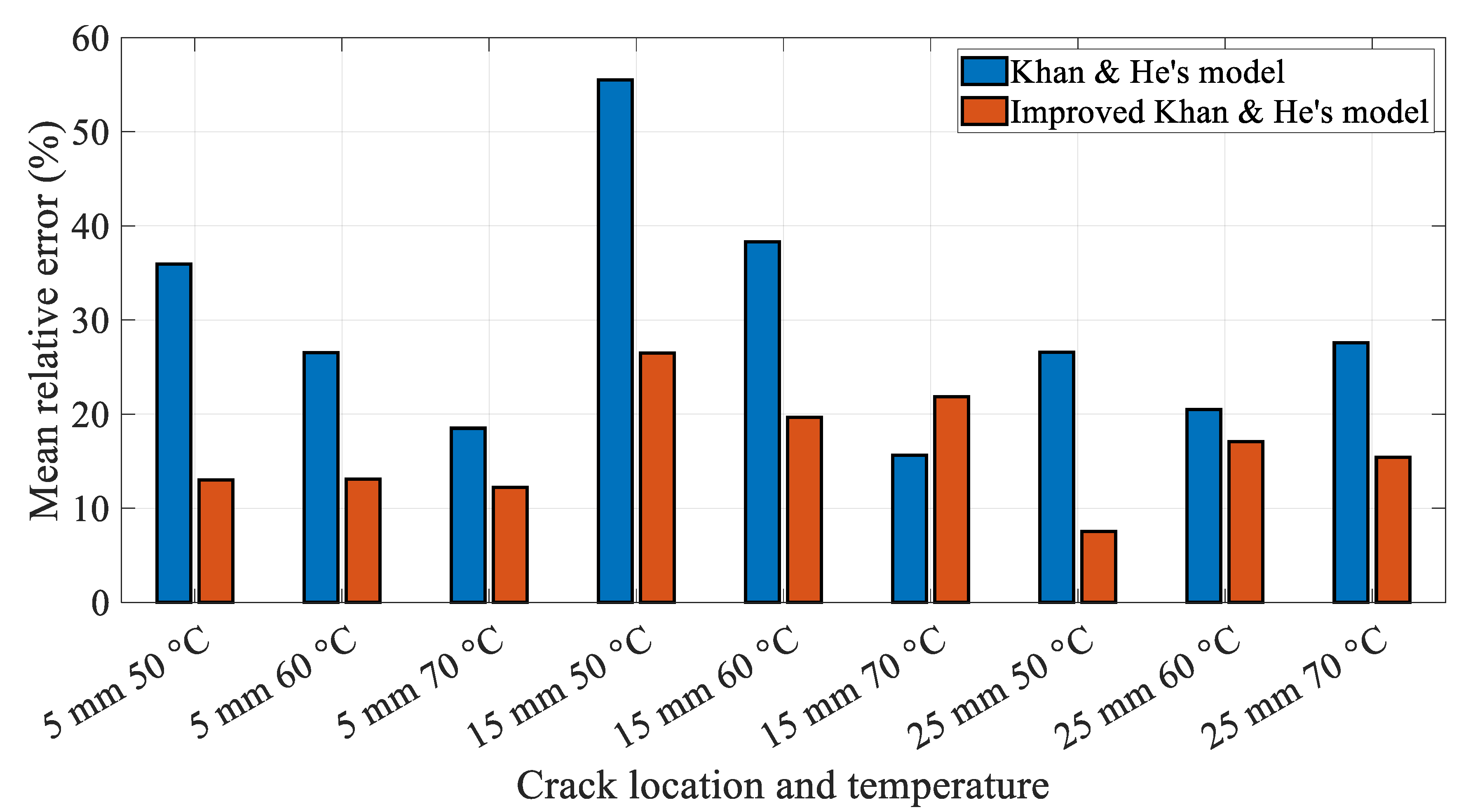
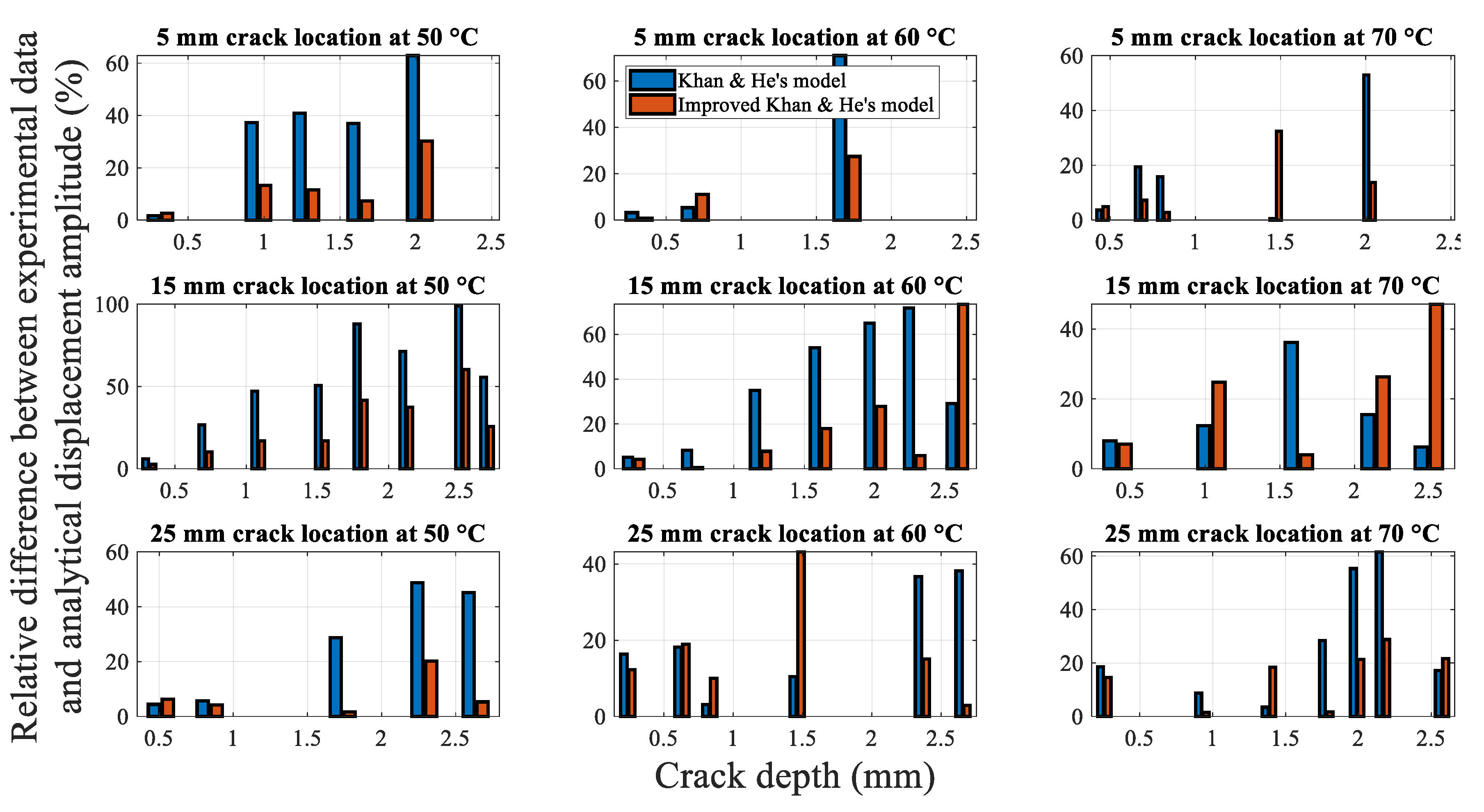
4.2.3.1. Influence of the Crack Depth on the Displacement Amplitude
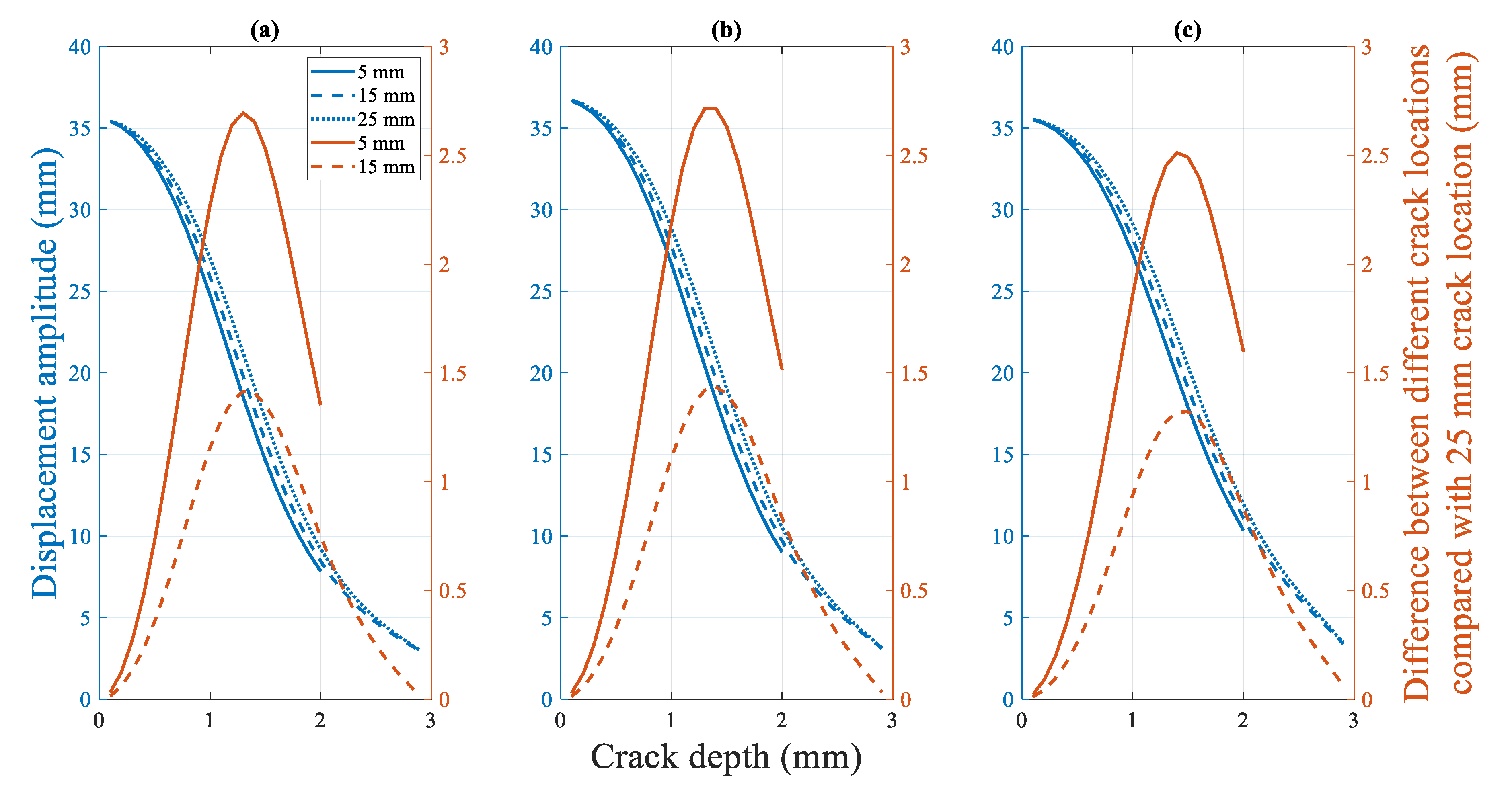
4.2.3.2. Influence of the Crack Location on the Displacement Amplitude
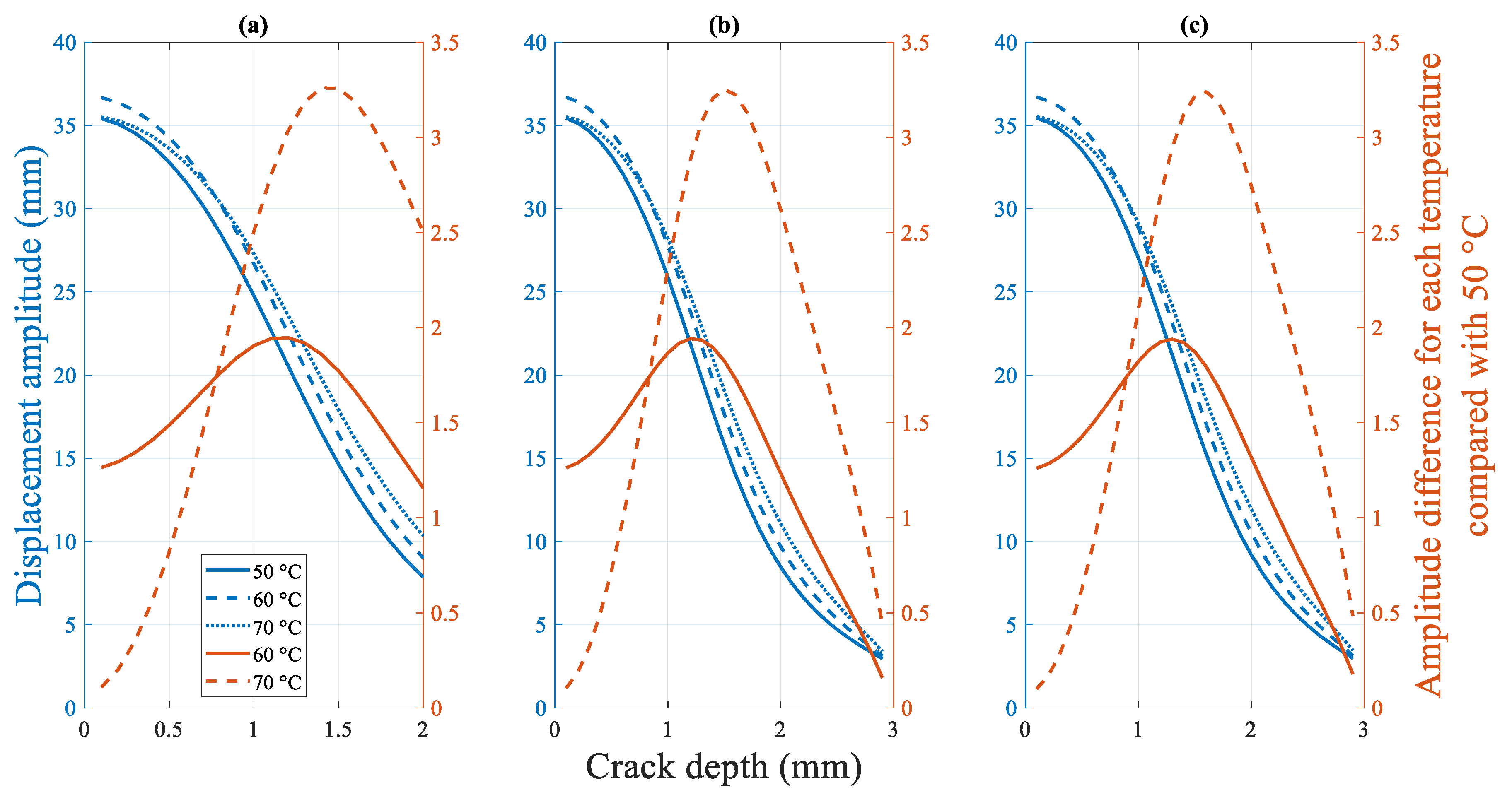
4.2.3.3. Influence of the Temperature on the Displacement Amplitude
4.2.4. Sensitivity of the Dynamic Response
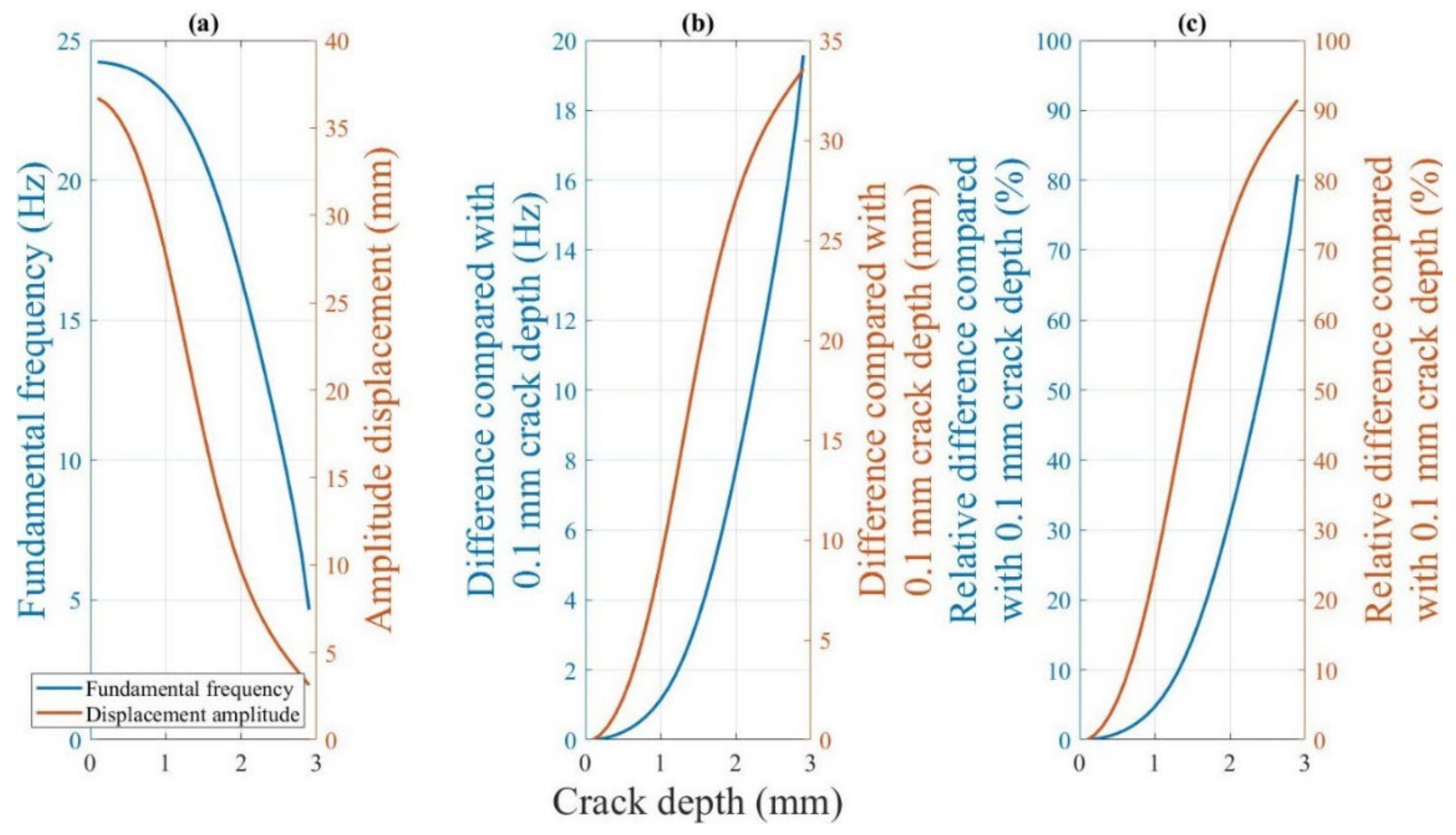
4.2.4.1. Sensitivity of the Dynamic Response to the Crack Depth
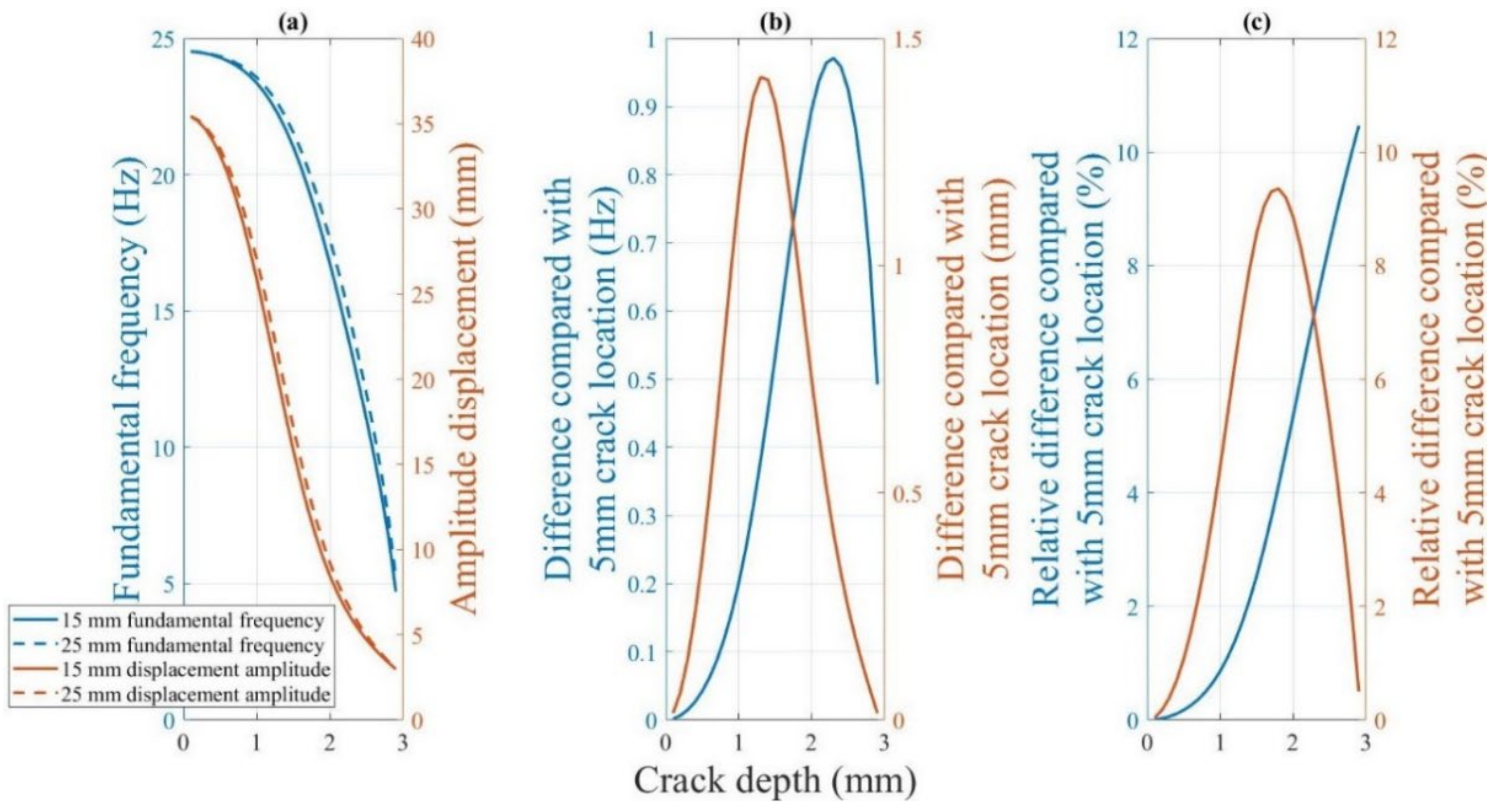
4.2.4.2. Sensitivity of the Dynamic Response to the Crack Location
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Crack depth | |
| Loss factor | |
| Beam section | |
| Coefficients | |
| Beam width | |
| Coefficient | |
| Coefficients | |
| Damping | |
| Coefficients | |
| Coefficients | |
| Elastic modulus | |
| Elastic modulus at | |
| Complex elastic modulus | |
| Storage modulus | |
| Loss modulus | |
| Frequency | |
| Shape function | |
| Beam thickness | |
| Area moment of inertia | |
| Momentum of inertia | |
| Torsional spring stiffness | |
| Distance between the crack location and fixed end of the beam | |
| Beam length | |
| End mass | |
| Accelerometer mass | |
| Angular frequency | |
| Angular frequency of a shaker | |
| Modal coordinate of the n-th mode | |
| Density | |
| Time | |
| Modal coordinate | |
| Shaker displacement | |
| Shaker displacement amplitude | |
| Beam displacement amplitude | |
| Modified beam displacement amplitude | |
| Beam total displacement | |
| Distance to the fixed end of the beam | |
| Beam displacement due to bending | |
| Fixed end side beam displacement | |
| Free end side beam displacement | |
| Mode shape of the beam | |
| n-th mode shape of the beam |
References
- Baqasah, H.; He, F.; Zai, B.A.; Asif, M.; Khan, K.A.; Thakur, V.K.; Khan, M.A. In-situ dynamic response measurement for damage quantification of 3D printed ABS cantilever beam under thermomechanical load. Polymers 2019, 11, 2079. [Google Scholar] [CrossRef]
- Arias, A.C.; MacKenzie, J.D.; McCulloch, I.; Rivnay, J.; Salleo, A. Materials and applications for large area electronics: Solution-based approaches. Chem. Rev. 2010, 110, 3–24. [Google Scholar] [CrossRef] [PubMed]
- Wong, J.Y.; Pfahnl, A.C. 3D printing of surgical instruments for long-duration space missions. Aviat. Sp. Environ. Med. 2014, 85, 758–763. [Google Scholar] [CrossRef] [PubMed]
- Espalin, D.; Muse, D.W.; MacDonald, E.; Wicker, R.B. 3D Printing multifunctionality: Structures with electronics. Int. J. Adv. Manuf. Technol. 2014, 72, 963–978. [Google Scholar] [CrossRef]
- Daneshmand, S.; Aghanajafi, C.; Shahverdi, H. Investigation of rapid manufacturing technology with ABS material for wind tunnel models fabrication. J. Polym. Eng. 2012, 32, 575–584. [Google Scholar] [CrossRef]
- Springer, A.; Coopert, K.; Roberts, F. Application of rapid prototyping models to transonic wind tunnel testing. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–10 January 1997; pp. 1–17. [Google Scholar]
- Zai, B.A.; Khan, M.A.; Khan, K.A.; Mansoor, A. A novel approach for damage quantification using the dynamic response of a metallic beam under thermo-mechanical loads. J. Sound Vib. 2020, 469, 115134. [Google Scholar] [CrossRef]
- Nandwana, B.P.; Maiti, S.K. Modelling of vibration of beam in presence of inclined edge or internal crack for its possible detection based on frequency measurements. Eng. Fract. Mech. 1997, 58, 193–205. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, X. Multi-cracks identification method for cantilever beam structure with variable cross-sections based on measured natural frequency changes. J. Sound Vib. 2017, 387, 53–65. [Google Scholar] [CrossRef]
- Boltezar, M.; Strancar, B.; Kuhelj, A. Identification of transverse crack location in flexural vibrations of free-free beams. J. Sound Vib. 1998, 211, 729–734. [Google Scholar] [CrossRef]
- Khiem, N.T.; Huyen, N.N. A method for crack identification in functionally graded Timoshenko beam. Nondestruct. Test. Eval. 2017, 32, 319–341. [Google Scholar] [CrossRef]
- Barad, K.H.; Sharma, D.S.; Vyas, V. Crack detection in cantilever beam by frequency based method. Procedia Eng. 2013, 51, 770–775. [Google Scholar] [CrossRef][Green Version]
- Douka, E.; Hadjileontiadis, L.J. Time-frequency analysis of the free vibration response of a beam with a breathing crack. NDT E Int. 2005, 38, 3–10. [Google Scholar] [CrossRef]
- Mazanoglu, K.; Sabuncu, M. A frequency based algorithm for identification of single and double cracked beams via a statistical approach used in experiment. Mech. Syst. Signal Process. 2012, 30, 168–185. [Google Scholar] [CrossRef]
- Revi, R.; Indu, V.S. Crack Detection of Propped Cantilever Beam Using Dynamic Analysis. Int. J. Tech. Res. Appl. 2015, 3, 2320–8163. [Google Scholar]
- Patil, D.P.; Maiti, S.K. Detection of multiple cracks using frequency measurements. Eng. Fract. Mech. 2003, 70, 1553–1572. [Google Scholar] [CrossRef]
- Fleet, T.; Kamei, K.; He, F.; Khan, M.A.; Khan, K.A.; Starr, A. A machine learning approach to model interdependencies between dynamic response and crack propagation. Sensors 2020, 20, 6847. [Google Scholar] [CrossRef]
- Rizos, P.F.; Aspragathos, N.; Dimarogonas, A.D. Identification of crack location and magnitude in a cantilever beam from the vibration modes. J. Sound Vib. 1990, 138, 381–388. [Google Scholar] [CrossRef]
- Nahvi, H.; Jabbari, M. Crack detection in beams using experimental modal data and finite element model. Int. J. Mech. Sci. 2005, 47, 1477–1497. [Google Scholar] [CrossRef]
- Agarwalla, D.K.; Parhi, D.R. Effect of crack on modal parameters of a cantilever beam subjected to vibration. Procedia Eng. 2013, 51, 665–669. [Google Scholar] [CrossRef][Green Version]
- Priyadarshini, A. Identification of Cracks in Beams Using Vibrational Analysis. Master’s Thesis, National Institute of Technology, Rourkela, India, 2013. [Google Scholar]
- Altunışık, A.C.; Okur, F.Y.; Kahya, V. Modal parameter identification and vibration based damage detection of a multiple cracked cantilever beam. Eng. Fail. Anal. 2017, 79, 154–170. [Google Scholar] [CrossRef]
- Jassim, Z.A.; Ali, N.N.; Mustapha, F.; Abdul Jalil, N.A. A review on the vibration analysis for a damage occurrence of a cantilever beam. Eng. Fail. Anal. 2013, 31, 442–461. [Google Scholar] [CrossRef]
- Hoshyar, A.N.; Samali, B.; Liyanapathirana, R.; Houshyar, A.N.; Yu, Y. Structural damage detection and localization using a hybrid method and artificial intelligence techniques. Struct. Health Monit. 2020, 19, 1507–1523. [Google Scholar] [CrossRef]
- Chati, M.; Rand, R.; Mukherjee, S. Modal analysis of a cracked beam. J. Sound Vib. 1997, 207, 249–270. [Google Scholar] [CrossRef]
- Mazanoglu, K.; Yesilyurt, I.; Sabuncu, M. Vibration analysis of multiple-cracked non-uniform beams. J. Sound Vib. 2009, 320, 977–989. [Google Scholar] [CrossRef]
- Gillich, G.R.; Furdui, H.; Abdel Wahab, M.; Korka, Z.I. A robust damage detection method based on multi-modal analysis in variable temperature conditions. Mech. Syst. Signal Process. 2019, 115, 361–379. [Google Scholar] [CrossRef]
- Hu, J.; Liang, R.Y. An integrated approach to detection of cracks using vibration characteristics. J. Frankl. Inst. 1993, 330, 841–853. [Google Scholar] [CrossRef]
- Gillich, G.R.; Praisach, Z.I. Modal identification and damage detection in beam-like structures using the power spectrum and time-frequency analysis. Signal Process. 2014, 96, 29–44. [Google Scholar] [CrossRef]
- Pandey, A.K.; Biswas, M.; Samman, M.M. Damage Detection from Mode Changes in Curvature. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, S.Z.; Sohail, W.; Khan, H.; Sohaib, M.; Nisar, S. Mechanical fatigue in aluminium at elevated temperature and remaining life prediction based on natural frequency evolution. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 897–903. [Google Scholar] [CrossRef]
- Loya, J.A.; Rubio, L.; Fernández-Sáez, J. Natural frequencies for bending vibrations of Timoshenko cracked beams. J. Sound Vib. 2006, 290, 640–653. [Google Scholar] [CrossRef]
- Khiem, N.T.; Tran, H.T. A procedure for multiple crack identification in beam-like structures from natural vibration mode. JVC J. Vib. Control 2014, 20, 1417–1427. [Google Scholar] [CrossRef]
- Gillich, G.-R.; Praisach, Z.-I.; Abdel Wahab, M.; Furdui, H. A new modal-based damage location indicator. In Proceedings of the International Conference on Noise and Vibration Engineering ISMA 2014, Leuven, Belgium, 15–17 September 2014; pp. 499–512. [Google Scholar]
- Nitesh, A.M.; Vaibhav, S.P. Analysis of Crack Detection of a Cantilever Beam using Finite Element Analysis. Int. J. Eng. Res. Technol. 2015, 4, 713–718. [Google Scholar]
- Shinde, Y.D.; Katekar, S.D. Vibration Analysis of Cantilever Beam with Single Crack using Experimental Method. Int. J. Eng. Res. Technol. 2014, 3, 1644–1648. [Google Scholar]
- Das, S.; Saha, P.; Patro, S.K. Vibration-based damage detection techniques used for health monitoring of structures: A review. J. Civ. Struct. Health Monit. 2016, 6, 477–507. [Google Scholar] [CrossRef]
- Zai, B.A.; Khan, M.A.; Mansoor, A.; Khan, S.Z.; Khan, K.A. Instant dynamic response measurements for crack monitoring in metallic beams. Insight Non-Destructive Test. Cond. Monit. 2019, 61, 222–229. [Google Scholar]
- Gupta, A.; Jain, N.K.; Salhotra, R.; Joshi, P.V. Effect of thermal environment on vibration analysis of isotropic micro plate with inclined crack based on modified couple stress theory. In Proceedings of the 24th International Congress on Sound and Vibration 2017 (ICSV 24), London, UK, 23–27 July 2017; pp. 1–7. [Google Scholar]
- Chondros, T.G.; Dimarogonas, A.D.; Yao, J. Vibration of a Beam with a Breathing Crack. J. Sound Vib. 2001, 239, 57–67. [Google Scholar] [CrossRef]
- Ghadimi, S.; Kourehli, S.S. Multiple crack identification in Euler beams using extreme learning machine. KSCE J. Civ. Eng. 2017, 21, 389–396. [Google Scholar] [CrossRef]
- Qian, G.L.; Gu, S.N.; Jiang, J.S. The dynamic behaviour and crack detection of a beam with a crack. J. Sound Vib. 1990, 138, 233–243. [Google Scholar] [CrossRef]
- Nguyen, K.V. Mode shapes analysis of a cracked beam and its application for crack detection. J. Sound Vib. 2014, 333, 848–872. [Google Scholar] [CrossRef]
- Gillich, G.R.; Maia, N.M.M.; Mituletu, I.C.; Praisach, Z.I.; Tufoi, M.; Negru, I. Early structural damage assessment by using an improved frequency evaluation algorithm. Lat. Am. J. Solids Struct. 2015, 12, 2311–2329. [Google Scholar] [CrossRef][Green Version]
- Zai, B.A.; Khan, M.A.; Khan, S.Z.; Asif, M.; Khan, K.A.; Saquib, A.N.; Mansoor, A.; Shahzad, M.; Mujtaba, A. Prediction of crack depth and fatigue life of an acrylonitrile butadiene styrene cantilever beam using dynamic response. J. Test. Eval. 2020, 48, 1520–1536. [Google Scholar] [CrossRef]
- Ostachowicz, W.M.; Krawczuk, M. Analysis of the effect of cracks on the natural frequencies of a cantilever beam. J. Sound Vib. 1991, 150, 191–201. [Google Scholar] [CrossRef]
- Akbarzadeh Khorshidi, M.; Soltani, D. Diagnosis of Type, Location and Size of Cracks by Using Generalized Differential Quadrature and Rayleigh Quotient Methods. J. Theor. Appl. Mech. 2013, 43, 61–70. [Google Scholar] [CrossRef]
- Moradi, S.; Makvandi, H.; Poorveis, D.; Shirazi, K.H. Free vibration analysis of cracked postbuckled plate. Appl. Math. Model. 2019, 66, 611–627. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Abbasi, M. A vibration analysis of a cracked micro-cantilever in an atomic force microscope by using transfer matrix method. Ultramicroscopy 2019, 196, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Manoach, E.; Warminski, J.; Kloda, L.; Teter, A. Numerical and experimental studies on vibration based methods for detection of damage in composite beams. Compos. Struct. 2017, 170, 26–39. [Google Scholar] [CrossRef]
- Zai, B.A.; Khan, M.; Khan, K.A.; Mansoor, A.; Shah, A.; Shahzad, M. The role of dynamic response parameters in damage prediction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4620–4636. [Google Scholar] [CrossRef]
- Alshammari, Y.L.A.; He, F.; Khan, M.A. Modelling and investigation of crack growth for 3d-printed acrylonitrile butadiene styrene (Abs) with various printing parameters and ambient temperatures. Polymers 2021, 13, 3737. [Google Scholar] [CrossRef]
- Ellyson, B.; Chekir, N.; Brochu, M.; Brochu, M. Characterization of bending vibration fatigue of WBD fabricated Ti-6Al-4V. Int. J. Fatigue 2017, 101, 36–44. [Google Scholar] [CrossRef]
- Hassanpour, P.A.; Esmailzadeh, E.; Cleghorn, W.L.; Mills, J.K. Generalized Orthogonality Condition for Beams with Intermediate Lumped Masses Subjected to Axial Force. J. Vib. Control 2010, 16, 665–683. [Google Scholar] [CrossRef]
- Romaszko, M.; Sapiński, B.; Sioma, A. Forced vibrations analysis of a cantilever beam using the vision method. J. Theor. Appl. Mech. 2015, 53, 243–254. [Google Scholar] [CrossRef]
- Aldosari, S.M.; Khan, M.A.; Rahatekar, S. Influence of High-Concentration LLDPE on the Manufacturing Process and Morphology of Pitch/LLDPE Fibres. Crystals 2021, 11, 1099. [Google Scholar] [CrossRef]
- Aldosari, S.M.; Khan, M.A.; Rahatekar, S. Manufacturing Pitch and Polyethylene Blends-Based Fibres as Potential Carbon Fibre Precursors. Polymers 2021, 13, 1445. [Google Scholar] [CrossRef] [PubMed]
- Aldosari, S.M.; Rahatekar, S. Extrusion Dwell Time and Its Effect on the Mechanical and Thermal Properties of Pitch/LLDPE Blend Fibres. Crystals 2021, 11, 1520. [Google Scholar] [CrossRef]
- Braconnier, D.J.; Jensen, R.E.; Peterson, A.M. Processing parameter correlations in material extrusion additive manufacturing. Addit. Manuf. 2020, 31, 100924. [Google Scholar] [CrossRef]
- He, F.; Khan, M. Effects of Printing Parameters on the Fatigue Behaviour of 3D-Printed ABS under Dynamic Thermo-Mechanical Loads. Polymers 2021, 13, 2362. [Google Scholar] [CrossRef]
- Wachtman, J.B.; Tefft, W.E.; Lam, D.G.; Apstein, C.S. Exponential Temperature Dependence of Young’s Modulus for Several Oxides. Phys. Rev. 1961, 122, 1754–1759. [Google Scholar] [CrossRef]
- Kharazan, M.; Irani, S.; Noorian, M.A. Effect of a breathing crack on the damping changes in nonlinear vibrations of a cracked beam: Experimental and theoretical investigations. J. Vib. Control 2020, 27, 2345–2353. [Google Scholar] [CrossRef]








| Printing Parameters | Settings |
|---|---|
| Infill density | 100% |
| Raster orientation | 0° |
| Nozzle size | 0.8 mm |
| Layer thickness | 0.15 mm |
| Nozzle temperature | 245 °C |
| Bed temperature | 90 °C |
| Crack Depth (mm) | 0.317 | 0.963 | 1.279 | 1.632 | 2.026 | 2.396 |
|---|---|---|---|---|---|---|
| Experimentally obtained fundamental frequency (Hz) | 23.39 | 23.26 | 21.88 | 19.88 | 15.99 | 12.96 |
| Fundamental frequency (Hz) obtained using Ostachowicz model | 24.44 | 23.66 | 22.91 | 21.76 | 20.19 | 18.7 |
| Fundamental frequency (Hz) obtained using Khan-He model | 24.42 | 23.27 | 21.9 | 19.42 | 15.59 | 10.3 |
| Difference between and (Hz) | 1.04 | 0.4 | 1.03 | 1.88 | 4.2 | 5.74 |
| Difference between and (Hz) | 1.03 | 0.018 | 0.014 | 0.46 | 0.4 | 2.66 |
| Difference between and (%) | 4.47 | 1.72 | 4.72 | 9.46 | 26.27 | 44.26 |
| Difference between and (%) | 4.42 | 0.08 | 0.07 | 2.33 | 2.49 | 20.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Khan, M.; Aldosari, S. Interdependencies between Dynamic Response and Crack Growth in a 3D-Printed Acrylonitrile Butadiene Styrene (ABS) Cantilever Beam under Thermo-Mechanical Loads. Polymers 2022, 14, 982. https://doi.org/10.3390/polym14050982
He F, Khan M, Aldosari S. Interdependencies between Dynamic Response and Crack Growth in a 3D-Printed Acrylonitrile Butadiene Styrene (ABS) Cantilever Beam under Thermo-Mechanical Loads. Polymers. 2022; 14(5):982. https://doi.org/10.3390/polym14050982
Chicago/Turabian StyleHe, Feiyang, Muhammad Khan, and Salem Aldosari. 2022. "Interdependencies between Dynamic Response and Crack Growth in a 3D-Printed Acrylonitrile Butadiene Styrene (ABS) Cantilever Beam under Thermo-Mechanical Loads" Polymers 14, no. 5: 982. https://doi.org/10.3390/polym14050982
APA StyleHe, F., Khan, M., & Aldosari, S. (2022). Interdependencies between Dynamic Response and Crack Growth in a 3D-Printed Acrylonitrile Butadiene Styrene (ABS) Cantilever Beam under Thermo-Mechanical Loads. Polymers, 14(5), 982. https://doi.org/10.3390/polym14050982






