Unscented Kalman Filter-Based Robust State and Parameter Estimation for Free Radical Polymerization of Styrene with Variable Parameters
Abstract
:1. Introduction
2. Foundations of UKF-Based SPE
2.1. Review of Standard UKF
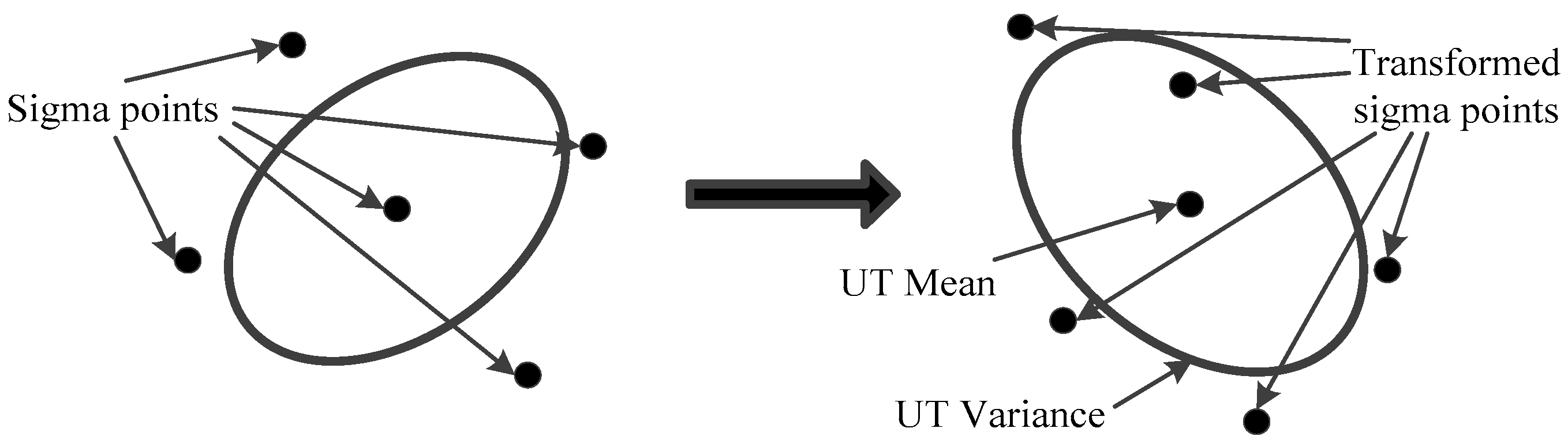
2.1.1. Unscented Transformation
2.1.2. UKF for State Estimation
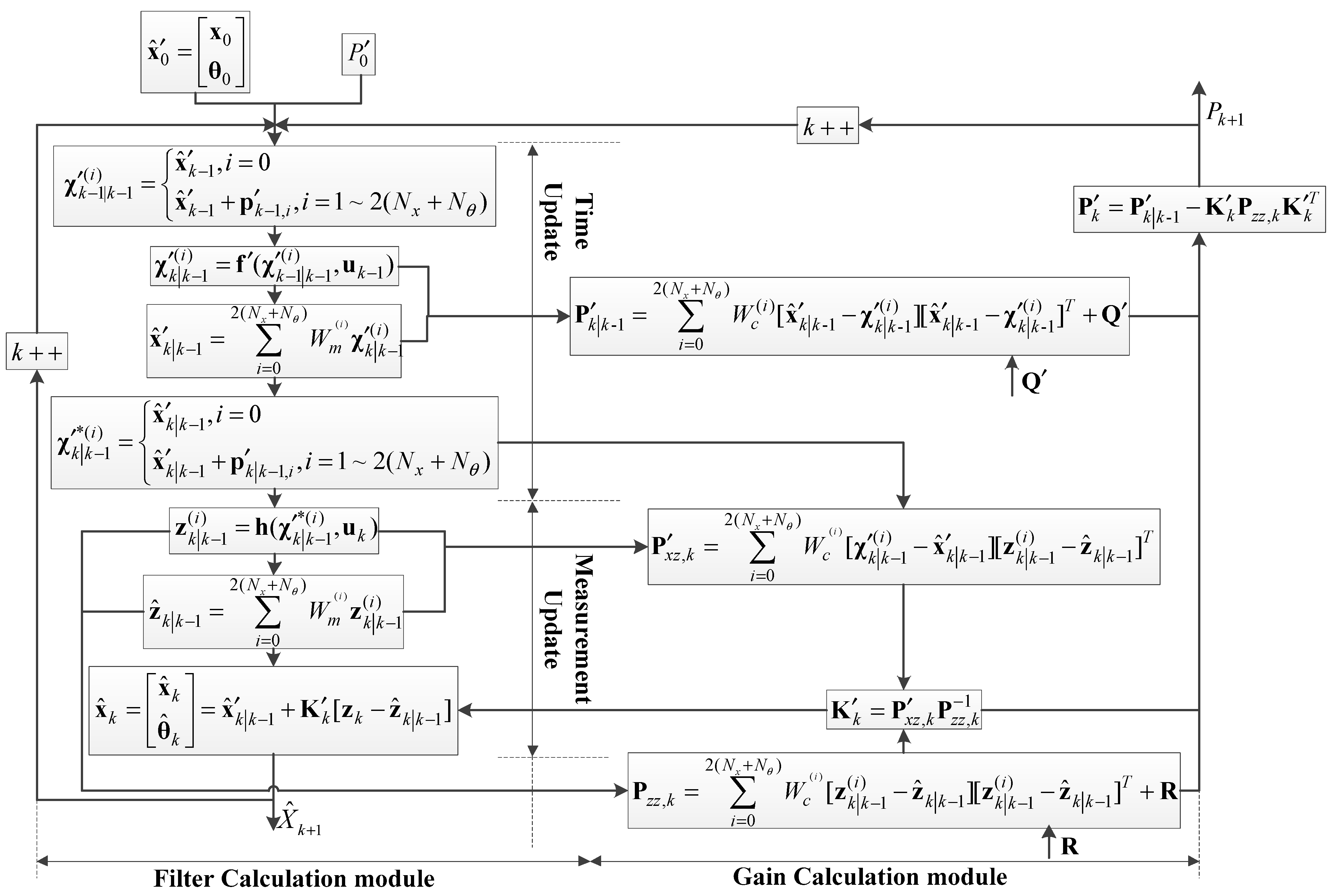
2.2. UKF-Based SPE
3. UKF-Based Robust SPE for System with Variable Parameters
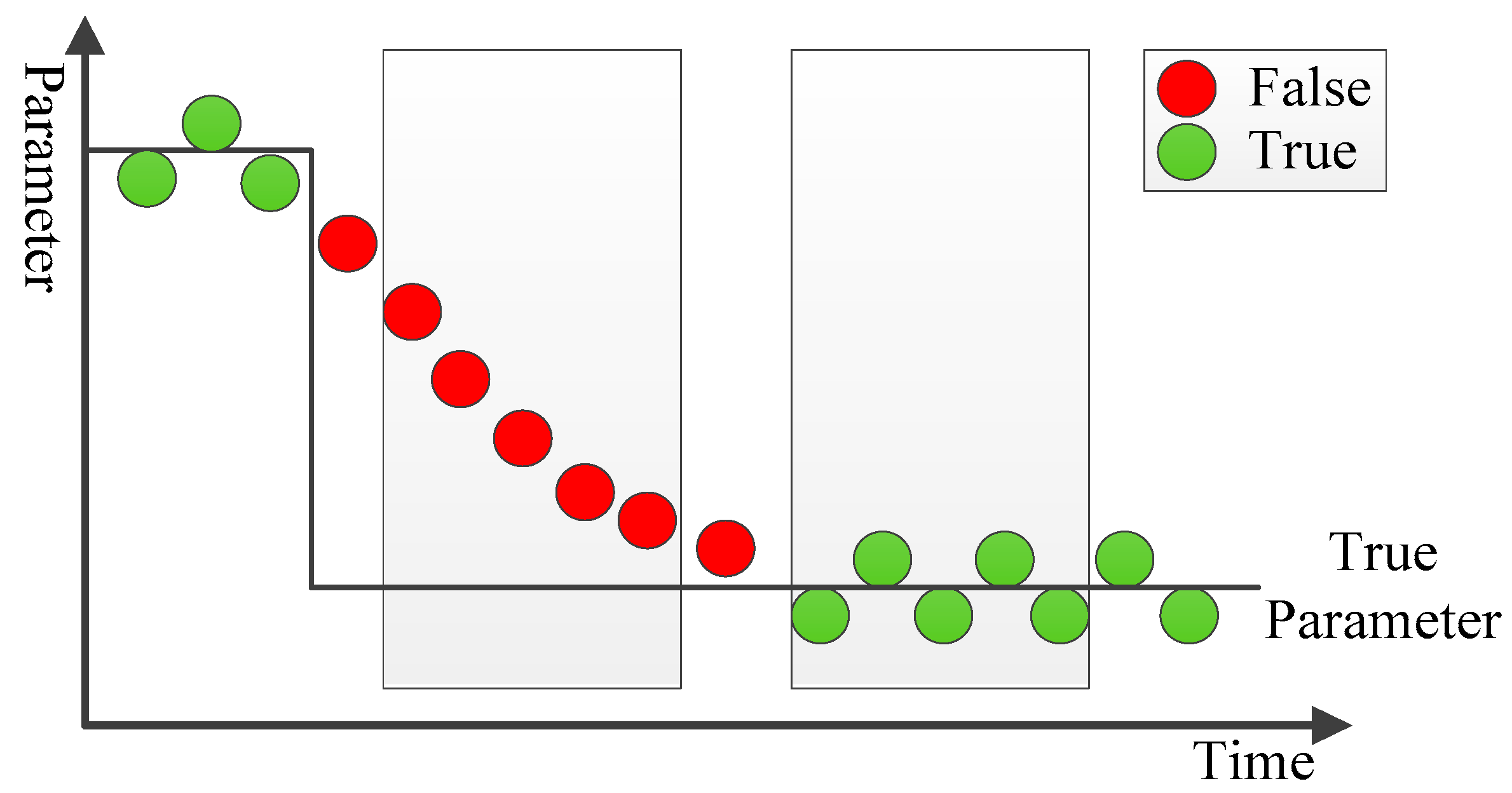
3.1. Parameters Test
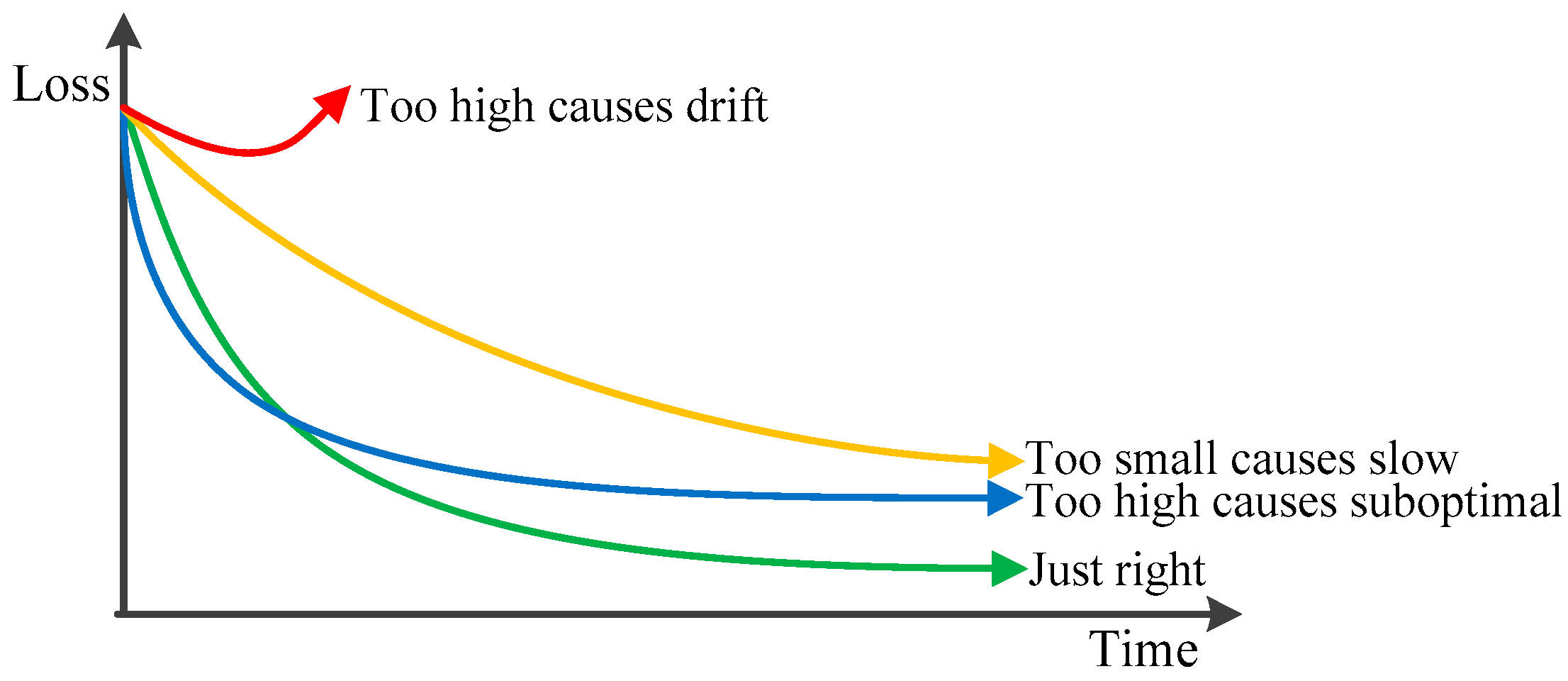
3.2. RMSProp Gradient Descent
| Algorithm1: UKF-based robust SPE |
| Input: ; ; Begin: Step 1. Extend the state vector to obtain . Step 2. Conduct UKF-SPE based on to estimate , , and reconcile . Step 3. Conduct parameters test: 1. Calculate the mean and variance of each estimated parameter in the window using Equations (43) and (44); 2. Performing hypothesis testing; For n = 1: If null hypothesis is accepted, , skip the following steps to output Else , proceed to the next step Step 4. Conduct RMSProp gradient descent: 1. Calculate loss using Equation (49); 2. Calculate the approximate gradient using Equation (53); 3. Calculate the learning rate for each parameter using Equation (56); 4. Modify parameters using Equation (57); Step 5. Re-conduct UKF-SPE based on the modified parameters to estimate , , and reconcile . End Output: ; ; |
4. Case Studies
4.1. Case Study 1: Typical Nonlinear Dynamic System
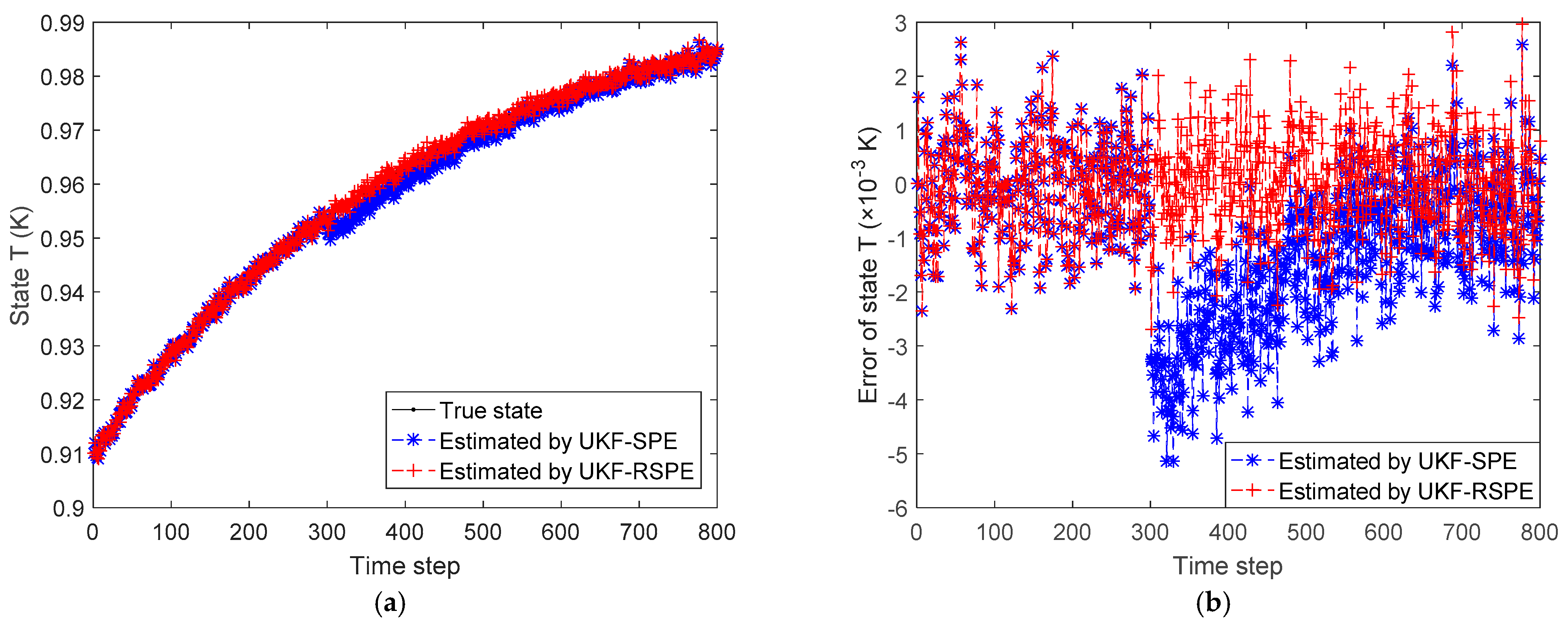
4.2. Case Study 2: Free Radical Polymerization of Styrene
4.2.1. Case Study 2.1: Robust SPE with Single Parameter
4.2.2. Case Study 2.2: Robust SPE with Multiple Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalman, R.E. A New approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Bucy, R.S.; Senne, K.D. Digital synthesis of non-linear filters. Automatica 1971, 7, 287–298. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, A.D.; Ray, W.H. The dynamic behavior of continuous polymerization reactors—I: Isothermal solution polymerization in a CSTR. Chem. Eng. Sci. 1981, 36, 1401–1410. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, J. Correntropy based data reconciliation and gross error detection and identification for nonlinear dynamic processes. Comput. Chem. Eng. 2015, 75, 120–134. [Google Scholar] [CrossRef]
- Hu, G.; Zhang, Z.; Armaou, A.; Yan, Z. Robust extended Kalman filter based state estimation for nonlinear dynamic processes with measurements corrupted by gross errors. J. Taiwan Inst. Chem. Eng. 2020, 106, 20–33. [Google Scholar] [CrossRef]
- Hu, G.; Zhang, Z.; Chen, J.; Zhang, Z.; Armaou, A.; Yan, Z. Elman neural networks combined with extended Kalman filters for data-driven dynamic data reconciliation in nonlinear dynamic process systems. Ind. Eng. Chem. Res. 2021, 60, 15219–15235. [Google Scholar] [CrossRef]
- Al-Harthi, M.; Soares, J.B.P.; Simon, L.C. Mathematical modeling of atom-transfer radical copolymerization. Macromol. React. Eng. 2007, 1, 468–479. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Pakdel, A.S.; Saeb, M.R.; Boodhoo, K. Monte Carlo simulation of free radical polymerization of styrene in a spinning disc reactor. Chem. Eng. J. 2014, 247, 231–240. [Google Scholar] [CrossRef]
- Maafa, I.M.; Soares, J.B.P.; Elkamel, A. Prediction of chain length distribution of polystyrene made in batch reactors with bifunctional free-radical initiators using dynamic monte carlo simulation. Macromol. React. Eng. 2007, 1, 364–383. [Google Scholar] [CrossRef]
- Woloszyn, J.D.; Hesse, P.; Hungenberg, K.-D.; McAuley, K.B. Parameter selection and estimation techniques in a styrene polymerization model. Macromol. React. Eng. 2013, 7, 293–310. [Google Scholar] [CrossRef]
- Meißner, P.; Watschke, H.; Winter, J.; Vietor, T. Artificial neural networks-based material parameter identification for numerical simulations of additively manufactured parts by material extrusion. Polymers 2020, 12, 2949. [Google Scholar] [CrossRef] [PubMed]
- Kiparissides, C.; Seferlis, P.; Mourikas, G.; Morris, A.J. Online optimizing control of molecular weight properties in batch free-radical polymerization reactors. Ind. Eng. Chem. Res. 2002, 41, 6120–6131. [Google Scholar] [CrossRef]
- Yousefi-Darani, A.; Paquet-Durand, O.; Hinrichs, J.; Hitzmann, B. Parameter and state estimation of backers yeast cultivation with a gas sensor array and unscented Kalman filter. Eng. Life Sci. 2021, 21, 170–180. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, G.; Wang, Y.; Du, H.; Hu, J.-S.; Yin, C. PTV Longitudinal-lateral state estimation considering unknown control inputs and uncertain model parameters. IEEE Trans. Veh. Technol. 2021, 70, 4366–4376. [Google Scholar] [CrossRef]
- Kim, S.-H.; Yang, H.-J.; Nguyen, N.A.T.; Mehmood, R.M.; Lee, S.-W. Parameter estimation using unscented Kalman filter on the gray-box model for dynamic EEG system modeling. IEEE Trans. Instrum. Meas. 2020, 69, 6175–6185. [Google Scholar] [CrossRef]
- Geraldi, E.L.; Fernandes, T.C.C.; Piardi, A.B.; Grilo, A.P.; Ramos, R.A. Parameter estimation of a synchronous generator model under unbalanced operating conditions. Electr. Power Syst. Res. 2020, 187, 106487. [Google Scholar] [CrossRef]
- Peng, X.; Li, Y.; Yang, W.; Garg, A. Real-time state of charge estimation of the extended Kalman filter and unscented Kalman filter algorithms under different working conditions. J. Electrochem. Energy Convers. Storage 2021, 18, 041007. [Google Scholar] [CrossRef]
- Kong, D.; Wang, S.; Ping, P. A novel parameter adaptive method for state of charge estimation Intelligent particle filter and its application on fault detection of nonlinear system of aged lithium batteries. J. Energy Storage 2021, 44, 103389. [Google Scholar] [CrossRef]
- Nakamura, R.; Kawamura, T. Building heat load estimation method including parameter estimation from actual data. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 1067–1075. [Google Scholar] [CrossRef]
- Li, Y.; Castiglione, J.; Astroza, R.; Chen, Y. Real-time thermal dynamic analysis of a house using RC models and joint state-parameter estimation. Build. Environ. 2021, 188, 107184. [Google Scholar] [CrossRef]
- Chen, Y.; Castiglione, J.; Astroza, R.; Li, Y. Parameter estimation of resistor-capacitor models for building thermal dynamics using the unscented Kalman filter. J. Build. Eng. 2021, 34, 101639. [Google Scholar] [CrossRef]
- Rodríguez, A.J.; Sanjurjo, E.; Pastorino, R.; Naya, M.N. State, parameter and input observers based on multibody models and Kalman filters for vehicle dynamics. Mech. Syst. Signal Process. 2021, 155, 107544. [Google Scholar] [CrossRef]
- Wan, W.; Feng, J.; Song, B.; Li, X. Huber-based robust unscented Kalman filter distributed drive electric vehicle state observation. Energies 2021, 14, 750. [Google Scholar] [CrossRef]
- Lee, S.-H.; Song, J. Regularization-based dual adaptive Kalman filter for identification of sudden structural damage using sparse measurements. Appl. Sci. 2020, 10, 850. [Google Scholar] [CrossRef] [Green Version]
- Ding, D.; He, K.F.; Qian, W.Q. A Bayesian adaptive unscented Kalman filter for aircraft parameter and noise estimation. J. Sens. 2021, 2021, 9002643. [Google Scholar] [CrossRef]
- Liu, J.; West, M. Combined parameter and state estimation in simulation-based filtering. In Sequential Monte Carlo Methods in Practice; Springer: New York, NY, USA, 2001; pp. 197–223. [Google Scholar] [CrossRef]
- Zhu, Z.; Meng, Z.; Cao, T.; Zhang, Z.; Dai, Y. Particle filter-based robust state and parameter estimation for nonlinear process systems with variable parameters. Meas. Sci. Technol. 2017, 28, 065003. [Google Scholar] [CrossRef]
- Wang, S.; Na, J.; Xing, Y. Adaptive optimal parameter estimation and control of servo mechanisms: Theory and experiments. IEEE Trans. Ind. Electron. 2021, 68, 598–608. [Google Scholar] [CrossRef]
- Jacobs, R.A. Increased rates of convergence through learning rate adaptation. Neural Netw. 1988, 1, 295–307. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:abs/1412.6980. Available online: https://arxiv.org/abs/1412.6980 (accessed on 22 December 2021).
- Long, B.; Zhu, Z.; Yang, W.; Chong, K.T.; Rodriguez, J.; Guerrero, J.M. Gradient descent optimization based parameter identification for FCS-MPC control of LCL-type grid connected converter. IEEE Trans. Ind. Electron. 2022, 69, 2631–2643. [Google Scholar] [CrossRef]
- Li, L.; Long, Z.; Ying, H.; Qiao, Z. An online gradient-based parameter identification algorithm for the neuro-fuzzy systems. Fuzzy Sets Syst. 2022, 426, 27–45. [Google Scholar] [CrossRef]
- Na, J.; Xing, Y.; Costa-Castello, R. Adaptive estimation of time-varying parameters with application to roto-magnet plant. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 731–741. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chen, J. Simultaneous data reconciliation and gross error detection for dynamic systems using particle filter and measurement test. Comput. Chem. Eng. 2014, 69, 66–74. [Google Scholar] [CrossRef]
- Hidalgo, P.M.; Brosilow, C.B. Nonlinear model predictive control of styrene polymerization at unstable operating points. Comput. Chem. Eng. 1990, 4, 481–494. [Google Scholar] [CrossRef]
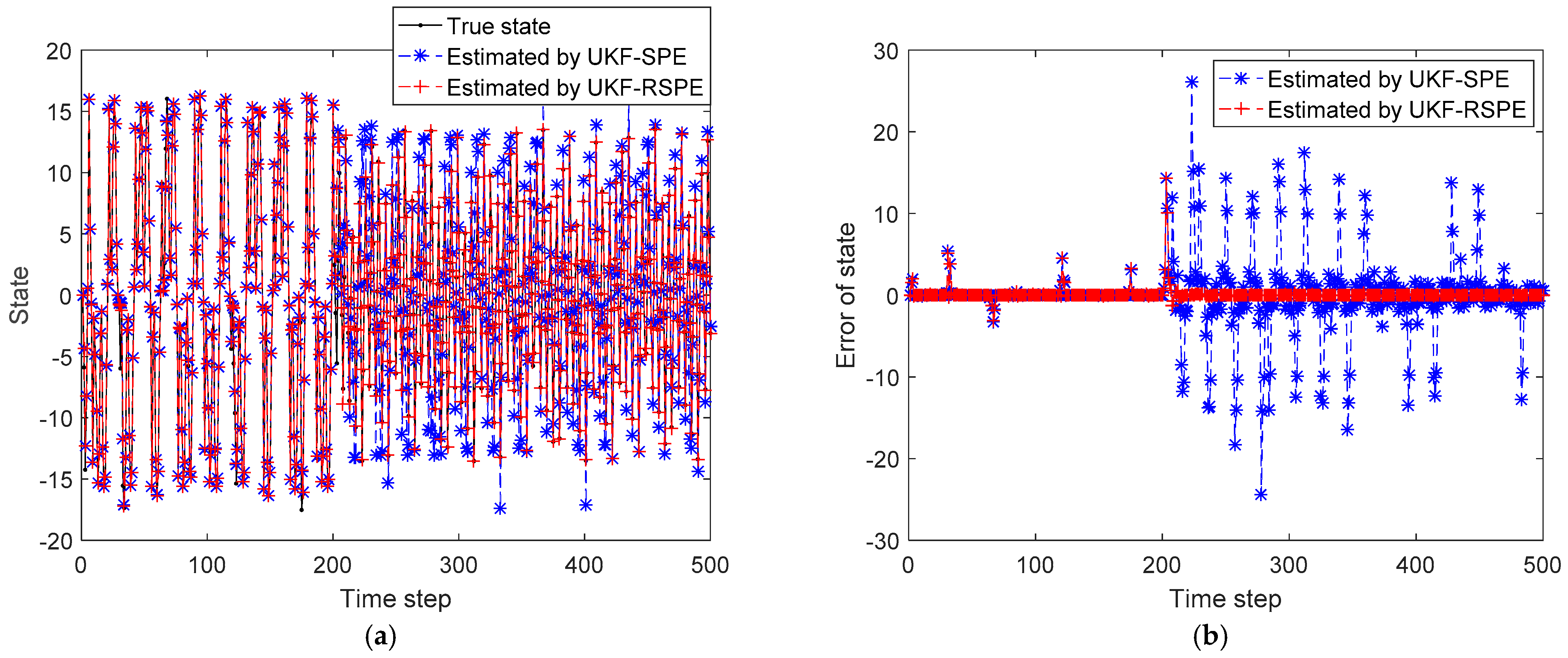
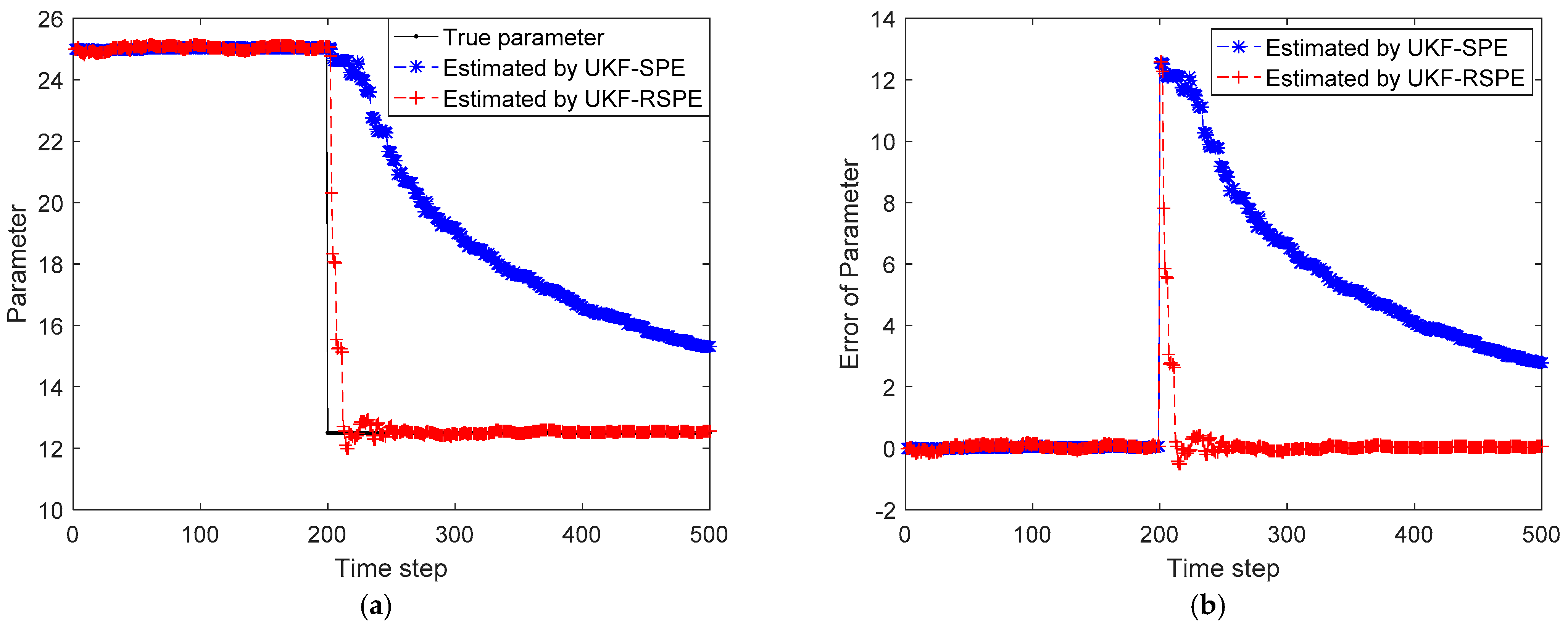
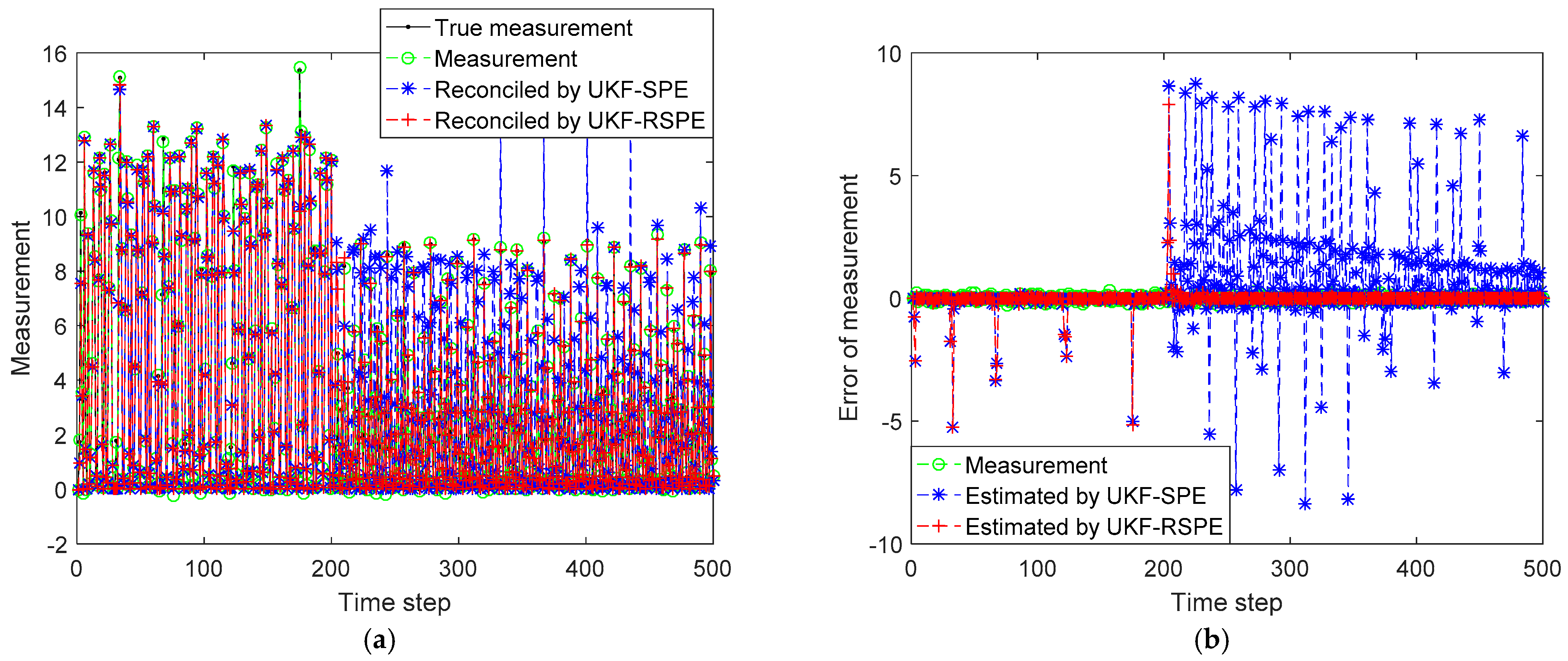

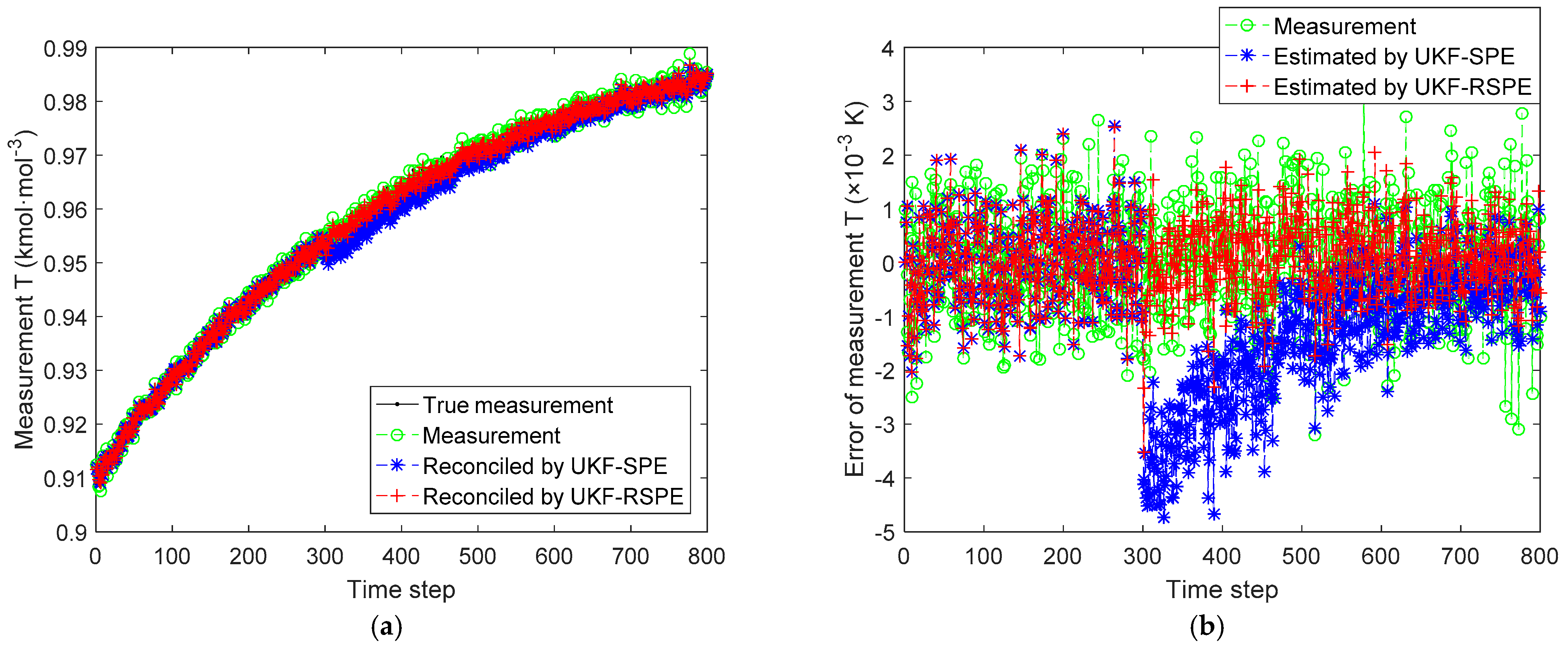
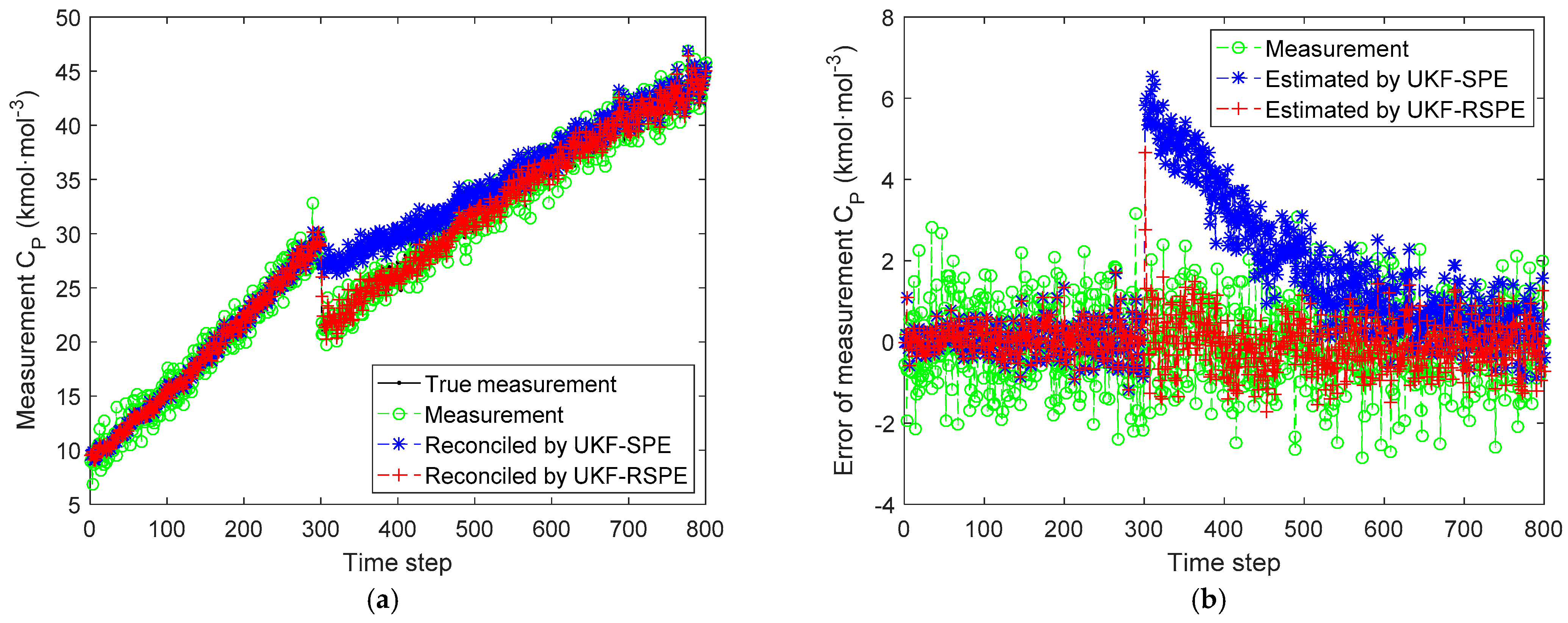
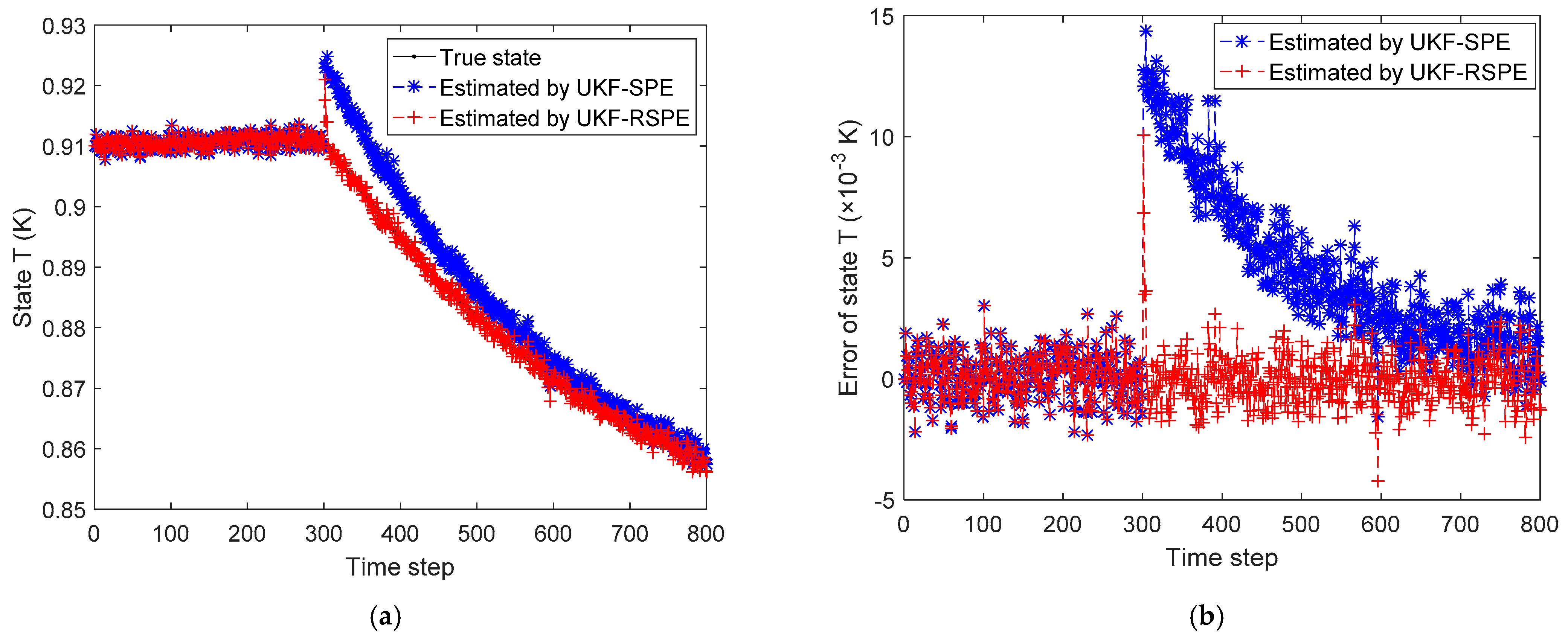
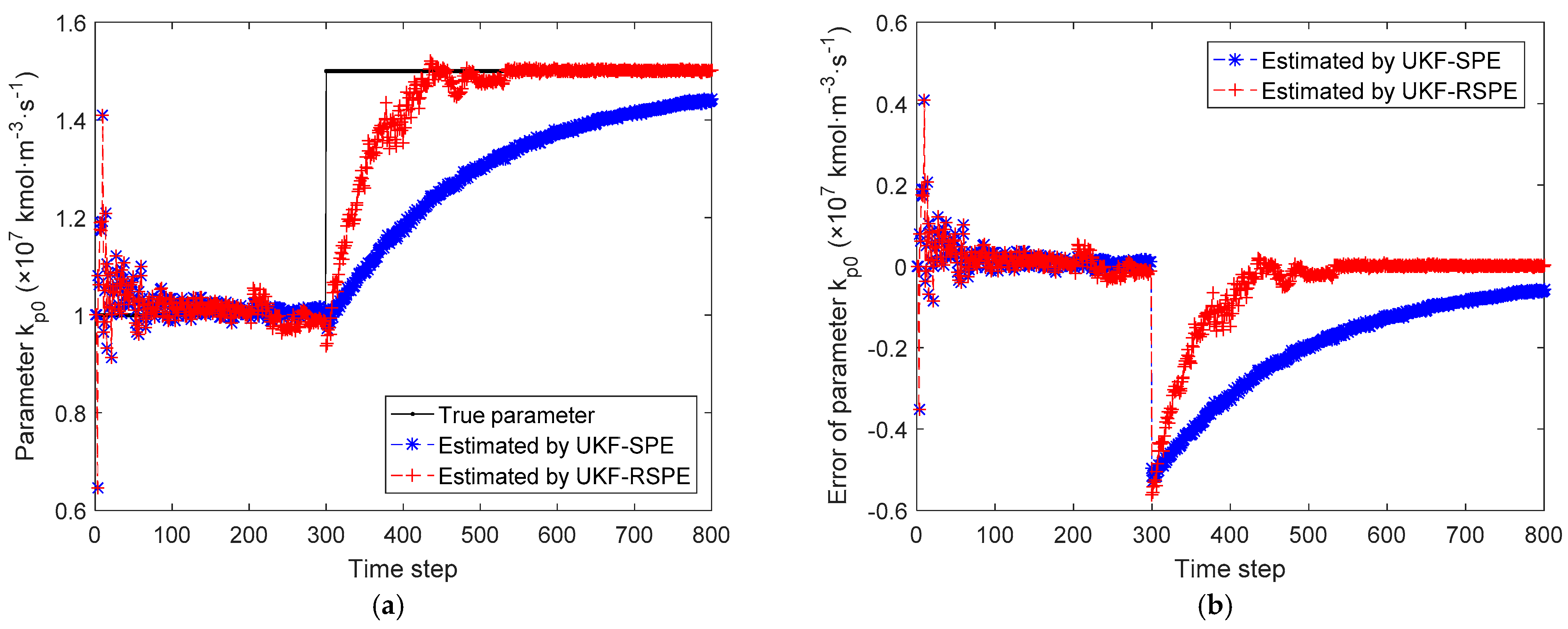
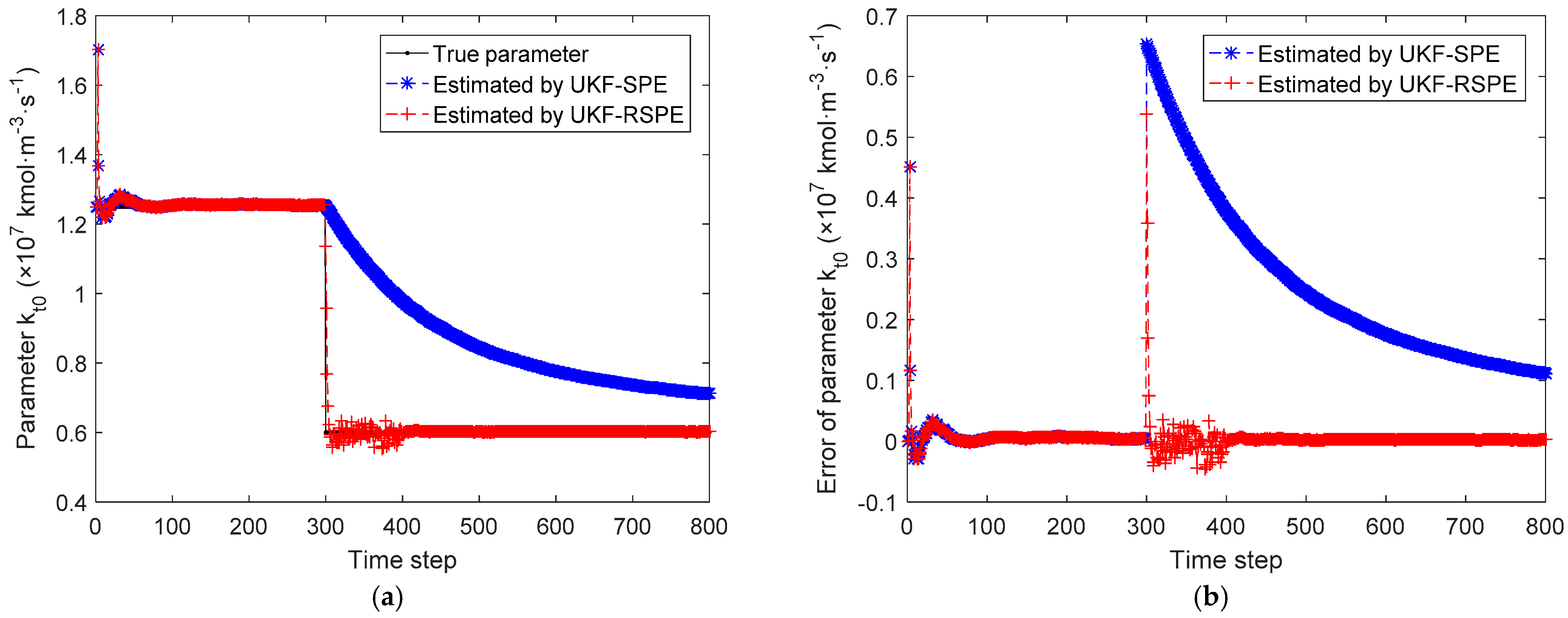

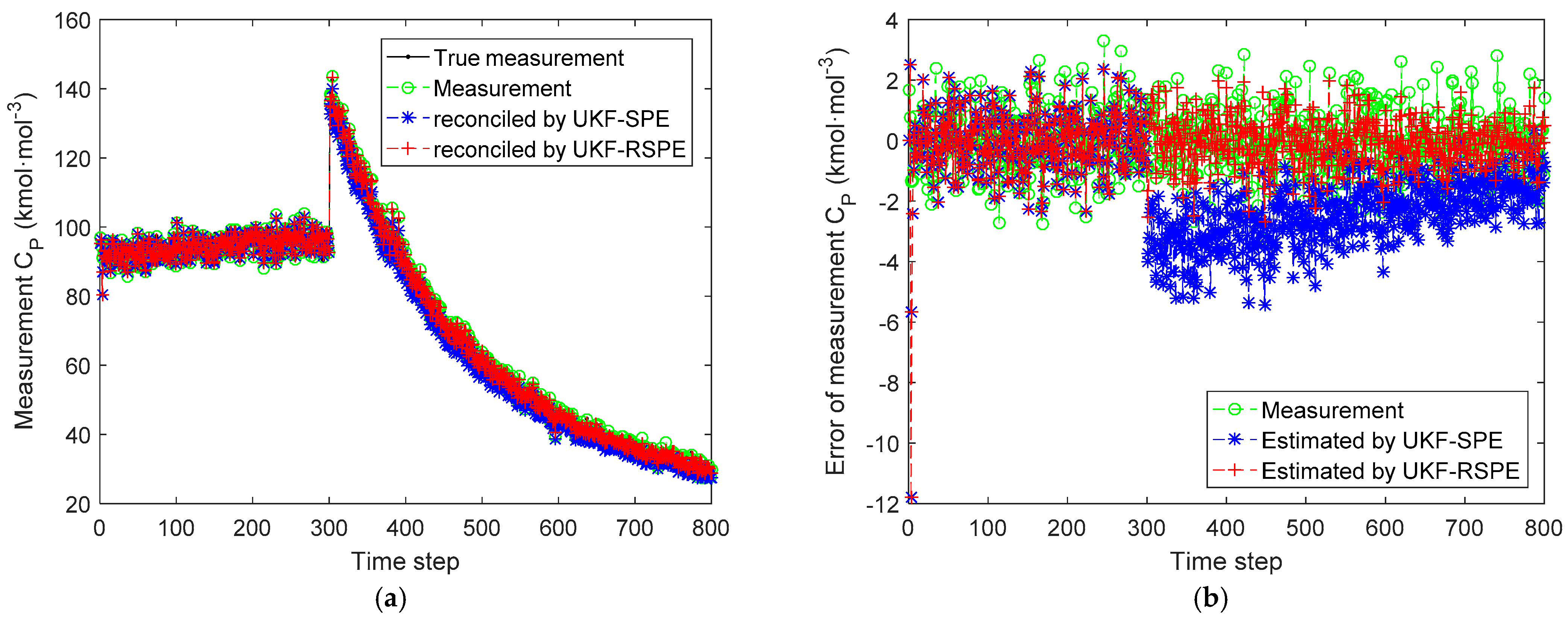
| Results | MSE | |
|---|---|---|
| UKF-SPE | UKF-RSPE | |
| States | 20.4359 | 0.8509 |
| Parameters | 26.4655 | 1.3346 |
| Measurements (MSE = 0.0106) | 4.3588 | 0.3375 |
| Process Parameters | Value |
|---|---|
| The reaction rate constant of the decomposition reaction | |
| The reaction rate constant of the propagation reaction | |
| The reaction rate constant of the termination reaction | |
| The energy of activation of the decomposition reaction | |
| The energy of activation of the propagation reaction | |
| The energy of activation of the termination reaction |
| Process States | Initial Value | Standard Deviation of Noise | Final Value at Steady State |
|---|---|---|---|
| Dimensionless concentration of initiator | 0.91 | 0.01 | 1 |
| Dimensionless concentration of monomer | 0.91 | 0.01 | 1 |
| Dimensionless temperature of reactor | 0.91 | 0.01 | 1 |
| Process Parameters | Value |
|---|---|
| The volumetric flow rates of inlet solvent | |
| The volumetric flow rates of inlet monomer | |
| The volumetric flow rates of inlet initiator | |
| The volumetric flow rates outlet streams | |
| The reactor volume | |
| The residence time | |
| The measured density | Obtained from simultaneous online measurements |
| The volumetric heat capacity of reacting mixture | |
| The heat of reaction due to the propagation reaction | |
| The amount of reaction mixture | |
| The heating rate at the steady state | |
| The inlet feed temperature |
| Results | MSE | |
|---|---|---|
| UKF-SPE | UKF-RSPE | |
| States | 1.51 × 10−6 | 8.67 × 10−7 |
| Parameters | 7.09 × 10−3 | 2.08 × 10−4 |
| Measurements (MSE = 2.49 × 10−1) | 1.03 | 8.58 × 10−2 |
| Results | MSE | |
|---|---|---|
| UKF-SPE | UKF-RSPE | |
| States | 7.17 × 10−6 | 9.20 × 10−7 |
| Parameters | 4.53 × 10−2 | 6.04 × 10−3 |
| Measurements (MSE = 2.59 × 10−1) | 1.22 | 2.35 × 10−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhang, Z.; Hong, Z. Unscented Kalman Filter-Based Robust State and Parameter Estimation for Free Radical Polymerization of Styrene with Variable Parameters. Polymers 2022, 14, 973. https://doi.org/10.3390/polym14050973
Zhang Z, Zhang Z, Hong Z. Unscented Kalman Filter-Based Robust State and Parameter Estimation for Free Radical Polymerization of Styrene with Variable Parameters. Polymers. 2022; 14(5):973. https://doi.org/10.3390/polym14050973
Chicago/Turabian StyleZhang, Zhenhui, Zhengjiang Zhang, and Zhihui Hong. 2022. "Unscented Kalman Filter-Based Robust State and Parameter Estimation for Free Radical Polymerization of Styrene with Variable Parameters" Polymers 14, no. 5: 973. https://doi.org/10.3390/polym14050973
APA StyleZhang, Z., Zhang, Z., & Hong, Z. (2022). Unscented Kalman Filter-Based Robust State and Parameter Estimation for Free Radical Polymerization of Styrene with Variable Parameters. Polymers, 14(5), 973. https://doi.org/10.3390/polym14050973






