Temperature-Dependent Conformation Behavior of Isolated Poly(3-hexylthiopene) Chains
Abstract
:1. Introduction
2. Simulation Models and Details
2.1. Molecular Dynamics Simulations
2.2. Lennard–Jones Model Polymer
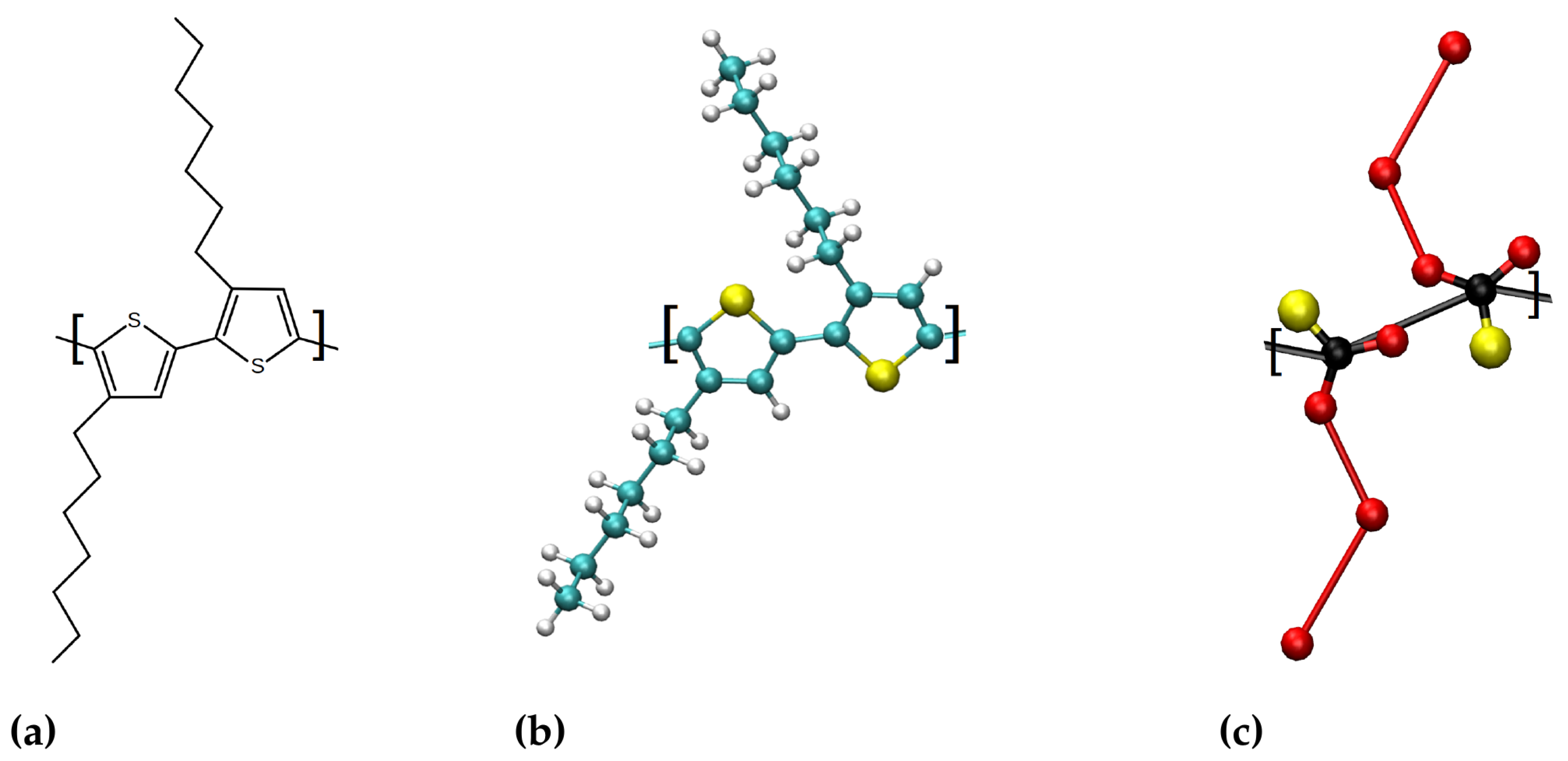
2.3. Atomistic Poly(3-hexylthiopene) Model
2.4. Coarse Grained Martini Poly(3-hexylthiopene) Model
3. Results
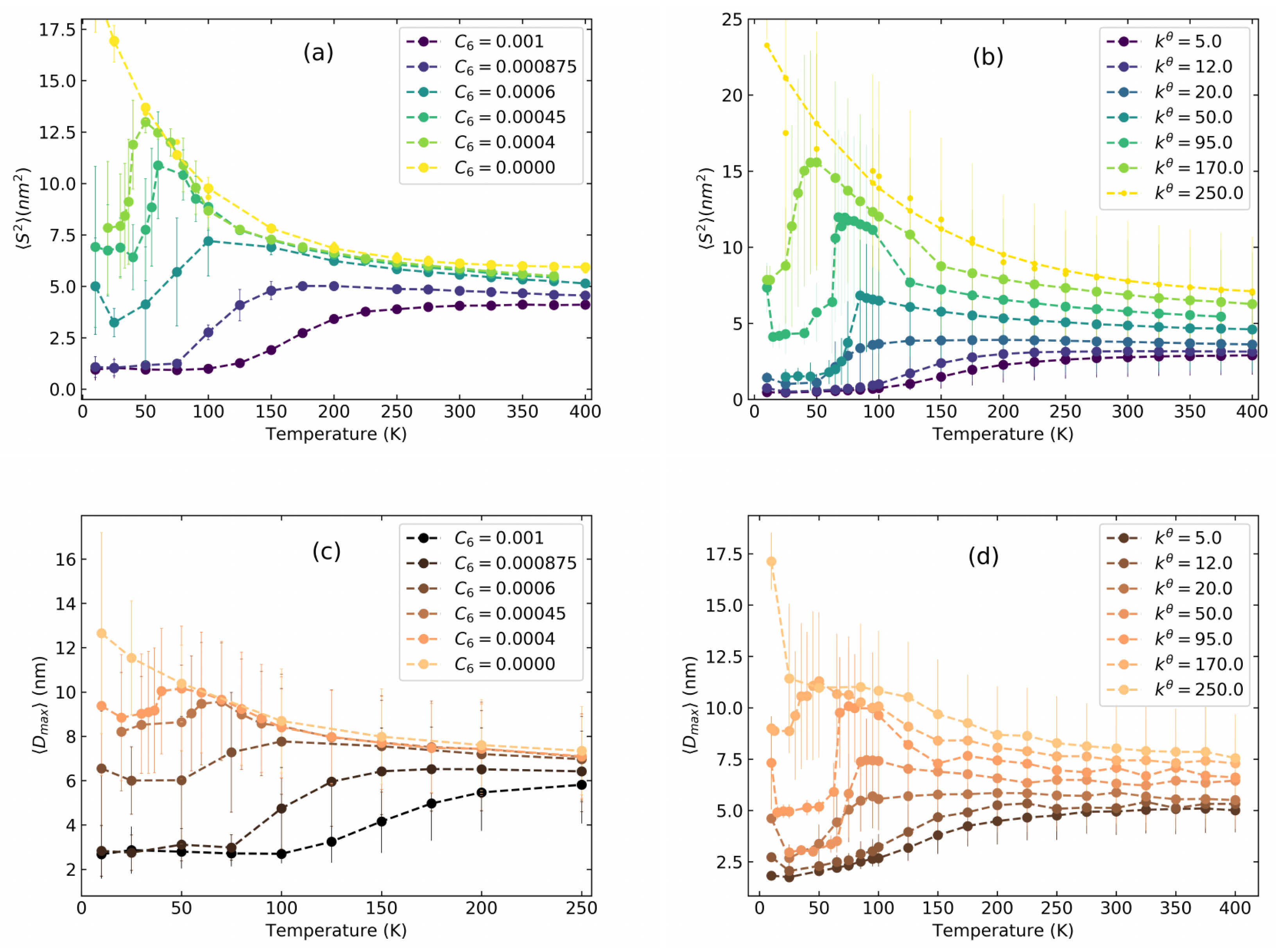
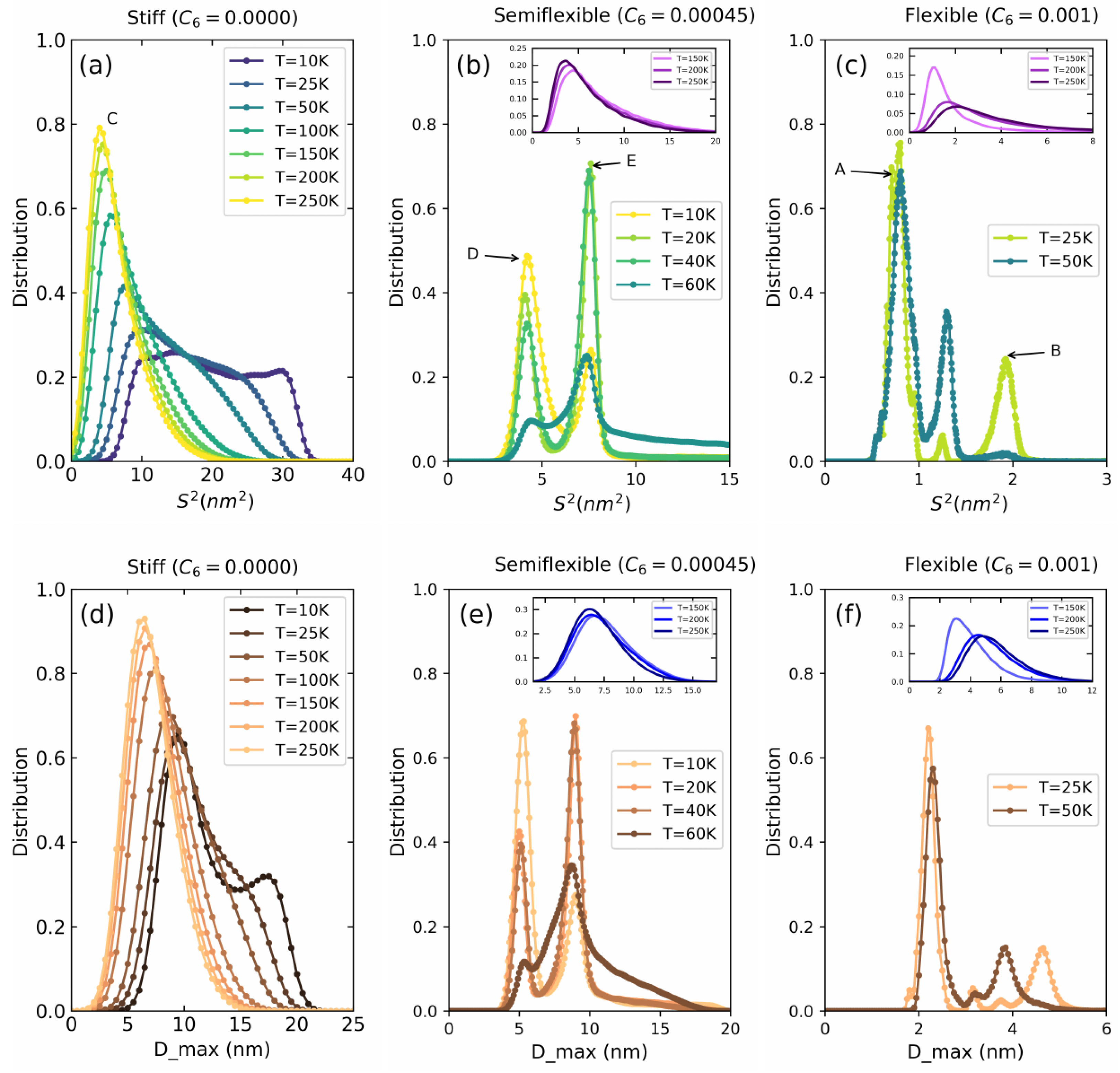
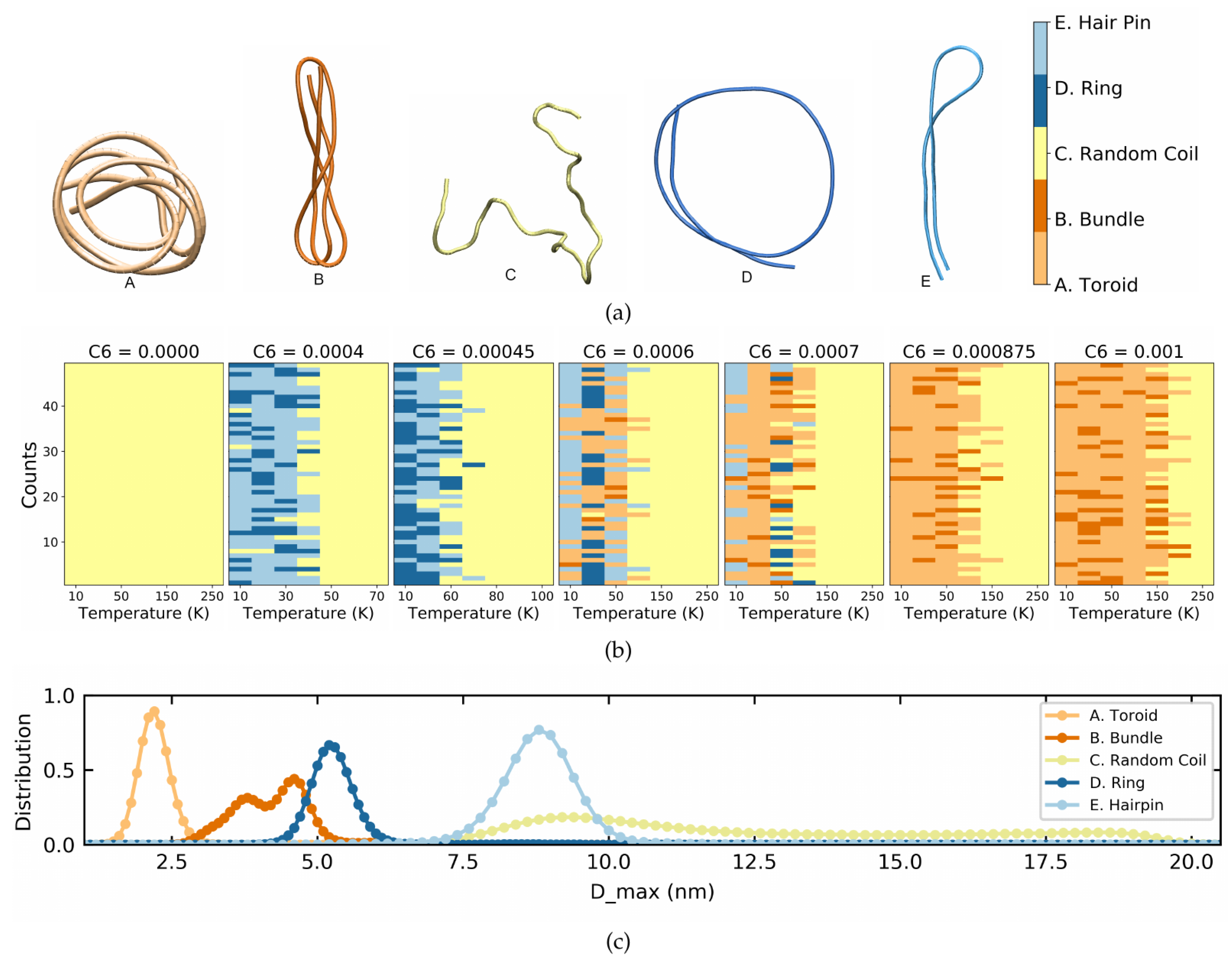
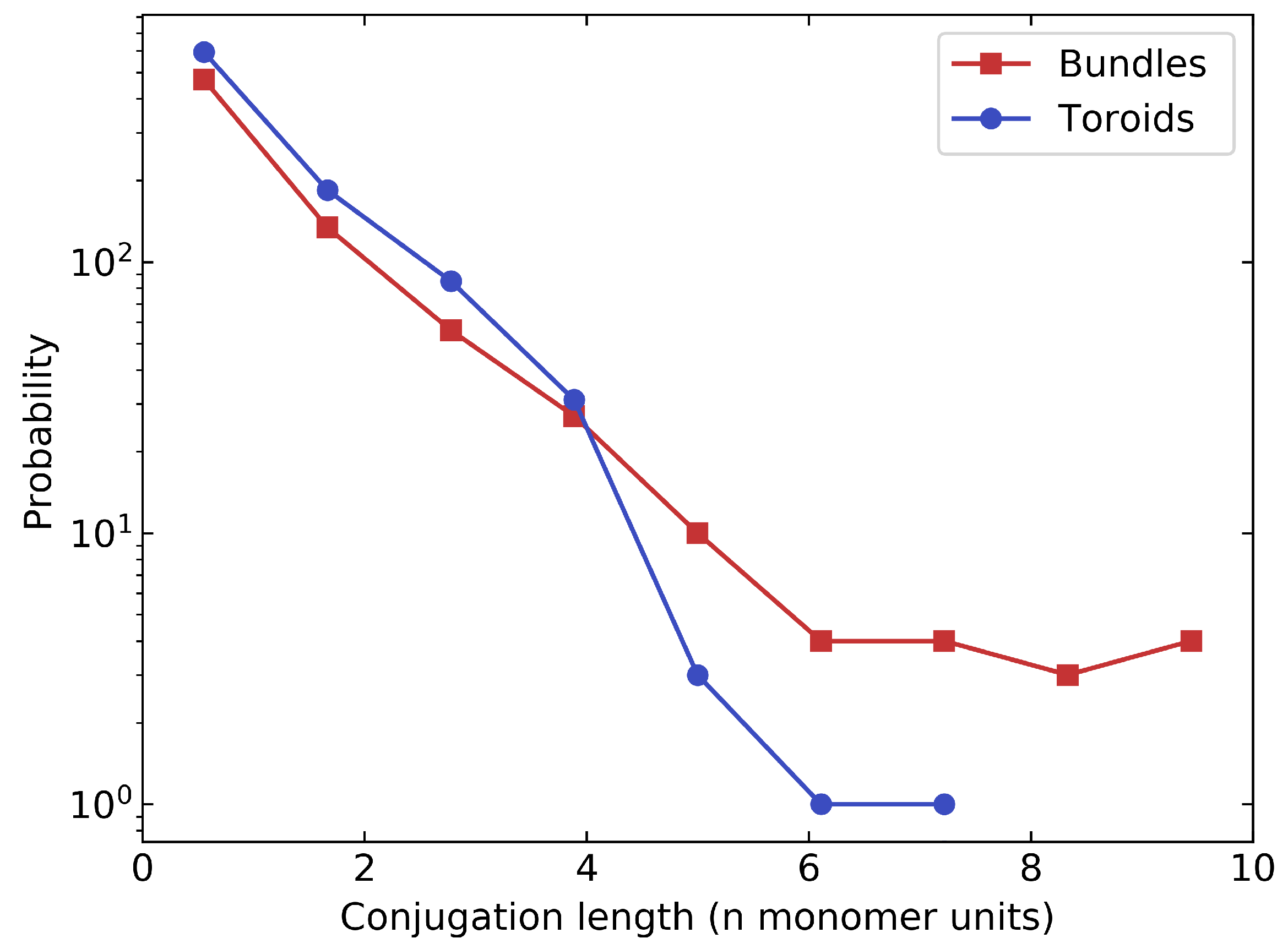
Lennard–Jones Model Polymers
4. Poly(3-hexylthiopene) (P3HT)
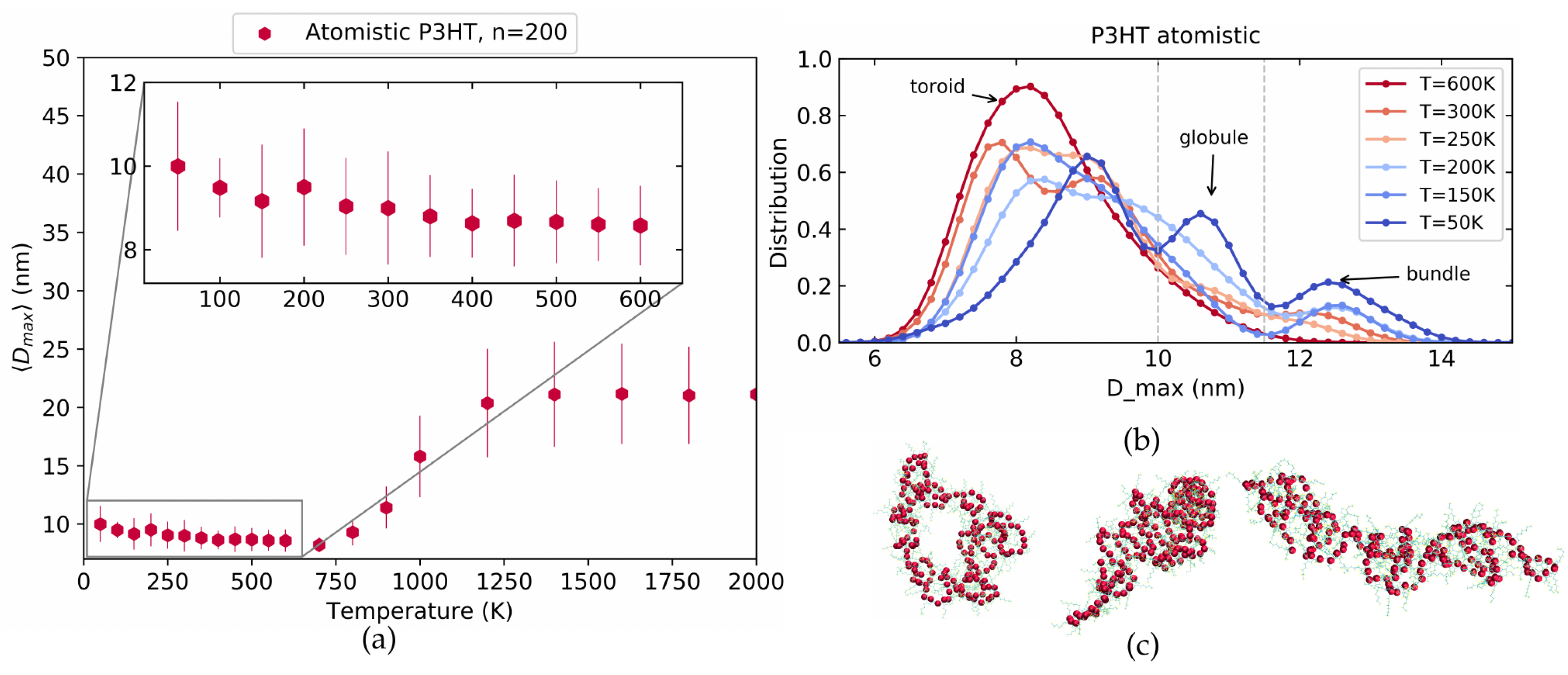
4.1. Atomistic P3HT
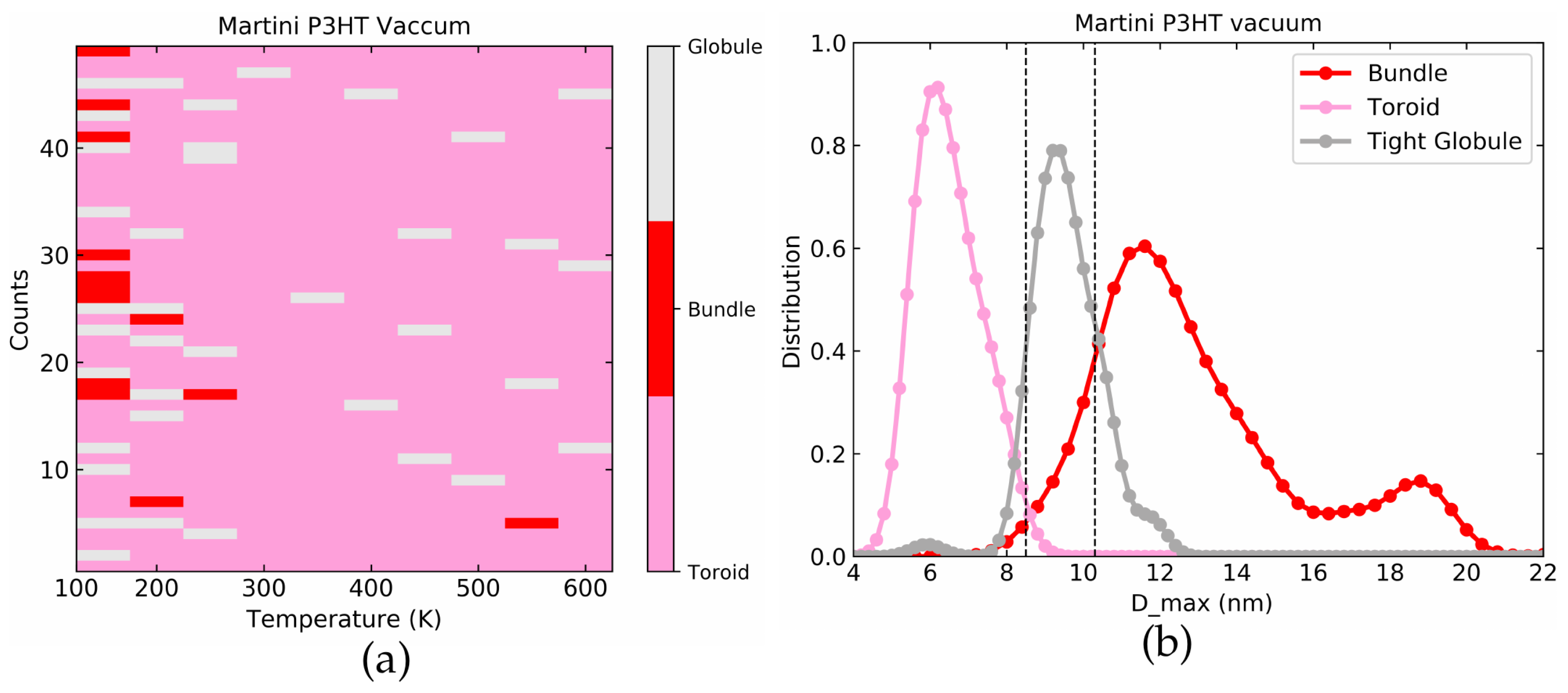
4.2. Martini P3HT in Vacuum
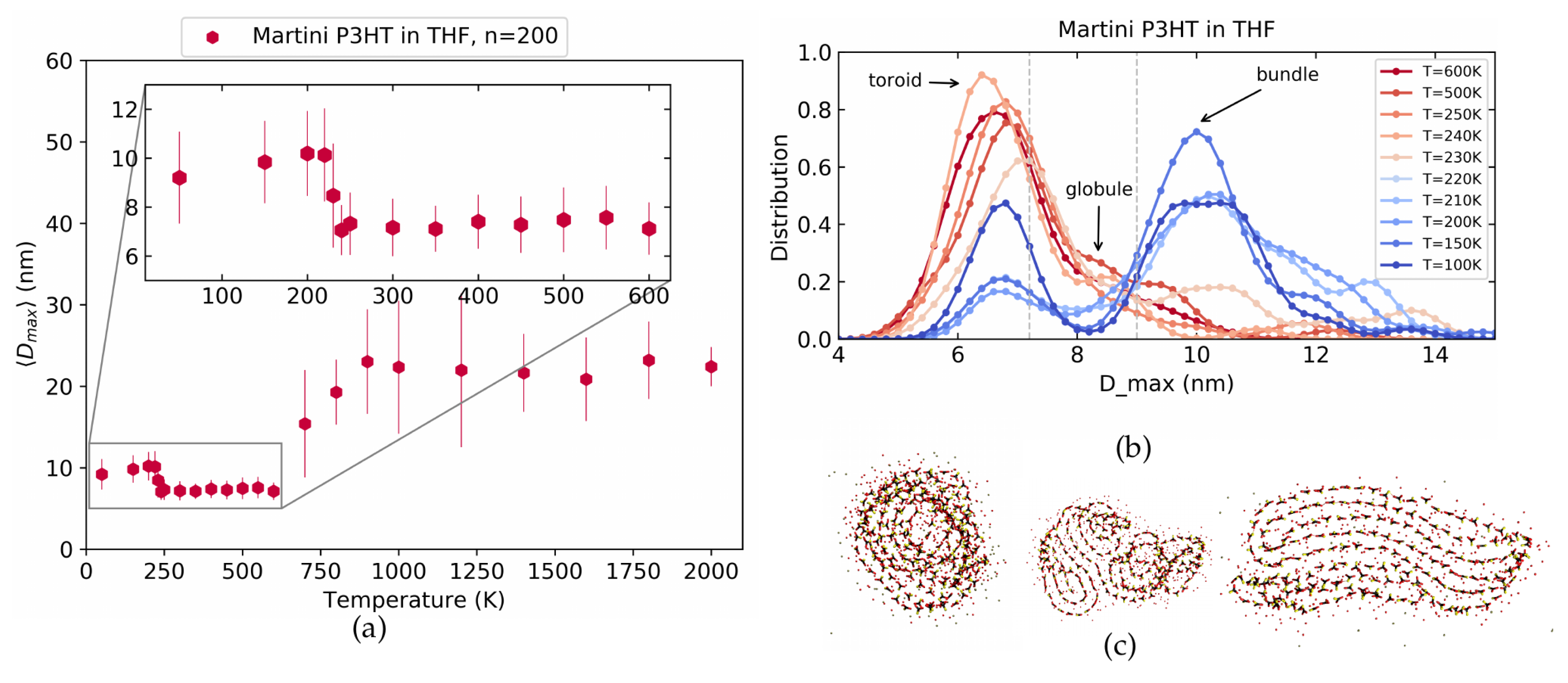
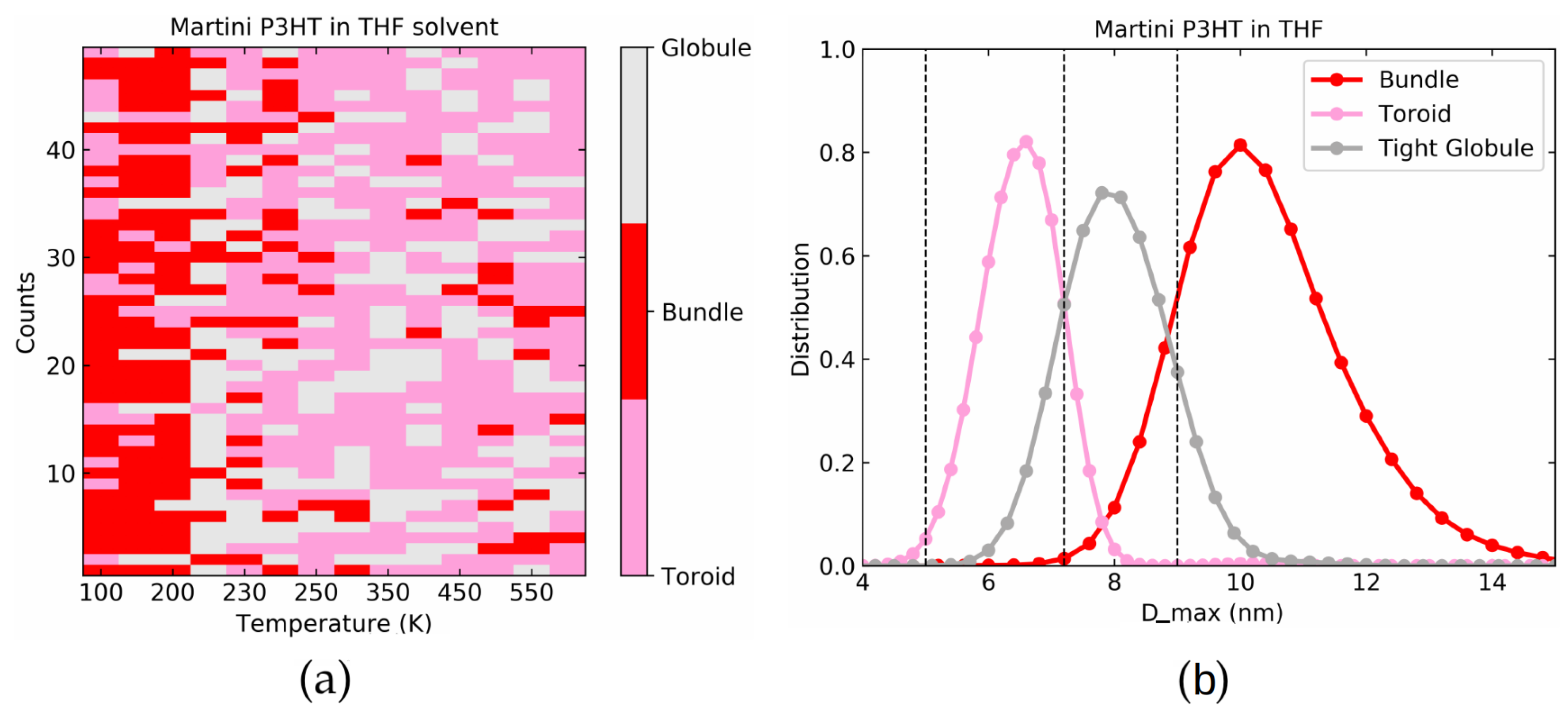
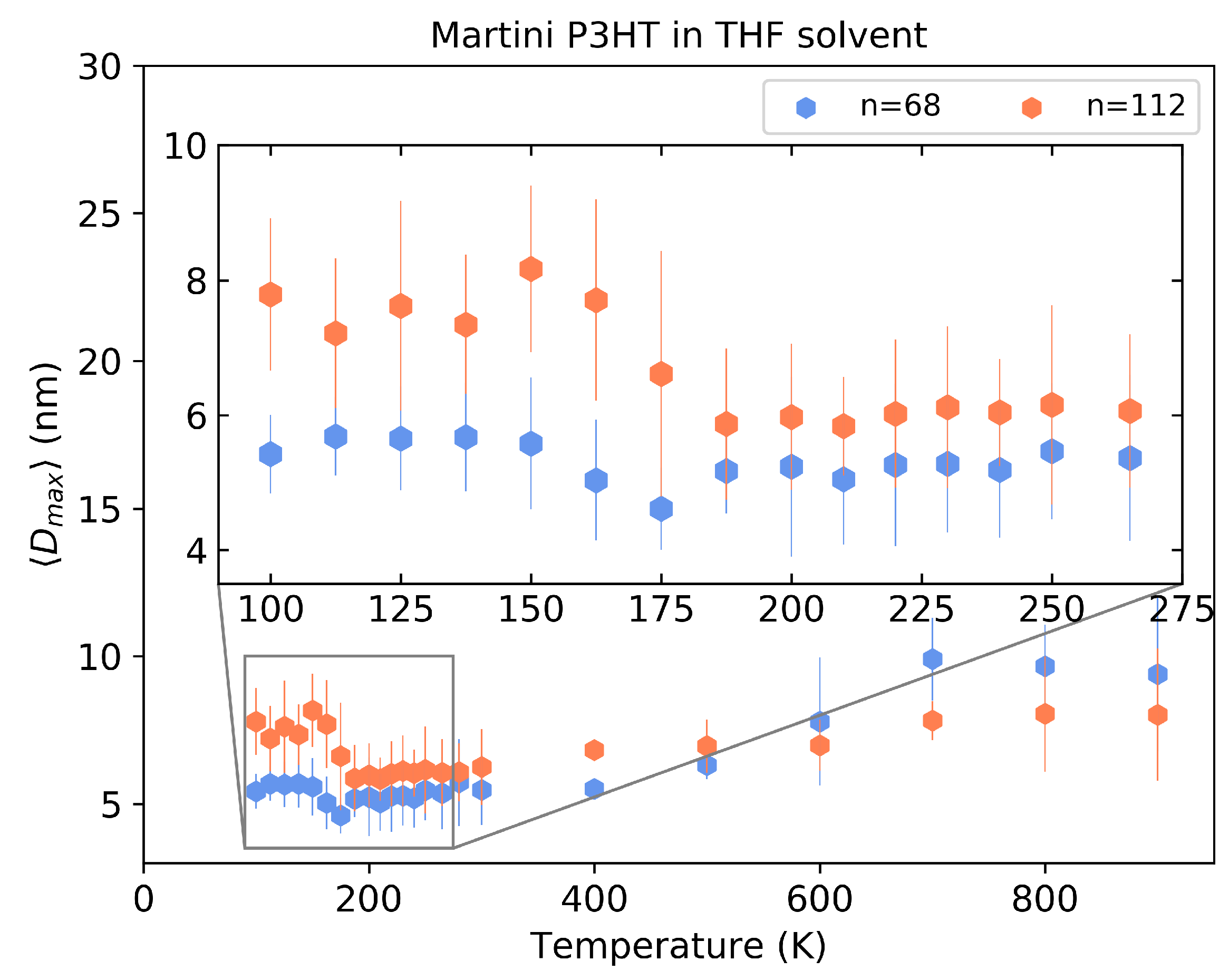
4.3. Martini P3HT in THF Solvent
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| P3HT | Poly(3-hexylthiopene) |
| THF | Tetrahydrofuran |
| MD | Molecular Dynamics |
| ATB | Automated Topology Builder and Repository |
References
- Poelking, C.; Andrienko, D. Effect of Polymorphism, Regioregularity and Paracrystallinity on Charge Transport in Poly(3-hexylthiophene) [P3HT] Nanofibers. Macromolecules 2013, 46, 8941–8956. [Google Scholar] [CrossRef]
- Bao, Z.; Dodabalapur, A.; Lovinger, A.J. Soluble and processable regioregular poly(3-hexylthiophene) for thin film field-effect transistor applications with high mobility. Appl. Phys. Lett. 1996, 69, 4108–4110. [Google Scholar] [CrossRef]
- Yang, H.; LeFevre, S.W.; Ryu, C.Y.; Bao, Z. Solubility-driven thin film structures of regioregular poly(3-hexyl thiophene) using volatile solvents. Appl. Phys. Lett. 2007, 90, 172116. [Google Scholar] [CrossRef]
- Goh, C.; Kline, R.J.; McGehee, M.D.; Kadnikova, E.N.; Fréchet, J.M.J. Molecular-weight-dependent mobilities in regioregular poly(3-hexyl-thiophene) diodes. Appl. Phys. Lett. 2005, 86, 122110. [Google Scholar] [CrossRef] [Green Version]
- Kuila, B.K.; Nandi, A.K. Structural Hierarchy in Melt-Processed Poly(3-hexyl thiophene)-Montmorillonite Clay Nanocomposites: Novel Physical, Mechanical, Optical, and Conductivity Properties. J. Phys. Chem. B 2006, 110, 1621–1631. [Google Scholar] [CrossRef]
- Heffner, G.W.; Pearson, D.S. Molecular characterization of poly(3-hexylthiophene). Macromolecules 1991, 24, 6295–6299. [Google Scholar] [CrossRef]
- McCulloch, B.; Ho, V.; Hoarfrost, M.; Stanley, C.; Do, C.; Heller, W.T.; Segalman, R.A. Polymer Chain Shape of Poly(3-alkylthiophenes) in Solution Using Small-Angle Neutron Scattering. Macromolecules 2013, 46, 1899–1907. [Google Scholar] [CrossRef]
- Nagai, M.; Huang, J.; Zhou, T.; Huang, W. Effect of molecular weight on conformational characteristics of poly(3-hexyl thiophene). J. Polym. Sci. Part B Polym. Phys. 2017, 55, 1273–1277. [Google Scholar] [CrossRef]
- Adachi, T.; Brazard, J.; Ono, R.J.; Hanson, B.; Traub, M.C.; Wu, Z.Q.; Li, Z.; Bolinger, J.C.; Ganesan, V.; Bielawski, C.W.; et al. Regioregularity and Single Polythiophene Chain Conformation. J. Phys. Chem. Lett. 2011, 2, 1400–1404. [Google Scholar] [CrossRef]
- Chen, P.Y.; Rassamesard, A.; Chen, H.L.; Macromolecules, S.C. Conformation and fluorescence property of poly (3-hexylthiophene) isolated chains studied by single molecule spectroscopy: Effects of solvent quality and Regioregularity. ACS Publ. 2013, 46, 5657–5663. [Google Scholar] [CrossRef]
- Raithel, D.; Baderschneider, S.; Queiroz, T.B.d.; Lohwasser, R.; Köhler, J.; Thelakkat, M.; Kümmel, S.; Hildner, R. Emitting Species of Poly(3-hexylthiophene): From Single, Isolated Chains to Bulk. Macromolecules 2016, 49, 9553–9560. [Google Scholar] [CrossRef]
- Schwarz, K.N.; Kee, T.W.; Huang, D.M. Coarse-grained simulations of the solution-phase self-assembly of poly(3-hexylthiophene) nanostructures. Nanoscale 2013, 5, 2017–2027. [Google Scholar] [CrossRef]
- Tapping, P.C.; Clafton, S.N.; Schwarz, K.N.; Kee, T.W.; Huang, D.M. Molecular-Level Details of Morphology-Dependent Exciton Migration in Poly(3-hexylthiophene) Nanostructures. J. Phys. Chem. C 2015, 119, 7047–7059. [Google Scholar] [CrossRef]
- Panzer, F.; Baessler, H.; Lohwasser, R.; Thelakkat, M.; Keohler, A. The impact of polydispersity and molecular weight on the order disorder transition in poly (3-hexylthiophene). J. Phys. Chem. Lett. 2014, 5, 2742–2747. [Google Scholar] [CrossRef]
- Panzer, F.; Baessler, H.; Koehler, A. Temperature induced order–disorder transition in solutions of conjugated polymers probed by optical spectroscopy. J. Phys. Chem. Lett. 2017, 8, 114–125. [Google Scholar] [CrossRef]
- Kolinski, A.; Skolnick, J.; Yaris, R. The collapse transition of semiflexible polymers. A Monte Carlo simulation of a model system. J. Chem. Phys. 1986, 85, 3585. [Google Scholar] [CrossRef]
- Noguchi, H.; Yoshikawa, K. Morphological variation in a collapsed single homopolymer chain. J. Chem. Phys. 1998, 109, 5070–5077. [Google Scholar] [CrossRef]
- Zierenberg, J.; Marenz, M.; Janke, W. Dilute Semiflexible Polymers with Attraction: Collapse, Folding and Aggregation. Polymers 2016, 8, 333. [Google Scholar] [CrossRef] [Green Version]
- Seaton, D.T.; Schnabel, S.; Landau, D.P.; Bachmann, M. From Flexible to Stiff: Systematic Analysis of Structural Phases for Single Semiflexible Polymers. Phys. Rev. Lett. 2013, 110, 028103. [Google Scholar] [CrossRef] [Green Version]
- Bhatta, R.S.; Yimer, Y.Y.; Perry, D.S.; Tsige, M. Improved Force Field for Molecular Modeling of Poly(3-hexylthiophene). J. Phys. Chem. B 2013, 117, 10035–10045. [Google Scholar] [CrossRef]
- Alessandri, R.; Uusitalo, J.J.; Vries, A.H.d.; Havenith, R.W.A.; Marrink, S.J. Bulk Heterojunction Morphologies with Atomistic Resolution from Coarse-Grain Solvent Evaporation Simulations. J. Am. Chem. Soc. 2017, 139, 3697–3705. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Borzdun, N.I.; Larin, S.V.; Falkovich, S.G.; Nazarychev, V.M.; Volgin, I.V.; Yakimansky, A.V.; Lyulin, A.V.; Negi, V.; Bobbert, P.A.; Lyulin, S.V. Molecular dynamics simulation of poly (3-hexylthiophene) helical structure In Vacuo and in amorphous polymer surrounding. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 2448–2456. [Google Scholar] [CrossRef] [Green Version]
- Wolf, C.M.; Kanekal, K.H.; Yimer, Y.Y.; Tyagi, M.; Omar-Diallo, S.; Pakhnyuk, V.; Luscombe, C.K.; Pfaendtner, J.; Pozzo, L.D. Assessment of molecular dynamics simulations for amorphous poly(3-hexylthiophene) using neutron and X-ray scattering experiments. Soft Matter 2019, 15, 5067–5083. [Google Scholar] [CrossRef]
- Tsourtou, F.D.; Peristeras, L.D.; Apostolov, R.; Mavrantzas, V.G. Molecular Dynamics Simulation of Amorphous Poly(3-hexylthiophene). Macromolecules 2020, 53, 7810–7824. [Google Scholar] [CrossRef]
- Lee, C.K.; Pao, C.W. Nanomorphology Evolution of P3HT/PCBM Blends during Solution-Processing from Coarse-Grained Molecular Simulations. J. Phys. Chem. C 2014, 118, 11224–11233. [Google Scholar] [CrossRef]
- Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef] [Green Version]
- Campos-Villalobos, G.; Siperstein, F.R.; Patti, A. Transferable coarse-grained MARTINI model for methacrylate-based copolymers. Mol. Syst. Des. Eng. 2019, 4, 186–198. [Google Scholar] [CrossRef] [Green Version]
- Flory, P.J. The Configuration of Real Polymer Chains. J. Chem. Phys. 1949, 17, 303–310. [Google Scholar] [CrossRef]
- Ivanov, V.; Stukan, M.; Vasilevskaya, V.; Paul, W.; Binder, K. Structures of stiff macromolecules of finite chain length near the coil-globule transition: A Monte Carlo simulation. Macromol. Theory Simulations 2000, 9, 488–499. [Google Scholar] [CrossRef]
- Marenz, M.; Janke, W. Knots as a Topological Order Parameter for Semiflexible Polymers. Phys. Rev. Lett. 2016, 116, 128301–128306. [Google Scholar] [CrossRef] [Green Version]
- Hu, D.; Yu, J.; Wong, K.; Bagchi, B.; Rossky, P.J.; Barbara, P.F. Collapse of stiff conjugated polymers with chemical defects into ordered, cylindrical conformations. Nature 2000, 405, 1030–1033. [Google Scholar] [CrossRef]
- Rodrigues, A.; Castro, M.C.R.; Farinha, A.S.; Oliveira, M.; Tomé, J.P.; Machado, A.V.; Raposo, M.M.M.; Hilliou, L.; Bernardo, G. Thermal stability of P3HT and P3HT: PCBM blends in the molten state. Polym. Test. 2013, 32, 1192–1201. [Google Scholar] [CrossRef]
- Bernardi, M.; Giulianini, M.; Grossman, J.C. Self-assembly and its impact on interfacial charge transfer in carbon nanotube/P3HT solar cells. ACS Nano 2010, 4, 6599–6606. [Google Scholar] [CrossRef] [Green Version]
- Vukmirovic, N.; Wang, L.W. Electronic structure of disordered conjugated polymers: Polythiophenes. J. Phys. Chem. B 2009, 113, 409–415. [Google Scholar] [CrossRef] [Green Version]
- Panzer, F.; Sommer, M.; Baessler, H.; Thelakkat, M.; Koehler, A. Spectroscopic signature of two distinct H-aggregate species in poly (3-hexylthiophene). Macromolecules 2015, 48, 1543–1553. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pantawane, S.; Gekle, S. Temperature-Dependent Conformation Behavior of Isolated Poly(3-hexylthiopene) Chains. Polymers 2022, 14, 550. https://doi.org/10.3390/polym14030550
Pantawane S, Gekle S. Temperature-Dependent Conformation Behavior of Isolated Poly(3-hexylthiopene) Chains. Polymers. 2022; 14(3):550. https://doi.org/10.3390/polym14030550
Chicago/Turabian StylePantawane, Sanwardhini, and Stephan Gekle. 2022. "Temperature-Dependent Conformation Behavior of Isolated Poly(3-hexylthiopene) Chains" Polymers 14, no. 3: 550. https://doi.org/10.3390/polym14030550
APA StylePantawane, S., & Gekle, S. (2022). Temperature-Dependent Conformation Behavior of Isolated Poly(3-hexylthiopene) Chains. Polymers, 14(3), 550. https://doi.org/10.3390/polym14030550






