Coarse Grained Modeling of Multiphase Flows with Surfactants
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dissipative Particle Dynamics
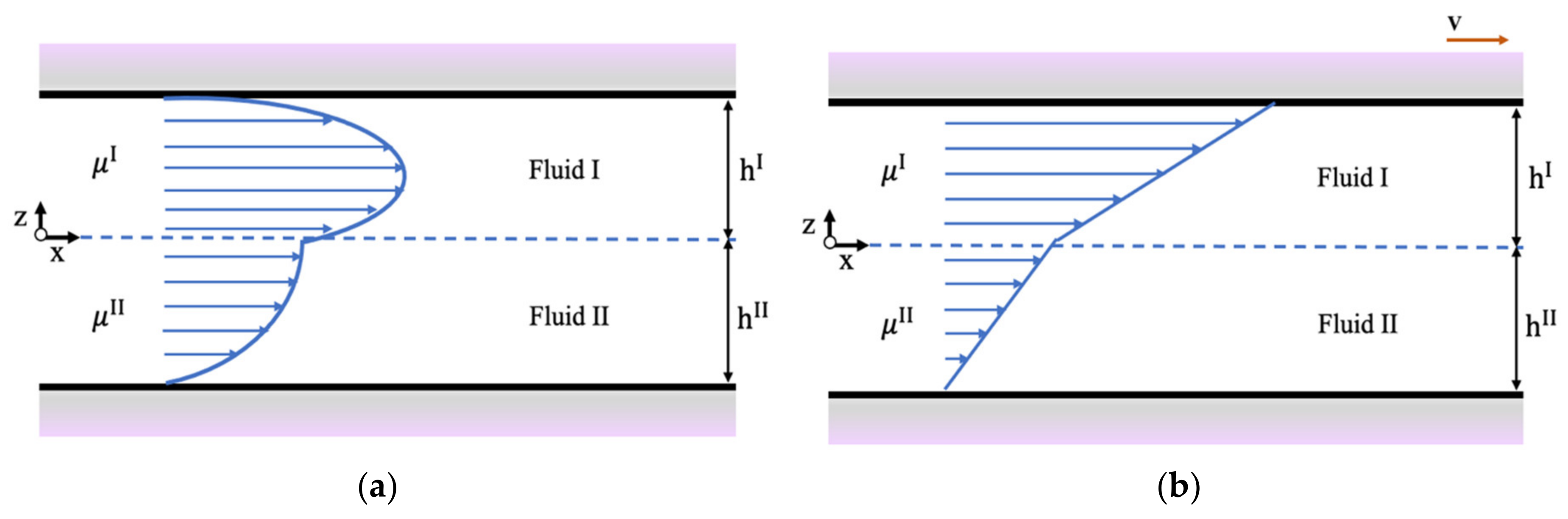
2.2. Velocity Distribution of Two Immiscible Liquids in Nanoslits
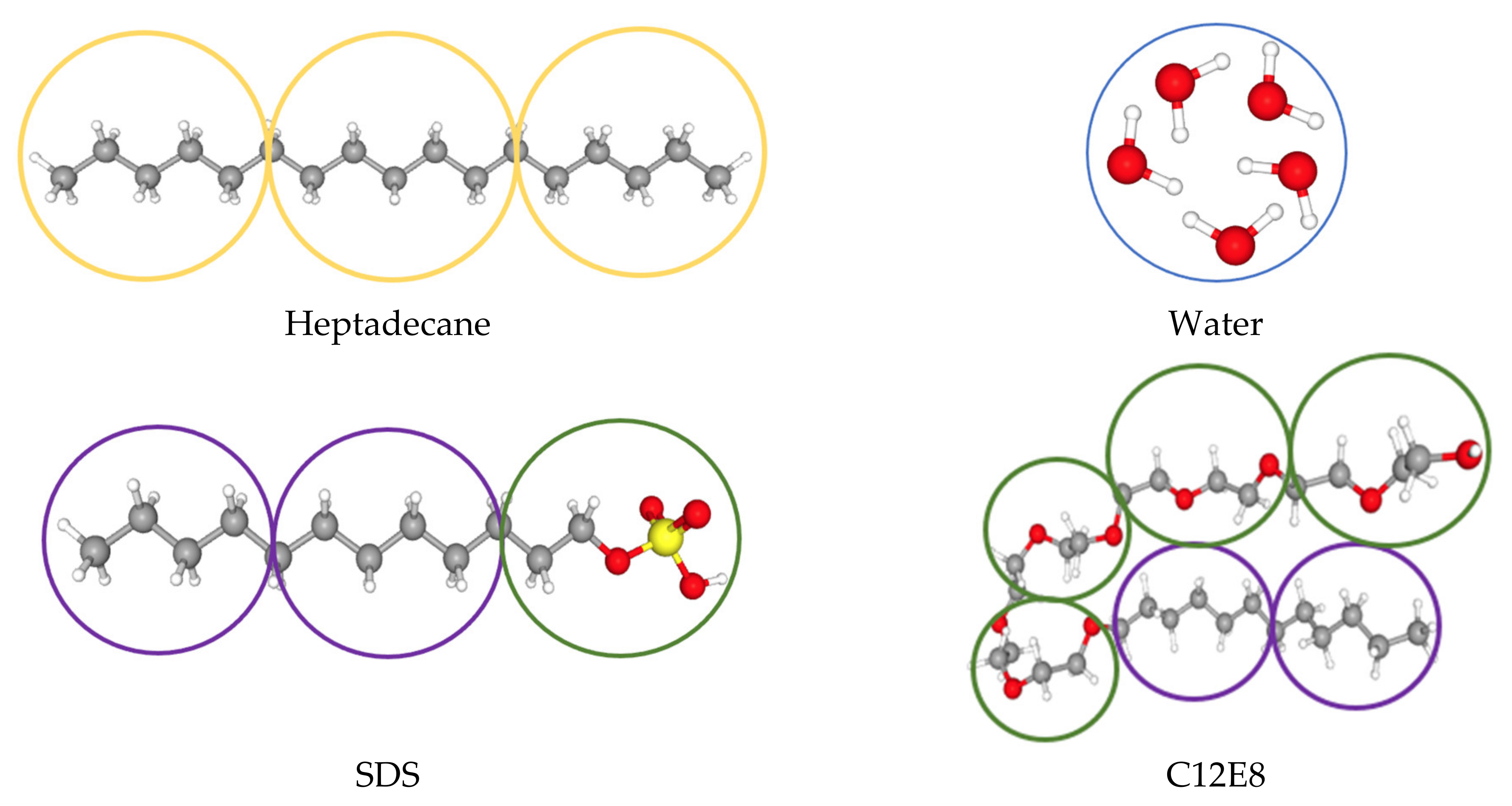
2.3. Details of the Computational Model
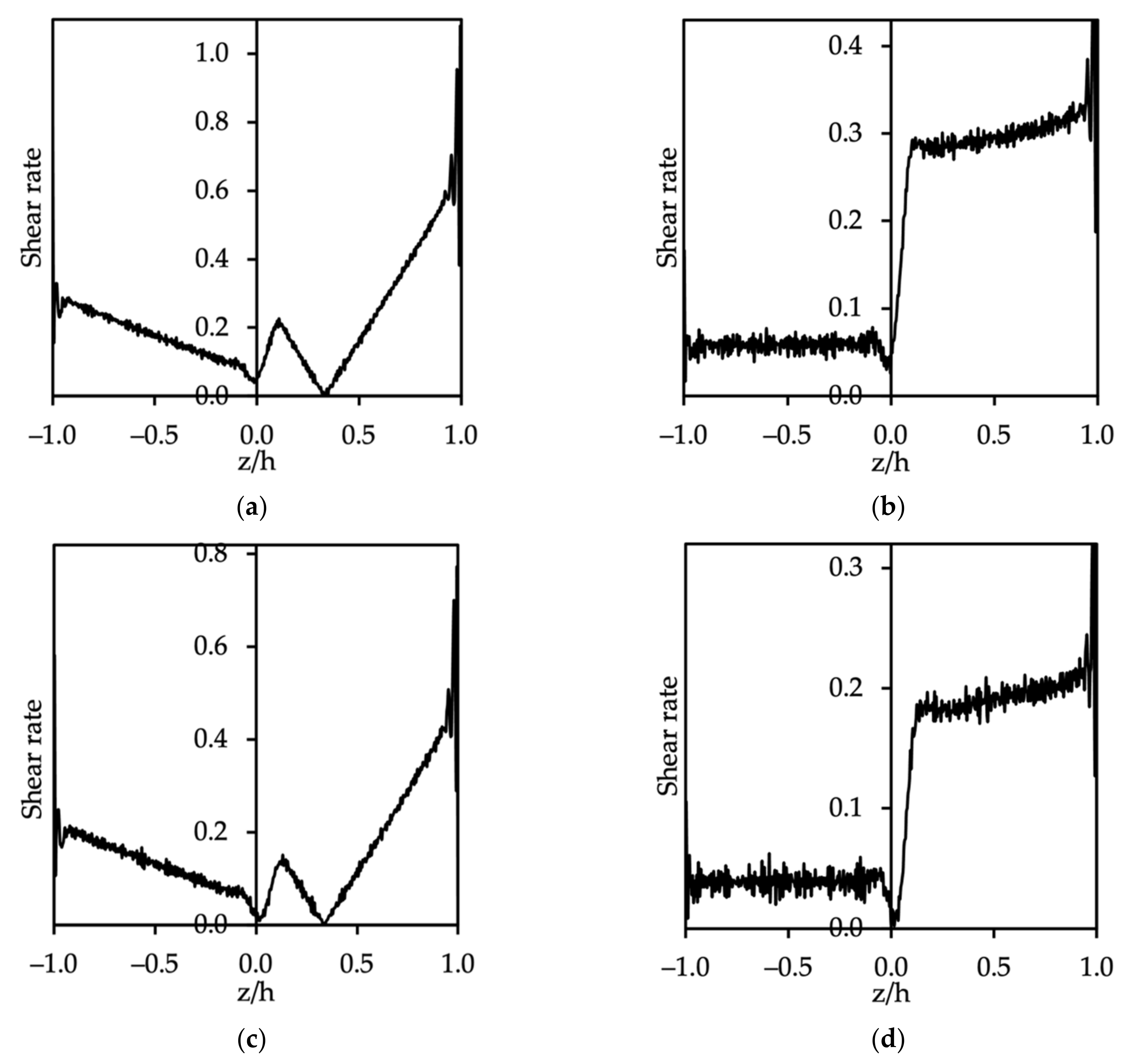
3. Results
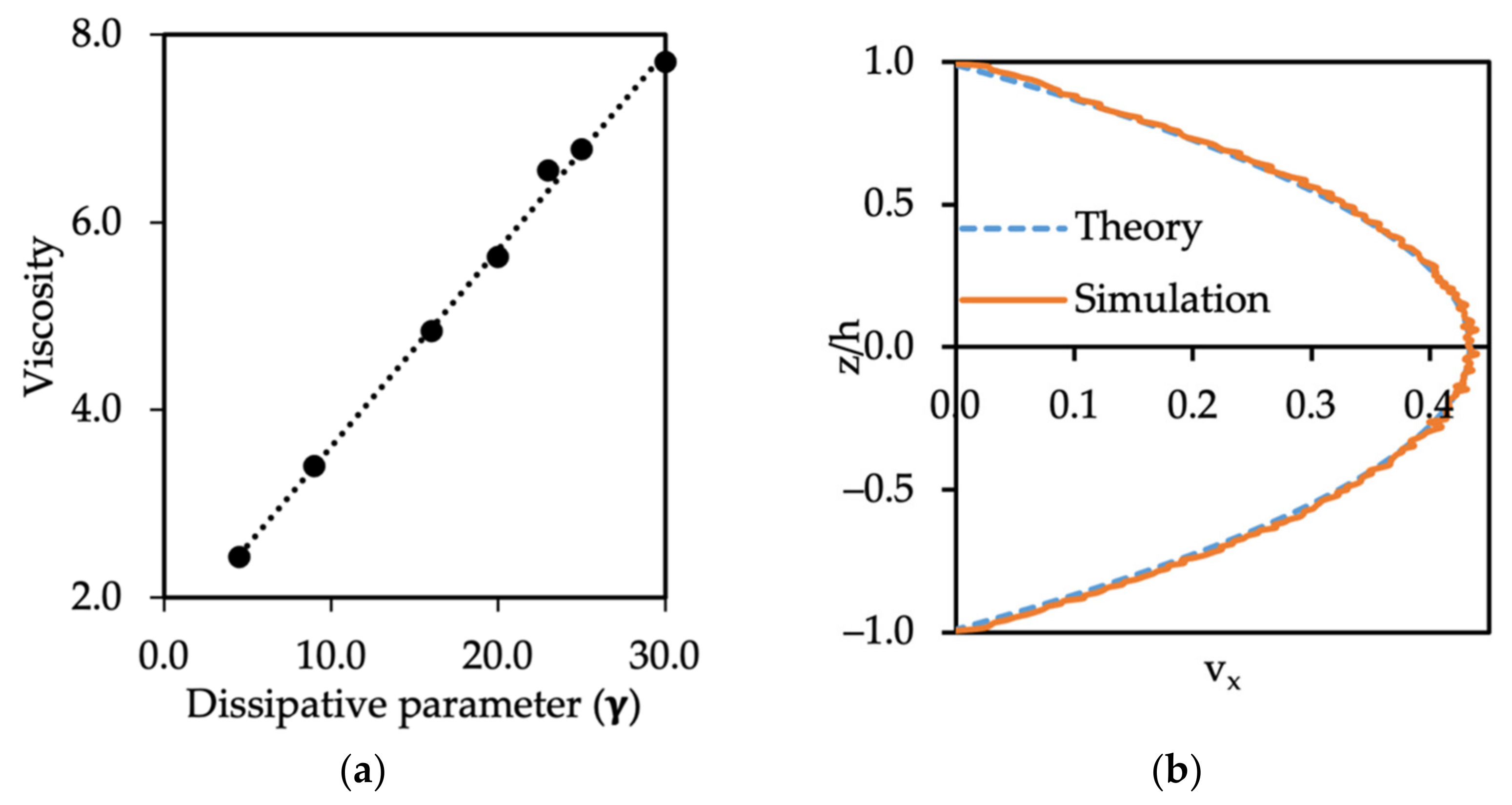
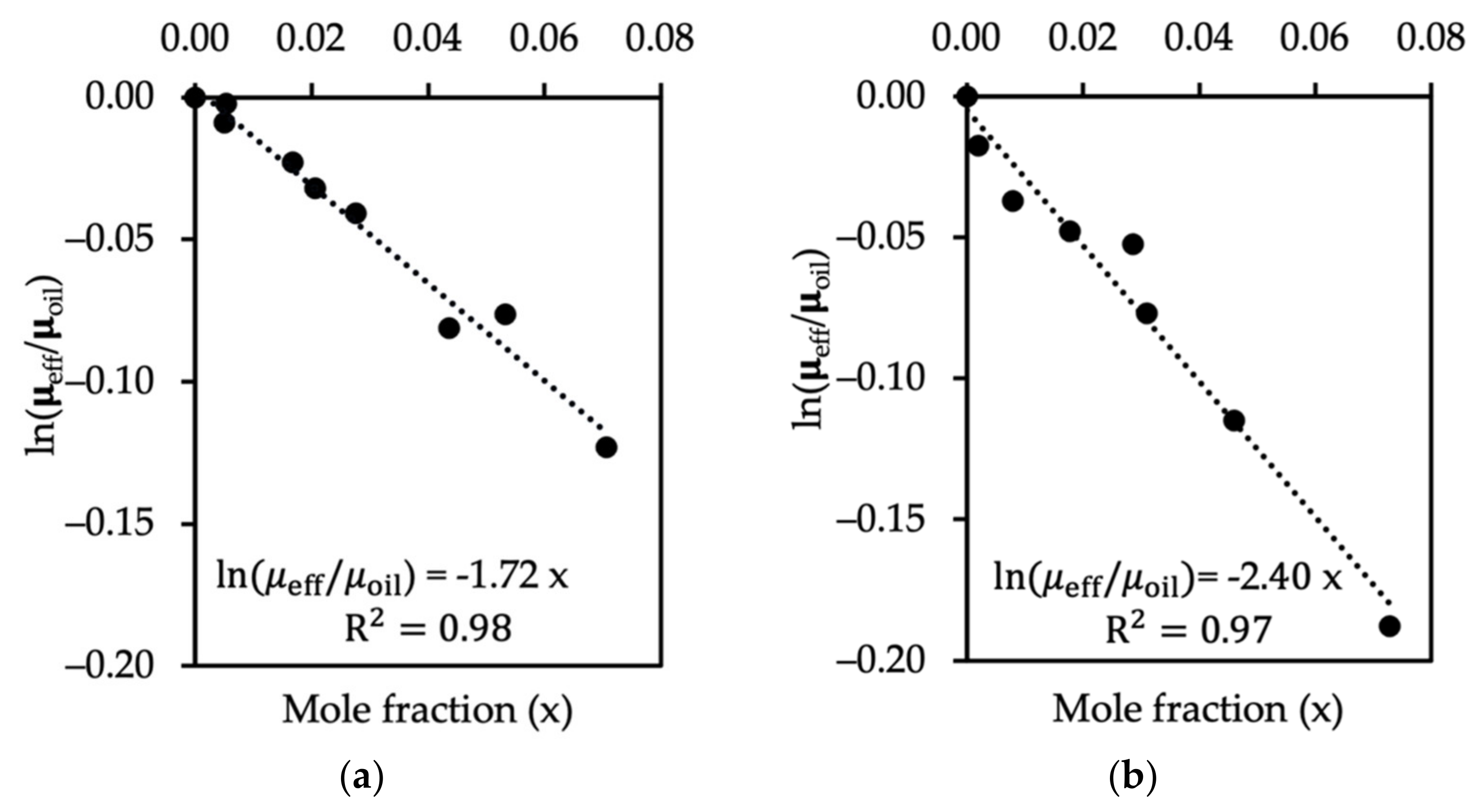
3.1. Single Phase Flow, No-Slip Boundary Conditions, and Determination of Fluid Viscosity
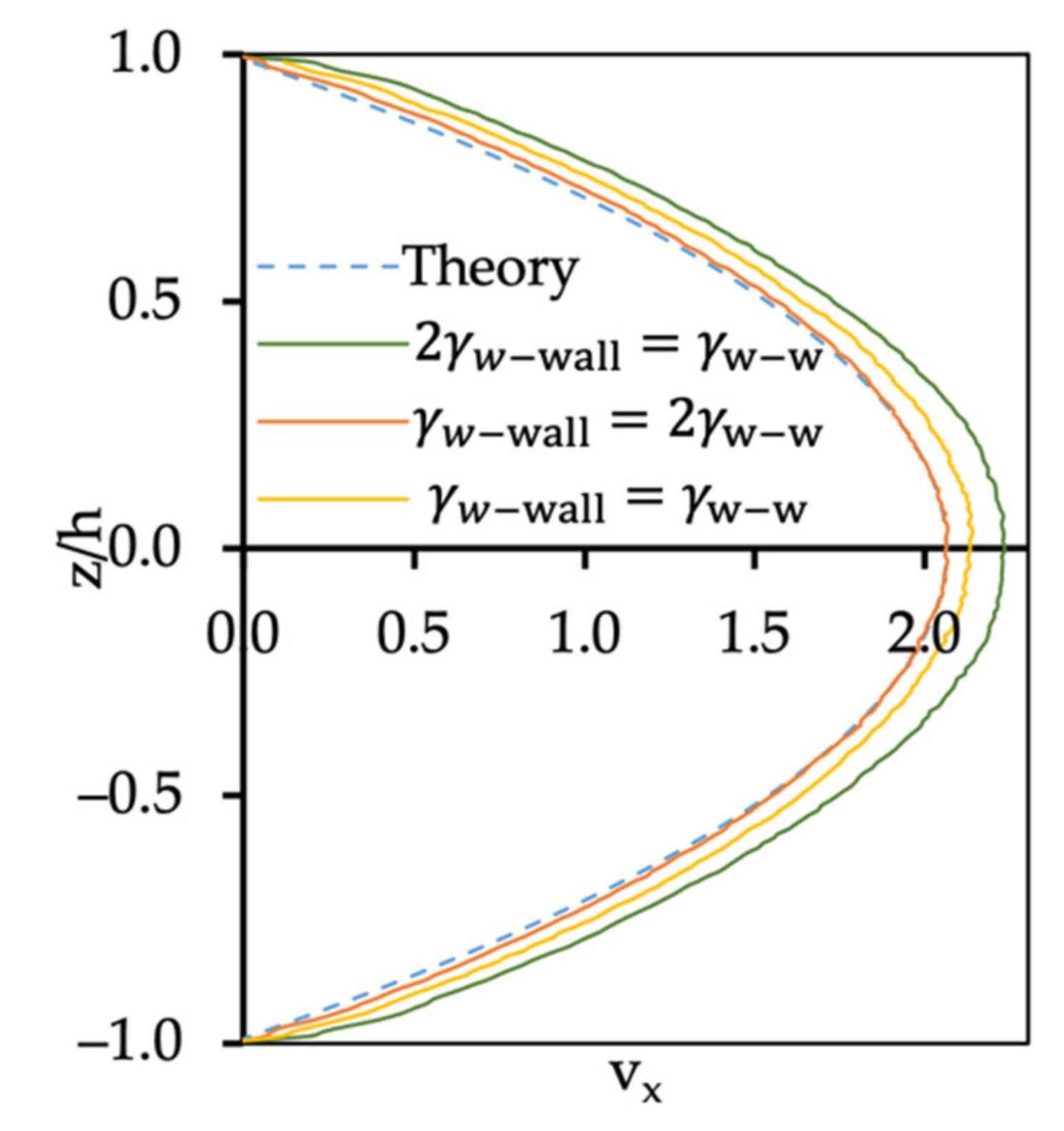
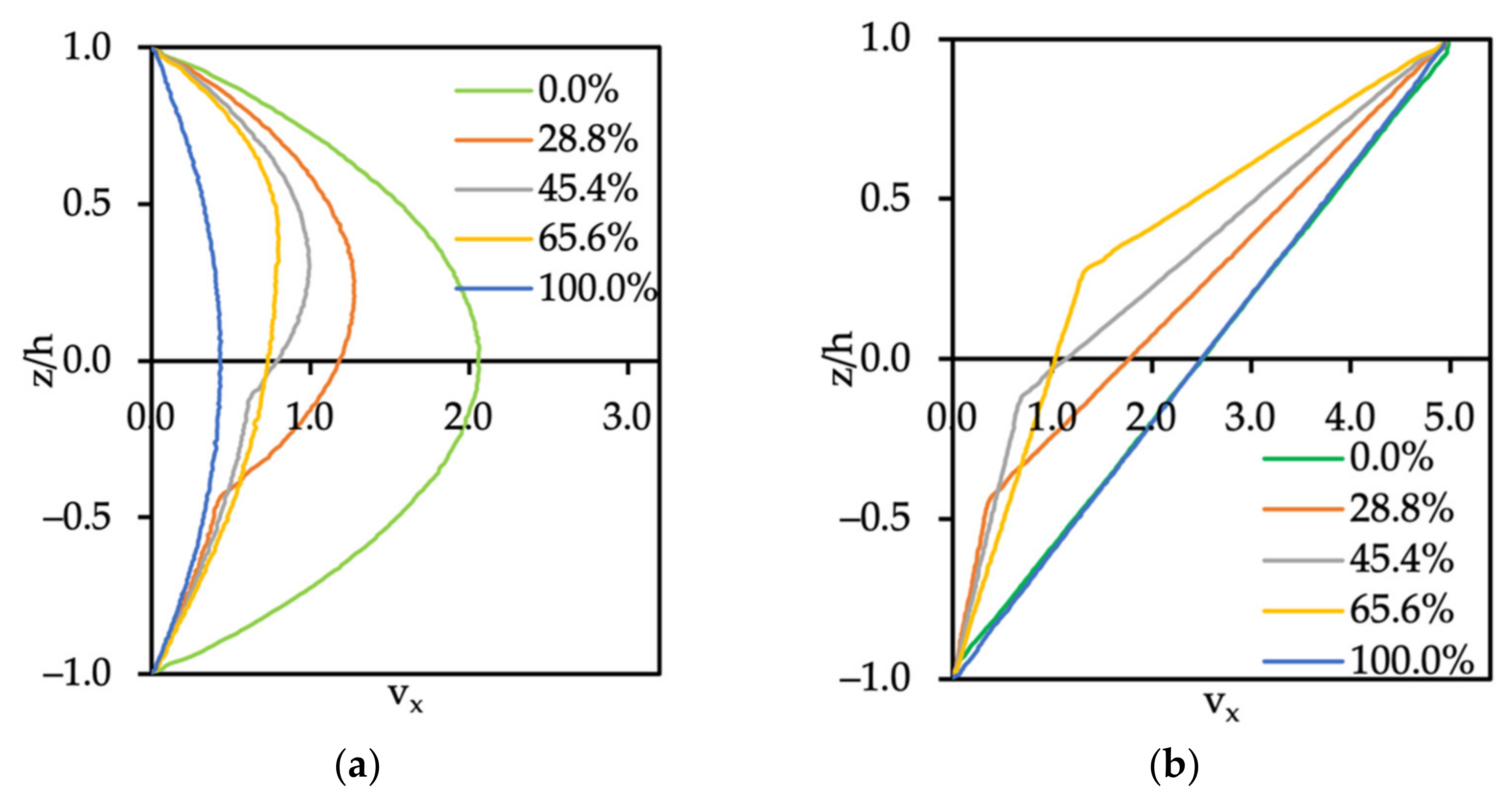
3.2. Flow of Two Immiscible Fluids
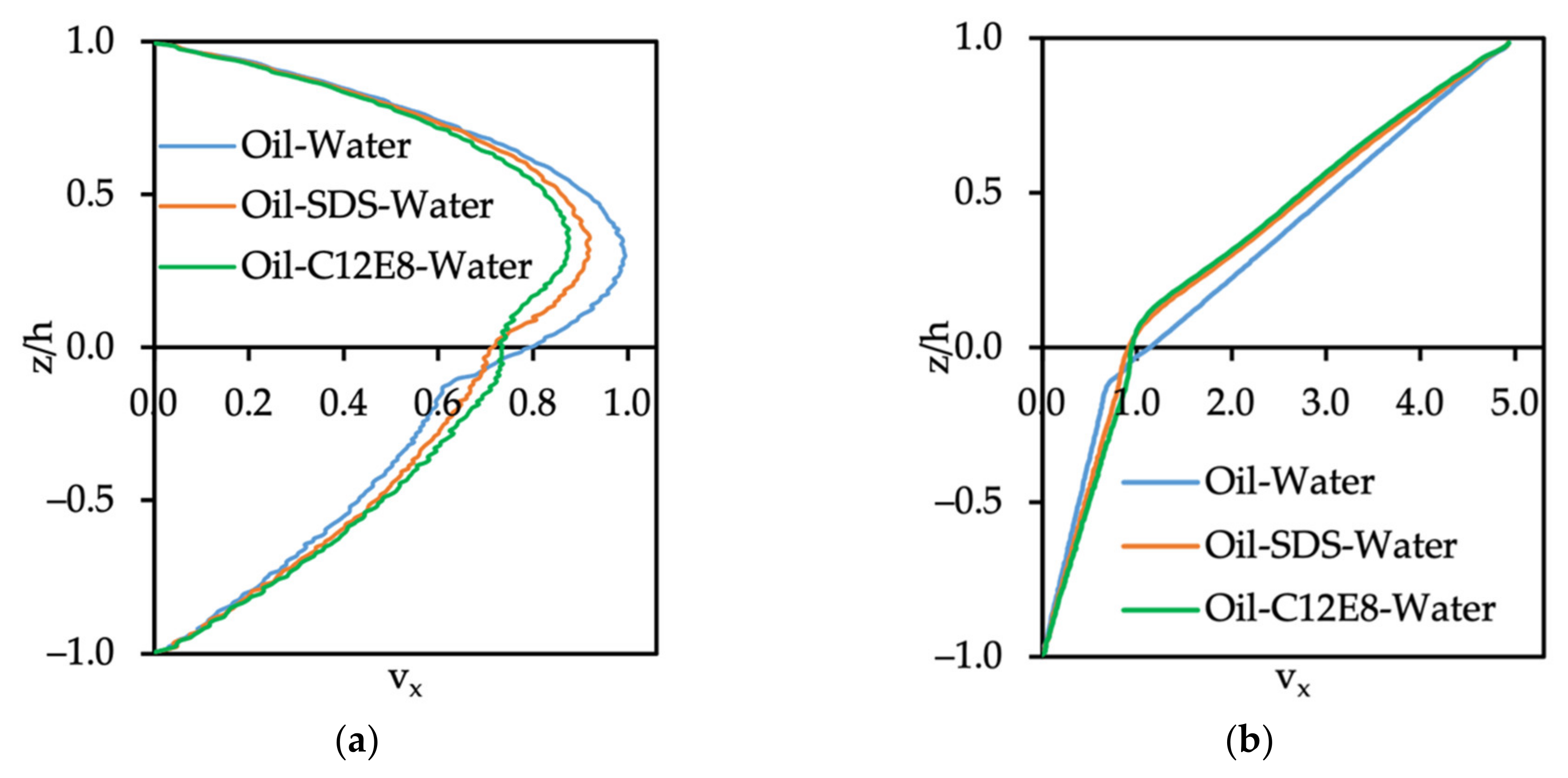
3.3. Dynamic Oil–Water System with Surfactants
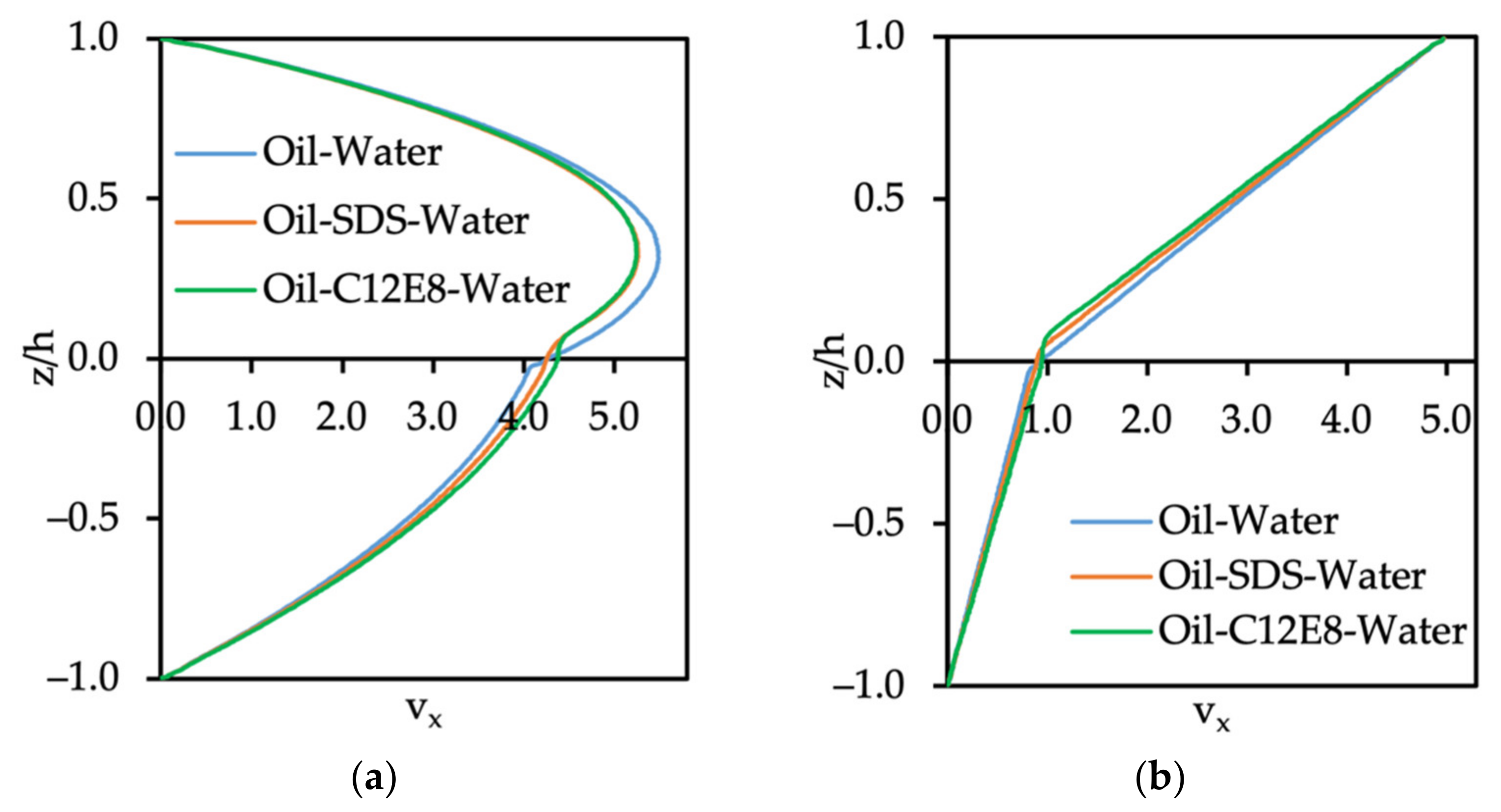
3.3.1. Velocity Profile of Oil–Water System with Surfactants
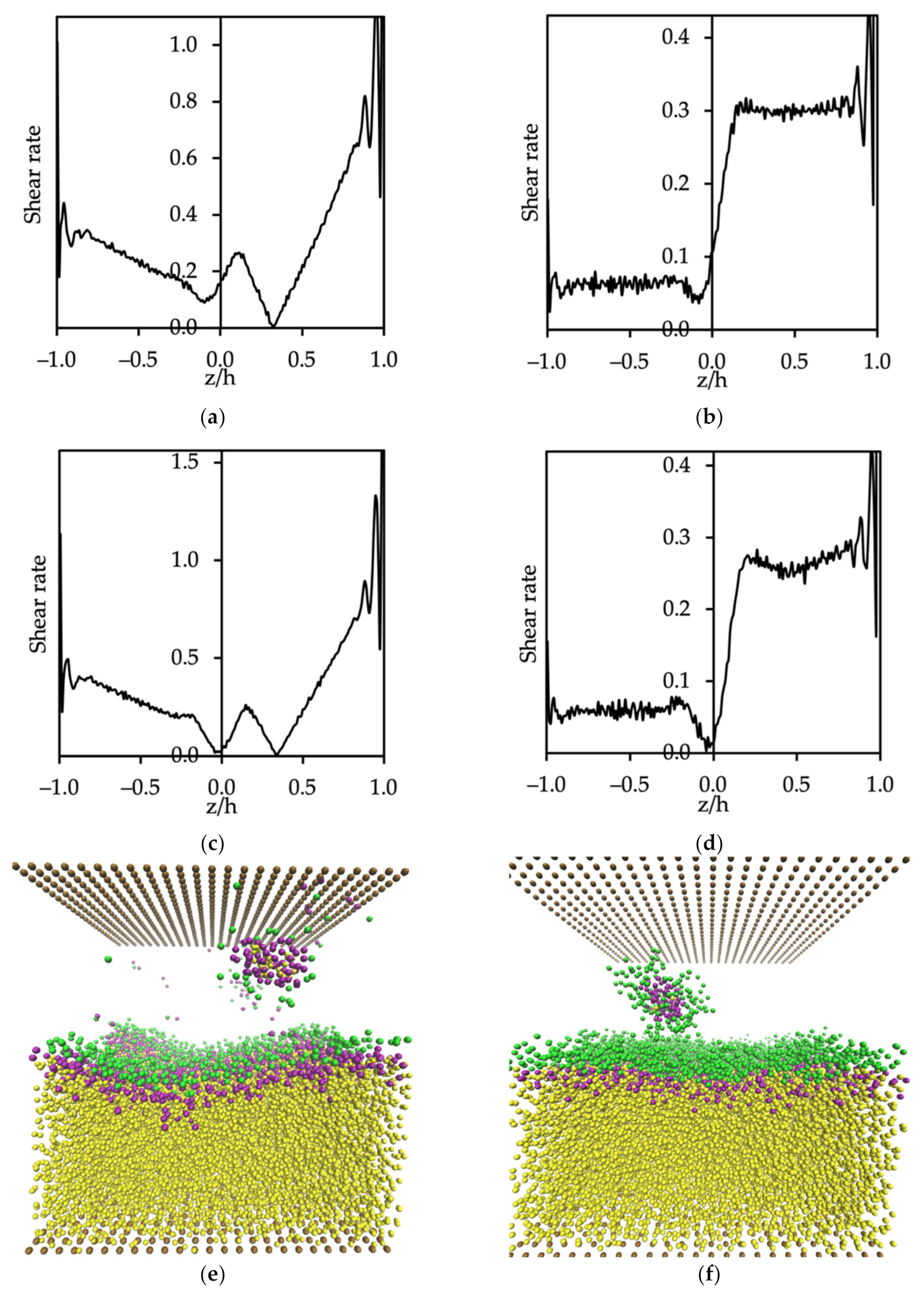
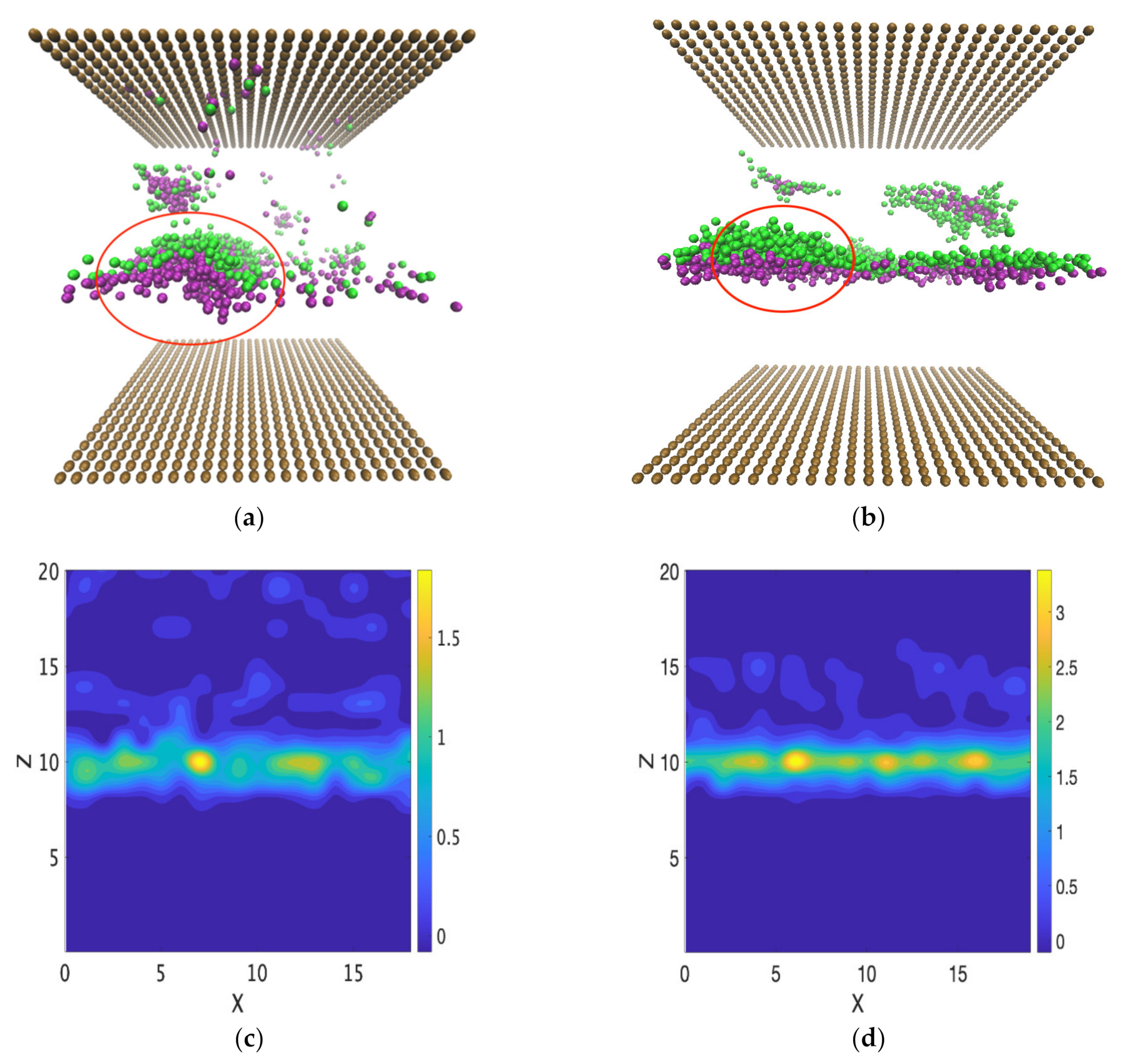
3.3.2. Micelle Formation
3.3.3. The Effect of Computational Box Size
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soares, E.J.; Thompson, R.L. Flow regimes for the immiscible liquid–liquid displacement in capillary tubes with complete wetting of the displaced liquid. J. Fluid Mech. 2009, 641, 63–84. [Google Scholar] [CrossRef]
- Zhao, H.; Ning, Z.; Kang, Q.; Chen, L.; Zhao, T. Relative permeability of two immiscible fluids flowing through porous media determined by lattice Boltzmann method. Int. Commun. Heat Mass Transf. 2017, 85, 53–61. [Google Scholar] [CrossRef]
- Li, J.; Sheeran, P.S.; Kleinstreuer, C. Analysis of multi-layer immiscible fluid flow in a microchannel. J. Fluids Eng. 2011, 133, 111202. [Google Scholar] [CrossRef]
- Gaddam, A.; Garg, M.; Agrawal, A.; Joshi, S.S. Modeling of liquid–gas meniscus for textured surfaces: Effects of curvature and local slip length. J. Micromech. Microeng. 2015, 25, 125002. [Google Scholar] [CrossRef]
- Tang, X.; Xiao, S.; Lei, Q.; Yuan, L.; Peng, B.; He, L.; Luo, J.; Pei, Y. Molecular dynamics simulation of surfactant flooding driven oil-detachment in nano-silica channels. J. Phys. Chem. B 2018, 123, 277–288. [Google Scholar] [CrossRef]
- Fan, J.C.; Wang, F.C.; Chen, J.; Zhu, Y.B.; Lu, D.T.; Liu, H.; Wu, H.A. Molecular mechanism of viscoelastic polymer enhanced oil recovery in nanopores. R. Soc. Open Sci. 2018, 5, 180076. [Google Scholar] [CrossRef] [Green Version]
- Karaborni, S.; Van Os, N.; Esselink, K.; Hilbers, P.A.J. Molecular dynamics simulations of oil solubilization in surfactant solutions. Langmuir 1993, 9, 1175–1178. [Google Scholar] [CrossRef]
- Smit, B.; Schlijper, A.; Rupert, L.; Van Os, N. Effects of chain length of surfactants on the interfacial tension: Molecular dynamics simulations and experiments. J. Phys. Chem. 1990, 94, 6933–6935. [Google Scholar] [CrossRef] [Green Version]
- Karniadakis, G.; Beskok, A.; Aluru, N. Microflows and Nanoflows: Fundamentals and Simulation; Springer Science & Business Media: Berlin, Germany, 2006; Volume 29. [Google Scholar]
- Rezaei, H.; Modarress, H. Dissipative particle dynamics (DPD) study of hydrocarbon–water interfacial tension (IFT). Chem. Phys. Lett. 2015, 620, 114–122. [Google Scholar] [CrossRef]
- Pivkin, I.V.; Karniadakis, G.E. A new method to impose no-slip boundary conditions in dissipative particle dynamics. J. Comput. Phys. 2005, 207, 114–128. [Google Scholar] [CrossRef]
- Xu, Z.; Meakin, P. A phase-field approach to no-slip boundary conditions in dissipative particle dynamics and other particle models for fluid flow in geometrically complex confined systems. J. Chem. Phys. 2009, 130, 234103. [Google Scholar] [CrossRef] [PubMed]
- Soares, J.S.; Gao, C.; Alemu, Y.; Slepian, M.; Bluestein, D. Simulation of platelets suspension flowing through a stenosis model using a dissipative particle dynamics approach. Ann. Biomed. Eng. 2013, 41, 2318–2333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Backer, J.; Lowe, C.; Hoefsloot, H.; Iedema, P. Poiseuille flow to measure the viscosity of particle model fluids. J. Chem. Phys. 2005, 122, 154503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belhaj, A.F.; Elraies, K.A.; Mahmood, S.M.; Zulkifli, N.N.; Akbari, S.; Hussien, O.S. The effect of surfactant concentration, salinity, temperature, and pH on surfactant adsorption for chemical enhanced oil recovery: A review. J. Pet. Explor. Prod. Technol. 2020, 10, 125–137. [Google Scholar] [CrossRef] [Green Version]
- Vu, T.V.; Papavassiliou, D.V. Oil-water interfaces with surfactants: A systematic approach to determine coarse-grained model parameters. J. Chem. Phys. 2018, 148, 204704. [Google Scholar] [CrossRef] [PubMed]
- Vu, T.V.; Razavi, S.; Papavassiliou, D.V. Effect of Janus particles and non-ionic surfactants on the collapse of the oil-water interface under compression. J. Colloid Interface Sci. 2022, 609, 158–169. [Google Scholar] [CrossRef] [PubMed]
- Green, D.W.; Willhite, G.P.; Henry, L. Enhanced Oil Recovery; Henry L. Doherty Memorial Fund of AIME; Society of Petroleum Engineer: Richardson, TX, USA, 1998; Volume 6. [Google Scholar]
- Shah, D.O. Improved Oil Recovery by Surfactant and Polymer Flooding; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hoogerbrugge, P.; Koelman, J. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. EPL (Europhys. Lett.) 1992, 19, 155. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Espanol, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. EPL (Europhys. Lett.) 1995, 30, 191. [Google Scholar] [CrossRef] [Green Version]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: New York, NY, USA, 2006; Volume 1. [Google Scholar]
- Plimpton, S. Computational limits of classical molecular dynamics simulations. Comput. Mater. Sci. 1995, 4, 361–364. [Google Scholar] [CrossRef]
- Groot, R.D.; Rabone, K. Mesoscopic simulation of cell membrane damage, morphology change and rupture by nonionic surfactants. Biophys. J. 2001, 81, 725–736. [Google Scholar] [CrossRef] [Green Version]
- Vu, T.V.; Papavassiliou, D.V. Modification of Oil–Water Interfaces by Surfactant-Stabilized Carbon Nanotubes. J. Phys. Chem. C 2018, 122, 27734–27744. [Google Scholar] [CrossRef]
- Vo, M.; Papavassiliou, D.V. Interaction parameters between carbon nanotubes and water in Dissipative Particle Dynamics. Mol. Simul. 2016, 42, 737–744. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Doolittle, A.K. Studies in Newtonian flow. II. The dependence of the viscosity of liquids on free-space. J. Appl. Phys. 1951, 22, 1471–1475. [Google Scholar] [CrossRef]
- Pan, D.; Phan-Thien, N.; Khoo, B.C. Dissipative particle dynamics simulation of droplet suspension in shear flow at low Capillary number. J. Non-Newton Fluid 2014, 212, 63–72. [Google Scholar] [CrossRef]
- Mondello, M.; Grest, G.S. Viscosity calculations of n-alkanes by equilibrium molecular dynamics. J. Chem. Phys. 1997, 106, 9327–9336. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon: Oxford, UK, 1986. [Google Scholar]
- Nissan, A.; Grunberg, L. Mixture law for viscosity. Nature 1949, 164, 799. [Google Scholar]
- Charru, F.; Fabre, J. Long waves at the interface between two viscous fluids. Phys. Fluids 1994, 6, 1223–1235. [Google Scholar] [CrossRef]
- Prhashanna, A.; Khan, S.A.; Chen, S.B. Micelle morphology and chain conformation of triblock copolymers under shear: LA-DPD study. Colloids Surf. A Physicochem. Eng. Asp. 2016, 506, 457–466. [Google Scholar] [CrossRef]
- Yaghoubi, S.; Shirani, E.; Pishevar, A.; Afshar, Y. New modified weight function for the dissipative force in the DPD method to increase the Schmidt number. EPL (Europhys. Lett.) 2015, 110, 24002. [Google Scholar] [CrossRef]
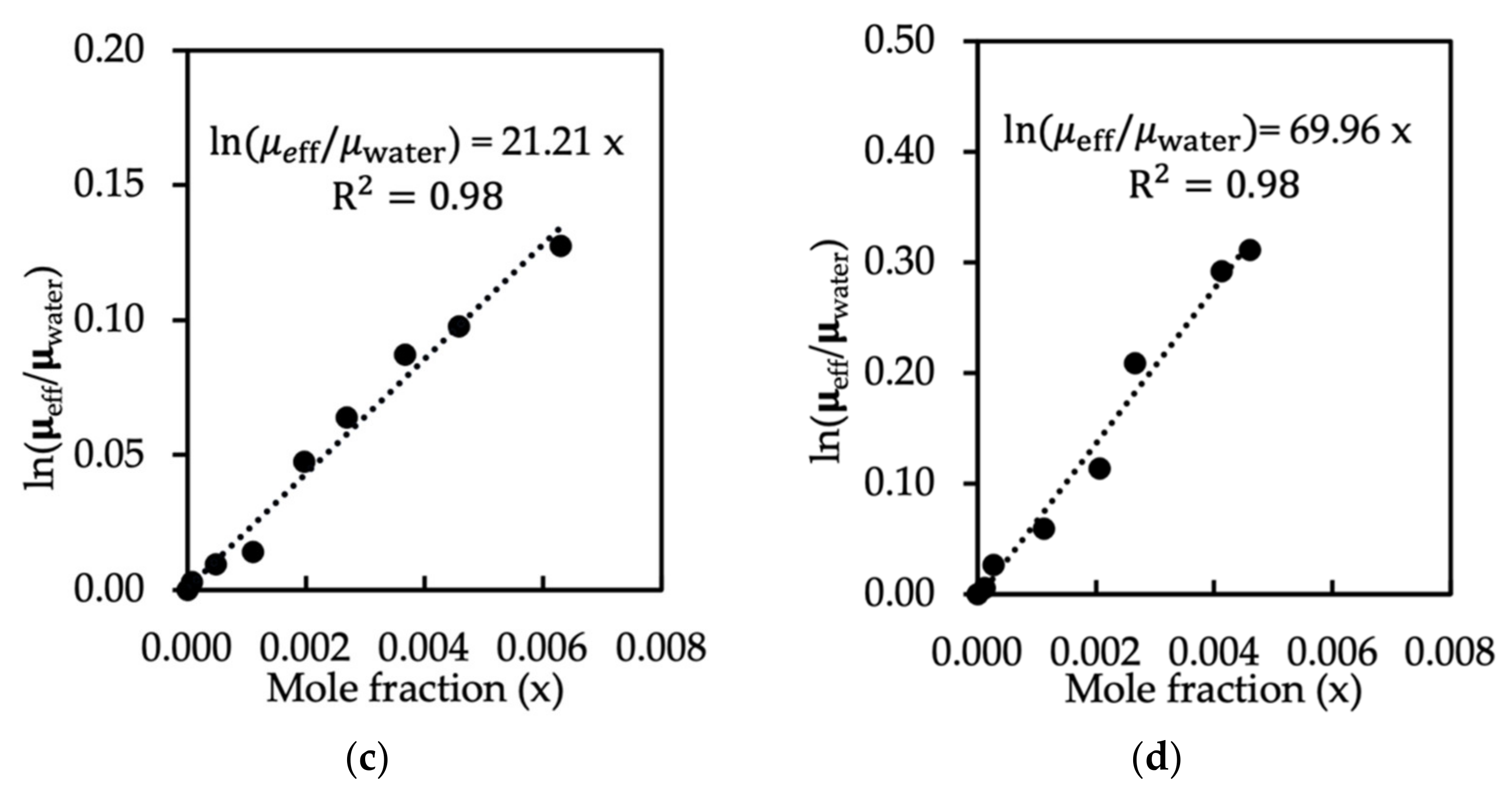
| Type of Surfactant | Density | Number of Water Molecules in One Bead | Mass Scale | Length Scale | Temperature Scale (K) | Time Scale |
|---|---|---|---|---|---|---|
| SDS | 5 | 5 | 1.5 | 9.09 | 298 | 5.48 |
| C12E8 | 5 | 6 | 1.8 | 9.66 | 298 | 6.38 |
| None | 5 | 5 | 1.5 | 9.09 | 298 | 5.48 |
| W | O | Wall | |
|---|---|---|---|
| W | 15 | 90 | 15 |
| O | 15 | 20 | |
| Wall | 15 |
| H | T | W | O | Wall | |
|---|---|---|---|---|---|
| H | 20 | 42 | 10 | 50 | 35 |
| T | 15 | 25 | 12 | 15.5 | |
| W | 15 | 90 | 15 | ||
| O | 15 | 20 | |||
| Wall | 15 |
| H | T | W | O | Wall | |
|---|---|---|---|---|---|
| H | 15 | 25 | 14 | 25 | 35 |
| T | 15 | 54 | 14.5 | 15.5 | |
| W | 15 | 100 | 15 | ||
| O | 15 | 20 | |||
| Wall | 15 |
| Percentage of oil | 0.0% | 28.8% | 45.4% | 65.6% | 100.0% |
| (Poiseullie flow) | 0.024 | 0.023 | 0.032 | 0.029 | 0.022 |
| (Couette flow) | 0.007 | 0.009 | 0.017 | 0.021 | 0.007 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.X.D.; Vu, T.V.; Razavi, S.; Papavassiliou, D.V. Coarse Grained Modeling of Multiphase Flows with Surfactants. Polymers 2022, 14, 543. https://doi.org/10.3390/polym14030543
Nguyen TXD, Vu TV, Razavi S, Papavassiliou DV. Coarse Grained Modeling of Multiphase Flows with Surfactants. Polymers. 2022; 14(3):543. https://doi.org/10.3390/polym14030543
Chicago/Turabian StyleNguyen, Thao X. D., Tuan V. Vu, Sepideh Razavi, and Dimitrios V. Papavassiliou. 2022. "Coarse Grained Modeling of Multiphase Flows with Surfactants" Polymers 14, no. 3: 543. https://doi.org/10.3390/polym14030543
APA StyleNguyen, T. X. D., Vu, T. V., Razavi, S., & Papavassiliou, D. V. (2022). Coarse Grained Modeling of Multiphase Flows with Surfactants. Polymers, 14(3), 543. https://doi.org/10.3390/polym14030543









