Experimental Study on the Bending and Shear Behaviors of Chinese Paulownia Wood at Elevated Temperatures
Abstract
:1. Introduction
2. Experimental Program
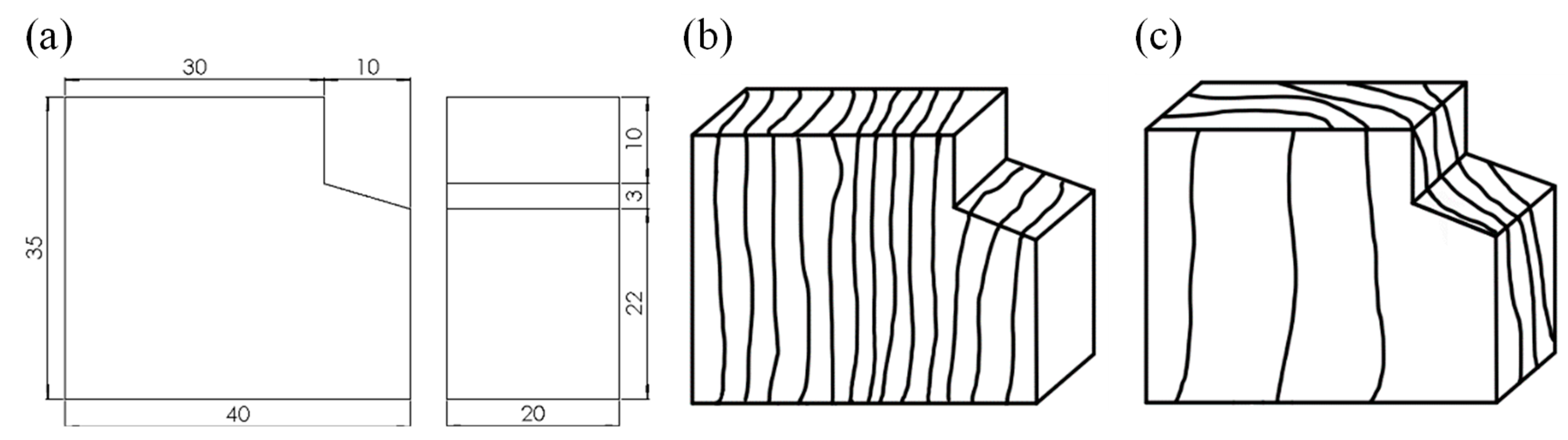
2.1. Material and Specimens
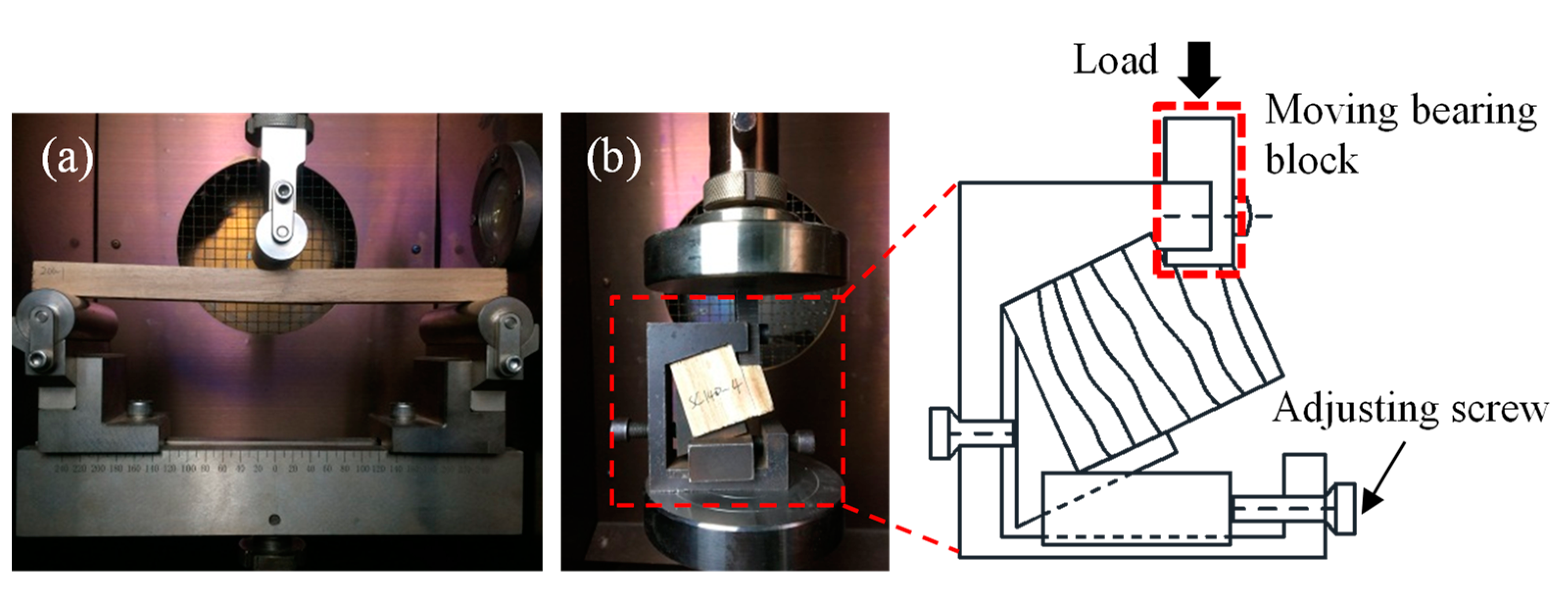
2.2. Experimental Instruments and Set-Up
2.3. Calculation of Bending and Shear Properties
3. Experimental Results and Discussion
3.1. Experimental Observation and Failure Mode
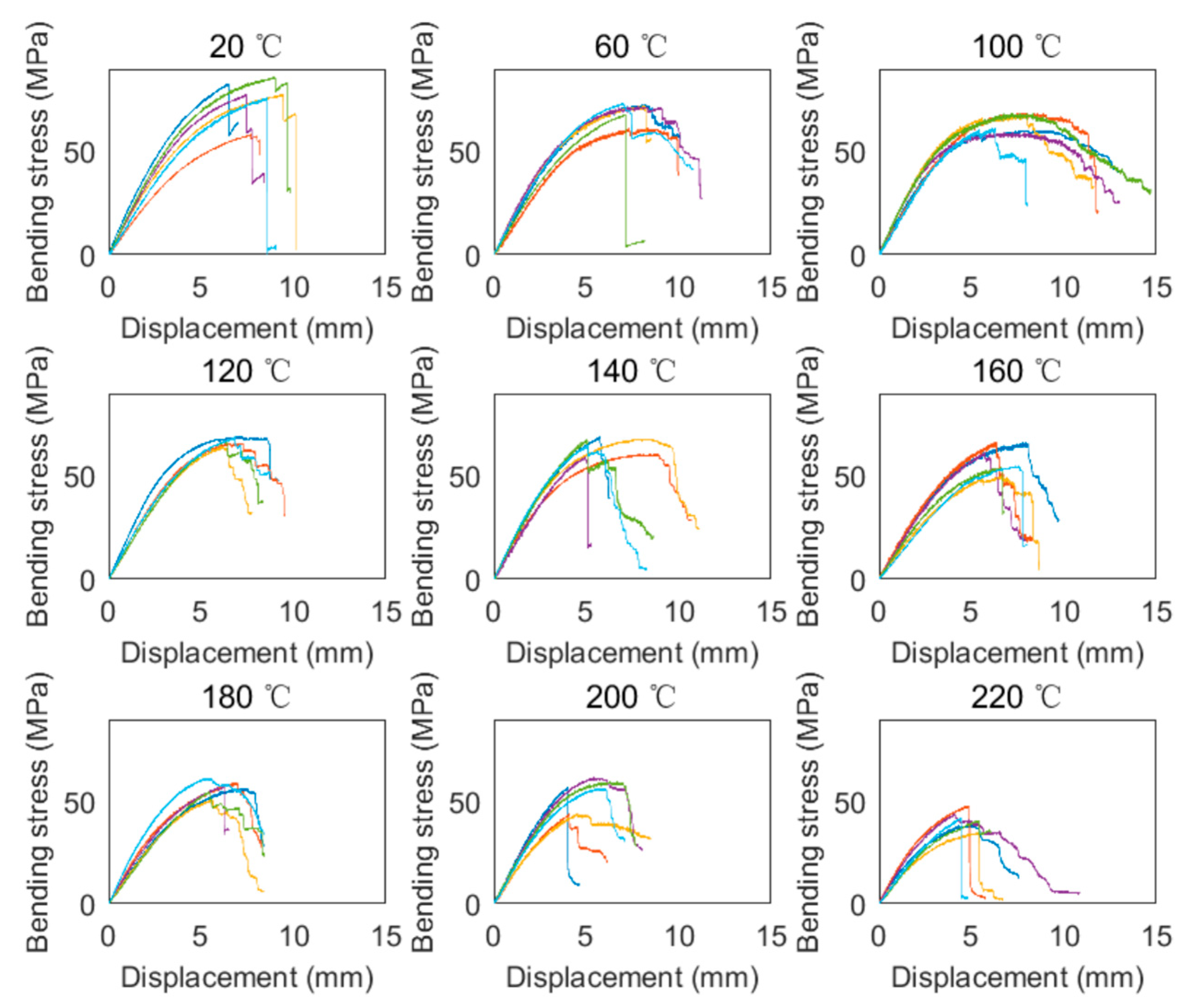
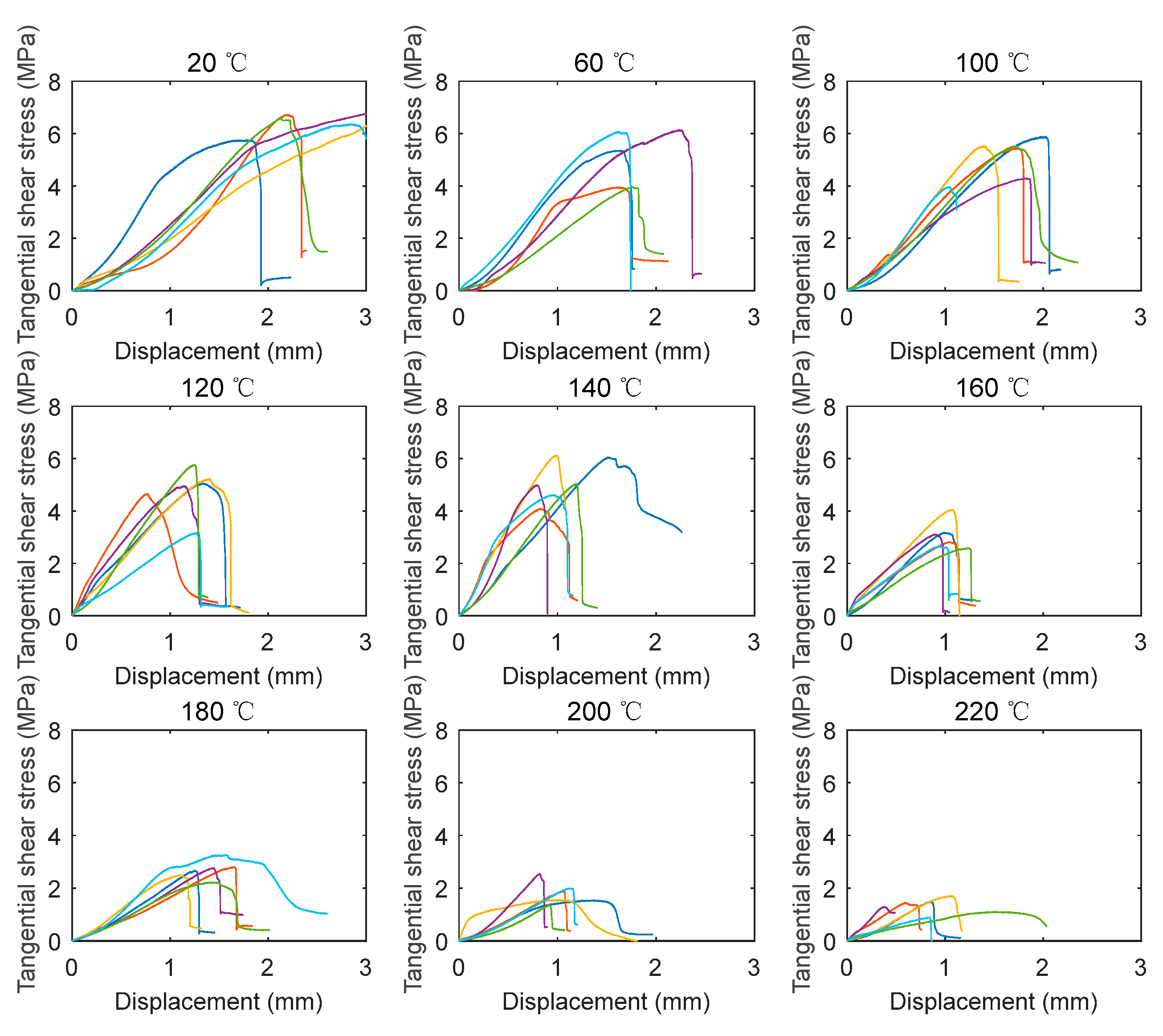
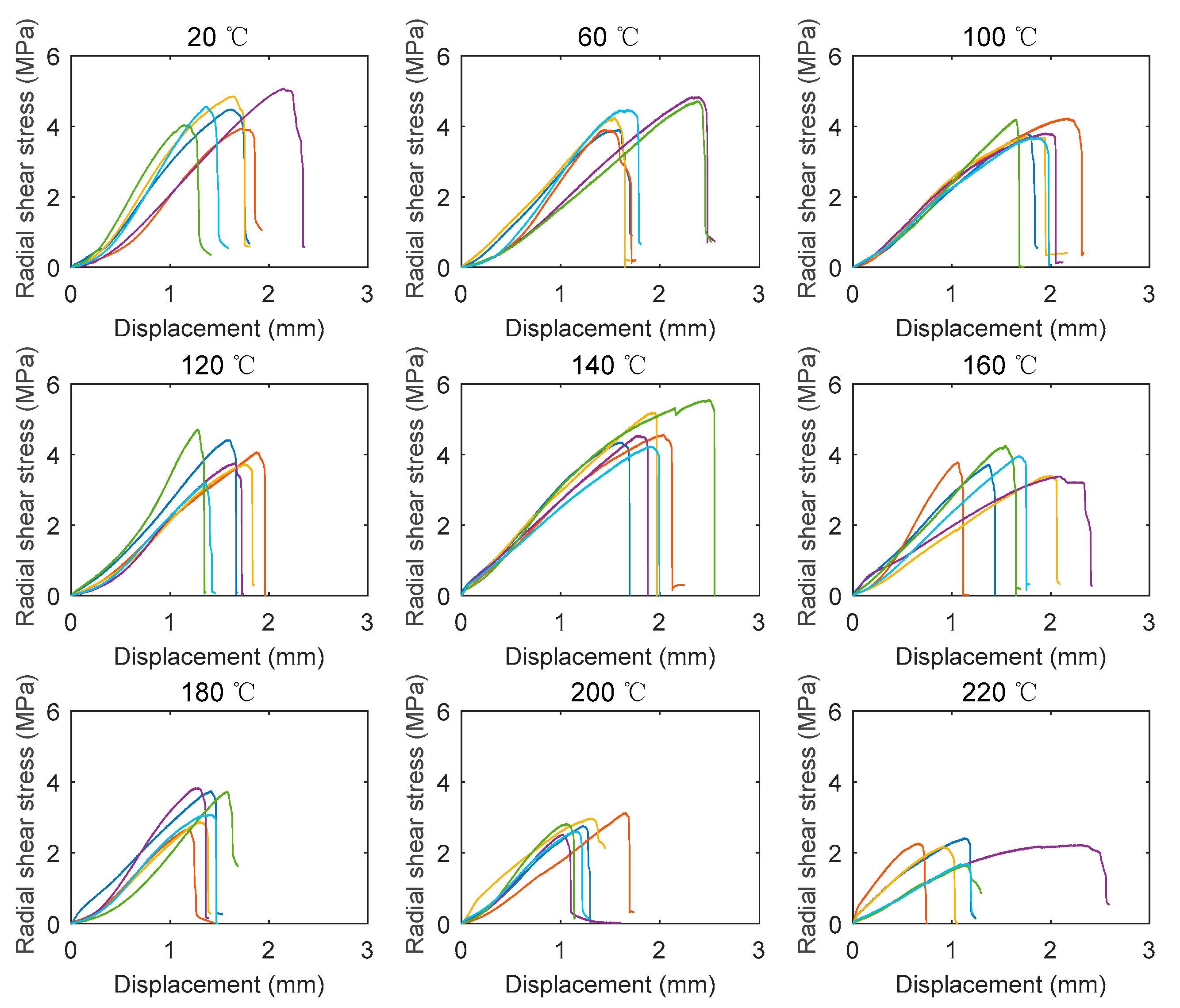
3.2. Stress-Displacement Curves
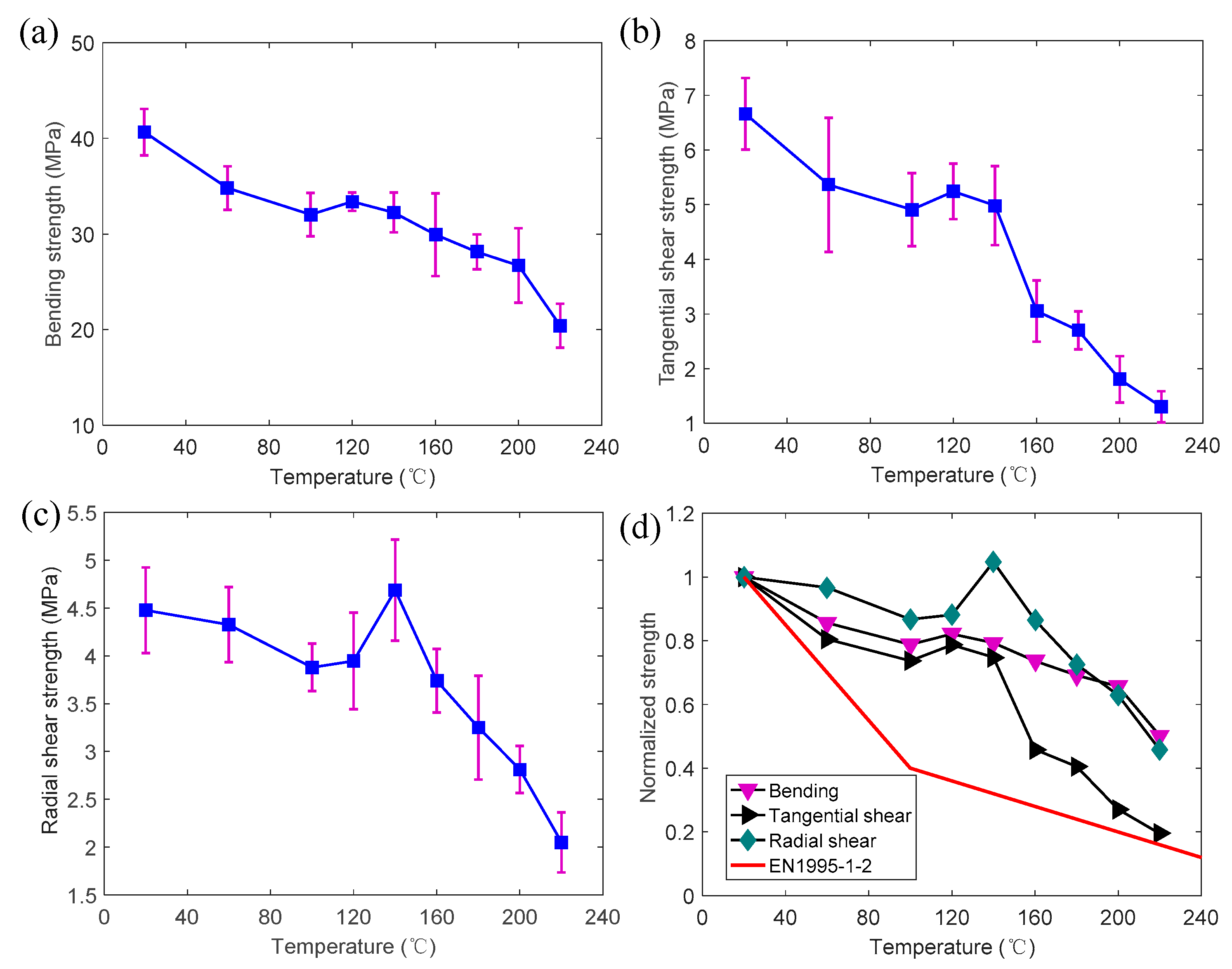
3.3. Temperature-Dependent Strength
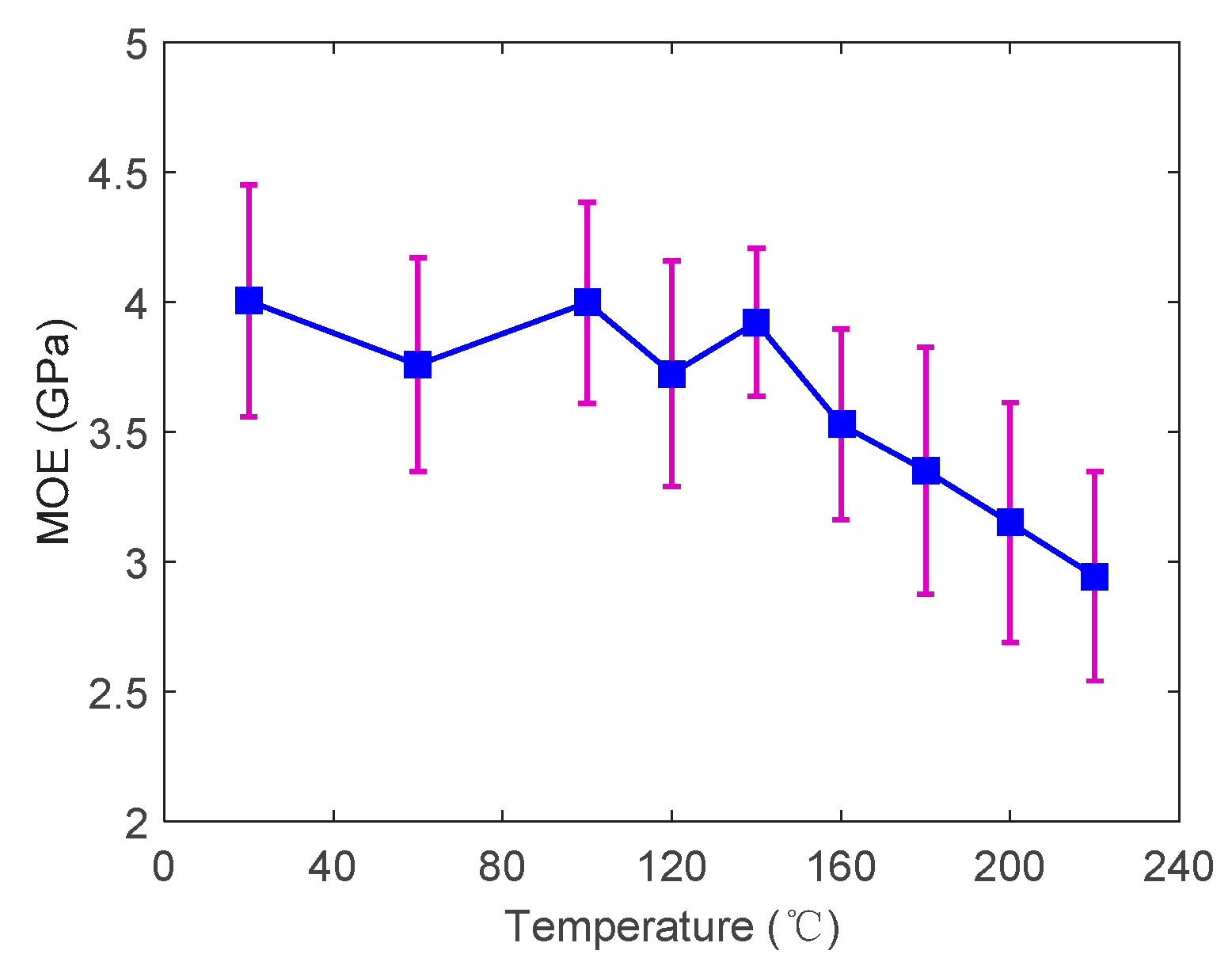
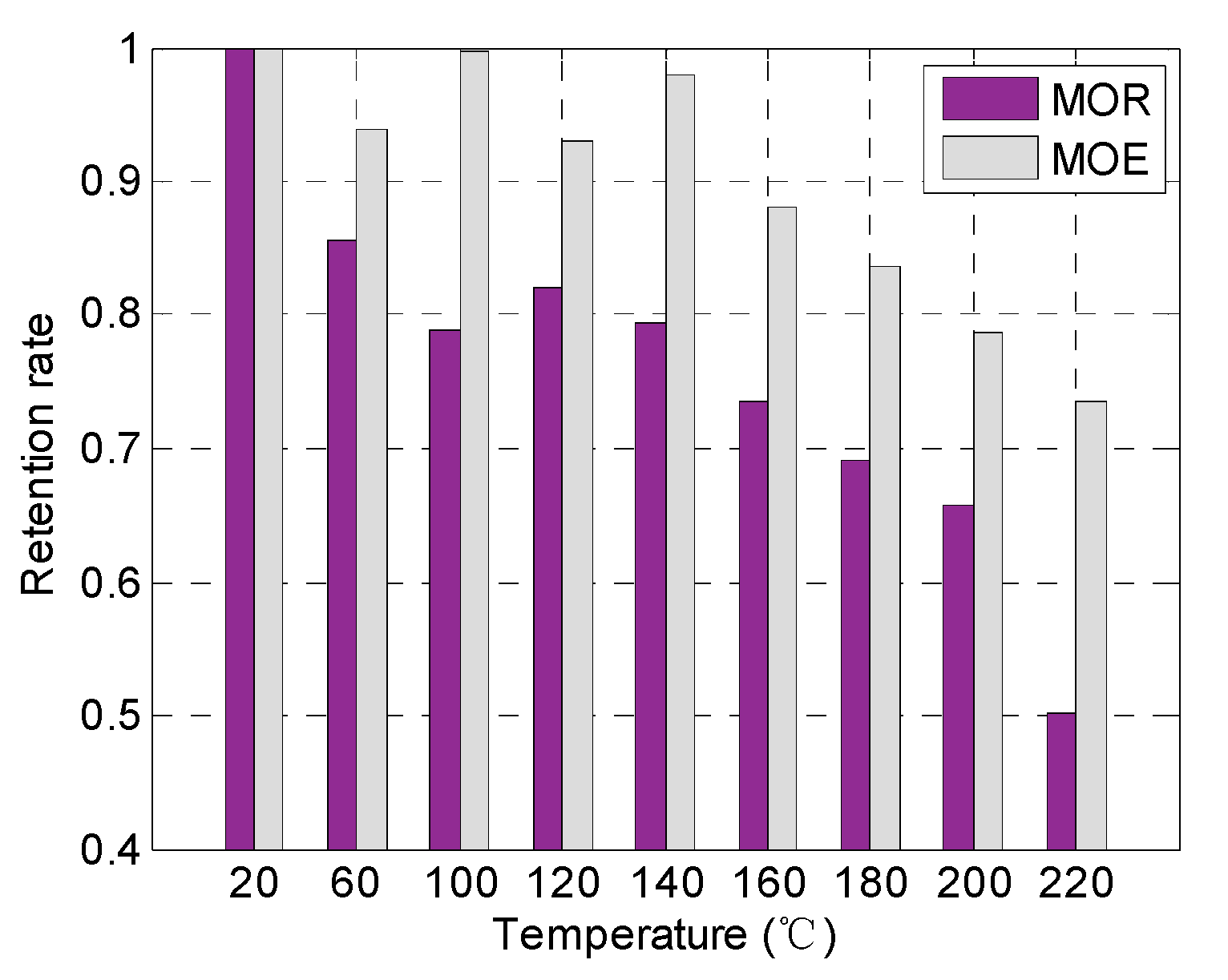
3.4. Temperature-Dependent Modulus of Elasticity and Modulus of Rupture
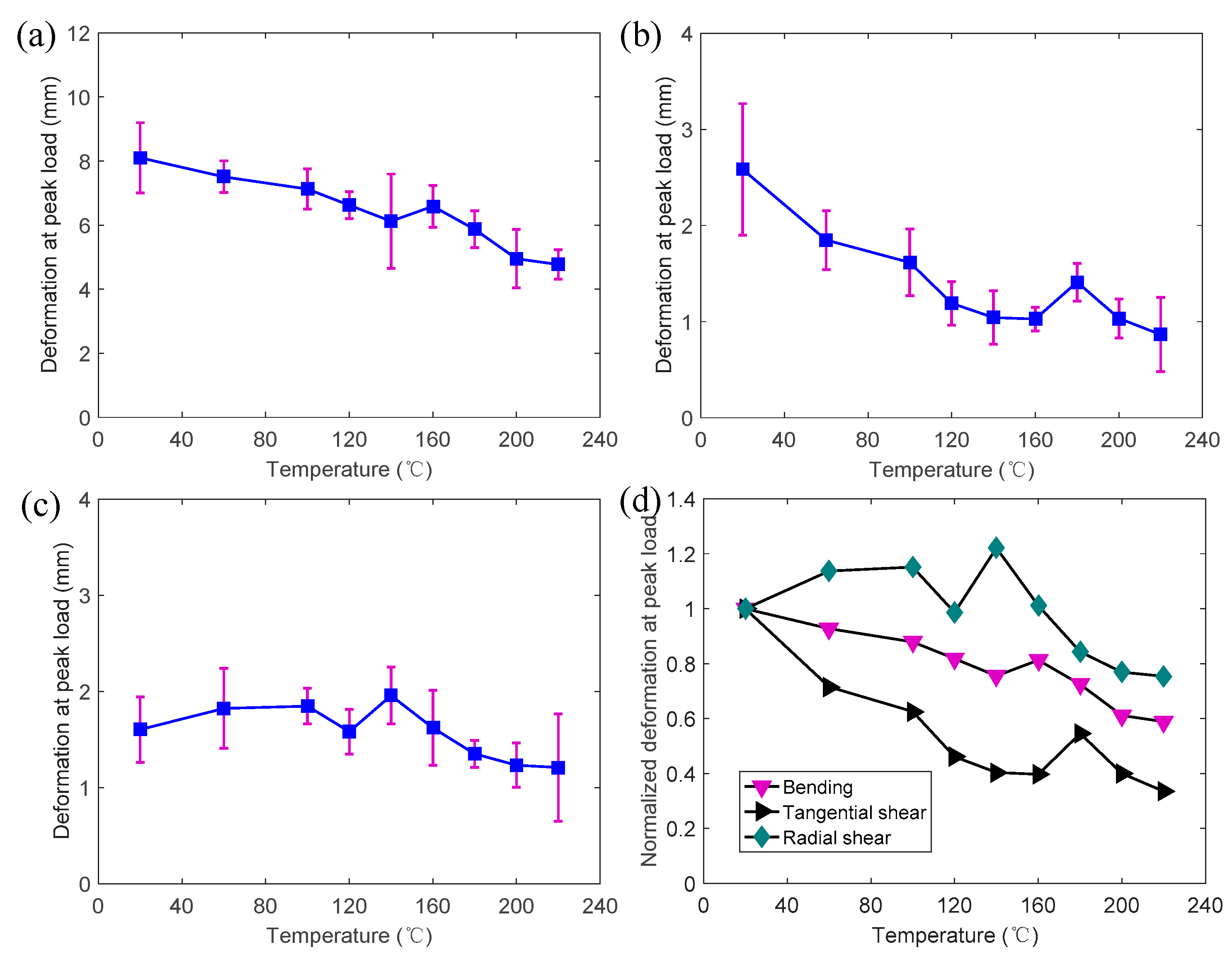
3.5. Temperature-Dependent Deformation Capacity
4. Conclusions
- (1)
- Crushing–tensile rupture at the middle-span cross-section was the main failure mode of the bending specimen. Moreover, shear cracks were found in a few bending specimens. The tangential shear specimens exhibited straight cracks while radial shear specimens exhibited wave-form cracks on the bottom surfaces. Elevated temperatures seemed to have little effect on the failure modes.
- (2)
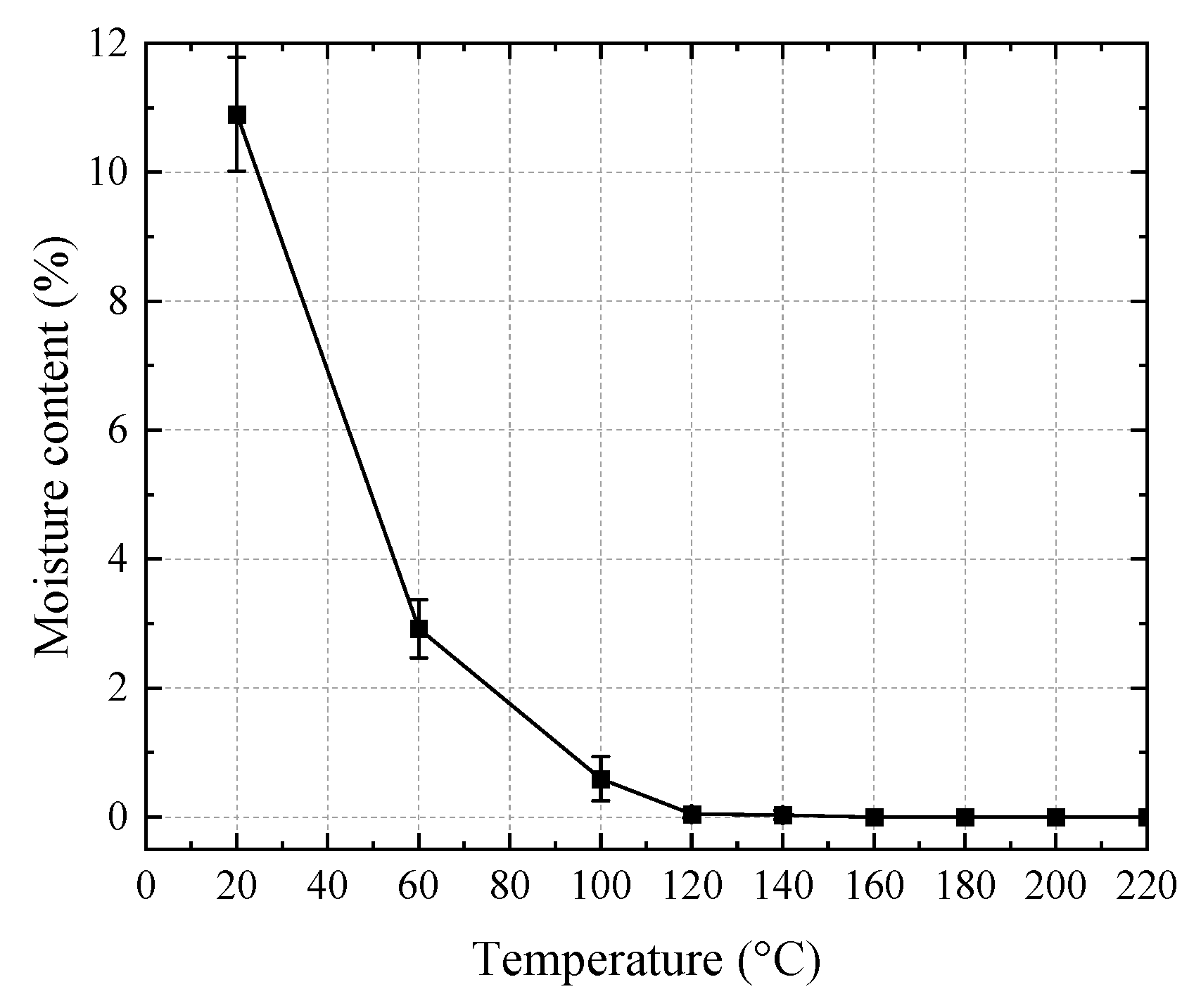
- The bending and shear strengths were simultaneously affected by the moisture content and the elevated temperature. The strengths decreased with the increase in moisture content and temperature. In the low (20 to 100 °C) and high (140 to 220 °C) temperature ranges, the effect of the increase in temperature was dominant, whereas in the intermediate temperature range (100 to 140 °C) the effect of moisture content was dominant.
- (3)
- The EN 1995-1-2 design curve for the shear strength of wood at elevated temperatures was conservative for both the tangential shear and radial shear specimens. However, the retention rate of the tangential shear strength was close to the predicted value from EN 1995-1-2 at 220 °C, indicating that the design curve may not be adopted to predict the tangential shear strengths at temperatures higher than 220 °C.
- (4)
- The modulus of rupture (MOR) and the modulus of elasticity (MOE) generally decreased with the increasing temperature. Under the same temperature, the retention rate of the MOE was significantly higher than that of the MOR. At 220 °C, the retention rate of the MOE was 1.5 times that of MOR.
- (5)
- The increase in the deformations at the peak load mainly resulted from the softening of the polymer components from 120 to 180 °C. The deformations of the radial shear specimens and the tangential shear specimens were much lower than those of the bending specimens. Moreover, most of the post-peak curves of the bending specimens exhibited pseudo-ductile characteristics due to the progressive damage. In contrast, the shear stress suddenly dropped after reaching the peak load, indicating that the shear specimens were much more brittle than the bending specimens.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Chen, K.; Liu, W.; Liu, Y.; Wang, K.; Ge, W.; Guo, K. Fire performance of pultruded wood-cored GFRP sandwich components for building construction. Case Stud. Constr. Mater. 2022, 17, e01555. [Google Scholar] [CrossRef]
- Menis, A.; Fragiacomo, M.; Clemente, I. Fire resistance of unprotected cross-laminated timber floor panels: Parametric study and simplified design. Fire Saf. J. 2019, 107, 104–113. [Google Scholar] [CrossRef]
- Gaff, M.; Čekovská, H.; Bouček, J.; Kačíková, D.; Kubovský, I.; Tribulová, T.; Zhang, L.; Marino, S.; Kačík, F. Flammability Characteristics of Thermally Modified Meranti Wood Treated with Natural and Synthetic Fire Retardants. Polymers 2021, 13, 2160. [Google Scholar] [CrossRef] [PubMed]
- Schmid, J.; Klippel, M.; Just, A.; Frangi, A. Review and analysis of fire resistance tests of timber members in bending, tension and compression with respect to the Reduced Cross-Section Method. Fire Saf. J. 2014, 68, 81–99. [Google Scholar] [CrossRef]
- Fragiacomo, M.; Menis, A.; Clemente, I.; Bochicchio, G.; Ceccotti, A. Fire resistance of cross-laminated timber panels loaded out of plane. J. Struct. Eng. 2013, 139, 04013018. [Google Scholar] [CrossRef]
- Schaffer, E.L.; Marx, C.M.; Bender, D.A.; Woeste, F.E. Strength Validation and Fire Endurance of Glued-Laminated Timber Beams; Research Paper FPL: Madison, WI, USA, 1980; Volume 467. [Google Scholar]
- Schmid, J.; Menis, A.; Fragiacomo, M.; Clemente, I.; Bochicchio, G. Behaviour of loaded cross-laminated timber wall elements in fire conditions. Fire Technol. 2015, 51, 1341–1370. [Google Scholar] [CrossRef]
- Suzuki, J.; Mizukami, T.; Naruse, T.; Araki, Y. Fire resistance of timber panel structures under standard fire exposure. Fire Technol. 2016, 52, 1015–1034. [Google Scholar] [CrossRef]
- Klippel, M.; Frangi, A. Fire Safety of Glued-Laminated Timber Beams in Bending. J. Struct. Eng. 2017, 143, 04017052. [Google Scholar] [CrossRef]
- Mindeguia, J.C.; Mohaine, S.; Bisby, L.; Robert, F.; McNamee, R.; Bartlett, A. Thermo-mechanical behaviour of cross-laminated timber slabs under standard and natural fires. Fire Mater. 2020, 45, 866–884. [Google Scholar] [CrossRef]
- Frangi, A.; Fontana, M.; Hugi, E.; Jübstl, R. Experimental analysis of cross-laminated timber panels in fire. Fire Saf. J. 2009, 44, 1078–1087. [Google Scholar] [CrossRef]
- Kippel, M.; Leyder, C.; Frangi, A.; Fontana, M. Fire tests on loaded cross-laminated timber wall and floor elements. Fire Saf. Sci. 2014, 11, 626–639. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, J.; Shen, H. Experimental and numerical analysis of residual load-carrying capacity of cross-laminated timber walls after fire. Structures 2021, 30, 50–61. [Google Scholar] [CrossRef]
- Mahr, K.; Sinha, A.; Barbosa, A.R. Elevated Temperature Effects on Performance of a Cross-Laminated Timber Floor-to-Wall Bracket Connections. J. Struct. Eng. 2020, 146, 04020173. [Google Scholar] [CrossRef]
- Mindeguia, J.-C.; Cueff, G.; Dréan, V.; Auguin, G. Simulation of charring depth of timber structures when exposed to non-standard fire curves. J. Struct. Fire Eng. 2018, 9, 63–76. [Google Scholar] [CrossRef]
- Yang, C. Study on the Changes of Physical and Mechanical Properties of Wood Used for Glulam at Different Temperature. Master’s Thesis, Nanjing Tech University, Nanjing, China, 2016. [Google Scholar]
- Zhong, Y.; Zhou, H.; Wen, L. The Effect of Elevated Temperature on Bending Properties of Normal Wood inside Chinese Larch Wood during Fire Events. BioResources 2015, 10, 2926–2935. [Google Scholar] [CrossRef]
- Korkut, S.; Budakçı, M. Effect of High-Temperature Treatment on the Mechanical Properties of Rowan (Sorbus aucuparia L.) Wood. Dry. Technol. 2009, 27, 1240–1247. [Google Scholar] [CrossRef]
- Tajvidi, M.; Mirzaei, B. Effects of temperature on the mechanical properties of beech (Fagus orientalis Lipsky) and lime (Tilia begonifolia) wood. Wood Mater. Sci. Eng. 2009, 4, 147–153. [Google Scholar] [CrossRef]
- Dhima, D.; Audebert, M.; Racher, P.; Bouchaïr, A.; Taazount, M. Shear tests of glulam at elevated temperatures. Fire Mater. 2014, 38, 827–842. [Google Scholar] [CrossRef]
- EN 1995-1-2: 2004; Eurocode5, Part 1–2: General-Structural Fire Design. CEN TC 250-SC5; EN: Brussels, Belgium, 2004.
- Garrido, M.; Melro, P.; Correia, J.R. Effects of elevated temperature on the shear response of end-grain balsa used in composite sandwich panels. J. Sandw. Struct. Mater. 2021, 23, 2106–2126. [Google Scholar] [CrossRef]
- GB/T 1931-2009; Method for Determination of Moisture Content of Wood. China Standard Press: Beijing, China, 2009.
- GB/T 1933-2009; Method for Determination of the Density of Wood. China Standard Press: Beijing, China, 2009.
- GB/T 1936.1-2009; Method of Testing in Bending Strength of Wood. China Standard Press: Beijing, China, 2009.
- GB/T 1937-2009; Method of Testing in Shearing Strength Parallel to Grain of Wood. China Standard Press: Beijing, China, 2009.
- GB/T 1936. 2-2009; Method for Determination of the Modulus of Elasticity in Static Bending of Wood. China Standard Press: Beijing, China, 2009.
- Schaffer, E.L. Effect of Pyrolytic Temperatures on the Longitudinal Strength of Dry Douglas-Fir. J. Test. Eval. 1973, 1, 319–329. [Google Scholar]
- Irvine, G.M. The glass transition of lignin, hemicellulose, cellulose and their measurement by differential thermal analysis. TAPPI 1984, 67, 118–121. [Google Scholar]
- Manríquez, M.J.; Moraes, P.D. Influence of the temperature on the compression strength parallel to grain of paricá. Constr. Build. Mater. 2010, 24, 99–104. [Google Scholar] [CrossRef]
- Yue, K.; Wu, J.; Wang, F.; Chen, Z.; Lu, W. Mechanical Properties of Douglas Fir Wood at Elevated Temperatures under Nitrogen Conditions. J. Mater. Civ. Eng. 2022, 34, 04021434. [Google Scholar] [CrossRef]
- Gerhards, C.C. Effect of moisture content and temperature on the mechanical properties of wood: An analysis of immediate effects. Wood Fiber 1982, 14, 4–36. [Google Scholar]
- Beall, F.C.; Eickner, H.W. Thermal Degradation of Wood Components: A Review of the Literature; USDA: Madison, WI, USA, 1970.



| Specimen | Time Required to Reach the Desired Temperature (min) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 20 °C | 60 °C | 100 °C | 120 °C | 140 °C | 160 °C | 180 °C | 200 °C | 220 °C | |
| Bending | 2.1 | 12.5 | 15.1 | 19.8 | 23.0 | 26.9 | 31.3 | 40.9 | 54.5 |
| Tangential shear | 2.5 | 15.9 | 28.4 | 32.1 | 35.4 | 37.5 | 44.4 | 52.3 | 64.8 |
| Radial shear | 2.5 | 16.1 | 30.3 | 34.2 | 36.8 | 38.6 | 44.9 | 53.1 | 65.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Xu, B.; Fang, Z.; Li, C.; Kong, X.; Li, Q.; Guo, K. Experimental Study on the Bending and Shear Behaviors of Chinese Paulownia Wood at Elevated Temperatures. Polymers 2022, 14, 5545. https://doi.org/10.3390/polym14245545
Zhang L, Xu B, Fang Z, Li C, Kong X, Li Q, Guo K. Experimental Study on the Bending and Shear Behaviors of Chinese Paulownia Wood at Elevated Temperatures. Polymers. 2022; 14(24):5545. https://doi.org/10.3390/polym14245545
Chicago/Turabian StyleZhang, Lingfeng, Biao Xu, Zhongjie Fang, Chen Li, Xijun Kong, Qianyi Li, and Kai Guo. 2022. "Experimental Study on the Bending and Shear Behaviors of Chinese Paulownia Wood at Elevated Temperatures" Polymers 14, no. 24: 5545. https://doi.org/10.3390/polym14245545
APA StyleZhang, L., Xu, B., Fang, Z., Li, C., Kong, X., Li, Q., & Guo, K. (2022). Experimental Study on the Bending and Shear Behaviors of Chinese Paulownia Wood at Elevated Temperatures. Polymers, 14(24), 5545. https://doi.org/10.3390/polym14245545







