An Approximate Method for Predicting the Friction Factor of Viscoplastic Shear-Thinning Fluids in Non-Circular Channels of Regular Cross-Sections
Abstract
1. Introduction
2. Materials and Methods
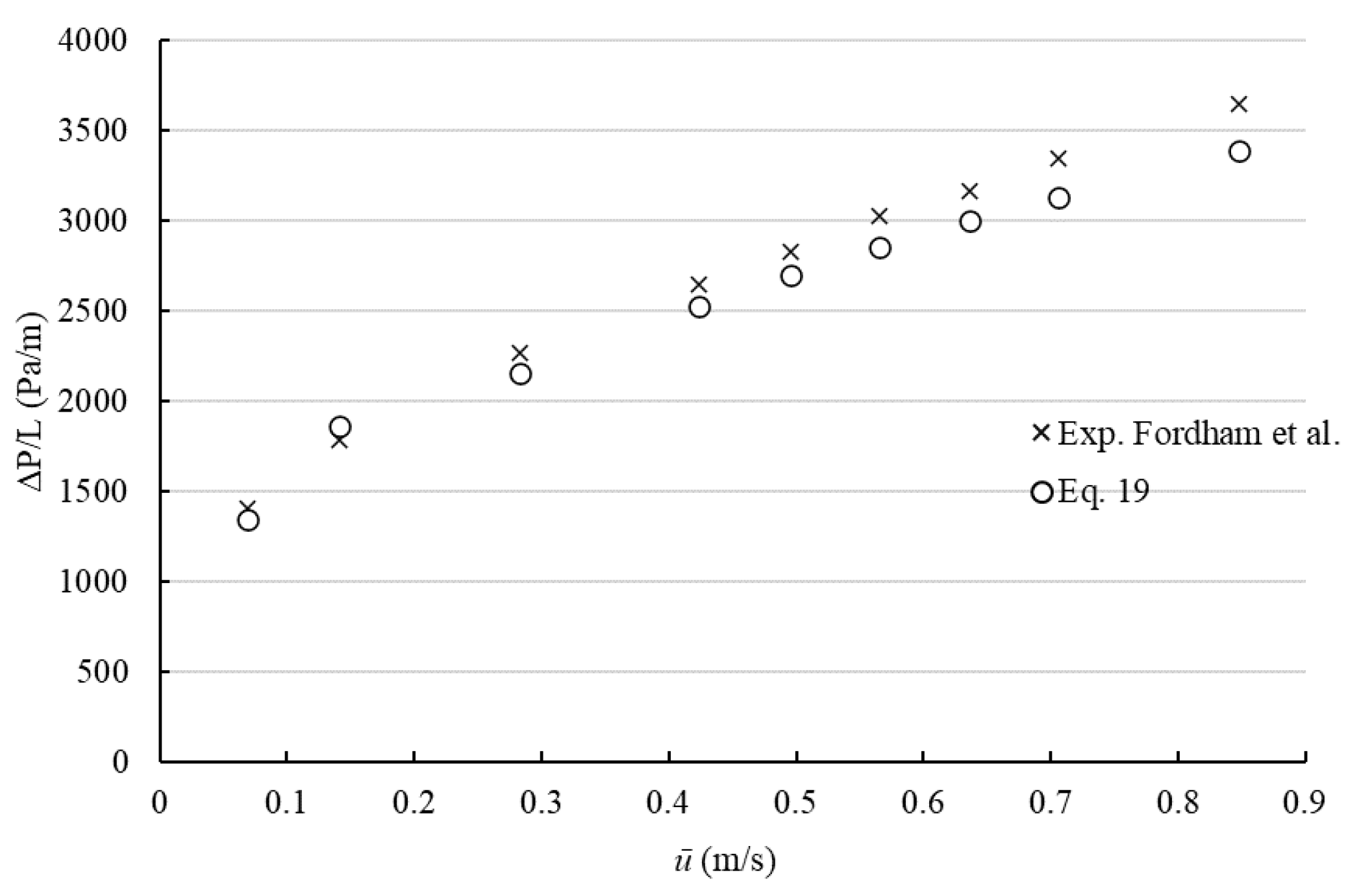
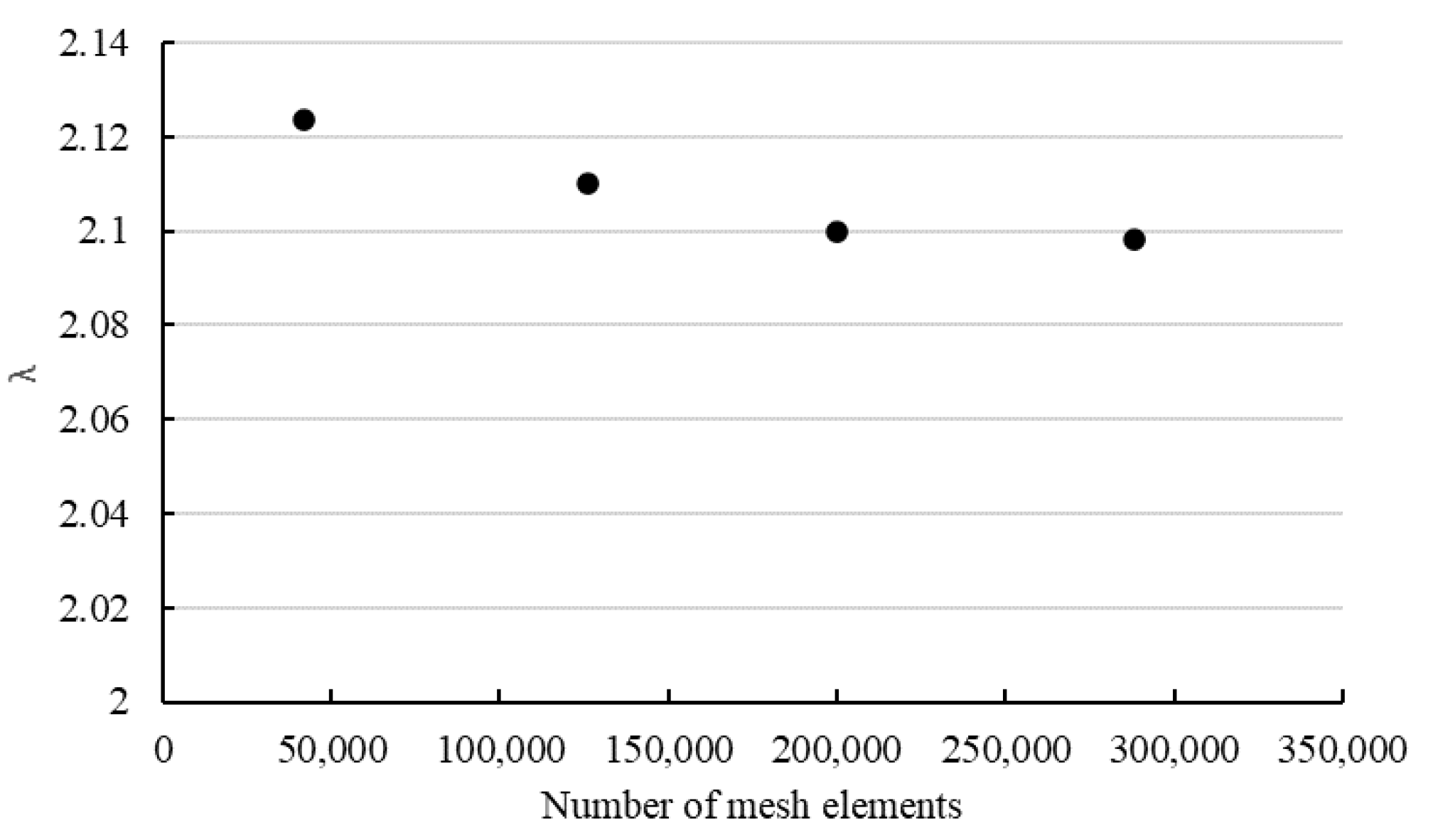
3. Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- Rheological parameters of the Herschel–Bulkley model (-consistency, -flow index, and yield stress τ0),
- (2)
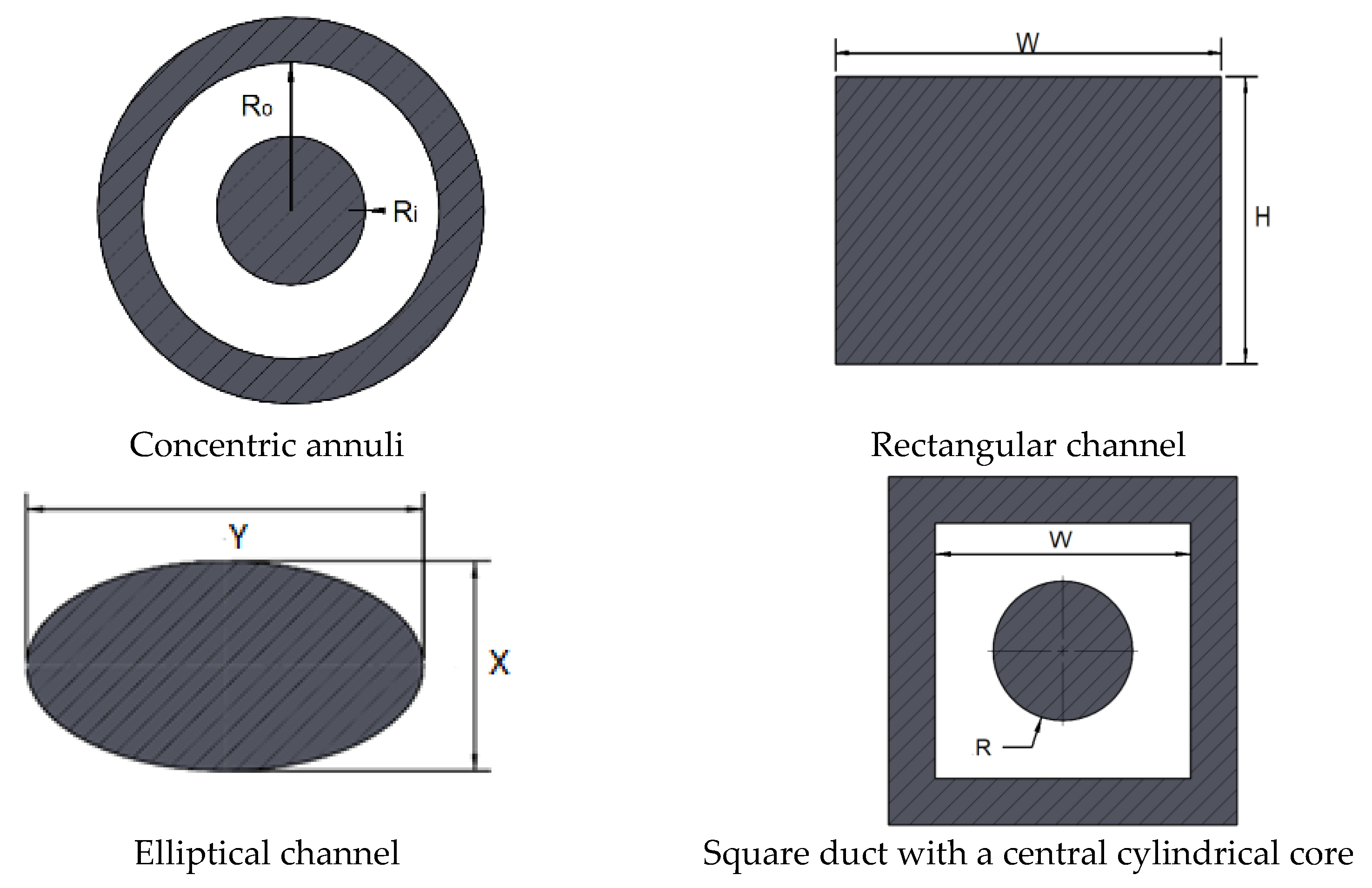
- Three geometry parameters characterizing the cross-section of pipe (equivalent diameter = and dimensionless parameters , designed by Kozicky, defining the shape of the cross-section.
- (3)
- Flowrate or mean velocity of the liquid , assuming fully developed laminar simple shear flow in a channel of arbitrary cross-section and length .
- (1)
- Calculate the Reynolds number derived by Kozicki,
- (2)
- Calculate dimensionless yield stress (Equation (21)) assuming friction factor λ from the previous iteration
- (3)
- Calculate auxiliary parameter θ Equation (19) or Equation (23) using
- (4)
- Calculate friction factor λ and iterate back to step 2 until sufficient accuracy is achieved
- (5)
- Calculate pressure drop from friction factor λ and mean velocity,
References
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2008; pp. 1–205. [Google Scholar]
- Delplace, F.; Leuliet, J.C. Generalized Reynolds number for the flow of Power-law fluids in cylindrical ducts of arbitrary cross-section. Chem. Eng. J. 1995, 56, 33–37. [Google Scholar] [CrossRef]
- Ayas, M.; Skocilas, J.; Jirout, T. Analysis of Power Input of an In-Line Rotor-Stator Mixer for Viscoplastic Fluids. Processes 2020, 8, 916. [Google Scholar] [CrossRef]
- Dinkgreve, M.; Fazilati, M.; Denn, M.M.; Bonn, D. Carbopol: From a simple to a thixotropic yield stress fluid. J. Rheol. 2018, 62, 773–780. [Google Scholar] [CrossRef]
- Macosko, C.W. Rheology: Principles, Measurements, and Applications; Wiley-VCH: New York, NY, USA, 1994; pp. 65–106. [Google Scholar]
- Ma, Z.; Cao, J.; Xu, X.; Xu, J. A shear stress model of water-based magnetorheological polishing fluids. J. Intell. Mater. Syst. Struct. 2022, 33, 160–169. [Google Scholar] [CrossRef]
- Baird, D.G.; Collias, D.I. Polymer Processing: Principles and Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 33–175. [Google Scholar]
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 79–135. [Google Scholar]
- Zachariades, A.E.; Porter, R.S. High Modulus Polymers: Approaches to Design and Development, 1st ed.; CRC Press: Boca Raton, FL, USA, 1988; pp. 1–36. [Google Scholar]
- Roland, W.; Marschik, C.; Krieger, M.; Löw-Baselli, B.; Miethlinger, J. Symbolic regression models for predicting viscous dissipation of three-dimensional non-Newtonian flows in single-screw extruders. J. Nonnewton Fluid Mech. 2019, 268, 12–29. [Google Scholar] [CrossRef]
- Štípek, J.; Skočilas, J.; Štancl, J.; Žitný, R. Extrusion rheometry of collagen dough. Czech J. Food Sci. 2021, 39, 384–392. [Google Scholar] [CrossRef]
- Crespi-Llorens, D.; Vicente, P.; Viedma, A. Generalized Reynolds number and viscosity definition for non-Newtonian fluid flow in ducts of non-uniform cross-sections. Exp. Therm. Fluid Sci. 2015, 64, 125–133. [Google Scholar] [CrossRef]
- Tang, M.; Yuan, L.; He, S.; Fu, T. Simplified modeling of YPL fluid flow through a concentric elliptical annular pipe. J. Pet. Sci. Eng. 2018, 162, 225–232. [Google Scholar] [CrossRef]
- Fernandes, C.S.; Dias, R.P.; Nóbrega, J.M.; Maia, J.M. Friction factors of power-law fluids in chevron-type plate heat exchangers. J. Food Eng. 2008, 89, 441–447. [Google Scholar] [CrossRef]
- Liu, T.J.; Hong, C.N. The pressure drop/flow rate equation for non-Newtonian flow in channels of irregular cross-section. Polym. Eng. Sci. 1988, 28, 1559–1564. [Google Scholar] [CrossRef]
- Burger, J.; Haldenwang, R.; Alderman, N. Experimental database for non-Newtonian flow in four channel shapes. J. Hydraul. Res. 2010, 48, 363–370. [Google Scholar] [CrossRef]
- Hanks, R.W.; Larsen, K.M. The flow of power-law Newtonian fluids in concentric annuli. Ind. Eng. Chem. Fundam. 1979, 18, 33–35. [Google Scholar] [CrossRef]
- Kelessidis, V.C.; Dalamarinis, P.; Maglione, R. Experimental study and predictions of pressure losses of fluids modeled as Herschel–Bulkley in concentric and eccentric annuli in laminar, transitional and turbulent flows. J. Pet. Sci. Eng. 2011, 77, 305–312. [Google Scholar] [CrossRef]
- Fordham, E.J.; Bittleston, S.H.; Tehrani, M.A. Viscoplastic flow in centered annuli, pipes, and slots. Ind. Eng. Chem. Res. 1991, 30, 517–524. [Google Scholar] [CrossRef]
- Kozicki, W.; Chou, C.H.; Tiu, C. Non-Newtonian flow in ducts of arbitrary cross-sectional shape. Chem. Eng. Sci. 1966, 21, 665–679. [Google Scholar] [CrossRef]
- Šesták, J.; Žitný, R.; Bukovský, J. A comparison of methods for rapid calculation of frictional pressure drop and heat transfer coefficient for the flow of non-Newtonian fluids in ducts with non-circular cross-sections. In Proceedings of the International Conference on Compact Heat Exchangers and Enhancement Technology for the Process Industries, Banff, AB, Canada, 18–23 July 1999. [Google Scholar]
- Ahmed, R. Experimental Study and Modeling of Yield Power-Law Fluid Flow in Pipes and Annuli; Report Prepared for TUDRP Advisory Board Meeting; The University of Tulsa: Tulsa, OK, USA, 2005. [Google Scholar]
- Tang, M.; Zhang, T.; He, S.; Li, H.; Li, Q. Modeling of laminar flow in an eccentric elliptical annulus for YPL fluid. J. Nat. Gas Sci. Eng. 2019, 64, 118–132. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayas, M.; Skočilas, J.; Štípek, J.; Gutiérrez, C.A.; Žitný, R.; Jirout, T. An Approximate Method for Predicting the Friction Factor of Viscoplastic Shear-Thinning Fluids in Non-Circular Channels of Regular Cross-Sections. Polymers 2022, 14, 5337. https://doi.org/10.3390/polym14245337
Ayas M, Skočilas J, Štípek J, Gutiérrez CA, Žitný R, Jirout T. An Approximate Method for Predicting the Friction Factor of Viscoplastic Shear-Thinning Fluids in Non-Circular Channels of Regular Cross-Sections. Polymers. 2022; 14(24):5337. https://doi.org/10.3390/polym14245337
Chicago/Turabian StyleAyas, Mehmet, Jan Skočilas, Jan Štípek, Carlos Arce Gutiérrez, Rudolf Žitný, and Tomáš Jirout. 2022. "An Approximate Method for Predicting the Friction Factor of Viscoplastic Shear-Thinning Fluids in Non-Circular Channels of Regular Cross-Sections" Polymers 14, no. 24: 5337. https://doi.org/10.3390/polym14245337
APA StyleAyas, M., Skočilas, J., Štípek, J., Gutiérrez, C. A., Žitný, R., & Jirout, T. (2022). An Approximate Method for Predicting the Friction Factor of Viscoplastic Shear-Thinning Fluids in Non-Circular Channels of Regular Cross-Sections. Polymers, 14(24), 5337. https://doi.org/10.3390/polym14245337





