Analysis of the Adsorption-Release Isotherms of Pentaethylenehexamine-Modified Sorbents for Rare Earth Elements (Y, Nd, La)
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
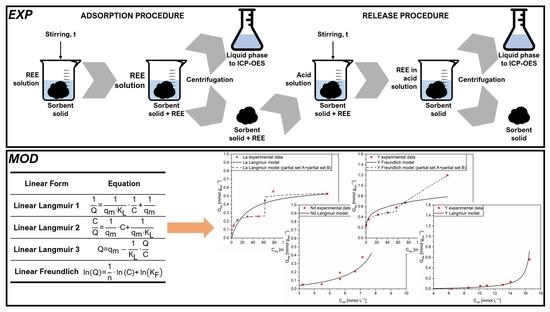
2.2. Methods
2.3. Mathematical Approach
3. Results
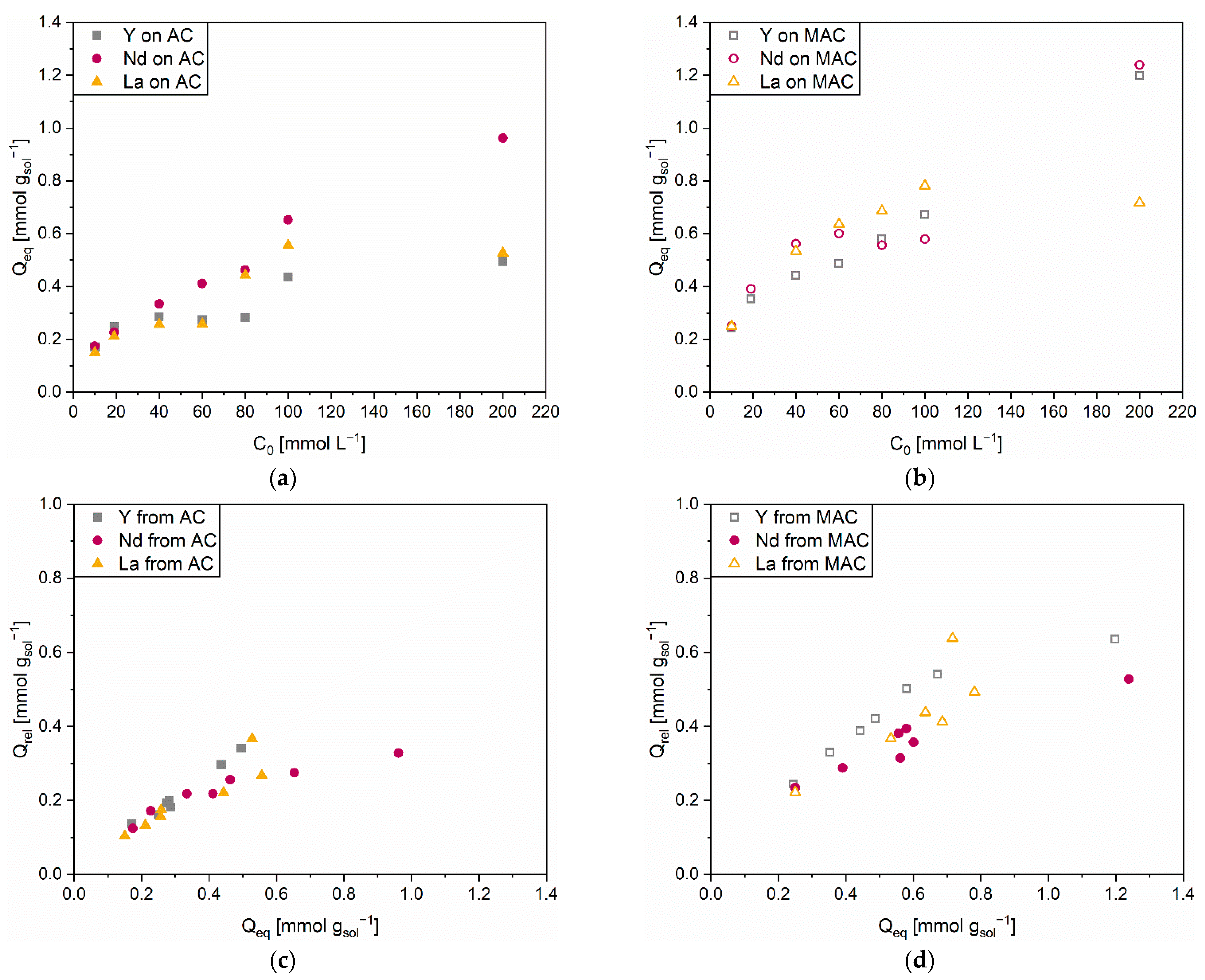
3.1. Activated Carbon
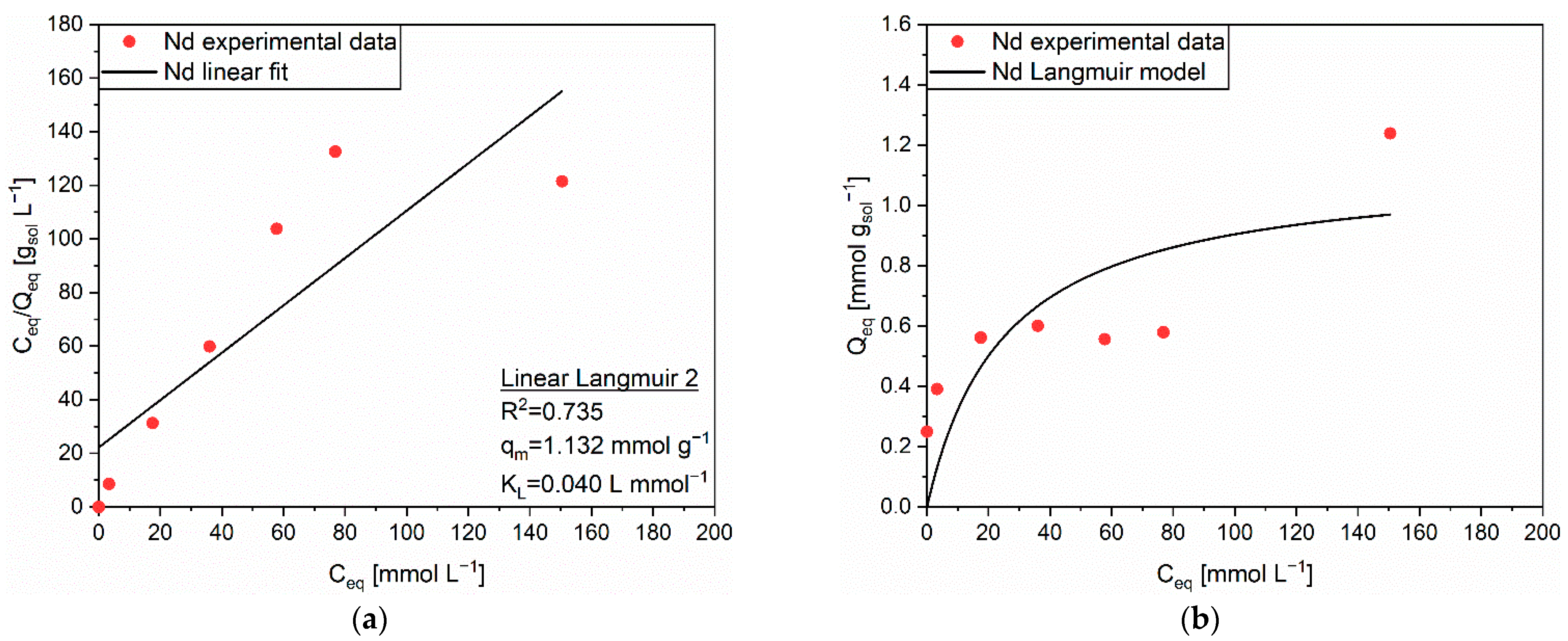
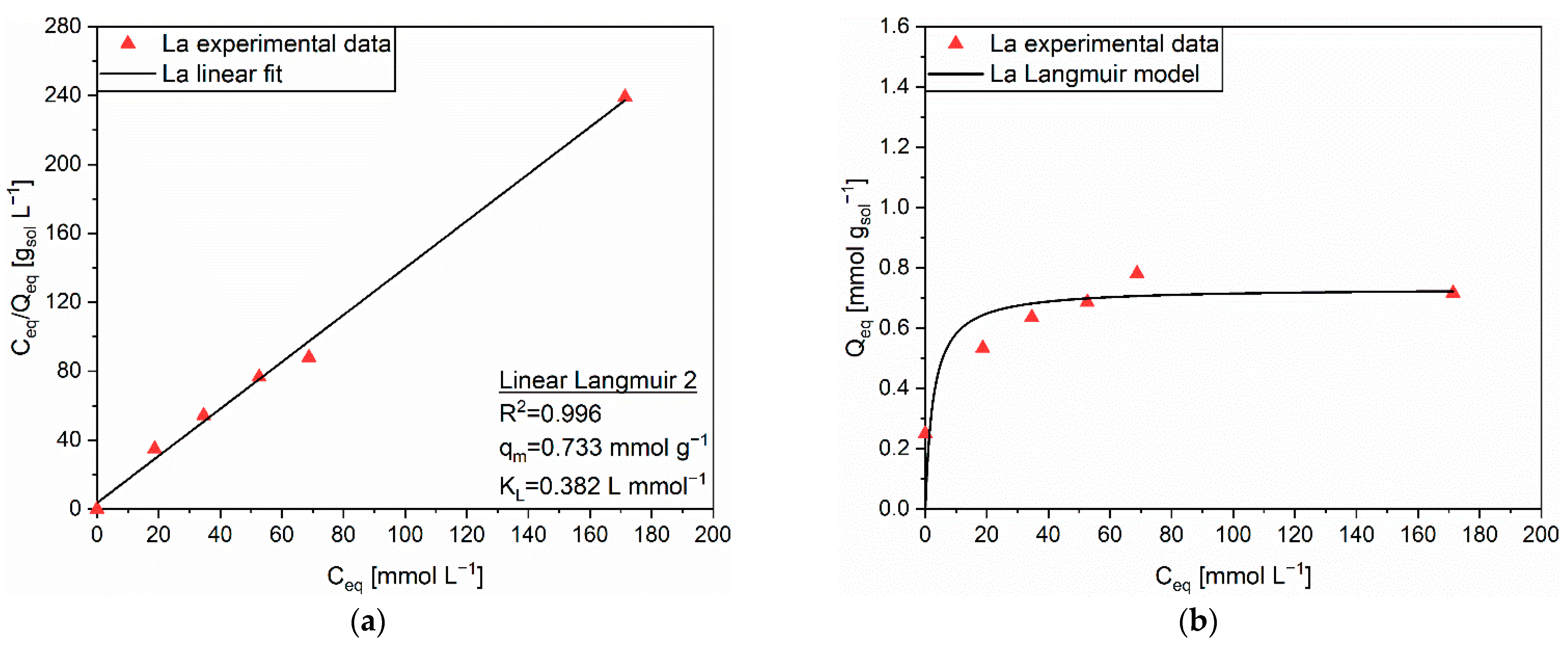
3.1.1. Adsorption
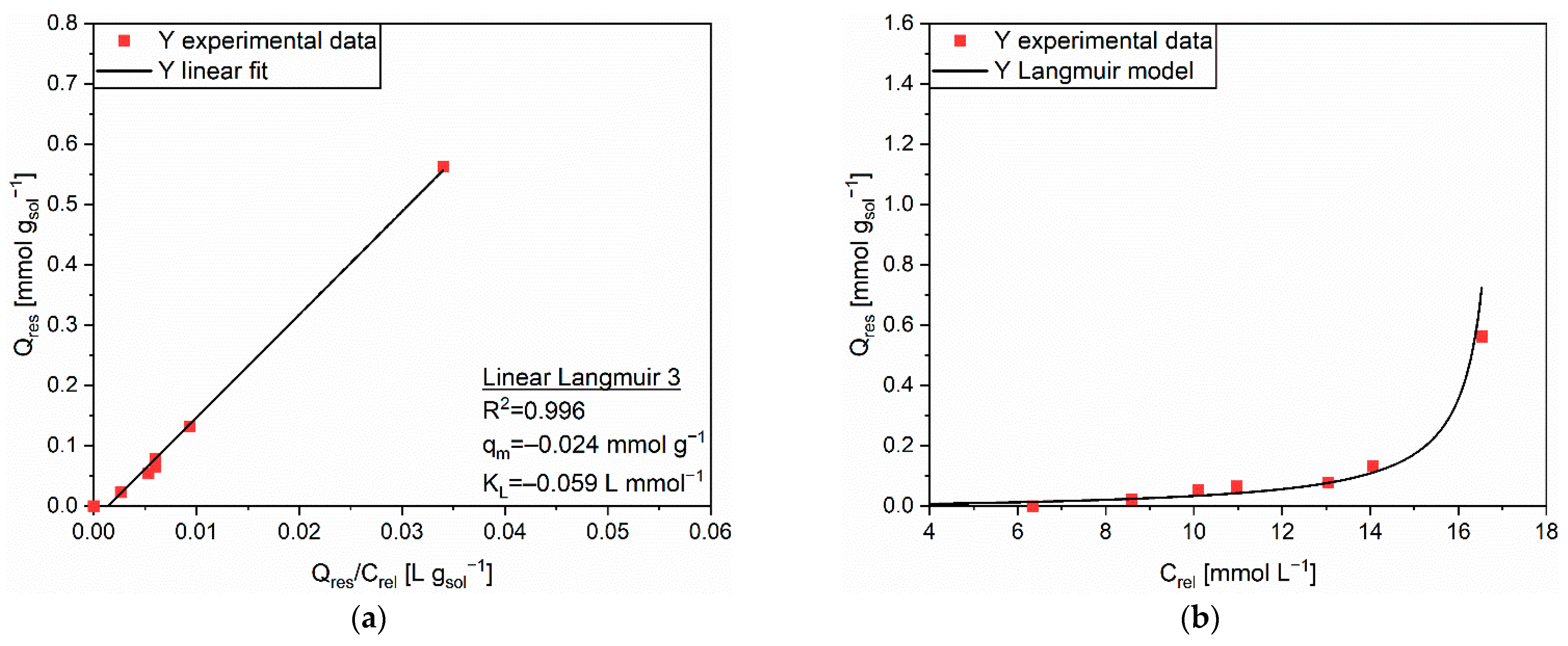
3.1.2. Release
3.2. Modified Activated Carbon
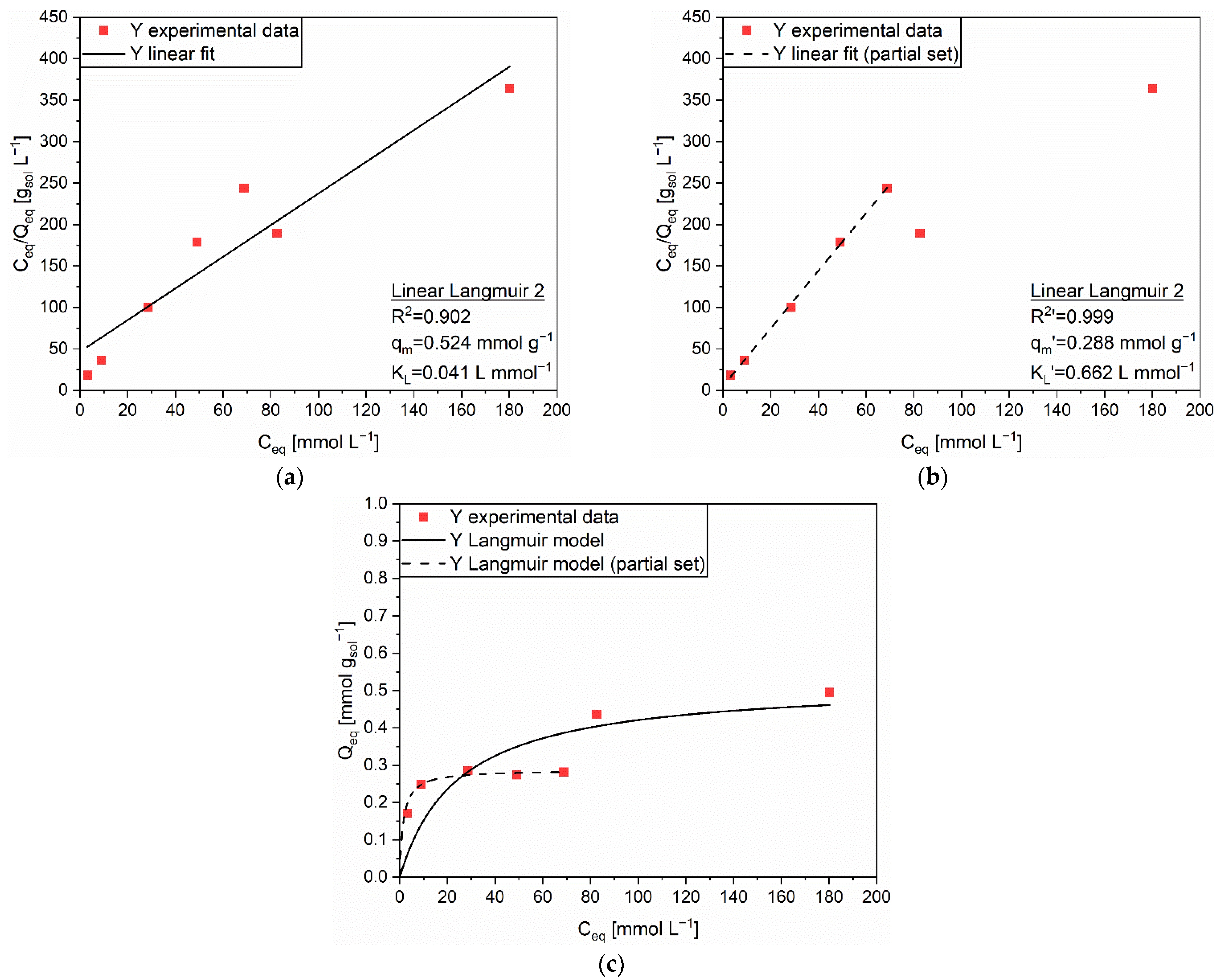
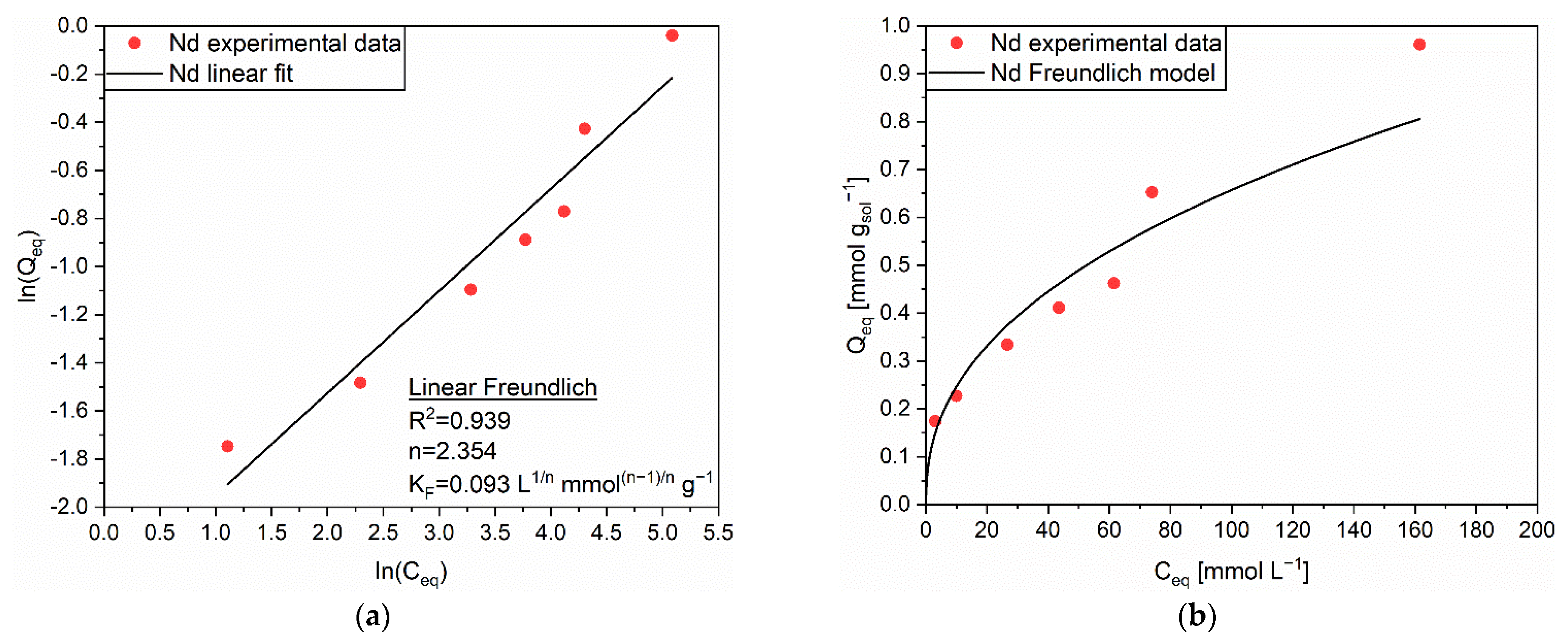
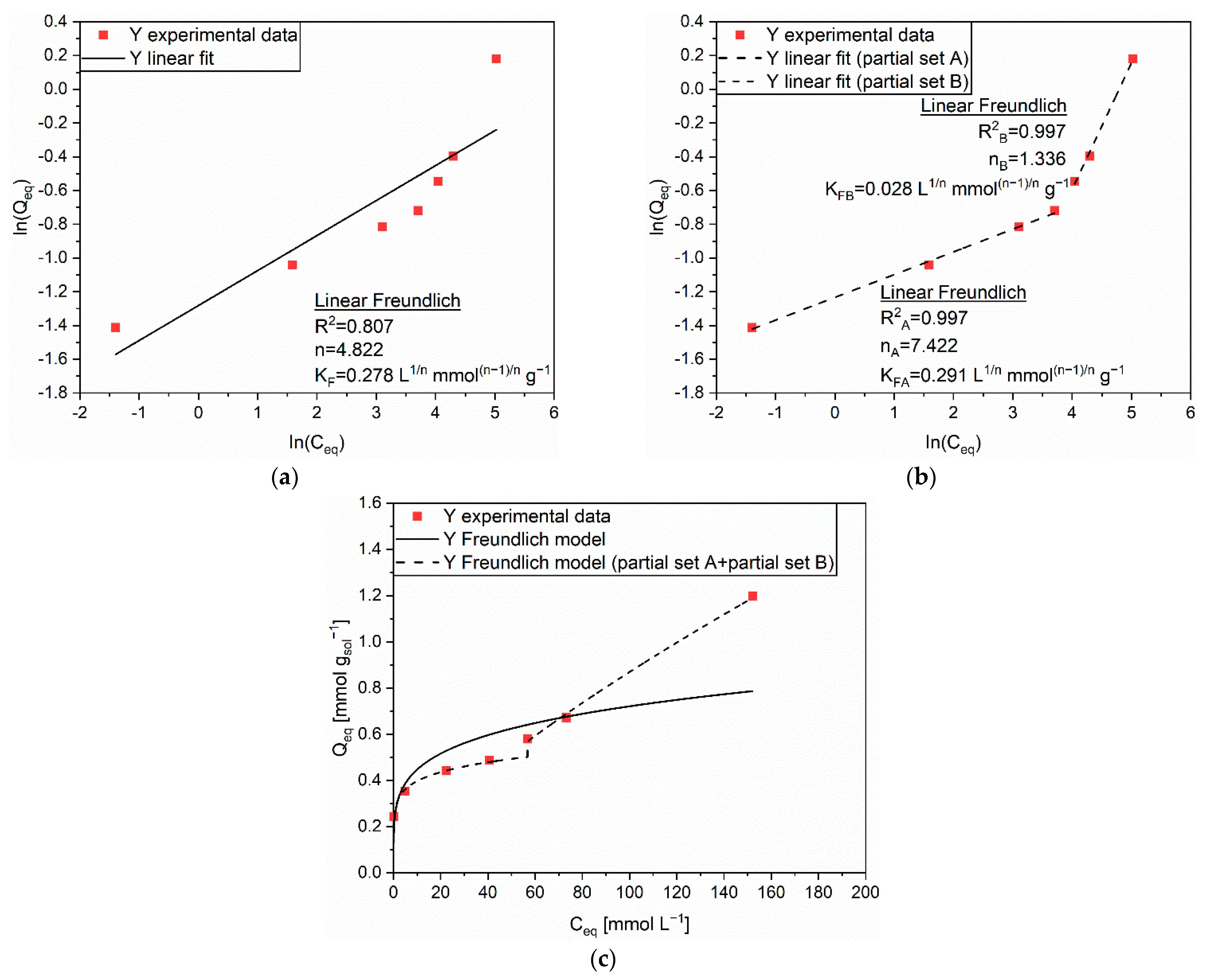
3.2.1. Adsorption
3.2.2. Release
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdelbasir, S.M.; Hassan, S.S.M.; Kamel, A.H.; El-Nasr, R.S. Status of electronic waste recycling techniques: A review. Environ. Sci. Pollut. Res. 2018, 25, 16533–16547. [Google Scholar] [CrossRef] [PubMed]
- Andrade, D.F.; Romanelli, J.P.; Pereira-Filho, E.R. Past and emerging topics related to electronic waste management: Top countries, trends, and perspectives. Environ. Sci. Pollut. Res. 2019, 26, 17135–17151. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Ge, L.; Shi, S.; Sun, Y.; Liu, M.; Wang, B.; Shang, Y.; Wu, J.; Tian, J. Global trends and future prospects of e-waste research: A bibliometric analysis. Environ. Sci. Pollut. Res. 2019, 26, 17809–17820. [Google Scholar] [CrossRef]
- Xavier, L.H.; Giese, E.C.; Ribeiro-Duthie, A.C.; Lins, F.A.F. Sustainability and the circular economy: A theoretical approach focused on e-waste urban mining. Resour. Policy 2021, 74, 101467. [Google Scholar] [CrossRef]
- Iannicelli Zubiani, E.M.; Cristiani, C.; Dotelli, G.; Stampino, P.G.; Pelosato, R. Recovery of rare earths and precious metals from waste electrical and electronic equipment by acid leaching and immobilized chelating agents. Chem. Eng. Trans. 2015, 43, 2413–2418. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Chen, J.; Kallem, P.; Banat, F.; Qiu, H. Recent advances in selective separation technologies of rare earth elements: A review. J. Environ. Chem. Eng. 2022, 10, 107104. [Google Scholar] [CrossRef]
- Shittu, O.S.; Williams, I.D.; Shaw, P.J. Global E-waste management: Can WEEE make a difference? A review of e-waste trends, legislation, contemporary issues and future challenges. Waste Manag. 2021, 120, 549–563. [Google Scholar] [CrossRef]
- Egedy, A.; Fogarasi, S.; Varga, T.; Imre-Lucaci, Á.; Chován, T. CFD models in the development of electrical waste recycling technologies. Chem. Eng. Trans. 2013, 35, 1327–1332. [Google Scholar] [CrossRef]
- Ambaye, T.G.; Vaccari, M.; Castro, F.D.; Prasad, S.; Rtimi, S. Emerging technologies for the recovery of rare earth elements (REEs) from the end-of-life electronic wastes: A review on progress, challenges, and perspectives. Environ. Sci. Pollut. Res. 2020, 27, 36052–36074. [Google Scholar] [CrossRef]
- European Commission. Critical Raw Materials Resilience: Charting a Path towards Greater Security and Sustainability 2021. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52020DC0474 (accessed on 10 November 2022).
- Royer-Lavallée, A.; Neculita, C.M.; Coudert, L. Removal and potential recovery of rare earth elements from mine water. J. Ind. Eng. Chem. 2020, 89, 47–57. [Google Scholar] [CrossRef]
- Liu, T.; Chen, J. Extraction and separation of heavy rare earth elements: A review. Sep. Purif. Technol. 2021, 276, 119263. [Google Scholar] [CrossRef]
- Wang, Y.; Wan, Q.; Liu, B.; Wei, Z.; Zhang, M.; Tang, Y. Co-transport and competitive retention of different ionic rare earth elements (REEs) in quartz sand: Effect of kaolinite. Sci. Total Environ. 2020, 722, 137779. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Shao, P.; Chen, Y.; Zhou, X.; Yang, L.; Shi, H.; Yu, K.; Luo, X.; Luo, X. A critical review of the recovery of rare earth elements from wastewater by algae for resources recycling technologies. Resour. Conserv. Recycl. 2021, 169, 105519. [Google Scholar] [CrossRef]
- Allam, E.M.; Lashen, T.A.; Abou El-Enein, S.A.; Hassanin, M.A.; Sakr, A.K.; Hanfi, M.Y.; Sayyed, M.I.; Al-Otaibi, J.S.; Cheira, M.F. Cetylpyridinium Bromide/Polyvinyl Chloride for Substantially Efficient Capture of Rare Earth Elements from Chloride Solution. Polymers 2022, 14, 954. [Google Scholar] [CrossRef] [PubMed]
- Iftekhar, S.; Ramasamy, D.L.; Srivastava, V.; Asif, M.B.; Sillanpää, M. Understanding the factors affecting the adsorption of Lanthanum using different adsorbents: A critical review. Chemosphere 2018, 204, 413–430. [Google Scholar] [CrossRef]
- Cristiani, C.; Bellotto, M.; Dotelli, G.; Latorrata, S.; Ramis, G.; Gallo Stampino, P.; Zubiani, E.M.I.; Finocchio, E. Rare Earths (La, Y, and Nd) Adsorption Behaviour towards Mineral Clays and Organoclays: Monoionic and Trionic Solutions. Minerals 2020, 11, 30. [Google Scholar] [CrossRef]
- Shrestha, R.; Ban, S.; Devkota, S.; Sharma, S.; Joshi, R.; Tiwari, A.P.; Kim, H.Y.; Joshi, M.K. Technological trends in heavy metals removal from industrial wastewater: A review. J. Environ. Chem. Eng. 2021, 9, 105688. [Google Scholar] [CrossRef]
- Anastopoulos, I.; Bhatnagar, A.; Lima, E.C. Adsorption of rare earth metals: A review of recent literature. J. Mol. Liq. 2016, 221, 954–962. [Google Scholar] [CrossRef]
- Iannicelli Zubiani, E.M.; Gallo Stampino, P.; Cristiani, C.; Dotelli, G. Enhanced lanthanum adsorption by amine modified activated carbon. Chem. Eng. J. 2018, 341, 75–82. [Google Scholar] [CrossRef]
- Zhao, Y.; Liang, T.; Miao, P.; Chen, T.; Han, X.; Hu, G.; Gao, J. Green Preparation of Aminated Magnetic PMMA Microspheres via EB Irradiation and Its Highly Efficient Uptake of Ce(III). Materials 2022, 15, 6553. [Google Scholar] [CrossRef]
- Kumrić, K.R.; Đukić, A.B.; Trtić-Petrović, T.M.; Vukelić, N.S.; Stojanović, Z.; Grbović Novaković, J.D.; Matović, L.L. Simultaneous Removal of Divalent Heavy Metals from Aqueous Solutions Using Raw and Mechanochemically Treated Interstratified Montmorillonite/Kaolinite Clay. Ind. Eng. Chem. Res. 2013, 52, 7930–7939. [Google Scholar] [CrossRef]
- Krajnák, A.; Viglašová, E.; Galamboš, M.; Krivosudský, L. Kinetics, thermodynamics and isotherm parameters of uranium(VI) adsorption on natural and HDTMA-intercalated bentonite and zeolite. Desalin. Water Treat. 2018, 127, 272–281. [Google Scholar] [CrossRef]
- Zhu, R.; Chen, Q.; Zhou, Q.; Xi, Y.; Zhu, J.; He, H. Adsorbents based on montmorillonite for contaminant removal from water: A review. Appl. Clay Sci. 2016, 123, 239–258. [Google Scholar] [CrossRef]
- Sakr, A.K.; Cheira, M.F.; Hassanin, M.A.; Mira, H.I.; Mohamed, S.A.; Khandaker, M.U.; Osman, H.; Eed, E.M.; Sayyed, M.I.; Hanfi, M.Y. Adsorption of Yttrium Ions on 3-Amino-5-Hydroxypyrazole Impregnated Bleaching Clay, a Novel Sorbent Material. Appl. Sci. 2021, 11, 10320. [Google Scholar] [CrossRef]
- Zhou, F.; Feng, J.; Xie, X.; Wu, B.; Liu, Q.; Wu, X.; Chi, R. Adsorption of lanthanum(III) and yttrium(III) on kaolinite: Kinetics and adsorption isotherms. Physicochem. Probl. Miner. Process. 2019, 55, 928–939. [Google Scholar] [CrossRef]
- Bouchmila, I.; Bejaoui Kefi, B.; Djebali, K.; Souissi, R. Optimization and modeling of solid-phase extraction of rare earth elements with chert using design methodology. Microchem. J. 2022, 176, 107182. [Google Scholar] [CrossRef]
- Tian, L.; Fu, K.; Chen, S.; Yao, J.; Bian, L. Comparison of microscopic adsorption characteristics of Zn(II), Pb(II), and Cu(II) on kaolinite. Sci. Rep. 2022, 12, 15936. [Google Scholar] [CrossRef]
- Qadeer, R. Adsorption of neodymium ions on activated charcoal from aqeous solutions. J. Radioanal. Nucl. Chem. 2005, 265, 377–381. [Google Scholar] [CrossRef]
- Chen, Q. Study on the adsorption of lanthanum(III) from aqueous solution by bamboo charcoal. J. Rare Earths 2010, 28, 125–131. [Google Scholar] [CrossRef]
- Qu, W.; Yuan, T.; Yin, G.; Xu, S.; Zhang, Q.; Su, H. Effect of properties of activated carbon on malachite green adsorption. Fuel 2019, 249, 45–53. [Google Scholar] [CrossRef]
- Brown, A.T.; Balkus, K.J. Critical Rare Earth Element Recovery from Coal Ash Using Microsphere Flower Carbon. ACS Appl. Mater. Interfaces 2021, 13, 48492–48499. [Google Scholar] [CrossRef]
- Gismondi, P.; Kuzmin, A.; Unsworth, C.; Rangan, S.; Khalid, S.; Saha, D. Understanding the Adsorption of Rare-Earth Elements in Oligo-Grafted Mesoporous Carbon. Langmuir 2022, 38, 203–210. [Google Scholar] [CrossRef]
- Slavković-Beškoski, L.; Ignjatović, L.; Bolognesi, G.; Maksin, D.; Savić, A.; Vladisavljević, G.; Onjia, A. Dispersive Solid–Liquid Microextraction Based on the Poly(HDDA)/Graphene Sorbent Followed by ICP-MS for the Determination of Rare Earth Elements in Coal Fly Ash Leachate. Metals 2022, 12, 791. [Google Scholar] [CrossRef]
- Bosacka, A.; Zienkiewicz-Strzałka, M.; Deryło-Marczewska, A.; Chrzanowska, A.; Wasilewska, M.; Sternik, D. Physicochemical, structural, and adsorption properties of chemically and thermally modified activated carbons. Colloids Surfaces A Physicochem. Eng. Asp. 2022, 647, 129130. [Google Scholar] [CrossRef]
- S, D.S.; Vishwakarma, V. Recovery and recycle of wastewater contaminated with heavy metals using adsorbents incorporated from waste resources and nanomaterials—A review. Chemosphere 2021, 273, 129677. [Google Scholar] [CrossRef] [PubMed]
- Cristiani, C.; Iannicelli-Zubiani, E.M.; Bellotto, M.; Dotelli, G.; Stampino, P.G.; Latorrata, S.; Ramis, G.; Finocchio, E. Capture Mechanism of La and Cu Ions in Mixed Solutions by Clay and Organoclay. Ind. Eng. Chem. Res. 2021, 60, 6803–6813. [Google Scholar] [CrossRef]
- Cristiani, C.; Iannicelli-Zubiani, E.M.; Dotelli, G.; Finocchio, E.; Gallo Stampino, P.; Licchelli, M. Polyamine-Based Organo-Clays for Polluted Water Treatment: Effect of Polyamine Structure and Content. Polymers 2019, 11, 897. [Google Scholar] [CrossRef] [PubMed]
- Cristiani, C.; Bellotto, M.; Dotelli, G.; Gallo Stampino, P.; Latorrata, S.; Finocchio, E. Capture and Release Mechanism of Ni and La Ions via Solid/Liquid Process: Use of Polymer-Modified Clay and Activated Carbons. Polymers 2022, 14, 485. [Google Scholar] [CrossRef]
- Bernal, V.; Giraldo, L.; Moreno-Piraján, J. Physicochemical Properties of Activated Carbon: Their Effect on the Adsorption of Pharmaceutical Compounds and Adsorbate–Adsorbent Interactions. C 2018, 4, 62. [Google Scholar] [CrossRef]
- Demey, H.; Lapo, B.; Ruiz, M.; Fortuny, A.; Marchand, M.; Sastre, A. Neodymium Recovery by Chitosan/Iron(III) Hydroxide [ChiFer(III)] Sorbent Material: Batch and Column Systems. Polymers 2018, 10, 204. [Google Scholar] [CrossRef] [PubMed]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and Interpretation of Adsorption Isotherms. J. Chem. 2017, 2017, 3039817. [Google Scholar] [CrossRef]
- Chen, X. Modeling of Experimental Adsorption Isotherm Data. Information 2015, 6, 14–22. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J. Comparison of linearization methods for modeling the Langmuir adsorption isotherm. J. Mol. Liq. 2019, 296, 111850. [Google Scholar] [CrossRef]
- Javadian, H.; Ruiz, M.; Taghvai, M.; Sastre, A.M. Novel magnetic nanocomposite of calcium alginate carrying poly(pyrimidine-thiophene-amide) as a novel green synthesized polyamide for adsorption study of neodymium, terbium, and dysprosium rare-earth ions. Colloids Surfaces A Physicochem. Eng. Asp. 2020, 603, 125252. [Google Scholar] [CrossRef]
- Koochaki-Mohammadpour, S.M.A.; Torab-Mostaedi, M.; Talebizadeh-Rafsanjani, A.; Naderi-Behdani, F. Adsorption Isotherm, Kinetic, Thermodynamic, and Desorption Studies of Lanthanum and Dysprosium on Oxidized Multiwalled Carbon Nanotubes. J. Dispers. Sci. Technol. 2014, 35, 244–254. [Google Scholar] [CrossRef]
- Pholosi, A.; Naidoo, E.B.; Ofomaja, A.E. Intraparticle diffusion of Cr(VI) through biomass and magnetite coated biomass: A comparative kinetic and diffusion study. S. Afr. J. Chem. Eng. 2020, 32, 39–55. [Google Scholar] [CrossRef]
- Zawisza, B.; Pytlakowska, K.; Feist, B.; Polowniak, M.; Kita, A.; Sitko, R. Determination of rare earth elements by spectroscopic techniques: A review. J. Anal. At. Spectrom. 2011, 26, 2373–2390. [Google Scholar] [CrossRef]
- Ticová, B.; Novotný, K.; Kanický, V. Comparison of different spectral resolution ICP-OES spectrometers for the determination of rare earth elements. Chem. Pap. 2019, 73, 2913–2921. [Google Scholar] [CrossRef]
- Kinraide, T.B.; Yermiyahu, U. A scale of metal ion binding strengths correlating with ionic charge, Pauling electronegativity, toxicity, and other physiological effects. J. Inorg. Biochem. 2007, 101, 1201–1213. [Google Scholar] [CrossRef]
- Berber, M.R. Surface-functionalization of activated carbon with polyglucosamine polymer for efficient removal of cadmium ions. Polym. Compos. 2020, 41, 3074–3086. [Google Scholar] [CrossRef]
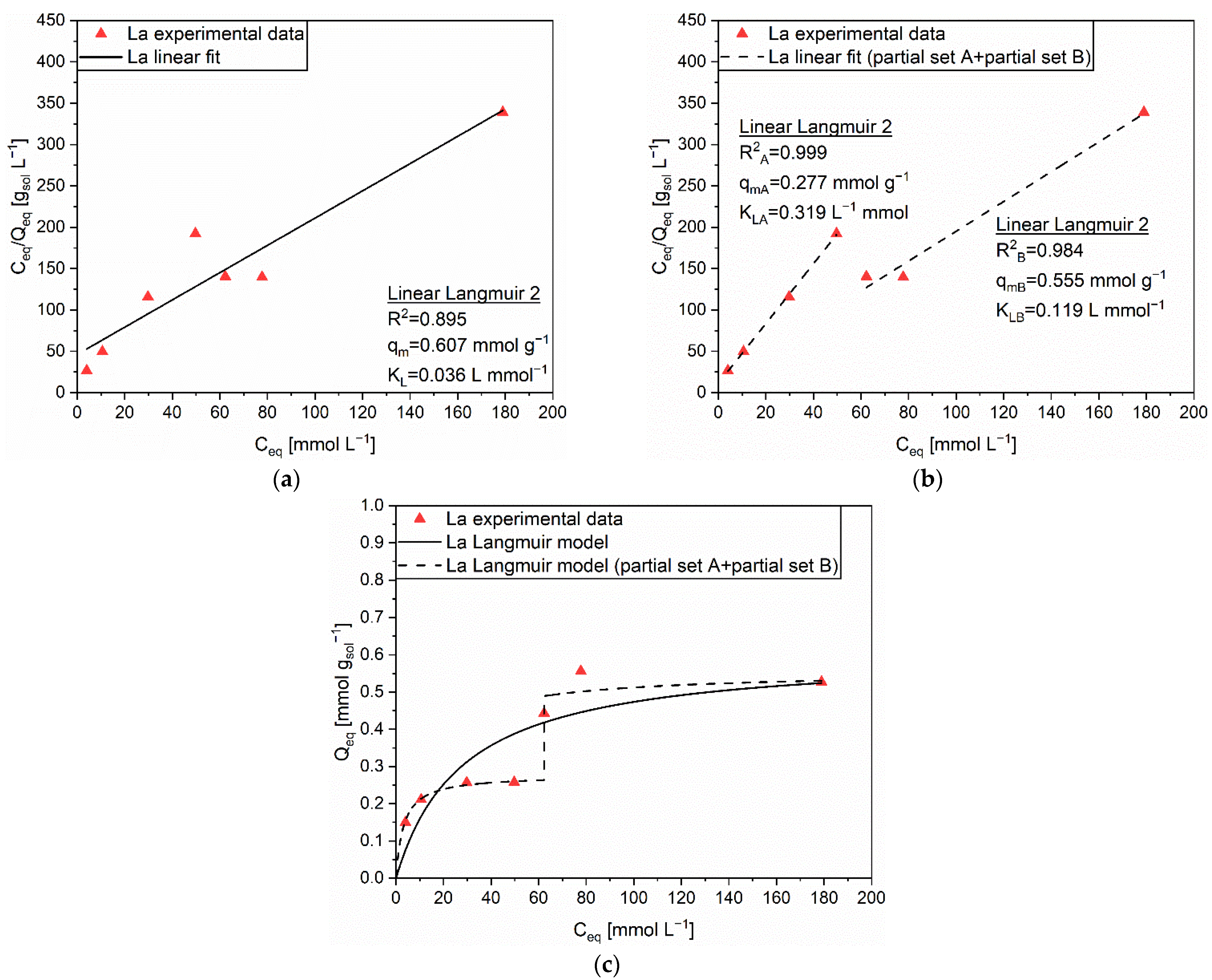
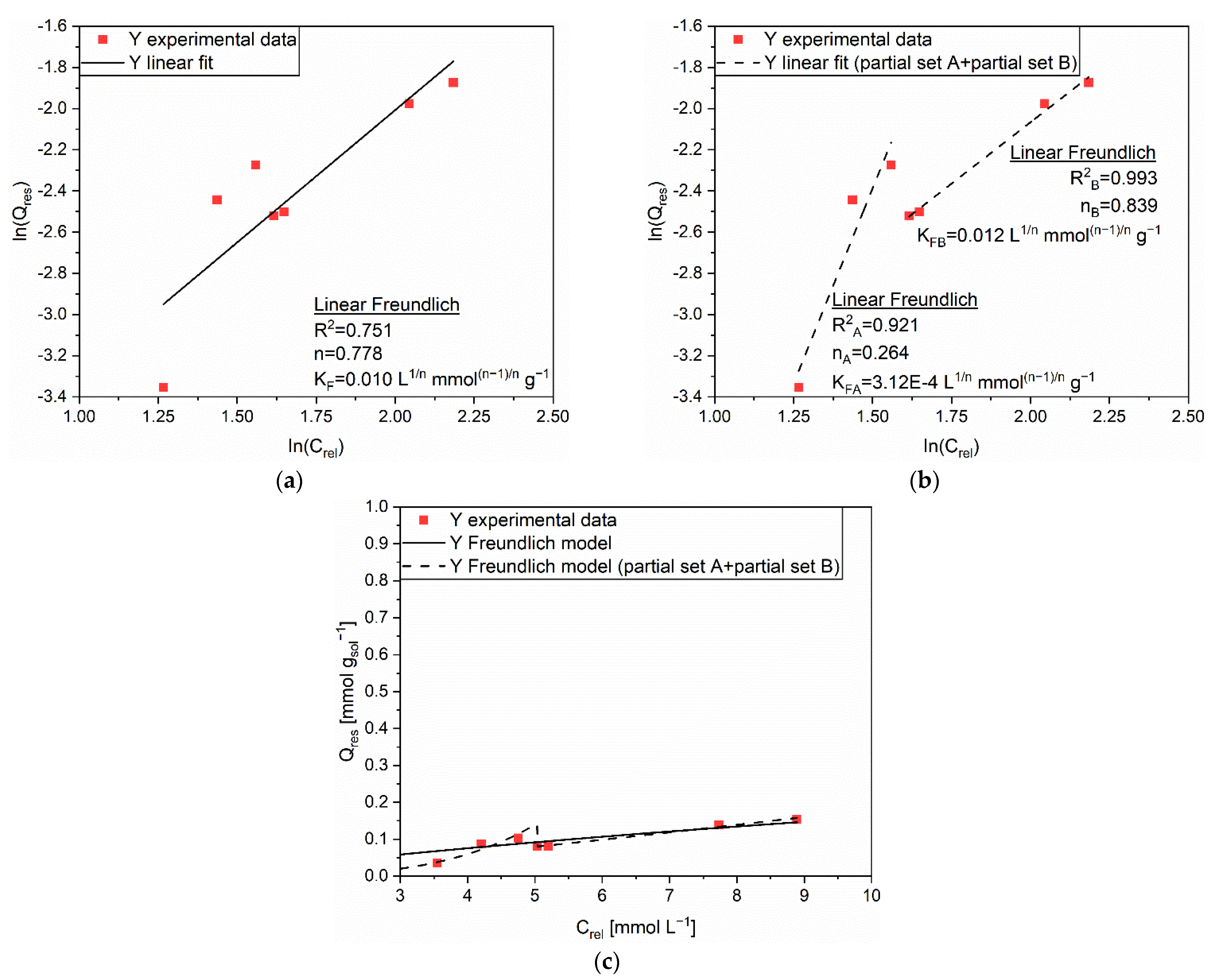
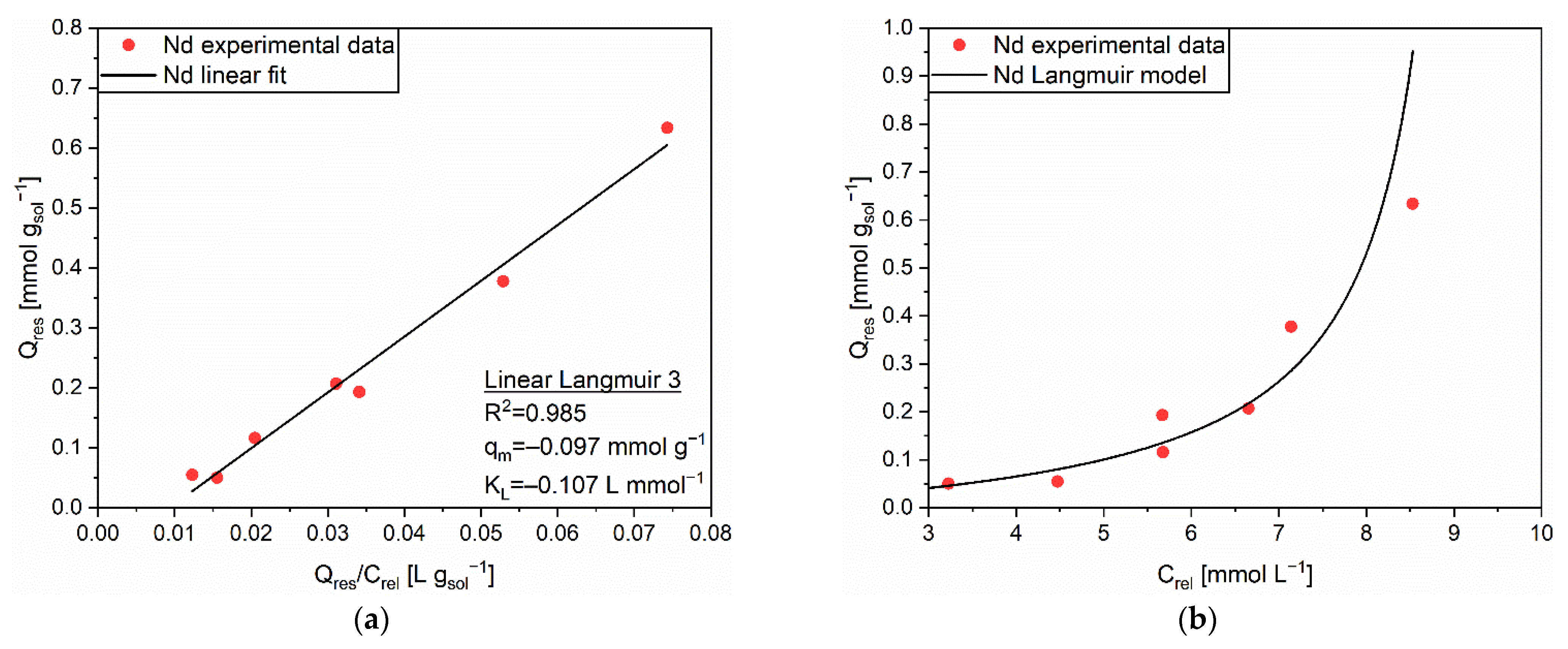
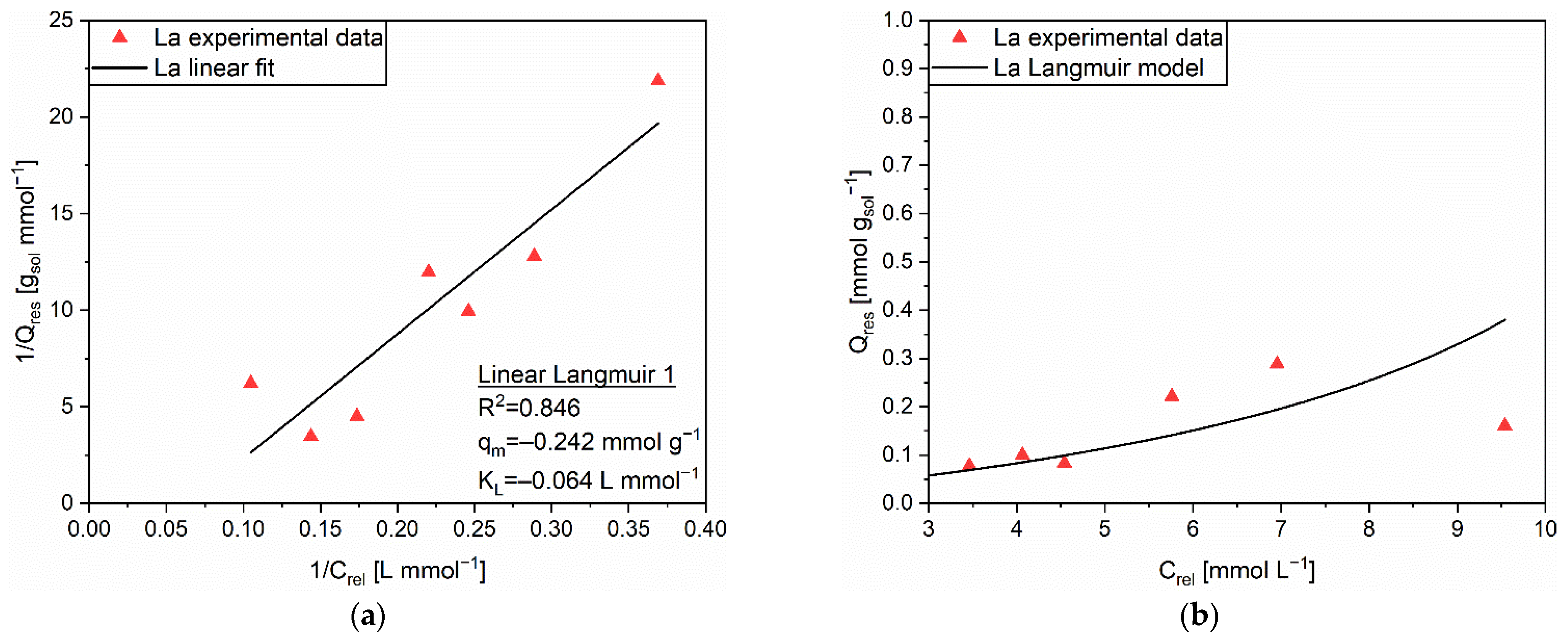

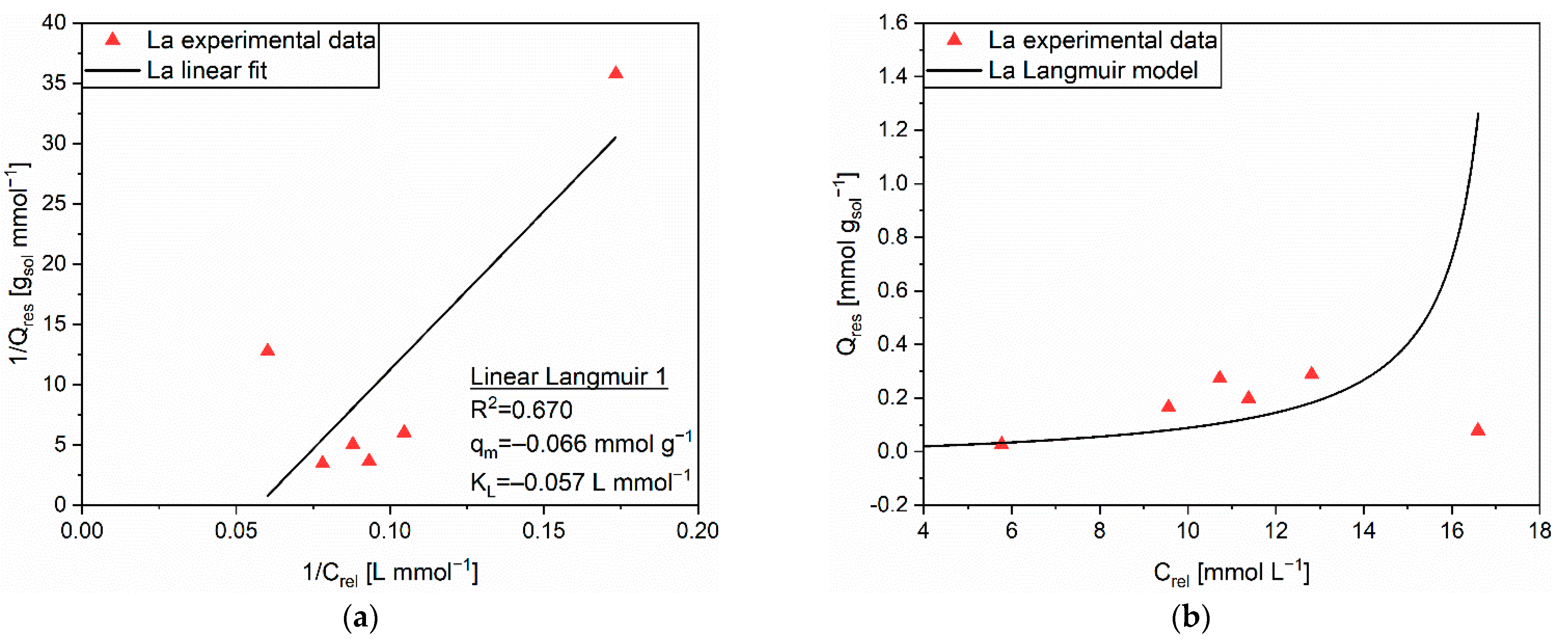
| Linear Form | Equation | Plot | Parameters |
| Linear Langmuir 1 | 1/Q vs. 1/C | qm, KL | |
| Linear Langmuir 2 | C/Q vs. C | qm, KL | |
| Linear Langmuir 3 | Q vs. Q/C | qm, KL | |
| Linear Freundlich | ln(Q) vs. ln(C) | n, KF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Virgilio, M.; Latorrata, S.; Cristiani, C.; Dotelli, G. Analysis of the Adsorption-Release Isotherms of Pentaethylenehexamine-Modified Sorbents for Rare Earth Elements (Y, Nd, La). Polymers 2022, 14, 5063. https://doi.org/10.3390/polym14235063
Di Virgilio M, Latorrata S, Cristiani C, Dotelli G. Analysis of the Adsorption-Release Isotherms of Pentaethylenehexamine-Modified Sorbents for Rare Earth Elements (Y, Nd, La). Polymers. 2022; 14(23):5063. https://doi.org/10.3390/polym14235063
Chicago/Turabian StyleDi Virgilio, Matteo, Saverio Latorrata, Cinzia Cristiani, and Giovanni Dotelli. 2022. "Analysis of the Adsorption-Release Isotherms of Pentaethylenehexamine-Modified Sorbents for Rare Earth Elements (Y, Nd, La)" Polymers 14, no. 23: 5063. https://doi.org/10.3390/polym14235063
APA StyleDi Virgilio, M., Latorrata, S., Cristiani, C., & Dotelli, G. (2022). Analysis of the Adsorption-Release Isotherms of Pentaethylenehexamine-Modified Sorbents for Rare Earth Elements (Y, Nd, La). Polymers, 14(23), 5063. https://doi.org/10.3390/polym14235063