Multifunctional Performance of Hybrid SrFe12O19/BaTiO3/Epoxy Resin Nanocomposites
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples Preparation
2.2. Scanning Electron Microscopy
2.3. X-ray Diffraction (XRD)
2.4. Broadband Dielectric Spectroscopy (BDS)
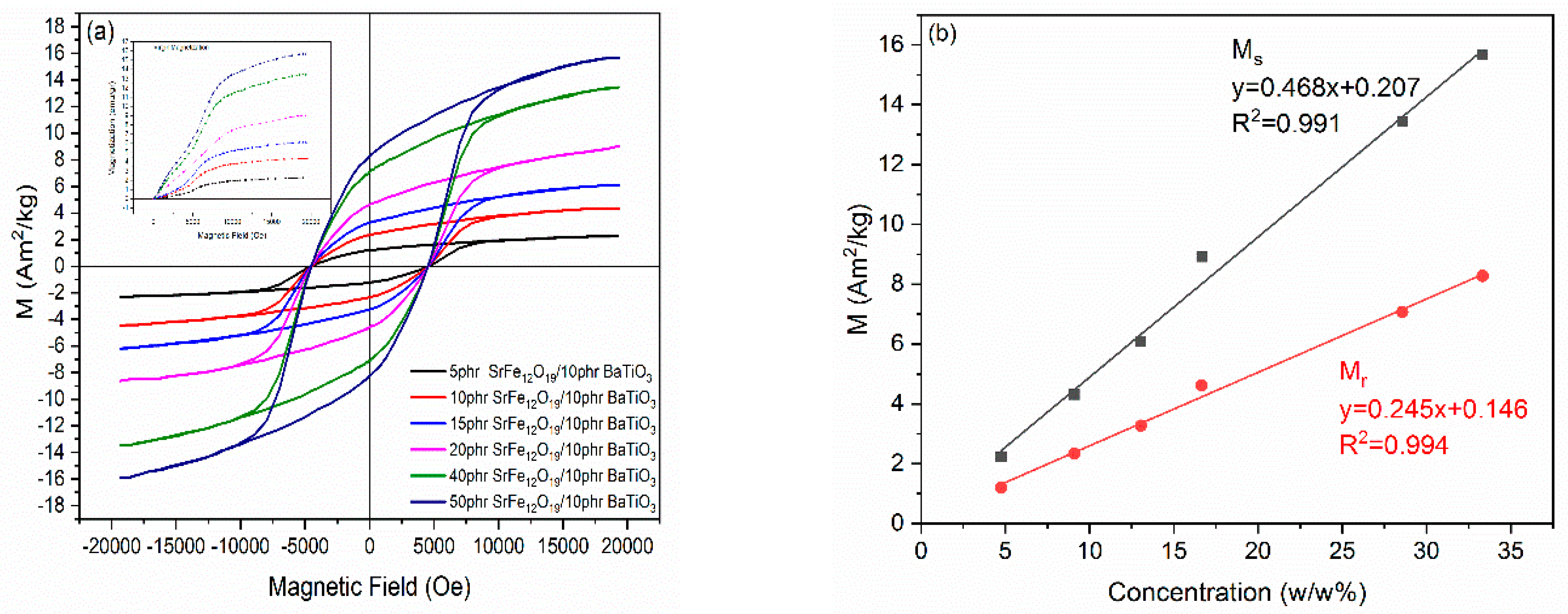
2.5. Magnetic Measurements
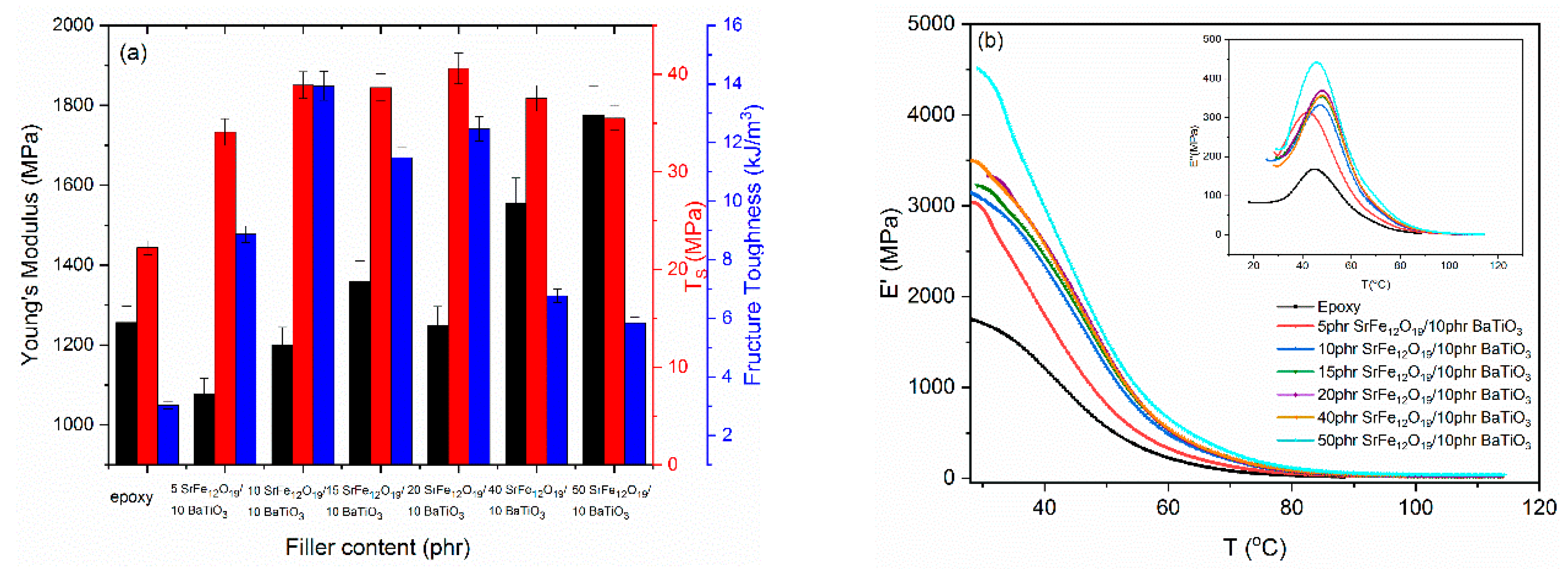
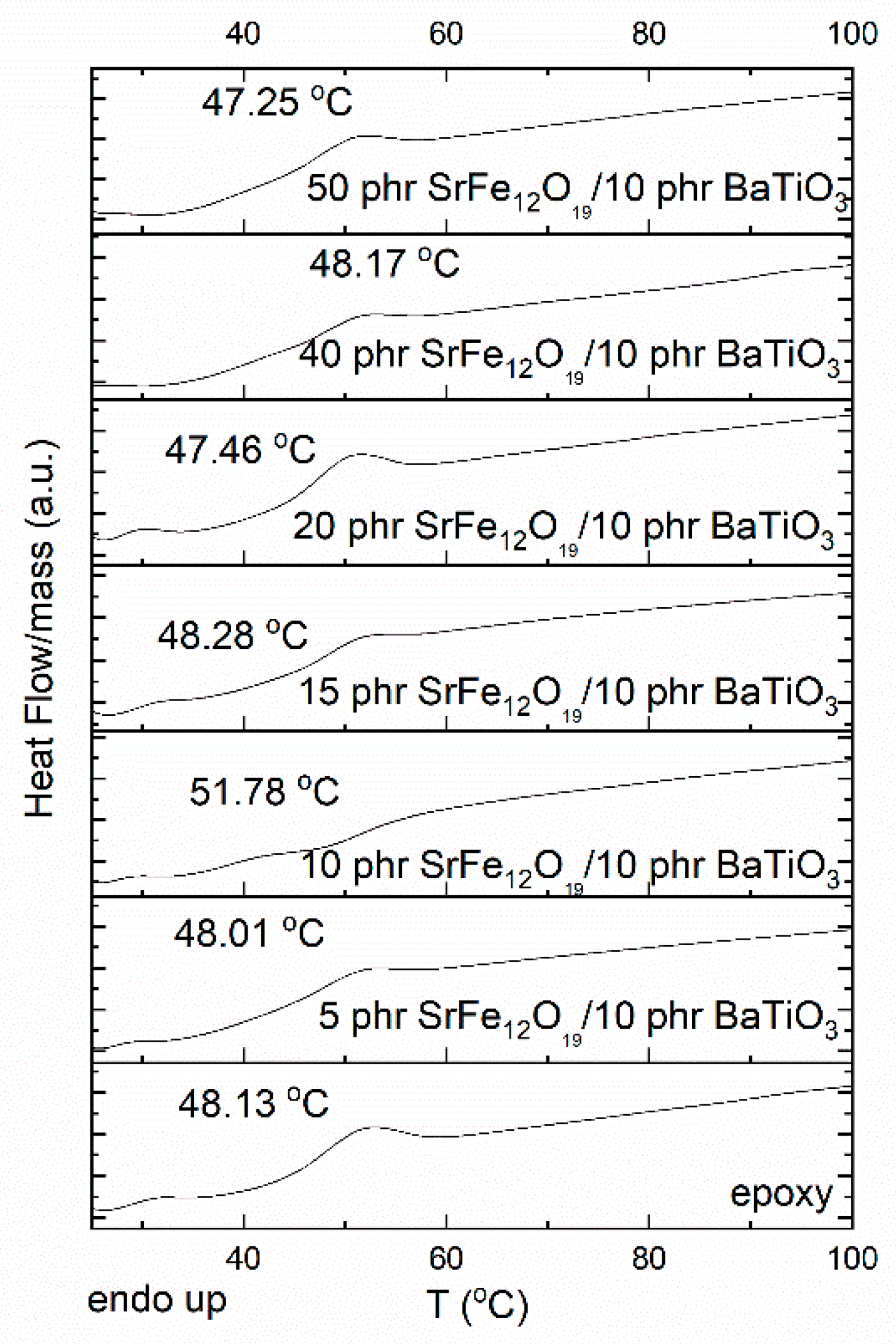
2.6. Thermomechanical Response
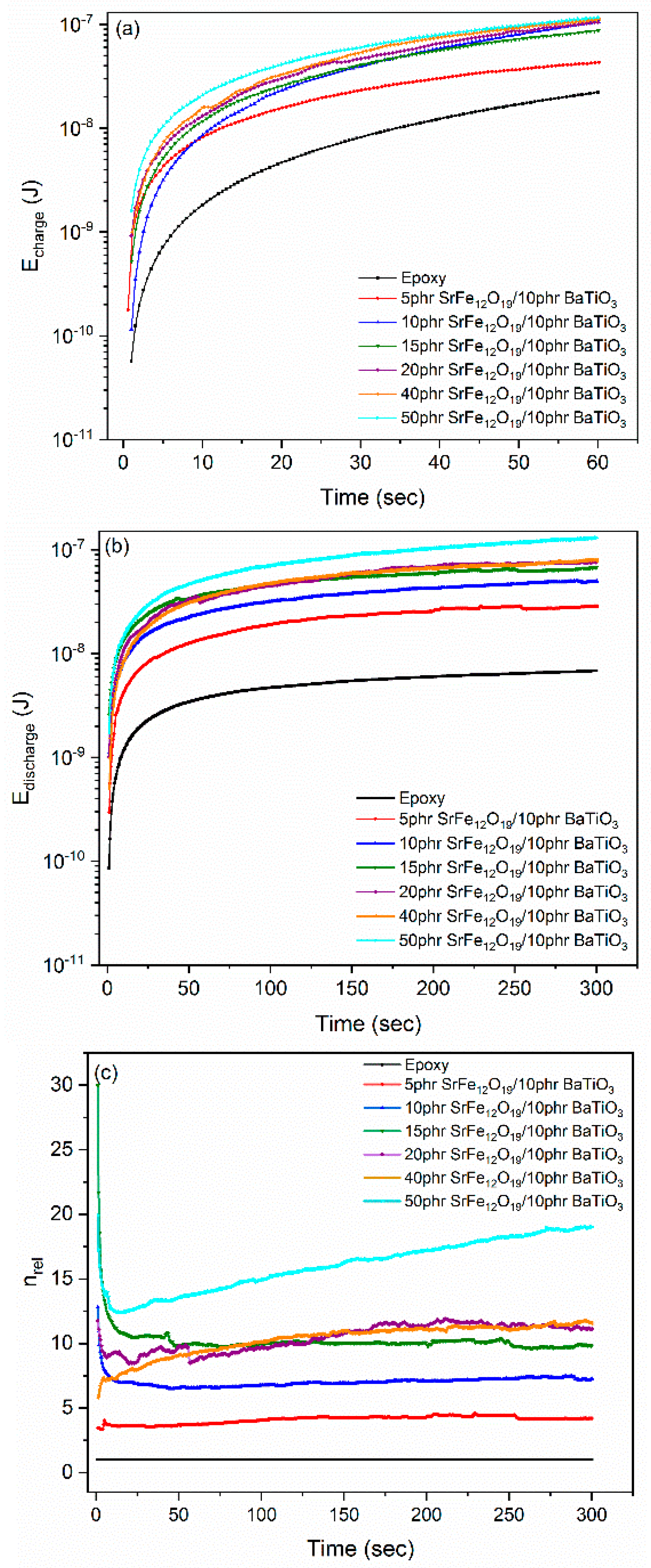
2.7. Energy Storing and Retrieving
3. Results
3.1. Morphological/Structural Characterization
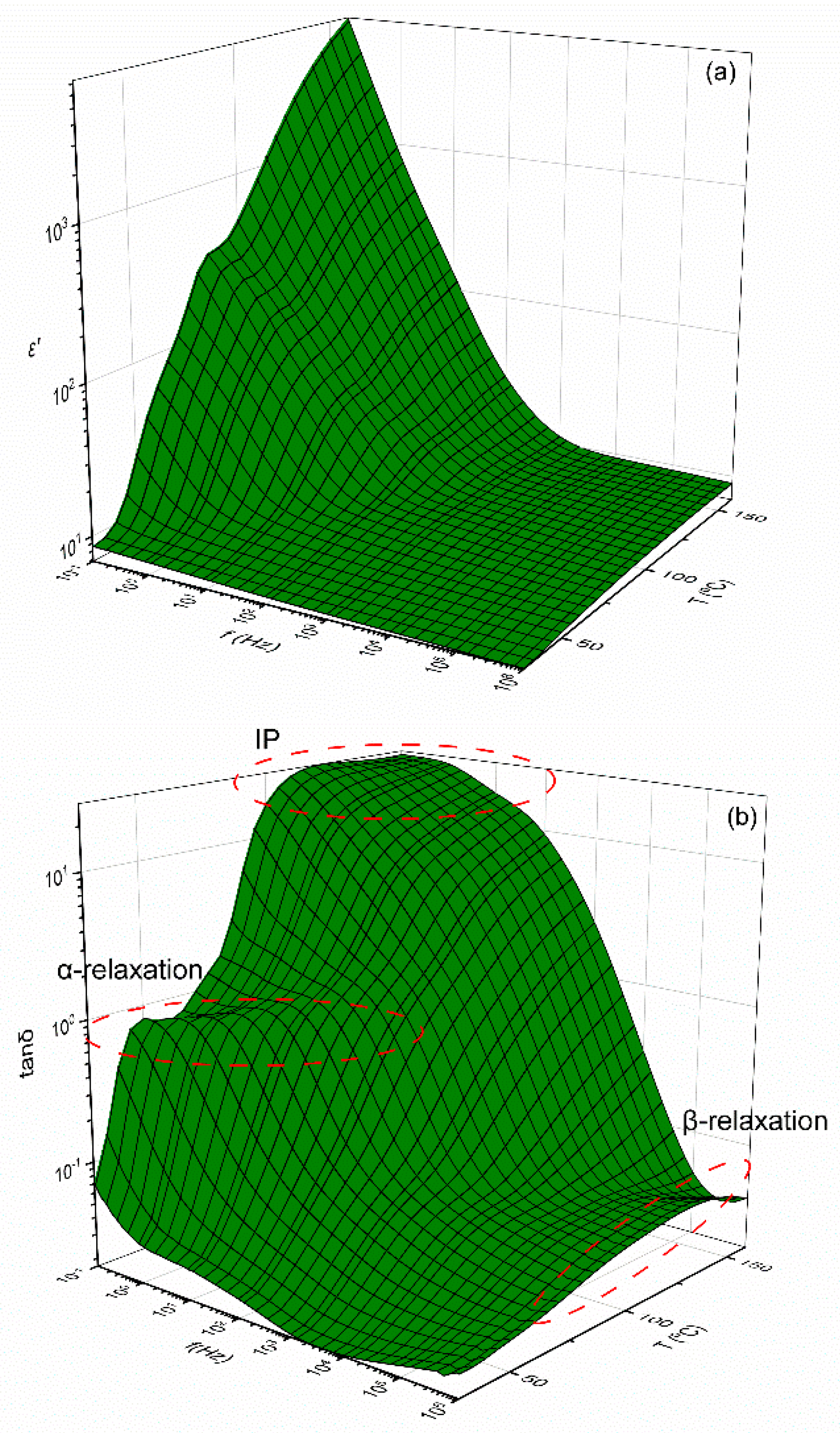
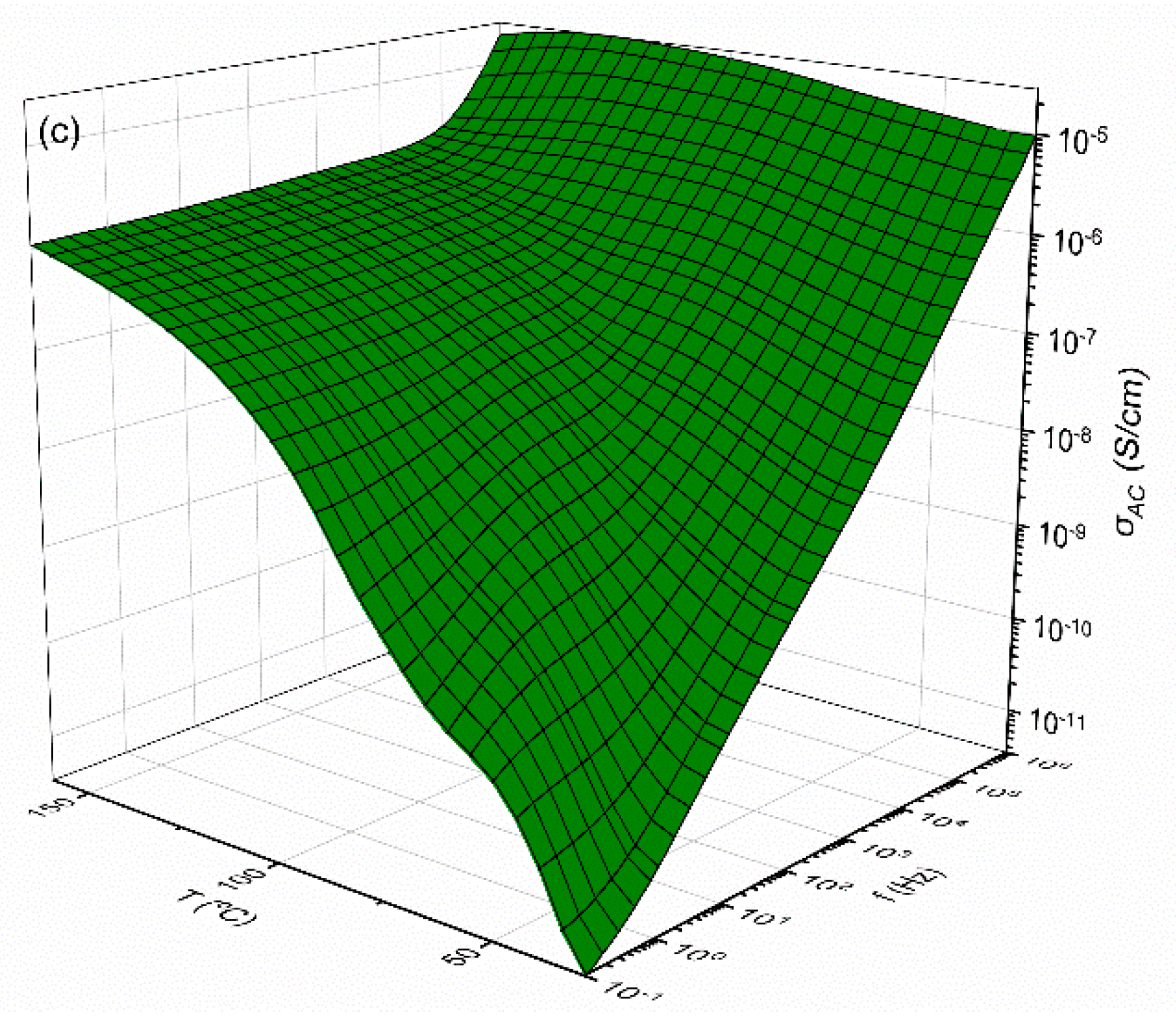
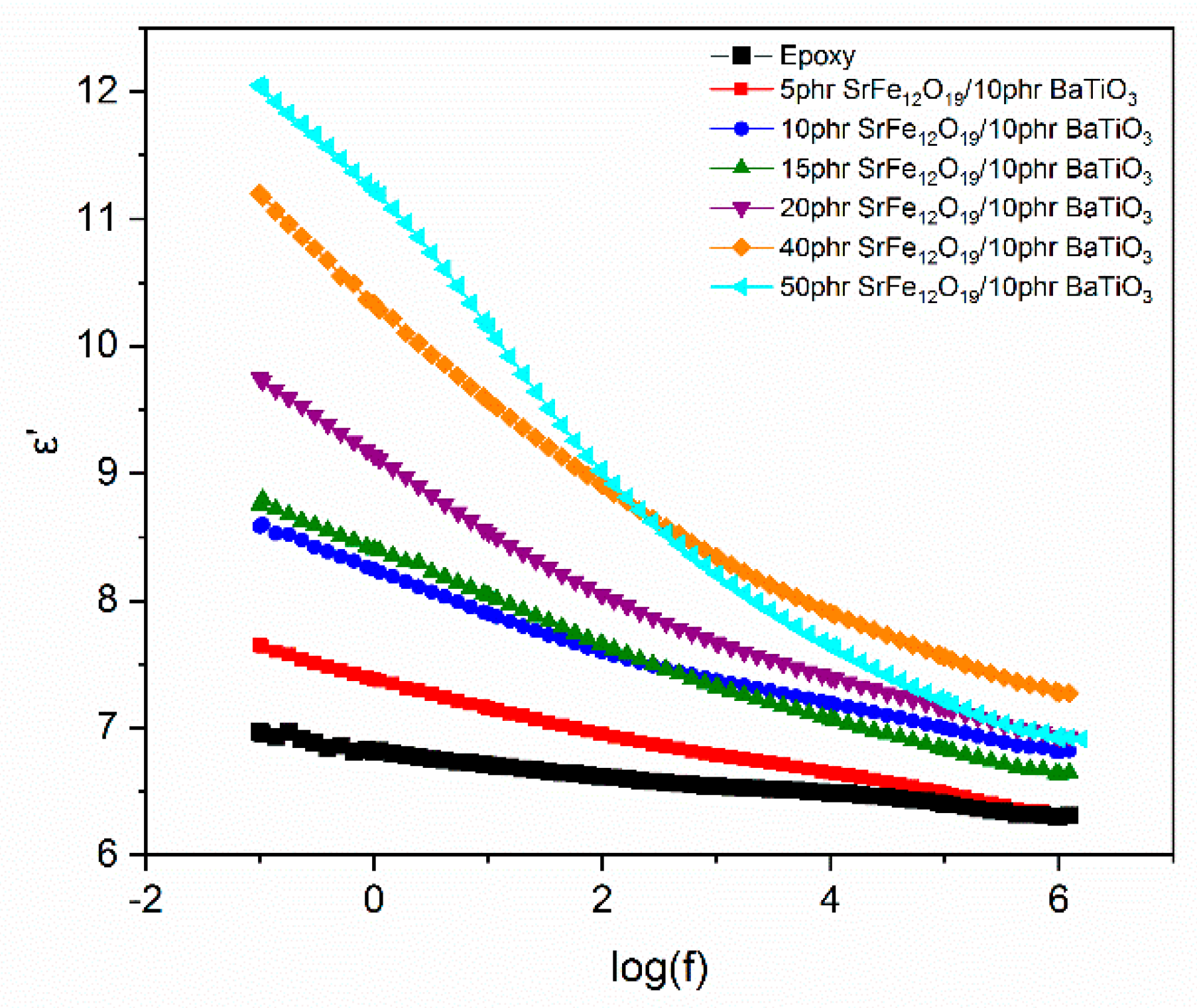
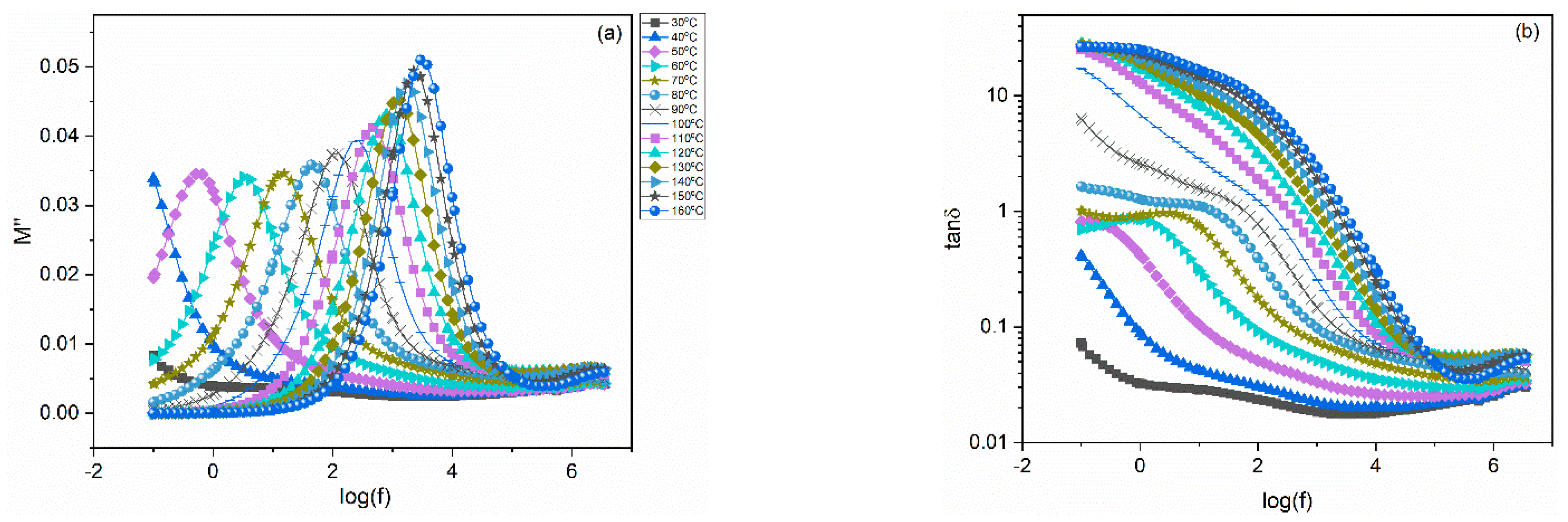
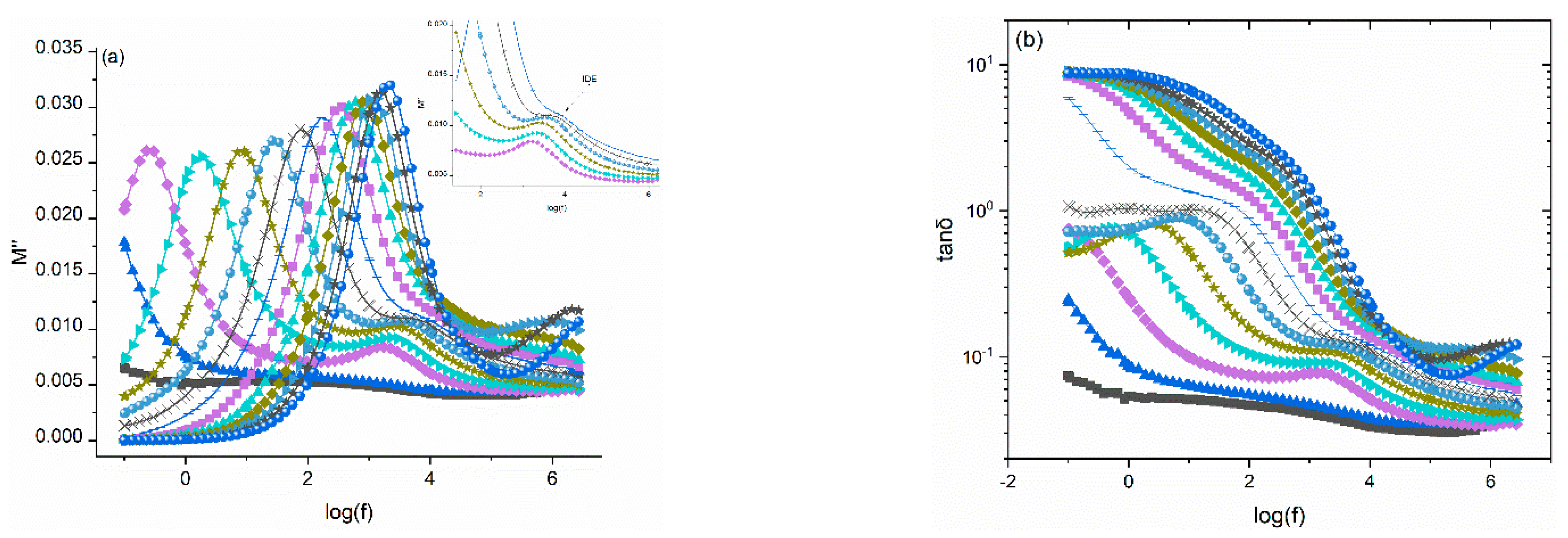
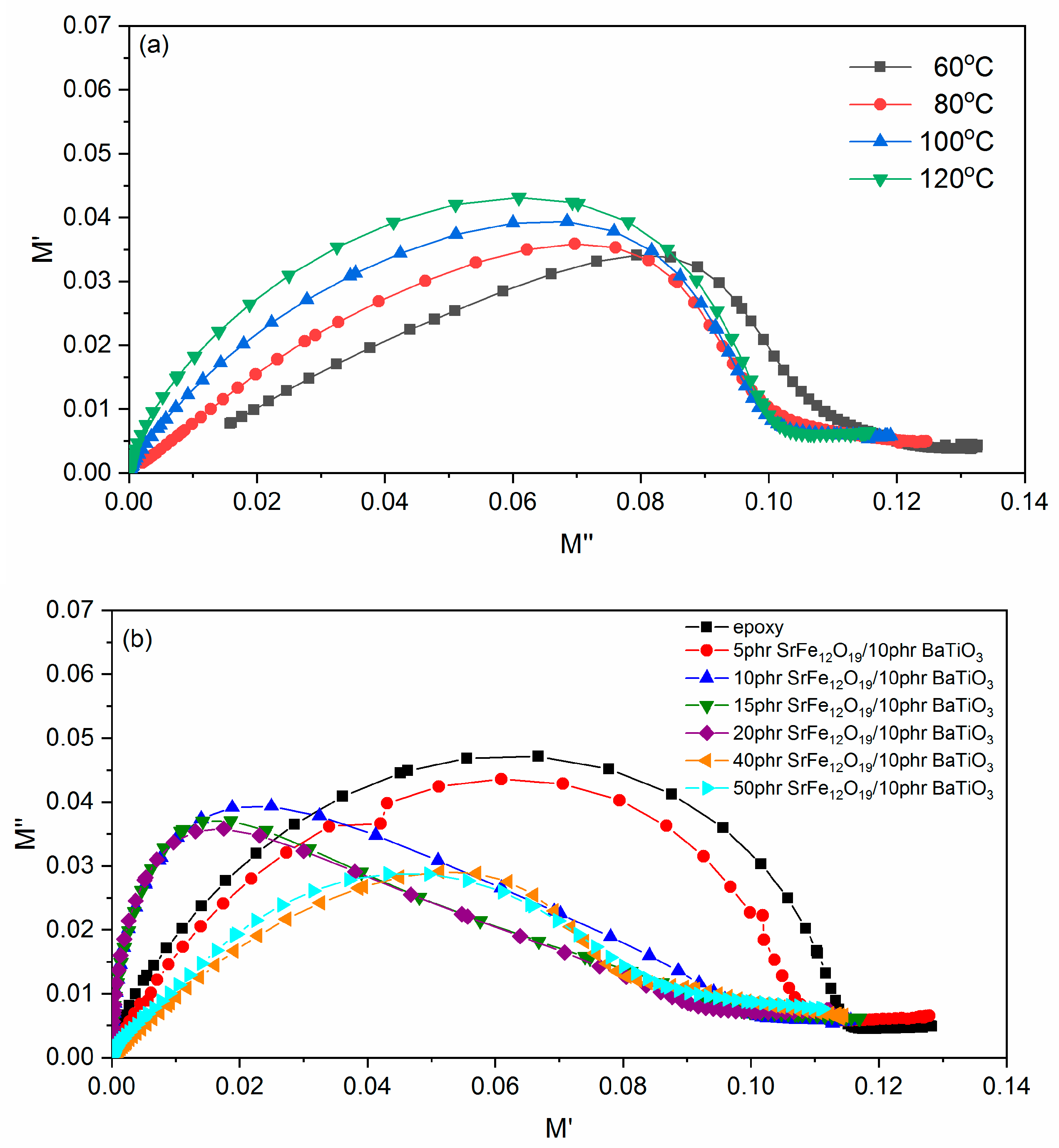
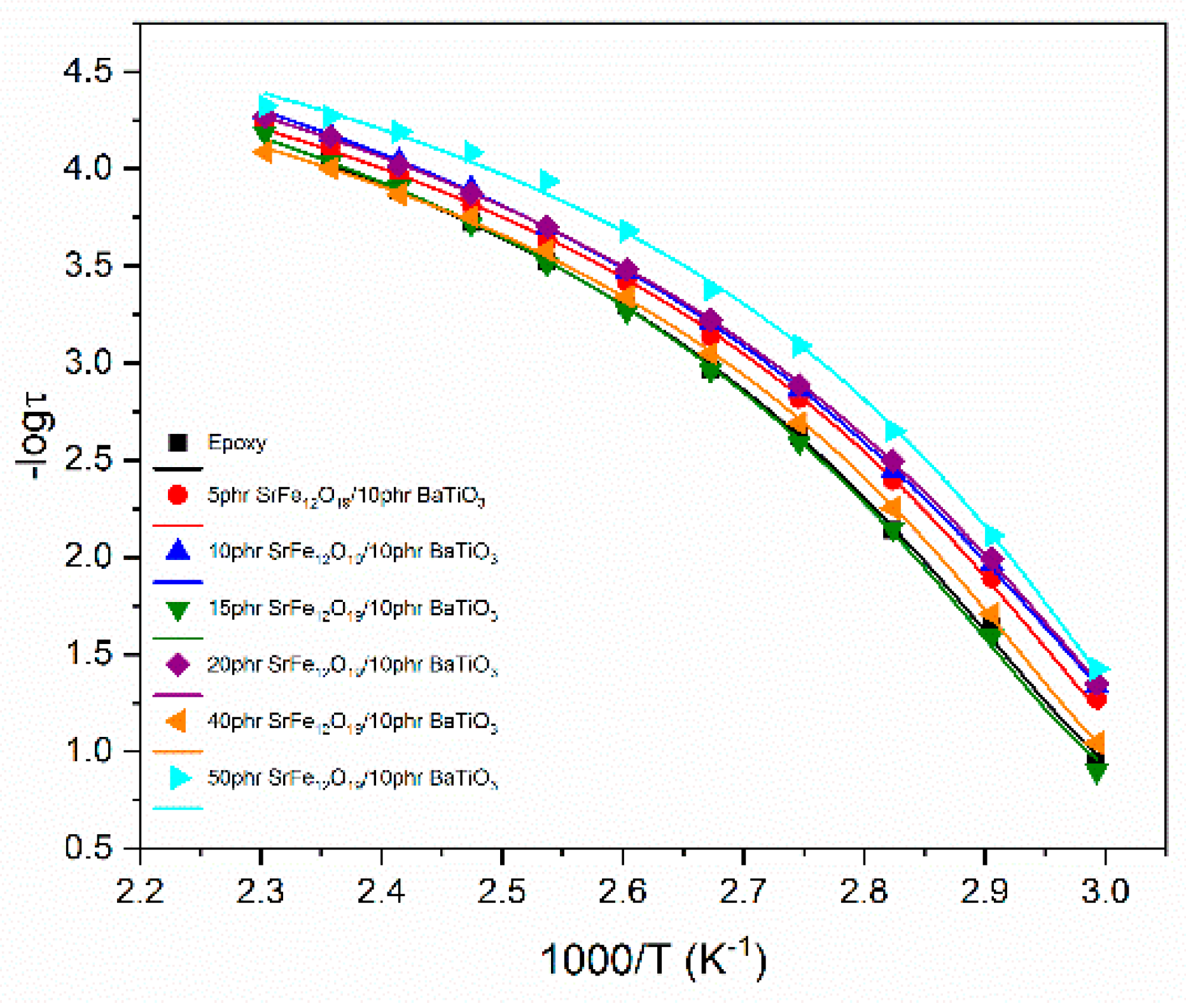
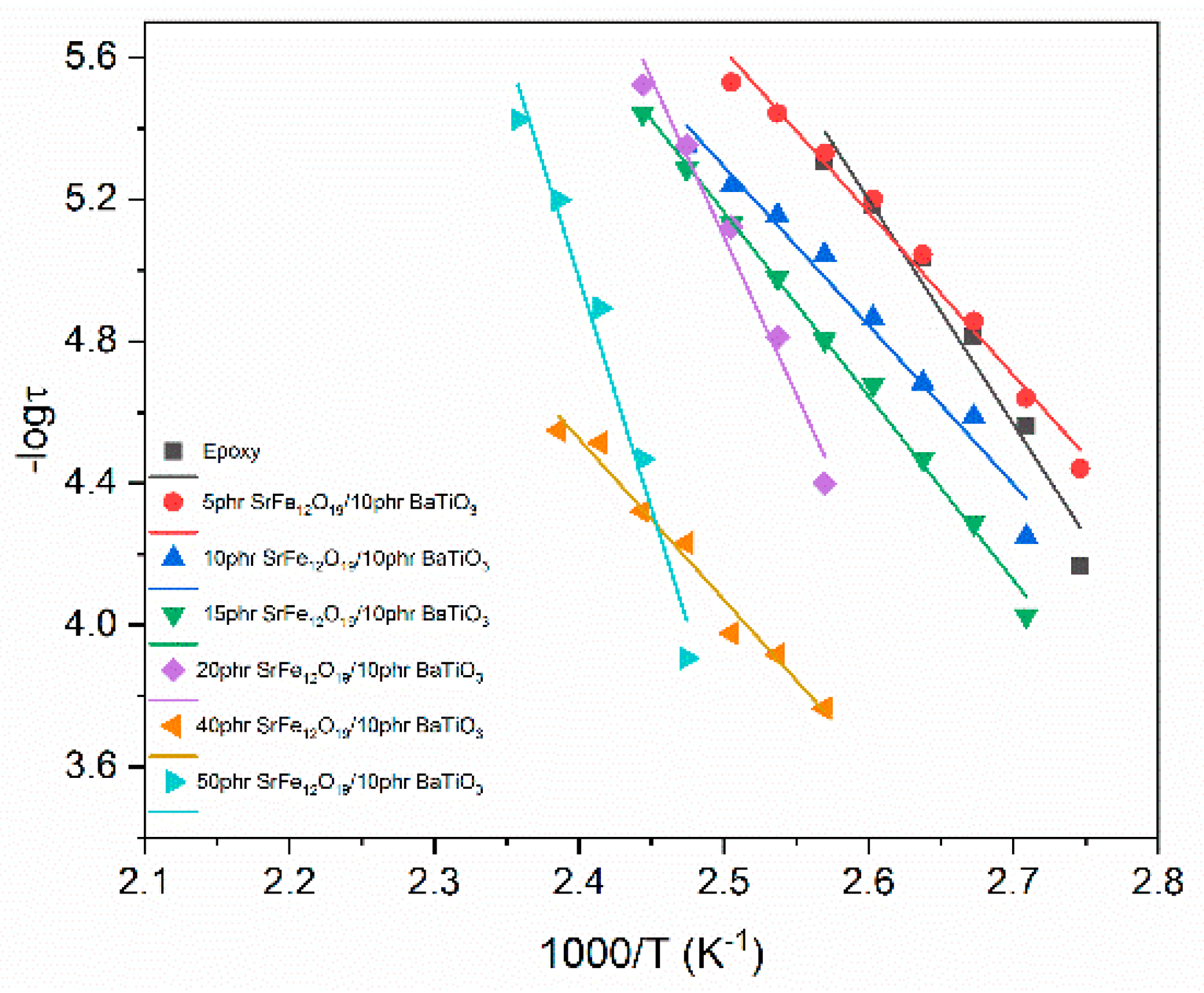
3.2. Dielectric Characterization
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, K.; Guo, J.Z.; Liu, C. Polymer-Based Multifunctional Nanocomposites and Their Applications; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780128150672. [Google Scholar]
- Friedrich, K. Routes for achieving multifunctionality in reinforced polymers and composite structures. In Multifunctionality of Polymer Composites; Friedrich, K., Breuer, U., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 3–41. ISBN 978-0-323-26434-1. [Google Scholar]
- Krawczak, P. Polymer composites: Evolve towards multifunctionality or perish. eXPRESS Polym. Lett. 2019, 13, 771. [Google Scholar] [CrossRef]
- Psarras, G.C. Ceramic/Polymer Nanodielectrics: Towards A Multifunctional or Smart Performance. In Proceedings of the ECCM18—18th European Conference on Composite Materials, Athens, Greece, 24–28 June 2018; pp. 24–28. [Google Scholar]
- Bafakeeh, O.T.; Shewakh, W.M.; Abu-Oqail, A.; Abd-Elaziem, W.; Ghafaar, M.A.; Bakafeeh, M.A.-O. Synthesis and Characterization of Hybrid Fiber-Reinforced Polymer by Adding Ceramic Nanoparticles for Aeronautical Structural Applications. Polymers 2021, 13, 4116. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Yin, L.J.; Hao, Y.N.; Zhong, S.L.; Zhang, D.L.; Bi, K.; Zhang, Y.X.; Zhao, Y.; Dang, Z.M. Flexible and Stretchable Capacitive Sensors with Different Microstructures. Adv. Mater. 2021, 33, 2008267. [Google Scholar] [CrossRef] [PubMed]
- Vikulova, M.; Nikityuk, T.; Artyukhov, D.; Tsyganov, A.; Bainyashev, A.; Burmistrov, I.; Gorshkov, N. High-k Three-Phase Epoxy/K1.6(Ni0.8Ti7.2)O16/CNT Composites with Synergetic Effect. Polymers 2022, 14, 448. [Google Scholar] [CrossRef]
- Psarras, G.C. Smart polymer systems: A journey from imagination to applications. eXPRESS Polym. Lett. 2011, 5, 1027. [Google Scholar] [CrossRef]
- Sanida, A.; Stavropoulos, S.G.; Speliotis, T.; Psarras, G.C. Evaluating the multifunctional performance of polymer matrix nanodielectrics incorporating magnetic nanoparticles: A comparative study. Polymer 2021, 236, 124311. [Google Scholar] [CrossRef]
- Gioti, S.; Sanida, A.; Mathioudakis, G.N.; Patsidis, A.C.; Speliotis, T.; Psarras, G.C. Multitasking Performance of Fe3O4/BaTiO3/Epoxy Resin Hybrid Nanocomposites. Materials 2022, 15, 1784. [Google Scholar] [CrossRef]
- Psarras, G.C. Conductivity and dielectric characterization of polymer nanocomposites. In Physical Properties and Applications of Polymer Nanocomposites; Tjong, S.C., Mai, Y.-W., Eds.; Woodhead Publishing: Cambridge, MA, USA, 2010; pp. 31–69. ISBN 9781845696726. [Google Scholar]
- Sanida, A.; Stavropoulos, S.G.; Speliotis, T.; Psarras, G.C. Investigating the Effect of Zn Ferrite Nanoparticles on the Thermomechanical, Dielectric and Magnetic Properties of Polymer Nanocomposites. Materials 2019, 12, 3015. [Google Scholar] [CrossRef]
- Sagar, R.; Gaur, M.S.; Rogachev, A.A. Piezoelectric and pyroelectric properties of ceramic nanoparticles-based nanostructured PVDF/PVC blend nanocomposites. J. Therm. Anal. Calorim. 2020, 146, 645–655. [Google Scholar] [CrossRef]
- Zheng, T.; Yu, Y.; Pang, Y.; Zhang, D.; Wang, Y.; Zhao, H.; Zhang, X.; Leng, H.; Yang, X.; Cai, Q. Improving bone regeneration with composites consisting of piezoelectric poly(l-lactide) and piezoelectric calcium/manganese co-doped barium titanate nanofibers. Compos. Part B Eng. 2022, 234, 109734. [Google Scholar] [CrossRef]
- Zha, J.W.; Zheng, M.S.; Fan, B.H.; Dang, Z.M. Polymer-based dielectrics with high permittivity for electric energy storage: A review. Nano Energy 2021, 89, 106438. [Google Scholar] [CrossRef]
- Xu, T.; Du, H.; Liu, H.; Liu, W.; Zhang, X.; Si, C.; Liu, P.; Zhang, K. Advanced nanocellulose-based composites for flexible functional energy storage devices. Adv. Mater. 2021, 33, 2101368. [Google Scholar] [CrossRef]
- Praveenkumara, J.; Madhu, P.; Yashas Gowda, T.G.; Sanjay, M.R.; Siengchin, S. A comprehensive review on the effect of synthetic filler materials on fiber-reinforced hybrid polymer composites. J. Text. Inst. 2022, 113, 1231–1239. [Google Scholar] [CrossRef]
- Feng, Q.-K.; Zhong, S.-L.; Pei, J.-Y.; Zhao, Y.; Zhang, D.-L.; Liu, D.-F.; Zhang, Y.-X.; Dang, Z.-M. Recent Progress and Future Prospects on All-Organic Polymer Dielectrics for Energy Storage Capacitors. Chem. Rev. 2022, 122, 3820–3878. [Google Scholar] [CrossRef]
- Buscaglia, V.; Buscaglia, M.T.; Viviani, M.; Mitoseriu, L.; Nanni, P.; Trefiletti, V.; Piaggio, P.; Gregora, I.; Ostapchuk, T.; Pokorný, J.; et al. Grain size and grain boundary-related effects on the properties of nanocrystalline barium titanate ceramics. J. Eur. Ceram. Soc. 2006, 26, 2889–2898. [Google Scholar] [CrossRef]
- Mandal, T.K. Characterization of tetragonal BaTiO3 nanopowders prepared with a new soft chemistry route. Mater. Lett. 2007, 61, 850–854. [Google Scholar] [CrossRef]
- Ram, S.; Jana, A.; Kundu, T.K. Ferroelectric BaTiO3 phase of orthorhombic crystal structure contained in nanoparticles. J. Appl. Phys. 2007, 102, 054107. [Google Scholar] [CrossRef]
- Patsidis, A.; Psarras, G.C. Dielectric behaviour and functionality of polymer matrix—Ceramic BaTiO3 composites. eXPRESS Polym. Lett. 2008, 2, 718–726. [Google Scholar] [CrossRef]
- Smith, M.B.; Page, K.; Siegrist, T.; Et, A. Crystal structure and the paraelectric-to-ferroelectric phase transition of nanoscale BaTiO3. J. Am. Chem. Soc. 2008, 130, 6955–6963. [Google Scholar] [CrossRef]
- Chávez, E.; Fuentes, S.; Zarate, R.A.; Padilla-Campos, L. Structural analysis of nanocrystalline BaTiO3. J. Mol. Struct. 2010, 984, 131–136. [Google Scholar] [CrossRef]
- Manika, G.C.; Andrikopoulos, K.S.; Psarras, G.C. On the Ferroelectric to Paraelectric Structural Transition of BaTiO3 Micro-/Nanoparticles and Their Epoxy Nanocomposites. Molecules 2020, 25, 2686. [Google Scholar] [CrossRef] [PubMed]
- Sanida, A.; Stavropoulos, S.G.; Speliotis, T.; Psarras, G.C. Development, characterization, energy storage and interface dielectric properties in SrFe12O19/epoxy nanocomposites. Polymer 2017, 120, 73–81. [Google Scholar] [CrossRef]
- Patsidis, A.C.; Kalaitzidou, K.; Psarras, G.C. Dielectric response, functionality and energy storage in epoxy nanocomposites: Barium titanate vs exfoliated graphite nanoplatelets. Mater. Chem. Phys. 2012, 135, 798–805. [Google Scholar] [CrossRef]
- Patsidis, A.C.; Psarras, G.C. Structural transition, dielectric properties and functionality in epoxy resin—Barium titanate nanocomposites. Smart Mater. Struct. 2013, 22, 115006. [Google Scholar] [CrossRef]
- Swanson, H.E.; McMurdie, H.F.; Morris, M.C.; Evans, E.H. Standard X-ray Diffraction Powder Patterns: NBS Monograph 25—Section 5; National Bureau of Standards Reports; Government Printing Office: Gaithersburg, MD, USA; Washington DC, USA, 1967. [Google Scholar]
- Patsidis, A.C.; Psarras, G.C. Dielectric and conductivity studies of epoxy composites. In Epoxy Composites. Fabrication, Characterization and Applications; Parameswaranpillai, J., Pulikkalparambil, H., Rangappa, S.M., Siengchin, S., Eds.; Wiley: New York, NY, USA, 2021; pp. 299–348. ISBN 978-3-527-34678-3. [Google Scholar]
- Jonscher, A.K. Universal Relaxation Law: A Sequel to Dielectric Relaxation in Solids; Chelsea Dielectrics Press: London, UK, 1996; Chapter 5. [Google Scholar]
- Tsangaris, G.M.; Psarras, G.C.; Manolakaki, E. DC and AC conductivity in polymeric particulate composites. Adv. Comp. Lett. 1999, 8, 25–29. [Google Scholar]
- Tsangaris, G.M.; Psarras, G.C.; Kouloumbi, N. Electric modulus and interfacial polarization in composite polymeric systems. J. Mater. Sci. 1998, 33, 2027–2037. [Google Scholar] [CrossRef]
- Hernández, M.; Carretero-González, J.; Verdejo, R.; Ezquerra, T.A.; López-Manchado, M.A. Molecular dynamics of natural rubber/layered silicate nanocomposites as studied by dielectric relaxation spectroscopy. Macromolecules 2010, 43, 643–651. [Google Scholar] [CrossRef]
- Belattar, J.; Achour, M.E.; Brosseau, C. A comparison between the permittivity and electric modulus representations of the microwave response of carbon black loaded polymer composites under uniaxial tension. J. Appl. Phys. 2011, 110, 054101. [Google Scholar] [CrossRef]
- Kontos, G.A.; Soulintzis, A.L.; Karahaliou, P.K.; Psarras, G.C.; Georga, S.N.; Krontiras, C.A.; Pisanias, M.N. Electrical relaxa-tion dynamics in TiO2—Polymer matrix composites. eXPRESS Polym. Lett. 2007, 1, 781–789. [Google Scholar] [CrossRef]
- Hao, N.; Böhning, M.; Goering, H.; Schönhals, A. Nanocomposites of Polyhedral Oligomeric Phenethylsilsesquioxanes and Poly(bisphenol A carbonate) as Investigated by Dielectric Spectroscopy. Macromolecules 2007, 40, 2955–2964. [Google Scholar] [CrossRef]
- Soulintzis, A.; Kontos, G.; Karahaliou, P.; Psarras, G.C.; Georga, S.N.; Krontiras, C.A. Dielectric relaxation processes in epoxy resin-ZnO composites. J. Polym. Sci. Polym. Phys. 2009, 47, 445–454. [Google Scholar] [CrossRef]
- Ramajo, L.A.; Cristóbal, A.A.; Botta, P.M.; Porto López, J.M.; Reboredo, M.M.; Castro, M.S. Dielectric and magnetic response of Fe3O4/epoxy composites. Compos. Part A Appl. Sci. Manuf. 2009, 40, 388–393. [Google Scholar] [CrossRef]
- Ioannou, G.; Patsidis, A.; Psarras, G.C. Dielectric and functional properties of polymer matrix/ZnO/BaTiO3 hybrid composites. Compos. Part A Appl. Sci. Manuf. 2011, 42, 104–110. [Google Scholar] [CrossRef]
- Tomara, G.N.; Kerasidou, A.P.; Patsidis, A.C.; Karahaliou, P.K.; Psarras, G.C.; Georga, S.N.; Krontiras, C.A. Dielectric response and energy storage efficiency of low content TiO2-polymer matrix nanocomposites. Compos. Part A Appl. S. 2015, 71, 204–211. [Google Scholar] [CrossRef]
- Psarras, G.C. Fundamentals of dielectric theories. In Dielectric Polymer Materials for High-Density Energy Storage; Dang, Z.M., Ed.; Elsevier Inc.: Cambridge, UK, 2018; pp. 11–57. [Google Scholar]
- Sanida, A.; Stavropoulos, S.G.; Speliotis, T.; Psarras, G.C. Magneto-dielectric behaviour of M-type hexaferrite/polymer nanocomposites. Materials 2018, 11, 2551. [Google Scholar] [CrossRef]



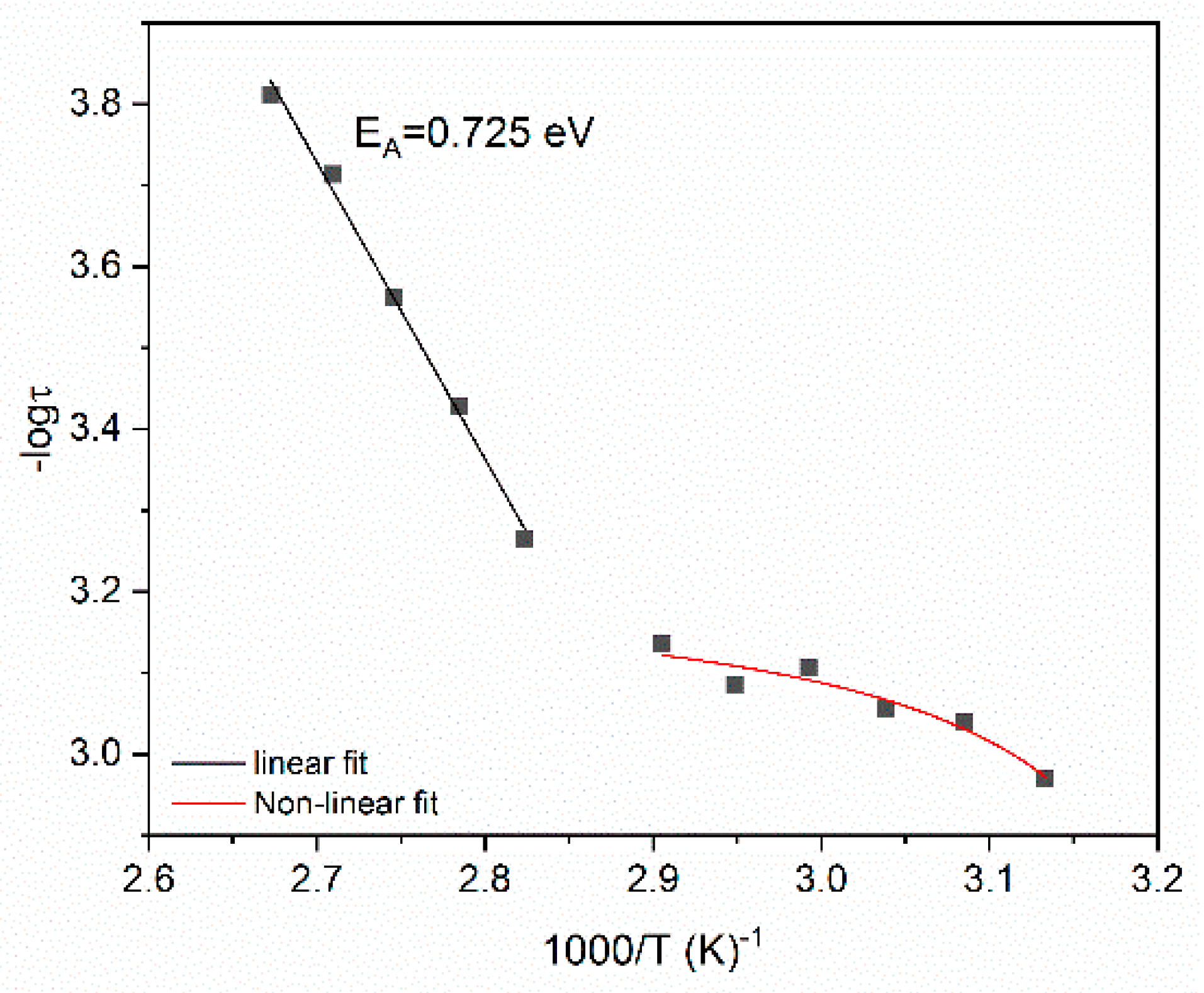
| Composites | α-Mode | β-Mode EA (eV) | |
|---|---|---|---|
| T0 (K) | A | ||
| Epoxy | 321.47 | 18.21 | 1.256 |
| 5 phr SrFe12O19 + 10 phr BaTiO3 | 315.28 | 19.10 | 0.910 |
| 10 phr SrFe12O19 + 10 phr BaTiO3 | 313.98 | 19.51 | 0.888 |
| 15 phr SrFe12O19 + 10 phr BaTiO3 | 321.74 | 18.34 | 1.029 |
| 20 phr SrFe12O19 + 10 phr BaTiO3 | 314.60 | 18.42 | 1.765 |
| 40 phr SrFe12O19 + 10 phr BaTiO3 | 321.10 | 16.52 | 0.900 |
| 50 phr SrFe12O19 + 10 phr BaTiO3 | 317.26 | 15.17 | 2.569 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manika, G.C.; Gioti, S.; Sanida, A.; Mathioudakis, G.N.; Abazi, A.; Speliotis, T.; Patsidis, A.C.; Psarras, G.C. Multifunctional Performance of Hybrid SrFe12O19/BaTiO3/Epoxy Resin Nanocomposites. Polymers 2022, 14, 4817. https://doi.org/10.3390/polym14224817
Manika GC, Gioti S, Sanida A, Mathioudakis GN, Abazi A, Speliotis T, Patsidis AC, Psarras GC. Multifunctional Performance of Hybrid SrFe12O19/BaTiO3/Epoxy Resin Nanocomposites. Polymers. 2022; 14(22):4817. https://doi.org/10.3390/polym14224817
Chicago/Turabian StyleManika, Georgia C., Sevasti Gioti, Aikaterini Sanida, Georgios N. Mathioudakis, Anxhela Abazi, Thanassis Speliotis, Anastasios C. Patsidis, and Georgios C. Psarras. 2022. "Multifunctional Performance of Hybrid SrFe12O19/BaTiO3/Epoxy Resin Nanocomposites" Polymers 14, no. 22: 4817. https://doi.org/10.3390/polym14224817
APA StyleManika, G. C., Gioti, S., Sanida, A., Mathioudakis, G. N., Abazi, A., Speliotis, T., Patsidis, A. C., & Psarras, G. C. (2022). Multifunctional Performance of Hybrid SrFe12O19/BaTiO3/Epoxy Resin Nanocomposites. Polymers, 14(22), 4817. https://doi.org/10.3390/polym14224817








