Force-Extension Curve of a Polymer Chain Entangled with a Static Ring-Shaped Obstacle
Abstract
1. Introduction
2. Methods
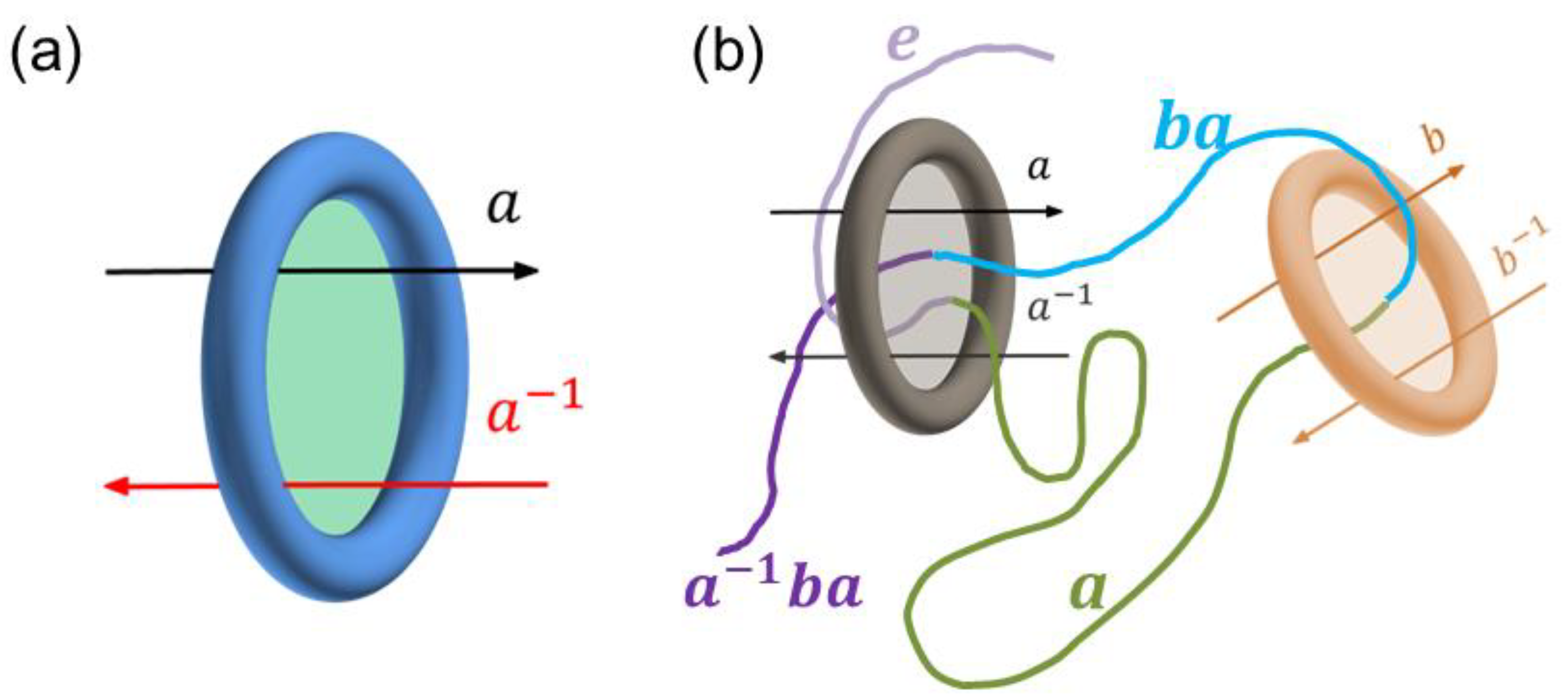
2.1. Superspace Approach for Static Topological Constraints
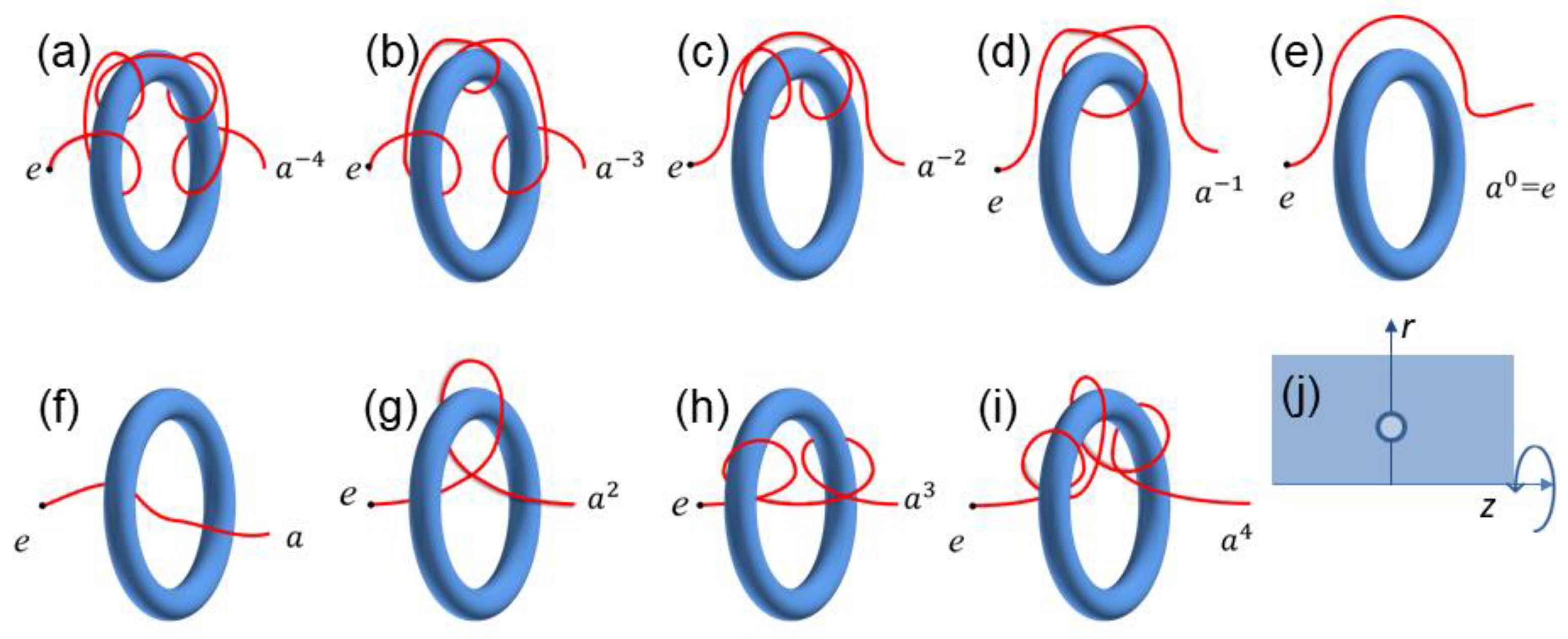
2.2. ADI Scheme in Cylindrical Coordinates and Boundary Conditions
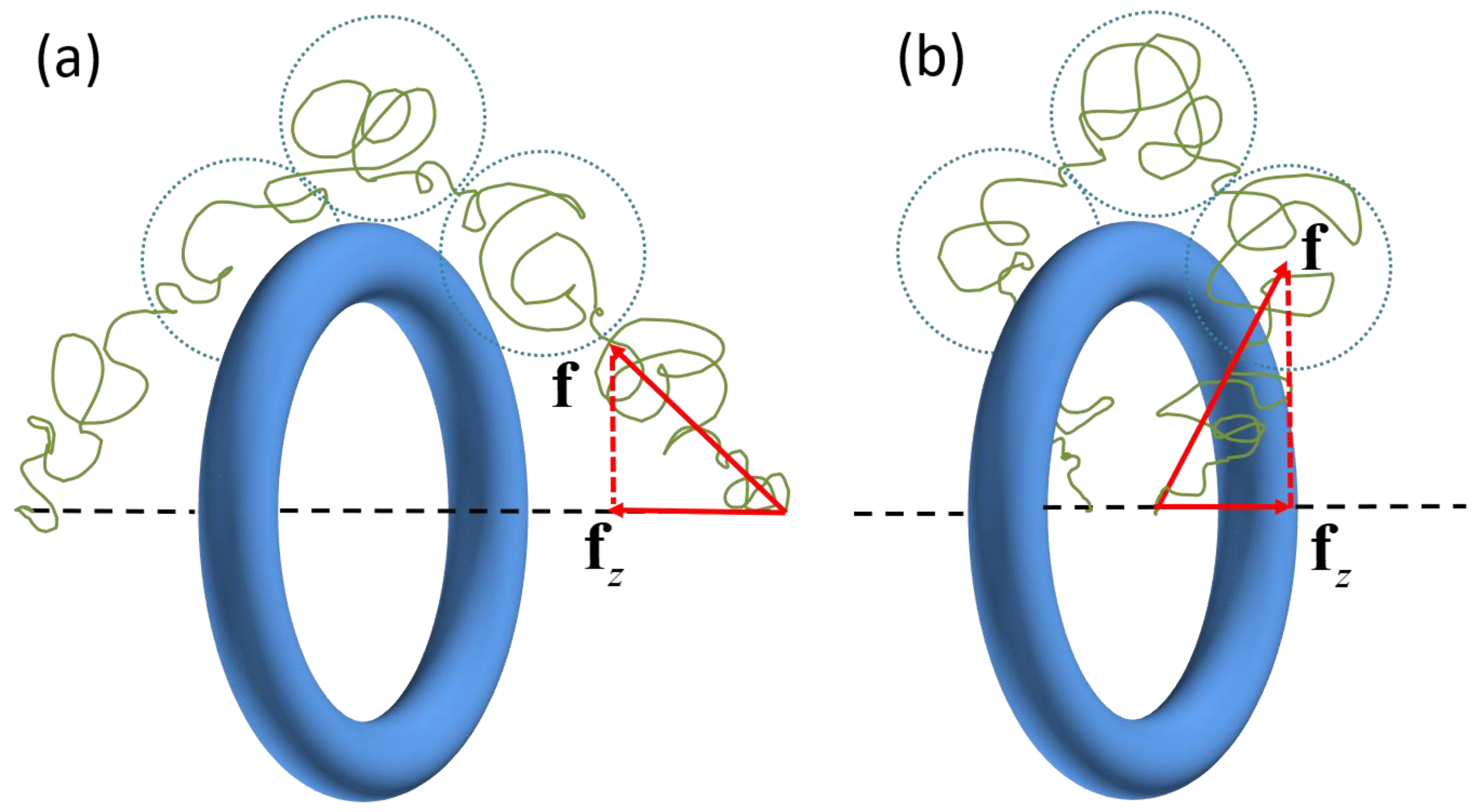
3. Results
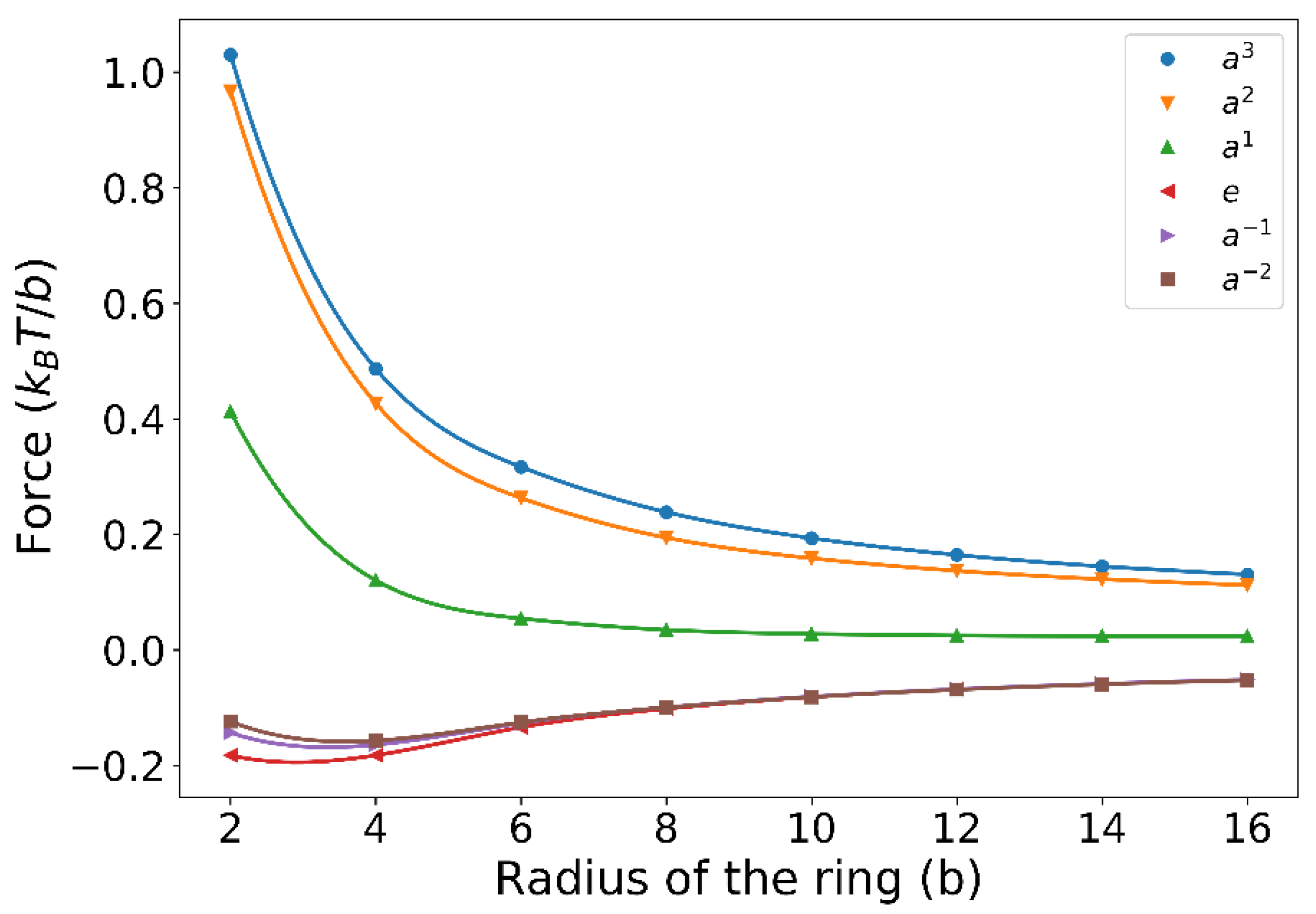
3.1. Attraction of the Ring to the Gaussian Chain
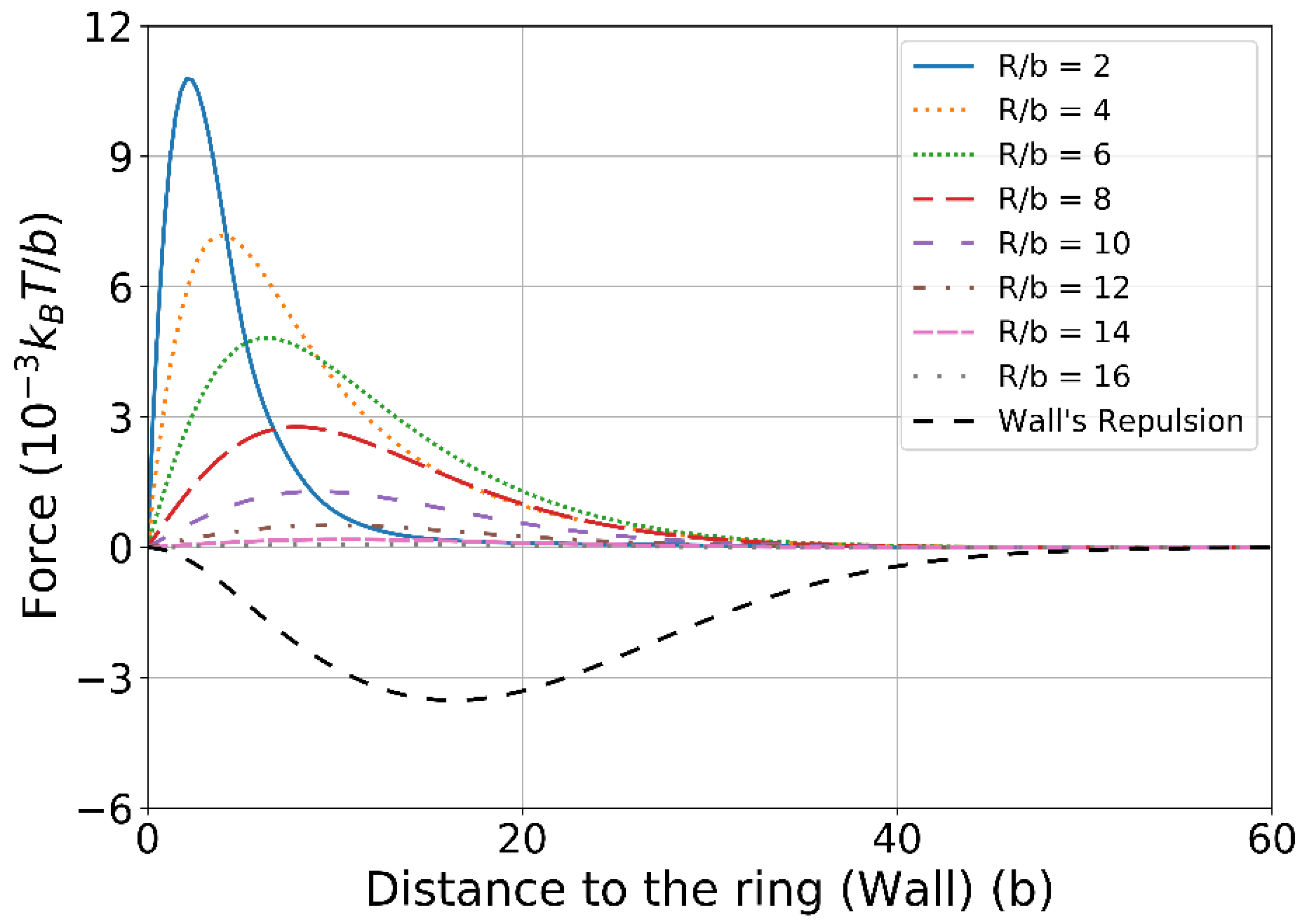
3.2. Force-Extension Curves of an Ideal Chain Entangled with a Ring
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vlassopoulos, D. Macromolecular topology and rheology: Beyond the tube model. Rheol. Acta. 2016, 55, 613–632. [Google Scholar] [CrossRef]
- De Gennes, P.G. Reptation of a Polymer Chain in the Presence of Fixed Obstacles. J. Chem. Phys. 1971, 55, 572. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 1 Brownian motion in the equilibrium state. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 2 Molecular motion under flow. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1802–1817. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 3 The constitutive equation. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1818–1832. [Google Scholar] [CrossRef]
- Doi, M. Explanation for the 3.4-power law for viscosity of polymeric liquids on the basis of the tube model. J. Polym. Sci. Polym. Phys. Ed. 1983, 21, 667–684. [Google Scholar] [CrossRef]
- Des Cloizeaux, J. Double reptation vs. simple reptation in polymer melts. Europhys. Lett. 1988, 5, 437–442. [Google Scholar] [CrossRef]
- Marrucci, G. Relaxation by reptation and tube enlargement: A model for polydisperse. J. Polym. Sci. B Polym. Phys. 1985, 23, 159–177. [Google Scholar] [CrossRef]
- Tsenoglou, C. Molecular weight polydispersity effects on the viscoelasticity of entangled linear polymers. Macromolecules 1991, 24, 1762–1767. [Google Scholar] [CrossRef]
- Viovy, J.L.; Rubinstein, M.; Colby, R.H. Constraint release in polymer melts: Tube reorganization versus tube dilation. Macromolecules 1991, 24, 3587–3596. [Google Scholar] [CrossRef]
- Watanabe, H. Viscoelasticity and dynamics of entangled polymers. Prog. Polym. Sci. 1999, 24, 1253–1403. [Google Scholar] [CrossRef]
- Edwards, S.F. The statistical mechanics of polymers with excluded volume. Proc. Phys. Soc. 1965, 85, 613. [Google Scholar] [CrossRef]
- Edwards, S.F. Statistical mechanics with topological constraints. Proc. Phys. Soc. 1967, 91, 513. [Google Scholar] [CrossRef]
- Grosberg, A.; Frisch, H. Winding angle distribution for planar random walk, polymer ring entangled with an obstacle, and all that: Spitzer–Edwards–Prager–Frisch model revisited. J. Phys. A Math. Gen. 2003, 36, 8955–8981. [Google Scholar] [CrossRef]
- Prager, S.; Frisch, H.L. Statistical mechanics of a simple entanglement. J. Chem. Phys. 1967, 46, 1475. [Google Scholar] [CrossRef]
- Rudnick, J.; Hu, Y. Winding angle of a self-avoiding random walk. Phys. Rev. Lett. 1988, 60, 712. [Google Scholar] [CrossRef]
- Gong, H.; Li, J.F.; Zhang, H.D.; Shi, A.C. Force-Extension Curve of an Entangled Polymer Chain: A Superspace Approach. Chin. J. Polym. Sci. 2021, 39, 345–1350. [Google Scholar] [CrossRef]
- Kong, D.J.; Banik, S.; Francisco, M.J.S.; Lee, M.; Anderson, R.M.R.; Schroeder, C.M.; Mckenna, G.B. Rheology of Entangled Solutions of Ring−Linear DNA Blends. Macromolecules 2022, 55, 1205–1217. [Google Scholar] [CrossRef]
- Doi, Y.; Takano, A.; Takahashi, Y.; Matsushita, Y. Melt rheology of tadpole-shaped polystyrenes with different ring sizes. Soft Matter 2020, 16, 8720–8724. [Google Scholar] [CrossRef]
- Halverson, J.D.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Rheology of Ring Polymer Melts: From Linear Contaminants to Ring-Linear Blends. Phys. Rev. Lett. 2012, 108, 038301. [Google Scholar] [CrossRef]
- Michieletto, D.; Sakaue, T. Dynamical Entanglement and Cooperative Dynamics in Entangled Solutions of Ring and Linear Polymers. Macro Lett. 2021, 10, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.J.; Zhang, J.G. Topological catenation induced swelling of ring polymers revealed by molecular dynamics simulation. Polymer 2020, 196, 122475. [Google Scholar] [CrossRef]
- Daitchman, D.; Greenblatt, H.M.; Levy, Y. Diffusion of ring-shaped proteins along DNA: Case study of sliding clamps. Nucleic Acids Res. 2018, 46, 5935–5949. [Google Scholar] [CrossRef] [PubMed]
- Oakley, A.J. Dynamics of open DNA sliding clamps. PLoS ONE 2016, 11, e0154899. [Google Scholar] [CrossRef] [PubMed]
- Thordarson, P.; Bijsterveld, J.A.; Rowan, A.E.; Nolte, R.J.M. Epoxidation of polybutadiene by a topologically linked catalyst. Nature 2003, 424, 915–918. [Google Scholar] [CrossRef] [PubMed]
- Lehn, L.M.; Atwood, J.L.; Davies, L.E.D.; MacNicol, D.D.; Voetle, F. Comprehensive Supramolecular Chemistry; Pergamon: New York, NY, USA, 1996; Volume 11. [Google Scholar]
- Liu, Y.; You, C.C.; Zhang, H.Y. Supramolecular Chemistry-Molecular Recognition and Assembly of Synthetic Receptions; Nankai University Press: Tianjing, China, 2001. [Google Scholar]
- Yang, Y.L.; Zhang, H.D.; Qiu, F. Threading-unthreading equilibrium in solution of molecular nanotubes and linear flexible polymer chains. J. Chem. Phys. 2005, 122, 084908. [Google Scholar] [CrossRef] [PubMed]
- Fredrickson, G.H. The Equilibrium Theory of Inhomogeneous Polymers; Clarendon Press: Oxford, UK, 2006. [Google Scholar]
- Helfand, E.J. Theory of inhomogeneous polymers: Fundamentals of the Gaussian random-walk model. J. Chem. Phys. 1975, 62, 999. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Metzler, R.; Kantor, Y.; Kardar, M. Force-extension relations for polymers with sliding links. Phys. Rev. E 2002, 66, 022102. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Li, J. Force-Extension Curve of a Polymer Chain Entangled with a Static Ring-Shaped Obstacle. Polymers 2022, 14, 4613. https://doi.org/10.3390/polym14214613
Zhang Q, Li J. Force-Extension Curve of a Polymer Chain Entangled with a Static Ring-Shaped Obstacle. Polymers. 2022; 14(21):4613. https://doi.org/10.3390/polym14214613
Chicago/Turabian StyleZhang, Qihao, and Jianfeng Li. 2022. "Force-Extension Curve of a Polymer Chain Entangled with a Static Ring-Shaped Obstacle" Polymers 14, no. 21: 4613. https://doi.org/10.3390/polym14214613
APA StyleZhang, Q., & Li, J. (2022). Force-Extension Curve of a Polymer Chain Entangled with a Static Ring-Shaped Obstacle. Polymers, 14(21), 4613. https://doi.org/10.3390/polym14214613







