Reduction of Thermal Residual Strain in a Metal-CFRP-Metal Hybrid Tube Using an Axial Preload Tool Monitored through Optical Fiber Sensors
Abstract
1. Introduction
2. Experimental Procedure
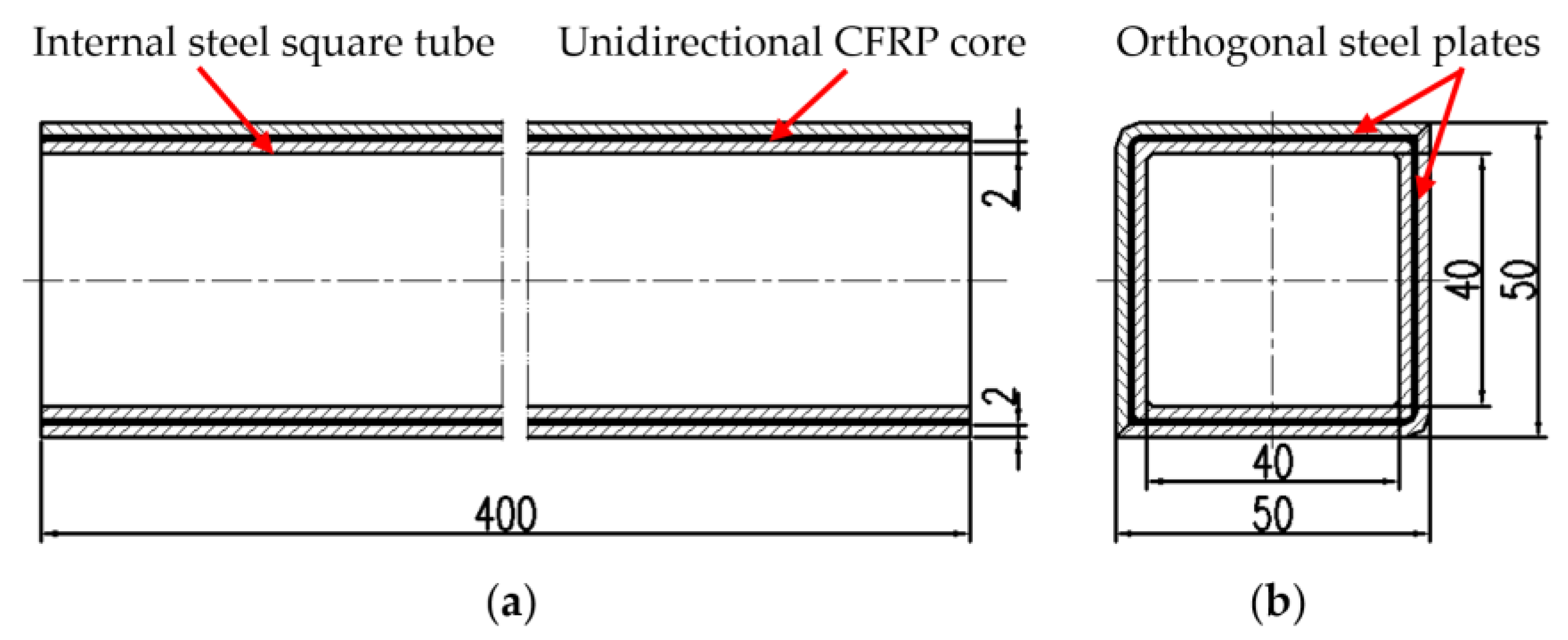
2.1. Material and Structure of the MCMHT
2.2. Fabrication Method of the MCMHT with the Axial Preload Tool
2.3. Measurement of Strains through Optical Fiber Sensors
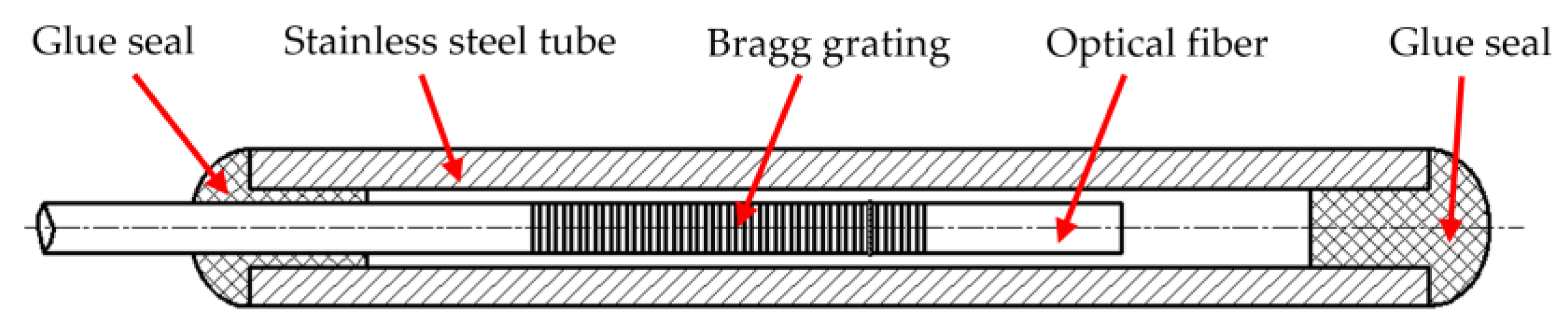
2.3.1. Sensing Principle of FBG Sensor
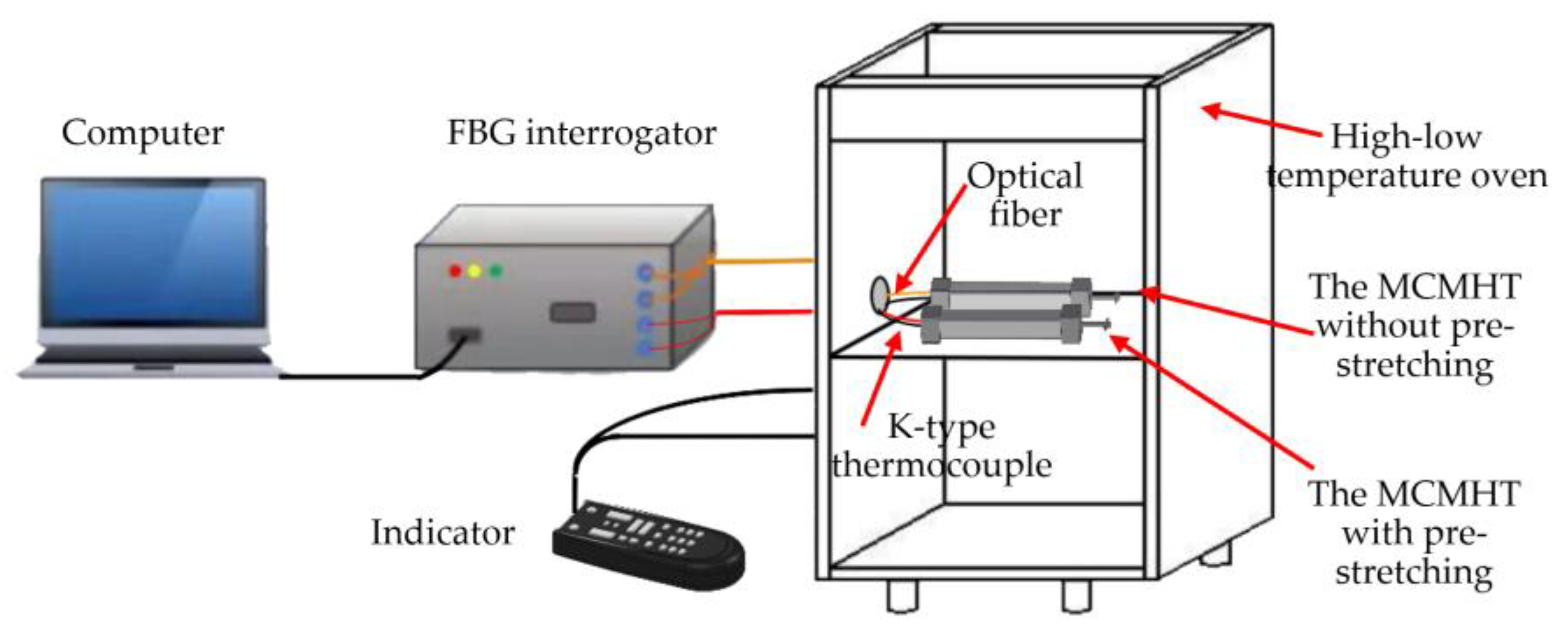
2.3.2. Temperature Calibration
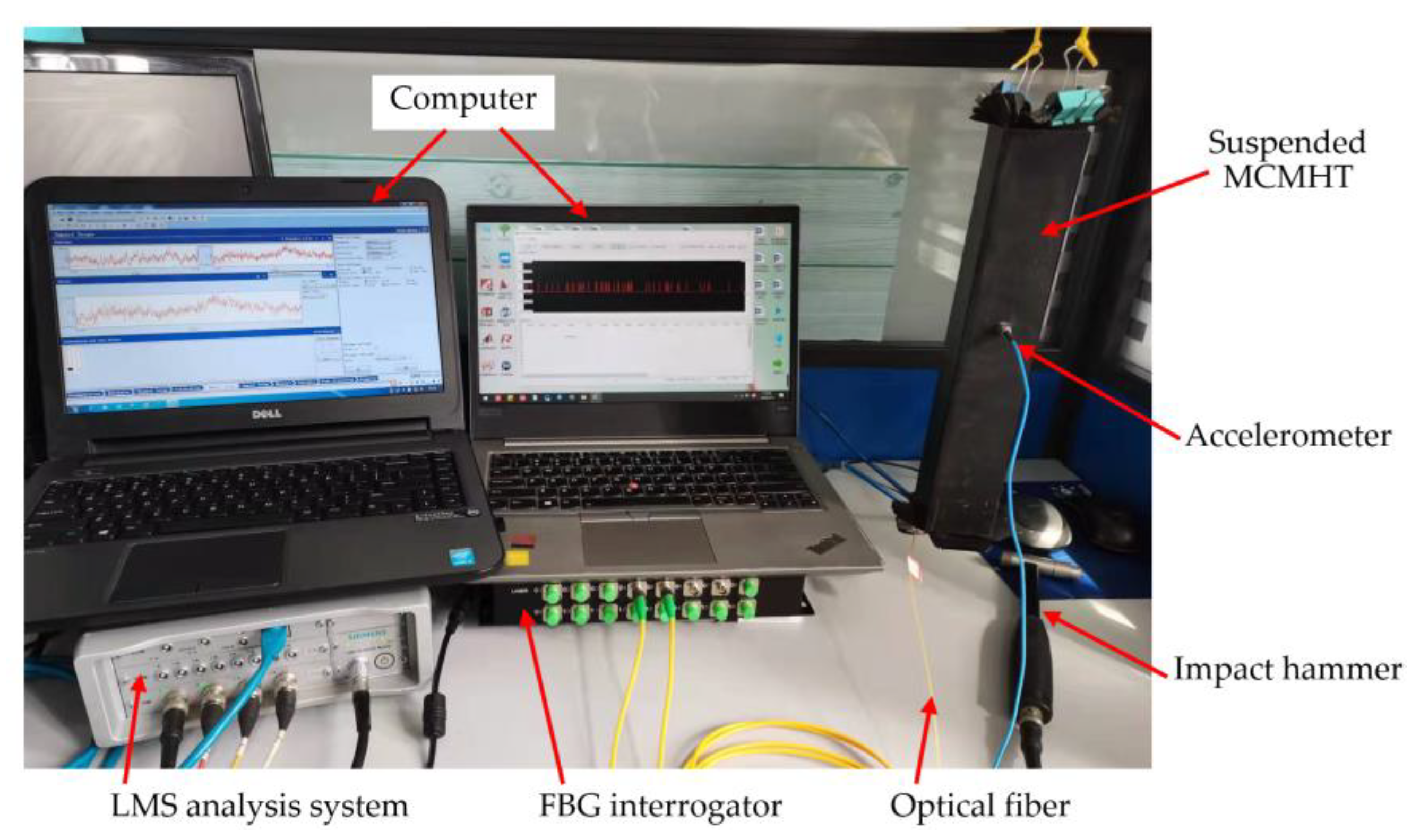
2.4. Experimental Setup of Modal Testing
3. Evaluation of Thermal Residual Strains Based on Classical Lamination Theory
3.1. Material Properties of the Laminate with Arbitrary Lamina Orientation Angle
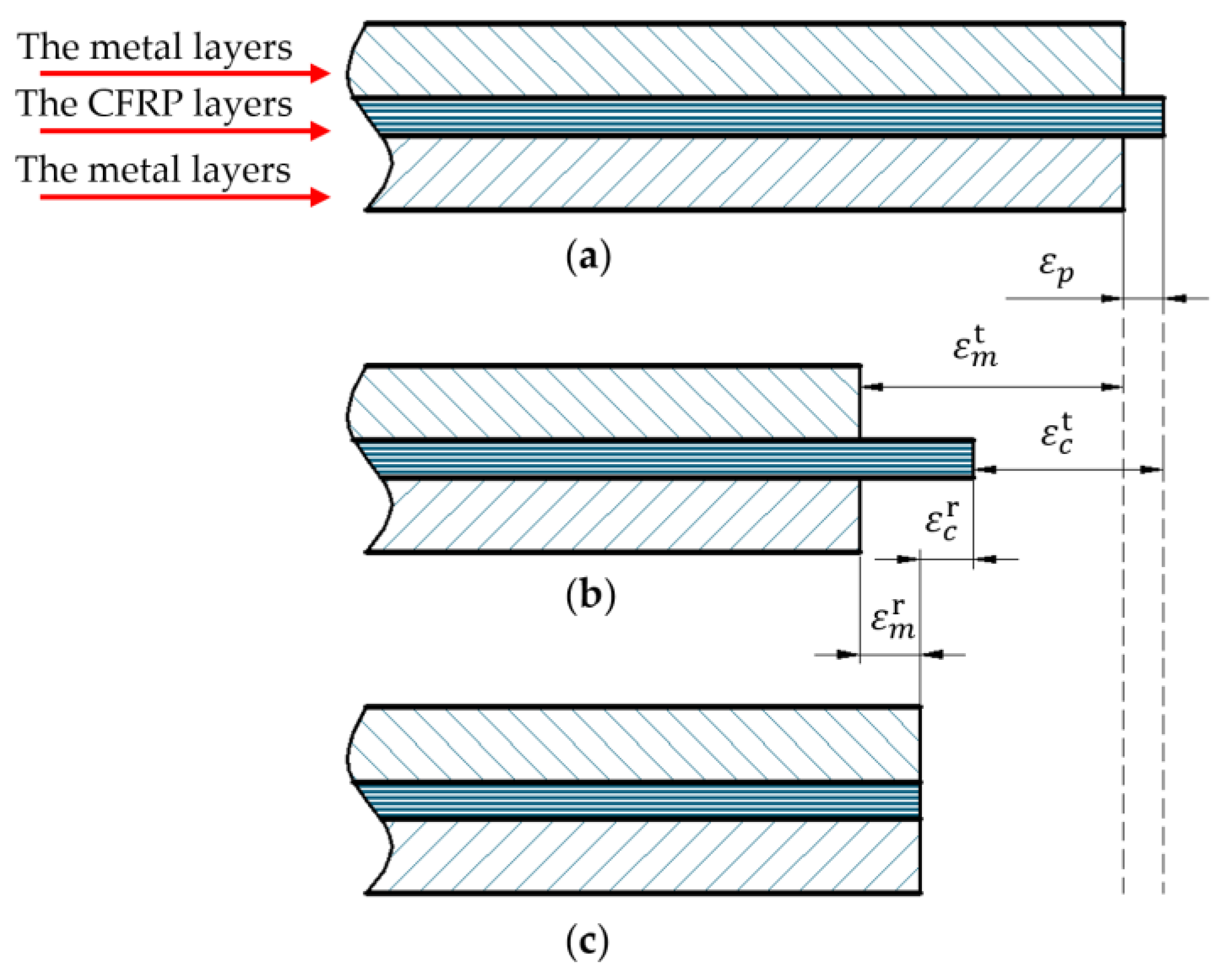
3.2. Strains in Metal-CFRP-Metal Hybrid Structure
4. Measurement Results and Discussion
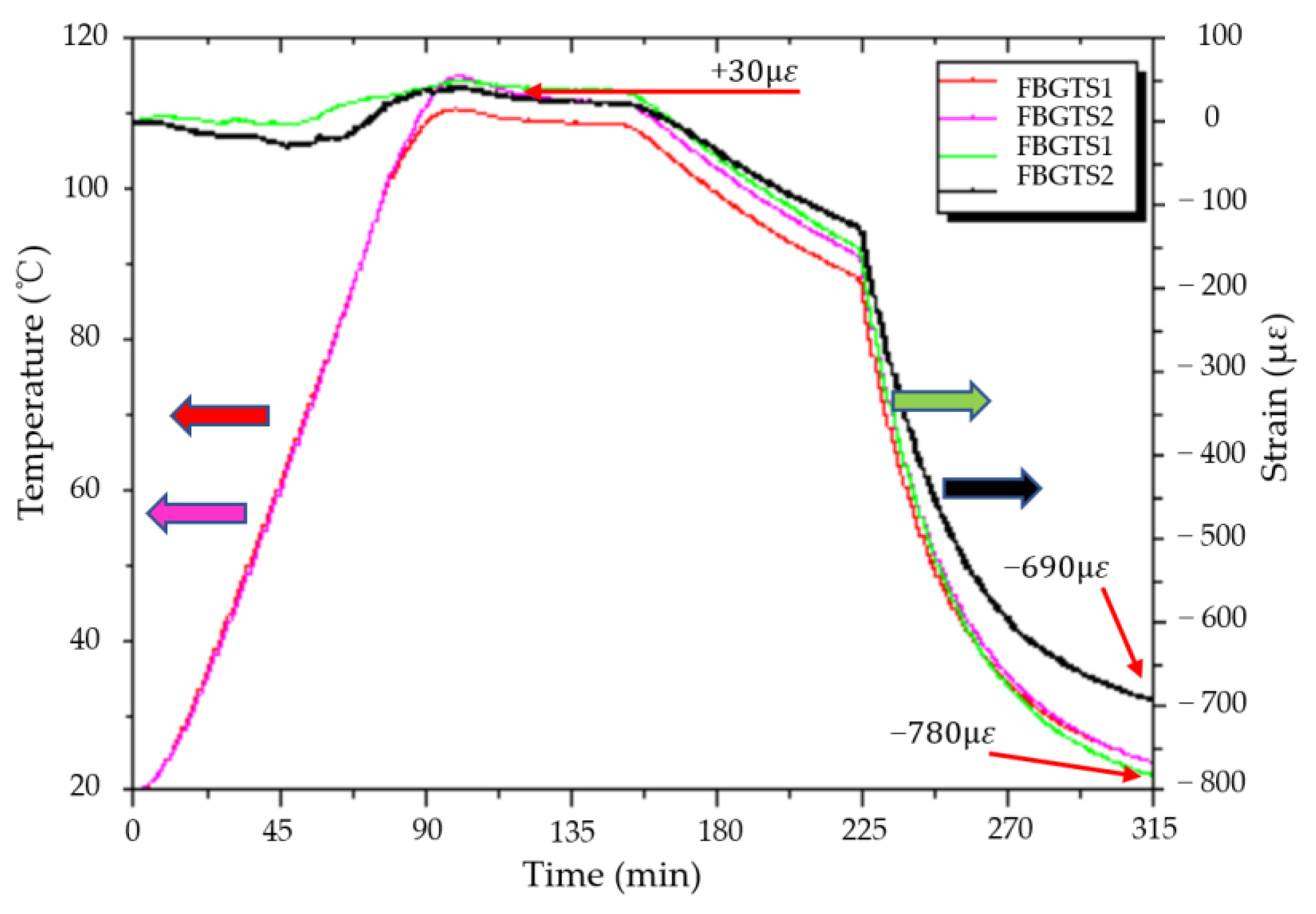
4.1. Comparison of Theoretical Calculation with Measurement by the FBGSS
4.2. The Dynamic Characteristics of the MCMHT
5. Conclusions
- To reduce thermal residual strain, the proposed axial preload tool can apply compressive forces to the metal layers or tensile forces to the CFRP layers by rotating the handwheel. This shows the axial preload tool can change the strain state of the metal-composite hybrid structure;
- Thermal residual strain of the metal-composite hybrid structure obtained from embedded optical fiber sensors show good agreement with the theoretical calculation based on classic laminate theory;
- The modal testing results imply that the reduction of residual strain increases the natural frequency of the metal-composite hybrid structure, but is detrimental to its damping capability. This shows that the intrinsic properties of the metal-composite hybrid structure can be modified by the proposed axial preload tool.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sinmazçelik, T.; Avcu, E.; Bora, M.Ö.; Çoban, O. A review: Fibre metal laminates, background, bonding types and applied test methods. Mater. Des. 2011, 32, 3671–3685. [Google Scholar] [CrossRef]
- Braga, D.F.O.; Tavares, S.M.O.; da Silva, L.F.M.; Moreira, P.M.G.P.; de Castro, P.M.S.T. Advanced design for lightweight structures: Review and prospects. Prog. Aerosp. Sci. 2014, 69, 29–39. [Google Scholar] [CrossRef]
- Hollaway, L.C. A review of the present and future utilisation of FRP composites in the civil infrastructure with reference to their important in-service properties. Constr. Build. Mater. 2010, 24, 2419–2445. [Google Scholar] [CrossRef]
- Pramanik, A.; Basak, A.K.; Dong, Y.; Sarker, P.K.; Uddin, M.S.; Littlefair, G.; Dixit, A.R.; Chattopadhyaya, S. Joining of carbon fibre reinforced polymer (CFRP) composites and aluminium alloys—A review. Compos. Part A 2017, 101, 1–29. [Google Scholar] [CrossRef]
- Nowak, T. Elastic-plastic behavior and failure analysis of selected Fiber Metal Laminates. Compos. Struct. 2018, 183, 450–456. [Google Scholar] [CrossRef]
- Yao, Y.; Shi, P.; Chen, M.; Chen, G.; Gao, C.; Boisse, P.; Zhu, Y. Experimental and numerical study on Mode I and Mode II interfacial fracture toughness of co-cured steel-CFRP hybrid composites. Int. J. Adhes. Adhes. 2022, 112, 103030. [Google Scholar] [CrossRef]
- Sun, G.; Chen, D.; Zhu, G.; Li, Q. Lightweight hybrid materials and structures for energy absorption: A state-of-the-art review and outlook. Thin-Walled Struct. 2022, 172, 108760. [Google Scholar] [CrossRef]
- Düring, D.; Weiß, L.; Stefaniak, D.; Jordan, N.; Hühne, C. Low-velocity impact response of composite laminates with steel and elastomer protective layer. Compos. Struct. 2015, 134, 18–26. [Google Scholar] [CrossRef]
- Alderliesten, R.C. Designing for damage tolerance in aerospace: A hybrid material technology. Mater. Des. 2015, 66, 421–428. [Google Scholar] [CrossRef]
- Dadej, K.; Bieniaś, J.; Surowska, B. Residual fatigue life of carbon fibre aluminium laminates. Int. J. Fatigue 2017, 100, 94–104. [Google Scholar] [CrossRef]
- Zafar, R.; Lihui, L.; Rongjing, Z. Analysis of hydro-mechanical deep drawing and the effects of cavity pressure on quality of simultaneously formed three-layer Al alloy parts. Int. J. Adv. Manuf. Technol. 2015, 80, 2117–2128. [Google Scholar] [CrossRef]
- Kotik, H.G.; Perez Ipiña, J.E. Short-beam shear fatigue behavior of fiber metal laminate (Glare). Int. J. Fatigue 2017, 95, 236–242. [Google Scholar] [CrossRef]
- Elsheikh, A. Bistable Morphing Composites for Energy-Harvesting Applications. Polymers 2022, 14, 1893. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.S.; Park, S.W.; Lee, D.G. Smart cure cycle with cooling and reheating for co-cure bonded steel/carbon epoxy composite hybrid structures for reducing thermal residual stress. Compos. Part A 2006, 37, 1708–1721. [Google Scholar] [CrossRef]
- Kim, H.C.; Shin, D.K.; Lee, J.J. Characteristics of aluminum/CFRP short square hollow section beam under transverse quasi-static loading. Compos. Part B Eng. 2013, 51, 345–358. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, X.; Xing, F.; Li, D.; Wang, Y.; Sui, L. Behavior and modeling of FRP-concrete-steel double-skin tubular columns made of full lightweight aggregate concrete. Constr. Build. Mater. 2017, 139, 52–63. [Google Scholar] [CrossRef]
- Parlevliet, P.P.; Bersee, H.E.N.; Beukers, A. Residual stresses in thermoplastic composites—a study of the literature. Part III: Effects of thermal residual stresses. Compos. Part A 2007, 38, 1581–1596. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Daneshvar, A.; Akbari, S. Reduction of thermal residual stresses of laminated polymer composites by addition of carbon nanotubes. Mater. Des. 2014, 53, 209–216. [Google Scholar] [CrossRef]
- Agius, S.L.; Joosten, M.; Trippit, B.; Wang, C.H.; Hilditch, T. Rapidly cured epoxy/anhydride composites: Effect of residual stress on laminate shear strength. Compos. Part A 2016, 90, 125–136. [Google Scholar] [CrossRef]
- White, S.R.; Hahn, H.T. Cure Cycle Optimization for the Reduction of Processing-Induced Residual Stresses in Composite Materials. J. Compos. Mater. 1993, 27, 1352–1378. [Google Scholar] [CrossRef]
- Kim, H.-S.; Yoo, S.-H.; Chang, S.-H. In situ monitoring of the strain evolution and curing reaction of composite laminates to reduce the thermal residual stress using FBG sensor and dielectrometry. Compos. Part B Eng. 2013, 44, 446–452. [Google Scholar] [CrossRef]
- Kim, S.S.; Murayama, H.; Kageyama, K.; Uzawa, K.; Kanai, M. Study on the curing process for carbon/epoxy composites to reduce thermal residual stress. Compos. Part A 2012, 43, 1197–1202. [Google Scholar] [CrossRef]
- Prussak, R.; Stefaniak, D.; Kappel, E.; Hühne, C.; Sinapius, M. Smart cure cycles for fiber metal laminates using embedded fiber Bragg grating sensors. Compos. Struct. 2019, 213, 252–260. [Google Scholar] [CrossRef]
- Hyun, D.; Lee, D.G. Manufacturing of co-cured composite aluminum shafts with compression during co-curing operation to reduce residual thermal stresses. J. Compos. Mater. 1998, 32, 1221–1241. [Google Scholar] [CrossRef]
- Xue, J.; Wang, W.-X.; Takao, Y.; Matsubara, T. Reduction of thermal residual stress in carbon fiber aluminum laminates using a thermal expansion clamp. Compos. Part A 2011, 42, 986–992. [Google Scholar] [CrossRef]
- Lee, D.G.; Kim, J.W.; Hwang, H.Y. Torsional Fatigue Characteristics of Aluminum–Composite Co-Cured Shafts with Axial Compressive Preload. J. Compos. Mater. 2004, 38, 737–756. [Google Scholar] [CrossRef]
- Khan, S.U.; Alderliesten, R.C.; Benedictus, R. Post-stretching induced stress redistribution in Fibre Metal Laminates for increased fatigue crack growth resistance. Compos. Sci. Technol. 2009, 69, 396–405. [Google Scholar] [CrossRef]
- Li, N.; Li, Y.; Hao, X.; Gao, J. A comparative experiment for the analysis of microwave and thermal process induced strains of carbon fiber/bismaleimide composite materials. Compos. Sci. Technol. 2015, 106, 15–19. [Google Scholar] [CrossRef]
- Li, N.; Li, Y.; Hang, X.; Gao, J. Analysis and optimization of temperature distribution in carbon fiber reinforced composite materials during microwave curing process. J. Mater. Process. Technol. 2014, 214, 544–550. [Google Scholar] [CrossRef]
- Wu, T.; Degener, S.; Tinkloh, S.; Liehr, A.; Zinn, W.; Nobre, J.P.; Tröster, T.; Niendorf, T. Characterization of residual stresses in fiber metal laminate interfaces—A combined approach applying hole-drilling method and energy-dispersive X-ray diffraction. Compos. Struct. 2022, 299, 116071. [Google Scholar] [CrossRef]
- Parlevliet, P.P.; Bersee, H.E.N.; Beukers, A. Residual stresses in thermoplastic composites—A study of the literature—Part II: Experimental techniques. Compos. Part A 2007, 38, 651–665. [Google Scholar] [CrossRef]
- Lee, D.-W.; Park, B.-J.; Park, S.-Y.; Choi, C.-H.; Song, J.-I. Fabrication of high-stiffness fiber-metal laminates and study of their behavior under low-velocity impact loadings. Compos. Struct. 2018, 189, 61–69. [Google Scholar] [CrossRef]
- Harhash, M.; Sokolova, O.; Carradó,, A.; Palkowski, H. Mechanical properties and forming behaviour of laminated steel/polymer sandwich systems with local inlays—Part 1. Compos. Struct. 2014, 118, 112–120. [Google Scholar] [CrossRef]
- Hill, K.O.; Meltz, G. Fiber Bragg Grating Technology Fundamentals and Overview. J. Lightwave Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Kuang, K.S.C.; Zhang, L.; Cantwell, W.J.; Bennion, I. Process monitoring of aluminum-foam sandwich structures based on thermoplastic fibre–metal laminates using fibre Bragg gratings. Compos. Sci. Technol. 2005, 65, 669–676. [Google Scholar] [CrossRef]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D.K. Fibre Bragg gratings in structural health monitoring—Present status and applications. Sens. Actuators A Phys. 2008, 147, 150–164. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, L.; Wang, X.; Dong, Q. Numerical analysis and fiber Bragg grating monitoring of thermocuring processes of carbon fiber/epoxy laminates. Polym. Test. 2017, 62, 287–294. [Google Scholar] [CrossRef]
- Xu, Y.; Li, H.; Yang, Y.; Hu, Y.; Tao, J. Determination of residual stresses in Ti/CFRP laminates after preparation using multiple methods. Compos. Struct. 2019, 210, 715–723. [Google Scholar] [CrossRef]
- Gibson, R.F. Principles of Composite Material Mechanics, 4th ed.; Taylor & Francis Group: Oxford, UK, 2016; pp. 338–343. [Google Scholar]


| Material Properties | USN 10000/T300 Prepreg | AISI 1045 |
|---|---|---|
| Longitudinal modulus, E1 (GPa) | 137 | 200 |
| Transverse modulus, E2 (GPa) | 9 | 200 |
| Shear modulus, G12 (GPa) | 3.78 | 80 |
| Major Poisson’s ratio, ν12 | 0.28 | 0.29 |
| Longitudinal CTE, α1 (10−6/°C) | −0.5 | 11 |
| Transverse CTE, α2 (10−6/°C) | 27 | 11 |
| Density (g/cm3) | 1.76 | 7.85 |
| Experimental Condition | MCMHT without Pre-Stretching | MCMHT with Pre-Stretching |
|---|---|---|
| Material | Unidirectional CFRP prepreg and AISI 1045 | |
| Curing equipment | The high-low temperature oven | |
| Sensor | FBGTS1 and FBGSS1 | FBGTS2 and FBGSS2 |
| Axial preload tool | Without pre-stretching | With pre-stretching of 4 mm |
| FBG | Initial Central Wavelength/nm | Fitting Linear Correlation Coefficient | |
|---|---|---|---|
| FBGTS1 | 1546.914 | 11.80 | 99.95% |
| FBGTS2 | 1546.860 | 11.84 | 99.91% |
| FBGSS1 | 1537.041 | 11.20 | 99.84% |
| FBGSS2 | 1546.936 | 11.07 | 99.82% |
| MCMHT | by the FBGSS/με | by Theoretical Calculation/με | Relative Difference |
|---|---|---|---|
| With pre-stretching | 720 | 659.2 | −8.4% |
| Without pre-stretching | 810 | 759.2 | −6.2% |
| Characteristics | without Pre-Stretching | with Pre-Stretching | Relative Difference |
|---|---|---|---|
| Natural frequency/Hz | 1883 | 1980 | 5.2% |
| Damping ratio | 0.96% | 0.85% | −11.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Ke, W.; Liu, M.; Zhou, Y. Reduction of Thermal Residual Strain in a Metal-CFRP-Metal Hybrid Tube Using an Axial Preload Tool Monitored through Optical Fiber Sensors. Polymers 2022, 14, 4368. https://doi.org/10.3390/polym14204368
Li Z, Ke W, Liu M, Zhou Y. Reduction of Thermal Residual Strain in a Metal-CFRP-Metal Hybrid Tube Using an Axial Preload Tool Monitored through Optical Fiber Sensors. Polymers. 2022; 14(20):4368. https://doi.org/10.3390/polym14204368
Chicago/Turabian StyleLi, Zhao, Wei Ke, Mingyao Liu, and Yang Zhou. 2022. "Reduction of Thermal Residual Strain in a Metal-CFRP-Metal Hybrid Tube Using an Axial Preload Tool Monitored through Optical Fiber Sensors" Polymers 14, no. 20: 4368. https://doi.org/10.3390/polym14204368
APA StyleLi, Z., Ke, W., Liu, M., & Zhou, Y. (2022). Reduction of Thermal Residual Strain in a Metal-CFRP-Metal Hybrid Tube Using an Axial Preload Tool Monitored through Optical Fiber Sensors. Polymers, 14(20), 4368. https://doi.org/10.3390/polym14204368






