Study on the Expansion and Compression Resistance of 3D-Textile-Reinforced Self-Stressing Concrete
Abstract
:1. Introduction
2. Materials and Methods
2.1. Matrix
2.2. Textile
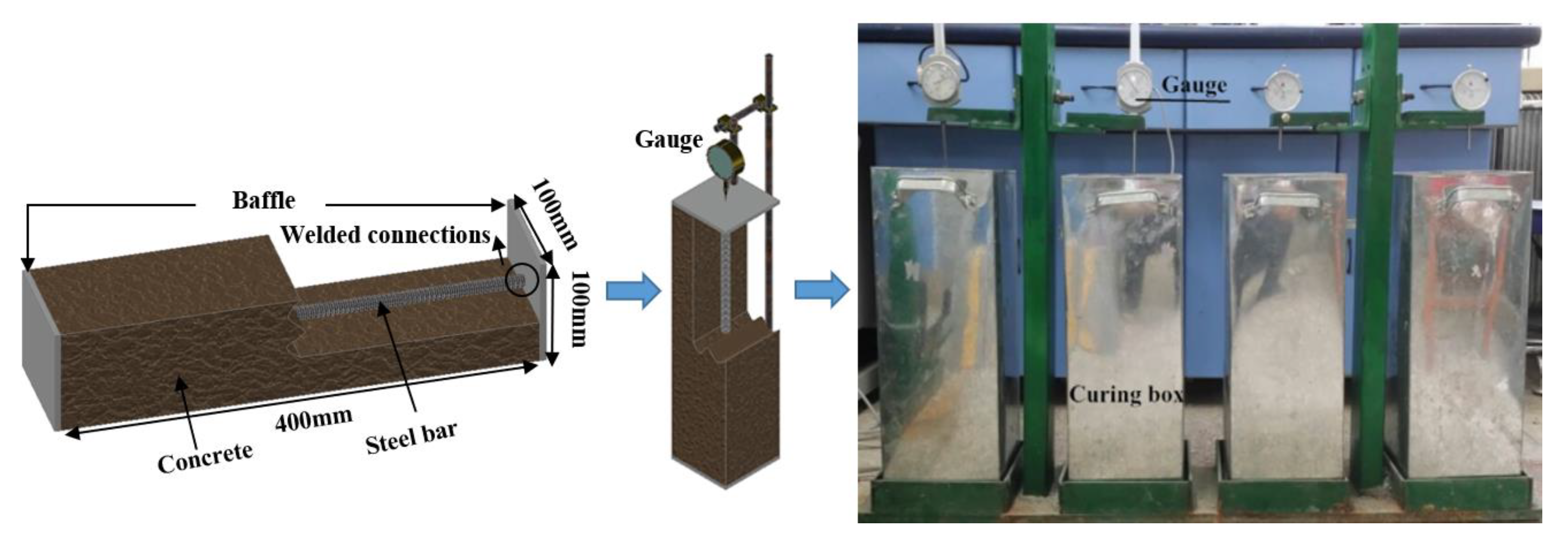
2.3. Self-Stress Value Test
2.4. Compression Test
3. Results and Discussion
3.1. Expansion Properties
- As: cross-sectional area of steel bar
- εs: strain of steel bar
- Es: modulus of elasticity of steel bar
- Ac: cross-sectional area of concrete
- σss: self-stress value of self-stressing concrete
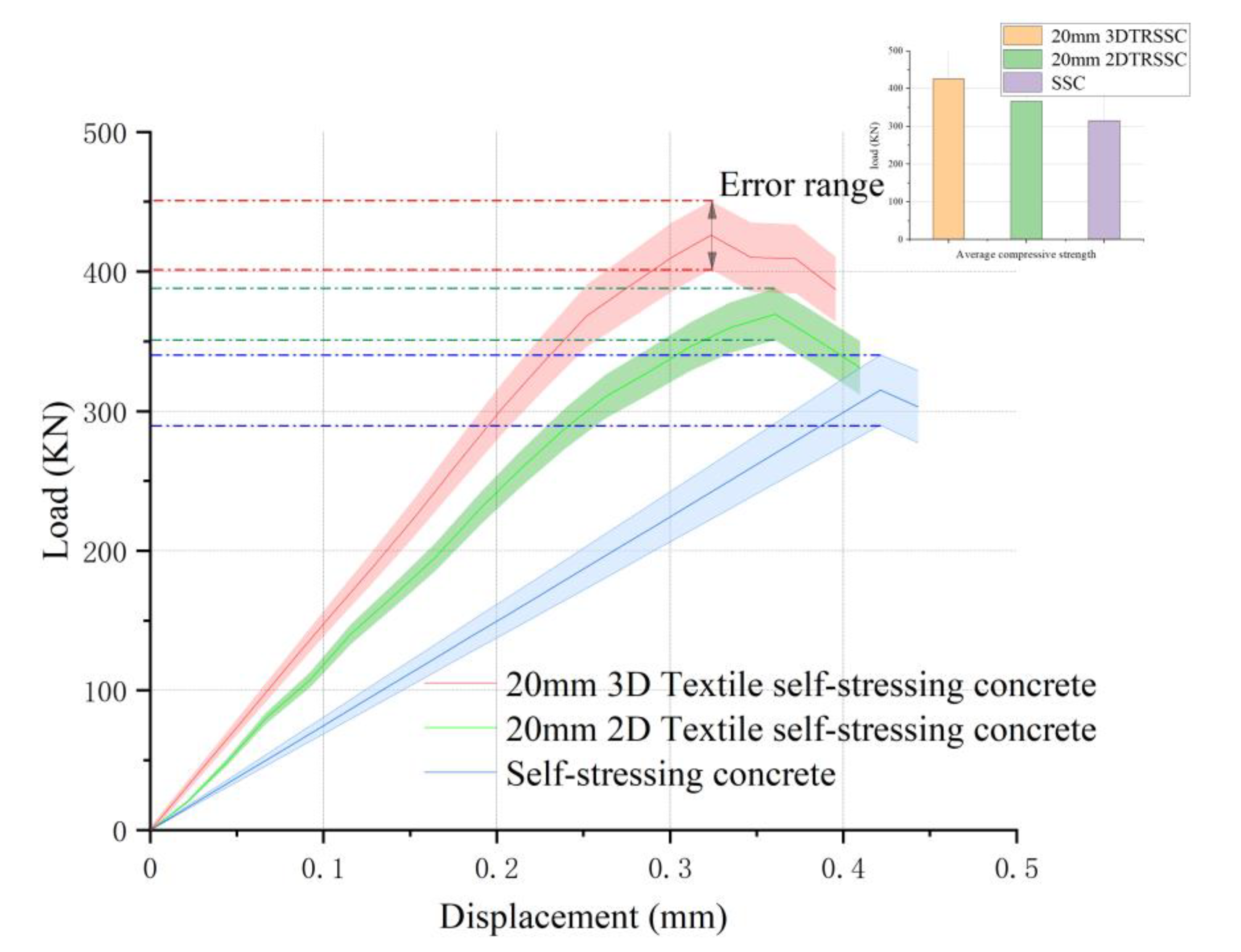
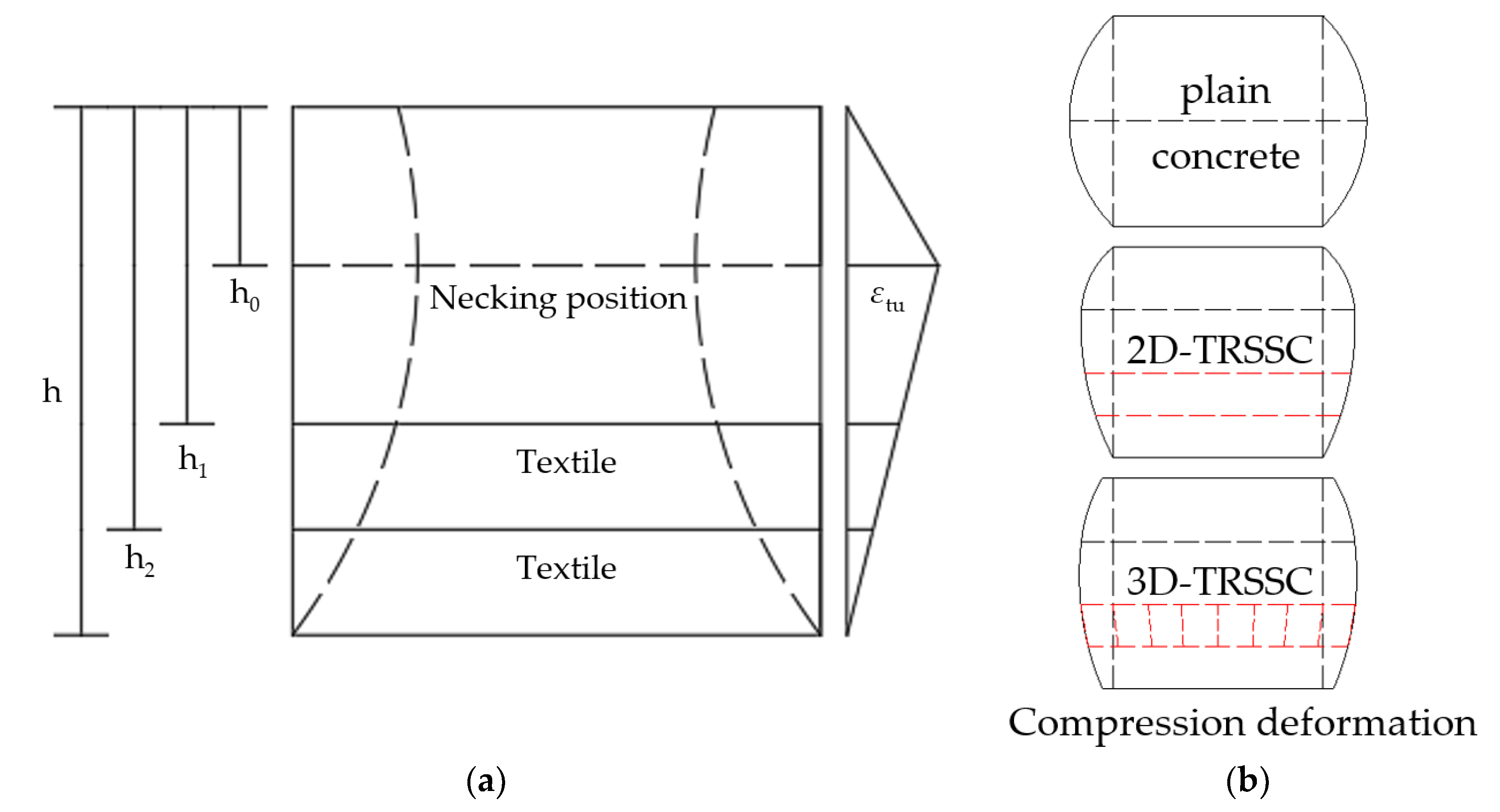
3.2. Compression Properties
- f3: conventional triaxial compressive strength
- fc: compressive strength of self-stressing concrete considering textile restraint but not self-stressing state
- f1: the self-stress value in the direction of σ1 and σ2
- Es: modulus of elasticity of fibers
- Ec: modulus of elasticity of concrete
- tu: ultimate tensile strain of concrete
- t: distance from necking position to the bottom of the specimen
- D: diameter of fiber bundle, 1 mm
- εe: ultimate expansion strain in the lateral direction
- b: width of the specimen
- a: spacing between textiles
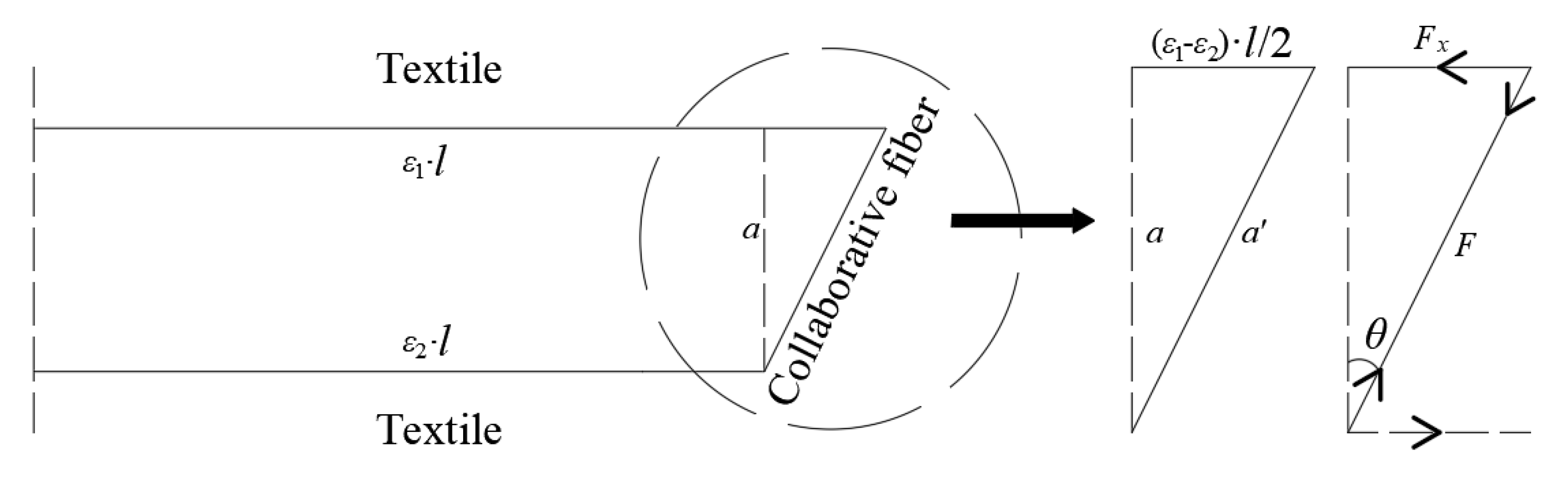
- ε1: strain of the upper textile layer
- ε2: strain of the lower textile layer
- θ: rotation angle of collaborative fiber
- F: internal force of collaborative fiber
- ρ: percentage of increase
4. Conclusions
- The 3D self-stress and 3D restraint effect introduced by the 3D collaborative textile can effectively ameliorate the compressive performance of the specimen and improve the compression failure mold form of the specimen. By observing the experimental data, due to the combined effect of 3D self-stress and collaborative fibers, the compressive performance of the 3D-TRSSC was improved by 16.3% compared to the 2D-TRSSC and 35.1% compared to the self-stressing concrete;
- The self-stress value was the same under the condition of using baffles and textile. Using this self-stress value and the triaxial stress model, the compressive strength of 3D-TRSSC was 24% higher than that of SSC, and the compressive strength of 2D-TRSSC was 15% higher than that of SSC in theory;
- A set of calculation methods for calculating the failure mode of 3D-TRSSC under compression and the increase in compressive strength of 3D-TRSSC compared with the 2D-TRSSC specimens was proposed. By calculation, the height of the neutral axis is 27.2mm, and the compressive strength of 3D-TRSSC is increased by 15% compared with that of 2D-TRSSC.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, X.; Xie, N.; Fortune, K.; Gong, J. Durability of steel reinforced concrete in chloride environments: An overview. Constr. Build. Mater. 2012, 30, 125–138. [Google Scholar] [CrossRef]
- Yin, S.-P.; Na, M.-W.; Yu, Y.-L.; Wu, J. Research on the flexural performance of RC beams strengthened with TRC under the coupling action of load and marine environment. Constr. Build. Mater. 2017, 132, 251–261. [Google Scholar] [CrossRef]
- Li, B.; Xiong, H.; Jiang, J.; Dou, X. Tensile behavior of basalt textile grid reinforced Engineering Cementitious Composite. Compos. Part B Eng. 2019, 156, 185–200. [Google Scholar] [CrossRef]
- Wang, B.; Yuan, K.; Lu, X.; Zhao, J. Calculation method of cracking load and deflection of textile reinforced self-stressing concrete. Constr. Build. Mater. 2021, 304, 124622. [Google Scholar] [CrossRef]
- Ali, I.; Burakov, A.E.; Melezhik, A.V.; Babkin, A.V.; Burakova, I.V.; Neskomornaya, M.E.; Galunin, E.V.; Tkachev, A.G.; Kuznetsov, D.V. Removal of Copper(II) and Zinc(II) Ions in Water on a Newly Synthesized Polyhydroquinone/Graphene Nanocomposite Material: Kinetics, Thermodynamics and Mechanism. ChemistrySelect 2019, 4, 12708–12718. [Google Scholar] [CrossRef]
- Ali, I.; Basheer, A.A.; Kucherova, A.; Memetov, N.; Pasko, T.; Ovchinnikov, K.; Pershin, V.; Kuznetsov, D.; Galunin, E.; Grachev, V.; et al. Advances in carbon nanomaterials as lubricants modifiers. J. Mol. Liq. 2019, 279, 251–266. [Google Scholar] [CrossRef]
- Ali, I.; Alharbi, O.M.; ALOthman, Z.A.; Alwarthan, A.; Al-Mohaimeed, A.M. Preparation of a carboxymethylcellulose-iron composite for uptake of atorvastatin in water. Int. J. Biol. Macromol. 2019, 132, 244–253. [Google Scholar] [CrossRef]
- Basheer, A.A. Advances in the smart materials applications in the aerospace industries. Aircr. Eng. Aerosp. Technol. 2020, 92, 1027–1035. [Google Scholar] [CrossRef]
- Schladitz, F.; Frenzel, M.; Ehlig, D.; Curbach, M. Bending load capacity of reinforced concrete slabs strengthened with textile reinforced concrete. Eng. Struct. 2012, 40, 317–326. [Google Scholar] [CrossRef]
- Yin, S.; Yang, Y.; Ye, T.; Li, Y. Experimental Research on Seismic Behavior of Reinforced Concrete Columns Strengthened with TRC under Corrosion Environment. J. Struct. Eng. 2017, 143, 04016231. [Google Scholar] [CrossRef]
- Goliath, K.B.; Cardoso, D.C.; Silva, F.D. Flexural behavior of carbon-textile-reinforced concrete I-section beams. Compos. Struct. 2021, 260, 113540. [Google Scholar] [CrossRef]
- Brückner, A.; Ortlepp, R.; Curbach, M. Anchoring of shear strengthening for T-beams made of textile reinforced concrete (TRC). Mater. Struct. 2008, 41, 407–418. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Papanicolaou, C.G. Shear strengthening of reinforced concrete members with textile reinforced mortar (TRM) jackets. Mater. Struct. Mater. Constr. 2006, 39, 93–103. [Google Scholar] [CrossRef]
- Brückner, A.; Ortlepp, R.; Curbach, M. Textile reinforced concrete for strengthening in bending and shear. Mater. Struct. 2006, 39, 741–748. [Google Scholar] [CrossRef]
- Preinstorfer, P.; Kollegger, J. New insights into the splitting failure of textile-reinforced concrete. Compos. Struct. 2020, 243, 112203. [Google Scholar] [CrossRef]
- Hegger, J.; Voss, S. Investigations on the bearing behaviour and application potential of textile reinforced concrete. Eng. Struct. 2008, 30, 2050–2056. [Google Scholar] [CrossRef]
- Yin, S.; Xu, S.; Lv, H. Flexural Behavior of Reinforced Concrete Beams with TRC Tension Zone Cover. J. Mater. Civ. Eng. 2014, 26, 320–330. [Google Scholar] [CrossRef]
- Yin, S.; Xu, S.; Li, H. Improved mechanical properties of textile reinforced concrete thin plate. J. Wuhan Univ. Technol. Sci. Ed. 2013, 28, 92–98. [Google Scholar] [CrossRef]
- El Kadi, M.; Tysmans, T.; Verbruggen, S.; Vervloet, J.; De Munck, M.; Wastiels, J.; Van Hemelrijck, D. Experimental study and benchmarking of 3D textile reinforced cement composites. Cem. Concr. Compos. 2019, 104, 103352. [Google Scholar] [CrossRef]
- Sasi, E.A.; Peled, A. Three dimensional (3D) fabrics as reinforcements for cement-based composites. Compos. Part A Appl. Sci. Manuf. 2015, 74, 153–165. [Google Scholar] [CrossRef]
- Haik, R.; Sasi, E.A.; Peled, A. Influence of three-dimensional (3D) fabric orientation on flexural properties of cement-based composites. Cem. Concr. Compos. 2017, 80, 1–9. [Google Scholar] [CrossRef]
- El Kadi, M.; Kapsalis, P.; Van Hemelrijck, D.; Wastiels, J.; Tysmans, T. Influence of Loading Orientation and Knitted Versus Woven Transversal Connections in 3D Textile Reinforced Cement (TRC) Composites. Appl. Sci. 2020, 10, 4517. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, J.; Wang, Q. Distributed models of self-stress value in textile-reinforced self-stressing concrete. Constr. Build. Mater. 2016, 126, 286–296. [Google Scholar] [CrossRef]
- He, H.; Dong, W.; Wu, Z. Study on long-term expansive deformation of self-stressing concrete with combined restrictions of steel fibers and steel bar. Key Eng. Mater. 2011, 452, 533–536. [Google Scholar] [CrossRef]
- Guo, Z. Strength and Constitutive Relation of Concrete; China Architecture & Building Press: Beijing, China, 2004; pp. 159–200. (In Chinese) [Google Scholar]
- Lu, X.; Hsu, C.-T.T. Behavior of high strength concrete with and without steel fiber reinforcement in triaxial compression. Cem. Concr. Res. 2007, 36, 1679–1685. [Google Scholar] [CrossRef]
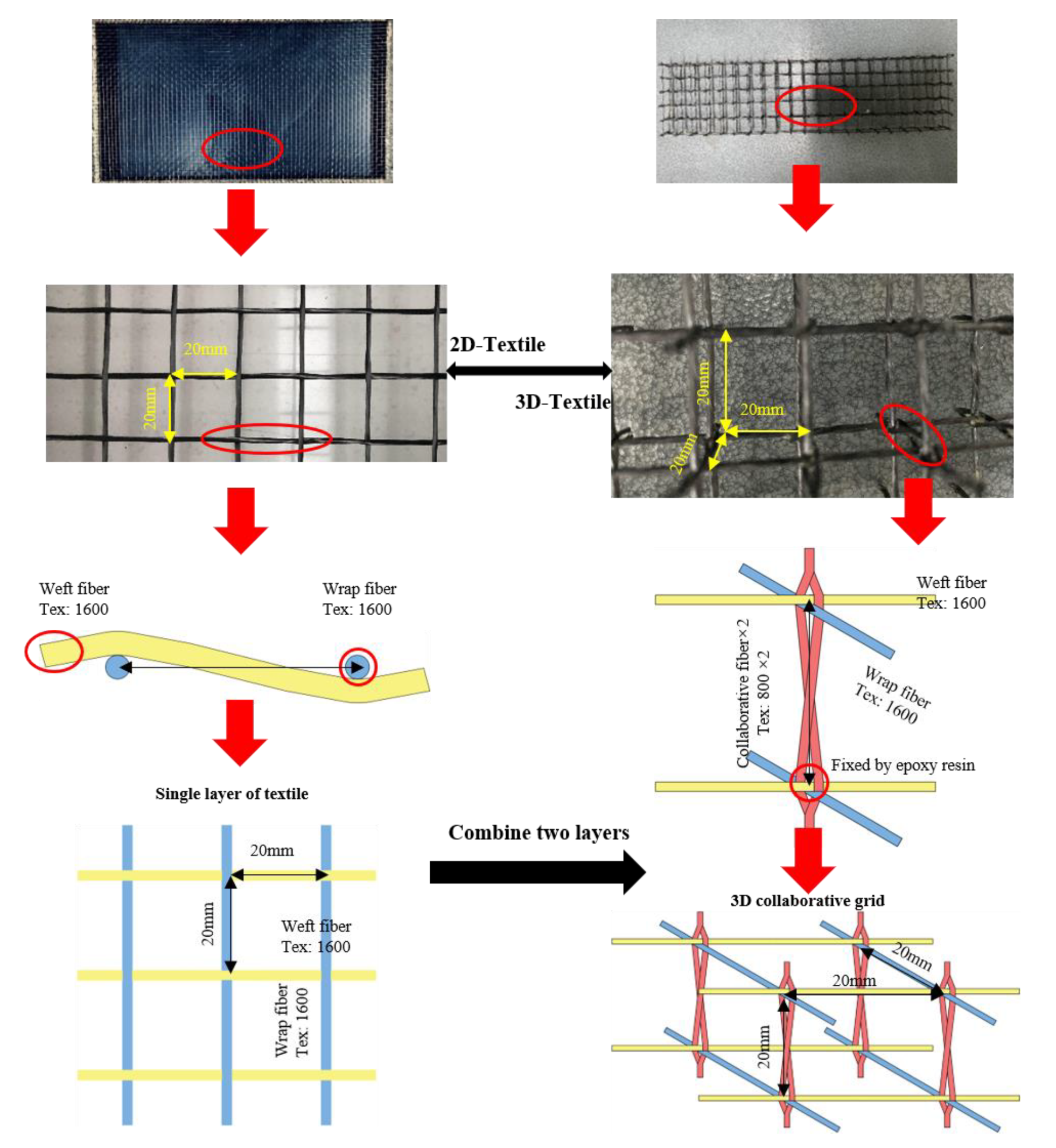


| Matrix | Type of Cement | Cement | Water | Fine Aggregate | Coarse Aggregate | Super Plasticizer |
|---|---|---|---|---|---|---|
| NC | Portland cement | 663 | 239 | 796 | 530 | 2.65 |
| SSC | Sulphate aluminate cement | 663 | 239 | 796 | 530 | 2.65 |
| Tensile Strength (MPa) | Tex (k) | Elastic Modulus (Gpa) | Density (g/cm3) | Theoretical Sectional Area (mm2) | Poisson’s Ratio |
|---|---|---|---|---|---|
| 4900 | 1600 | 230 | 1.76 | 9.09 | 0.307 |
| 4900 | 800 | 115 | 1.76 | 2.27 | 0.307 |
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Matrix | NC | NC | SSC | SSC | SSC | SSC | NC | SSC |
| Type of textile | Double- layer | 3D | Double- layer | 3D | Double- layer | 3D | / | / |
| Size of textile (mm) | 20 | 20 | 20 | 20 | 30 | 30 | / | / |
| Type of Constraint | Deformation of Reinforcement (mm) | Strain Value of Reinforcement (×10−3) | Self-Stress Value (mPa) |
|---|---|---|---|
| Steel bar and baffles | 0.79–1.83 | 1.97–4.58 | 1.12–2.59 |
| Textile | / | / | 1.10–2.50 |
| Group | Type of Matrix | Type of Textile | Size of Textile (mm) | Average Compressive Strength (mPa) | Standard Deviation |
|---|---|---|---|---|---|
| 1 | NC | Double- layer | 20 | 40.97 | 1.13 |
| 2 | NC | 3D | 20 | 40.77 | 2.25 |
| 3 | SSC | Double- layer | 20 | 36.63 | 0.44 |
| 4 | SSC | 3D | 20 | 42.60 | 1.28 |
| 5 | SSC | Double- layer | 30 | 34.87 | 2.88 |
| 6 | SSC | 3D | 30 | 37.67 | 1.12 |
| 7 | NC | None | 0 | 38.62 | 2.30 |
| 8 | SSC | None | 0 | 31.53 | 1.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Wang, B.; Guo, J.; Zhang, T. Study on the Expansion and Compression Resistance of 3D-Textile-Reinforced Self-Stressing Concrete. Polymers 2022, 14, 4336. https://doi.org/10.3390/polym14204336
Lu X, Wang B, Guo J, Zhang T. Study on the Expansion and Compression Resistance of 3D-Textile-Reinforced Self-Stressing Concrete. Polymers. 2022; 14(20):4336. https://doi.org/10.3390/polym14204336
Chicago/Turabian StyleLu, Xinyu, Boxin Wang, Jiahuan Guo, and Tianqi Zhang. 2022. "Study on the Expansion and Compression Resistance of 3D-Textile-Reinforced Self-Stressing Concrete" Polymers 14, no. 20: 4336. https://doi.org/10.3390/polym14204336
APA StyleLu, X., Wang, B., Guo, J., & Zhang, T. (2022). Study on the Expansion and Compression Resistance of 3D-Textile-Reinforced Self-Stressing Concrete. Polymers, 14(20), 4336. https://doi.org/10.3390/polym14204336






