Adsorption of Methylene Blue on the Surface of Polymer Membrane; Dependence on the Isotopic Composition of Liquid Matrix
Abstract
1. Introduction
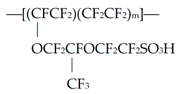
2. Materials and Methods
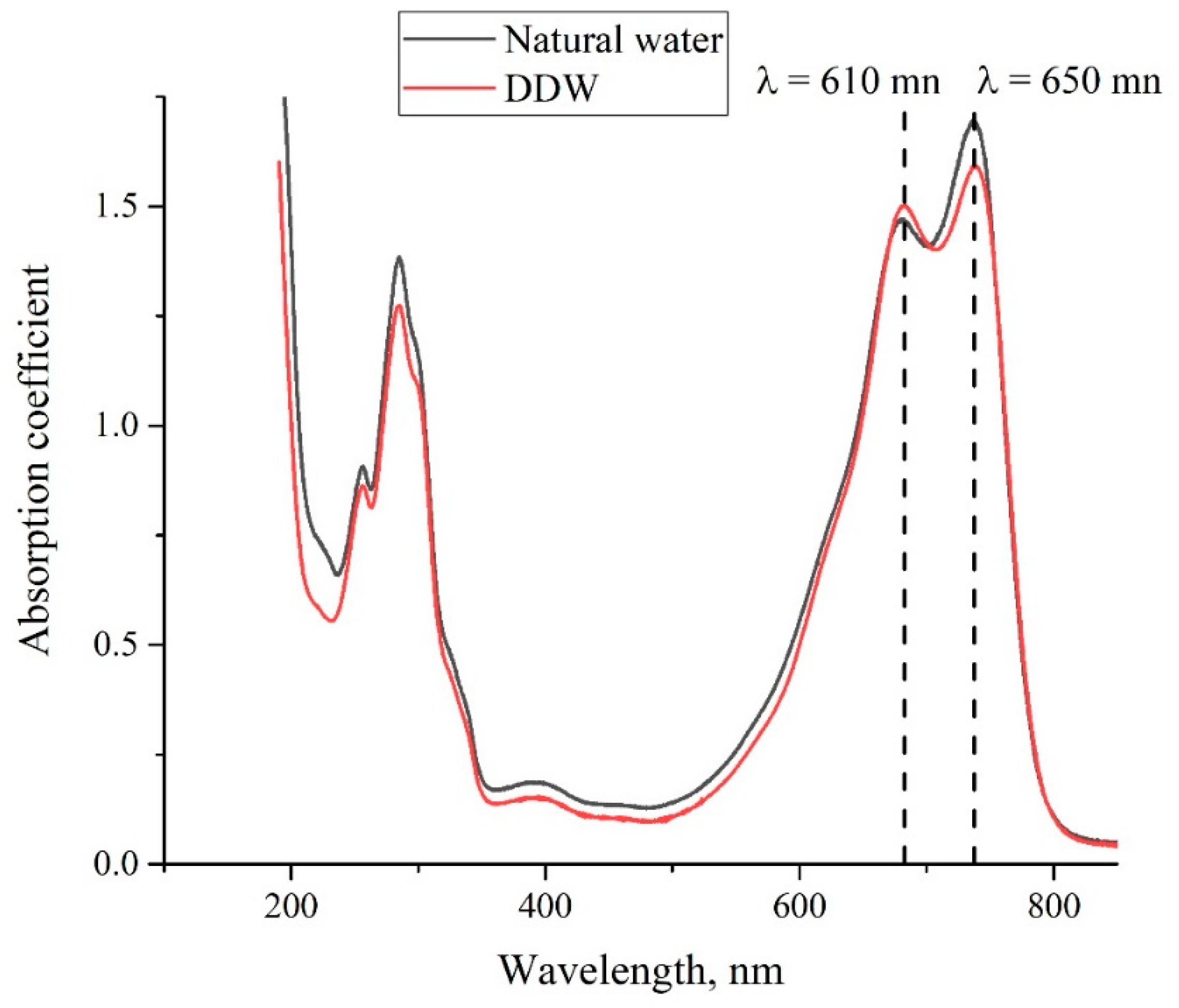
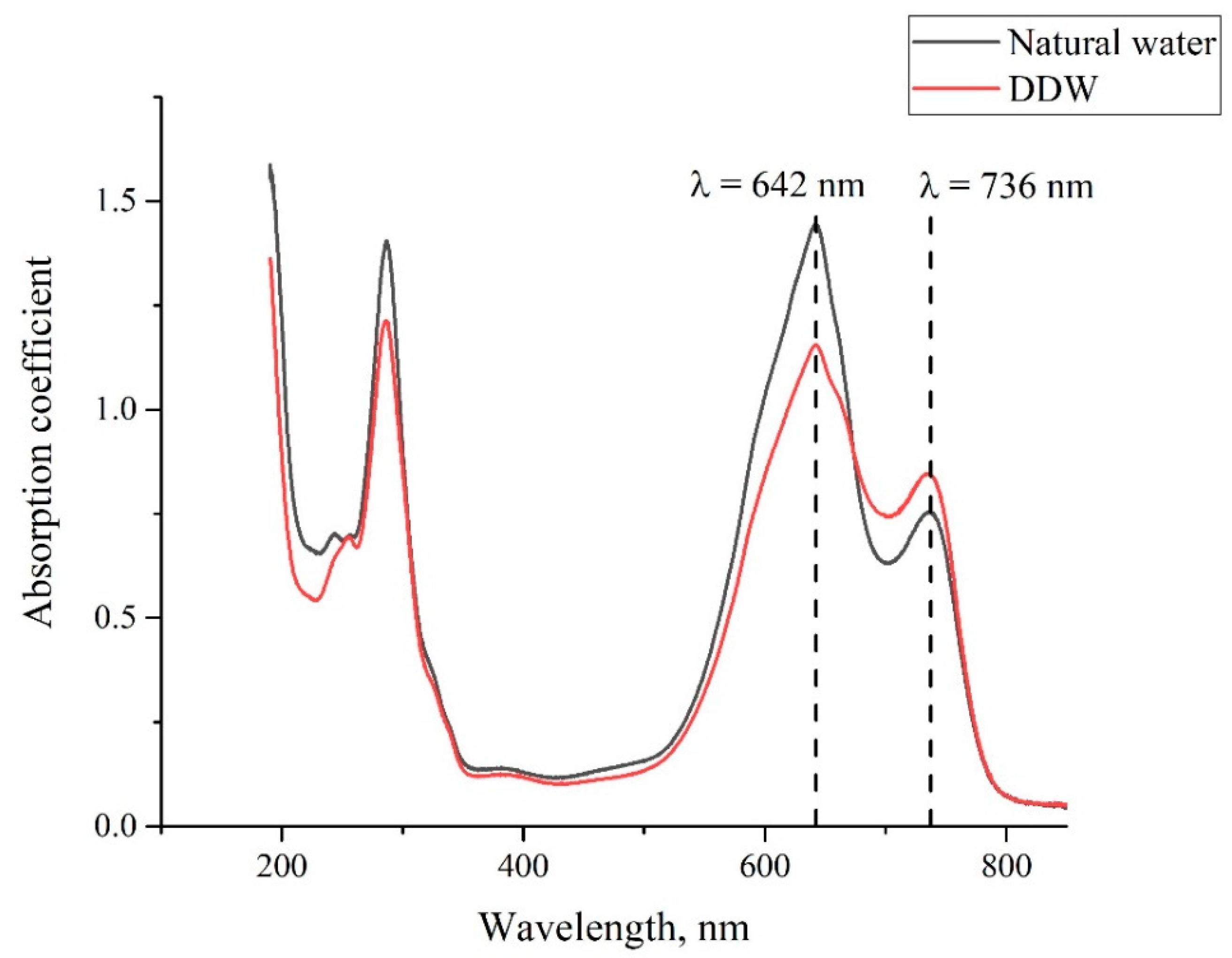
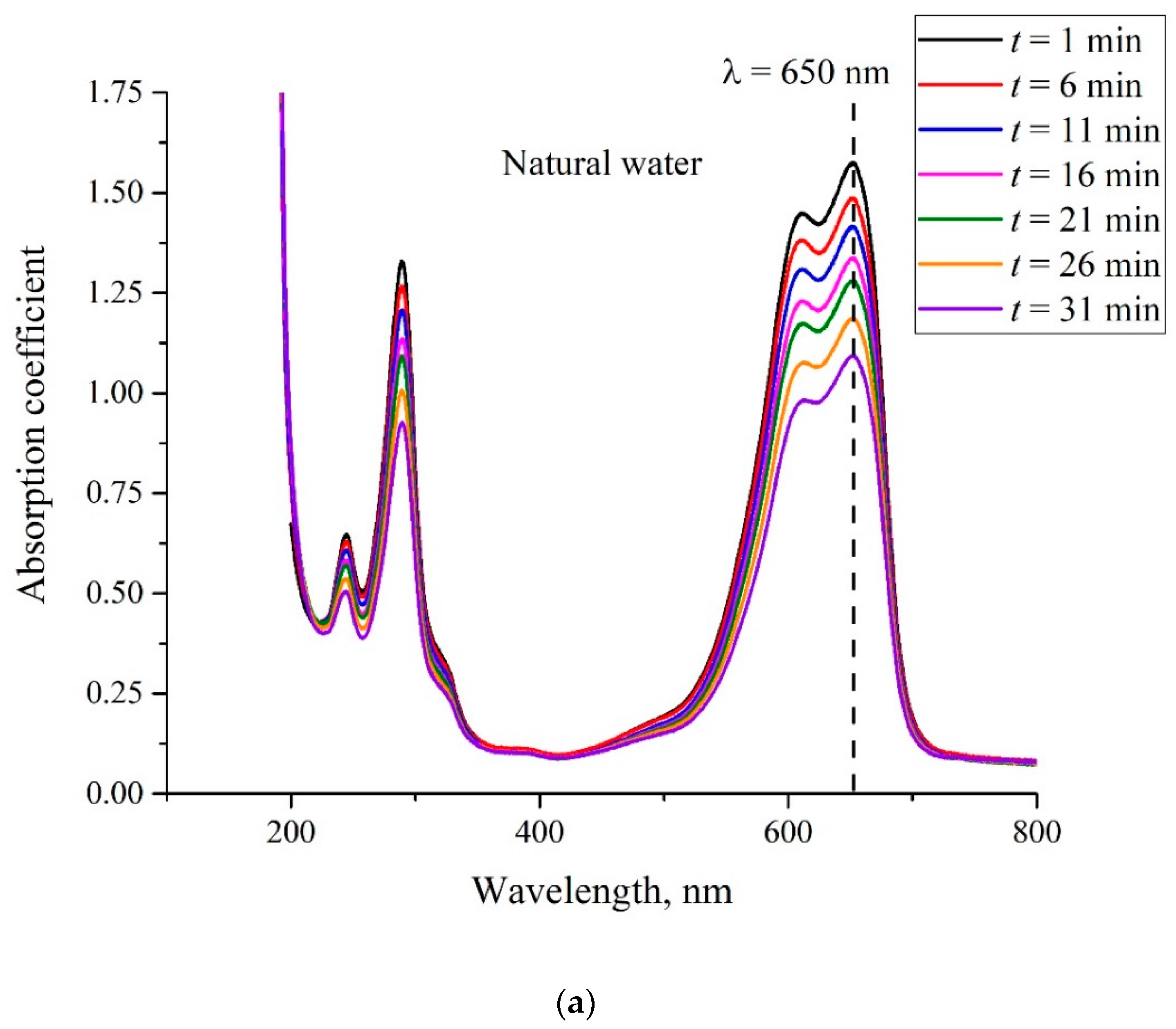
3. Experimental Results
4. Discussion
5. Conclusions
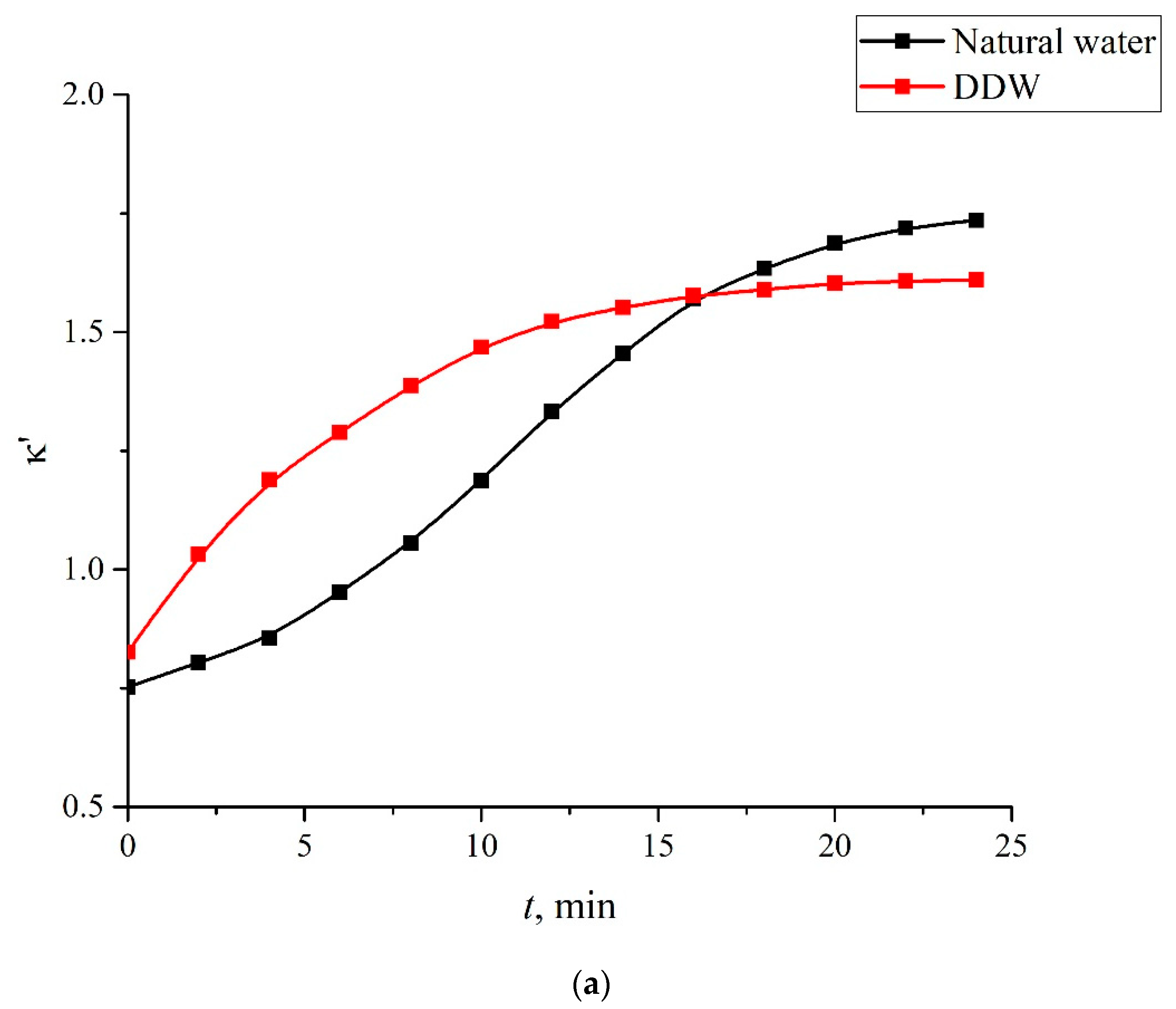
- The rate of MB adsorption on the Nafion surface depends on the isotopic composition of the MB aqueous solution, which is associated with the effect of unwinding polymer fibers from the membrane surface into the liquid bulk. This is due to the fact that adsorption is controlled by diffusion, and diffusion processes are slowed down inside the layer of unwound fibers, whereas the unwinding effect is controlled by the isotopic composition of liquid.
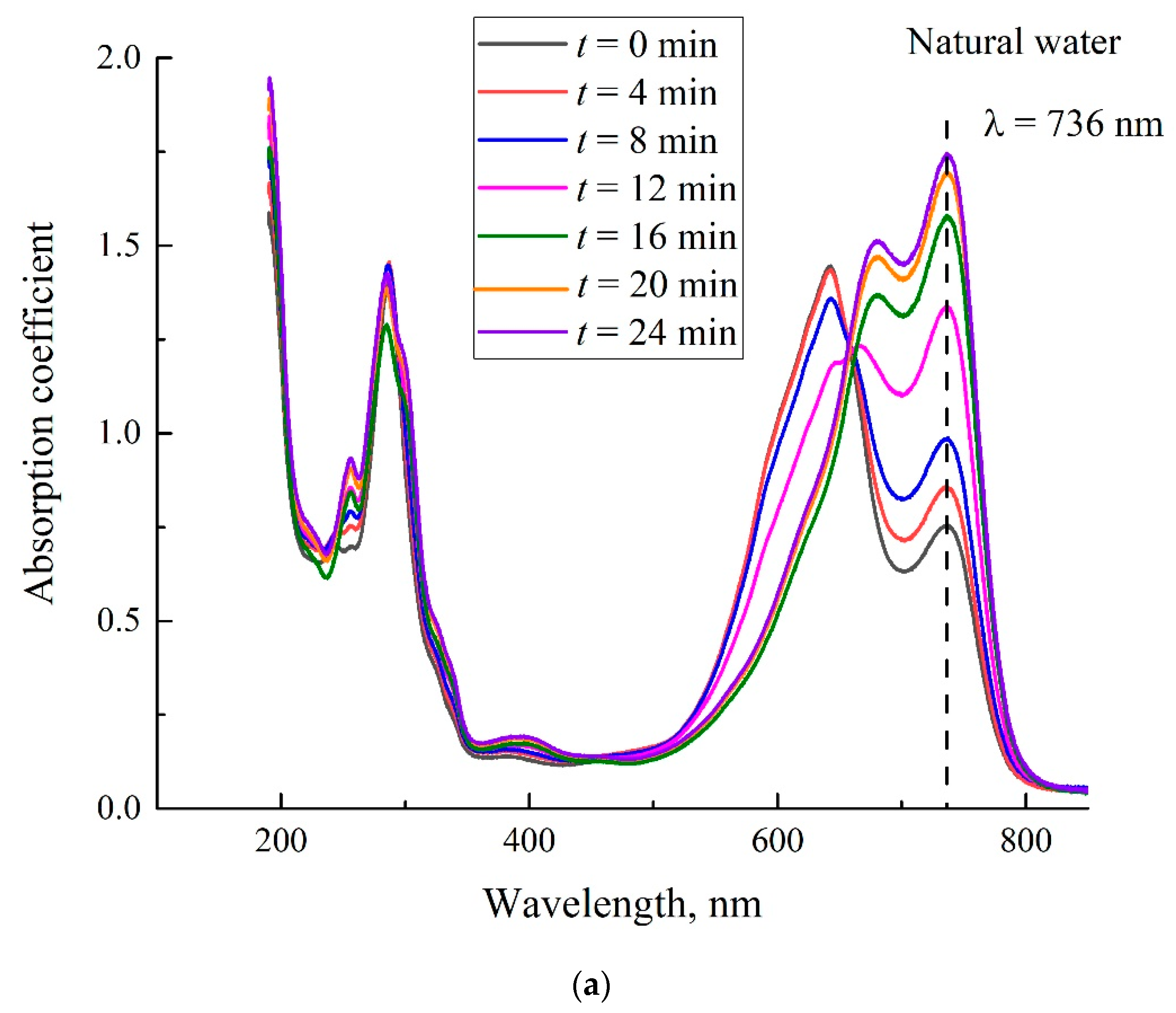
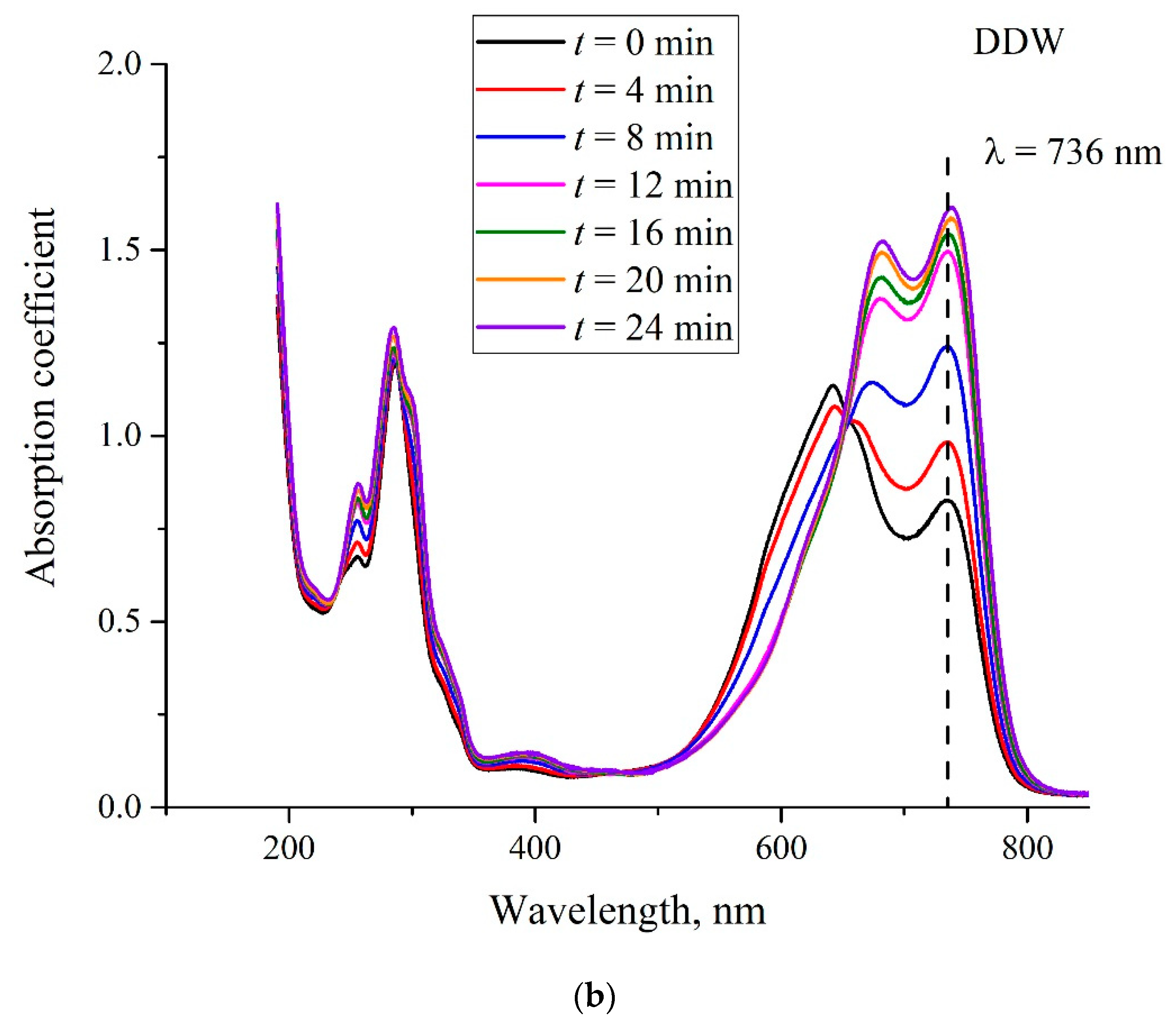
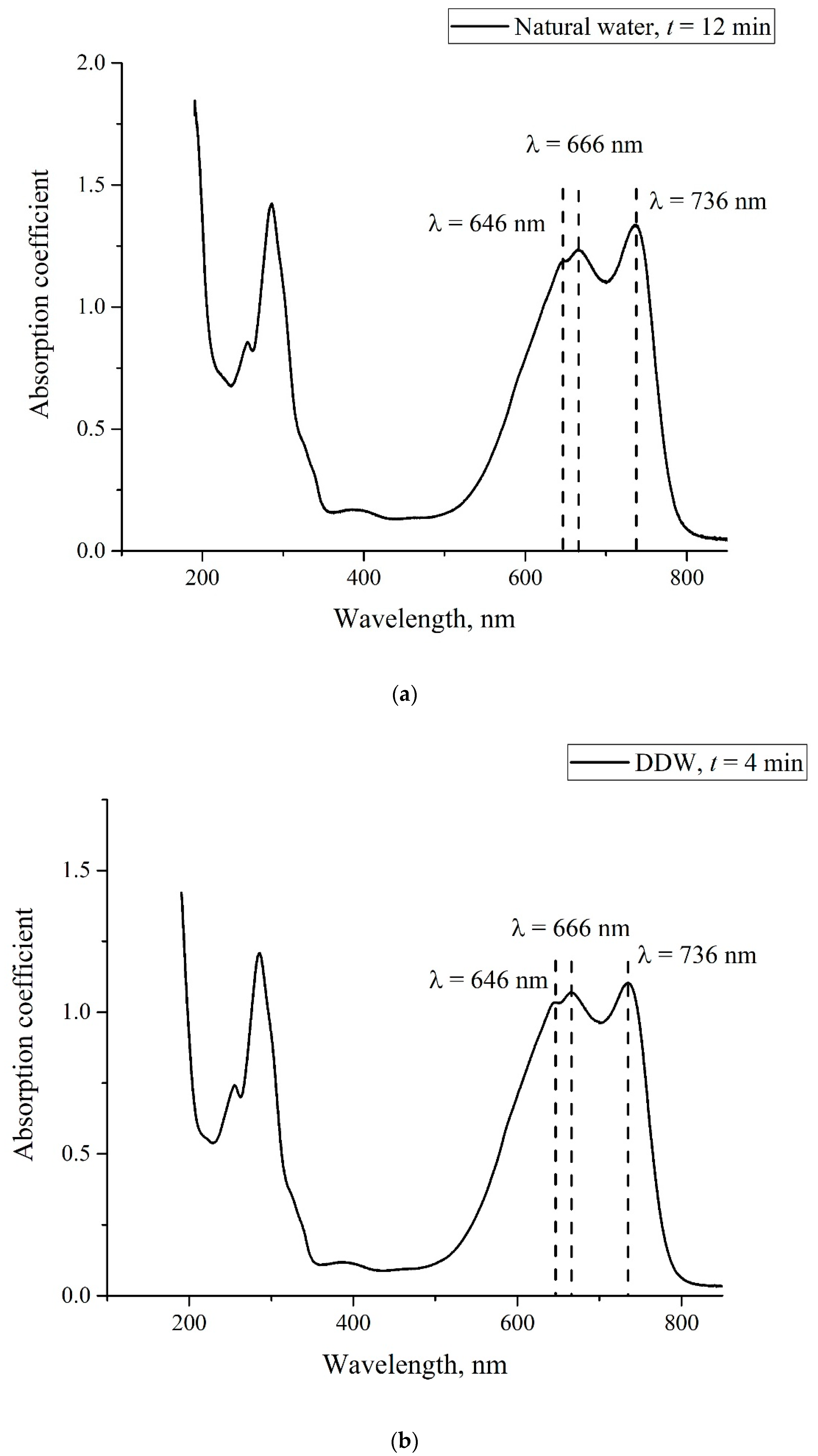
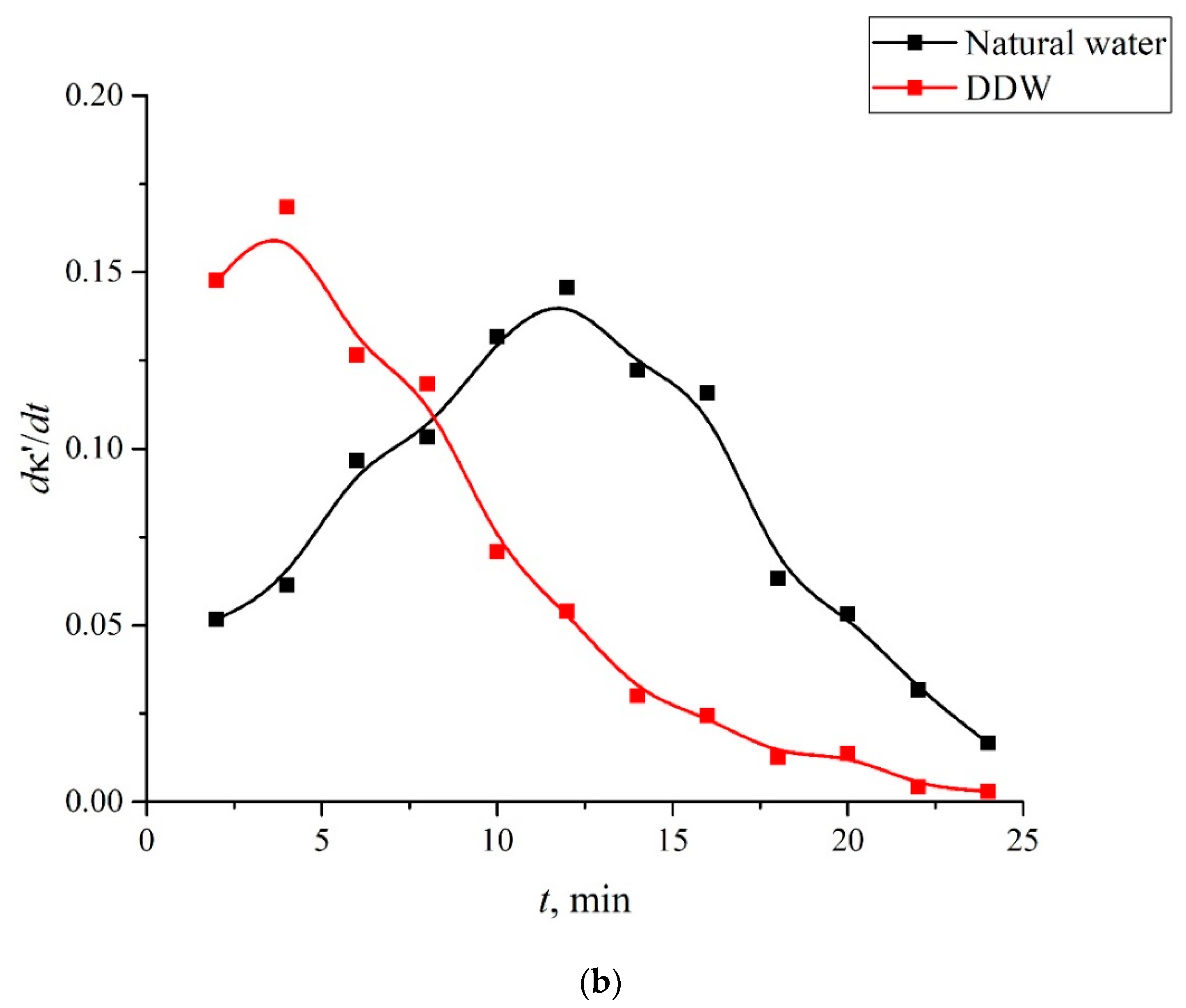
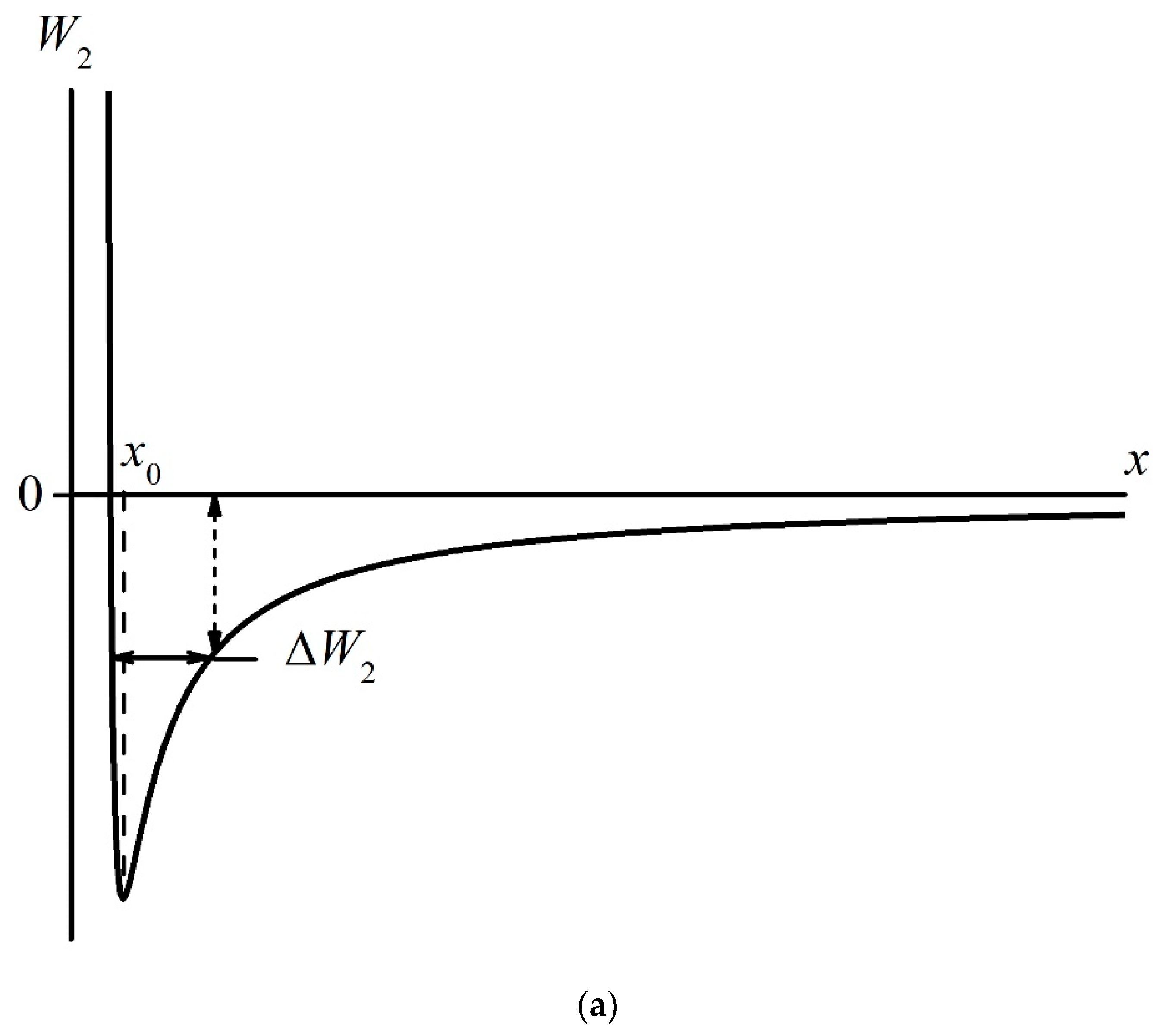
- Certain bands of the absorption spectrum of MB, adsorbed on the Nafion surface, are redshifted as compared to the same bands in the MB solution. The effect is associated with the formation of molecular complexes between MB, water, and Nafion. These complexes are formed due to short-range dispersion forces and long-range Coulomb forces; Coulomb forces are caused by the presence of negative charge on the membrane surface, resulting from the dissociation of terminal sulfonic groups and the transfer of protons into the liquid bulk. When the Nafion plate is removed from the liquid, the charge on the membrane surface is reduced to zero level, which leads to the disappearance of the Coulomb attraction and, accordingly, to a decrease in the desorption barrier for water molecules. The decrease in charge on the membrane surface is controlled by the diffusion kinetics. This is manifested in the behavior of the derivative dκ‘/dt. We can claim that in the case of polymer fibers, unwound into the bulk of liquid, the charge on the surface decreases slower than in the absence of the unwinding effect.
- We can claim that it is possible to control the dynamics of adsorption and desorption processes by infinitesimal changes in the deuterium content (from 3 to 157 ppm) in an aqueous solution, in which a polymer membrane swells.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A and B | Dimensional constants in Equations (6) and (7); |
| Cb | The concentration of adsorbed substance in the bulk of the solution in Equation (1); |
| C0 | The value of Cb at t = 0; |
| CS0 | The number of free adsorption sites per the surface unit before the beginning of the adsorption process in Equation (1); |
| C(t) | Time-dependent dimensional parameter in Equations (6) and (7); |
| d′ | Dipole moment of complex “MB + water”; |
| D | The diffusivity of adsorbing particles in Equation (3); |
| E | The electric field strength vector near the Nafion surface; |
| ni0 | The equilibrium volume number density of ions in MB solution; |
| n | The number of adsorbed molecules on the surface unit in Equation (1); |
| RD | The Debye screening radius; |
| Y01 | The equilibrium percentage of MB, removed from the solution based on natural water; |
| Y02 | The equilibrium percentage of MB, removed from the solution based on DDW; |
| σ | The area of adsorbed molecules in Equation (1); |
| σ′(t) | The surface charge density on the Nafion membrane; |
| φ | The subsurface concentration of adsorbed substance in Equation (4); |
| κ(t) | The absorption coefficient of MB solution; |
| κ′(t) | The absorption coefficient of Nafion after removing from MB solution; |
| η and ξ | Variables of integration in Equation (4); |
| τ1 | The characteristic time of MB adsorption from MB solution based on natural water; |
| τ1′ | The characteristic time of water desorption from MB solution based on natural water; |
| τ2 | The characteristic time of MB adsorption from MB solution based on DDW; |
| τ2′ | The characteristic time of water desorption from MB solution based on DDW; |
| ω | The oscillator frequency. |
References
- Mauritz, K.A.; Moore, R.B. State of understanding of Nafion. Chem. Rev. 2004, 104, 4535–4585. [Google Scholar] [CrossRef] [PubMed]
- Belov, N.A.; Pashkevich, D.S.; Alentiev, A.Y.; Tressaud, A. Effect of Direct Fluorination on the Transport Properties and Swelling of Polymeric Materials: A Review. Membranes 2021, 11, 713. [Google Scholar] [CrossRef] [PubMed]
- Samsudin, A.M.; Bodner, M.; Hacker, V. A Brief Review of Poly(Vinyl Alcohol)-Based Anion Exchange Membranes for Alkaline Fuel Cells. Polymers 2022, 14, 3565. [Google Scholar] [CrossRef] [PubMed]
- Tsioptsias, C.; Foukas, G.-R.P.; Papaioannou, S.-M.; Tzimpilis, E.; Tsivintzelis, I. On the Thermochemical Transition Depression of Cellulose Acetate Composite Membranes. Polymers 2022, 14, 3434. [Google Scholar] [CrossRef] [PubMed]
- Chausov, D.N.; Smirnova, V.V.; Burmistrov, D.E.; Sarimov, R.M.; Kurilov, A.D.; Astashev, M.E.; Uvarov, O.V.; Dubinin, M.V.; Kozlov, V.A.; Vedunova, M.V.; et al. Synthesis of a Novel, Biocompatible and Bacteriostatic Borosiloxane Composition with Silver Oxide Nanoparticles. Materials 2022, 15, 527. [Google Scholar] [CrossRef]
- Astashev, M.E.; Sarimov, R.M.; Serov, D.A.; Matveeva, T.A.; Simakin, A.V.; Ignatenko, D.N.; Burmistrov, D.; Smirnova, V.; Kurilov, A.; Mashchenko, V.; et al. Antibacterial behavior of organosilicon composite with nano aluminum oxide without influencing animal cells. React. Funct. Polym. 2022, 170, 105143. [Google Scholar] [CrossRef]
- Burmistrov, D.E.; Simakin, A.V.; Smirnova, V.V.; Uvarov, O.V.; Ivashkin, P.I.; Kucherov, R.N.; Ivanov, V.E.; Bruskov, V.I.; Sevostyanov, M.A.; Baikin, A.S.; et al. Bacteriostatic and Cytotoxic Properties of Composite Material Based on ZnO Nanoparticles in PLGA Obtained by Low Temperature Method. Polymers 2022, 14, 49. [Google Scholar] [CrossRef]
- Canaparo, R.; Foglietta, F.; Limongi, T.; Serpe, L. Biomedical applications of reactive oxygen species generation by metal nanoparticles. Materials 2021, 14, 53. [Google Scholar] [CrossRef]
- Mu, P.; Dong, T.; Jiang, H.; Jiang, M.; Chen, Z.; Xu, H.; Zhang, H.; Cui, G. Crucial challenges and recent optimization Progress of metal–sulfur battery electrolytes. Energy Fuels 2021, 35, 1966–1988. [Google Scholar] [CrossRef]
- Kodir, A.; Shin, S.H.; Park, S.; Arbi, M.R.; Yang, T.H.; Lee, H.; Shin, D.; Bae, B. Macromolecular antioxidants for chemically durable polymer electrolyte fuel cell membranes. Int. J. Energy Res. 2022, 46, 7186–7200. [Google Scholar] [CrossRef]
- Xiong, Z.M.; O’Donovan, M.; Sun, L.; Choi, J.Y.; Ren, M.; Cao, K. Anti-Aging Potentials of Methylene Blue for Human Skin Longevity. Sci. Rep. 2017, 7, 2475. [Google Scholar] [CrossRef] [PubMed]
- Te Velthuis, A.J.W.; Van den Worml, S.H.E.; Sims, A.C.; Baric, R.S.; Snijder, E.J.; Van Hemert, M.J. Zn(2+) inhibits coronavirus and arterivirus RNA polymerase activity in vitro and zinc ionophores block the replication of these viruses in cell culture. PLoS Pathog. 2010, 6, 1001176. [Google Scholar] [CrossRef] [PubMed]
- Alamdari, H.; Moghaddam, D.B.; Amini, A.S.; Hamidi Alamdari, A.; Damsaz, M.; Yarahmadi, A. The Application of a Reduced Dye Used in Orthopedics as a Novel Treatment against Coronavirus (COVID-19): A Suggested Therapeutic Protocol. Arch. Bone Jt. Surg. 2020, 8, 291–294. [Google Scholar]
- Dabholkar, N.; Gorantla, S.; Dubey, S.K.; Alexander, A.; Taliyan, R.; Singhvi, G. Repurposing methylene blue in the management of COVID-19: Mechanistic aspects and clinical investigations. Biomed. Pharmacother. 2021, 142, 112023. [Google Scholar] [CrossRef]
- Bojadzic, D.; Alcazar, O.; Buchwald, P. Methylene Blue Inhibits theSARS-CoV-2 Spike–ACE2Protein-Protein Interaction–a Mechanism that can Contribute to its Antiviral Activity Against COVID-19. Front. Pharm. 2021, 11, 600372. [Google Scholar] [CrossRef] [PubMed]
- Cagno, V.; Medaglia, C.; Cerny, A.; Cerny, T.; Zwygart, A.C.A.; Cerny, E.; Tapparel, C. Methylene Blue has a potent antiviral activity against SARS-CoV-2 and H1N1 influenza virus in the absence of UV-activation in vitro. Sci. Rep. 2021, 11, 14295. [Google Scholar] [CrossRef]
- Alemany, A.; Millat-Martinez, P.; Corbacho-Monné, M.; Malchair, P.; Ouchi, D.; Ruiz-Comellas, A.; Ramírez-Morros, A.; Codina, J.R.; Simon, R.A.; Videla, S.; et al. High-titre methylene blue-treated convalescent plasma as an early treatment for outpatients with COVID-19: A randomised, placebo-controlled trial. Lancet Respir. Med. 2022, 10, 278–288. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Bolotskova, P.N.; Bondarchuk, E.V.; Gryaznov, V.G.; Kozlov, V.A.; Okuneva, M.A.; Ovchinnikov, O.V.; Smoliy, O.P.; Turkanov, I.F.; Galkina, C.A.; et al. Stochastic Ultralow-Frequency Oscillations of the Luminescence Intensity from the Surface of a Polymer Membrane Swelling in Aqueous Salt Solutions. Polymers 2022, 14, 688. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Astashev, M.E.; Bolotskova, P.N.; Kozlov, V.A.; Kravchenko, A.O.; Nagaev, E.I.; Okuneva, M.A. Possibility to Alter Dynamics of Luminescence from Surface of Polymer Membrane with Ultrasonic Waves. Polymers 2022, 14, 2542. [Google Scholar] [CrossRef]
- Ninham, B.W.; Bolotskova, P.N.; Gudkov, S.V.; Baranova, E.N.; Kozlov, V.A.; Shkirin, A.V.; Vu, M.T. Nafion Swelling in Salt Solutions in a Finite Sized Cell: Curious Phenomena Dependent on Sample Preparation Protocol. Polymers 2022, 14, 1511. [Google Scholar] [CrossRef]
- Craig, H. Standard reporting concentrations of deuterium and oxygen-18 in natural water. Science 1961, 133, 1833–1834. [Google Scholar] [CrossRef] [PubMed]
- Goodsell, D.S. The Machinery of Life; Springer Science + Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Khawar, I.A.; Kim, J.H.; Kuh, H.J. Improving Drug Delivery to Solid Tumors: Priming the Tumor Microenvironment. J. Control Release 2015, 201, 78–89. [Google Scholar] [CrossRef]
- Buhren, B.A.; Schrumpf, H.; Hoff, N.P.; Bölke, E.; Hilton, S.; Gerber, P.A. Hyaluronidase: From Clinical Applications to Molecular and Cellular Mechanisms. Eur. J. Med. Res. 2016, 21, 5. [Google Scholar] [CrossRef]
- Nagy, N.; Kuipers, H.F.; Frymoyer, A.R.; Ishak, H.D.; Bollyky, J.B.; Wight, T.N.; Bollyky, P.L. 4-Methylumbelliferone Treatment and Hyaluronan Inhibition as a Therapeutic Strategy in Inflammation, Autoimmunity, and Cancer. Front. Immunol. 2015, 6, 123. [Google Scholar] [CrossRef] [PubMed]
- Shepard, H.M. Breaching the Castle Walls: Hyaluronan Depletion as a Therapeutic Approach to Cancer Therapy. Front. Oncol. 2015, 5, 192. [Google Scholar] [CrossRef] [PubMed]
- Rezaei-Zarchi, S.; Saboury, A.A.; Javed, A. Characterization Study for Nanocompositions of Methylene Blue and Riboflavin-Nafion on the Electrode Surface. Iran. J. Pharm. Sci. 2008, 4, 119–126. [Google Scholar]
- Al-Ghouti, M.A.; Al-Absi, R.S. Mechanistic understanding of the adsorption and thermodynamic aspects of cationic methylene blue dye onto cellulosic olive stones biomass from wastewater. Sci. Rep. 2020, 10, 15928. [Google Scholar] [CrossRef]
- Munir, M.; Nazar, M.F.; Zafar, M.N.; Zubair, M.; Ashfaq, M.; Hosseini-Bandegharaei, A.; Khan, S.U.; Ahmad, A. Effective Adsorptive Removal of Methylene Blue from Water by Didodecyldimethylammonium Bromide-Modified Brown Clay. ACS Omega 2020, 5, 16711–16721. [Google Scholar] [CrossRef]
- Cheng, J.; Zhan, C.; Wu, J.; Cui, Z.; Si, J.; Wang, Q.; Peng, X.; Turng, L.S. Highly Efficient Removal of Methylene Blue Dye from an Aqueous Solution Using Cellulose Acetate Nanofibrous Membranes Modified by Polydopamine. ACS Omega 2020, 5, 5389–5400. [Google Scholar] [CrossRef]
- Thang, N.H.; Khang, D.S.; Hai, T.D.; Nga, D.T.; Tuan, P.D. Methylene blue adsorption mechanism of activated carbon synthesised from cashew nut shells. RSC Adv. 2021, 11, 26563–26570. [Google Scholar] [CrossRef]
- El-Bery, H.M.; Saleh, M.; El-Gendy, R.A.; Saleh, M.R.; Thabet, S.M. High adsorption capacity of phenol and methylene blue using activated carbon derived from lignocellulosic agriculture wastes. Sci. Rep. 2022, 12, 5499. [Google Scholar] [CrossRef] [PubMed]
- De Almeida, S.H.; Kawano, Y. Ultraviolet-visible spectra of Nafion membrane. Eur. Polym. J. 1997, 33, 1307–1311. [Google Scholar] [CrossRef]
- Baret, J.F. Kinetics of Adsorption from a Solution. Role of the Diffusion and of the Adsorption-Desorption Antagonism. J. Phys. Chem. 1968, 72, 2755–2758. [Google Scholar] [CrossRef]
- Miller, R.; Kretzschmar, G. Adsorption kinetics of surfactants at fluid interfaces. Adv. Col. Int. Sci. 1991, 37, 97–121. [Google Scholar] [CrossRef]
- Ge, S.H.; Li, X.G.; Yi, B.L.; Hsing, I.M. Absorption, desorption, and transport of water in polymer electrolyte membranes for fuel cells. J. Electrochem. Soc. 2005, 152, A1149. [Google Scholar] [CrossRef]
- Majsztrik, P.W.; Satterfield, M.B.; Bocarsly, A.B.; Benziger, J.B. Water sorption, desorption and transport in Nafion membranes. J. Membr. Sci. 2007, 301, 93–106. [Google Scholar] [CrossRef]
- Mahmood, T.; Anwer, F.; Mahmood, I.; Kishwar, F.; Wahab, A. Solvatochromic effect of Methylene Blue in different solvents with different polarity. Eur. Acad. Res. 2013, 1, 1100–1109. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press Inc.: New York, NY, USA, 1971. [Google Scholar]
- Debye, P.; Hückel, E. ZurTheorie der Elektrolyte. Phys. Ztschr. 1923, 24, 185–206. [Google Scholar]
- Chai, B.; Yoo, H.; Pollack, G.H. Effect of Radiant Energy on Near-Surface Water. J. Phys. Chem. B 2009, 113, 13953–13958. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Physical Kinetics; Pergamon Press Inc.: New York, NY, USA, 1981. [Google Scholar]



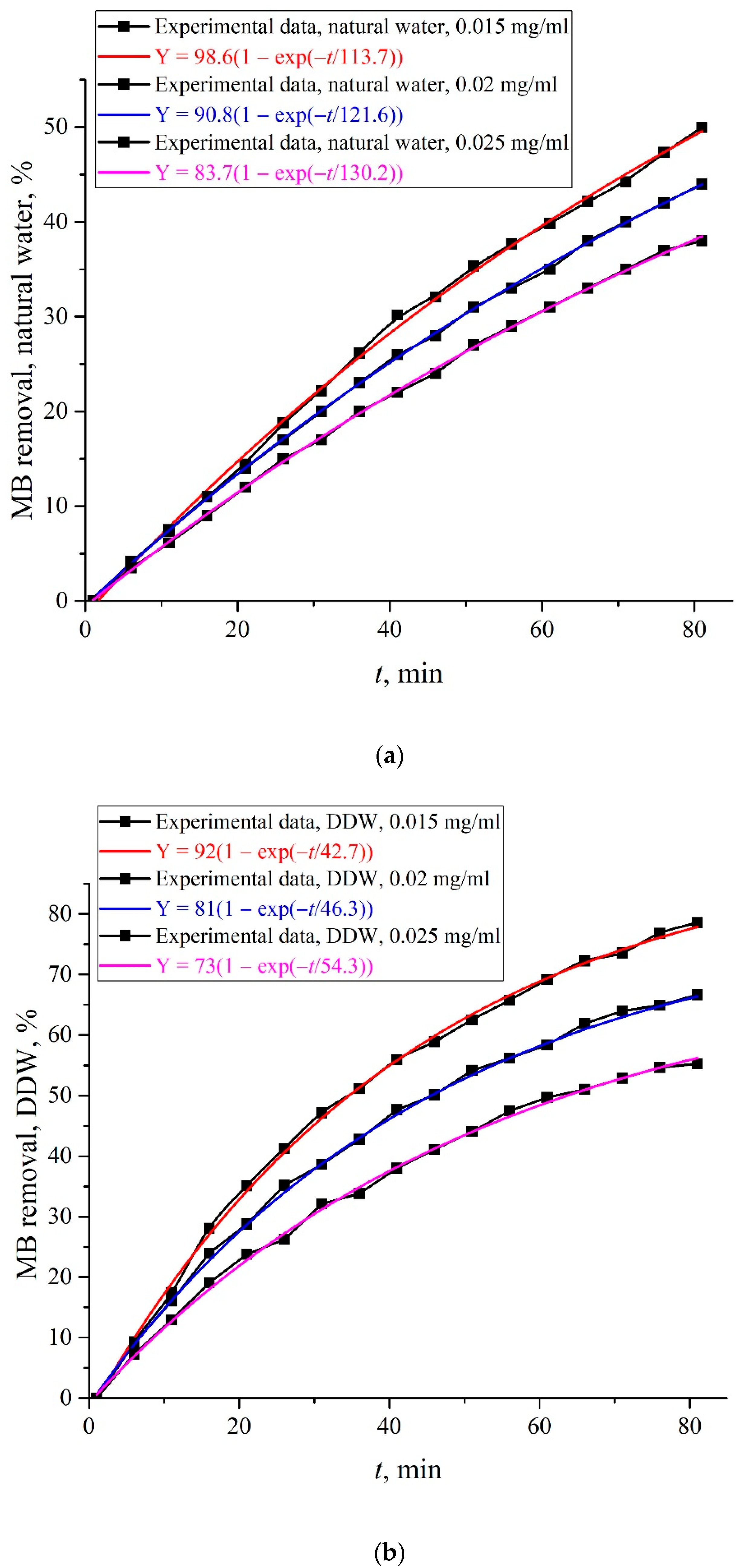

| C0, mg/mL | Y01, % | τ1, min |
|---|---|---|
| 0.015 | 98.6 | 113.7 |
| 0.02 | 90.8 | 121.6 |
| 0.025 | 83.7 | 130.2 |
| C, mg/mL | Y02, % | τ2, min |
|---|---|---|
| 0.015 | 92 | 42.7 |
| 0.02 | 81 | 46.3 |
| 0.025 | 73 | 54.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bunkin, N.F.; Bolotskova, P.N.; Gladysheva, Y.V.; Kozlov, V.A.; Timchenko, S.L. Adsorption of Methylene Blue on the Surface of Polymer Membrane; Dependence on the Isotopic Composition of Liquid Matrix. Polymers 2022, 14, 4007. https://doi.org/10.3390/polym14194007
Bunkin NF, Bolotskova PN, Gladysheva YV, Kozlov VA, Timchenko SL. Adsorption of Methylene Blue on the Surface of Polymer Membrane; Dependence on the Isotopic Composition of Liquid Matrix. Polymers. 2022; 14(19):4007. https://doi.org/10.3390/polym14194007
Chicago/Turabian StyleBunkin, Nikolai F., Polina N. Bolotskova, Yana V. Gladysheva, Valeriy A. Kozlov, and Svetlana L. Timchenko. 2022. "Adsorption of Methylene Blue on the Surface of Polymer Membrane; Dependence on the Isotopic Composition of Liquid Matrix" Polymers 14, no. 19: 4007. https://doi.org/10.3390/polym14194007
APA StyleBunkin, N. F., Bolotskova, P. N., Gladysheva, Y. V., Kozlov, V. A., & Timchenko, S. L. (2022). Adsorption of Methylene Blue on the Surface of Polymer Membrane; Dependence on the Isotopic Composition of Liquid Matrix. Polymers, 14(19), 4007. https://doi.org/10.3390/polym14194007










