On the Response of a Herschel–Bulkley Fluid Due to a Moving Plate
Abstract
1. Introduction
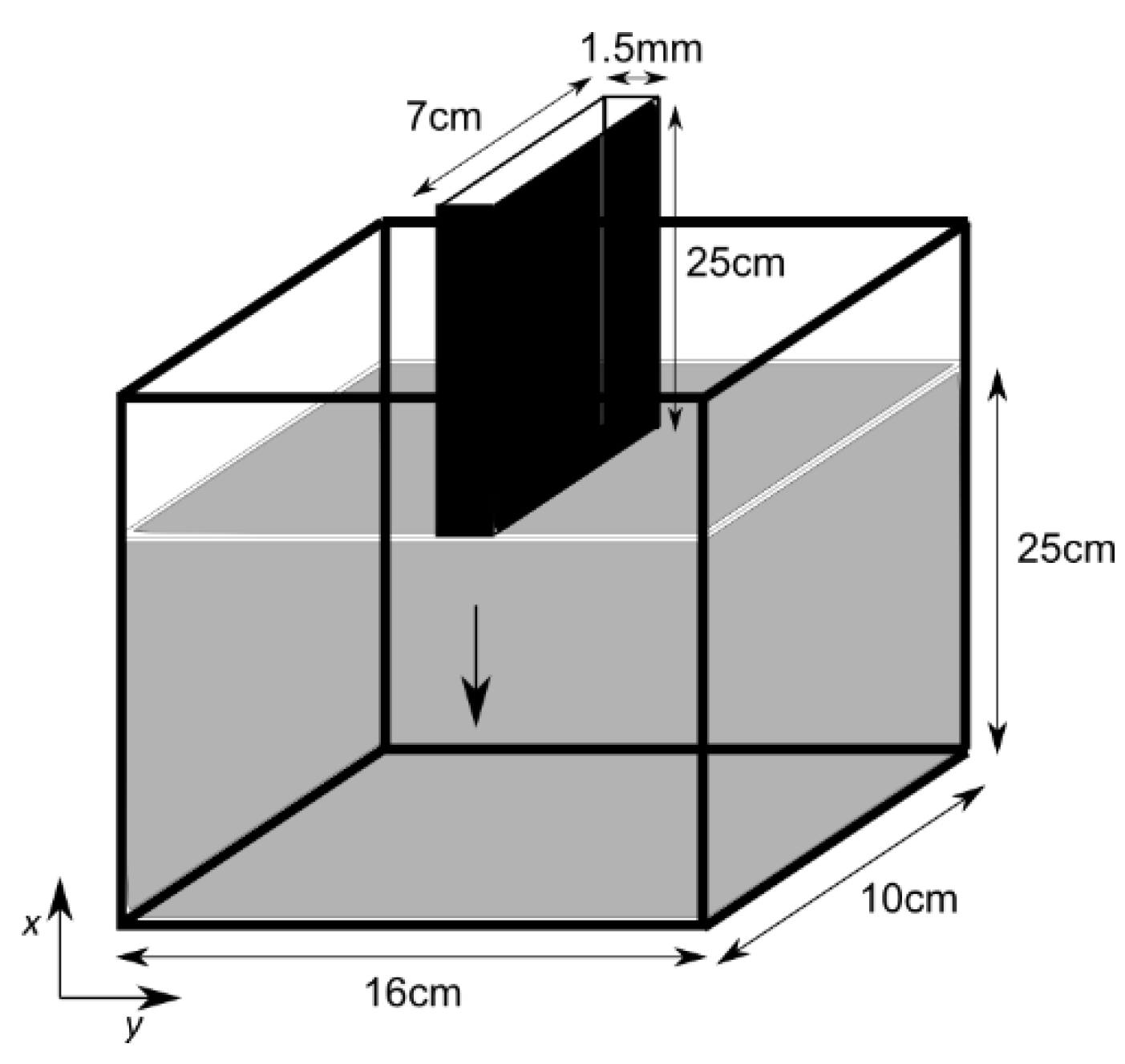
2. Problem Statement
3. Governing Equations
3.1. Conservation of Mass
3.2. Conservation of Linear Momentum
3.3. Conservation of Angular Momentum
4. Constitutive Relation for the Stress Tensor
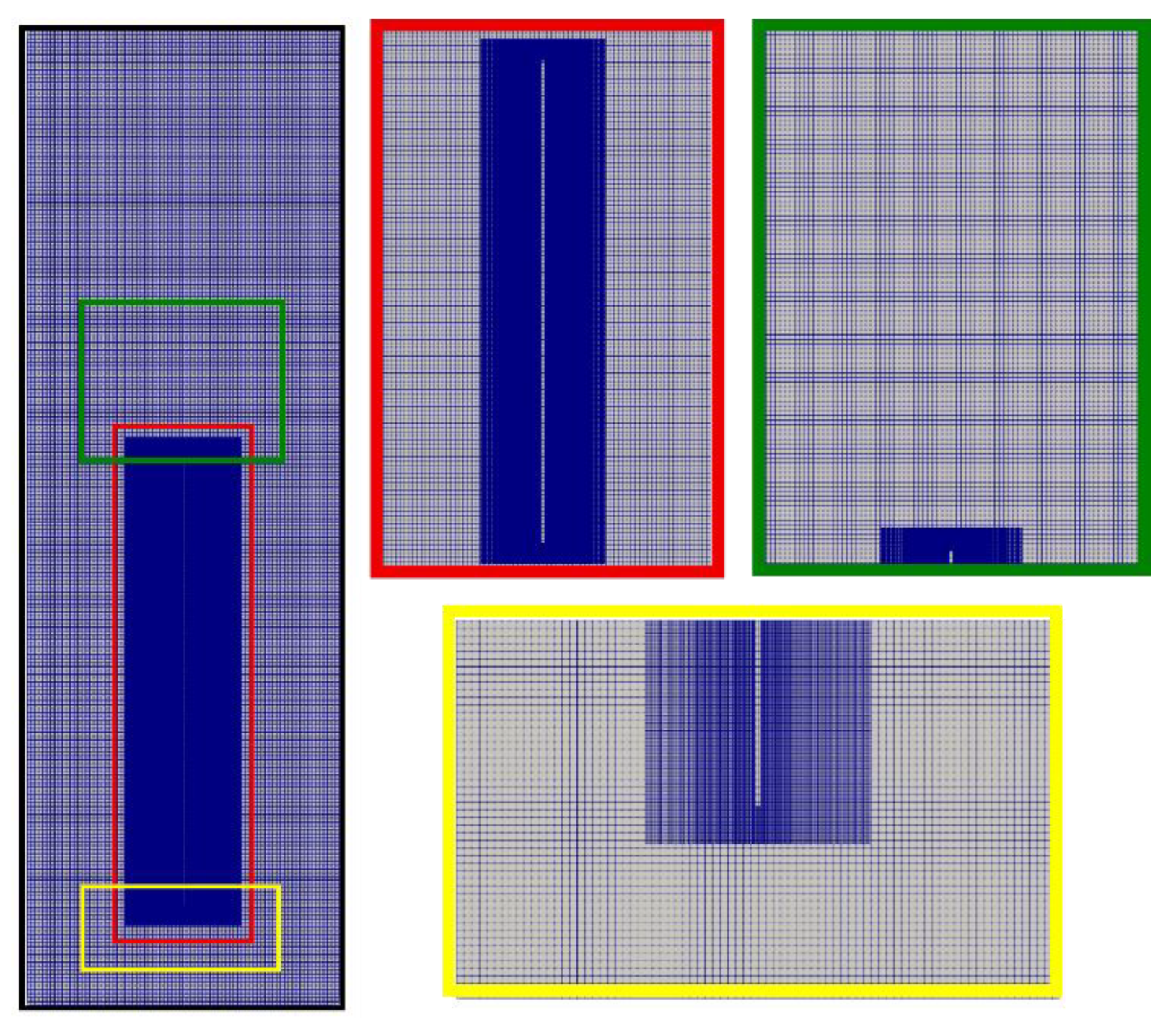
5. Numerical Approach
- at the moving plate:
- at the container’s walls:
6. Results
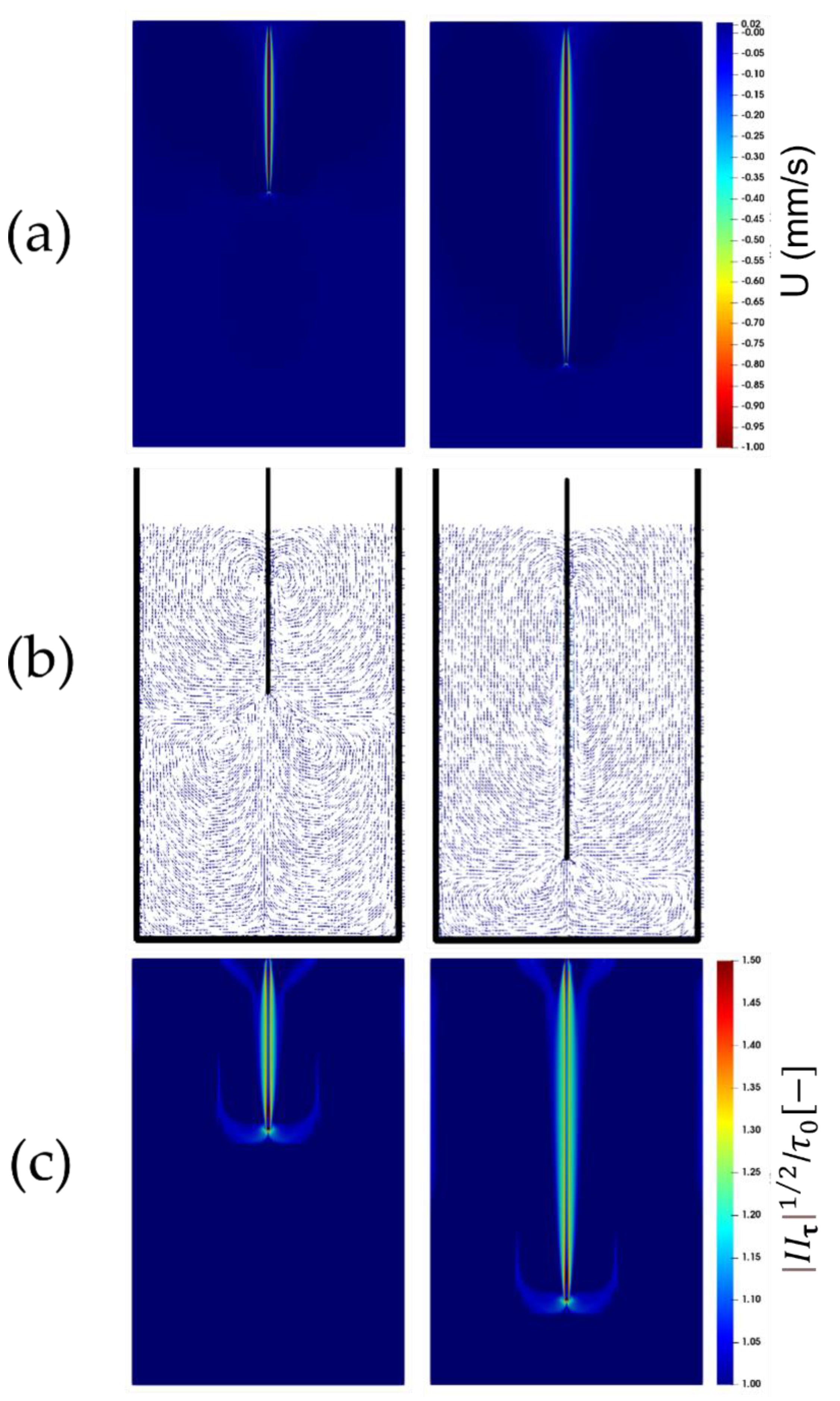
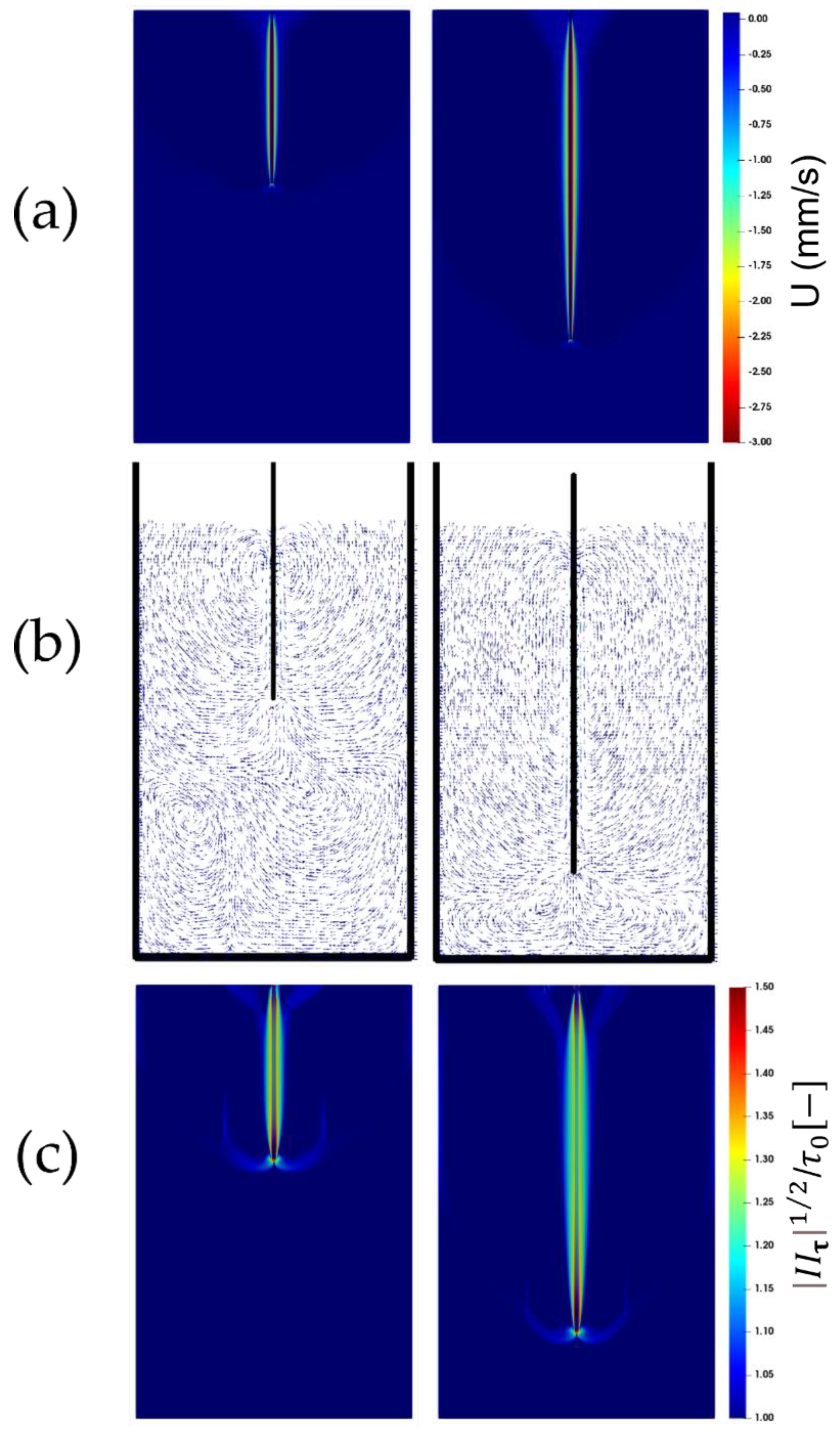
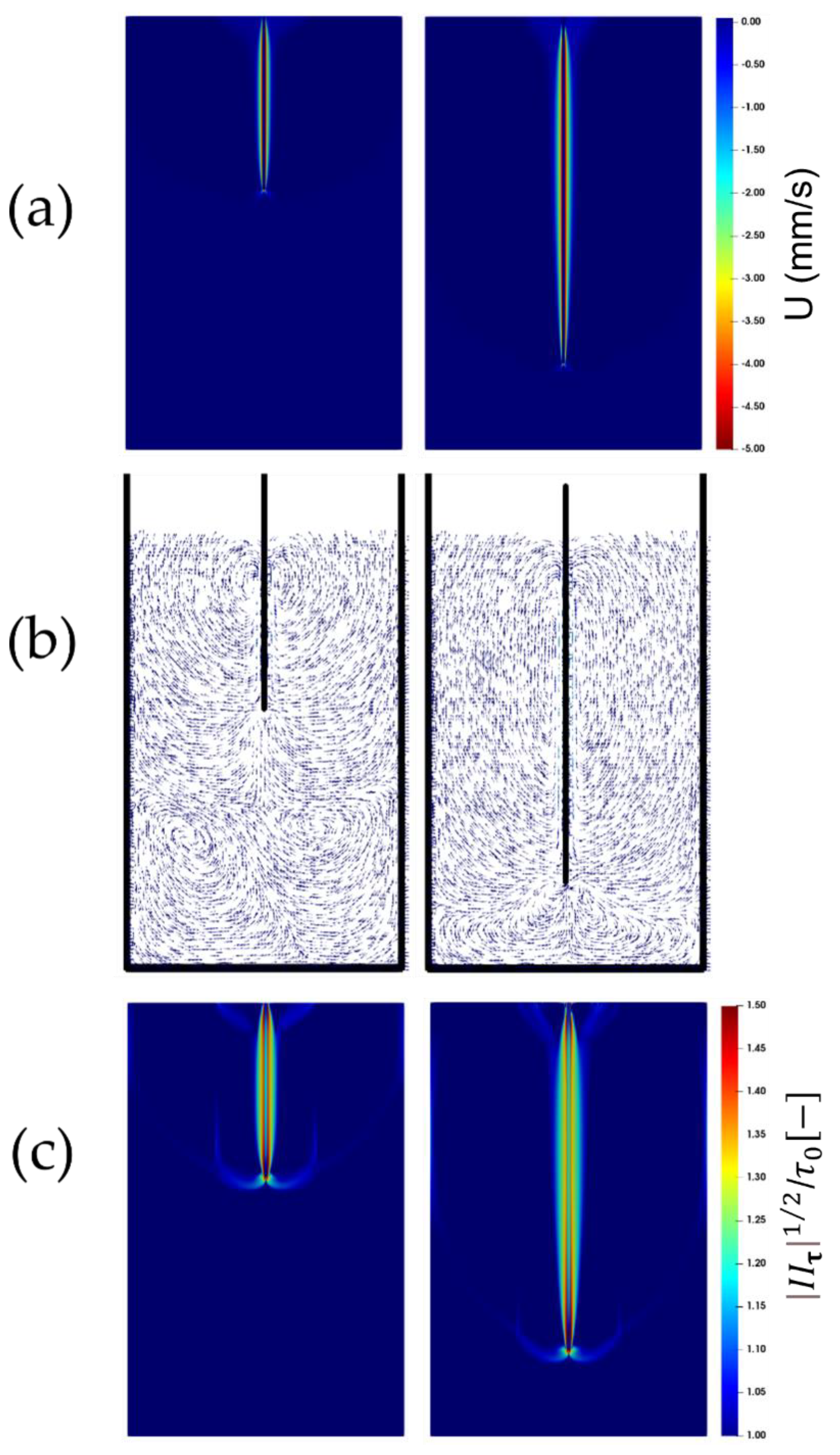
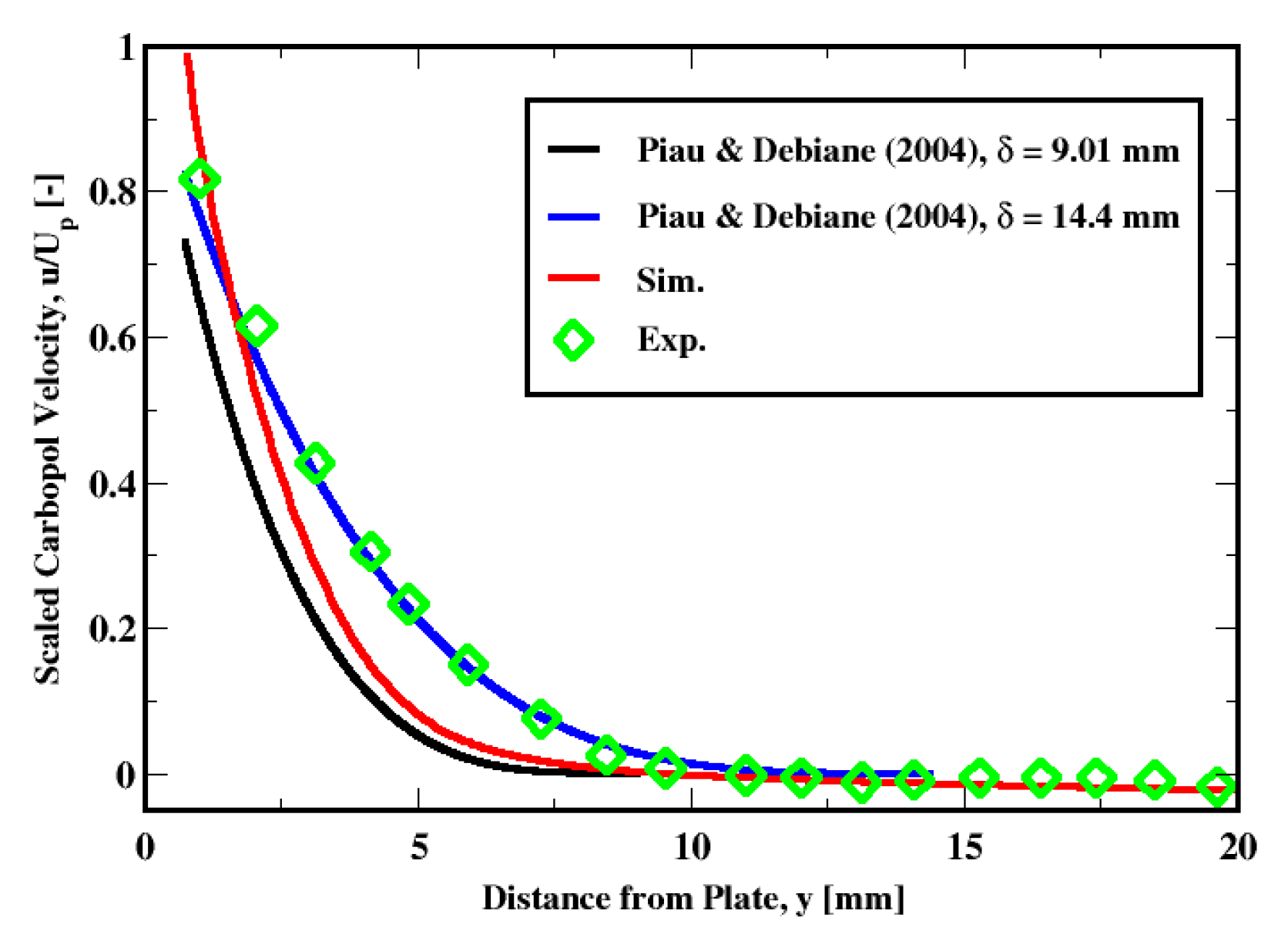
6.1. Flow Visualization
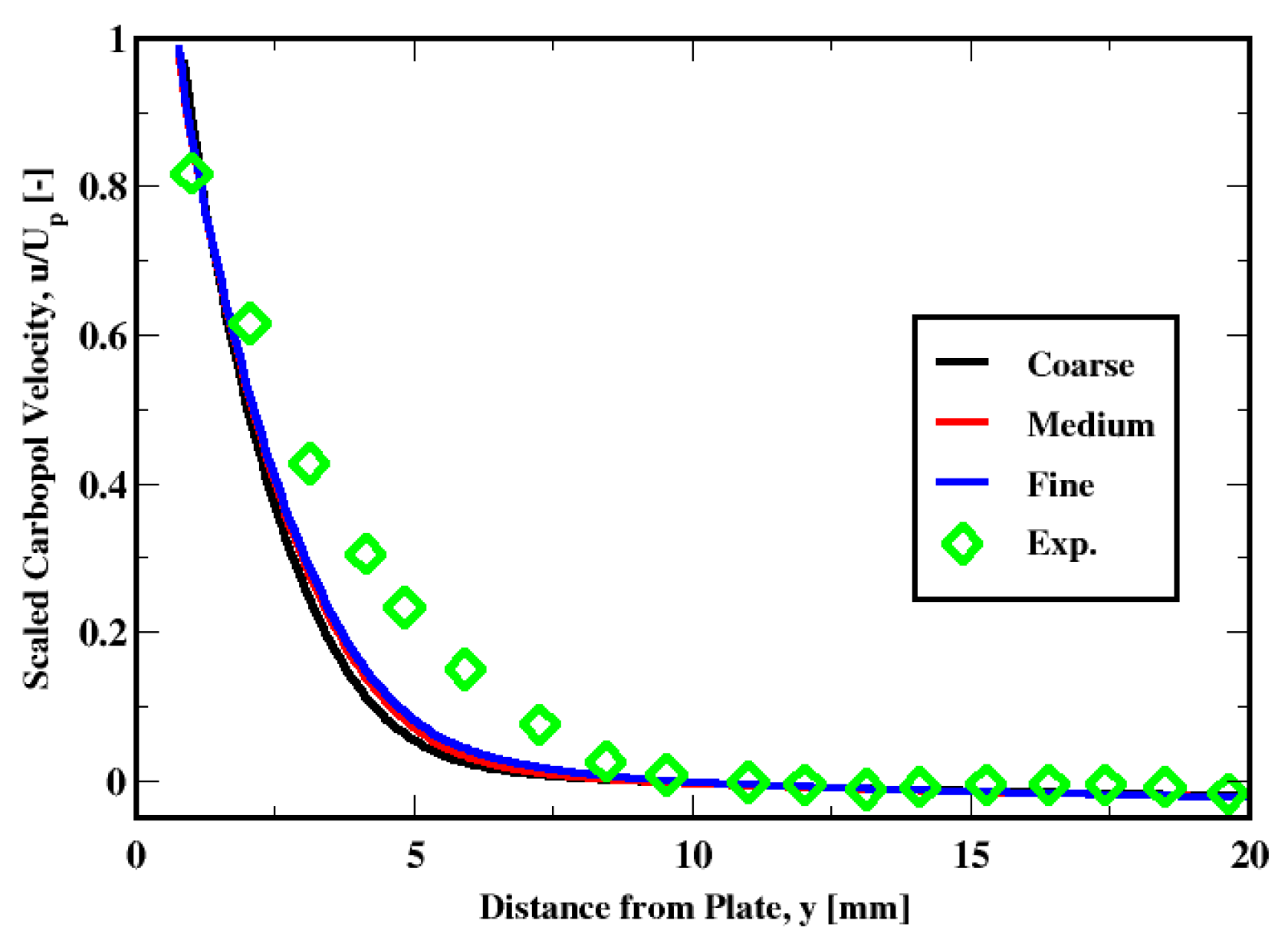
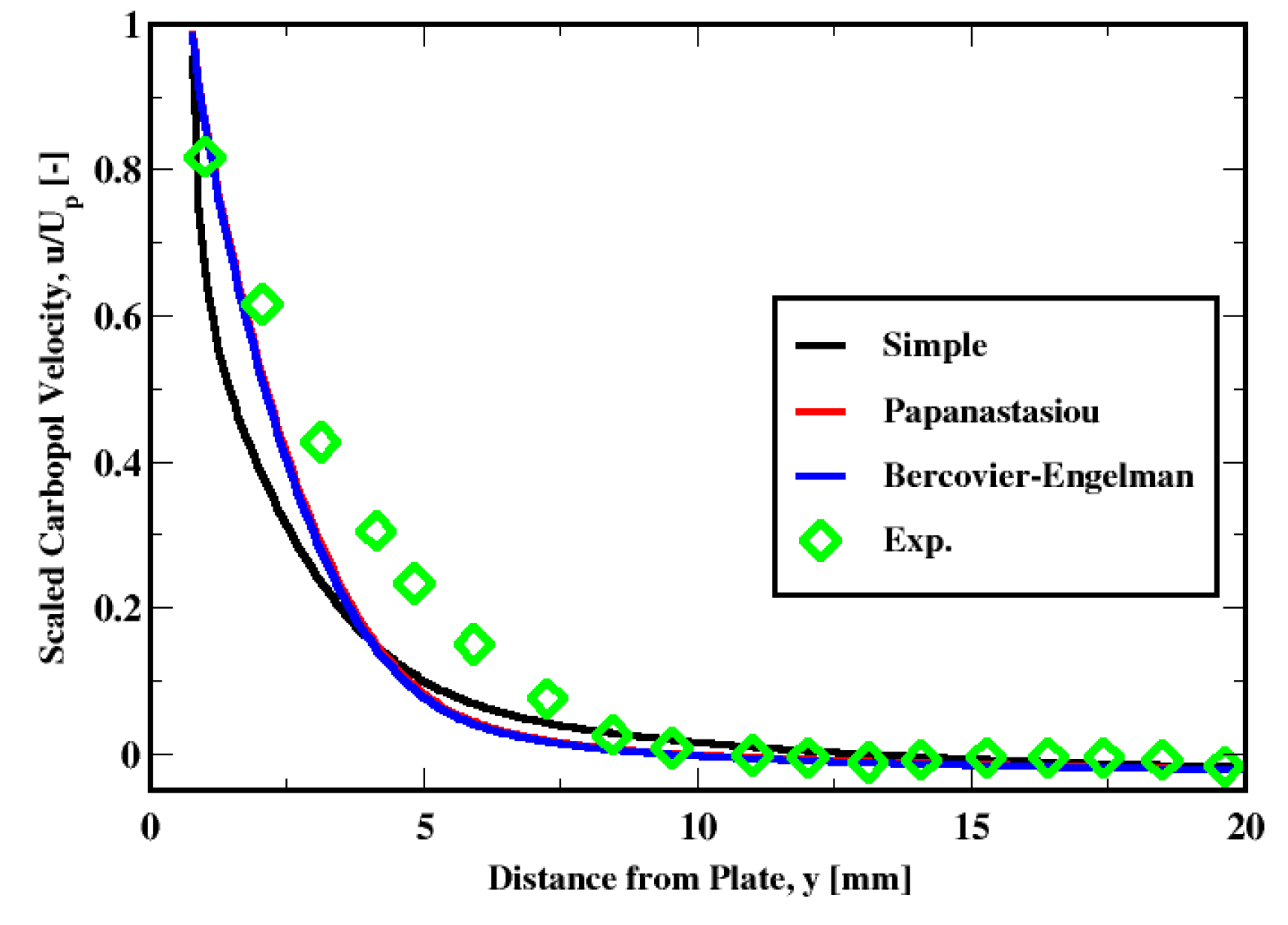
6.2. Mesh and Regularization Sensitivities
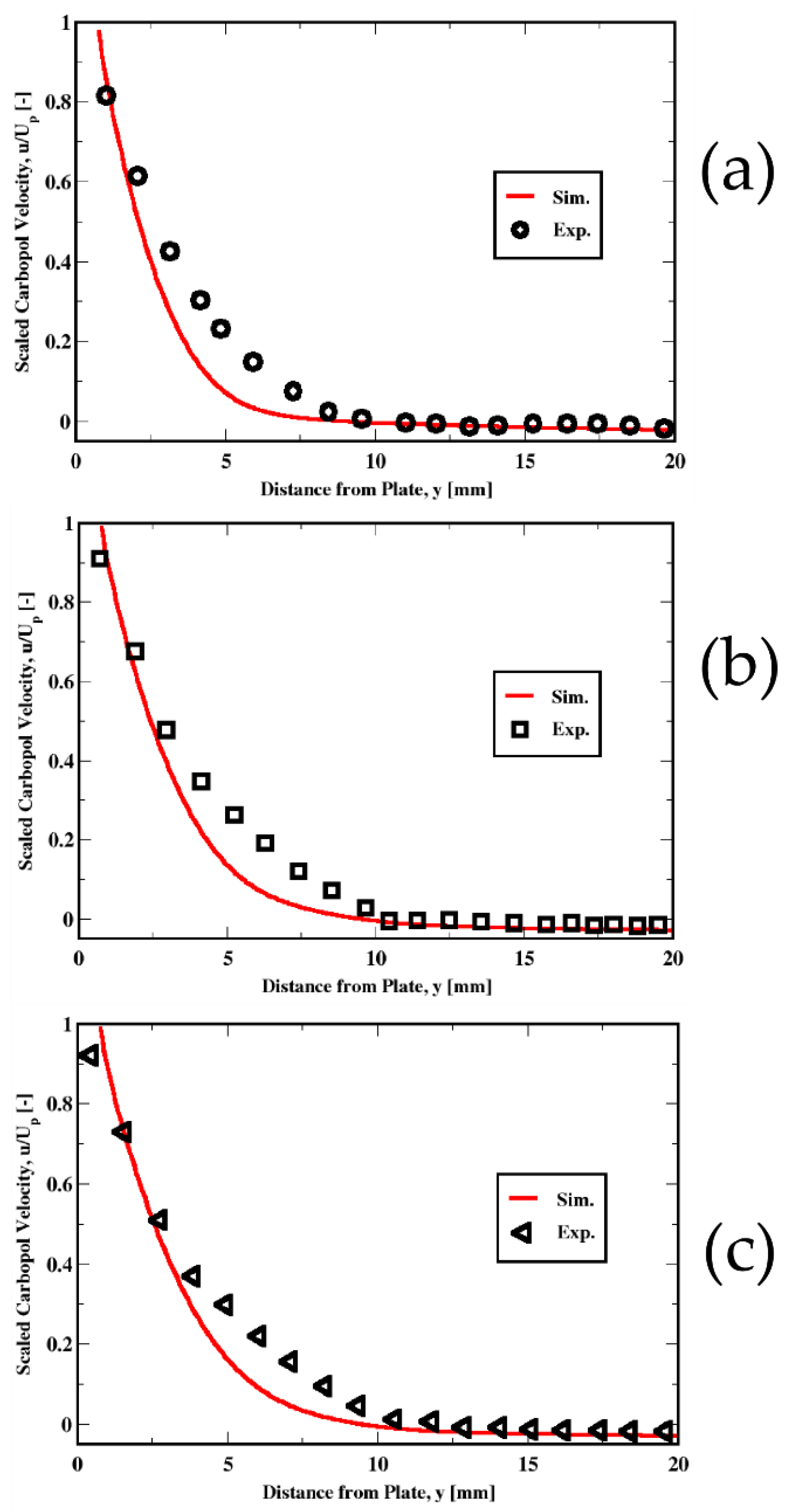
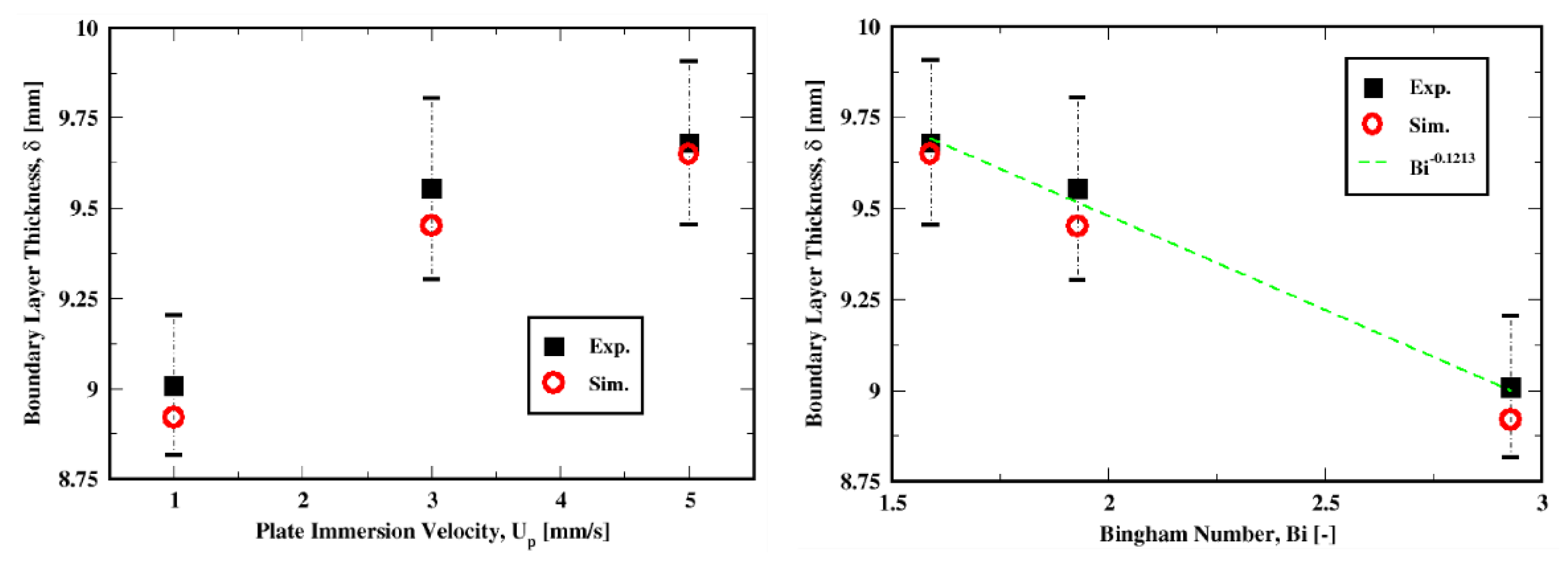
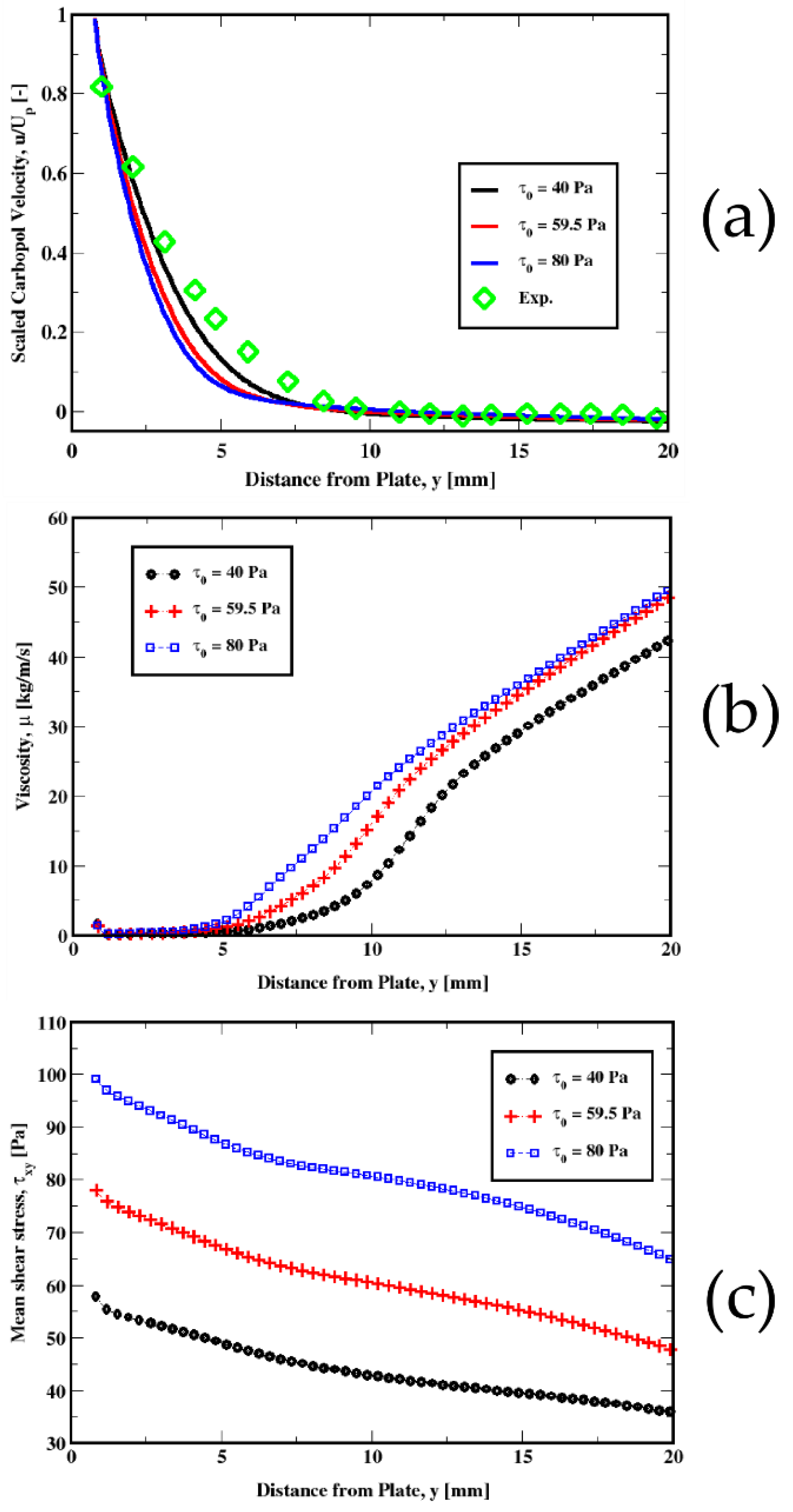
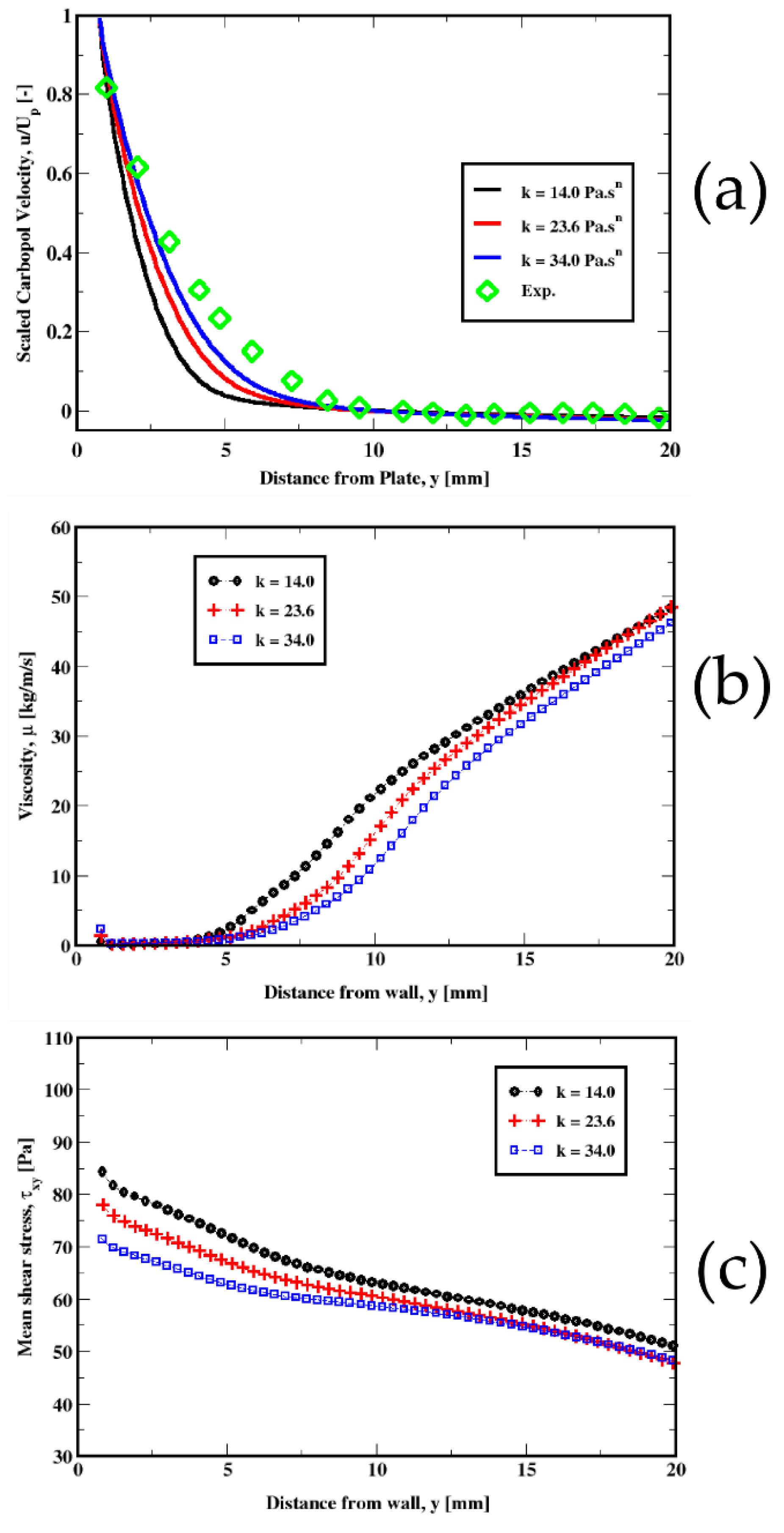
6.3. Results for Different Fluid Properties
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Disclaimer
Appendix A
References
- Boujlel, J.; Maillard, M.; Lindner, A.; Ovarlez, G.; Chateau, X.; Coussot, P. Boundary layer in pastes—Displacement of a long object through a yield stress fluid. J. Rheol. 2012, 56, 1083. [Google Scholar] [CrossRef]
- Schowalter, E.R. Mechanics of Non-Newtonian Fluids; Pergamon Press: New York, NY, USA, 1978. [Google Scholar]
- Oldroyd, J.G. An approach to non-Newtonian fluid mechanics. J. Non-Newton. Fluid Mech. 1984, 14, 9–46. [Google Scholar] [CrossRef]
- Larson, R.G. The Structure and Rheology of Complex Fluids; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Li, M.-G.; Feng, F.; Wu, W.-T.; Massoudi, M. Numerical Simulations of the Flow of a Dense Suspension Exhibiting Yield-Stress and Shear-Thinning Effects. Energies 2020, 13, 6635. [Google Scholar] [CrossRef]
- Fernandes, C.; Fakhari, A.; Tukovic, Ž. Non-Isothermal Free-Surface Viscous Flow of Polymer Melts in Pipe Extrusion Using an Open-Source Interface Tracking Finite Volume Method. Polymers 2021, 13, 4454. [Google Scholar] [CrossRef]
- Wong, L.S. Durability Performance of Geopolymer Concrete: A Review. Polymers 2022, 14, 868. [Google Scholar] [CrossRef] [PubMed]
- Batra, R.C. Elements of Continuum Mechanics; American Institute of Aeronautics and Astronautics (AIAA) Inc.: Reston, VA, USA, 2006. [Google Scholar]
- Haupt, P. Continuum Mechanics and Theory of Materials, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Liu, I.S. Continuum Mechanics; Springer-Verlag: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Massoudi, M.; Vaidya, A. On some generalizations of the second grade fluid model. Nonlinear Anal. Part II Real World Appl. 2008, 9, 1169–1183. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Ericksen, J.L. Stress deformation relations for isotropic materials. J. Rat. Mech. Anal. 1955, 4, 323–425. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics; Springer: New York, NY, USA, 1992. [Google Scholar]
- Deshpande, A.P.; Krishnan, J.M.; Sunil, P.B. Rheology of Complex Fluids, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-1-4419-6493-9. [Google Scholar]
- Denn, M.M.; Bonn, D. Issues in the flow of yield-stress liquids. Rheol. Acta 2011, 50, 307–315. [Google Scholar] [CrossRef]
- Beris, A.N.; Tsamopoulos, J.A.; Armstrong, R.C.; Brown, R.A. Creeping motion of a sphere through a Bingham plastic. J. Fluid Mech. 1985, 158, 219–244. [Google Scholar] [CrossRef]
- Lootens, D.; Hébraud, P.; Lécolier, E.; Van Damme, H. Gelation, Shear-Thinning and Shear-Thickening in Cement Slurries. Oil Gas Sci. Technol. 2004, 59, 31–40. [Google Scholar] [CrossRef]
- Banfill, P.F. The rheology of fresh cement and concrete-a review. In Proceedings of the 11th International Cement Chemistry Congress, Durban, South Africa, 11–16 May 2003; Volume 1, pp. 50–62. [Google Scholar]
- Tao, C.; Rosenbaum, E.; Kutchko, B.G.; Massoudi, M. A Brief Review of Gas Migration in Oilwell Cement Slurries. Energies 2021, 14, 2369. [Google Scholar] [CrossRef]
- Carreau, P.J.; De Kee, D.; Chhabra, R.J. Rheology of Polymeric System; Hanser/Gardner Publications: Cincinnati, OH, USA, 1997. [Google Scholar]
- Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Wu, W.-T.; Massoudi, M. Steady Flow of a Cement Slurry. Energies 2019, 12, 2604. [Google Scholar] [CrossRef]
- Mewis, J.; Spaull, A.J.B. Rheology of Concentrated Dispersions. Adv. Colloid Interface Sci. 1976, 6, 173–200. [Google Scholar] [CrossRef]
- Mewis, J.; Wagner, N.J. Colloidal Suspension Rheology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Agassant, J.F.; Avenas, P.; Carreau, P.J.; Vergnes, B.; Vincent, M. Polymer Processing: Principles and Modeling; Carl Hanser Verlag GmbH Co KG.: Munich, Germany, 2017. [Google Scholar]
- Denn, M.M. Simulation of polymer melt processing. AIChE J. 2009, 55, 1641–1647. [Google Scholar] [CrossRef]
- Middleman, S. Fundamentals of Polymer Processing; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Ziaee, H.; Arabloo, M.; Ghazanfari, M.H.; Rashtchian, D. Herschel–Bulkley rheological parameters of lightweight colloidal gas aphron (CGA) based fluids. Chem. Eng. Res. Des. 2015, 93, 21–29. [Google Scholar] [CrossRef]
- Wang, S.; Yuan, C.; Zhang, C.; Chen, L.; Liu, J. Rheological properties with temperature response characteristics and a mechanism of solid-free polymer drilling fluid at low temperatures. Appl. Sci. 2016, 7, 18. [Google Scholar] [CrossRef]
- Shafiei, M.; Bryant, S.; Balhoff, M.; Huh, C.; Bonnecaze, R.T. Hydrogel formulation for sealing cracked wellbores for CO2 storage. Appl. Rheol. 2017, 27, 27–34. [Google Scholar]
- Chauhan, G.; Verma, A.; Das, A.; Ojha, K. Rheological studies and optimization of Herschel-Bulkley flow parameters of viscous karaya polymer suspensions using GA and PSO algorithms. Rheol. Acta 2018, 57, 267–285. [Google Scholar] [CrossRef]
- Zheng, W.; Wu, X.; Huang, Y. Impact of polymer addition, electrolyte, clay and antioxidant on rheological properties of polymer fluid at high temperature and high pressure. J. Pet. Explor. Prod. Technol. 2020, 10, 663–671. [Google Scholar] [CrossRef]
- Milián, D.; Roux, D.C.; Caton, F.; El Kissi, N. Rheological behavior of gel polymer electrolytes: Yield stress and viscoelasticity. Rheol. Acta 2022, 61, 401–413. [Google Scholar] [CrossRef]
- Oldroyd, J.G. Two-dimensional plastic flow of a Bingham solid. A plastic boundary-layer theory for slow motion. Proc. Camb. Philos. Society. Math. Phys. Sci. 1947, 43, 383–395. [Google Scholar] [CrossRef]
- Piau, J.-M. Viscoplastic boundary layer. J. Non-Newton. Fluid Mech. 2002, 102, 193–218. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Craster, R.V.; Hewitt, D.R. Building on Oldroyd’s viscoplastic legacy: Perspectives and new developments. J. Non-Newton. Fluid Mech. 2021, 294, 104580. [Google Scholar] [CrossRef]
- Piau, J.-M.; Debiane, K. The adhesive or slippery flat plate viscoplastic boundary layer for a shear-thinning power-law viscosity. J. Non-Newton. Fluid Mech. 2004, 117, 97–107. [Google Scholar] [CrossRef]
- Ahonguio, F.; Jossic, L.; Magnin, A. Influence of slip on the flow of a yield stress fluid around a flat plate. AIChE J. 2016, 62, 1356–1363. [Google Scholar] [CrossRef]
- Ahonguio, F.; Jossic, L.; Magnin, A.; Dufour, F. Flow of an elasto-viscoplastic fluid around a flate plate: Experimental and numerical data. J. Non-Newton. Fluid Mech. 2016, 238, 131–139. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Craster, R.V.; Hewitt, D.R.; Hormozi, S.; Maleki, A. Viscoplastic boundary layers. J. Fluid Mech. 2017, 813, 929–954. [Google Scholar] [CrossRef]
- Chevalier, T.; Rodts, S.; Chateau, X.; Boujlel, J.; Maillard, M.; Coussot, P. Boundary layer (shear-band) in frustrated viscoplastic flows. EPL 2013, 102, 48002. [Google Scholar] [CrossRef][Green Version]
- Herschel, W.H.; Bulkley, R. Measurement of Consistency as Applied to Rubber-Benzene Solutions. Am. Soc. Test Proc. 1926, 26, 621–633. [Google Scholar]
- Headrick, E.D.; Spaulding, R.; Rosenbaum, E.; Kutchko, B.; Massoudi, M. The Effects of Conditioning and Additives on the Viscosity Measurement of Cement Slurries; NETL Technical Report Series; U.S. Department of Energy: Washington, DC, USA, 2022; submitted.
- Slattery, J.C. Advanced Transport Phenomena; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Barnes, H.A. The yield stress—A review or ‘παντα ρει’—Everything flows? J. Non-Newton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Barnes, H.A. The ‘yield stress myth?’ paper–21 years on. Appl. Rheol. 2007, 17, 43110-1–43110-5. [Google Scholar] [CrossRef]
- Barnes, H.A.; Walters, K. The yield stress myth? Rheol. Acta 1985, 24, 323–326. [Google Scholar] [CrossRef]
- Assaad, J.J.; Harb, J.; Maalouf, Y. Measurement of Yield Stress of Cement Pastes Using the Direct Shear Test. J. Non-Newton. Fluid Mech. 2014, 214, 18–27. [Google Scholar] [CrossRef]
- Assaad, J.J.; Harb, J.; Maalouf, Y. Effect of Vane Configuration on Yield Stress Measurements of Cement Pastes. J. Non-Newton. Fluid Mech. 2016, 230, 31–42. [Google Scholar] [CrossRef]
- Watts, B.; Tao, C.; Ferraro, C.; Masters, F. Proficiency analysis of VCCTL results for heat of hydration and mortar cube strength. Constr. Build. Mater. 2018, 161, 606–617. [Google Scholar] [CrossRef]
- Moller, P.; Fall, A.; Chikkadi, V.; Derks, D.; Bonn, D. An Attempt to Categorize Yield Stress Fluid Behaviour. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 5139–5155. [Google Scholar] [CrossRef] [PubMed]
- Dinkgreve, M.; Paredes, J.; Denn, M.M.; Bonn, D. On Different Ways of Measuring ‘the’ Yield Stress. J. Non-Newton. Fluid Mech. 2016, 238, 233–241. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Boger, D.V. Measuring the Flow Properties of Yield Stress Fluids. Annu. Rev. Fluid Mech. 1992, 24, 47–88. [Google Scholar] [CrossRef]
- Coussot, P. Yield Stress Fluid Flows: A Review of Experimental Data. J. Non-Newton. Fluid Mech. 2014, 211, 31–49. [Google Scholar] [CrossRef]
- Coussot, P.; Nguyen, Q.D.; Huynh, H.T.; Bonn, D. Viscosity Bifurcation in Thixotropic, Yielding Fluids. J. Rheol. 2002, 46, 573–589. [Google Scholar] [CrossRef]
- Tao, C.; Rosenbaum, E.; Kutchko, B.; Massoudi, M. The Importance of Vane Configuration on Yield Stress Measurements of Cement Slurry; DOE/NETL-2020/2116; NETL Technical Report Series; U.S. Department of Energy, National Energy Technology Laboratory: Morgantown, WV, USA, 2020; p. 24. [CrossRef]
- Saak, A.W.; Jennings, H.M.; Shah, S.P. The Influence of Wall Slip on Yield Stress and Viscoelastic Measurements of Cement Paste. Cem. Concr. Res. 2001, 31, 205–212. [Google Scholar] [CrossRef]
- Barnes, H.A. A Review of the Slip (Wall Depletion) of Polymer Solutions, Emulsions and Particle Suspensions in Viscometers: Its Cause, Character, and Cure. J. Non-Newton. Fluid Mech. 1995, 56, 221–251. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Boger, D.V. Direct Yield Stress Measurement with the Vane Method. J. Rheol. 1985, 29, 335–347. [Google Scholar]
- Liddel, P.V.; Boger, D.V. Yield Stress Measurements with the Vane. J. Non-Newton. Fluid Mech. 1996, 63, 235–261. [Google Scholar] [CrossRef]
- Banfill, P.F.G.; Saunders, D.C. On the Viscometric Examination of Cement Pastes. Cem. Concr. Res. 1981, 11, 363–370. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Boger, D.V. Yield Stress Measurement for Concentrated Suspensions. J. Rheol. 1983, 27, 321–349. [Google Scholar] [CrossRef]
- Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Massoudi, M. A Review of Rheological Modeling of Cement Slurry in Oil Well Applications. Energies 2020, 13, 570. [Google Scholar] [CrossRef]
- Krieger, I.M.; Dougherty, T.J. A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Bingham, E.C. Fluidity and Plasticity; McGraw Hill: New York, NY, USA, 1922. [Google Scholar]
- Denn, M.M. Polymer Melt Processing: Foundations in Fluid Mechanics and Heat Transfer; Cambridge University Press: Cambridge, UK, 2008; ISBN 1-316-58314-7. [Google Scholar]
- Macosko, C.W. Rheology: Principles, Measurements, and Applications; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- OpenFOAM v2012. Available online: http://www.openfoam.org (accessed on 3 August 2022).
- Papanastasiou, T.C. Flows of materials with yield. J. Rheol. 1987, 31, 385–404. [Google Scholar] [CrossRef]
- Allouche, M.; Frigaard, I.A.; Sona, G. Static wall layers in the displacement of two viscoplastic fluids in a plane channel. J. Fluid Mech. 2000, 424, 243–277. [Google Scholar] [CrossRef]
- Bercovier, M.; Engelman, M. A finite-element method for incompressible non-Newtonian flows. J. Comput. Phys. 1980, 36, 313–326. [Google Scholar] [CrossRef]
- Frigaard, I.A.; Nouar, C. On the usage of viscosity regularisation methods for visco-plastic fluid flow computation. J. Non-Newtonian Fluid Mech. 2005, 127, 1–26. [Google Scholar] [CrossRef]
- Saramito, P.; Wachs, A. Progress in numerical simulation of yield stress fluid flows. Rheol. Acta 2017, 56, 211–230. [Google Scholar] [CrossRef]
- Putz, A.M.V.; Burghelea, T.I. The solid–fluid transition in a yield stress shear thinning physical gel. Rheol. Acta 2009, 48, 673–689. [Google Scholar] [CrossRef]
- Piau, J.-M. Carbopol gels: Elastoviscoplastic and slippery glasses made of individual swollen sponges meso- and macroscopic properties, constitutive equations and scaling laws. J. Non-Newton. Fluid Mech. 2007, 144, 1–29. [Google Scholar] [CrossRef]


| Case | |||
|---|---|---|---|
| 1 | 1 | 5.2 × 10−5 | 2.93 |
| 2 | 3 | 3.1 × 10−4 | 1.93 |
| 3 | 5 | 7.0 × 10−4 | 1.59 |
| Mesh Details | Coarse | Medium | Finer | |
|---|---|---|---|---|
| Wall-normal [mm] | 0.2 | 0.15 | 0.1 | |
| 0.4 | 0.3 | 0.2 | ||
| [mm] | 1.25 | 1 | 0.8 | |
| Mesh size | 60,404 | 89,940 | 138,824 | |
| Experiments [mm] | Simulations | |||||
|---|---|---|---|---|---|---|
| 9.01 ± 0.20 | Mesh Sensitivity [mm] | Regularization Sensitivity [mm] | ||||
| Coarse | Medium | Fine | Simple | Bercovier–Engelman | Papanastasiou | |
| 8.64 | 8.92 | 9.33 | 12.67 | 9.21 | 8.92 | |
| (*) Bi [-] | ||||
|---|---|---|---|---|
| Baseline | 59.5 | 23.6 | 0.38 | 2.94 |
| Yield stress | 40.0 | - | - | 1.98 |
| 80.0 | - | - | 3.95 | |
| Consistency | - | 14.0 | - | 4.96 |
| - | 34.0 | - | 2.04 | |
| Power-law exponent | - | - | 0.25 | 2.79 |
| - | - | 0.50 | 3.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konan, N.A.; Rosenbaum, E.; Massoudi, M. On the Response of a Herschel–Bulkley Fluid Due to a Moving Plate. Polymers 2022, 14, 3890. https://doi.org/10.3390/polym14183890
Konan NA, Rosenbaum E, Massoudi M. On the Response of a Herschel–Bulkley Fluid Due to a Moving Plate. Polymers. 2022; 14(18):3890. https://doi.org/10.3390/polym14183890
Chicago/Turabian StyleKonan, N’dri Arthur, Eilis Rosenbaum, and Mehrdad Massoudi. 2022. "On the Response of a Herschel–Bulkley Fluid Due to a Moving Plate" Polymers 14, no. 18: 3890. https://doi.org/10.3390/polym14183890
APA StyleKonan, N. A., Rosenbaum, E., & Massoudi, M. (2022). On the Response of a Herschel–Bulkley Fluid Due to a Moving Plate. Polymers, 14(18), 3890. https://doi.org/10.3390/polym14183890









