Polyetherimide-Reinforced Smart Inlays for Bondline Surveillance in Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulation
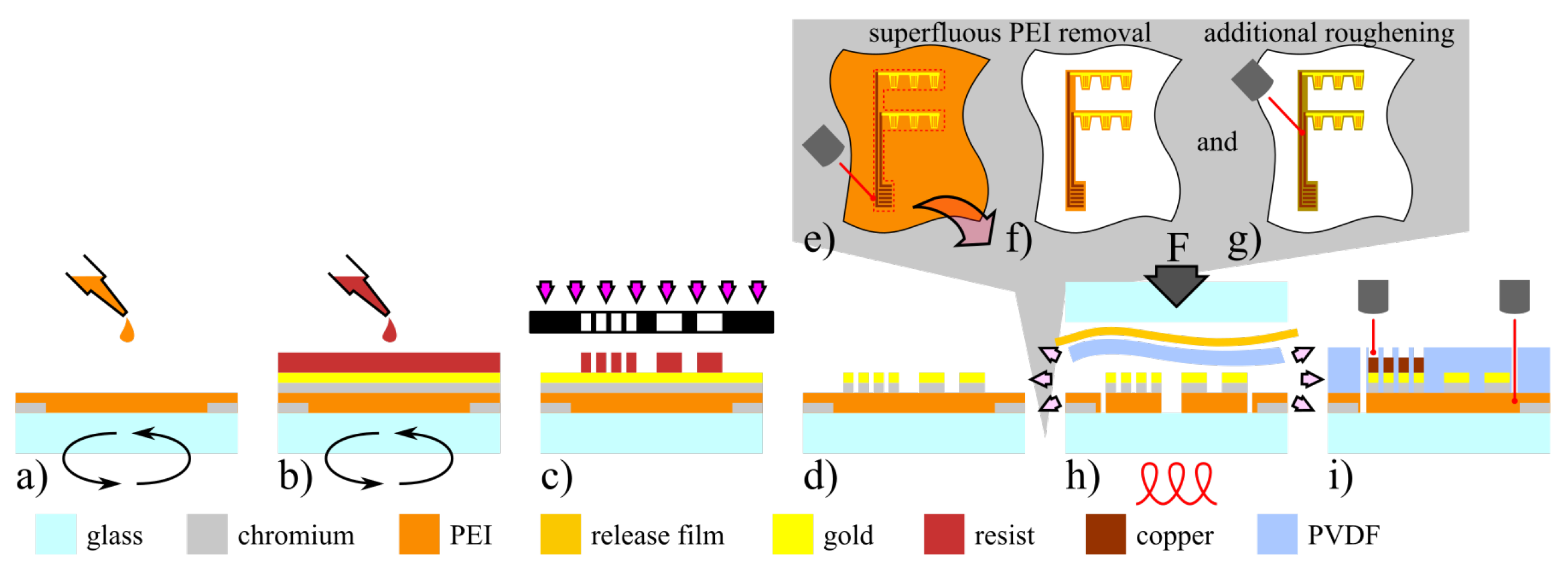
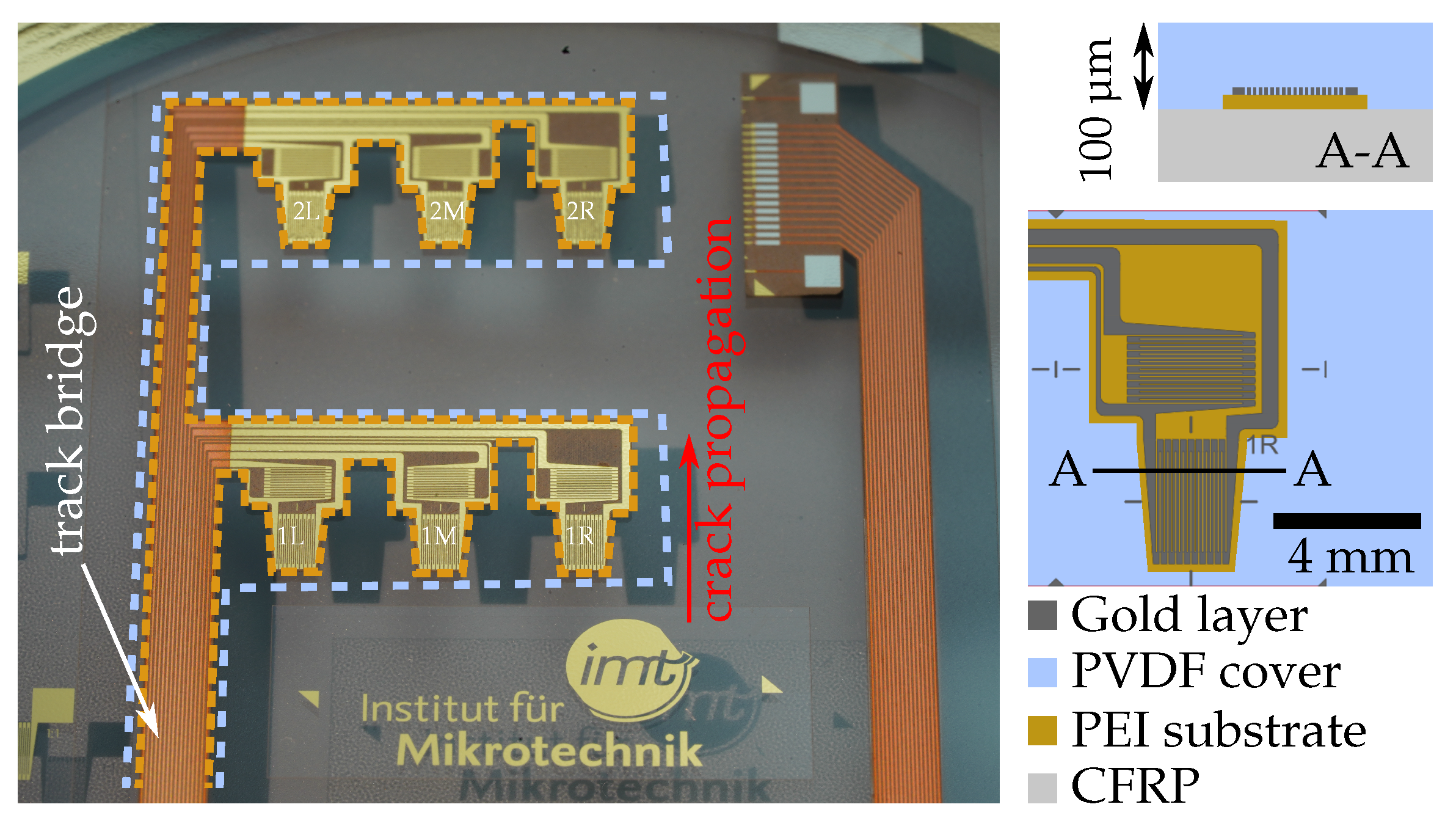
2.2. Smart Inlay Fabrication and Integration
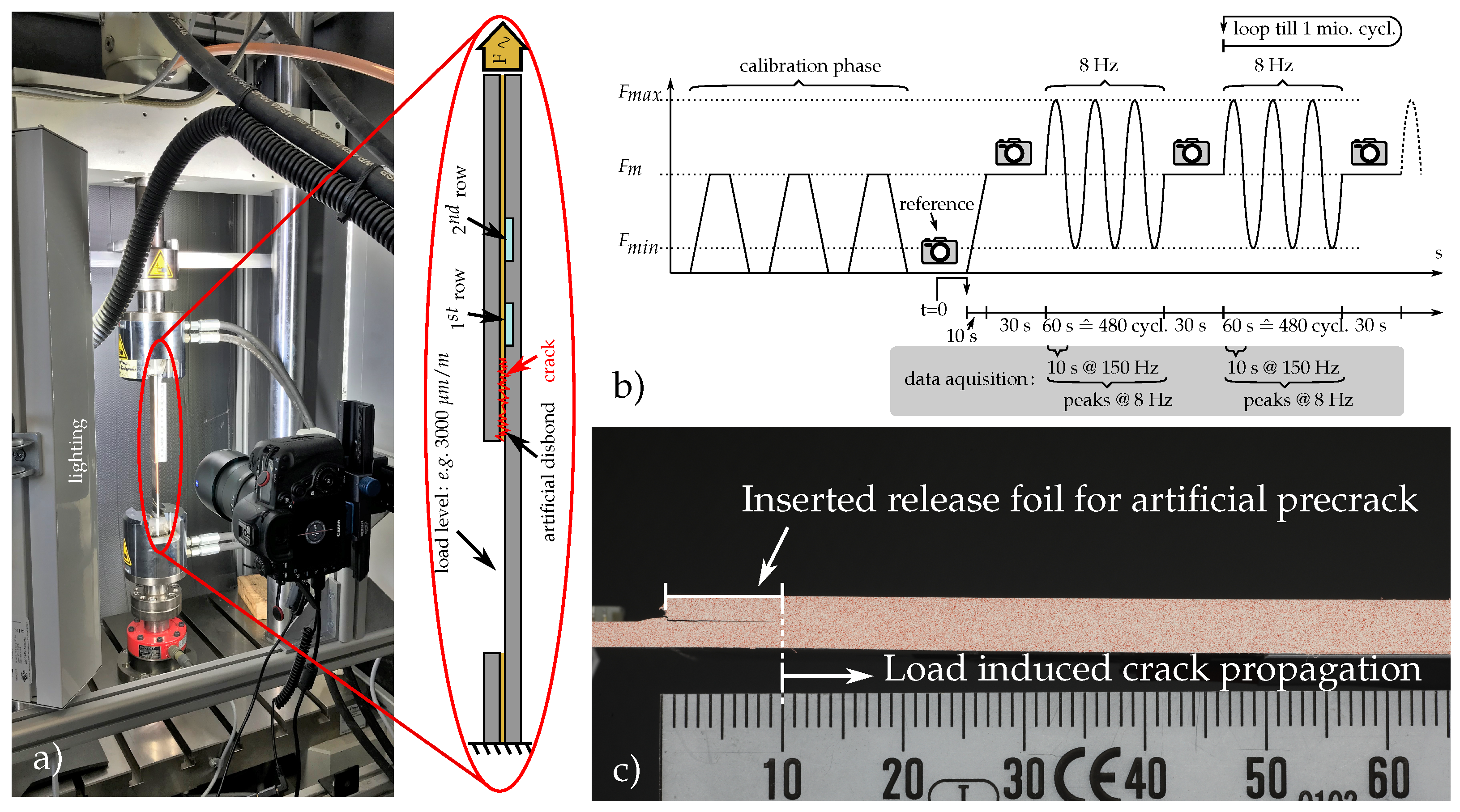
2.3. Mechanical Testing
2.3.1. Inlay Calibration
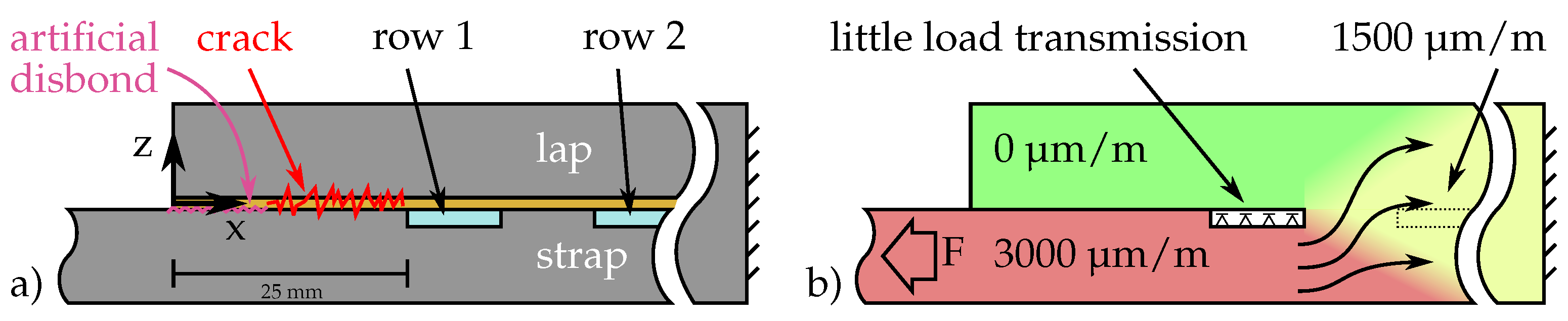
2.3.2. Quasi-Static Testing with Various Crack Lengths
2.3.3. Dynamic Fatigue Testing
3. Smart Inlay Concept and Evaluation of Reinforced Design
3.1. Basic Inlay Functionality
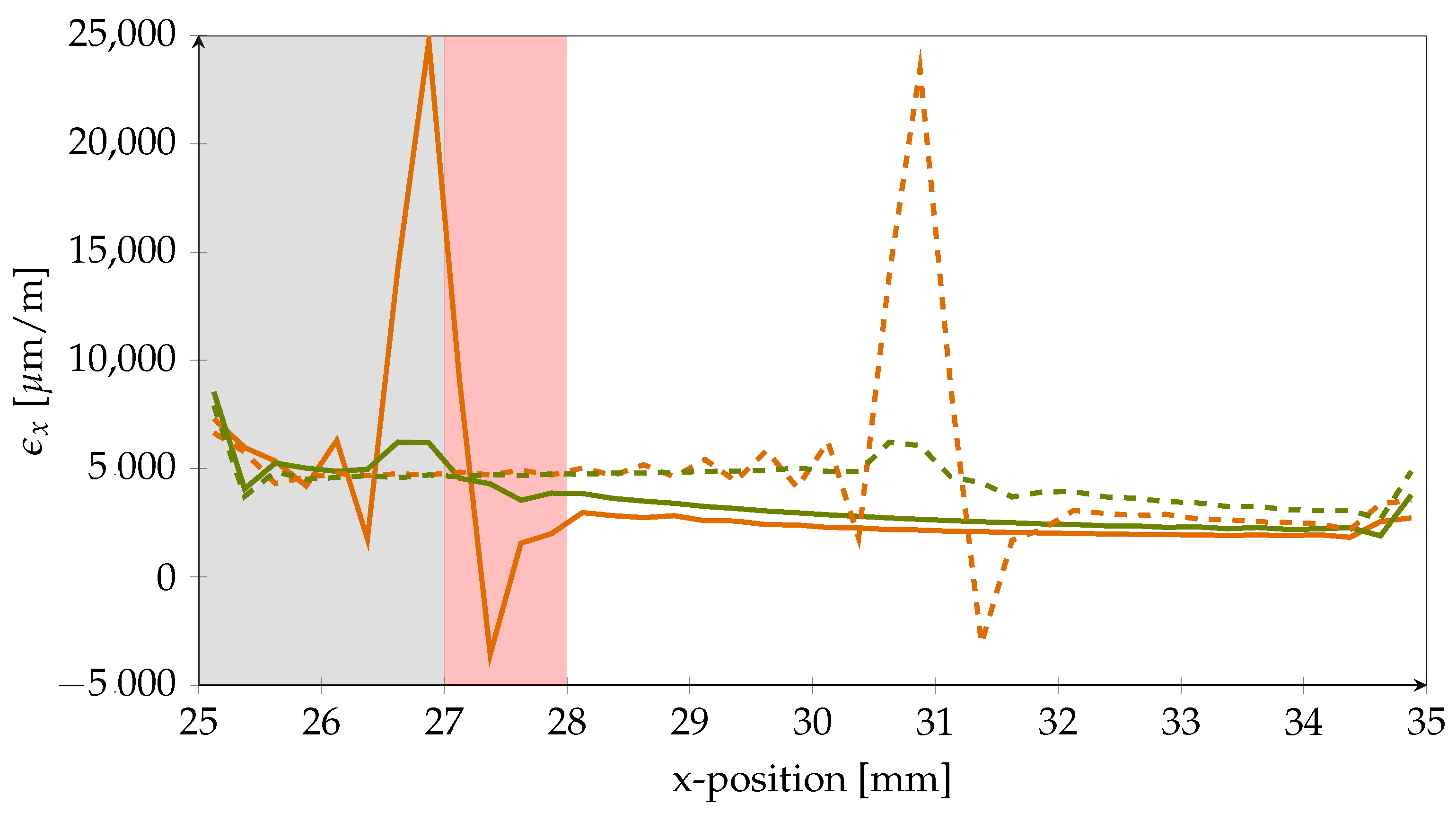
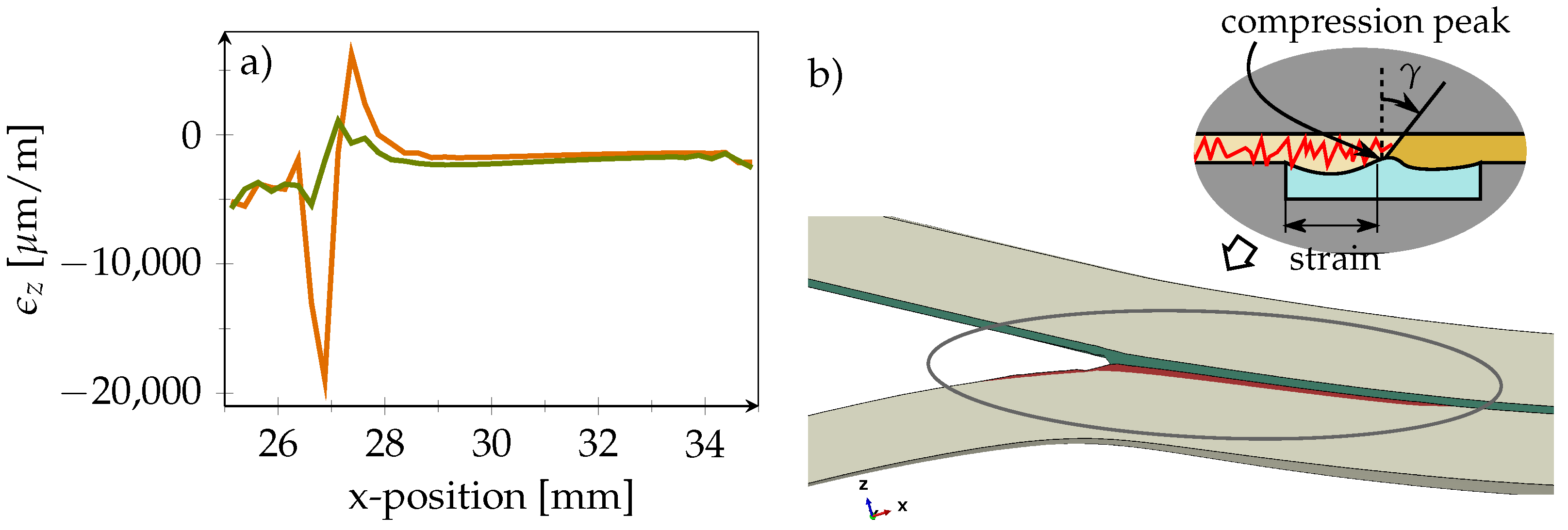
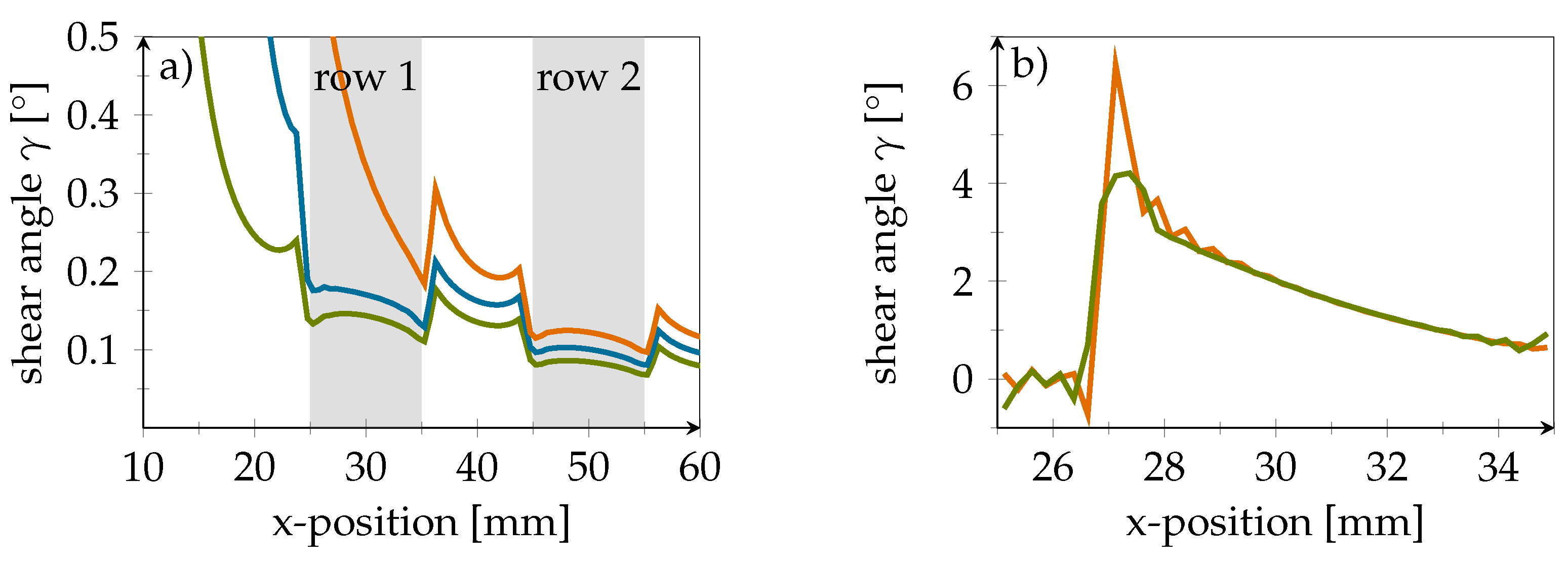
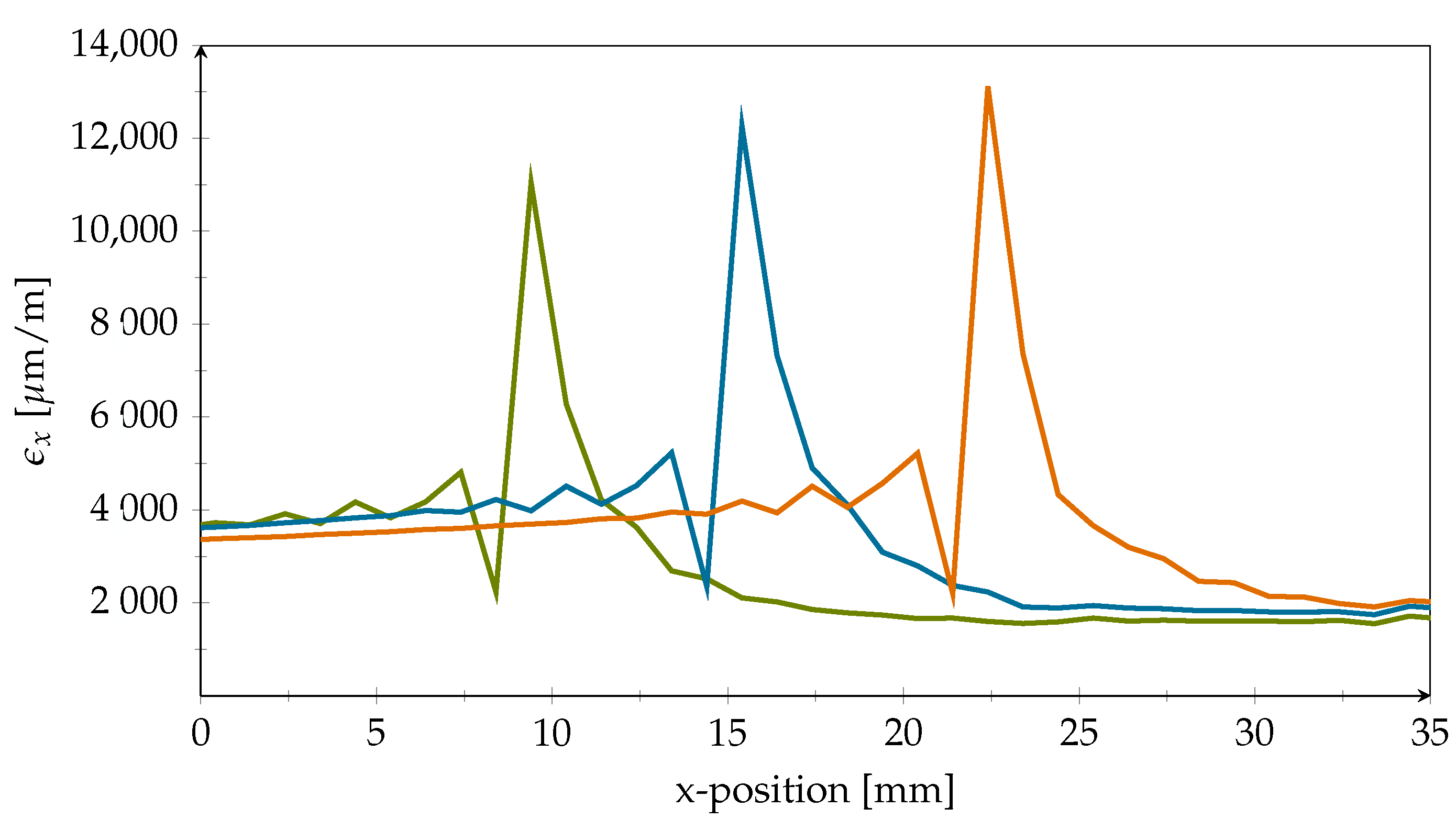
3.2. Strain Field Simulations
4. Results
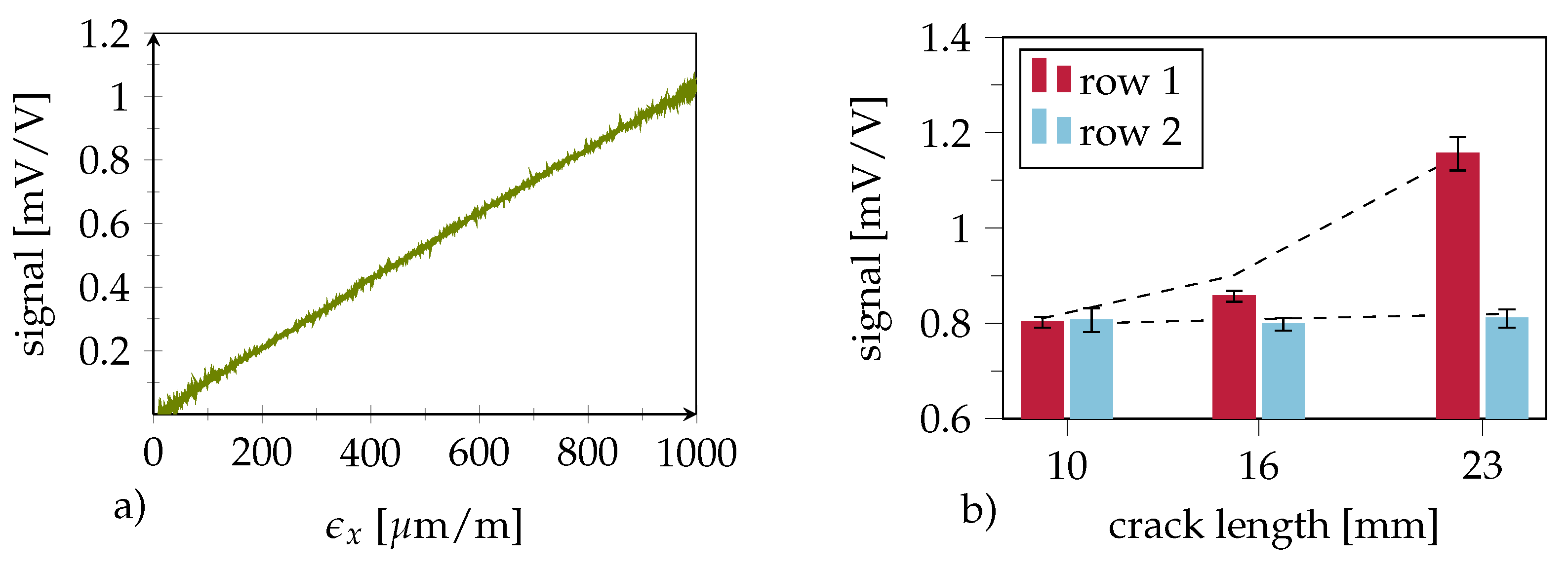
4.1. Smart Inlay Calibration
4.2. Crack Sensing in Quasi-Static Testing
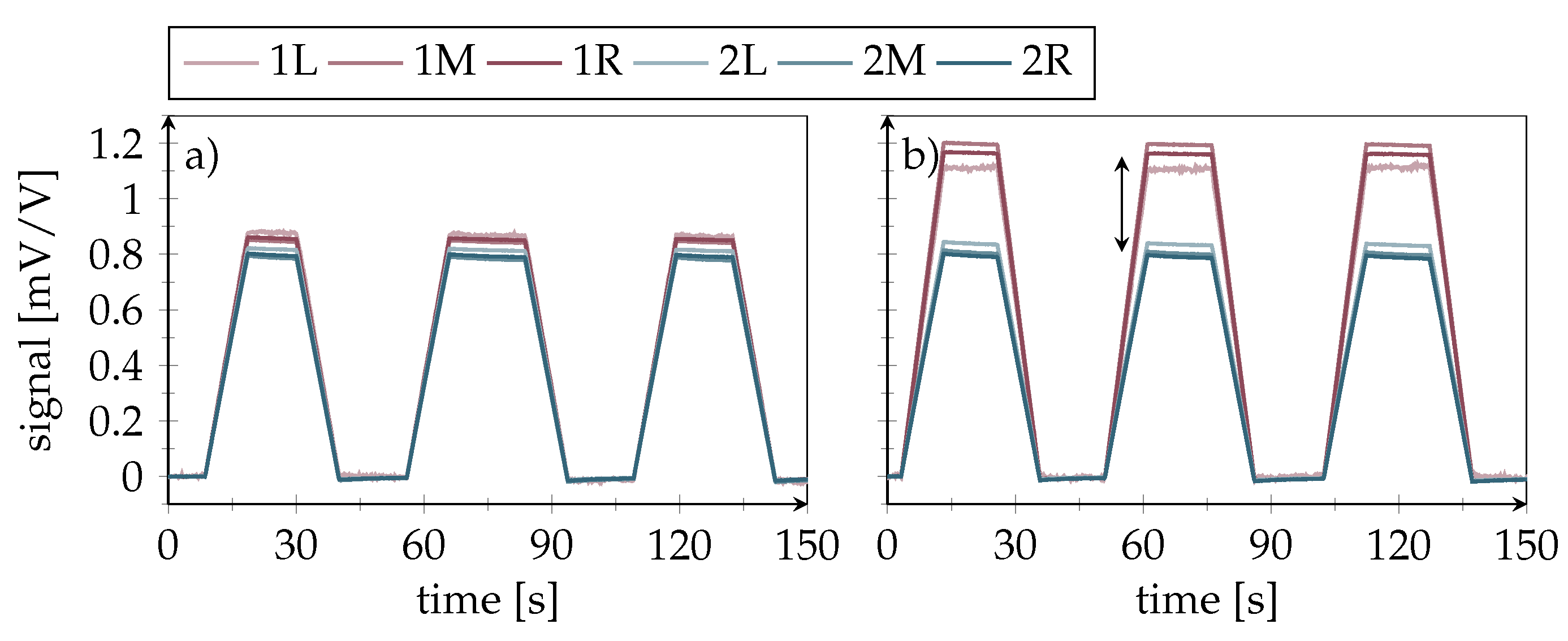
4.3. Fatigue Testing of Passive Bonds
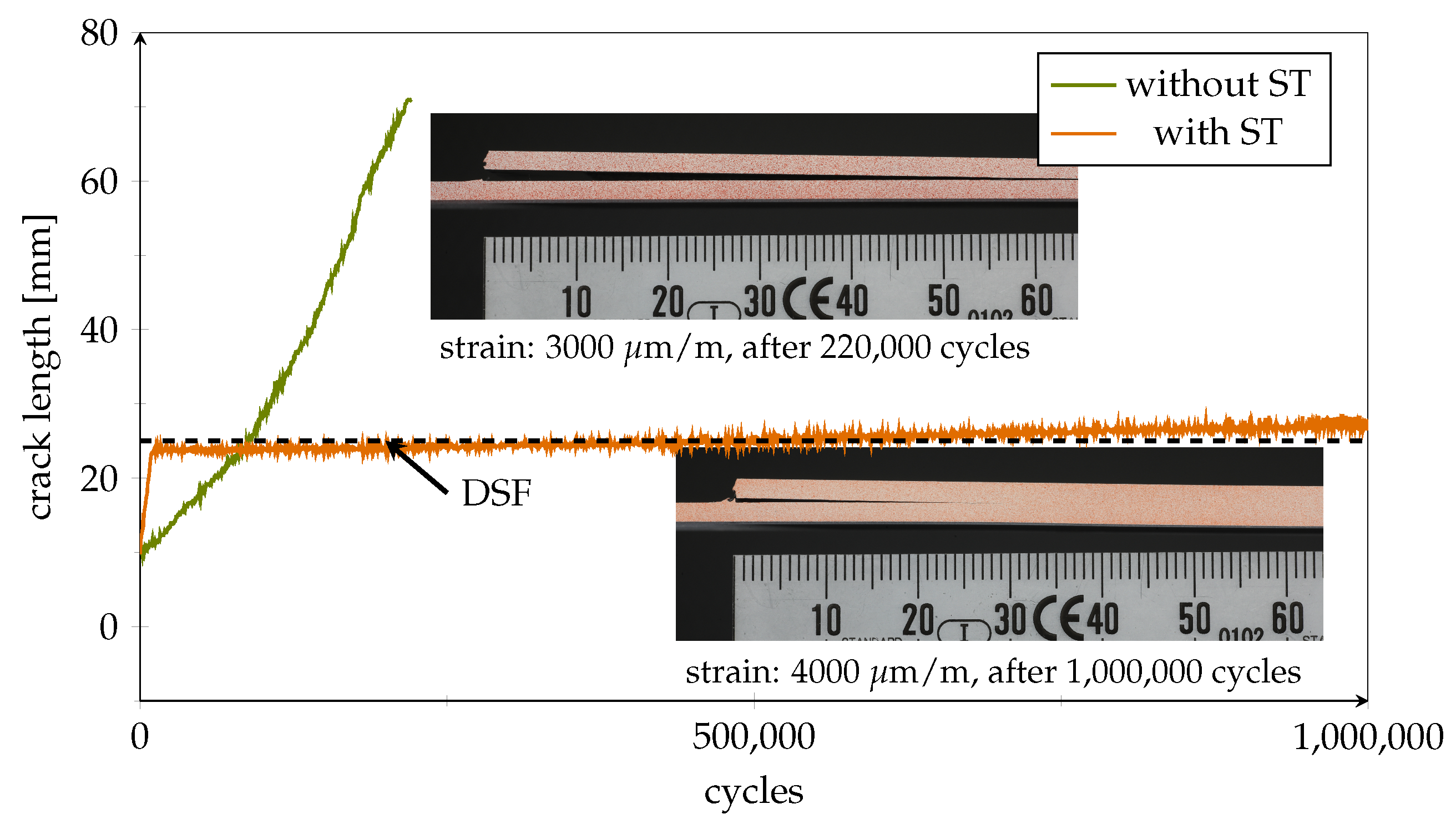
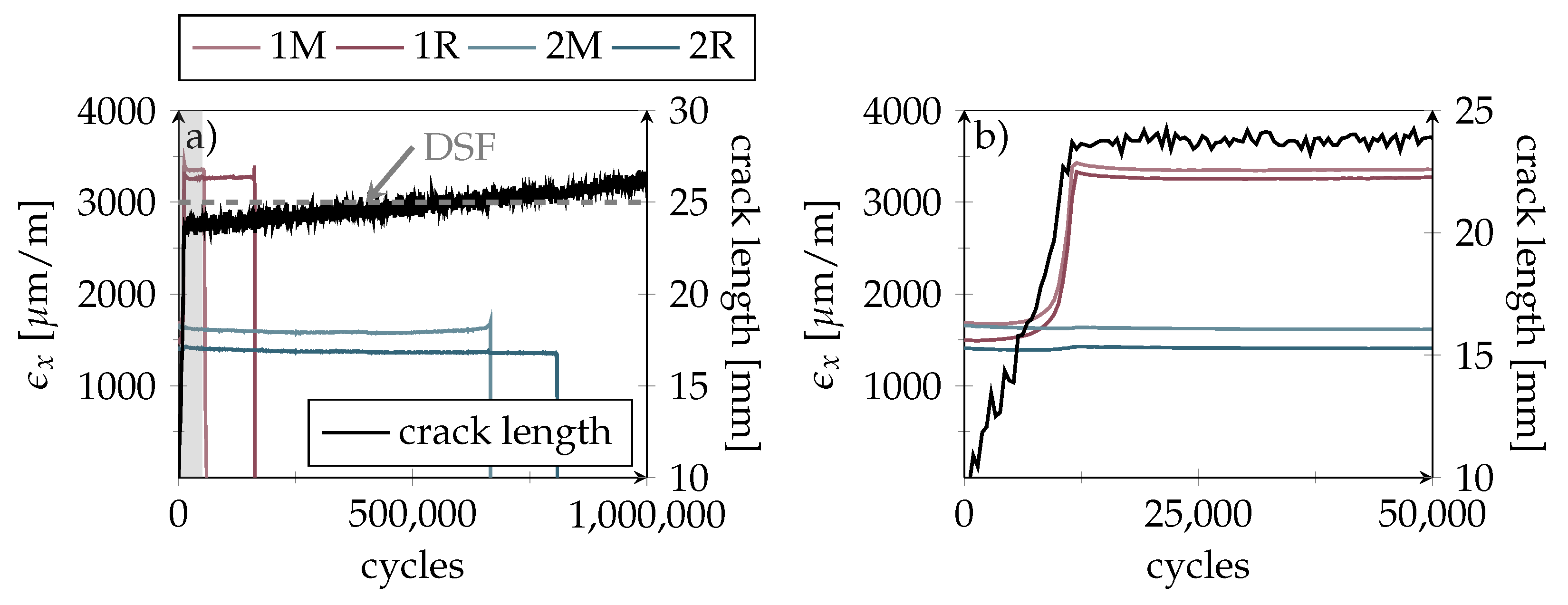
4.4. Detection of Emerging and Progressing Cracks using Smart Inlays
5. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFRP | carbon fiber-reinforced plastic |
| CLS | cracked lap shear |
| DSF | disbond-stopping feature |
| FE | finite element |
| MDAF | multifunctional disbond arrest feature |
| PEI | polyetherimide |
| PVDF | poly(vinyliden fluoride) |
| ST | surface toughening |
References
- Baker, A.A.; Scott, M.L. Composite Materials for Aircraft Structures, 3rd ed.; AIAA Education Series; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2016. [Google Scholar] [CrossRef]
- Markatos, D.N.; Tserpes, K.I.; Rau, E.; Markus, S.; Ehrhart, B.; Pantelakis, S. The effects of manufacturing-induced and in-service related bonding quality reduction on the mode-I fracture toughness of composite bonded joints for aeronautical use. Compos. Part B Eng. 2013, 45, 556–564. [Google Scholar] [CrossRef]
- Thrall, E.W. Primary Adhesively Bonded Structure Technology (PABST). J. Aircr. 1977, 14, 588–594. [Google Scholar] [CrossRef]
- Ashcroft, I.A.; Wahab, M.; Crocombe, A.; Hughes, D.; Shaw, S. The effect of environment on the fatigue of bonded composite joints. Part 1: Testing and fractography. Compos. Part A Appl. Sci. Manuf. 2001, 32, 45–58. [Google Scholar] [CrossRef]
- Bardenstein, D.; Lukatsky, A.; Deutsch, Z.; Kressel, I.; Shemesh, N.; Clay, S.B. Design and Experimental Validation of a bonded structure Fail Safe Damage Arrest Concept. In AIAA SCITECH 2022 Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Bonded Joints and Structures—Technical Issues and Certification Considerations: PS-ACE100-2005-10038; Federal Aviation Administration: Washington, DC, USA, 2005.
- Kelly, G. Load transfer in hybrid (bonded/bolted) composite single-lap joints. Compos. Struct. 2005, 69, 35–43. [Google Scholar] [CrossRef]
- Cheung, C.H.; Gray, P.; Lin, K.Y. Fastener as Fail-Safe Disbond/Delamination Arrest for Laminated Composite Structures. In Proceedings of the 18th Internationel Conference on Composite Materials, Jeju, Korea, 21–26 August 2011. [Google Scholar]
- Kadlec, M.; Růžek, R.; Bělský, P. Concurrent use of Z-pins for crack arrest and structural health monitoring in adhesive-bonded composite lap joints. Compos. Sci. Technol. 2020, 188, 107967. [Google Scholar] [CrossRef]
- European Aviation Safety Agency. Annex II to ED Decision 2010/003/R of 19/07/2010; EASA: Cologne, Germany, 2010.
- Murayama, H.; Kageyama, K.; Uzawa, K.; Ohara, K.; Igawa, H. Strain monitoring of a single-lap joint with embedded fiber-optic distributed sensors. Struct. Health Monit. 2012, 11, 325–344. [Google Scholar] [CrossRef]
- Webb, S.; Shin, P.; Peters, K.; Zikry, M.A.; Stan, N.; Chadderdon, S.; Selfridge, R.; Schultz, S. Characterization of fatigue damage in adhesively bonded lap joints through dynamic, full-spectral interrogation of fiber Bragg grating sensors: 1. Experiments. Smart Mater. Struct. 2014, 23, 025016. [Google Scholar] [CrossRef]
- Preisler, A.; Sadeghi, Z.; Adomeit, A.; Schröder, K.U. Damage Assessment in Adhesively Bonded Structures by Using SmartSHM. In Structural Health Monitoring 2015; Chang, F.K., Kopsaftopoulos, F., Eds.; Destech Publications: Lancaster, PA, USA, 2015. [Google Scholar] [CrossRef]
- Weiland, J.; Luber, M.; Rostan, K.; Schiebahn, A.; Engelbrecht, R.; Reisgen, U. Strain Monitoring of a Structural Adhesive Bond by Embedding a Polymer Optical Fiber. In European Workshop on Structural Health Monitoring; Springer eBook Collection; Rizzo, P., Milazzo, A., Eds.; Springer International Publishing: Cham, Switzerland; Imprint Springer: Cham, Switzerland, 2022; Volume 253, pp. 745–754. [Google Scholar] [CrossRef]
- Department of Defense. Joint Service Specification Guide JSSG-2006; Department of Defense: Arlington, VA, USA, 1998.
- Holzhüter, D.; Löbel, T.; Hühne, C.; Kühn, M. Faserverbundstruktur und Verfahren zur Herstellung. DE 10 2013 107 849 B4, 7 April 2016. [Google Scholar]
- Tao, R.; Li, X.; Yudhanto, A.; Alfano, M.; Lubineau, G. Toughening adhesive joints through crack path engineering using integrated polyamide wires. Compos. Part A Appl. Sci. Manuf. 2022, 158, 106954. [Google Scholar] [CrossRef]
- Schollerer, M.J.; Kosmann, J.; Völkerink, O.; Holzhüter, D.; Hühne, C. Surface toughening—A concept to decrease stress peaks in bonded joints. J. Adhes. 2018, 95, 495–514. [Google Scholar] [CrossRef]
- Schollerer, M.J.; Kosmann, J.; Holzhüter, D.; Bello-Larroche, C.; Hühne, C. Surface toughening—An industrial approach to increase the robustness of pure adhesive joints with film adhesives. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 1980–1987. [Google Scholar] [CrossRef]
- von der Heide, C.; Steinmetz, J.; Schollerer, M.J.; Hühne, C.; Sinapius, M.; Dietzel, A. Smart Inlays for Simultaneous Crack Sensing and Arrest in Multifunctional Bondlines of Composites. Sensors 2021, 21, 3852. [Google Scholar] [CrossRef] [PubMed]
- Kyriazis, A.; Asali, K.; Sinapius, M.; Rager, K.; Dietzel, A. Adhesion of Multifunctional Substrates for Integrated Cure Monitoring Film Sensors to Carbon Fiber Reinforced Polymers. J. Compos. Sci. 2020, 4, 138. [Google Scholar] [CrossRef]
- Marlett, K.; Ng, Y.; Tomblin, J. Hexcel 8552 IM7 Unidirectional Prepreg 190 Gsm & 35% RC Qualification Material Property Data Report; Test Report CAM-RP-2009-015; Rev. A’ National Center for Advanced Materials Performance: Wichita, KS, USA, 2011; pp. 1–238. [Google Scholar]
- Völkerink, O.; Kosmann, J.; Schollerer, M.; Holzhüter, D.; Hühne, C. Strength prediction of adhesively bonded single lap joints with the eXtended Finite Element Method. J. Adhes. 2019, 95, 474–494. [Google Scholar] [CrossRef]
- Tomblin, J.; Seneviratne, W.; Escobar, P.; Yoon-Khian, Y. Shear Stress-Strain Data for Structural Adhesives; Technical Report; Wichita State University Department of Aeronautical Engineering: Wichita, KS, USA, 2002. [Google Scholar]
- ARKEMA. Datenblatt Kynar 740-PVDF. 2021. Available online: https://www.campusplastics.com/material/pdf/138634/Kynar740?sLg=de (accessed on 30 June 2022).
- Rager, K.; Jaworski, D.; von der Heide, C.; Kyriazis, A.; Sinapius, M.; Constantinou, I.; Dietzel, A. Space-Filling Curve Resistor on Ultra-Thin Polyetherimide Foil for Strain Impervious Temperature Sensing. Sensors 2021, 21, 6479. [Google Scholar] [CrossRef] [PubMed]
- Löbel, T. The Hybrid Bondline: A Novel Disbond-Stopping Design for Adhesively Bonded Composite Joints. Ph.D. Thesis, Technische Universität Carolo-Wilhelmina zu Braunschweig, Braunschweig, Germany, 2016. [Google Scholar]
- Steinmetz, J.; Löbel, T.; Völkerink, O.; Hühne, C.; Sinapius, M.; von der Heide, C.; Dietzel, A. The Working Principles of a Multifunctional Bondline with Disbond Stopping and Health Monitoring Features for Composite Structures. J. Compos. Sci. 2021, 5, 51. [Google Scholar] [CrossRef]
- Keil, S. Dehnungsmessstreifen, 2nd ed.; Springer: Wiesbaden, Germany, 2017. [Google Scholar]

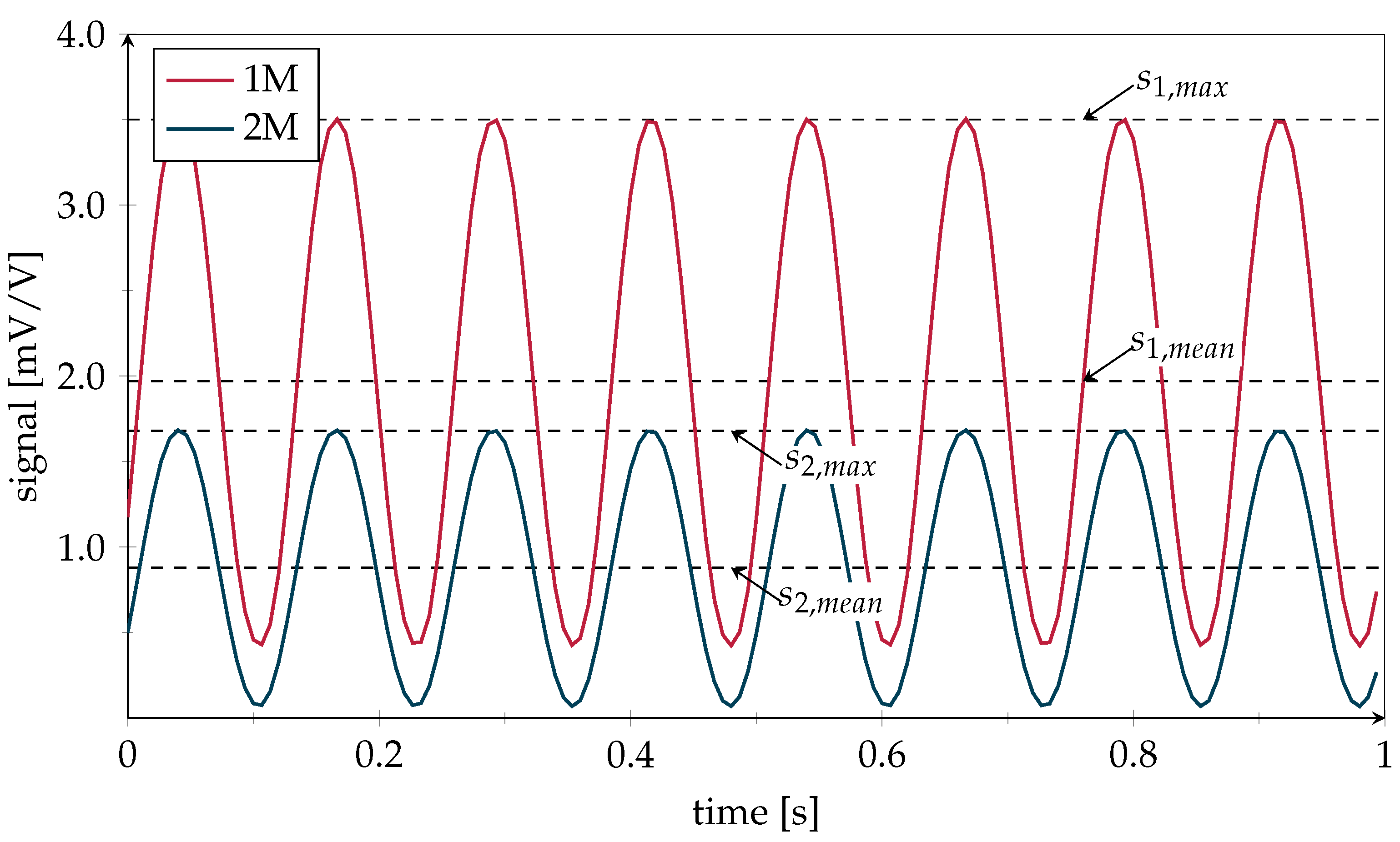
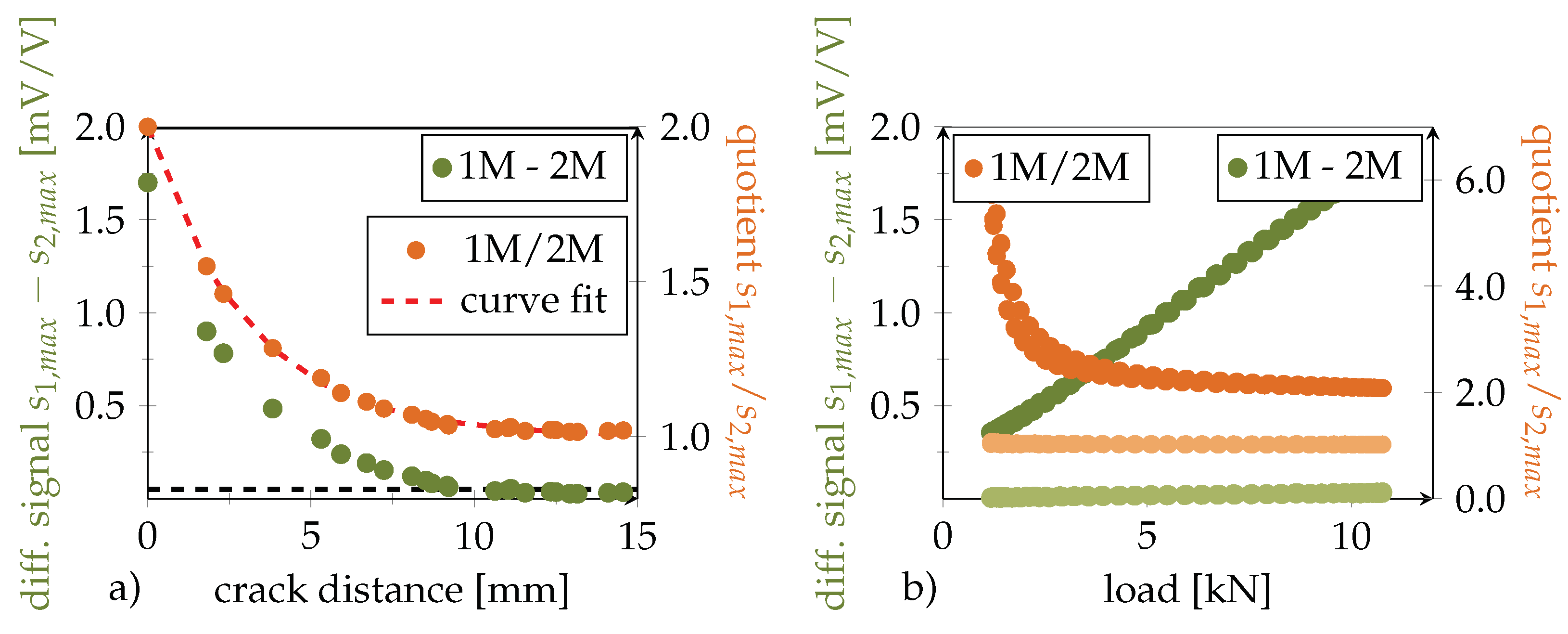
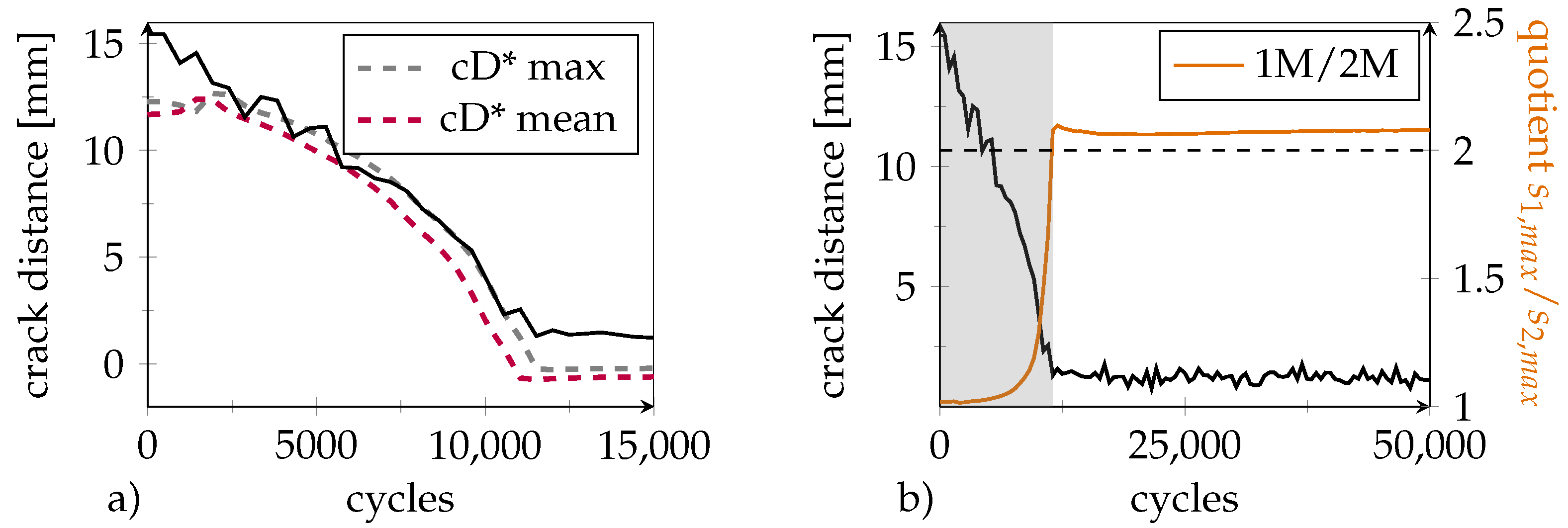
| Max. Strain | Load levelmean ± Oszi. Amplitude | Fmax |
|---|---|---|
| 3000 | 5.104 kN ± 4.176 kN @ 8 Hz | 9.280 kN |
| 3500 | 5.973 kN ± 4.887 kN @ 8 Hz | 10.860 kN |
| 4000 | 6.837 kN ± 5.594 kN @ 8 Hz | 12.431 kN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
von der Heide, C.; Steinmetz, J.; Völkerink, O.; Makiela, P.; Hühne, C.; Sinapius, M.; Dietzel, A. Polyetherimide-Reinforced Smart Inlays for Bondline Surveillance in Composites. Polymers 2022, 14, 3816. https://doi.org/10.3390/polym14183816
von der Heide C, Steinmetz J, Völkerink O, Makiela P, Hühne C, Sinapius M, Dietzel A. Polyetherimide-Reinforced Smart Inlays for Bondline Surveillance in Composites. Polymers. 2022; 14(18):3816. https://doi.org/10.3390/polym14183816
Chicago/Turabian Stylevon der Heide, Chresten, Julian Steinmetz, Oliver Völkerink, Patrick Makiela, Christian Hühne, Michael Sinapius, and Andreas Dietzel. 2022. "Polyetherimide-Reinforced Smart Inlays for Bondline Surveillance in Composites" Polymers 14, no. 18: 3816. https://doi.org/10.3390/polym14183816
APA Stylevon der Heide, C., Steinmetz, J., Völkerink, O., Makiela, P., Hühne, C., Sinapius, M., & Dietzel, A. (2022). Polyetherimide-Reinforced Smart Inlays for Bondline Surveillance in Composites. Polymers, 14(18), 3816. https://doi.org/10.3390/polym14183816











