Low-Velocity Impact Behavior of Sandwich Plates with FG-CNTRC Face Sheets and Negative Poisson’s Ratio Auxetic Honeycombs Core
Abstract
:1. Introduction
2. Modeling and Materials of Sandwich Plates
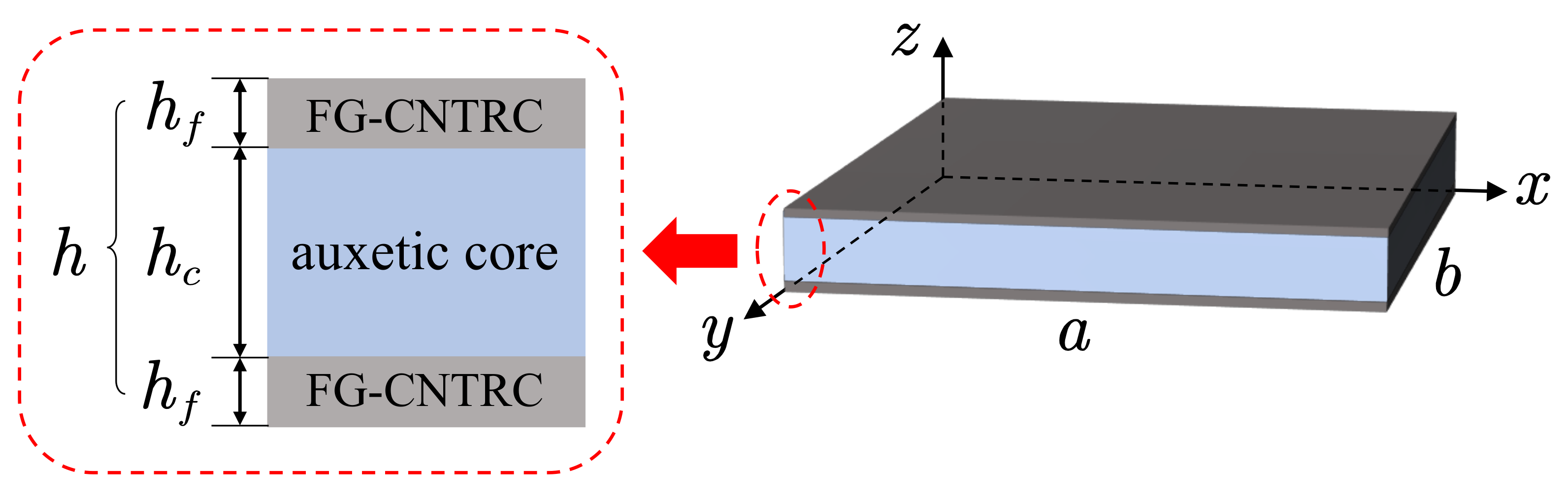
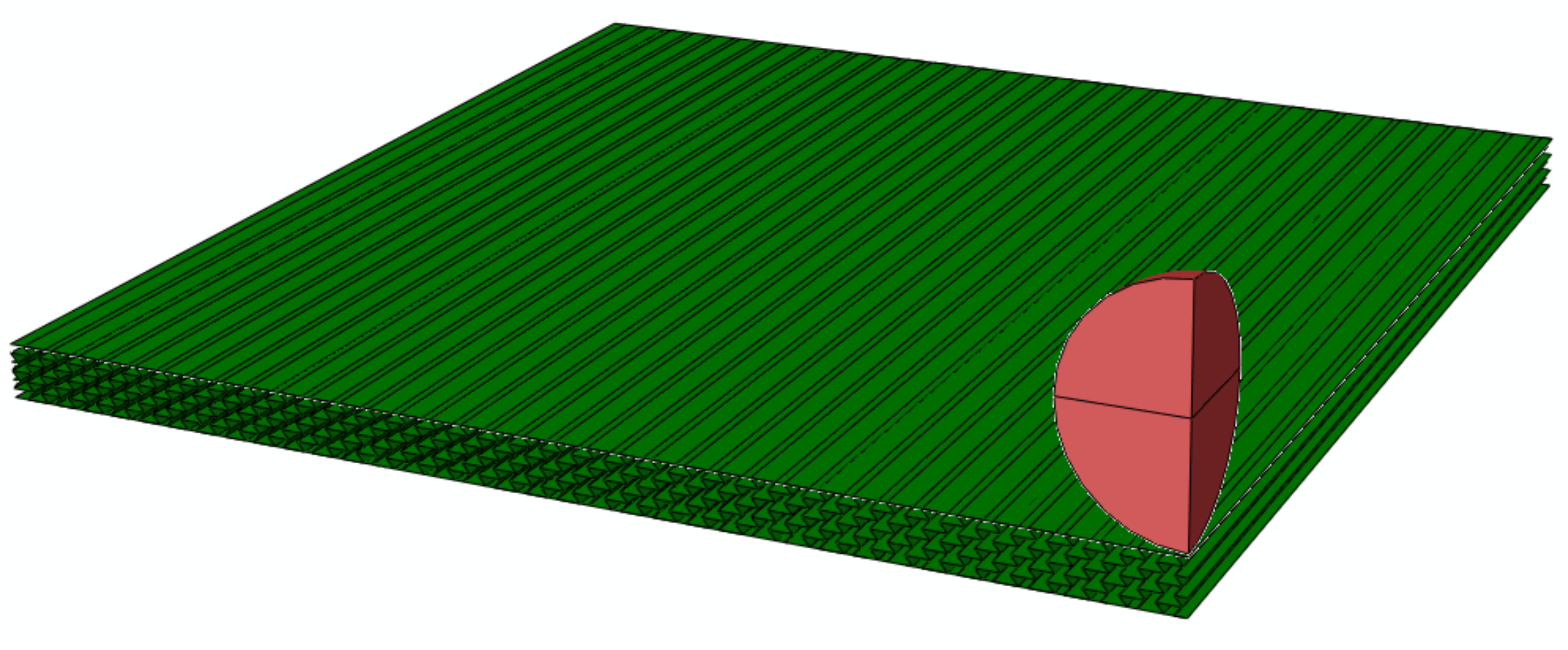
2.1. Modeling of Sandwich Plates
2.2. Materials of FG-CNTRC Face Sheets
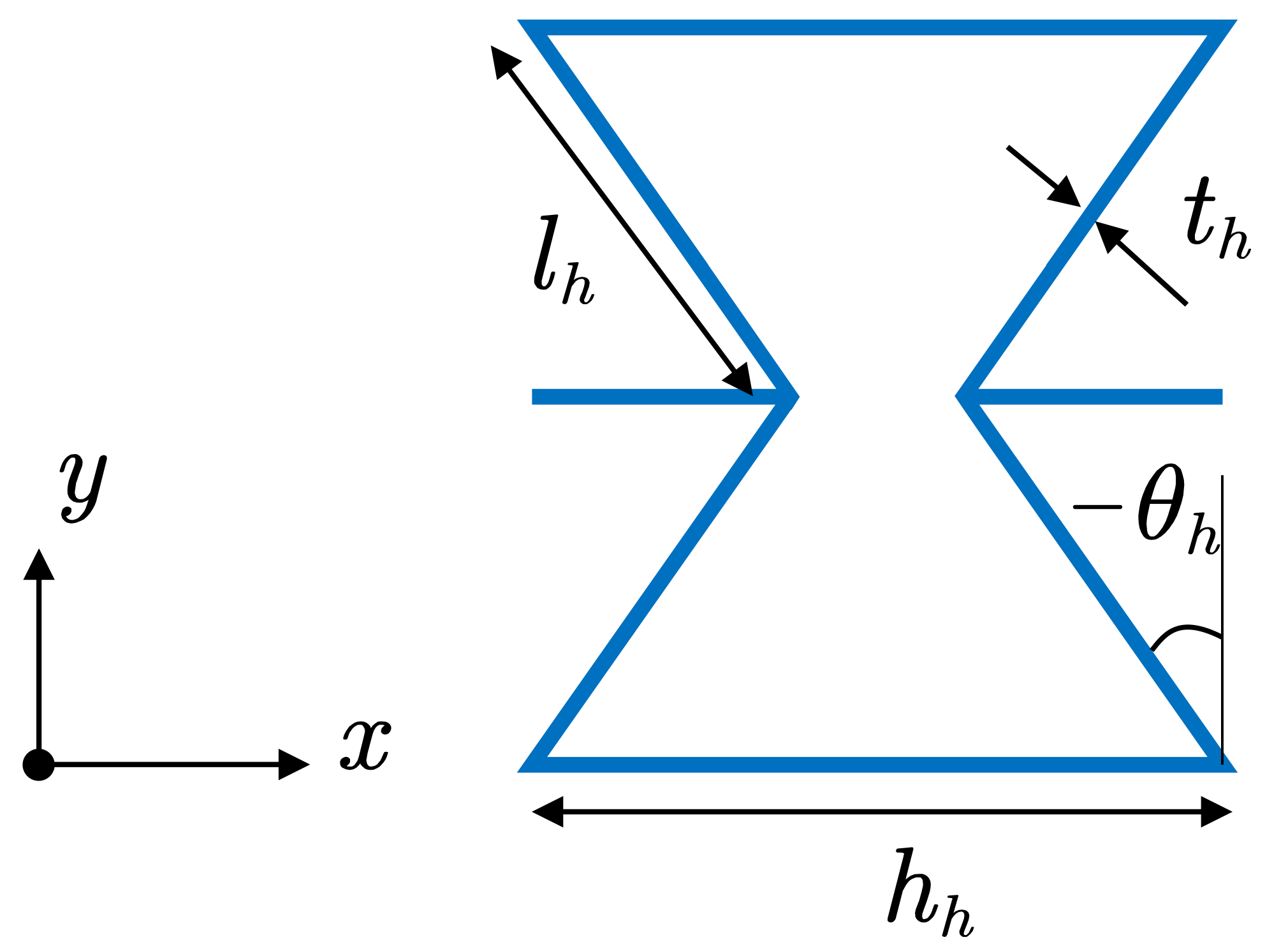
2.3. Materials of Auxetic Honeycomb Core
3. Computational Methods
3.1. Governing Equations
3.2. Low-Velocity Impact Response
3.3. Solution Procedure
4. Results and Discussion
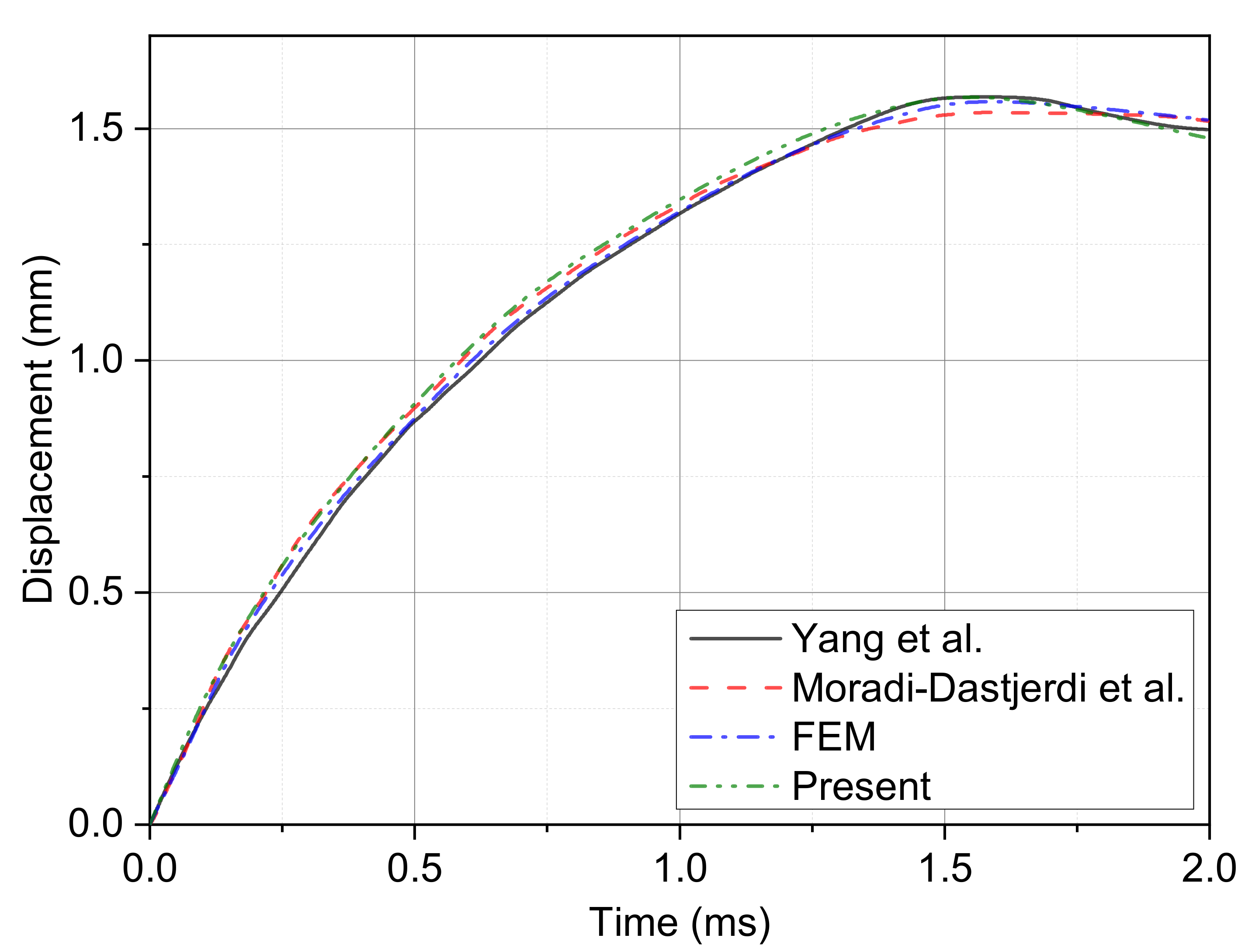
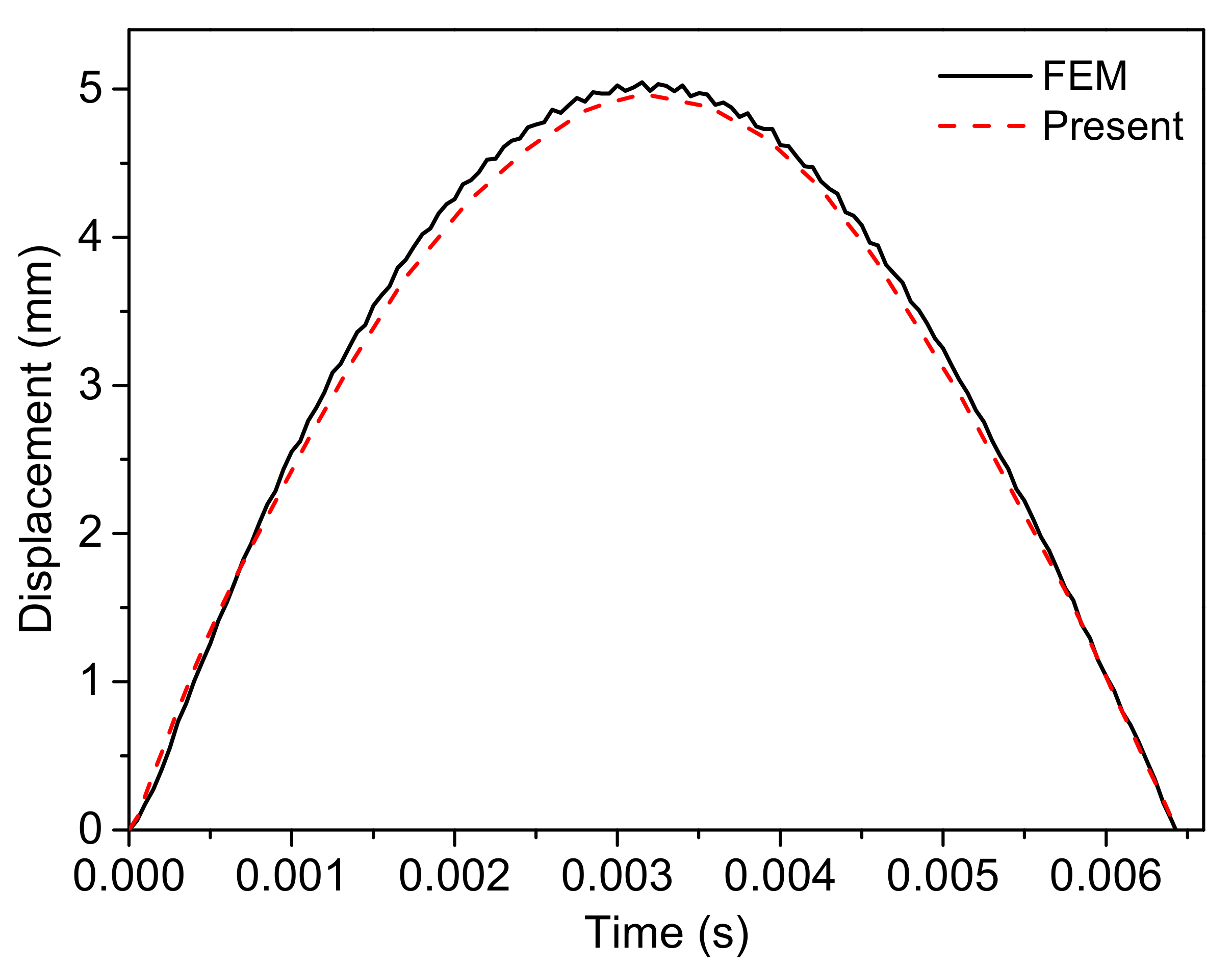
4.1. Validation Studies
4.2. Parameter Studies
- Sandwich plate—length/width ratio = 1, total thickness h = 25.4 mm;
- FG-CNTRC surface—thickness = 1.2 mm, gradient form FG-V;
- Honeycomb core—thickness = 23 mm, length of inclined cell rib = 5 mm, length of the vertical cell rib = 10 mm, inclined angle = −40;
- Calculate conditions—temperature T = 300 K, impact velocity = 2 m/s, boundary conditions clamped.
4.2.1. Gradient Forms of FG-CNTRC Surfaces
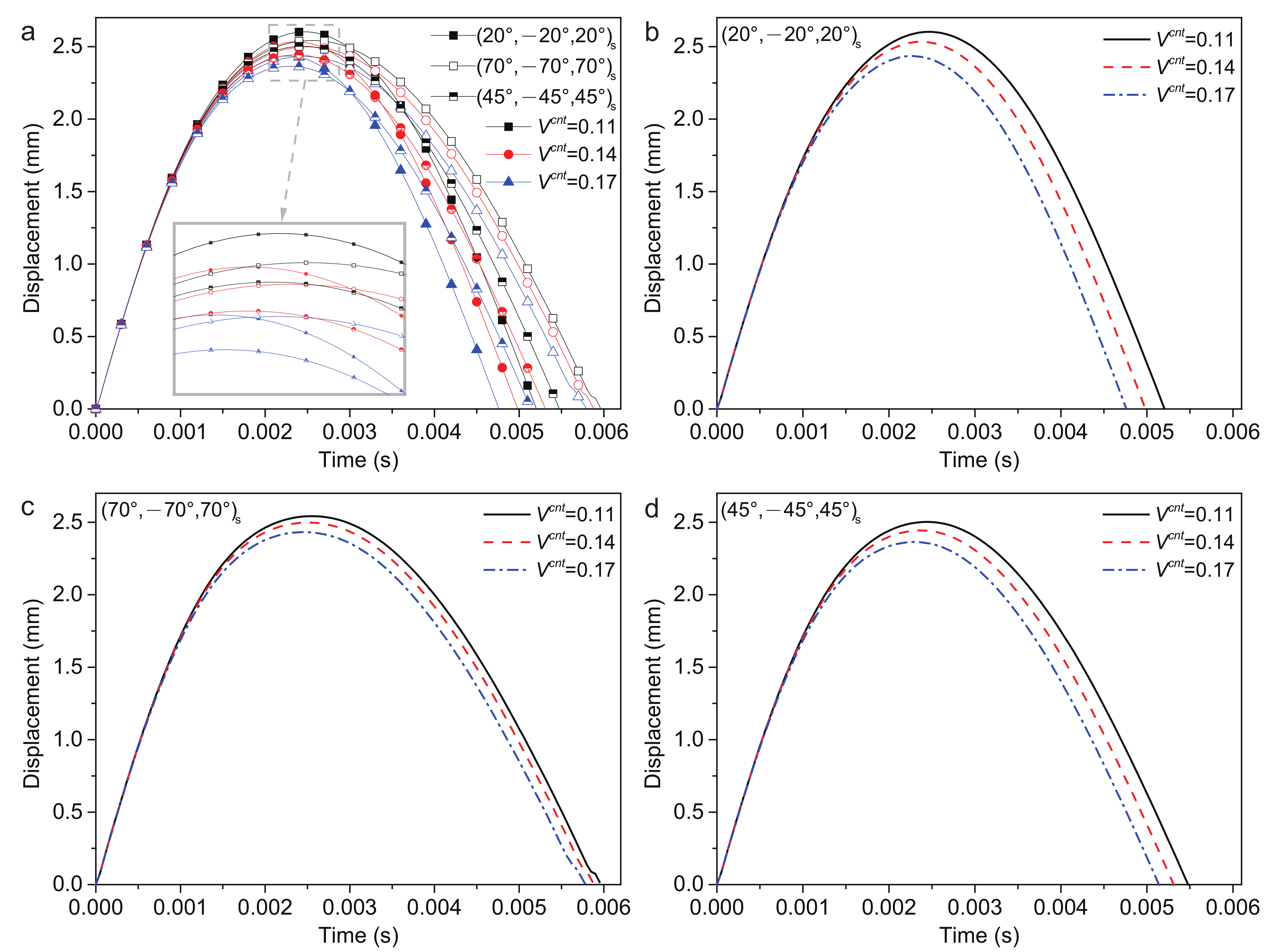
4.2.2. Volume Fractions of CNTs
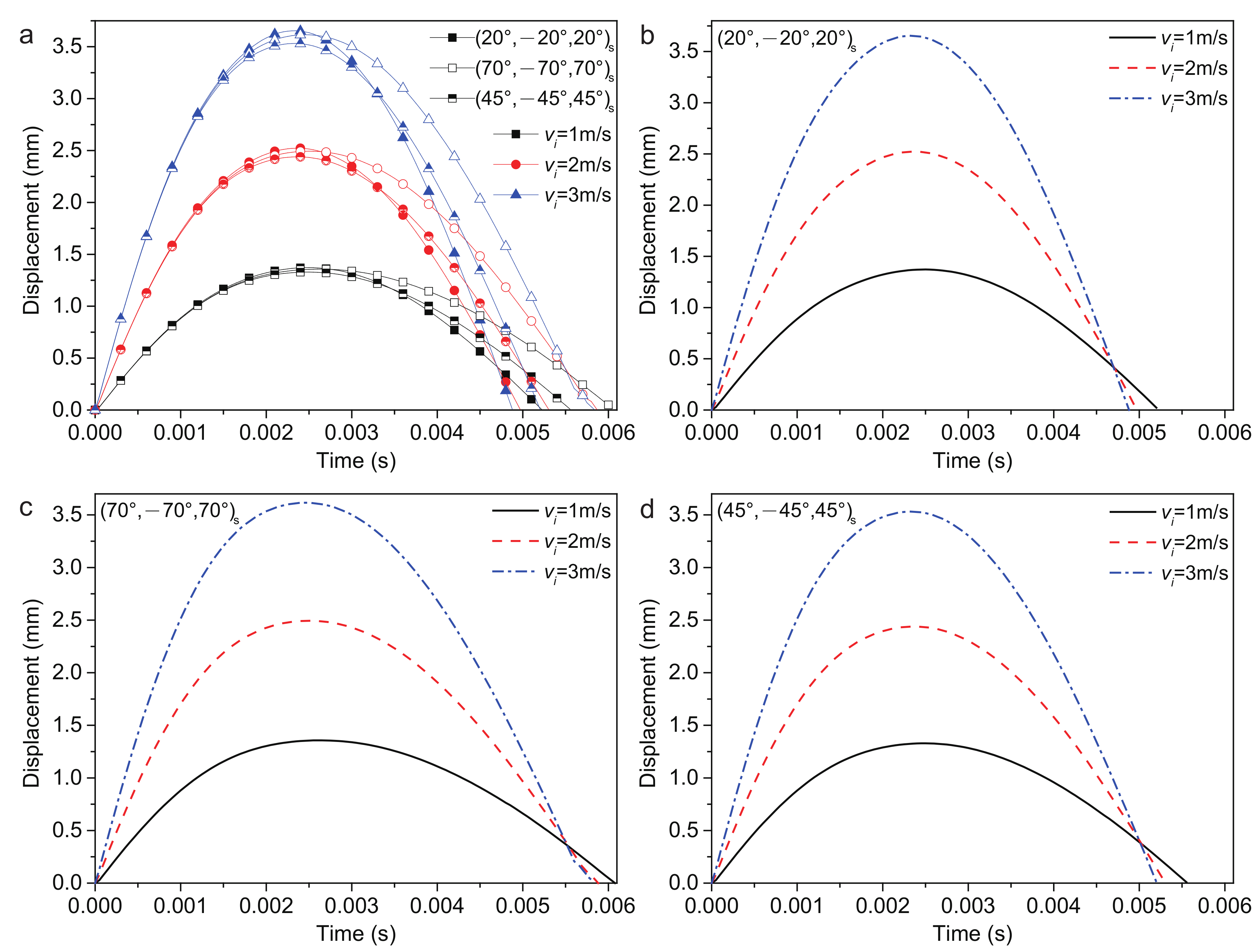
4.2.3. Impact Velocity
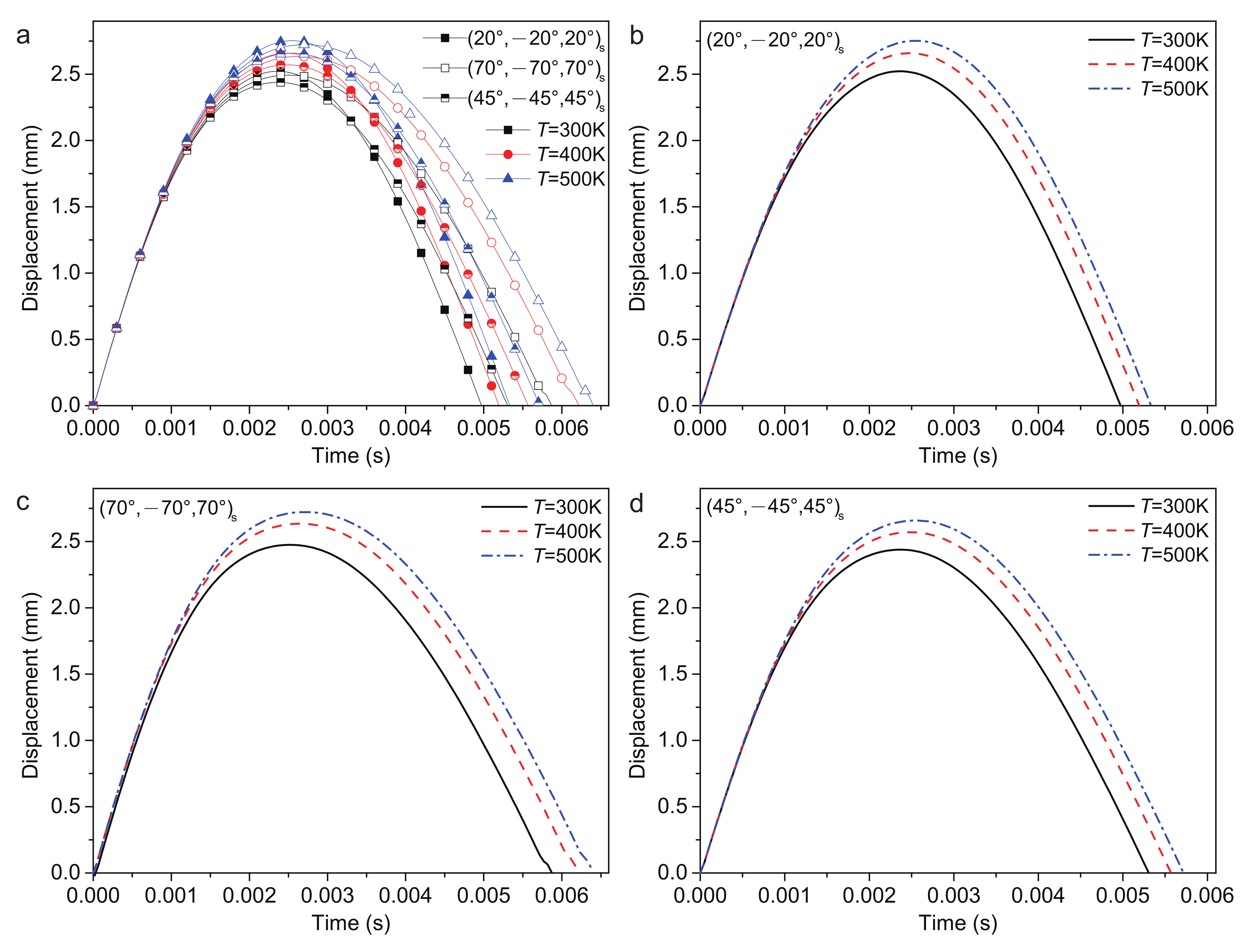
4.2.4. Temperature
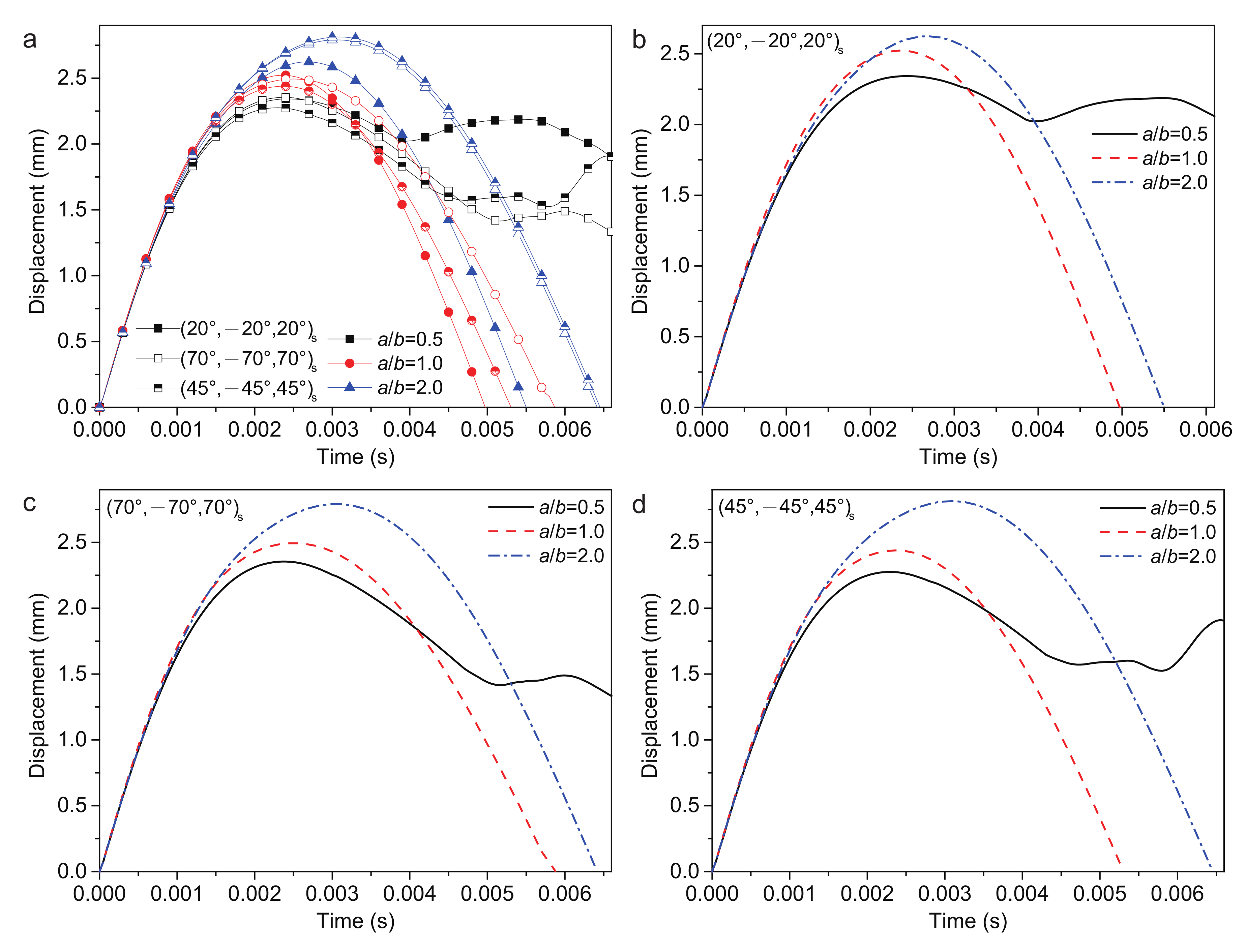
4.2.5. Ratio of Plate Length and Width
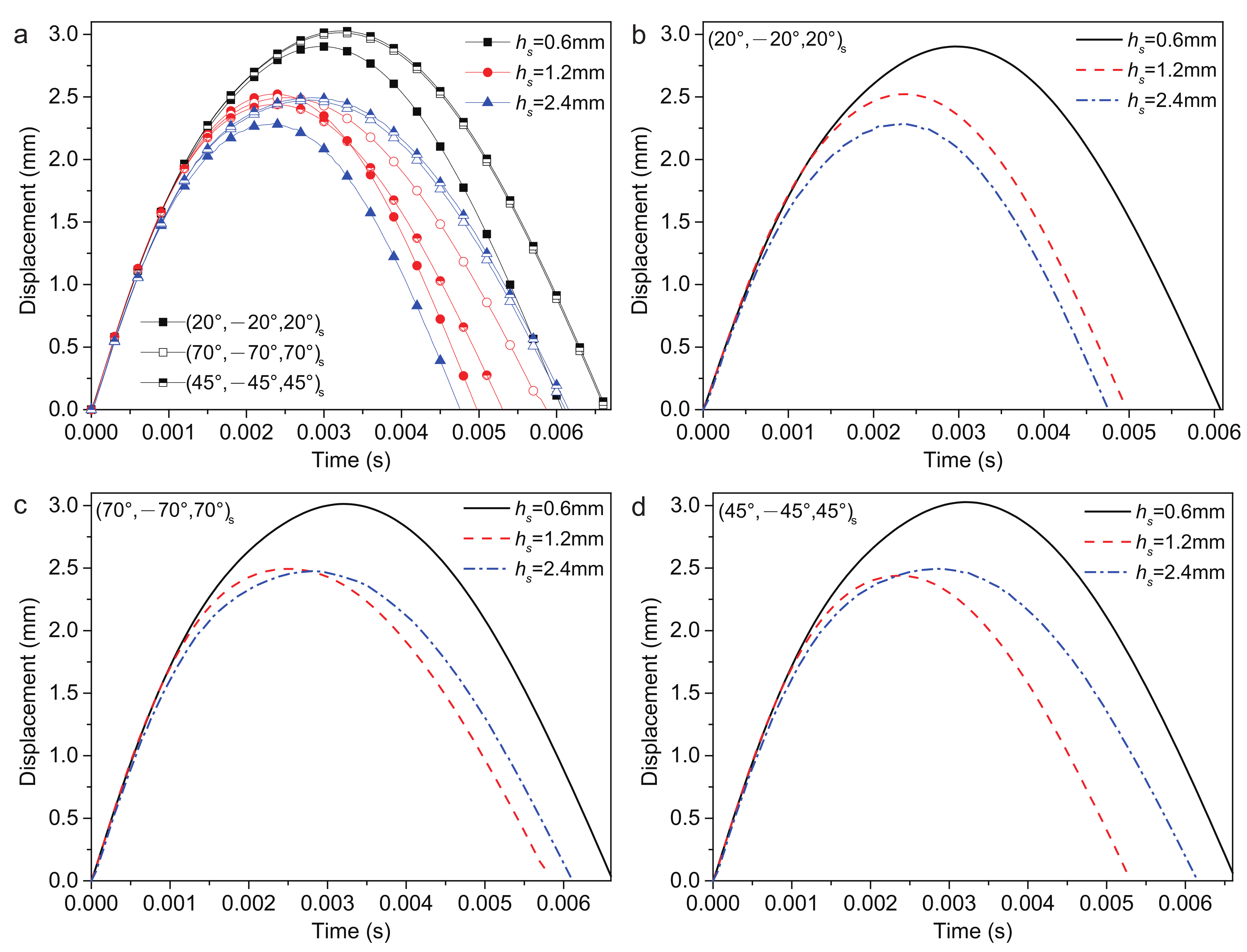
4.2.6. Thickness of Surface Layer
| Type | (mm) | (N) | (ms) | (ms) | |
|---|---|---|---|---|---|
| 0.5 | 2.342 | 1147.677 | 9.380 | 3.900 | |
| (20/−20/20)s | 1.0 | 2.522 | 1154.605 | 4.972 | 5.250 |
| 2.0 | 2.624 | 1044.604 | 5.498 | 5.600 | |
| 0.5 | 2.275 | 1165.578 | 8.125 | 4.350 | |
| (45/−45/45)s | 1.0 | 2.439 | 1162.674 | 5.306 | 5.650 |
| 2.0 | 2.813 | 955.473 | 6.454 | 6.550 | |
| 0.5 | 2.354 | 1111.640 | 8.070 | 4.750 | |
| (70/−70/70)s | 1.0 | 2.494 | 1105.591 | 5.879 | 5.750 |
| 2.0 | 2.791 | 965.506 | 6.417 | 6.500 |
5. Conclusions
- Gradient forms of FG-CNTRC surfaces:(20/−20/20)s ply—the UD form has the largest , smallest and longest ; and the FG-O form has the smallest , largest and shortest ;(45/−45/45)s ply—the UD form has the largest and longest ; the FG-X form has the largest and shortest ; the FG-O form has the smallest ; and the FG-V form has the smallest ;(70/−70/70)s ply—the UD form has the largest , smallest and longest ; the FG-X form has the smallest , largest and shortest .Within three stacking sequences and five gradient forms, the (45/−45/45)s ply with FG-O type has the smallest , while the (70/−70/70)s ply with the UD type has the smallest . The percentage decrease is approximately 5% by changing the stacking sequence and gradient form of the surface sheets.
- Volume fractions of CNTs:The (20/−20/20)s ply has the largest and shortest . The (45/−45/45)s ply has the smallest and the (70/−70/70)s ply has the longest ;The plate center displacement , recovery time of deformation and contact time decreased, while the contact force increased with the increased volume fractions of CNTs.Increasing the volume fraction of CNTs from 0.11 to 0.17 can lead to a reduction in the and an increase in the . Furthermore, this phenomenon is more sensitive to (20/−20/20)s ply with a reduction in by approximately 6.4%.
- Impact velocities:The (20/−20/20)s ply has the largest and has the shortest . The (45/−45/45)s ply has the smallest . The (70/−70/70)s ply has the longest .The plate center displacement and contact force increased, while the recovery time of deformation and contact time decreased as the impact velocity increased.The three stacking sequences have a slight impact on the variable ratio of and . Increasing the impact velocity from 1 m/s to 3 m/s can lead to an increase in the and of approximately 62.5% and 68%, respectively.
- Temperatures:The (20/−20/20)s ply has the largest and the shortest . The (45/−45/45)s ply has the smallest . The (70/−70/70)s ply has the longest .The plate center displacement , recovery time of deformation and contact time increased, while the contact force decreased as the temperature increased.The stiffness of the structure will reduce by increasing the temperature. From 300 K to 500 K, the will increase by approximately 8.4%.
- Ratio of plate length and width:(20/−20/20)s ply: = 2.0 has the smallest and largest .(45/−45/45)s ply: = 0.5 has the smallest and largest ; = 2.0 has the largest and smallest .(70/−70/70)s ply: = 0.5 has the largest and smallest .The decreased at first and then increased as increased.The increased as increased.Due to the anisotropic honeycomb core, the geometry scale has more influence on the impact response. Using the honeycomb section as the long side of the structure can reduce the .
- Thickness of surface layers:(20/−20/20)s ply: = 0.6 mm has the smallest , largest and shortest and ; = 2.4 mm has the smallest , largest and shortest and .(45/−45/45)s ply: = 0.6 mm has the largest , longest and ; = 2.4 mm has the largest , smallest and longest and .(70/−70/70)s ply: = 0.6 mm has the smallest .Increasing can lead to a reduction in the and an increase in the by increasing the stiffness of the structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Iijima, S. Carbon nanotubes: Past, present, and future. Phys. B Condens. Matter 2002, 323, 1–5. [Google Scholar] [CrossRef]
- Esawi, A.M.; Farag, M.M. Carbon nanotube reinforced composites: Potential and current challenges. Mater. Des. 2007, 28, 2394–2401. [Google Scholar] [CrossRef]
- Hu, K.; Kulkarni, D.D.; Choi, I.; Tsukruk, V.V. Graphene-polymer nanocomposites for structural and functional applications. Prog. Polym. Sci. 2014, 39, 1934–1972. [Google Scholar] [CrossRef]
- Shen, H.S. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Kwon, H.; Bradbury, C.R.; Leparoux, M. Fabrication of Functionally Graded Carbon Nanotube-Reinforced Aluminum Matrix Composite. Adv. Eng. Mater. 2011, 13, 325–329. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments, Part II: Pressure-loaded shells. Compos. Struct. 2011, 93, 2496–2503. [Google Scholar] [CrossRef]
- Jafari Mehrabadi, S.; Sobhani Aragh, B.; Khoshkhahesh, V.; Taherpour, A. Mechanical buckling of nanocomposite rectangular plate reinforced by aligned and straight single-walled carbon nanotubes. Compos. Part Eng. 2012, 43, 2031–2040. [Google Scholar] [CrossRef]
- Zhang, L.; Lei, Z.; Liew, K. An element-free IMLS-Ritz framework for buckling analysis of FG–CNT reinforced composite thick plates resting on Winkler foundations. Eng. Anal. Bound. Elem. 2015, 58, 7–17. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, H. Nonlinear bending and postbuckling analysis of matrix cracked hybrid laminated plates containing carbon nanotube reinforced composite layers in thermal environments. Compos. Part B Eng. 2016, 86, 1–16. [Google Scholar] [CrossRef]
- Zhang, L.; Liew, K. Postbuckling analysis of axially compressed CNT reinforced functionally graded composite plates resting on Pasternak foundations using an element-free approach. Compos. Struct. 2016, 138, 40–51. [Google Scholar] [CrossRef]
- Zhang, L.; Liew, K.; Reddy, J. Postbuckling of carbon nanotube reinforced functionally graded plates with edges elastically restrained against translation and rotation under axial compression. Comput. Methods Appl. Mech. Eng. 2016, 298, 1–28. [Google Scholar] [CrossRef]
- Kiani, Y. Buckling of FG-CNT-reinforced composite plates subjected to parabolic loading. Acta Mech. 2017, 228, 1303–1319. [Google Scholar] [CrossRef]
- Kiani, Y. Thermal buckling of temperature-dependent FG-CNT-reinforced composite skew plates. J. Therm. Stress. 2017, 40, 1442–1460. [Google Scholar] [CrossRef]
- Kiani, Y. Thermal post-buckling of temperature dependent sandwich plates with FG-CNTRC face sheets. J. Therm. Stress. 2018, 41, 866–882. [Google Scholar] [CrossRef]
- Kiani, Y.; Mirzaei, M. Rectangular and skew shear buckling of FG-CNT reinforced composite skew plates using Ritz method. Aerosp. Sci. Technol. 2018, 77, 388–398. [Google Scholar] [CrossRef]
- Ansari, R.; Hassani, R.; Gholami, R.; Rouhi, H. Thermal postbuckling analysis of FG-CNTRC plates with various shapes and temperature-dependent properties using the VDQ-FEM technique. Aerosp. Sci. Technol. 2020, 106, 106078. [Google Scholar] [CrossRef]
- Hieu, P.T.; Van Tung, H. Thermomechanical postbuckling of pressure loaded CNT reinforced composite cylindrical shells under tangential edge constraints and various temperature conditions. Polym. Compos. 2020, 41, 244–257. [Google Scholar] [CrossRef]
- Wang, Z.X.; Shen, H.S. Nonlinear vibration of nanotube-reinforced composite plates in thermal environments. Comput. Mater. Sci. 2011, 50, 2319–2330. [Google Scholar] [CrossRef]
- Zhu, P.; Lei, Z.; Liew, K. Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos. Struct. 2012, 94, 1450–1460. [Google Scholar] [CrossRef]
- Lei, Z.; Liew, K.; Yu, J. Free vibration analysis of functionally graded carbon nanotube-reinforced composite plates using the element-free kp-Ritz method in thermal environment. Compos. Struct. 2013, 106, 128–138. [Google Scholar] [CrossRef]
- Abdollahzadeh Shahrbabaki, E.; Alibeigloo, A. Three-dimensional free vibration of carbon nanotube-reinforced composite plates with various boundary conditions using Ritz method. Compos. Struct. 2014, 111, 362–370. [Google Scholar] [CrossRef]
- Kamarian, S.; Shakeri, M.; Yas, M.; Bodaghi, M.; Pourasghar, A. Free vibration analysis of functionally graded nanocomposite sandwich beams resting on Pasternak foundation by considering the agglomeration effect of CNTs. J. Sandw. Struct. Mater. 2015, 17, 632–665. [Google Scholar] [CrossRef]
- Mehar, K.; Panda, S.K. Geometrical nonlinear free vibration analysis of FG-CNT reinforced composite flat panel under uniform thermal field. Compos. Struct. 2016, 143, 336–346. [Google Scholar] [CrossRef]
- Wu, C.P.; Li, H.Y. Three-dimensional free vibration analysis of functionally graded carbon nanotube-reinforced composite plates with various boundary conditions. J. Vib. Control 2016, 22, 89–107. [Google Scholar] [CrossRef]
- Wang, Q.; Qin, B.; Shi, D.; Liang, Q. A semi-analytical method for vibration analysis of functionally graded carbon nanotube reinforced composite doubly-curved panels and shells of revolution. Compos. Struct. 2017, 174, 87–109. [Google Scholar] [CrossRef]
- Thomas, B.; Roy, T. Vibration and damping analysis of functionally graded carbon nanotubes reinforced hybrid composite shell structures. J. Vib.Control 2017, 23, 1711–1738. [Google Scholar] [CrossRef]
- Hasrati, E.; Ansari, R.; Torabi, J. Nonlinear Forced Vibration Analysis of FG-CNTRC Cylindrical Shells Under Thermal Loading Using a Numerical Strategy. Int. J. Appl. Mech. 2017, 9, 1750108. [Google Scholar] [CrossRef]
- Ansari, R.; Hasrati, E.; Torabi, J. Nonlinear vibration response of higher-order shear deformable FG-CNTRC conical shells. Compos. Struct. 2019, 222, 110906. [Google Scholar] [CrossRef]
- Sofiyev, A.; Hui, D. On the vibration and stability of FGM cylindrical shells under external pressures with mixed boundary conditions by using FOSDT. Thin-Walled Struct. 2019, 134, 419–427. [Google Scholar] [CrossRef]
- Maji, P.; Rout, M.; Karmakar, A. The free vibration response of temperature-dependent carbon nanotube-reinforced composite stiffened plate. Mech. Adv. Mater. Struct. 2021, 29, 2555–2569. [Google Scholar] [CrossRef]
- Quoc, T.H.; Van Tham, V.; Tu, T.M. Active vibration control of a piezoelectric functionally graded carbon nanotube-reinforced spherical shell panel. Acta Mech. 2021, 232, 1005–1023. [Google Scholar] [CrossRef]
- Wang, Z.X.; Xu, J.; Qiao, P. Nonlinear low-velocity impact analysis of temperature-dependent nanotube-reinforced composite plates. Compos. Struct. 2014, 108, 423–434. [Google Scholar] [CrossRef]
- Jam, J.; Kiani, Y. Low velocity impact response of functionally graded carbon nanotube reinforced composite beams in thermal environment. Compos. Struct. 2015, 132, 35–43. [Google Scholar] [CrossRef]
- Song, Z.G.; Zhang, L.W.; Liew, K.M. Dynamic responses of CNT reinforced composite plates subjected to impact loading. Compos. Part B Eng. 2016, 99, 154–161. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Dehbozorgi, M. Low velocity impact analysis of functionally graded carbon nanotubes reinforced composite skew plates. Compos. Struct. 2016, 140, 728–748. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Habibi, S. Low-velocity impact response of laminated FG-CNT reinforced composite plates in thermal environment. Adv. Nano Res. 2017, 5, 69–97. [Google Scholar]
- Yang, C.H.; Ma, W.N.; Ma, D.W.; He, Q.; Zhong, J.L. Analysis of the low velocity impact response of functionally graded carbon nanotubes reinforced composite spherical shells. J. Mech. Sci. Technol. 2018, 32, 2681–2691. [Google Scholar] [CrossRef]
- Yang, C.H.; Ma, W.N.; Ma, D.W. Low-velocity impact analysis of carbon nanotube reinforced composite laminates. J. Mater. Sci. 2018, 53, 637–656. [Google Scholar] [CrossRef]
- Fallah, M.; Daneshmehr, A.R.; Zarei, H.; Bisadi, H.; Minak, G. Low velocity impact modeling of functionally graded carbon nanotube reinforced composite (FG-CNTRC) plates with arbitrary geometry and general boundary conditions. Compos. Struct. 2018, 187, 554–565. [Google Scholar] [CrossRef]
- Bayat, M.R.; Rahmani, O.; Mosavi Mashhadi, M. Nonlinear low-velocity impact analysis of functionally graded nanotube-reinforced composite cylindrical shells in thermal environments. Polym. Compos. 2018, 39, 730–745. [Google Scholar] [CrossRef]
- Ma, W.; Yang, C.; Ma, D.; Zhong, J. Low-velocity impact response of nanotube-reinforced composite sandwich curved panels. Sādhanā 2019, 44, 227. [Google Scholar] [CrossRef] [Green Version]
- Khalkhali, A.; Geran Malek, N.; Bozorgi Nejad, M. Effects of the impactor geometrical shape on the non-linear low-velocity impact response of sandwich plate with CNTRC face sheets. J. Sandw. Struct. Mater. 2020, 22, 962–990. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Shen, H.S.; Li, C.; Reddy, J. Large amplitude vibration of FG-CNTRC laminated cylindrical shells with negative Poisson’s ratio. Comput. Methods Appl. Mech. Eng. 2020, 360, 112727. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X.H.; Shen, H.S. Nonlinear vibration of temperature-dependent FG-CNTRC laminated plates with negative Poisson’s ratio. Thin-Walled Struct. 2020, 148, 106514. [Google Scholar] [CrossRef]
- Whitty, J.; Alderson, A.; Myler, P.; Kandola, B. Towards the design of sandwich panel composites with enhanced mechanical and thermal properties by variation of the in-plane Poisson’s ratios. Compos. Part A Appl. Sci. Manuf. 2003, 34, 525–534. [Google Scholar] [CrossRef]
- Scarpa, F.; Blain, S.; Lew, T.; Perrott, D.; Ruzzene, M.; Yates, J. Elastic buckling of hexagonal chiral cell honeycombs. Compos. Part A Appl. Sci. Manuf. 2007, 38, 280–289. [Google Scholar] [CrossRef]
- Evans, K.E. Auxetic polymers: A new range of materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Scarpa, F.; Yates, J.R.; Ciffo, L.G.; Patsias, S. Dynamic crushing of auxetic open-cell polyurethane foam. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2002, 216, 1153–1156. [Google Scholar] [CrossRef]
- Liu, W.; Wang, N.; Luo, T.; Lin, Z. In-plane dynamic crushing of re-entrant auxetic cellular structure. Mater. Des. 2016, 100, 84–91. [Google Scholar] [CrossRef]
- Mohsenizadeh, S.; Alipour, R.; Shokri Rad, M.; Farokhi Nejad, A.; Ahmad, Z. Crashworthiness assessment of auxetic foam-filled tube under quasi-static axial loading. Mater. Des. 2015, 88, 258–268. [Google Scholar] [CrossRef]
- Hou, S.; Liu, T.; Zhang, Z.; Han, X.; Li, Q. How does negative Poisson’s ratio of foam filler affect crashworthiness? Mater. Des. 2015, 82, 247–259. [Google Scholar] [CrossRef]
- Lakes, R. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Evans, K.E.; Alderson, A. Auxetic Materials: Functional Materials and Structures from Lateral Thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef] [Green Version]
- Duc, N.D.; Seung-Eock, K.; Tuan, N.D.; Tran, P.; Khoa, N.D. New approach to study nonlinear dynamic response and vibration of sandwich composite cylindrical panels with auxetic honeycomb core layer. Aerosp. Sci. Technol. 2017, 70, 396–404. [Google Scholar] [CrossRef]
- Cong, P.H.; Khanh, N.D.; Khoa, N.D.; Duc, N.D. New approach to investigate nonlinear dynamic response of sandwich auxetic double curves shallow shells using TSDT. Compos. Struct. 2018, 185, 455–465. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.S.; Wang, H. Nonlinear Vibration of Sandwich Beams with Functionally Graded Negative Poisson’s Ratio Honeycomb Core. Int. J. Struct. Stab. Dyn. 2019, 19, 1950034. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.S.; Wang, H. Nonlinear bending of sandwich beams with functionally graded negative Poisson’s ratio honeycomb core. Compos. Struct. 2019, 212, 317–325. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.S.; Wang, H. Thermal post-buckling of sandwich beams with functionally graded negative Poisson’s ratio honeycomb core. Int. J. Mech. Sci. 2019, 152, 289–297. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.S.; Wang, H.; Yu, Z. Large amplitude vibration of sandwich plates with functionally graded auxetic 3D lattice core. Int. J. Mech. Sci. 2020, 174, 105472. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.S.; Wang, H. Postbuckling behavior of sandwich plates with functionally graded auxetic 3D lattice core. Compos. Struct. 2020, 237, 111894. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.S.; Wang, H. Nonlinear dynamic response of sandwich plates with functionally graded auxetic 3D lattice core. Nonlinear Dyn. 2020, 100, 3235–3252. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.S.; Wang, H. Full-scale finite element modeling and nonlinear bending analysis of sandwich plates with functionally graded auxetic 3D lattice core. J. Sandw. Struct. Mater. 2020, 23, 109963622092465. [Google Scholar] [CrossRef]
- Wan, H.; Ohtaki, H.; Kotosaka, S.; Hu, G. A study of negative Poisson’s ratios in auxetic honeycombs based on a large deflection model. Eur. J. Mech.-A/Solids 2004, 23, 95–106. [Google Scholar] [CrossRef]
- Grima, J.N.; Oliveri, L.; Attard, D.; Ellul, B.; Gatt, R.; Cicala, G.; Recca, G. Hexagonal Honeycombs with Zero Poisson’s Ratios and Enhanced Stiffness. Adv. Eng. Mater. 2010, 12, 855–862. [Google Scholar] [CrossRef]
- Assidi, M.; Ganghoffer, J.F. Composites with auxetic inclusions showing both an auxetic behavior and enhancement of their mechanical properties. Compos. Struct. 2012, 94, 2373–2382. [Google Scholar] [CrossRef]
- Grujicic, M.; Galgalikar, R.; Snipes, J.; Yavari, R.; Ramaswami, S. Multi-physics modeling of the fabrication and dynamic performance of all-metal auxetic-hexagonal sandwich-structures. Mater. Des. 2013, 51, 113–130. [Google Scholar] [CrossRef]
- Liu, X.F.; Wang, Y.F.; Wang, Y.S.; Zhang, C. Wave propagation in a sandwich plate with a periodic composite core. J. Sandw. Struct. Mater. 2014, 16, 319–338. [Google Scholar] [CrossRef]
- Qiao, J.; Chen, C. Impact resistance of uniform and functionally graded auxetic double arrowhead honeycombs. Int. J. Impact Eng. 2015, 83, 47–58. [Google Scholar] [CrossRef]
- Zhang, X.C.; An, L.Q.; Ding, H.M.; Zhu, X.Y.; El-Rich, M. The influence of cell micro-structure on the in-plane dynamic crushing of honeycombs with negative Poisson’s ratio. J. Sandw. Struct. Mater. 2015, 17, 26–55. [Google Scholar] [CrossRef]
- Zhang, G.; Ghita, O.R.; Evans, K.E. Dynamic thermo-mechanical and impact properties of helical auxetic yarns. Compos. Part B Eng. 2016, 99, 494–505. [Google Scholar] [CrossRef] [Green Version]
- Hadi Harkati, E.; Bezazi, A.; Scarpa, F.; Alderson, K.; Alderson, A. Modelling the influence of the orientation and fibre reinforcement on the Negative Poisson’s ratio in composite laminates. Phys. Status Solidi 2007, 244, 883–892. [Google Scholar] [CrossRef]
- Lim, T.C. Vibration of thick auxetic plates. Mech. Res. Commun. 2014, 61, 60–66. [Google Scholar] [CrossRef]
- Zhang, R.; Yeh, H.L.; Yeh, H.Y. A Preliminary Study of Negative Poisson’s Ratio of Laminated Fiber Reinforced Composites. J. Reinf. Plast. Compos. 1998, 17, 1651–1664. [Google Scholar] [CrossRef]
- Shen, H.S.; Huang, X.H.; Yang, J. Nonlinear bending of temperature-dependent FG-CNTRC laminated plates with negative Poisson’s ratio. Mech. Adv. Mater. Struct. 2020, 27, 1141–1153. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X.H.; Shen, H.S. Nonlinear flexural behavior of temperature-dependent FG-CNTRC laminated beams with negative Poisson’s ratio resting on the Pasternak foundation. Eng. Struct. 2020, 207, 110250. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X.H.; Shen, H.S. Nonlinear Vibration of Temperature-Dependent FG-CNTRC Laminated Beams with Negative Poisson’s Ratio. Int. J. Struct. Stab. Dyn. 2020, 20, 2050043. [Google Scholar] [CrossRef]
- Yu, Y.; Shen, H.S. A comparison of nonlinear vibration and bending of hybrid CNTRC/metal laminated plates with positive and negative Poisson’s ratios. Int. J. Mech. Sci. 2020, 183, 105790. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, Y. The effect of negative Poisson’s ratio on the low-velocity impact response of an auxetic nanocomposite laminate beam. Int. J. Mech. Mater. Des. 2021, 17, 153–169. [Google Scholar] [CrossRef]
- Huang, X.h.; Yang, J.; Bai, L.; Wang, X.e.; Ren, X. Theoretical solutions for auxetic laminated beam subjected to a sudden load. Structures 2020, 28, 57–68. [Google Scholar] [CrossRef]
- Huang, X.h.; Yang, J.; Wang, X.e.; Azim, I. Combined analytical and numerical approach for auxetic FG-CNTRC plate subjected to a sudden load. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Abrate, S. Hull Slamming. Appl. Mech. Rev. 2013, 64, 060803. [Google Scholar] [CrossRef]
- Lin, F.; Xiang, Y. Numerical Analysis on Nonlinear Free Vibration of Carbon Nanotube Reinforced Composite Beams. Int. J. Struct. Stab. Dyn. 2014, 14, 1350056. [Google Scholar] [CrossRef]
- Lin, F.; Xiang, Y. Vibration of carbon nanotube reinforced composite beams based on the first and third order beam theories. Appl. Math. Model. 2014, 38, 3741–3754. [Google Scholar] [CrossRef]
- Moradi-Dastjerdi, R.; Payganeh, G.; Tajdari, M. Resonance in functionally graded nanocomposite cylinders reinforced by wavy carbon nanotube. Polym. Compos. 2017, 38, E542–E552. [Google Scholar] [CrossRef]


| 0.11 | 0.149 | 0.934 | 0.934 |
| 0.14 | 0.150 | 0.941 | 0.941 |
| 0.17 | 0.149 | 1.381 | 1.381 |
| Temp (K) | (TPa) | (TPa) | (TPa) | (×10/K) | (×10/K) | |
|---|---|---|---|---|---|---|
| 300 | 5.6466 | 7.0800 | 1.9445 | 0.175 | 3.4584 | 5.1682 |
| 400 | 5.5308 | 6.9348 | 1.9643 | 0.175 | 4.1496 | 5.0905 |
| 500 | 5.4744 | 6.8641 | 1.9644 | 0.175 | 4.5361 | 5.0189 |
| Temp (K) | (GPa) | (/K) | |
|---|---|---|---|
| 300 | 2.10 | 0.34 | 45.00 |
| 400 | 1.63 | 0.34 | 47.25 |
| 500 | 1.16 | 0.34 | 49.50 |
| Material Properties | (GPa) | (g/cm) | |
|---|---|---|---|
| Ti-6Al-4V | (1–4.586 | 0.342 | 4.43 |
| Type | Gradient Forms | (mm) | (N) | (ms) | (ms) |
|---|---|---|---|---|---|
| (20/−20/20)s | FG-A | 2.522 | 1155.943 | 4.970 | 5.250 |
| FG-O | 2.518 | 1156.313 | 4.966 | 5.250 | |
| UD | 2.534 | 1149.806 | 4.982 | 5.250 | |
| FG-V | 2.522 | 1154.605 | 4.972 | 5.250 | |
| FG-X | 2.521 | 1155.906 | 4.969 | 5.250 | |
| (45/−45/45)s | FG-A | 2.436 | 1164.017 | 5.304 | 5.650 |
| FG-O | 2.433 | 1164.171 | 5.303 | 5.650 | |
| UD | 2.444 | 1163.188 | 5.311 | 5.650 | |
| FG-V | 2.439 | 1162.674 | 5.306 | 5.650 | |
| FG-X | 2.434 | 1164.324 | 5.300 | 5.650 | |
| (70/−70/70)s | FG-A | 2.491 | 1106.108 | 5.876 | 5.750 |
| FG-O | 2.490 | 1106.045 | 5.875 | 5.750 | |
| UD | 2.498 | 1104.619 | 5.888 | 5.750 | |
| FG-V | 2.494 | 1105.591 | 5.879 | 5.750 | |
| FG-X | 2.488 | 1107.330 | 5.874 | 5.750 |
| Type | Volume Fraction | (mm) | (N) | (ms) | (ms) |
|---|---|---|---|---|---|
| 0.11 | 2.602 | 1120.218 | 5.202 | 5.500 | |
| (20/−20/20)s | 0.14 | 2.534 | 1149.936 | 4.978 | 5.250 |
| 0.17 | 2.436 | 1196.062 | 4.762 | 5.000 | |
| 0.11 | 2.503 | 1134.566 | 5.478 | 5.800 | |
| (45/−45/45)s | 0.14 | 2.444 | 1163.188 | 5.311 | 5.650 |
| 0.17 | 2.365 | 1194.500 | 5.139 | 5.450 | |
| 0.11 | 2.436 | 1092.485 | 5.969 | 5.850 | |
| (70/−70/70)s | 0.14 | 2.498 | 1104.619 | 5.880 | 5.750 |
| 0.17 | 2.433 | 1121.323 | 5.783 | 5.600 |
| Type | Impact Velocity (m/s) | (mm) | (N) | (ms) | (ms) |
|---|---|---|---|---|---|
| 1 | 1.372 | 563.495 | 5.223 | 5.500 | |
| (20/−20/20)s | 2 | 2.522 | 1154.605 | 4.972 | 5.250 |
| 3 | 3.654 | 1784.333 | 4.881 | 5.150 | |
| 1 | 1.329 | 575.804 | 5.558 | 5.850 | |
| (45/−45/45)s | 2 | 2.439 | 1162.674 | 5.306 | 5.650 |
| 3 | 3.532 | 1777.370 | 5.201 | 5.350 | |
| 1 | 1.357 | 551.596 | 6.074 | 7.300 | |
| (70/−70/70)s | 2 | 2.494 | 1105.591 | 5.879 | 5.750 |
| 3 | 3.616 | 1706.855 | 5.848 | 7.200 |
| Type | Temperature (K) | (mm) | (N) | (ms) | (ms) |
|---|---|---|---|---|---|
| 300 | 2.522 | 1154.605 | 4.972 | 5.250 | |
| (20/−20/20)s | 400 | 2.659 | 1092.760 | 5.193 | 5.550 |
| 500 | 2.753 | 1119.235 | 5.332 | 5.560 | |
| 300 | 2.439 | 1162.674 | 5.306 | 5.650 | |
| (45/−45/45)s | 400 | 2.571 | 1104.613 | 5.570 | 5.950 |
| 500 | 2.659 | 1098.925 | 5.714 | 6.100 | |
| 300 | 2.494 | 1105.591 | 5.879 | 5.750 | |
| (70/−70/70)s | 400 | 2.635 | 1044.606 | 6.221 | 6.050 |
| 500 | 2.723 | 1011.190 | 6.405 | 6.250 |
| Type | h (mm) | (mm) | (N) | (ms) | (ms) |
|---|---|---|---|---|---|
| 0.6 | 2.903 | 946.210 | 6.072 | 6.250 | |
| (20/−20/20)s | 1.2 | 2.522 | 1154.605 | 4.970 | 5.250 |
| 2.4 | 2.287 | 1746.733 | 4.746 | 4.850 | |
| 0.6 | 3.027 | 904.395 | 6.650 | 6.900 | |
| (45/−45/45)s | 1.2 | 2.439 | 1162.674 | 5.302 | 5.650 |
| 2.4 | 2.494 | 1209.172 | 6.149 | 6.350 | |
| 0.6 | 3.013 | 902.615 | 6.625 | 6.850 | |
| (70/−70/70)s | 1.2 | 2.494 | 1105.591 | 5.877 | 5.750 |
| 2.4 | 2.476 | 1469.982 | 6.102 | 6.300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Ma, W.; Zhang, Z.; Zhong, J. Low-Velocity Impact Behavior of Sandwich Plates with FG-CNTRC Face Sheets and Negative Poisson’s Ratio Auxetic Honeycombs Core. Polymers 2022, 14, 2938. https://doi.org/10.3390/polym14142938
Yang C, Ma W, Zhang Z, Zhong J. Low-Velocity Impact Behavior of Sandwich Plates with FG-CNTRC Face Sheets and Negative Poisson’s Ratio Auxetic Honeycombs Core. Polymers. 2022; 14(14):2938. https://doi.org/10.3390/polym14142938
Chicago/Turabian StyleYang, Chunhao, Wuning Ma, Zhendong Zhang, and Jianlin Zhong. 2022. "Low-Velocity Impact Behavior of Sandwich Plates with FG-CNTRC Face Sheets and Negative Poisson’s Ratio Auxetic Honeycombs Core" Polymers 14, no. 14: 2938. https://doi.org/10.3390/polym14142938
APA StyleYang, C., Ma, W., Zhang, Z., & Zhong, J. (2022). Low-Velocity Impact Behavior of Sandwich Plates with FG-CNTRC Face Sheets and Negative Poisson’s Ratio Auxetic Honeycombs Core. Polymers, 14(14), 2938. https://doi.org/10.3390/polym14142938







