Self-Jumping of a Liquid Crystal Elastomer Balloon under Steady Illumination
Abstract
:1. Introduction
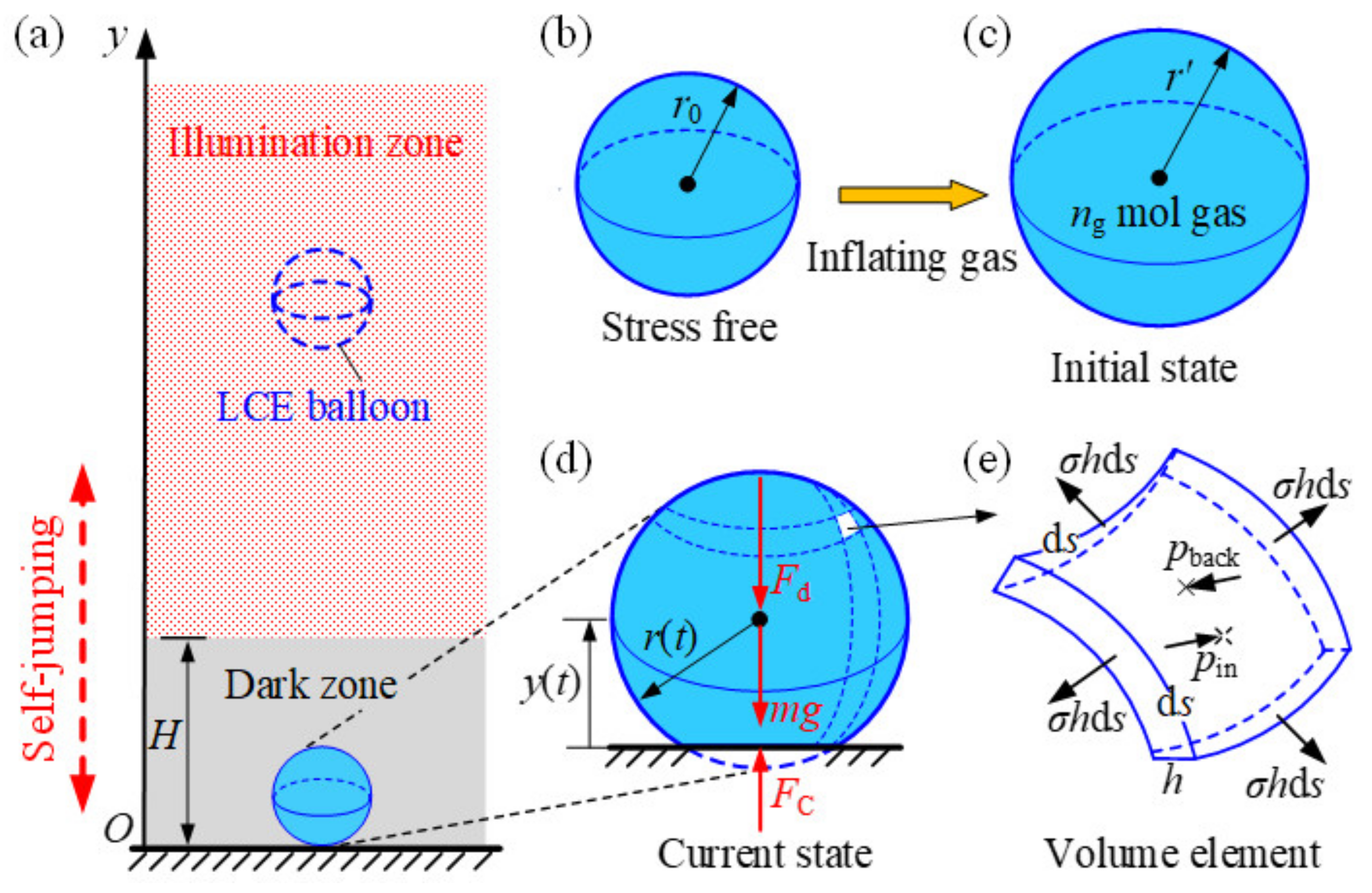
2. Model and Formulation
2.1. Dynamic of the Spherical LCE Balloon
2.2. Dynamic LCE Model
2.3. Solution Method
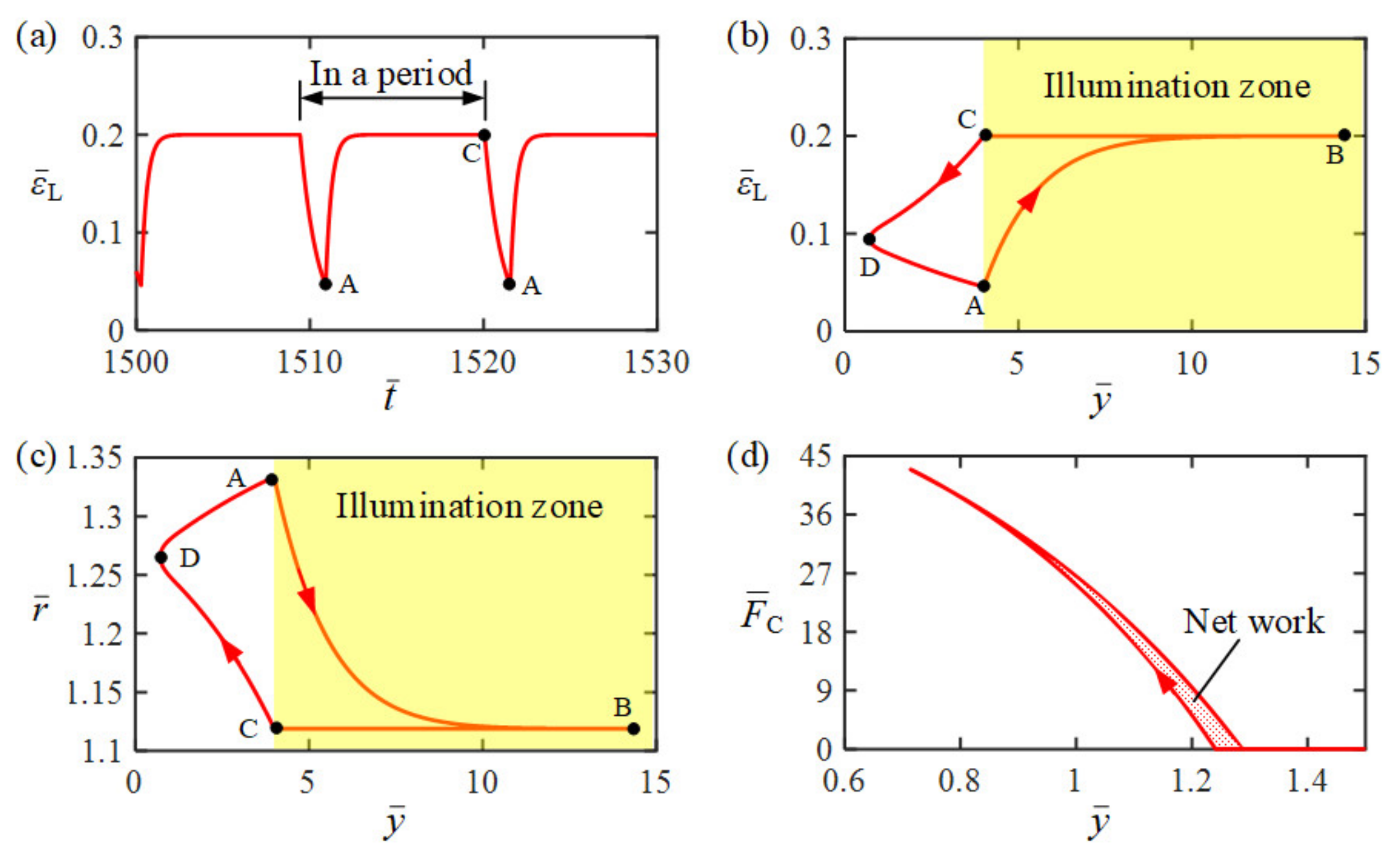
3. Two Motion Regimes and Mechanism of the Self-Jumping
3.1. Two Motion Regimes
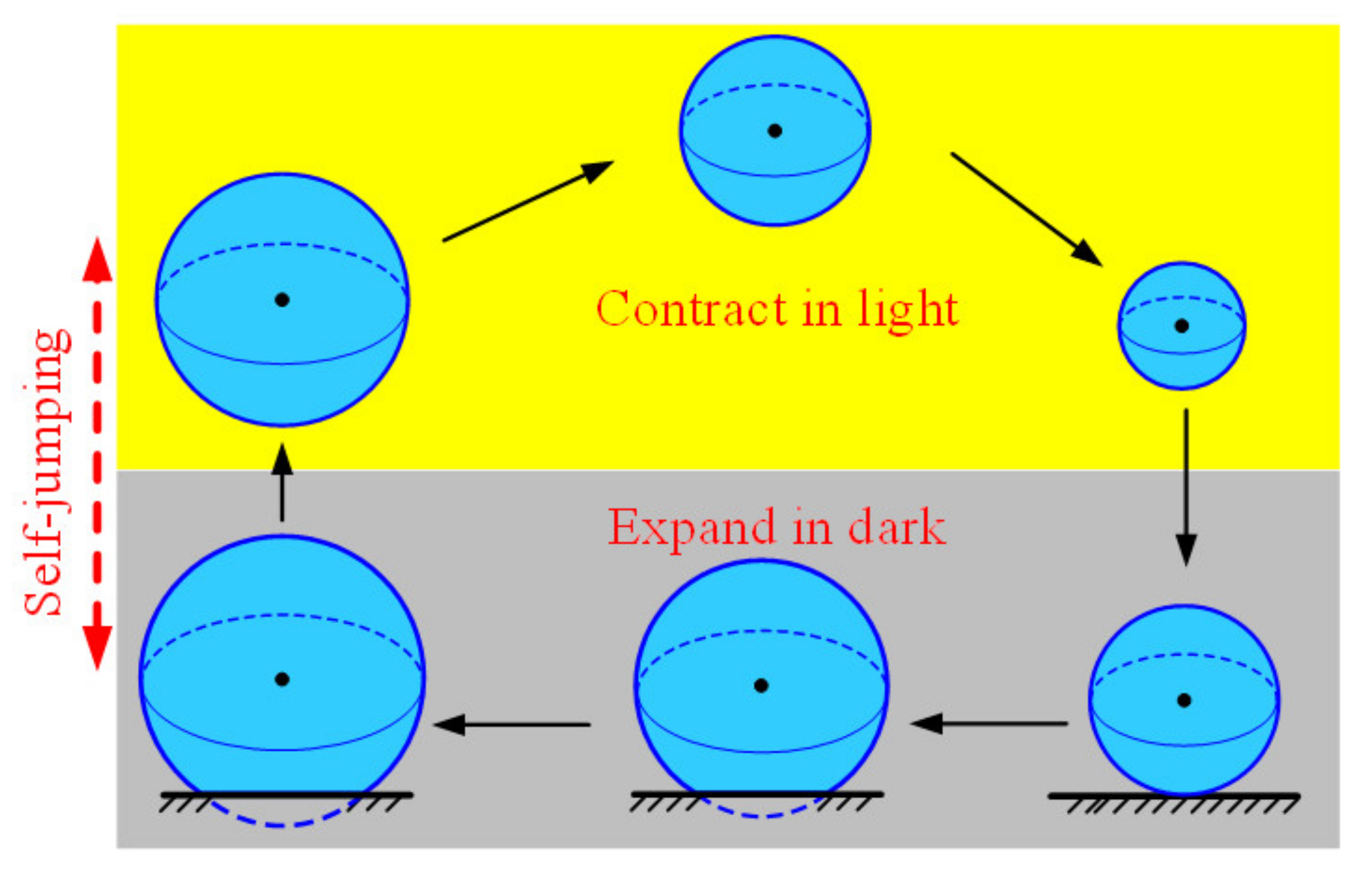
3.2. Mechanisms of the Self-Jumping
4. Influence of System Parameters on the Self-Jumping
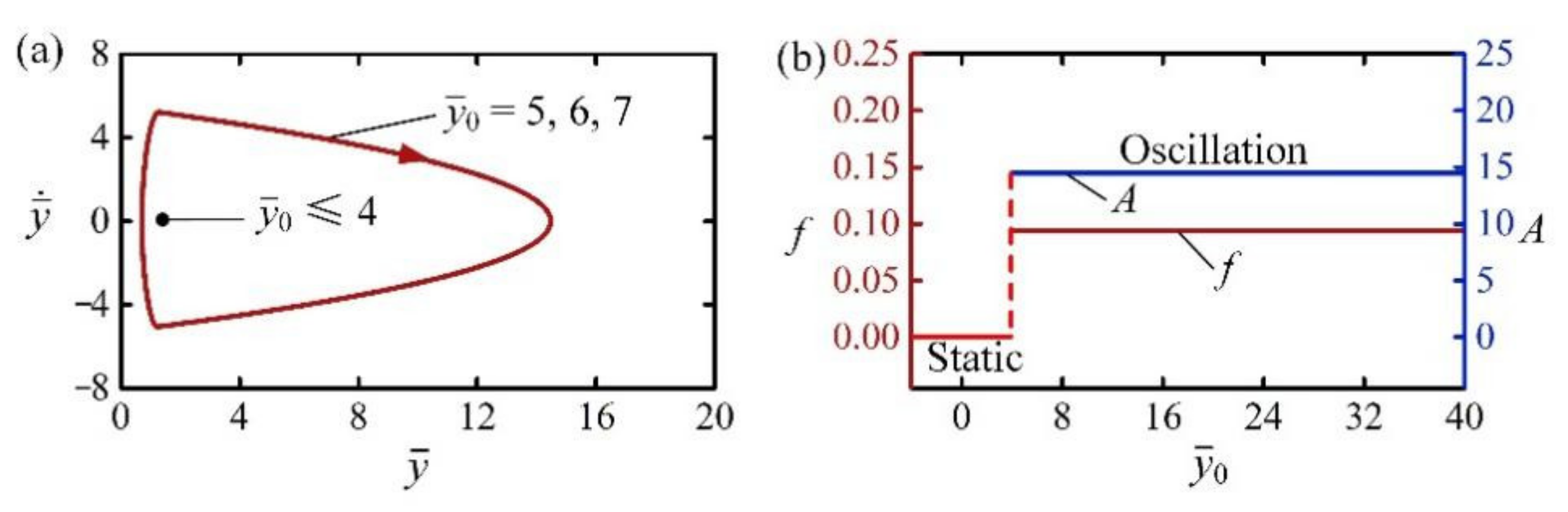
4.1. Effect of Initial Position
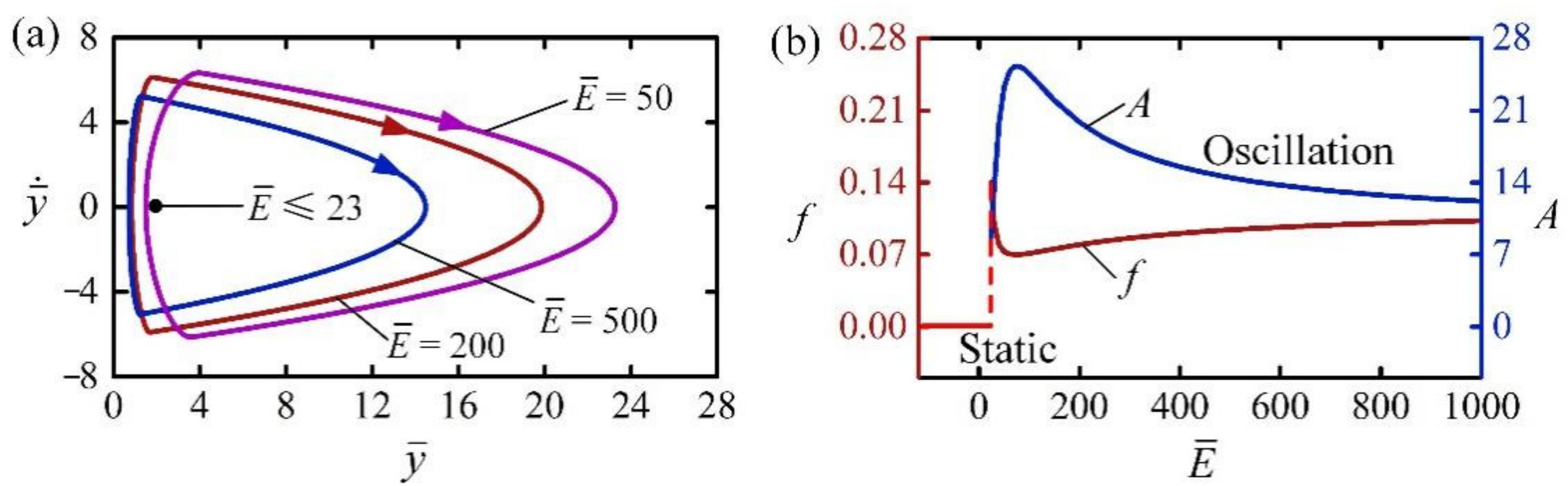
4.2. Effect of Light Intensity
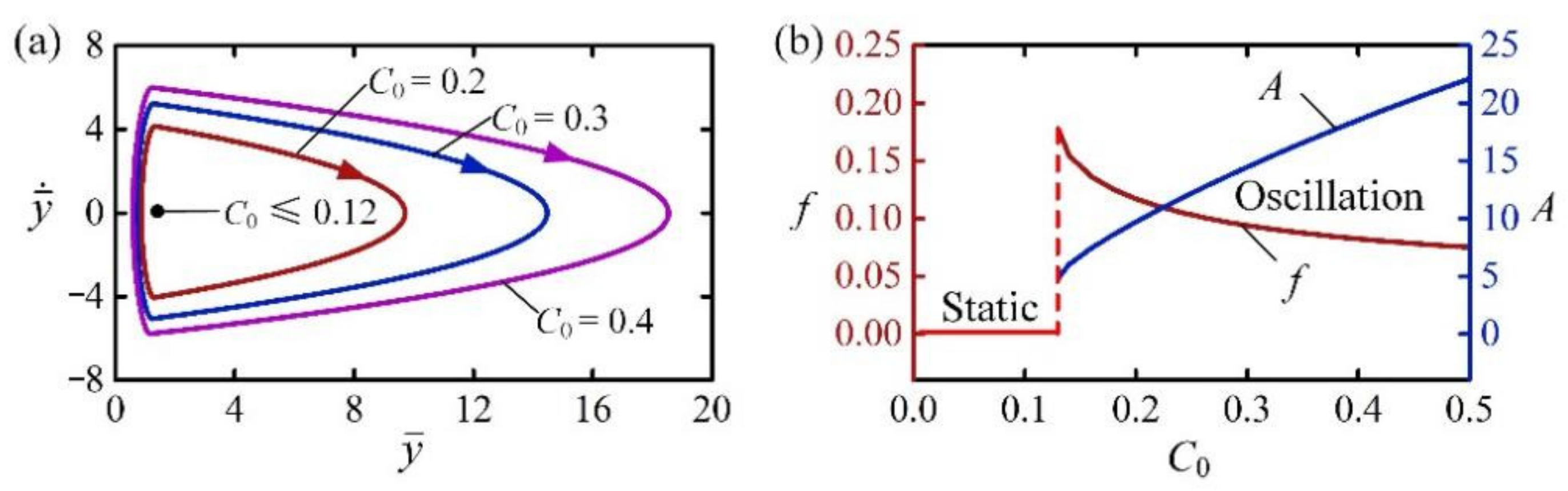
4.3. Effect of Contraction Coefficient
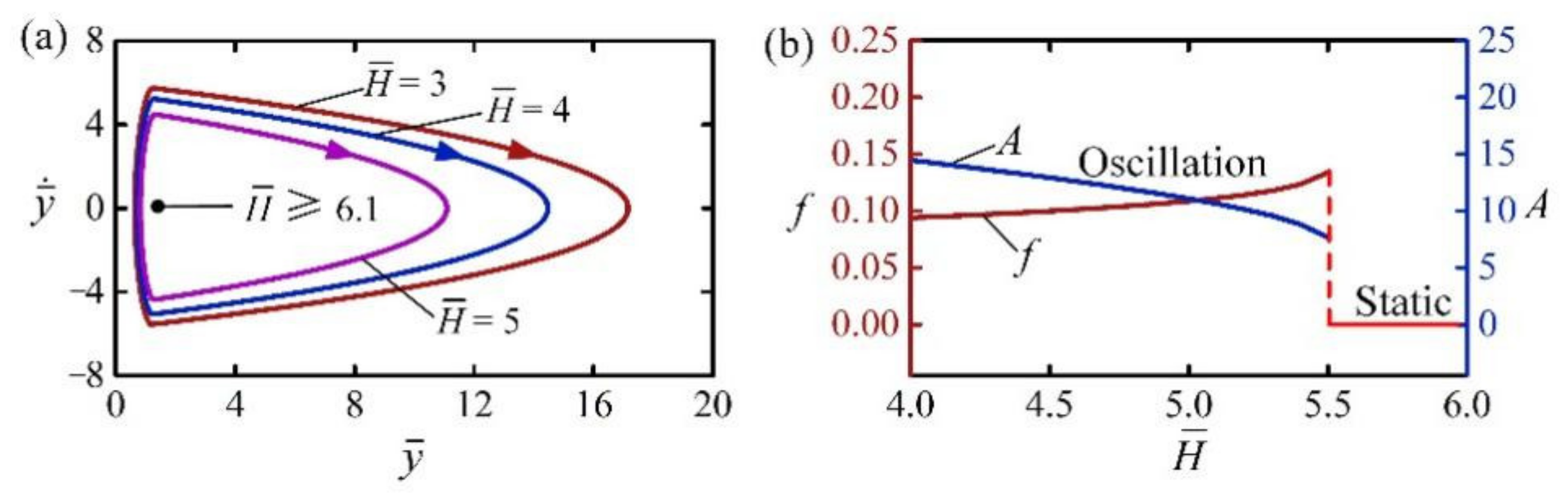
4.4. Effect of Dark Zone
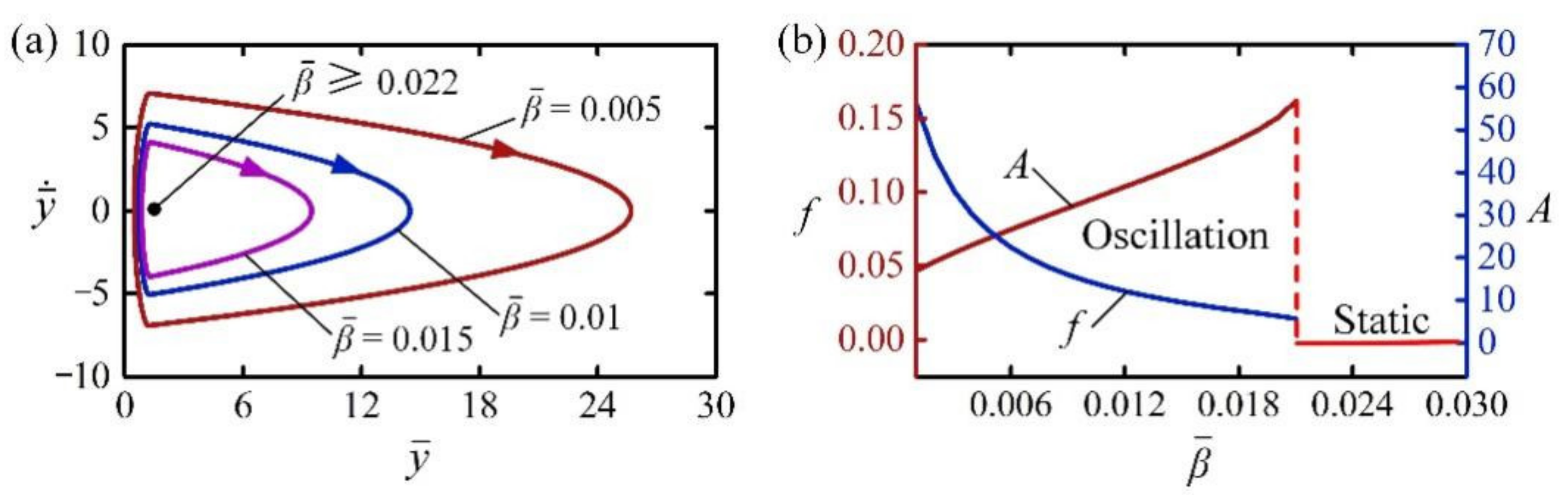
4.5. Effect of Damping Coefficient
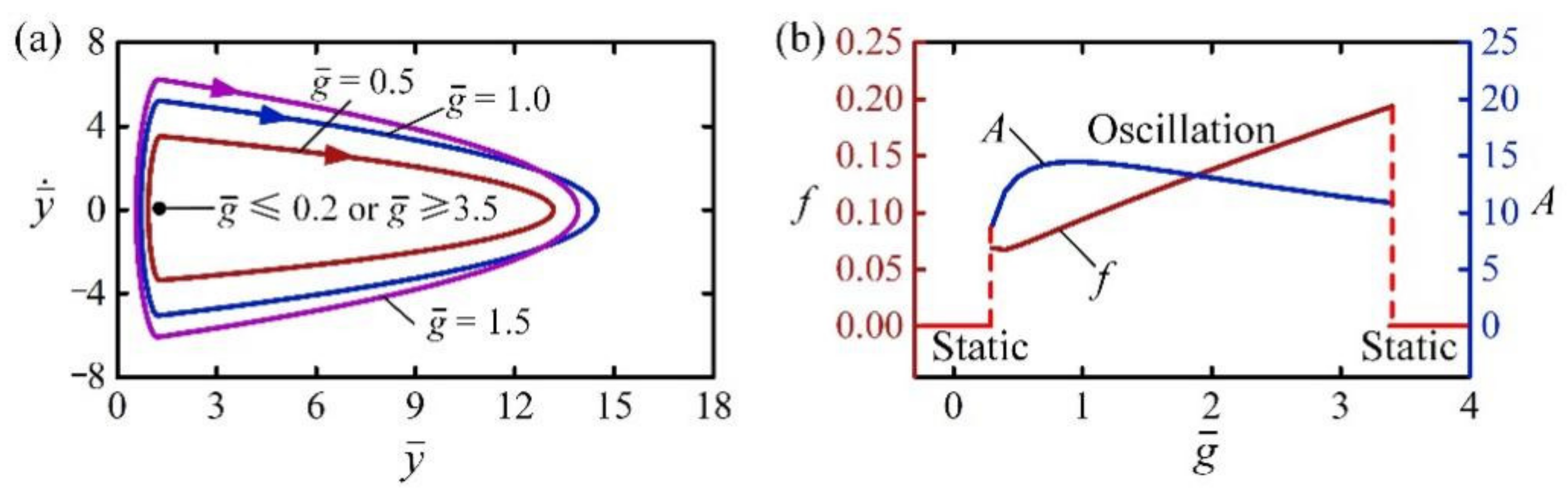
4.6. Effect of Gravitational Acceleration
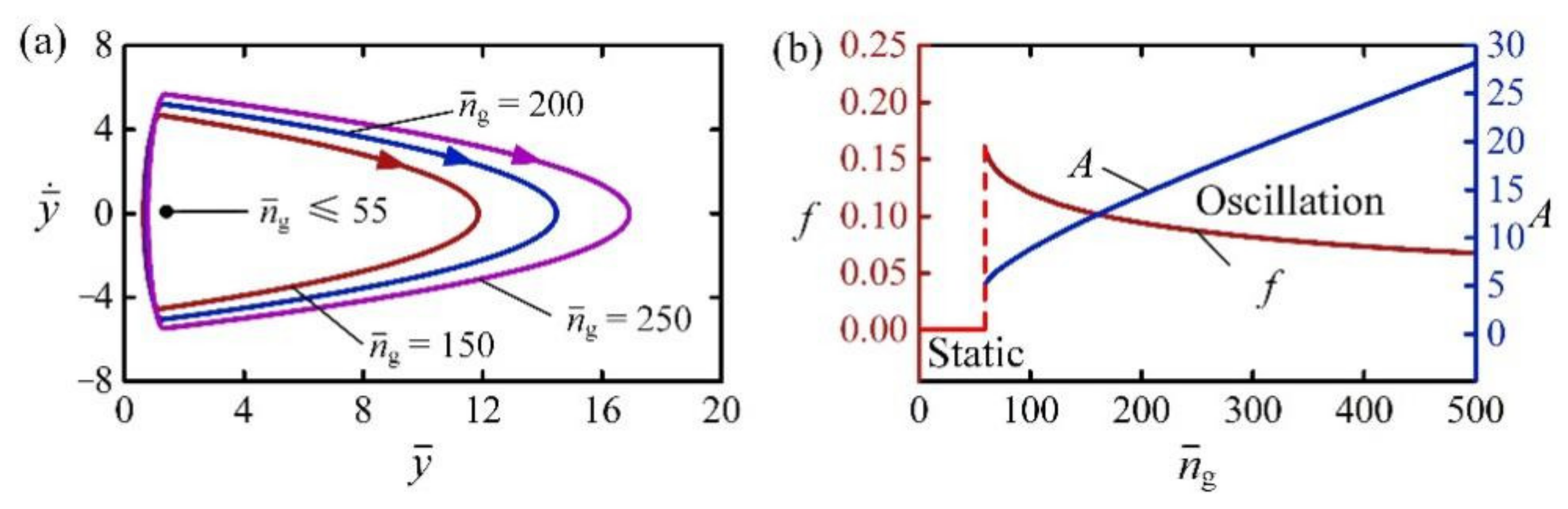
4.7. Effect of Amount of Substance
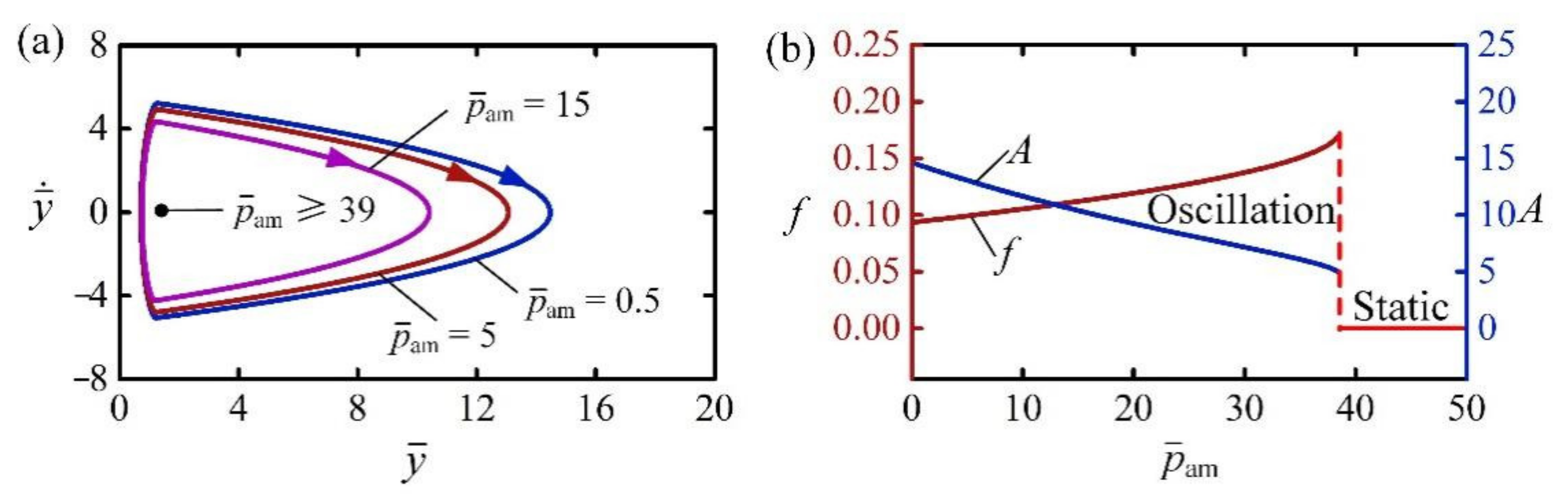
4.8. Effect of Ambient Pressure
4.9. Effect of Equivalent Elastic Modulus
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thomson, W.T. Theory of Vibration with Applications, 5th ed.; Prentice-Hall: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ding, W.J. Self-Excited Vibration; Tsing-Hua University Press: Beijing, China, 2009. [Google Scholar]
- Du, C.; Cheng, Q.; Li, K.; Yu, Y. A Light-powered liquid crystal elastomer spring oscillator with self-shading coatings. Polymers 2022, 14, 1525. [Google Scholar] [CrossRef]
- Sangwan, V.; Taneja, A.; Mukherjee, S. Design of a robust self-excited biped walking mechanism. Mech. Mach. Theory 2004, 39, 1385–1397. [Google Scholar] [CrossRef]
- Wang, X.; Ho, G.W. Design of untethered soft material micromachine for life-like locomotion. Mater. Today 2022, 53, 197–216. [Google Scholar] [CrossRef]
- Cheng, Y.; Lu, H.; Lee, X.; Zeng, H.; Priimagi, A. Kirigami-based light-induced shape-morphing and locomotion. Adv. Mater. 2020, 32, 1906233. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Chang, L.; Hu, Y.; Huang, M.; Ji, Q.; Lu, P.; Liu, J.; Chen, W.; Wu, Y. An autonomous soft actuator with light-driven self-sustained wavelike oscillation for phototactic self-locomotion and power generation. Adv. Funct. Mater. 2020, 30, 1908842. [Google Scholar] [CrossRef]
- Li, K.; Chen, Z.; Xu, P. Light-propelled self-sustained swimming of a liquid crystal elastomer torus at low Reynolds number. Int. J. Mech. Sci. 2022, 219, 107128. [Google Scholar] [CrossRef]
- Chun, S.; Pang, C.; Cho, S.B. A micropillar-assisted versatile strategy for highly sensitive and efficient triboelectric energy generation under in-plane stimuli. Adv. Mater. 2020, 32, 1905539. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Liu, Y. A prototype for light-electric harvester based on light sensitive liquid crystal elastomer cantilever. Energy 2020, 198, 117351. [Google Scholar] [CrossRef]
- Tang, R.; Liu, Z.; Xu, D.; Liu, J.; Yu, L.; Yu, H. Optical pendulum generator based on photomechanical liquid-crystalline actuators. ACS Appl. Mater. Interfaces 2015, 7, 8393–8397. [Google Scholar] [CrossRef] [PubMed]
- Rothemund, P.; Ainla, A.; Belding, L.; Preston, D.J.; Kurihara, S.; Suo, Z.; Whitesides, G.M. A soft, bistable valve for autonomous control of soft actuators. Sci. Robot. 2018, 3, eaar7986. [Google Scholar] [CrossRef] [Green Version]
- White, T.J.; Broer, D.J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 2015, 14, 1087–1098. [Google Scholar] [CrossRef]
- Yoshida, R. Self-oscillating gels driven by the Belousov-Zhabotinsky reaction as novel smart materials. Adv. Mater. 2010, 22, 3463–3483. [Google Scholar] [CrossRef]
- Hua, M.; Kim, C.; Du, Y.; Wu, D.; Bai, R.; He, X. Swaying gel: Chemo-mechanical self-oscillation based on dynamic buckling. Matter 2021, 4, 1029–1041. [Google Scholar] [CrossRef]
- Wu, J.; Yao, S.; Zhang, H.; Man, W.; Bai, Z.; Zhang, F.; Wang, X.; Fang, D.; Zhang, Y. Liquid crystal elastomer metamaterials with giant biaxial thermal shrinkage for enhancing skin regeneration. Adv. Mater. 2021, 33, 2170356. [Google Scholar] [CrossRef]
- Boissonade, J.; Kepper, P.D. Multiple types of spatio-temporal oscillations induced by differential diffusion in the Landolt reaction. Phys. Chem. Chem. Phys. 2011, 13, 4132–4137. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Yang, S. Multi-functional liquid crystal elastomer composites. Appl. Phys. Rev. 2022, 9, 011301. [Google Scholar] [CrossRef]
- Bubnov, A.; Domenici, V.; Hamplová, V.; Kašpar, M.; Zalar, B. First liquid single crystal elastomer containing lactic acid derivative as chiral co-monomer: Synthesis and properties. Polymer 2011, 52, 4490–4497. [Google Scholar] [CrossRef]
- Milavec, J.; Domenici, V.; Zupančič, B.; Rešetič, A.; Bubnov, A.; Zalar, B. Deuteron nmr resolved mesogen vs. crosslinker molecular order and reorientational exchange in liquid single crystal elastomers. Phys. Chem. Chem. Phys. 2016, 18, 4071–4077. [Google Scholar] [CrossRef]
- Rešetič, A.; Milavec, J.; Domenici, V.; Zupančič, B.; Bubnov, A.; Zalar, B. Stress-strain and thermomechanical characterization of nematic to smectic a transition in a strongly-crosslinked bimesogenic liquid crystal elastomer. Polymer 2018, 158, 96–102. [Google Scholar] [CrossRef]
- Shen, Q.; Trabia, S.; Stalbaum, T.; Palmre, V.; Kim, K.; Oh, I. A multiple-shape memory polymer-metal composite actuator capable of programmable control, creating complex 3D motion of bending, twisting, and oscillation. Sci. Rep. 2016, 6, 24462. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Ji, Q.; Huang, M.; Chang, L.; Zhang, C.; Wu, G.; Zi, B.; Bao, N.; Chen, W.; Wu, Y. Light-driven self-oscillating actuators with pototactic locomotion based on black phosphorus heterostructure. Angew. Chem. Int. Ed. 2021, 60, 20511–20517. [Google Scholar] [CrossRef]
- Sun, J.; Hu, W.; Zhang, L.; Lan, R.; Yang, H.; Yang, D. Light-driven self-oscillating behavior of liquid-crystalline networks triggered by dynamic isomerization of molecular motors. Adv. Funct. Mater. 2021, 31, 2103311. [Google Scholar] [CrossRef]
- Manna, R.K.; Shklyaev, O.E.; Balazs, A.C. Chemical pumps and flexible sheets spontaneously form self-regulating oscillators in solution. Proc. Natl. Acad. Sci. USA 2021, 118, e2022987118. [Google Scholar] [CrossRef]
- Li, Z.; Myung, N.V.; Yin, Y. Light-powered soft steam engines for self-adaptive oscillation and biomimetic swimming. Sci. Robot. 2021, 6, eabi4523. [Google Scholar] [CrossRef]
- Kuenstler, A.S.; Chen, Y.; Bui, P.; Kim, H.; DeSimone, A.; Jin, L.; Hayward, R. Blueprinting photothermal shape-morphing of liquid crystal elastomers. Adv. Mater. 2020, 32, 2000609. [Google Scholar] [CrossRef]
- Ge, D.; Li, K. Self-oscillating buckling and postbuckling of a liquid crystal elastomer disk under steady illumination. Int. J. Mech. Sci. 2022, 221, 107233. [Google Scholar] [CrossRef]
- Shen, B.; Kang, S. Designing self-oscillating matter. Matter 2021, 4, 766–769. [Google Scholar] [CrossRef]
- Zhao, T.; Fan, Y.; Lv, J. Photomorphogenesis of Diverse Autonomous Traveling Waves in a Monolithic Soft Artificial Muscle. ACS Appl. Mater. Interfaces 2022, 14, 23839–23849. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Li, Y.; Lv, J. Phototunable self-oscillating system driven by a self-winding fiber actuator. Nat. Commun. 2021, 12, 3211. [Google Scholar] [CrossRef]
- Zhao, Y.; Chi, Y.; Hong, Y.; Li, Y.; Yang, S.; Yin, J. Twisting for soft intelligent autonomous robot in unstructured environments. Proc. Natl. Acad. Sci. USA 2022, 119, e2200265119. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; Wang, Y.; Wang, Z.; Li, C.; Annapooranan, R.; Zeng, J.; Chen, R.; Cai, S. Electrospun liquid crystal elastomer microfiber actuator. Sci. Robot. 2021, 6, eabi9704. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Du, C.; Wang, W.; Li, K. A thermally-responsive fiber engine in a linear temperature field. Int. J. Mech. Sci. 2022, 225, 107291. [Google Scholar] [CrossRef]
- Ahn, C.; Li, K.; Cai, S. Light or thermally-powered autonomous rolling of an elastomer rod. ACS Appl. Mater. Interfaces 2018, 10, 25689–25696. [Google Scholar] [CrossRef] [PubMed]
- Bazir, A.; Baumann, A.; Ziebert, F.; Kulić, I.M. Dynamics of fiberboids. Soft Matter 2020, 16, 5210–5223. [Google Scholar] [CrossRef]
- Serak, S.; Tabiryan, N.V.; Vergara, R.; White, T.; Vaia, R.; Bunning, T. Liquid crystalline polymer cantilever oscillators fueled by light. Soft Matter 2010, 6, 779–783. [Google Scholar] [CrossRef]
- Liang, X.; Chen, Z.; Zhu, L.; Li, K. Light-powered self-excited oscillation of a liquid crystal elastomer pendulum. Mech. Syst. Signal Processing 2022, 163, 108140. [Google Scholar] [CrossRef]
- Xu, T.; Pei, D.; Yu, S.; Zhang, X.; Yi, M.; Li, C. Design of MXene composites with biomimetic rapid and self-oscillating actuation under ambient circumstances. ACS Appl. Mater. Interfaces 2021, 13, 31978–31985. [Google Scholar] [CrossRef]
- Zeng, H.; Lahikainen, M.; Liu, L.; Ahmed, Z.; Wani, O.M.; Wang, M.; Priimagi, A. Light-fuelled freestyle self-oscillators. Nat. Commun. 2019, 10, 5057. [Google Scholar] [CrossRef] [Green Version]
- Cunha, M.; Peeketi, A.R.; Ramgopal, A.; Annabattula, R.K.; Schenning, A. Light-driven continual oscillatory rocking of a polymer film. Chem. Open 2020, 9, 1149–1152. [Google Scholar]
- Graeber, G.; Regulagadda, K.; Hodel, P.; Küttel, C.; Landolf, D.; Schutzius, T.; Poulikakos, D. Leidenfrost droplet trampolining. Nat. Commun. 2021, 12, 1727. [Google Scholar] [CrossRef]
- Kim, Y.; Berg, J.; Crosby, A.J. Autonomous snapping and jumping polymer gels. Nat. Mater. 2021, 20, 1695–1701. [Google Scholar] [CrossRef]
- Xu, P.; Jin, J.; Li, K. Light-powered self-excited bouncing of a liquid crystal elastomer ball. Int. J. Mech. Sci. 2021, 208, 106686. [Google Scholar] [CrossRef]
- Cheng, Q.; Liang, X.; Li, K. Light-powered self-excited motion of a liquid crystal elastomer rotator. Nonlinear Dynam. 2021, 103, 2437–2449. [Google Scholar] [CrossRef]
- Baumann, A.; Sánchez-Ferrer, A.; Jacomine, L.; Martinoty, P.; Houerou, V.; Ziebert, F.; Kulić, I. Motorizing fibers with geometric zero-energy modes. Nat. Mater. 2018, 17, 523–527. [Google Scholar] [CrossRef]
- Li, K.; Chen, Z.; Wang, Z.; Cai, S. Self-sustained eversion or inversion of a thermally responsive torus. Phys. Rev. E 2021, 103, 033004. [Google Scholar] [CrossRef]
- Vantomme, G.; Elands, L.C.M.; Gelebart, A.H.; Meijer, E.W.; Pogromsky, A.Y.; Nijmeijer, H.; Broer, D.J. Coupled liquid crystalline oscillators in Huygens’ synchrony. Nat. Mater. 2021, 20, 1702–1706. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Choi, G.P.T.; Mahadevan, L. Self-excited motions of volatile drops on swellable sheets. Phys. Rev. Lett. 2020, 124, 258002. [Google Scholar] [CrossRef]
- Lv, X.; Yu, M.; Wang, W.; Yu, H. Photothermal pneumatic wheel with high loadbearing capacity. Comp. Comm. 2021, 24, 100651. [Google Scholar] [CrossRef]
- Lendlein, A.; Jiang, H.; Jünger, O.; Langer, R. Light-induced shape-memory polymers. Nature 2005, 434, 879–882. [Google Scholar] [CrossRef]
- Yu, Y.; Li, L.; Liu, E.; Han, X.; Wang, J.; Xie, Y.; Lu, C. Light-driven core-shell fiber actuator based on carbon nanotubes/liquid crystal elastomer for artificial muscle and phototropic locomotion. Carbon 2022, 187, 97–107. [Google Scholar] [CrossRef]
- Ula, S.W.; Traugutt, N.A.; Volpe, R.H.; Patel, R.R.; Yu, K.; Yakacki, C.M. Liquid crystal elastomers, an introduction and review of emerging technologies. Liq. Cryst. Rev. 2018, 6, 78–107. [Google Scholar] [CrossRef]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press London: London, UK, 2007. [Google Scholar]
- Domenici, V.; Milavec, J.; Bubnov, A.; Pociecha, D.; Zupančič, B.; Rešetič, A.; Hamplová, V.; Gorecka, E.; Zalar, B. Effect of co-monomers’ relative concentration on self-assembling behaviour of side-chain liquid crystalline elastomers. RSC Adv. 2014, 4, 44056–44064. [Google Scholar] [CrossRef]
- Domenici, V.; Milavec, J.; Zupančič, B.; Bubnov, A.; Hamplová, V.; Zalar, B. Brief overview on 2H NMR studies of polysiloxane-based side-chain nematic elastomers. Magn. Reson. Chem. 2014, 52, 649–655. [Google Scholar] [CrossRef]
- Milavec, J.; Rešetič, A.; Bubnov, A.; Zalar, B.; Domenici, V. Dynamic investigations of liquid crystalline elastomers and their constituents by 2H NMR spectroscopy. Liq. Cryst. 2018, 45, 2158–2173. [Google Scholar] [CrossRef]
- Rešetič, A.; Milavec, J.; Domenici, V.; Zupančič, B.; Zalar, B.; Zalar, B. Deuteron NMR investigation on orientational order parameter in polymer dispersed liquid crystal elastomers. Phys. Chem. Chem. Phys. 2020, 22, 23064–23072. [Google Scholar] [CrossRef]
- Parrany, M. Nonlinear light-induced vibration behavior of liquid crystal elastomer beam. Int. J. Mech. Sci. 2018, 136, 179–187. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, Y. Photomechanical vibration energy harvesting based on liquid crystal elastomer cantilever. Smart Mater. Struct. 2019, 28, 075017. [Google Scholar] [CrossRef]
- Haldane, D.W.; Plecnik, M.M.; Yim, J.K.; Fearing, R.S. Robotic vertical jumping agility via series-elastic power modulation. Sci. Robot. 2016, 1, eaag2048. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Wang, X.; Dong, B.; Sitti, M. In-air fast response and high speed jumping and rolling of a light-driven hydrogel actuator. Nat. Comm. 2020, 11, 3988. [Google Scholar] [CrossRef]
- Sternad, D.; Duarte, M.; Katsumata, H.; Schaal, S. Dynamics of a bouncing ball in human performance. Phys. Rev. E 2000, 63, 011902. [Google Scholar] [CrossRef] [Green Version]
- Halev, A.; Harris, D.M. Bouncing ball on a vibrating periodic surface. Chaos 2018, 28, 096103. [Google Scholar] [CrossRef] [PubMed]
- Shanahan, M.E.R. A novel test for the appraisal of solid/solid interfacial interactions. J. Adhesion 1997, 65, 15–29. [Google Scholar] [CrossRef]
- Yu, Y.; Nakano, M.; Ikeda, T. Directed bending of a polymer film by light. Nature 2003, 425, 425145a. [Google Scholar] [CrossRef] [PubMed]
- Ge, F.J.; Yang, R.; Tong, X.; Camerel, F.; Zhao, Y. A multifunctional dyedoped liquid crystal polymer actuator: Light-guided transportation, turning in locomotion, and autonomous motion. Angew. Chem. Int. Ed. 2018, 130, 11932–11937. [Google Scholar] [CrossRef]
- Camacho, L.M.; Finkelmann, H.; Palffy, M.P.; Shelley, M. Fast liquid-crystal elastomer swims into the dark. Nat. Mater. 2004, 5, 307–310. [Google Scholar] [CrossRef]


| Parameter | Definition | Value | Units |
|---|---|---|---|
| Contraction coefficient | 0.2~0.5 | / | |
| trans-to-cis thermal relaxation time | 1~100 | ms | |
| Light intensity | 0~1000 | kW/m2 | |
| Light-absorption constant | 0.0003 | m2/(s∙W) | |
| Reference radius of LCE balloon | 0~5 | mm | |
| Volume of the LCE balloon | 0~2 | mm3 | |
| Mass of LCE balloon | 0~2 | mg | |
| Elastic modulus of LCE balloon | 1~10 | MPa | |
| Amount of substance of the gas | 0~10−7 | mol | |
| Ideal gas constant | 8.314 | J/(mol·K) | |
| Ambient pressure | 0~0.1 | MPa | |
| Damping coefficient | 0~0.001 | kg/s | |
| Gravitational acceleration | 10 | m/s2 |
| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Value | 0~102 | 0~20 | 0~104 | 0~107 | 0~50 | 102~107 | 10−2~102 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, D.; Jin, J.; Dai, Y.; Xu, P.; Li, K. Self-Jumping of a Liquid Crystal Elastomer Balloon under Steady Illumination. Polymers 2022, 14, 2770. https://doi.org/10.3390/polym14142770
Ge D, Jin J, Dai Y, Xu P, Li K. Self-Jumping of a Liquid Crystal Elastomer Balloon under Steady Illumination. Polymers. 2022; 14(14):2770. https://doi.org/10.3390/polym14142770
Chicago/Turabian StyleGe, Dali, Jielin Jin, Yuntong Dai, Peibao Xu, and Kai Li. 2022. "Self-Jumping of a Liquid Crystal Elastomer Balloon under Steady Illumination" Polymers 14, no. 14: 2770. https://doi.org/10.3390/polym14142770







