Faraday Instability in Viscous Fluids Covered with Elastic Polymer Films
Abstract
1. Introduction
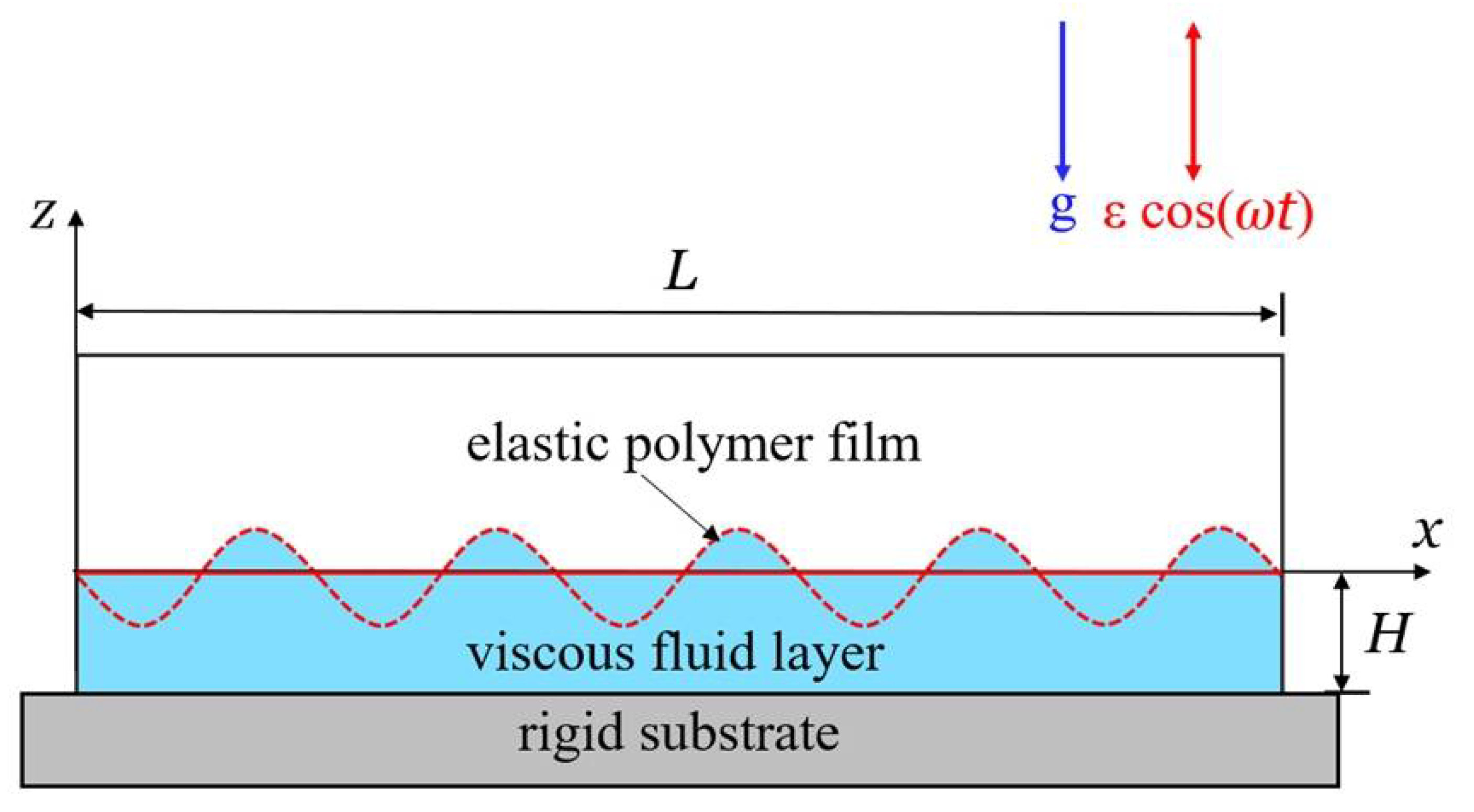
2. Model and Formulation
2.1. Governing Equations
2.2. Stability Analysis
2.3. Solution
3. Results and Discussion
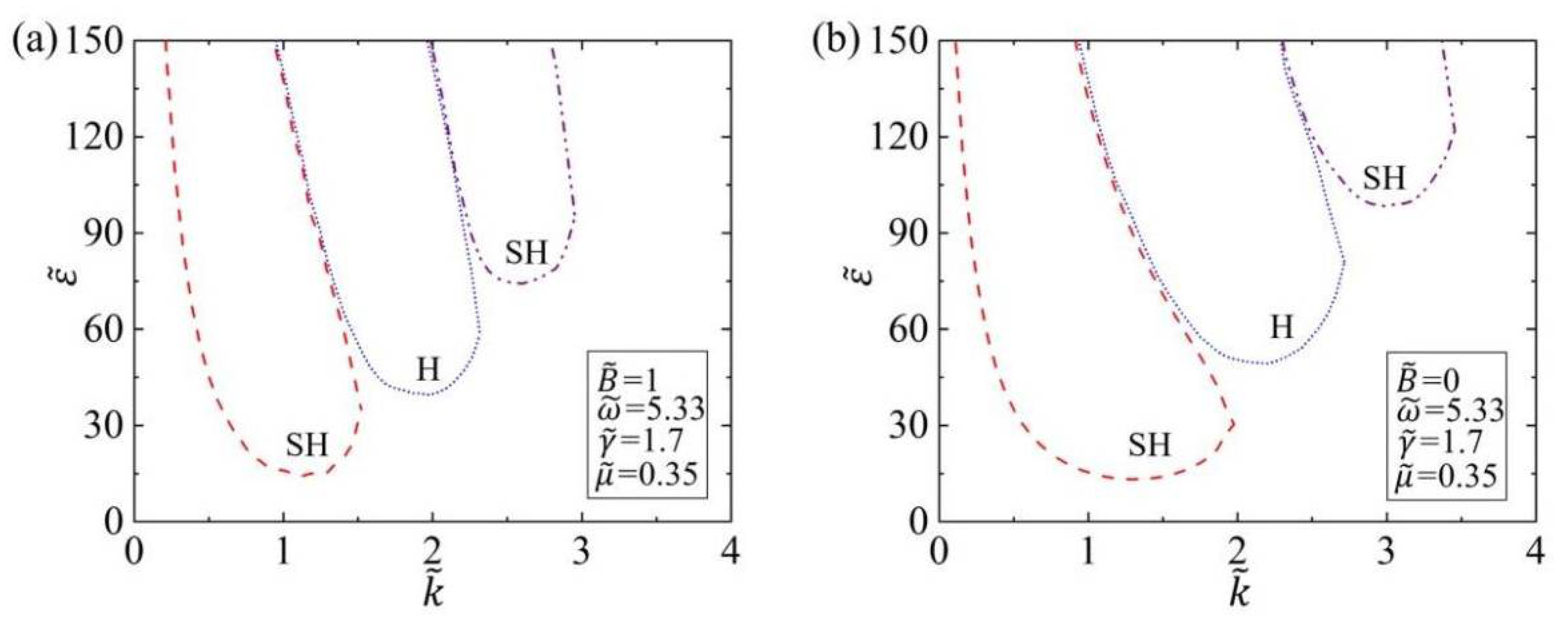
3.1. Stability Criterion
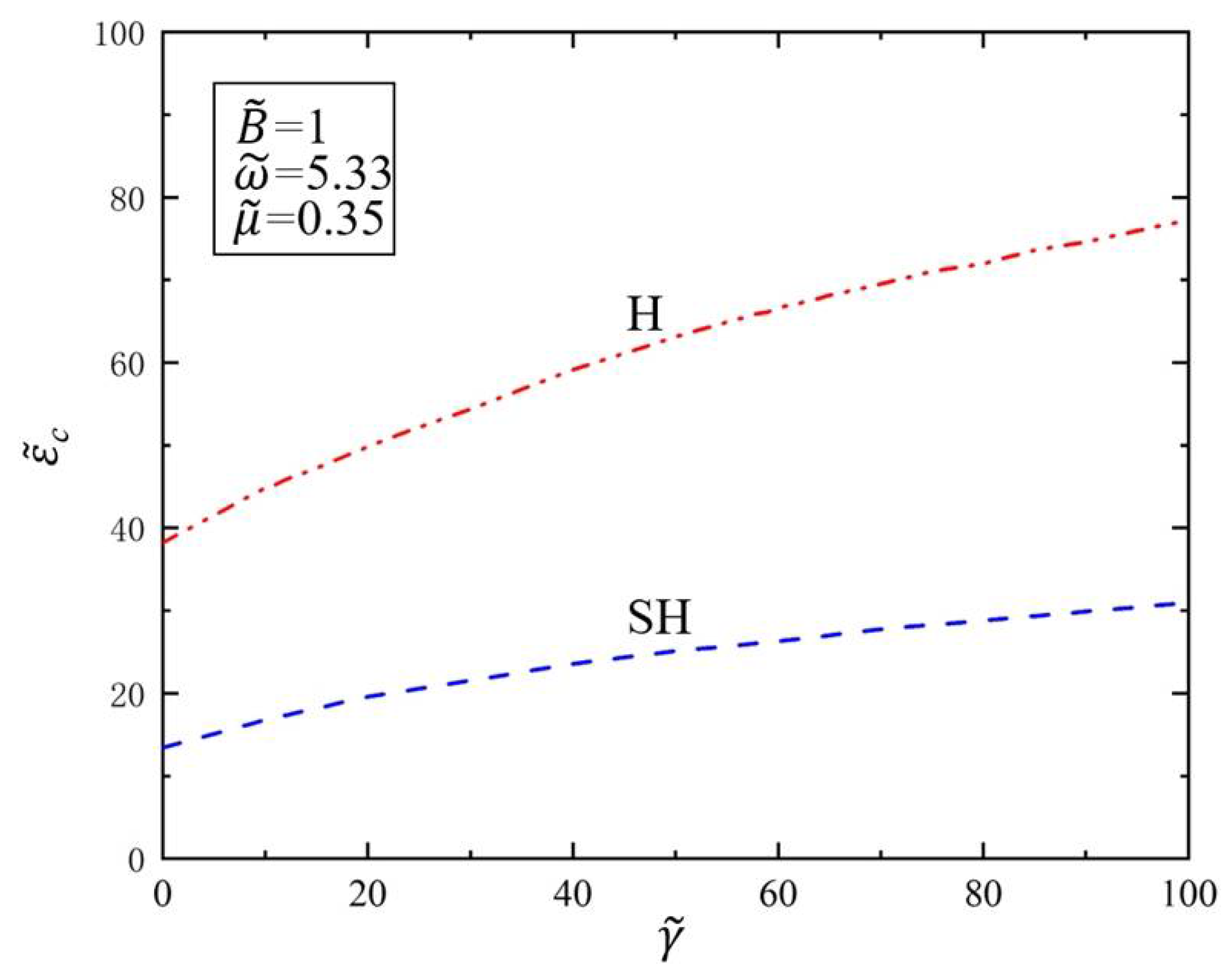
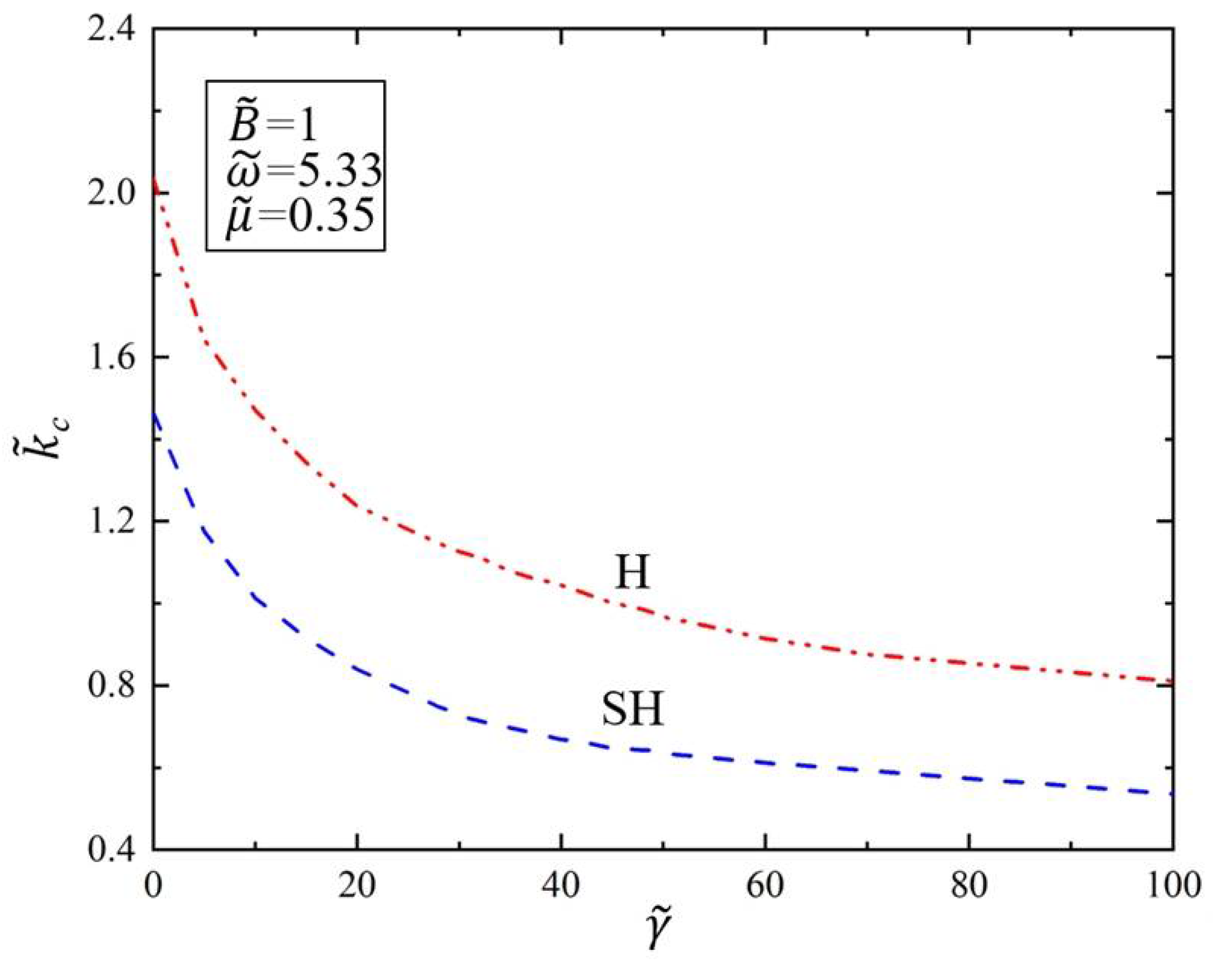
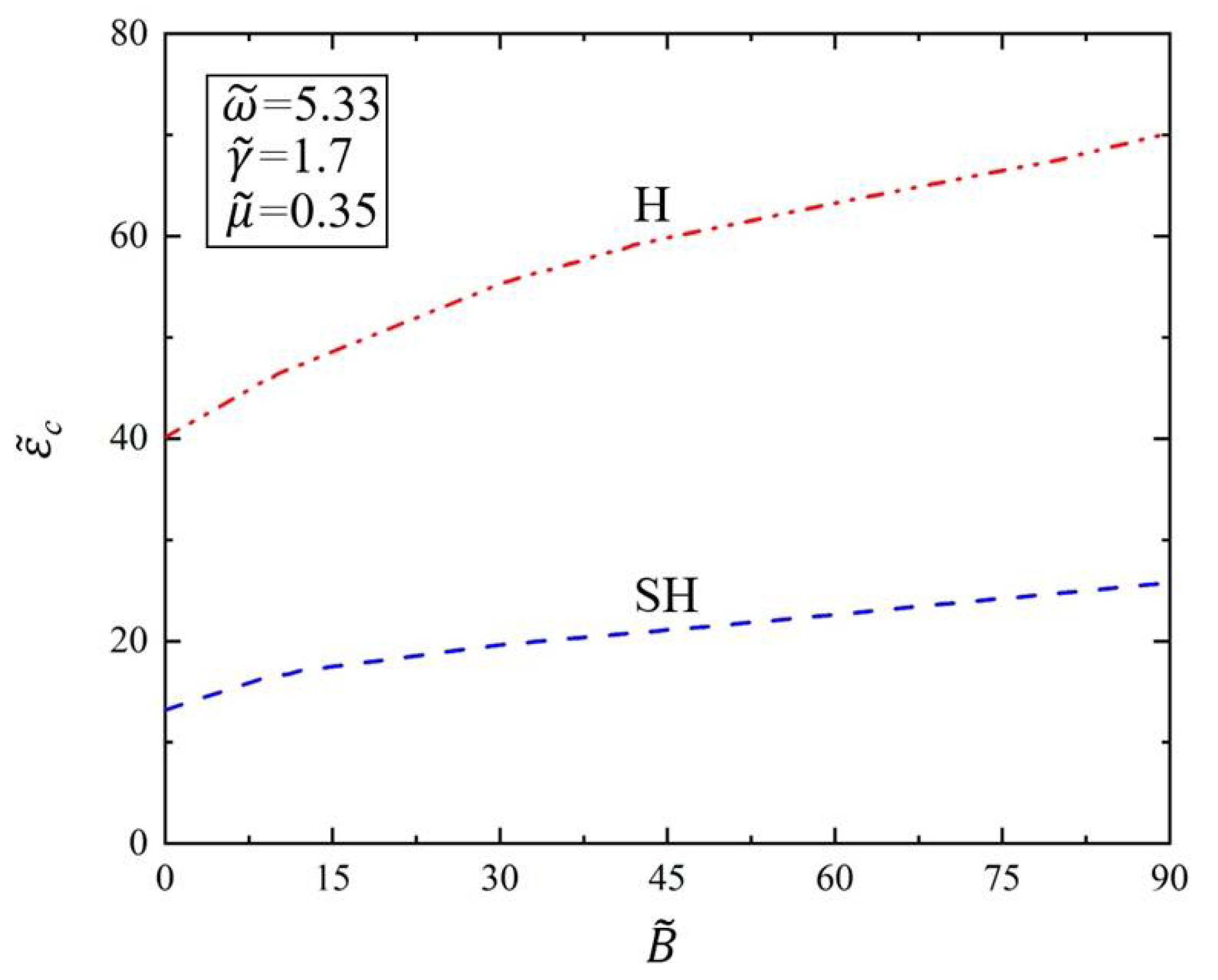
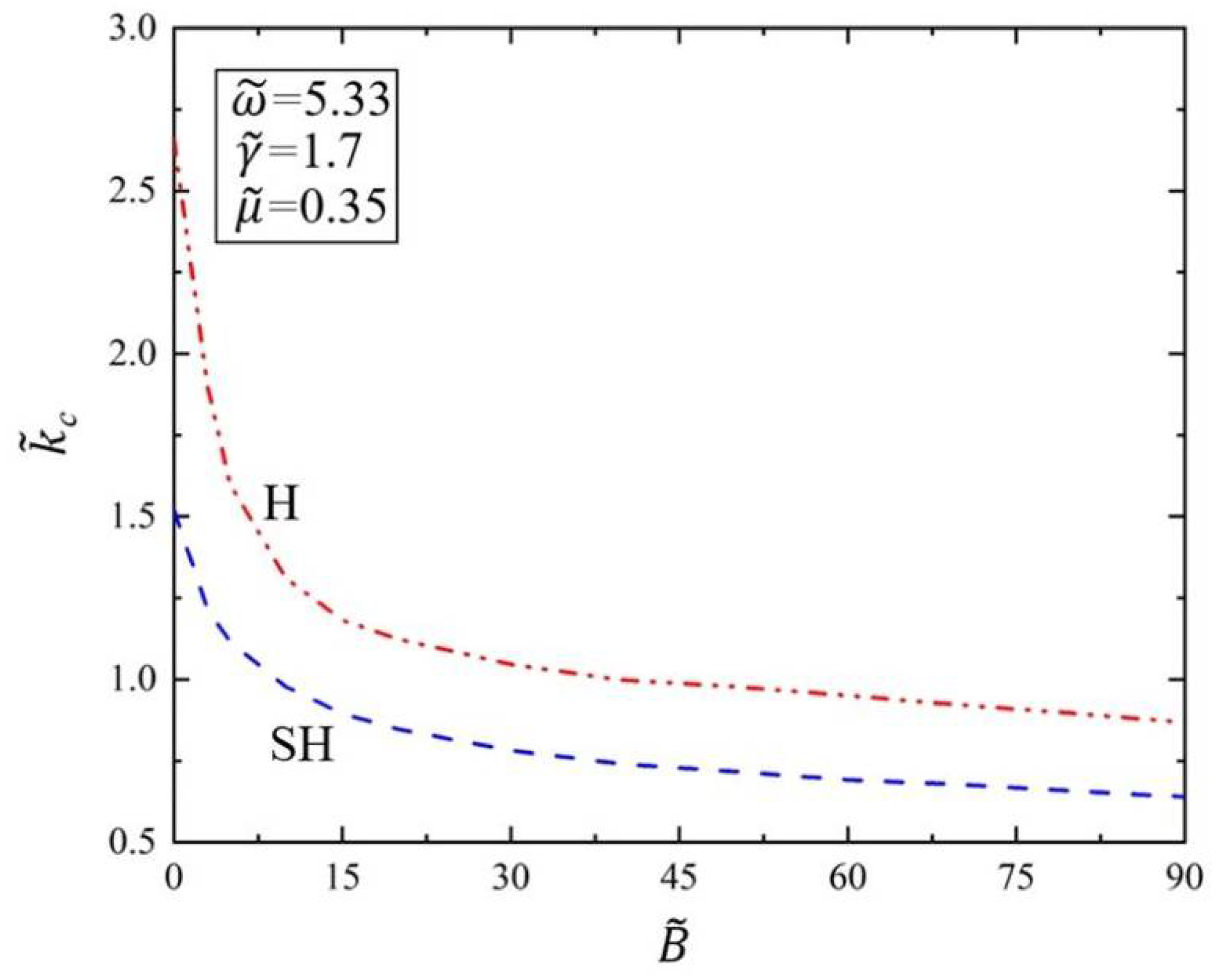
3.2. Effect of Surface Tension and Bending Stiffness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Faraday, M. On a Peculiar Class of Acoustical Figures; and on Certain Forms Assumed by Groups of Particles upon Vibrating Elastic Surfaces. Phil. Trans. R. Soc. Lond. 1831, 121, 299–340. [Google Scholar]
- Rayleigh, L. On the crispations of fluid resting upon a vibrating support. Phil. Mag. 1883, 16, 50–58. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Ursell, F.J. The stability of the plane free surface of a liquid in vertical periodic motion. Proc. Roy. Soc. A 1954, 225, 505–515. [Google Scholar]
- Rajchenbach, J.; Clamond, D. Faraday waves: Their dispersion relation, nature of bifurcation and wavenumber selection revisited. J. Fluid. Mech. 2015, 777, R2. [Google Scholar] [CrossRef]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Francois, N.; Xia, H.; Punzmann, H.; Ramsden, S.; Shats, M. Three-Dimensional Fluid Motion in Faraday Waves: Creation of Vorticity and Generation of Two-Dimensional Turbulence. Phys. Rev. X 2014, 4, 021021. [Google Scholar] [CrossRef]
- Shao, X.; Saylor, J.R.; Bostwick, J.B. Extracting the surface tension of soft gels from elastocapillary wave behavior. Soft Matter 2018, 14, 7347–7353. [Google Scholar] [CrossRef]
- Tarasov, N.; Perego, A.M.; Churkin, D.V.; Staliunas, K.; Turitsyn, S.K. Mode-locking via dissipative Faraday instability in a fiber laser. Nat. Commun. 2016, 7, 12441. [Google Scholar] [CrossRef]
- Huang, S.-W.; Vinod, A.K.; Yang, J.; Yu, M.; Wong, C.W. Multispectral optical frequency comb based on microresonator Faraday instability. In Proceedings of the 2017 IEEE Photonics Conference (IPC), Orlando, FL, USA, 1–5 October 2017; pp. 343–344. [Google Scholar]
- Domino, L.; Tarpin, M.; Patinet, S.; Eddi, A. Faraday wave lattice as an elastic metamaterial. Phys. Rev. E 2016, 93, 050202. [Google Scholar] [CrossRef]
- Francois, N.; Xia, H.; Punzmann, H.; Fontana, P.W.; Shats, M. Wave-based liquid-interface metamaterials. Nat. Commun. 2017, 8, 14325. [Google Scholar] [CrossRef]
- Sheldrake, M.; Sheldrake, R. Determinants of Faraday Wave-Patterns in Water Samples Oscillated Vertically at a Range of Frequencies from 50–200 Hz. Water 2017, 9, 1–27. [Google Scholar]
- Takagi, S.; Krinsky, V.; Pumir, A.; Frelin, C. The use of Faraday instability to produce defined topological organization in cultures of mammalian cells. Int. J. Bifurc. Chaos 2002, 12, 2009–2019. [Google Scholar] [CrossRef]
- Hong, S.-H.; Gorce, J.B.; Punzmann, H.; Francois, N.; Xia, H. Surface waves control bacterial attachment and formation of biofilms in thin layers. Sci. Adv. 2020, 6, aaz9386. [Google Scholar] [CrossRef] [PubMed]
- Maksymov, I.S.; Pototsky, A. Excitation of Faraday-like body waves in vibrated living earthworms. Sci. Rep. 2020, 10, 8564. [Google Scholar] [CrossRef] [PubMed]
- Mitra, O.; Callaham, M.A.; Smith, M.L.; Yack, J.E. Grunting for worms: Seismic vibrations cause Diplocardia earthworms to emerge from the soil. Biol. Lett. 2008, 5, 16–19. [Google Scholar] [CrossRef]
- Blakemore, R.; Hochkirch, A. Restore earthworms to rebuild topsoil. Nature 2017, 545, 30. [Google Scholar] [CrossRef]
- Lacoste, M.; Ruiz, S.; Or, D. Listening to earthworms burrowing and roots growing-acoustic signatures of soil biological activity. Sci. Rep. 2018, 8, 10236. [Google Scholar] [CrossRef]
- Ruiz, S.A.; Or, D. Biomechanical limits to soil penetration by earthworms: Direct measurements of hydroskeletal pressures and peristaltic motions. J. R. Soc. Interface 2018, 15, 20180127. [Google Scholar] [CrossRef]
- Emelianov, S. Light, sound, nanobubbles: New approach to contrast-enhanced ultrasound and photoacoustic imaging. J. Acoust. Soc. Am. 2019, 145, 1779. [Google Scholar] [CrossRef]
- Ballmann, C.W.; Meng, Z.; Yakovlev, V.V. Nonlinear Brillouin spectroscopy: What makes it a better tool for biological viscoelastic measurements. Biomed. Opt. Express 2019, 10, 1750–1759. [Google Scholar] [CrossRef]
- Blamey, J.; Yeo, L.Y.; Friend, J.R. Microscale Capillary Wave Turbulence Excited by High Frequency Vibration. Langmuir 2013, 29, 3835–3845. [Google Scholar] [CrossRef] [PubMed]
- Zinin, P.V.; Allen, J.S., III; Levin, V.M. Mechanical resonances of bacteria cells. Phys. Rev. E 2006, 72, 061907. [Google Scholar] [CrossRef] [PubMed]
- Ivanova, E.P.; Hasan, J.; Webb, H.K.; Gervinskas, G.; Crawfoed, R.J. Bactericidal activity of black silicon. Nat. Commun. 2013, 4, 2838. [Google Scholar] [CrossRef] [PubMed]
- Boyd, B.; Suslov, S.A.; Becker, S.; Greentree, A.D.; Maksymov, I.S. Beamed UV sonoluminescence by aspherical air bubble collapse near liquid-metal microparticles. Sci. Rep. 2020, 10, 1501. [Google Scholar] [CrossRef] [PubMed]
- Lyubimova, T.; Ivantsov, A.; Garrabos, Y.; Lecoutre, C.; Beysens, D. Faraday waves on band pattern under zero gravity conditions. Phys. Rev. Fluids 2019, 4, 064001. [Google Scholar] [CrossRef]
- Lioubashevski, O.; Arbell, H.; Fineberg, J. Dissipative Solitary States in Driven Surface Waves. Phys. Rev. Lett. 1996, 76, 3959. [Google Scholar] [CrossRef] [PubMed]
- Lioubashevski, O.; Fineberg, J.; Tuckerman, L.S. Scaling of the transition to parametrically driven surface waves in highly dissipative systems. Phys. Rev. E 1997, 55, R3832–R3835. [Google Scholar] [CrossRef]
- Kumar, K. Linear theory of Faraday instability in viscous liquids. Proc. R. Soc. Lond. A 1996, 452, 1113–1126. [Google Scholar]
- Kumar, K.; Tuckerman, L.S. Parametric instability of the interface between two fluids. J. Fluid Mech. 1994, 279, 49–68. [Google Scholar] [CrossRef]
- Beyer, J.; Friedrich, R. Faraday instability: Linear analysis for viscous fluids. Phys. Rev. E 1995, 51, 1162–1168. [Google Scholar] [CrossRef]
- Christiansen, B.; Alstrom, P.; Levinsen, M.T. Ordered capillary-wave states: Quasicrystals, hexagons, and radial waves. Phys. Rev. Lett. 1992, 68, 2157–2160. [Google Scholar] [CrossRef]
- Kudrolli, A.; Gullob, J.P. Patterns and spatiotemporal chaos in parametrically forced surface waves: A systematic survey at large aspect ratio. J. Physica. D 1996, 97, 133–154. [Google Scholar] [CrossRef]
- Wagner, C.; Müller, H.W.; Knorr, K. Faraday Waves on a Viscoelastic Liquid. Phys. Rev. Lett. 1999, 83, 308–311. [Google Scholar] [CrossRef]
- Chen, P.; Viñals, J. Amplitude equation and pattern selection in Faraday waves. Phys. Rev. E 1999, 60, 559–570. [Google Scholar] [CrossRef]
- Zhang, W.; Viñals, J. Square patterns and quasipatterns in weakly damped Faraday waves. Phys. Rev. E 1996, 53, 4283–4286. [Google Scholar] [CrossRef]
- Raynal, F.; Kumar, S.; Fauve, S. Faraday instability with a polymer solution. Eur. Phys. J. B 1999, 9, 175–178. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Z.; Güven, S.; Tasoglu, S.; Ganesan, A.V.; Weng, A.; Demirci, U. Microscale Assembly Directed by Liquid-based Template. Adv. Mater. 2014, 26, 5936–5941. [Google Scholar] [CrossRef]
- Engels, P.; Atherton, C.; Hoefer, M.A. Observation of Faraday Waves in a Bose-Einstein Condensate. Phys. Rev. Lett. 2007, 98, 2–5. [Google Scholar] [CrossRef]
- Nguyen, J.H.V.; Tsatsos, M.C.; Luo, D.; Lode, A.U.J.; Telles, G.D.; Bagnato, V.S.; Hulet, R.G. Parametric Excitation of a Bose-Einstein Condensate: From Faraday Waves to Granulation. Phys. Rev. X 2019, 9, 11052. [Google Scholar] [CrossRef]
- Gross, C.; Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 2017, 357, 995–1001. [Google Scholar] [CrossRef]
- Müller, H.W.; Zimmermann, W. Faraday instability in a linear viscoelastic fluid. Europhys. Lett. 1999, 45, 169. [Google Scholar] [CrossRef]
- Bevilacqua, G.; Shao, X.; Saylor, J.R.; Bostwick, J.B.; Ciarletta, P. Faraday waves in soft elastic solids. Proc. R. Soc. A-Math. Phy. 2020, 476, 2241. [Google Scholar] [CrossRef] [PubMed]
- Douady, S. Experimental study of the Faraday instability. J. Fluid Mech. 1990, 221, 383–409. [Google Scholar] [CrossRef]
- Lam, K.D.N.T.; Caps, H. Effect of a capillary meniscus on the Faraday instability threshold. Eur. Phys. J. E 2011, 34, 112. [Google Scholar]
- Douady, S.; Fauve, S. Pattern Selection in Faraday Instability. Europhys. Lett. 1988, 6, 221. [Google Scholar] [CrossRef]
- Wright, P.H.; Saylor, J.R. Patterning of particulate films using Faraday waves. Rev. Sci. Instrum. 2003, 74, 4063–4070. [Google Scholar] [CrossRef]
- Mahr, T.; Rehberg, I. Magnetic Faraday-Instability. Europhys. Lett. 1998, 43, 23–28. [Google Scholar] [CrossRef][Green Version]
- Samanta, A. Effect of porous layer on the Faraday instability in viscous liquid. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 2239. [Google Scholar] [CrossRef]
- Kumar, S.; Matar, O.K. On the Faraday instability in a surfactant-covered liquid. Phys. Fluids 2004, 16, 39. [Google Scholar] [CrossRef]
- Giavedoni, M.D.; Ubal, S. Onset of Faraday Waves in a Liquid Layer Covered with a Surfactant with Elastic and Viscous Properties. Ind. Eng. Chem. Res. 2007, 46, 5228–5237. [Google Scholar] [CrossRef]
- Kharbedia, M.; Caselli, N.; Herráez-Aguilar, D.; López-Menéndez, H.; Enciso, E.; Santiago, J.A.; Monroy, F. Moulding hydrodynamic 2D-crystals upon parametric Faraday waves in shear-functionalized water surfaces. Nat. Commun. 2021, 12, 1130. [Google Scholar] [CrossRef] [PubMed]
- Bahri, K.; Eslami, H.; Müller-Plathe, F. Self-Assembly of Model Triblock Janus Colloidal Particles in Two Dimensions. J. Chem. Theory Comput. 2022, 18, 1870–1882. [Google Scholar] [CrossRef] [PubMed]
- Eslami, H.; Gharibi, A.; Müller-Plathe, F. Mechanisms of nucleation and solid–solid-phase transitions in Triblock Janus Assemblies. J. Chem. Theory Comput. 2021, 17, 1742–1754. [Google Scholar] [CrossRef] [PubMed]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Huang, R.; Suo, Z. Wrinkling of a compressed elastic film on a viscous layer. J. Appl. Phys. 2002, 91, 1135–1142. [Google Scholar] [CrossRef]
- Zhou, T.; Wu, Z.; Das, S.; Eslami, H.; Müller-Plathe, F. How Ethanolic Disinfectants Disintegrate Coronavirus Model Membranes: A Dissipative Particle Dynamics Simulation Study. J. Chem. Theory Comput. 2022, 18, 2597–2615. [Google Scholar] [CrossRef]


| Parameter | Definition | Value | Units |
|---|---|---|---|
| Thickness of viscous fluid layer | |||
| Thickness of the elastic polymer film | |||
| Surface tension | |||
| Driving frequency | |||
| Kinematic viscosity | |||
| Bending stiffness |
| Parameter | ||||
| Value |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Song, W.; Ma, G.; Li, K. Faraday Instability in Viscous Fluids Covered with Elastic Polymer Films. Polymers 2022, 14, 2334. https://doi.org/10.3390/polym14122334
Liu J, Song W, Ma G, Li K. Faraday Instability in Viscous Fluids Covered with Elastic Polymer Films. Polymers. 2022; 14(12):2334. https://doi.org/10.3390/polym14122334
Chicago/Turabian StyleLiu, Junxiu, Wenqiang Song, Gan Ma, and Kai Li. 2022. "Faraday Instability in Viscous Fluids Covered with Elastic Polymer Films" Polymers 14, no. 12: 2334. https://doi.org/10.3390/polym14122334
APA StyleLiu, J., Song, W., Ma, G., & Li, K. (2022). Faraday Instability in Viscous Fluids Covered with Elastic Polymer Films. Polymers, 14(12), 2334. https://doi.org/10.3390/polym14122334








