Flow Behaviors of Polymer Solution in a Lid-Driven Cavity
Abstract
:1. Introduction
2. Methodology
2.1. Governing Equations
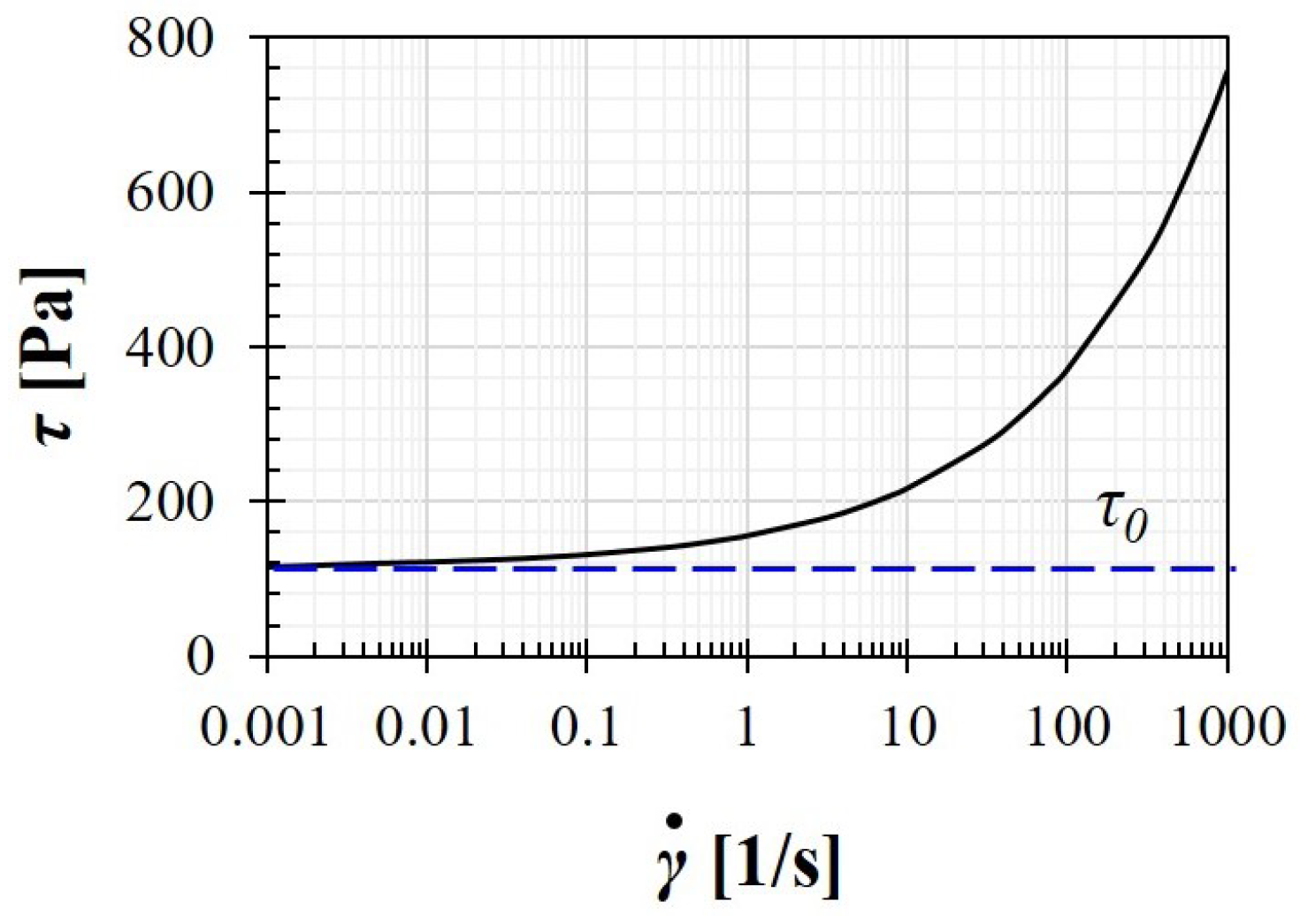
2.2. Fluid Materials
2.3. Computational Approach
2.3.1. Regularization Scheme
2.3.2. Computational Implementation
3. Results and Discussion
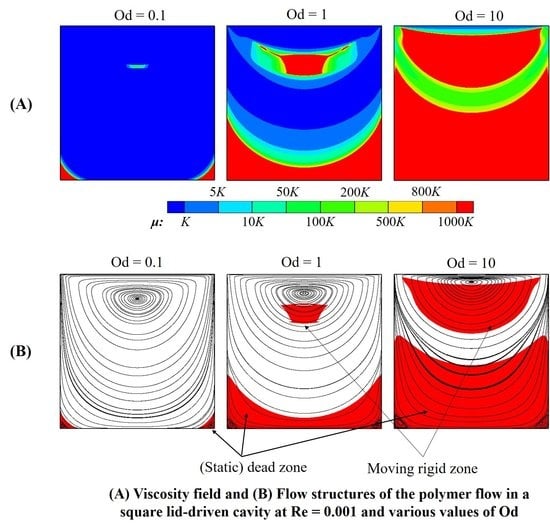
3.1. Polymer Flow Morphology
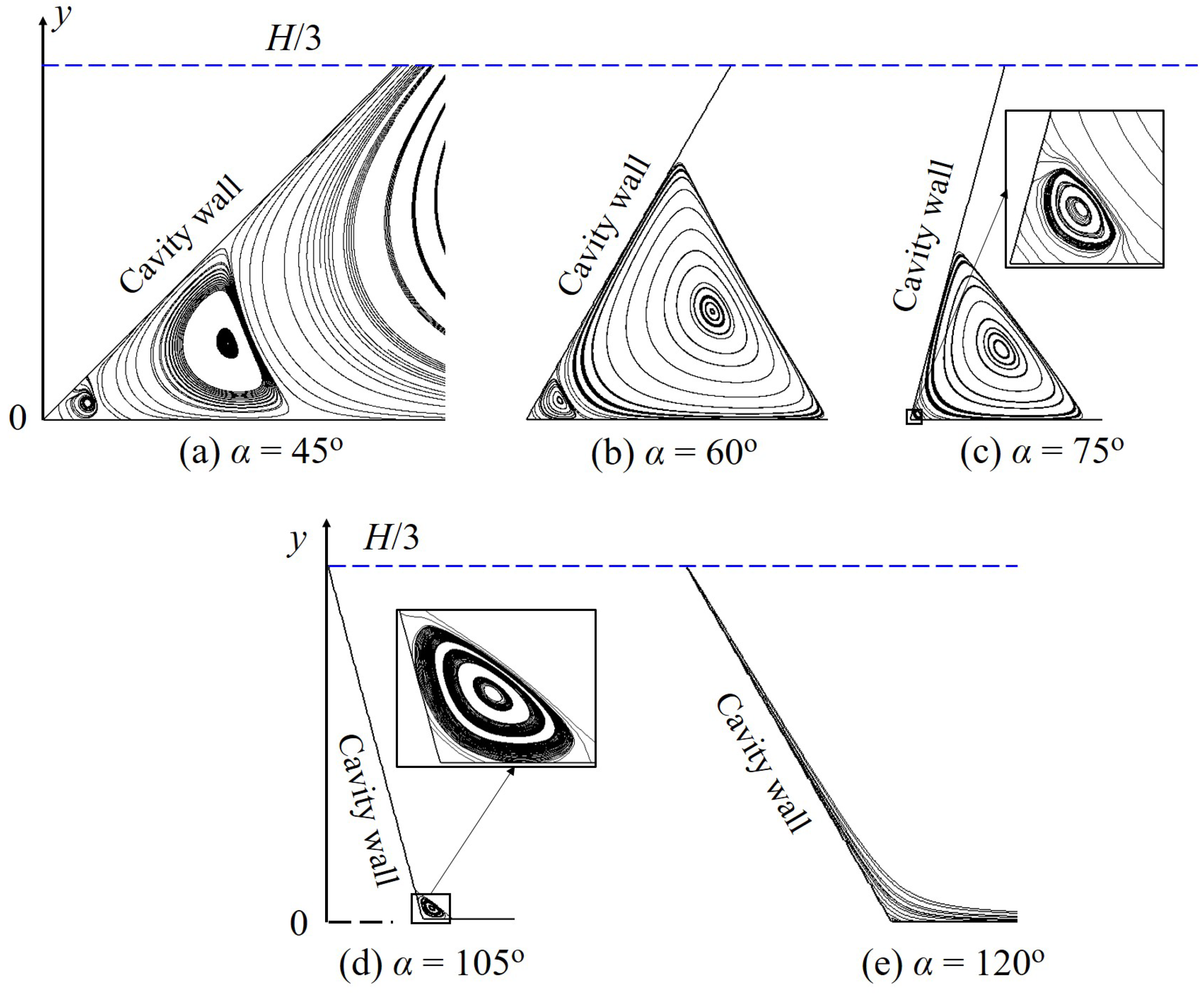
3.2. Cavity Configurations
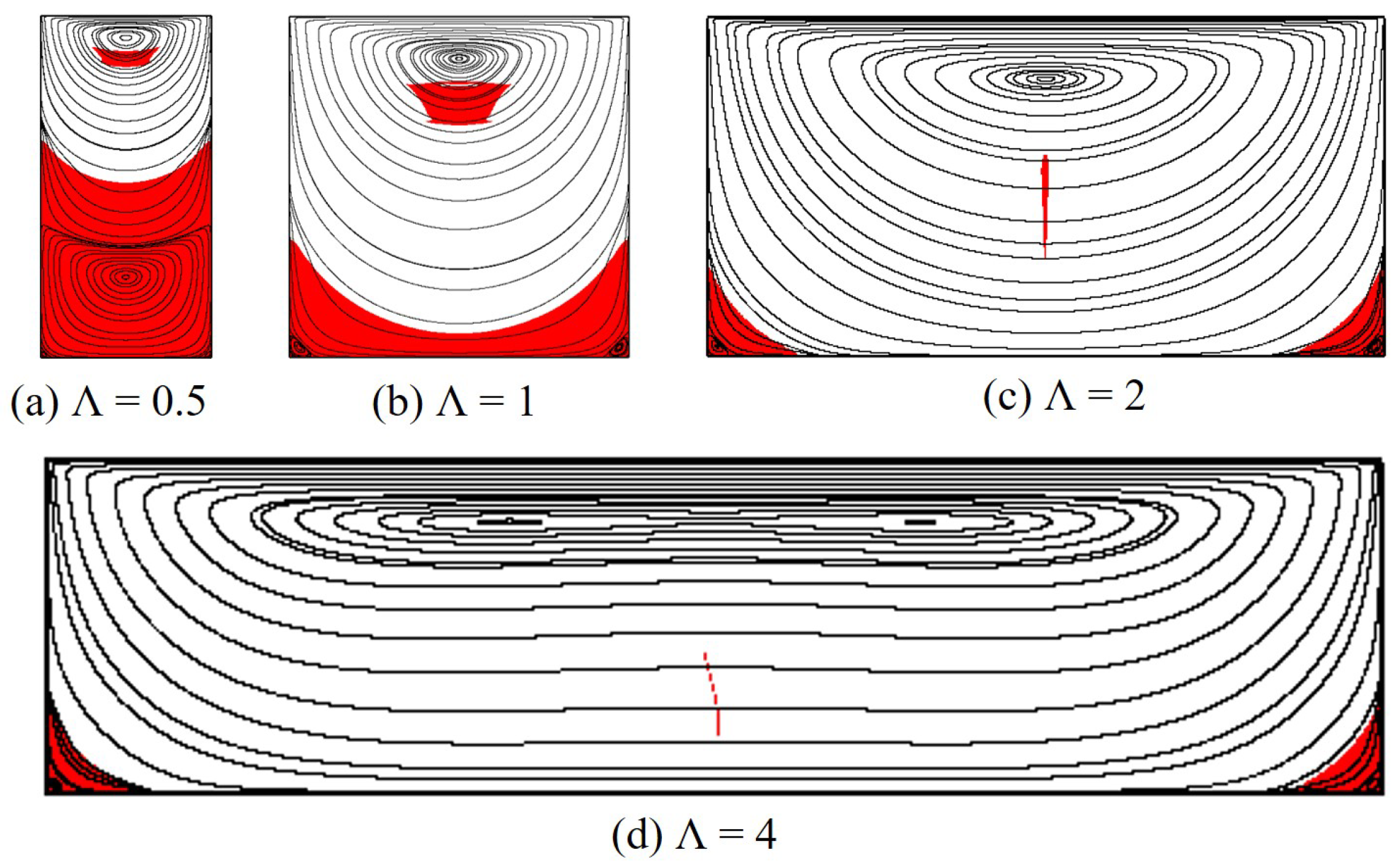
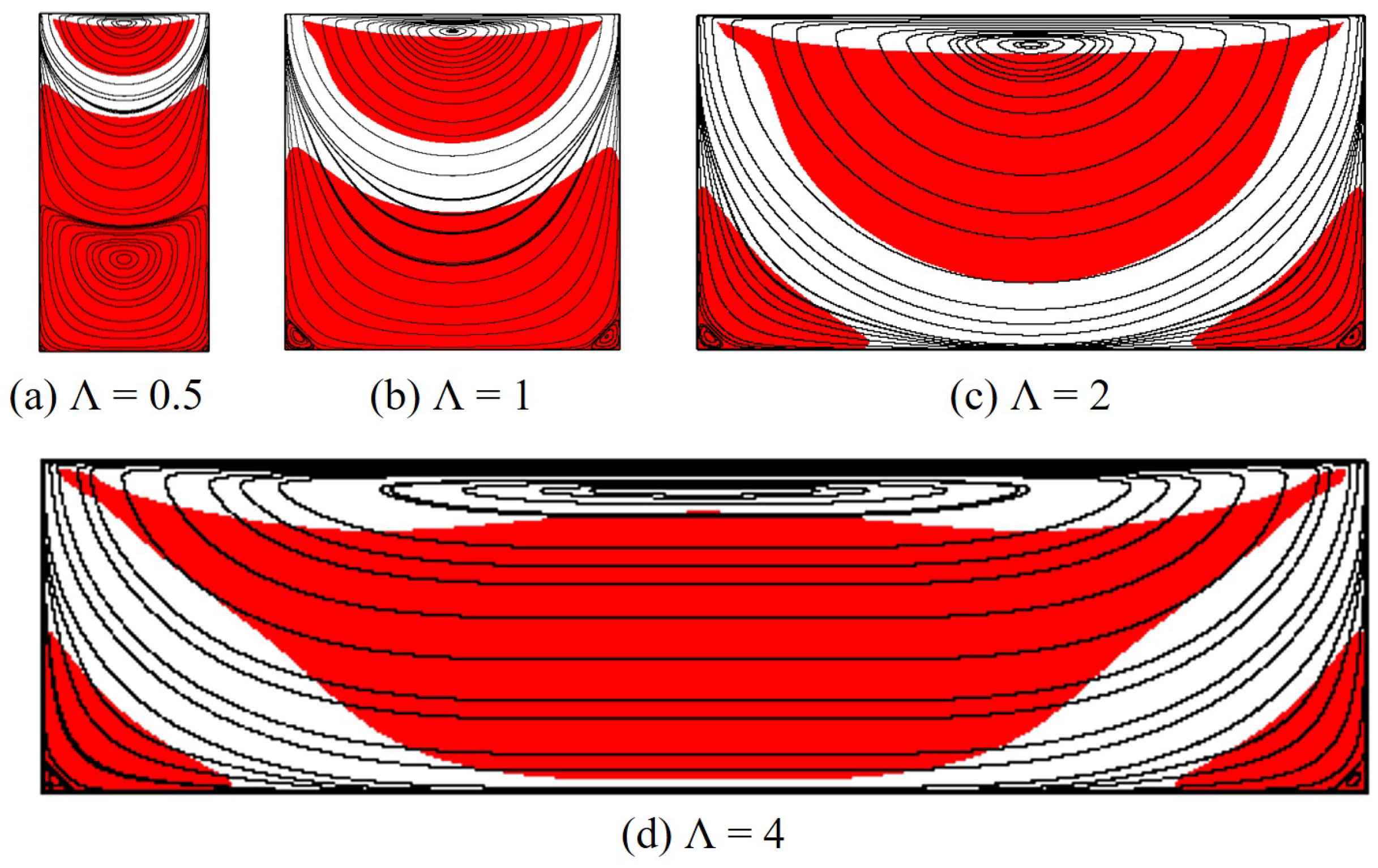
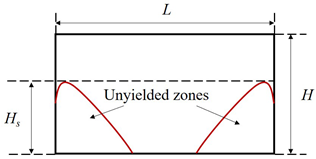
3.2.1. Rectangular cavity
3.2.2. Skewed Cavity
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zdanski, P.; Ortega, M.; Fico, N.G., Jr. Numerical study of the flow over shallow cavities. Comput. Fluids 2003, 32, 953–974. [Google Scholar] [CrossRef]
- Chella, R.; Viñals, J. Mixing of a two-phase fluid by cavity flow. Phys. Rev. E 1996, 53, 3832. [Google Scholar] [CrossRef] [PubMed]
- Gaskell, P.; Summers, J.; Thompson, H.; Savage, M. Creeping flow analyses of free surface cavity flows. Theor. Comput. Fluid Dyn. 1996, 8, 415–433. [Google Scholar] [CrossRef]
- Shankar, P.; Deshpande, M. Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 2000, 32, 93–136. [Google Scholar] [CrossRef] [Green Version]
- Ghia, U.; Ghia, K.N.; Shin, C.T. High-Re Solutions for Incompressible Flow Using the Navier-Stokes Equations and a Multigrid Method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Mochizuki, O.; Yamabe, H.; Yamada, H. Flow in a two-dimensional square cavity: A comparison between flow visualization experiment and numerical calculations. Bull. JSME 1986, 29, 4103–4106. [Google Scholar] [CrossRef]
- Xu, R.; Stansby, P.; Laurence, D. Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 2009, 228, 6703–6725. [Google Scholar] [CrossRef]
- Khorasanizade, S.; Sousa, J.M. A detailed study of lid-driven cavity flow at moderate Reynolds numbers using Incompressible SPH. Int. J. Numer. Methods Fluids 2014, 76, 653–668. [Google Scholar] [CrossRef]
- Zheng, E.; Rudman, M.; Kuang, S.; Chryss, A. Turbulent coarse-particle non-Newtonian suspension flow in a pipe. Int. J. Multiph. Flow 2021, 142, 103698. [Google Scholar] [CrossRef]
- Yan, Z.; Li, Z.; Cheng, S.; Wang, X.; Zhang, L.; Zheng, L.; Zhang, J. From Newtonian to non-Newtonian fluid: Insight into the impact of rheological characteristics on mineral deposition in urine collection and transportation. Sci. Total Environ. 2022, 823, 153532. [Google Scholar] [CrossRef]
- Hato, M.J.; Zhang, K.; Ray, S.S.; Choi, H.J. Rheology of organoclay suspension. Colloid Polym. Sci. 2011, 289, 1119–1125. [Google Scholar] [CrossRef]
- Spearman, J. An examination of the rheology of flocculated clay suspensions. Ocean Dyn. 2017, 67, 485–497. [Google Scholar] [CrossRef]
- Lev, E.; Spiegelman, M.; Wysocki, R.J.; Karson, J.A. Investigating lava flow rheology using video analysis and numerical flow models. J. Volcanol. Geotherm. Res. 2012, 247, 62–73. [Google Scholar] [CrossRef] [Green Version]
- Harris, A.J.; Rowland, S.K. Lava flows and rheology. In The Encyclopedia of Volcanoes; Elsevier: Amsterdam, The Netherlands, 2015; pp. 321–342. [Google Scholar]
- Ghannam, M.T.; Hasan, S.W.; Abu-Jdayil, B.; Esmail, N. Rheological properties of heavy & light crude oil mixtures for improving flowability. J. Pet. Sci. Eng. 2012, 81, 122–128. [Google Scholar]
- Souas, F.; Safri, A.; Benmounah, A. On the rheological behavior of light crude oil: A review. Pet. Sci. Technol. 2020, 38, 849–857. [Google Scholar] [CrossRef]
- Souas, F.; Safri, A.; Benmounah, A. A review on the rheology of heavy crude oil for pipeline transportation. Pet. Res. 2021, 6, 116–136. [Google Scholar] [CrossRef]
- Guo, L.; Kawano, Y.; Zhang, S.; Suzuki, T.; Morita, K.; Fukuda, K. Numerical simulation of rheological behavior in melting metal using finite volume particle method. J. Nucl. Sci. Technol. 2010, 47, 1011–1022. [Google Scholar] [CrossRef]
- Jeyakumar, M.; Hamed, M.; Shankar, S. Rheology of liquid metals and alloys. J. Non-Newton. Fluid Mech. 2011, 166, 831–838. [Google Scholar] [CrossRef]
- Lower, G.W.; Walker, W.C.; Zettlemoyer, A.C. The rheology of printing inks. II. temperature control studies in the rotational viscometer. J. Colloid Sci. 1953, 8, 116–129. [Google Scholar] [CrossRef]
- Zettlemoyer, A.; Lower, G. The rheology of printing inks. III. Studies of simple dispersions. J. Colloid Sci. 1955, 10, 29–45. [Google Scholar] [CrossRef]
- Snabre, P.; Mills, P. Rheology of concentrated suspensions of viscoelastic particles. Colloids Surf. A Physicochem. Eng. Asp. 1999, 152, 79–88. [Google Scholar] [CrossRef]
- Mossaz, S.; Jay, P.; Magnin, A. Experimental study of stationary inertial flows of a yield-stress fluid around a cylinder. J. Non-Newton. Fluid Mech. 2012, 189–190, 40–52. [Google Scholar] [CrossRef]
- Kamal, M.S.; Sultan, A.S.; Al-Mubaiyedh, U.A.; Hussein, I.A. Review on polymer flooding: Rheology, adsorption, stability, and field applications of various polymer systems. Polym. Rev. 2015, 55, 491–530. [Google Scholar] [CrossRef]
- Rueda, M.M.; Auscher, M.C.; Fulchiron, R.; Perie, T.; Martin, G.; Sonntag, P.; Cassagnau, P. Rheology and applications of highly filled polymers: A review of current understanding. Prog. Polym. Sci. 2017, 66, 22–53. [Google Scholar] [CrossRef]
- Ouattara, Z.; Jay, P.; Blésès, D.; Magnin, A. Drag of a cylinder moving near a wall in a yield stress fluid. AIChE J. 2018, 64, 4118–4130. [Google Scholar] [CrossRef]
- Wilczyński, K.; Buziak, K.; Lewandowski, A.; Nastaj, A.; Wilczyński, K.J. Rheological Basics for Modeling of Extrusion Process of Wood Polymer Composites. Polymers 2021, 13, 622. [Google Scholar] [CrossRef]
- Xin, X.; Yu, G.; Wu, K.; Dong, X.; Chen, Z. Polymer Flooding in Heterogeneous Heavy Oil Reservoirs: Experimental and Simulation Studies. Polymers 2021, 13, 2636. [Google Scholar] [CrossRef]
- Bishop, J.J.; Popel, A.S.; Intaglietta, M.; Johnson, P.C. Rheological effects of red blood cell aggregation in the venous network: A review of recent studies. Biorheology 2001, 38, 263–274. [Google Scholar]
- Beris, A.N.; Horner, J.S.; Jariwala, S.; Armstrong, M.; Wagner, N.J. Recent advances in blood rheology: A review. Soft Matter 2021, 17, 10591–10613. [Google Scholar] [CrossRef]
- Yu, Z.; Wachs, A. A fictitious domain method for dynamic simulation of particle sedimentation in Bingham fluids. J. Non-Newton. Fluid Mech. 2007, 145, 78–91. [Google Scholar] [CrossRef]
- Olshanskii, M.A. Analysis of semi-staggered finite-difference method with application to Bingham flows. Comput. Methods Appl. Mech. Eng. 2009, 198, 975–985. [Google Scholar] [CrossRef]
- Zhang, J. An augmented Lagrangian approach to Bingham fluid flows in a lid-driven square cavity with piecewise linear equal-order finite elements. Comput. Methods Appl. Mech. Eng. 2010, 199, 3051–3057. [Google Scholar] [CrossRef]
- dos Santos, D.D.; Frey, S.; Naccache, M.F.; de Souza Mendes, P. Numerical approximations for flow of viscoplastic fluids in a lid-driven cavity. J. Non-Newton. Fluid Mech. 2011, 166, 667–679. [Google Scholar] [CrossRef]
- Syrakos, A.; Georgiou, G.C.; Alexandrou, A.N. Solution of the square lid-driven cavity flow of a Bingham plastic using the finite volume method. J. Non-Newton. Fluid Mech. 2013, 195, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, R.; Kousar, N.; Yaqub, M.; Jabeen, K. Numerical simulations of the square lid driven cavity flow of Bingham fluids using nonconforming finite elements coupled with a direct solver. Adv. Math. Phys. 2017, 2017, 5210708. [Google Scholar] [CrossRef]
- Hoang-Trong, C.N.; Bui, C.M.; Ho, T.X. Lid-driven cavity flow of sediment suspension. Eur. J. Mech.-B/Fluids 2021, 85, 312–321. [Google Scholar] [CrossRef]
- Pakdel, P.; McKinley, G.H. Elastic Instability and Curved Streamlines. Phys. Rev. Lett. 1996, 77, 2459–2462. [Google Scholar] [CrossRef]
- Pakdel, P.; Spiegelberg, S.H.; McKinley, G.H. Cavity flows of elastic liquids: Two-dimensional flows. Phys. Fluids 1997, 9, 3123–3140. [Google Scholar] [CrossRef]
- Pakdel, P.; McKinley, G.H. Cavity flows of elastic liquids: Purely elastic instabilities. Phys. Fluids 1998, 10, 1058–1070. [Google Scholar] [CrossRef] [Green Version]
- Pan, T.W.; Hao, J.; Glowinski, R. On the simulation of a time-dependent cavity flow of an Oldroyd-B fluid. Int. J. Numer. Methods Fluids 2009, 60, 791–808. [Google Scholar] [CrossRef]
- Yapici, K.; Karasozen, B.; Uludag, Y. Finite volume simulation of viscoelastic laminar flow in a lid-driven cavity. J. Non-Newton. Fluid Mech. 2009, 164, 51–65. [Google Scholar] [CrossRef]
- Sousa, R.; Poole, R.; Afonso, A.; Pinho, F.; Oliveira, P.; Morozov, A.; Alves, M. Lid-driven cavity flow of viscoelastic liquids. J. Non-Newton. Fluid Mech. 2016, 234, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, R.; Bilal, S.; Khan, I.; Kousar, N.; Seikh, A.H.; Sherif, E.S.M. A comprehensive finite element examination of Carreau Yasuda fluid model in a lid driven cavity and channel with obstacle by way of kinetic energy and drag and lift coefficient measurements. J. Mater. Res. Technol. 2020, 9, 1785–1800. [Google Scholar] [CrossRef]
- Shuguang, L. Numerical simulation of non-Newtonian Carreau fluid in a lid-driven cavity. J. Phys. Conf. Ser. 2021, 2091, 012068. [Google Scholar] [CrossRef]
- Herschel, W.; Bulkley, R. Measurement of consistency as applied to rubber-benzene solutions. Am. Soc. Test Proc. 1926, 26, 621–633. [Google Scholar]
- Papanastasiou, T. Flows of Materials with Yield. J. Rheol. 1987, 31, 385. [Google Scholar] [CrossRef]
- Bui, C.M.; Ho, T.X. Numerical study of an unsteady flow of thixotropic liquids past a cylinder. AIP Adv. 2019, 9, 115002. [Google Scholar] [CrossRef]
- Bui, C.; Ho, T. Effects of the regularization parameter on the flow characteristics of a viscoplastic fluid. In Proceedings of the 1st International Conference on Innovations for Computing, Engineering and Materials, 2021: ICEM, Ho Chi Minh City, Vietnam, 27 June 2021; AIP Publishing LLC: Melville, NY, USA, 2021; Volume 2420, p. 020032. [Google Scholar]












| 0.1 | 1 | 5 | 10 | 20 | 50 | |
| 0.8 | 1.2 | 1.6 | 1.8 | >4 | >4 |
| 0.5 | 1 | 2 | 4 | |||
|---|---|---|---|---|---|---|
 | 0.46 | 0.12 | 0.11 | 0.11 | ||
| 0.63 | 0.34 | 0.26 | 0.26 | |||
| 0.75 | 0.54 | 0.42 | 0.4 | |||
| 0.79 | 0.6 | 0.49 | 0.48 | |||
| 0.82 | 0.65 | 0.56 | 0.56 | |||
| 0.99 | 0.99 | 0.99 | 0.99 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bui, C.M.; Ho, A.-N.T.; Nguyen, X.B. Flow Behaviors of Polymer Solution in a Lid-Driven Cavity. Polymers 2022, 14, 2330. https://doi.org/10.3390/polym14122330
Bui CM, Ho A-NT, Nguyen XB. Flow Behaviors of Polymer Solution in a Lid-Driven Cavity. Polymers. 2022; 14(12):2330. https://doi.org/10.3390/polym14122330
Chicago/Turabian StyleBui, Cuong Mai, Anh-Ngoc Tran Ho, and Xuan Bao Nguyen. 2022. "Flow Behaviors of Polymer Solution in a Lid-Driven Cavity" Polymers 14, no. 12: 2330. https://doi.org/10.3390/polym14122330
APA StyleBui, C. M., Ho, A.-N. T., & Nguyen, X. B. (2022). Flow Behaviors of Polymer Solution in a Lid-Driven Cavity. Polymers, 14(12), 2330. https://doi.org/10.3390/polym14122330