Fabrication of High-Quality Straight-Line Polymer Composite Frame with Different Radius Parts Using Fiber Winding Process
Abstract
:1. Introduction
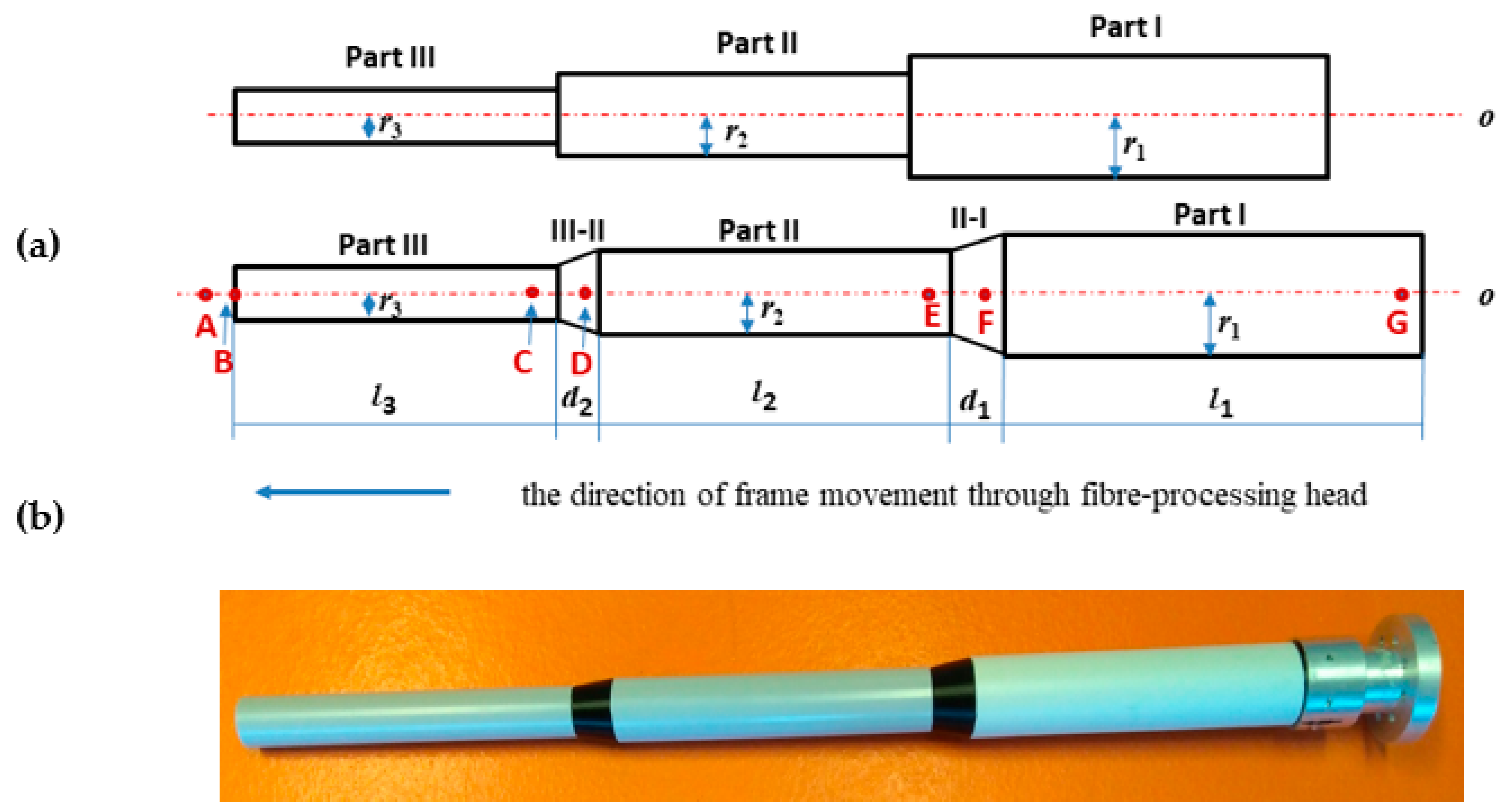
2. Manufacturing of Polymer Composite Frame
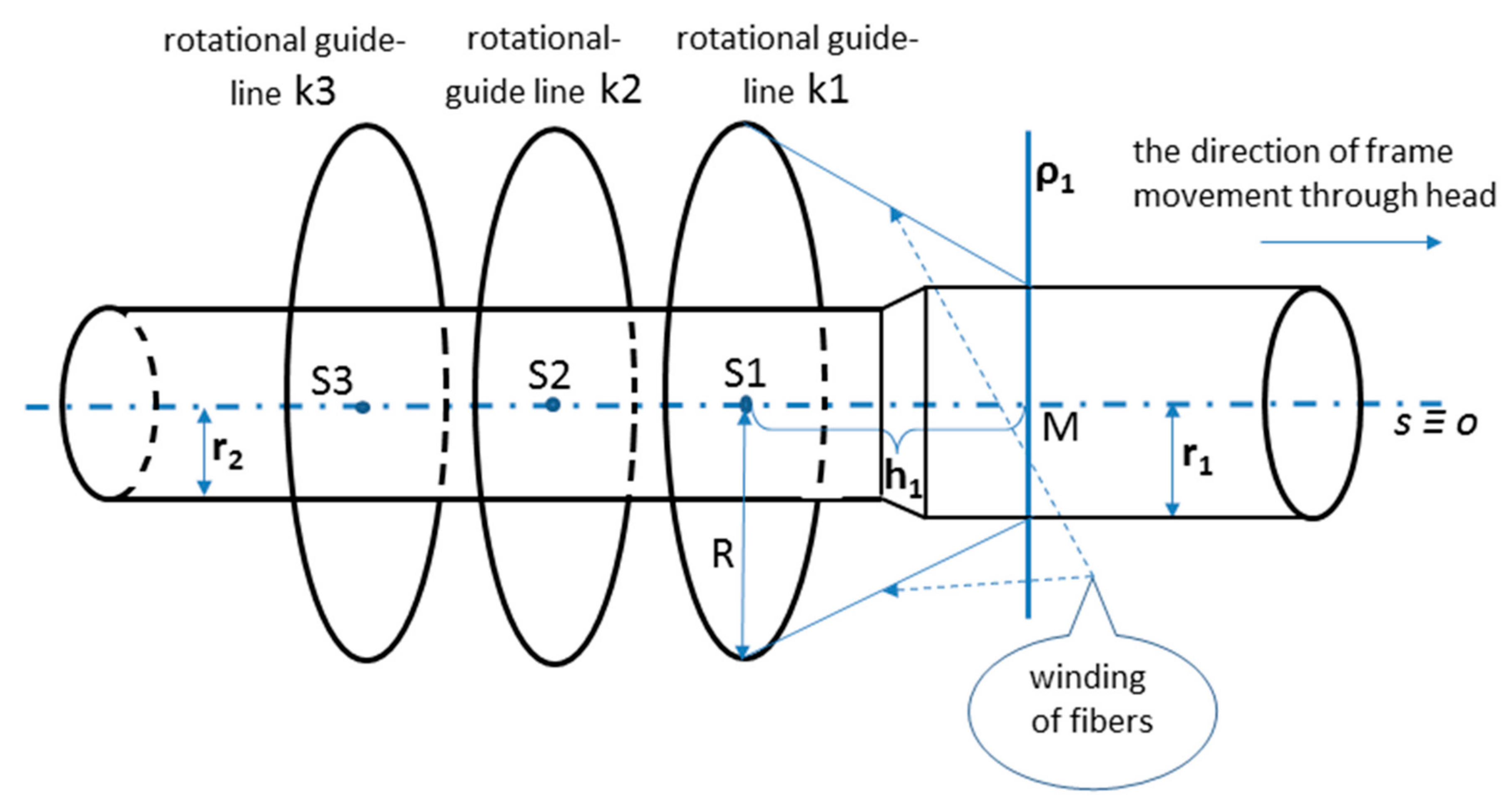
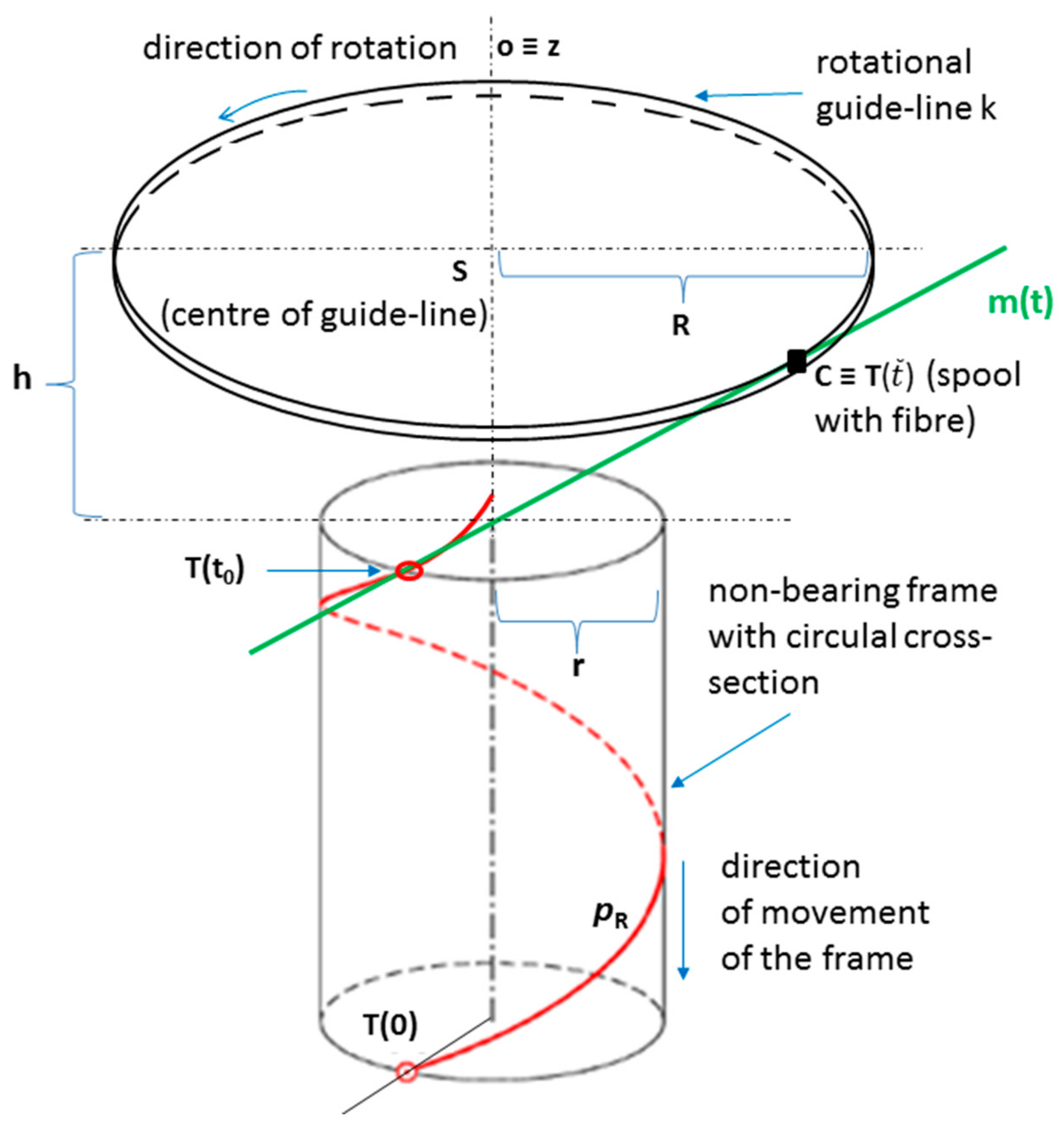
2.1. Determination of the Winding Plane
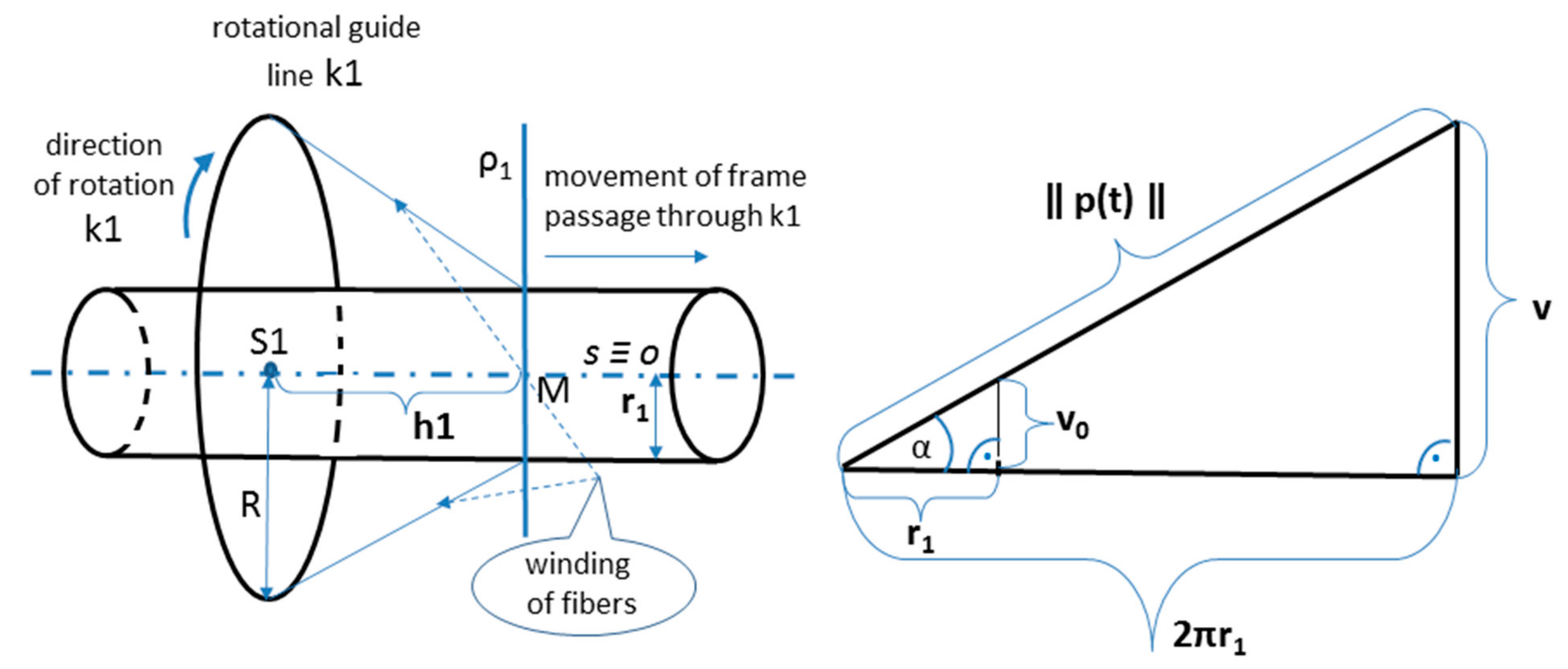
2.2. Controlling of the Speed of Fibers Winding
Note
General Procedure
- Determination of the distance h1 of the fiber winding on Part I of the frame from guide-line (use Relation (4)).
- Calculation of angular speed ω1 needed to ensure the required angle of the fibers winding on Part I (use Relation (7)).
- Determination of distance h2 of the fiber winding on Part II of the frame from guide-line (use Relation (4)).
- Calculation of angular speed ω2 needed to ensure the required angle of winding of the fibers on Part II (use Relation (7)).
- 5.
- Termination of angular speed ω1 of guide-line in distance h1 before the end of Part I when the frame goes through the guide-line.
- 6.
- Smooth transition from angular velocities ω1 to ω2 of guide-line.
- 7.
- Starting angular speed ω2 of guide-line, when the beginning of Part II is in distance before guide-line h2.
3. Results and Discussions
3.1. Verification Example
3.2. Composite Frame Production
Note
- realization of simultaneous winding of three layers of fibers on the frame at different angles,
- ensure the winding of individual parts (including parts with different radii of their cross-sections) of the frame at specified different angles for given winding layer,
- possibility of ensuring the same winding angle for each winding layer for all parts of the frame with different radii of their cross-sections,
- adjacent parts of the frame with different radii have a continuous transition of wound fibers for a given layer.
4. Conclusions
- Calculate the distance of winding the fibers (on the frame) from the corresponding guide-line. This distance depends on the size of the required winding angle, the radius of the guide-line, and the radius of the relevant wound part of the frame.
- Determine the angular speed of the guide-line so that the fibers are wound at the desired angle. Angular speed depends on the defined winding angle, the radius of the relevant part of the frame, and the constant size of passage speed of the frame through the head.
- Based on the previous two points and assuming a constant speed of passage of the frame through the head, we can determine:
- when and with what angular speed is started and ended winding by guide-line so that the fibers are wound at a desired angle on a specified part of the frame;
- the continuous transition between two individual parts of the frame with different radii is wound at a gradually varying angle from the finished winding angle to the next desired winding angle on the following part of the frame, while the gradual change of winding angle is performed based on the continuous change of angular speed of guide-line;
- the continuous change of winding angle on a straight-line frame with a constant cross-sectional radius;
- the same winding angle on the parts of the frame with different radii of the cross-section.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mlýnek, J.; Petrů, M.; Martinec, T.; Koloor, S.S.R. Fabrication of High-Quality Polymer Composite Frame by a New Method of Fiber Winding Process. Polymers 2020, 12, 1037. [Google Scholar] [CrossRef]
- Abdi, B.; Koloor, S.S.R.; Abdullah, M.R.; Ayob, A.; Yahya, M.Y.B. Effect of strain-rate on flexural behavior of composite sandwich panel. Appl. Mech. Mater. 2012, 229–231, 766–770. [Google Scholar] [CrossRef]
- Koloor, S.; Abdullah, M.; Tamin, M.; Ayatollahi, M. Fatigue damage of cohesive interfaces in fiber-reinforced polymer composite laminates. Compos. Sci. Technol. 2019, 183, 107779. [Google Scholar] [CrossRef]
- Gay, D. Composite Materials: Design and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Sharma, S.; Sowntharya, L.; Kar, K.K. Polymer-Based Composite Structures: Processing and Applications. In Composite Materials; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–36. [Google Scholar]
- McIlhagger, A.; Archer, E.; McIlhagger, R. Manufacturing processes for composite materials and components for aerospace applications. In Polymer Composites in the Aerospace Industry; Elsevier: Amsterdam, The Netherlands, 2020; pp. 59–81. [Google Scholar]
- Koloor, S.S.R.; Tamin, M. Mode-II interlaminar fracture and crack-jump phenomenon in CFRP composite laminate materials. Compos. Struct. 2018, 204, 594–606. [Google Scholar] [CrossRef]
- Martinec, T.; Mlýnek, J.; Petrů, M. Calculation of the robot trajectory for the optimum directional orientation of fibre placement in the manufacture of composite profile frames. Robot. Comput.-Integr. Manuf. 2015, 35, 42–54. [Google Scholar] [CrossRef]
- Davies, P.; Choqueuse, D.; Bigourdan, B.; Chauchot, P. Composite cylinders for deep sea applications: An overview. J. Press. Vessel Technol. 2016, 138, 060904. [Google Scholar] [CrossRef]
- Tian, Z.-S.; Jia, X.-L.; Liu, B.-Y.; Li, W.-S. Research and application progress of large-sized carbon fiber composite cylinder in storage and transportation of compressed natural gas. Fiber Reinf. Plast. Compos. 2013, 5, 62–66. [Google Scholar]
- Koloor, S.S.R.; Tamin, M.N. Effects of lamina damages on flexural stiffness of CFRP composites. Proceedings of 8th Asian-Australasian Conference on Composite Materials 2012, ACCM 2012—Composites: Enabling Tomorrow’s Industry Today, Kuala Lumpur, Malaysia, 6–8 November 2012; pp. 237–243. [Google Scholar]
- Chen, G. Advances in Agricultural Machinery and Technologies; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Grande, D.H.; Greist, S.; Jessie, T.; Daniel, J. 3.18 Composites in Sports Applications. In Comprehensive Composite Materials II; Beaumont, P.W.R., Zweben, C.H., Eds.; Elsevier: Oxford, UK, 2018; pp. 469–526. [Google Scholar] [CrossRef]
- Bai, X.; Li, N. The application of carbon fiber composite material for sports equipment. Adv. Mater. Res. 2012, 496, 480–483. [Google Scholar] [CrossRef]
- Sogard, D.; Shoemaker, S.; Smith, S.R. Support Structure/Membrane Composite Medical Device. U.S. Patent 6,699,276, 2 March 2004. [Google Scholar]
- Reimink, M.S.; Ogle, M.F. Medical Devices with Polymer/Inorganic Substrate Composites. U.S. Patent 7,604,663, 20 October 2009. [Google Scholar]
- Laney, P. Use of composite pipe materials in the transportation of natural gas. INEEL Field Work Proposal 2002. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.165.1163&rep=rep1&type=pdf (accessed on 25 December 2020).
- Sebaey, T.A. Design of Oil and Gas Composite Pipes for Energy Production. Energy Procedia 2019, 162, 146–155. [Google Scholar] [CrossRef]
- Taheri, F. 18—Advanced fiber-reinforced polymer (FRP) composites for the manufacture and rehabilitation of pipes and tanks in the oil and gas industry. In Advanced Fibre-Reinforced Polymer (FRP) Composites for Structural Applications; Bai, J., Ed.; Woodhead Publishing: Cambridge, UK, 2013; pp. 662–704. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Khosravani, M.R.; Hamzah, R.; Tamin, M. FE model-based construction and progressive damage processes of FRP composite laminates with different manufacturing processes. Int. J. Mech. Sci. 2018, 141, 223–235. [Google Scholar] [CrossRef]
- Mlýnek, J.; Petrů, M.; Martinec, T. Design of composite frames used in agricultural machinery. In Proceedings of the 7th TAE, Prague, Czech Republic, 17–20 September 2019. [Google Scholar]
- Mlýnek, J.; Knobloch, R. Model of shell metal mould heating in the automotive industry. Appl. Math. 2018, 63, 111–124. [Google Scholar] [CrossRef]
- Mlynek, J.; Petru, M.; Martinec, T. Optimization of Industrial Robot Trajectory in Composite Production. In Proceedings of the 18th International Conference on Mechatronics-Mechatronika (ME), Brno, Czech Republic, 5–7 December 2018; pp. 270–275. [Google Scholar]
- Bratukhin, A.G.; Bogolyubov, V.S. Composite Manufacturing Technology; Springer Netherlands: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Quanjin, M.; Rejab, M.; Idris, M.; Kumar, N.M.; Merzuki, M. Robotic Filament Winding Technique (RFWT) in Industrial Application: A Review of State of the Art and Future Perspectives. Int. Res. J. Eng. Technol. 2018, 5, 1668–1676. [Google Scholar]
- Durand, R.D.; Miller, M.F. Method for Manufacturing Vehicle Frame Components Using Composite Fiber Pultrusion Techniques. U.S. Patent 5,882,460, 16 March 1999. [Google Scholar]
- Kim, J.-S.; Lee, W.-G. Manufacturing and structural behavior evaluation of composite side beams using autoclave curing and resin transfer moulding method. Int. J. Precis. Eng. Manuf. 2012, 13, 723–730. [Google Scholar] [CrossRef]
- Hart, D.C. Development of a Progressive Failure Finite Element Analysis for a Braided Composite Fuselage Frame; Virginia Tech: Blacksburg, VA, USA, 2002. [Google Scholar]
- Groppe, D. Robots improve the quality and cost-effectiveness of composite structures. Ind. Robot Int. J. 2000, 27, 96–102. [Google Scholar] [CrossRef]
- Shirinzadeh, B.; Alici, G.; Foong, C.W.; Cassidy, G. Fabrication process of open surfaces by robotic fibre placement. Robot. Comput. Integr. Manuf. 2004, 20, 17–28. [Google Scholar] [CrossRef]
- Fowler, C.P.; Orifici, A.C.; Wang, C.H. A review of toroidal composite pressure vessel optimisation and damage tolerant design for high pressure gaseous fuel storage. Int. J. Hydrogen Energy 2016, 41, 22067–22089. [Google Scholar] [CrossRef]
- Liu, C.; Shi, Y. Design optimization for filament wound cylindrical composite internal pressure vessels considering process-induced residual stresses. Compos. Struct. 2020, 235, 111755. [Google Scholar] [CrossRef]
- Anderson, J.P.; Altan, M.C. Properties of Composite Cylinders Fabricated by Bladder Assisted Composite Manufacturing. J. Eng. Mater. Technol. 2012, 134. [Google Scholar] [CrossRef]
- Kehrl, D.J.; Johnson, K.E.; McCarville, D.A. Curved Composite Frames and Method of Making the Same. U.S. Patent 8,349,105, 8 January 2013. [Google Scholar]
- Sofi, T.; Neunkirchen, S.; Schledjewski, R. Path calculation, technology and opportunities in dry fiber winding: A review. Adv. Manuf. Polym. Compos. Sci. 2018, 4, 57–72. [Google Scholar] [CrossRef]
- Polini, W.; Sorrentino, L. Influence of winding speed and winding trajectory on tension in robotized filament winding of full section parts. Compos. Sci. Technol. 2005, 65, 1574–1581. [Google Scholar] [CrossRef]
- Azevedo, C.B.; Almeida Jr, J.H.S.; Flores, H.F.; Eggers, F.; Amico, S.C. Influence of mosaic pattern on hygrothermally-aged filament wound composite cylinders under axial compression. J. Compos. Mater. 2020, 54, 2651–2659. [Google Scholar] [CrossRef]
- Klimchik, A.; Ambiehl, A.; Garnier, S.; Furet, B.; Pashkevich, A. Efficiency evaluation of robots in machining applications using industrial performance measure. Robot. Comput. Integr. Manuf. 2017, 48, 12–29. [Google Scholar] [CrossRef]
- Gao, J.; Pashkevich, A.; Caro, S. Manipulator motion planning in redundant robotic system for fiber placement process. In New Trends in Mechanism and Machine Science; Springer: Berlin/Heidelberg, Germany, 2017; pp. 243–252. [Google Scholar]
- Gao, J.; Pashkevich, A.; Caro, S. Optimization of the robot and positioner motion in a redundant fiber placement workcell. Mech. Mach. Theory 2017, 114, 170–189. [Google Scholar] [CrossRef]
- Mlýnek, J.; Martinec, T. Mathematical model of composite manufacture and calculation of robot trajectory. In Proceedings of the 16th International Conference on Mechatronics-Mechatronika, Brno, Czech Republic, 3–5 December 2014; pp. 345–351. [Google Scholar]
- Xiao, Y.; Du, Z.; Dong, W. Smooth and near time-optimal trajectory planning of industrial robots for online applications. Ind. Robot Int. J. 2012, 39, 169–177. [Google Scholar] [CrossRef]
- Piao, S.; Zhong, Q.; Wang, X.; Gao, C. Optimal Trajectory Generation for Soccer Robot Based on Genetic Algorithms. In International Workshop on Computer Science for Environmental Engineering and EcoInformatics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 447–451. [Google Scholar]
- Chen, Y.; Yan, L.; Wei, H.; Wang, T. Optimal trajectory planning for industrial robots using harmony search algorithm. Ind. Robot Int. J. 2013, 40, 502–512. [Google Scholar] [CrossRef]
- Simba, K.R.; Uchiyama, N.; Sano, S. Real-time smooth trajectory generation for nonholonomic mobile robots using Bézier curves. Robot. Comput. Integr. Manuf. 2016, 41, 31–42. [Google Scholar] [CrossRef]
- Andulkar, M.V.; Chiddarwar, S.S. Incremental approach for trajectory generation of spray painting robot. Ind. Robot Int. J. 2015. [Google Scholar] [CrossRef]
- Zhuo, M.; Lingling, Y.; Jianqiu, B.; Yize, S. Prediction method for offset compensation on three-dimensional mandrel with spatial irregular shape. J. Ind. Text. 2019. [Google Scholar] [CrossRef]
- Pressley, A.N. Elementary Differential Geometry; Springer Science & Business Media: King’s College, London, UK, 2010. [Google Scholar]
- Shankar, R. Fundamentals of Physics I: Mechanics, Relativity, and Thermodynamics; Yale University Press: London, UK, 2019. [Google Scholar]





| R [mm] | r [mm] | α [º] | δ [º] | h [mm] |
|---|---|---|---|---|
| 50 | 20 | 30 | 60 | 26.4575 |
| 45 | 45 | 45.8258 | ||
| 60 | 30 | 79.3735 | ||
| 30 | 30 | 60 | 23.0940 | |
| 45 | 45 | 40.0000 | ||
| 60 | 30 | 69.2820 | ||
| 40 | 30 | 60 | 17.3205 | |
| 45 | 45 | 30.0000 | ||
| 60 | 30 | 51.9615 | ||
| 80 | 20 | 30 | 60 | 44.7213 |
| 45 | 45 | 77.4597 | ||
| 60 | 30 | 134.1641 | ||
| 30 | 30 | 60 | 42.8174 | |
| 45 | 45 | 74.1620 | ||
| 60 | 30 | 128.4524 | ||
| 40 | 30 | 60 | 39.1000 | |
| 45 | 45 | 69.2820 | ||
| 60 | 30 | 119.1000 |
| w [mm/s] | r [mm] | α [º] | tgα | ω [rad/s] |
|---|---|---|---|---|
| 25 | 20 | 30 | 0.5774 | 2.1649 |
| 45 | 1 | 1.2500 | ||
| 60 | 1.7321 | 0.7217 | ||
| 30 | 30 | 0.5774 | 1.4433 | |
| 45 | 1 | 0.8333 | ||
| 60 | 1.7321 | 0.4811 | ||
| 40 | 30 | 0.5774 | 1.0824 | |
| 45 | 1 | 0.6250 | ||
| 60 | 1.7321 | 0.3608 | ||
| 100 | 20 | 30 | 0.5774 | 8.6600 |
| 45 | 1 | 5.0000 | ||
| 60 | 1.7321 | 2.8867 | ||
| 30 | 30 | 0.5774 | 5.7730 | |
| 45 | 1 | 3.3333 | ||
| 60 | 1.7321 | 1.9244 | ||
| 40 | 30 | 0.5774 | 4.3467 | |
| 45 | 1 | 2.5000 | ||
| 60 | 1.7321 | 1.4433 |
| R [mm] | w [mm/s] | Part I, α1 = | ||
|---|---|---|---|---|
| 50 | 50 | r1 [mm] | h1 [mm] | ω1 [rad/s] |
| 40 | 30,000 | 1250 | ||
| Part II, α2 = | ||||
| r2 [mm] | h2 [mm] | ω2 [rad/s] | ||
| 30 | 23,094 | 2887 | ||
| Part III, α3 = | ||||
| r3 [mm] | h3 [mm] | ω3 [rad/s] | ||
| 20 | 79,371 | 1443 | ||
| Value of the Point Lying on Axis o of the Frame [mm] | Description Position of the Point | Angular Speed ω [rad/s] | Action When Point Goes Through Guide-Line k1 |
|---|---|---|---|
| A = 0 | corresponding point of begin of Part III is B = A+h3 | ω3 = 1.443 | start of fiber winding on Part III at angle of α3 = |
| C= 500 | C = A + l3 | end of fiber winding on Part III at angle of α3 = | |
| D = 636,287 | D = h3 + l3+ d2 − h2 | ω2=2.887 | start of fiber winding on Part II at angle of α2 = |
| E = 1136,277 | E = h3 + l3 + d2 + l2 − h2 | end of fiber winding on Part II at angle of α2 = | |
| F = 1209,371 | F = h3 + l3 + d2 + l2 + d1 − h1 | ω1 = 1.250 | start of fiber winding on Part I at angle of α1 = |
| G= 1709,371 | G = h3 + l3 + d2 + l2 +d1 + l1 − h1 | end of fiber winding on Part I at angle of α1 = |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mlýnek, J.; Rahimian Koloor, S.S.; Martinec, T.; Petrů, M. Fabrication of High-Quality Straight-Line Polymer Composite Frame with Different Radius Parts Using Fiber Winding Process. Polymers 2021, 13, 497. https://doi.org/10.3390/polym13040497
Mlýnek J, Rahimian Koloor SS, Martinec T, Petrů M. Fabrication of High-Quality Straight-Line Polymer Composite Frame with Different Radius Parts Using Fiber Winding Process. Polymers. 2021; 13(4):497. https://doi.org/10.3390/polym13040497
Chicago/Turabian StyleMlýnek, Jaroslav, Seyed Saeid Rahimian Koloor, Tomáš Martinec, and Michal Petrů. 2021. "Fabrication of High-Quality Straight-Line Polymer Composite Frame with Different Radius Parts Using Fiber Winding Process" Polymers 13, no. 4: 497. https://doi.org/10.3390/polym13040497
APA StyleMlýnek, J., Rahimian Koloor, S. S., Martinec, T., & Petrů, M. (2021). Fabrication of High-Quality Straight-Line Polymer Composite Frame with Different Radius Parts Using Fiber Winding Process. Polymers, 13(4), 497. https://doi.org/10.3390/polym13040497








