Effect of Needle Heating on the Sewing of Medical Textiles
Abstract
:1. Introduction
1.1. Medical Gowns
1.2. Basic Thermal Mechanism of Needle Heating
- Heat flux is generated between the outer surface of the needle and the fabric; this phenomenon depends on the needle-penetration force, withdrawal, and the frictional coefficient.
- Heat conduction between the needle and the thread is another major source of heating, and depends on the friction coefficient of the needle and thread, as well as the material parameters.
1.3. Contactless Method of Needle Temperature Measurement
1.4. Sewing Needle Temperature
2. Materials and Methods
- Lockstitch machine (Brother Company, Berlin, Germany DD7100-905).
- Thermocouple by Omega (K type 5SC-TT-(K)-36-(36)).
- Thermocouple by Omega—wireless device and receiver (MWTC-D-K-868).
- Needles (Groz–Beckert, Stuttgart, Germany 100/16) R-type.
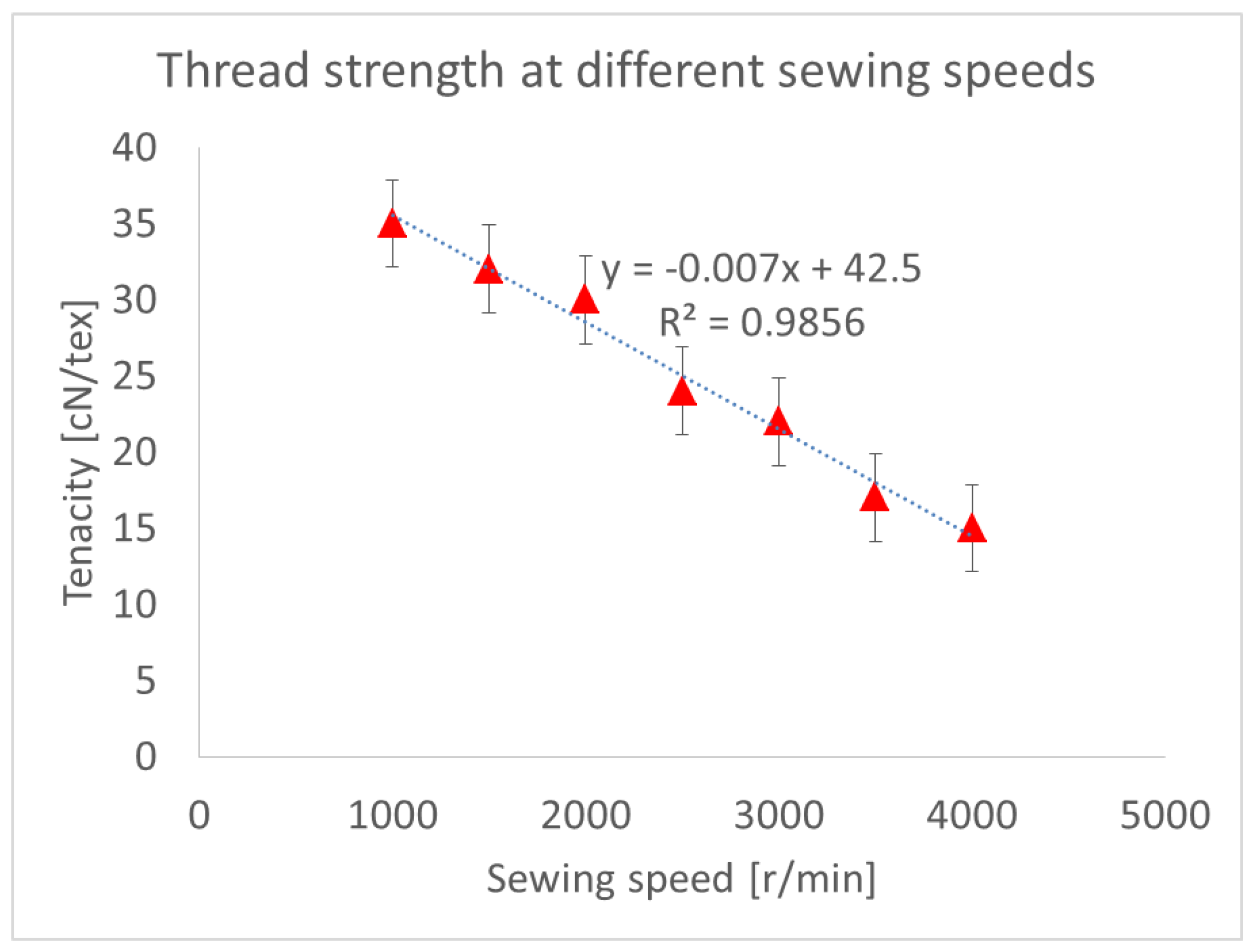
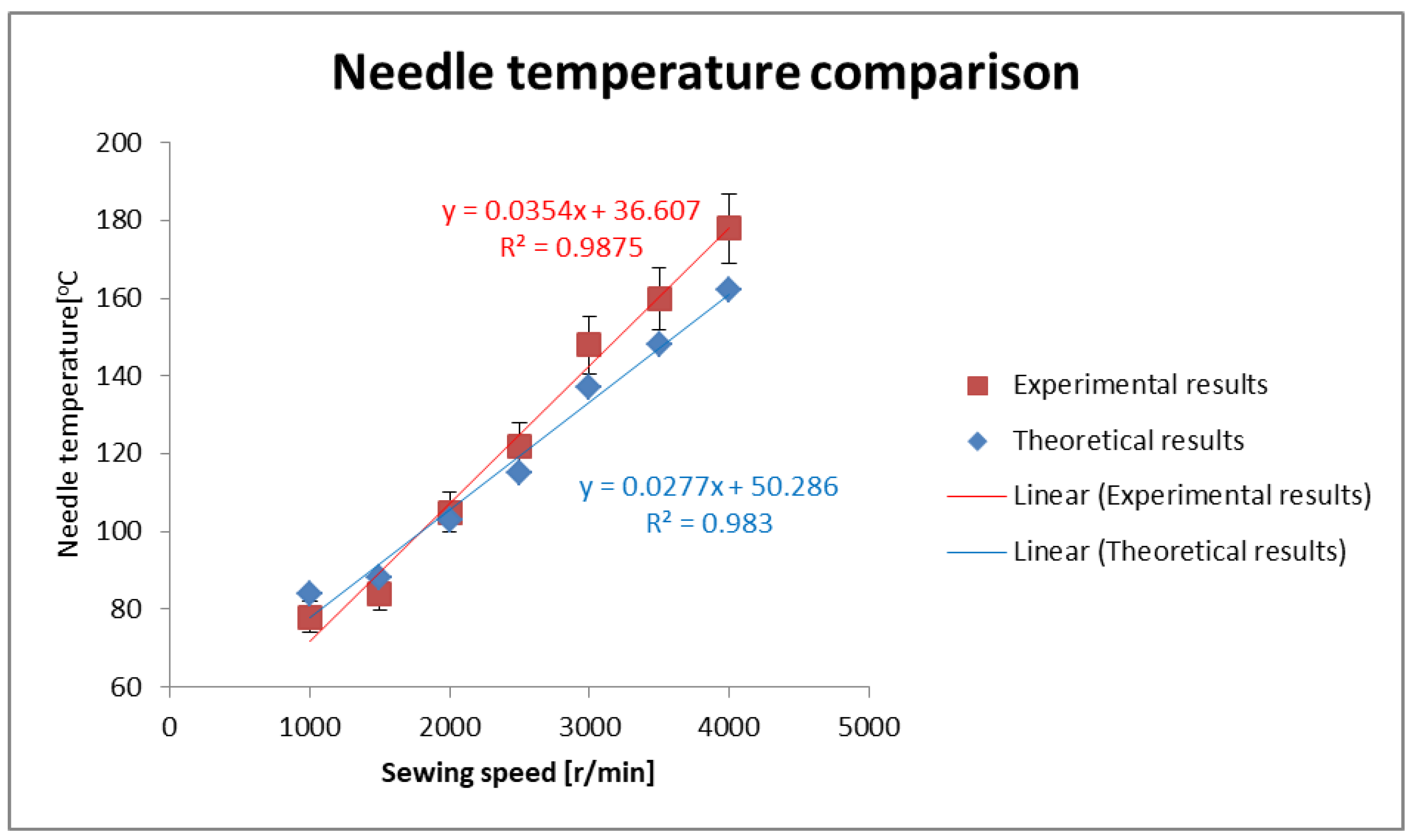
3. Results and Discussion
Theoretical Analysis
- 1-
- The needle, thread, and fabric are all at room temperature.
- 2-
- The needle is a cylinder with the same material composition throughout.
- 3-
- λN is the thermal conductivity of the needle material, and is significantly higher than that of the sewing thread λy and fabric λF. Here it is discreetly assumed that both the thread and fabric have lumped thermal properties, i.e., each has unchanging thermal conductivities, represented by single value.
- 4-
- The thread and textile fabric are considered homogenous, with constant thermal conductivity value throughout.
- 5-
- Radiation heat can be neglected due to the small size of the needle and a smaller contribution compared to other factors.
- 6-
- In this model, it is estimated that friction heat is assumed as Q = F*v [18], where F is friction force and v is the relative velocity of the two surfaces.
- 7-
- γ is the ratio determining the amount of heat distribution when two materials rub together. Partition ratio is calculated, using the Charron’s relation [24], as:where , N denotes the needle, i denotes the other rubbing material in contact, and b is the thermal absorptivity of the respective materials. The calculated value is given as , where ρ is the density of the material, C is the specific heat of the material, and is the thermal conductivity.
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Graham, F. A Brief History of the Sewing Machine. International Sewing Machine Collectors’ Society. Available online: http://ismacs.net/sewingmachine_history.html (accessed on 1 October 2021).
- Maja, J.; Goran, D. The influence of the sewing speed and fabric thickness on sewing machine stitch formation parameters. Adv. Technol. 2017, 6, 72–77. [Google Scholar]
- Carvalho, M.; Carvalho, H.; Silva, L.F. Problems relating to sewing. In Joining Textiles; Woodhead Publishing Series in Textiles; Jones, I., Stylios, G.K., Eds.; Woodhead Publishing: Duxford, UK, 2013; pp. 149–174. [Google Scholar]
- Nayak, R.; Padhye, R. Automation in Garment Manufacturing; Woodhead Publishing: Duxford, UK, 2018; pp. 1–290. [Google Scholar]
- Kumar, C.S.S.; Ramachandralu, K. Study on Relationship between Sewing Thread Tension and Fabric. Eur. J. Adv. Eng. Technol. 2015, 2, 105–107. [Google Scholar]
- Mazari, A.; Zhu, G.; Havelka, A. Sewing needle temperature of an industrial lockstitch machine. Ind. Text. 2014, 65, 335–339. [Google Scholar]
- Gribaa, S.; Amar, S.B.; Dogui, A. Influence of sewing parameters upon the tensile behavior of textile assembly. Int. J. Cloth. Sci. Technol. 2006, 18, 235–346. [Google Scholar] [CrossRef] [Green Version]
- Juciene, M.; Vobolis, J. Influence of fabric external friction force and certain parameters of a sewing machine upon stitch length. Mater. Sci. 2004, 10, 101–104. [Google Scholar]
- Mazari, A.; Havelka, A.; Wiener, J.; Rozek, Z. A study on DLC-coated industrial lockstitch sewing needle. Ind. Text. 2015, 66, 43–47. [Google Scholar]
- Lee, S.; Rho, S.H.; Lee, S.; Lee, J.; Lee, S.W.; Lim, D.; Jeong, W. Implementation of an automated manufacturing process for smart clothing: The Case Study a Smart Sports Bra. Processes 2021, 9, 289. [Google Scholar] [CrossRef]
- Gersak, J. Analysis of loading of the thread in the process of stitch forming. Tekstil 1987, 36, 481–489. [Google Scholar]
- Liasi, E.; Du, R.; Simon, D.; Dimitrejevic, J.; Liburdi, F. An experimental study of needle heating in sewing heavy materials using infrared radiometry. Int. J. Cloth. Sci. Technol. 1989, 11, 300–314. [Google Scholar] [CrossRef]
- Hersh, S.; Grady, P. Needle heating during high speed sewing. Text. Res. J. 1969, 39, 101–120. [Google Scholar] [CrossRef]
- Yukseloglu, M.; Citoglu, F.; Catinkaya, B. A study on the needle heating in polyester blend upholstery fabrics. Ind. Text. 2013, 63, 246–253. [Google Scholar]
- Li, Q.; Liasi, E.; Simon, D.; Du, R. Heating of industrial sewing machine needles: FEA model and verification using IR radiometry. In Thermosense XXI; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; Volume 3700, pp. 347–357. [Google Scholar]
- Mazari, A.; Bal, K.; Havelka, A. Prediction of needle heating in an industrial sewing machine. Text. Res. J. 2016, 86, 302–310. [Google Scholar] [CrossRef]
- Khan, R.; Hersh, S.; Grady, P. Simulation of needle-fabric interaction in sewing operation. Text. Res. J. 1970, 41, 489–497. [Google Scholar] [CrossRef]
- Li, Q.; Liasi, E. A study on the needle heating in heavy industrial sewing part-1. Int. J. Cloth. Sci. Technol. 2001, 13, 351–367. [Google Scholar] [CrossRef]
- Laughlin, R. Needle temperature measurement by infrared pyrometry. Text. Res. J. 1963, 33, 35–39. [Google Scholar] [CrossRef]
- Sondhelm, W. Causes of seam damage: Needle heating. J. Text. Inst. 1953, 44, 580–585. [Google Scholar] [CrossRef]
- Gurarda, A.; Yukseltan, E.; Kaplangiray, B.M.; Kanik, M. The effects of various lubricants on the friction properties of sewing threads. Text. Res. J. 2008, 83, 1273–1282. [Google Scholar] [CrossRef]
- Groz-Beckert Newsletter. Available online: https://www.groz-beckert.com (accessed on 1 April 2021).
- Mazari, A.; Havelka, A.; Hes, L. Experimental techniques for measuring sewing needle temperature. Textile Ve Konfeksiyon 2014, 24, 111–118. [Google Scholar]
- Charron, F. Partage de la Chaleur Entre Deux Corps Frottants; Blondel La Rougery: Paris, France, 1943. [Google Scholar]
- James, S. Lange’s Handbook of Chemistry, 16 ed.; McGraw-Hill Professional: New York, NY, USA, 2005; pp. 2758–2807. [Google Scholar]
- Thermal Conductivity. Available online: http://www.engineeringtoolbox.com/ (accessed on 20 October 2021).
- Sakthivel, J.C.; Mukhopadhyay, S.; Palanisamy, N.K. Some Studies on Mudar Fiber. J. Ind. Text. 2005, 35, 63–76. [Google Scholar] [CrossRef]
- ASTM. International 10th ed. Metals Handbook. Available online: http://products.asminternational.org/hbk/index.jsp (accessed on 24 October 2020).
- Rengasamy, R.; Wesley, D. Study on Dynamic Needle Thread Tensions in a Single Needle Lock Stitch (SNLS). Fibers Polym. 2014, 15, 1773–1778. [Google Scholar] [CrossRef]
- Rudolf, A.; Geršak, J.; Ujhelyiová, A.; Smole, M.S. Study of PES Sewing Thread Properties. Fibers Polym. 2007, 8, 212–217. [Google Scholar] [CrossRef]
- Li, Q.; Liasi, E. A study on the needle heating in heavy industrial sewing-part II. Int. J. Cloth. Sci. Technol. 2001, 13, 87–105. [Google Scholar] [CrossRef]



| Material | Manufacturing Technique | Weight [g/m2] | Thickness [mm] (S.D) | Layers Used |
|---|---|---|---|---|
| PP | Spun-bonded melt-blown polypropylene | 75 | 1.2 (±0.15) | 3 |
| Material | Twist | Count [tex] | Producer |
|---|---|---|---|
| PET | Z/S | 40 | Amman® (Liberec, Czech Republic) |
| Partition ratio of heat gain between needle and thread using Charron’s relation. | |
| Partition ratio of heat gain between needle and fabric using Charron’s relation. | |
| Coefficient of friction between needle and sewing thread. | |
| Coefficient of friction between fabric and sewing thread. | |
| Maximum tension of sewing thread during sewing cycle. | |
| Angle of sewing thread with respect to the needle. | |
| Velocity of needle with respect to the fabric. | |
| Needle penetration force with respect to the fabric. | |
| Velocity of thread with respect to the needle. |
| Property | Symbol | Value | Unit |
|---|---|---|---|
| Heat partition ratio (fabric & needle) [24]. | 0.945 | - | |
| Heat partition ratio (thread & needle) [24]. | 0.958 | - | |
| Density thread [25]. | y | 1400 | kg/m3 |
| Specific heat of thread [26]. | Cy | 750 | J/kgK |
| Thermal conductivity of thread [26]. | y | 0.15 | W/mK |
| Density of fabric [27]. | f | 920 | kg/m3 |
| Specific heat of fabric [26]. | Cf | 1700 | J/kgK |
| Thermal conductivity of fabric [experimental]. | f | 0.04 | W/mK |
| Density of needle [28]. | n | 7850 | kg/m3 |
| Specific heat of needle [28]. | Cn | 523 | J/kgK |
| Thermal conductivity of needle [28]. | n | 40 | W/mK |
| Friction coefficient of needle and thread [experimental value]. | 0.3 | - | |
| Friction coefficient of needle and fabric [experimental value]. | 0.21 | - | |
| Tension thread maximum [29,30]. | 1.05 | N | |
| Needle velocity [experimental value]. | 2.3 | m/s | |
| Machine speed (to be used with constant to balance the equation). | Vm | 1000–4500 | r/min |
| Needle and thread angle of contact [31]. | 60 | o | |
| Frictional normal penetration force to needle from fabric [experimental value]. | 2.5 | N |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazari, A. Effect of Needle Heating on the Sewing of Medical Textiles. Polymers 2021, 13, 4405. https://doi.org/10.3390/polym13244405
Mazari A. Effect of Needle Heating on the Sewing of Medical Textiles. Polymers. 2021; 13(24):4405. https://doi.org/10.3390/polym13244405
Chicago/Turabian StyleMazari, Adnan. 2021. "Effect of Needle Heating on the Sewing of Medical Textiles" Polymers 13, no. 24: 4405. https://doi.org/10.3390/polym13244405
APA StyleMazari, A. (2021). Effect of Needle Heating on the Sewing of Medical Textiles. Polymers, 13(24), 4405. https://doi.org/10.3390/polym13244405





