Artificial Neural Network Modeling of Glass Transition Temperatures for Some Homopolymers with Saturated Carbon Chain Backbone
Abstract
1. Introduction
2. Materials and Methods
2.1. Database Construction
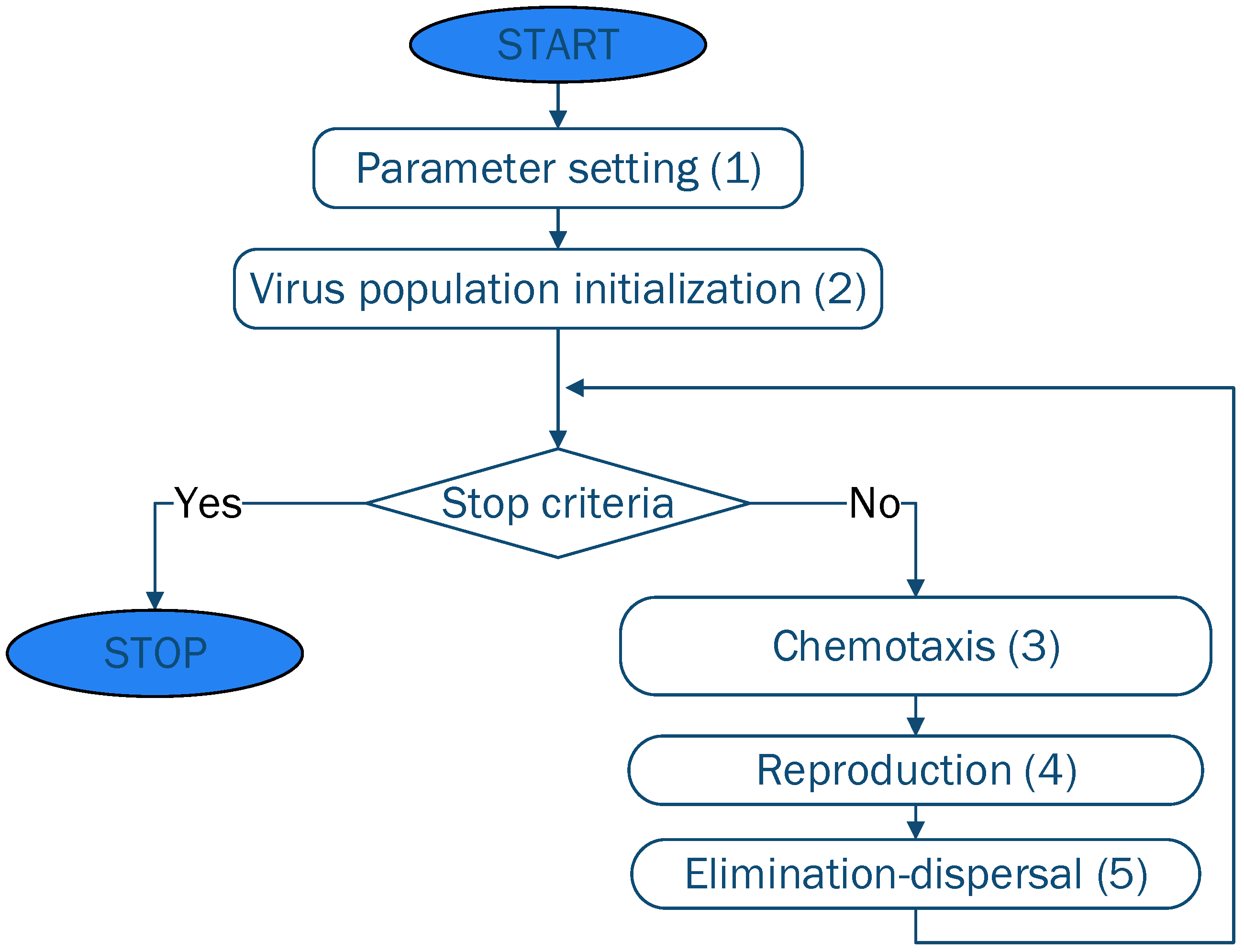
2.2. Bacterial Foraging Optimization
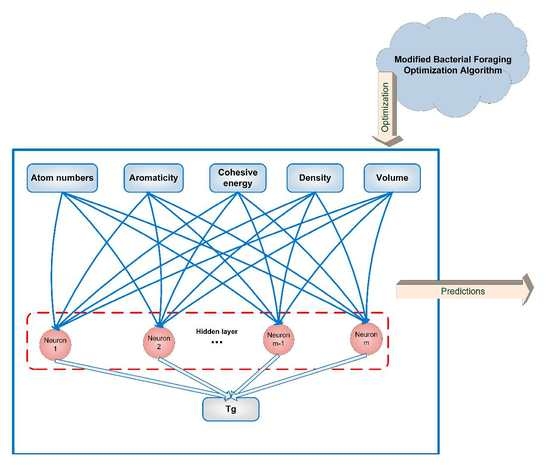
2.3. Artificial Neural Networks
2.4. Sensitivity Analysis
3. Results
3.1. Database
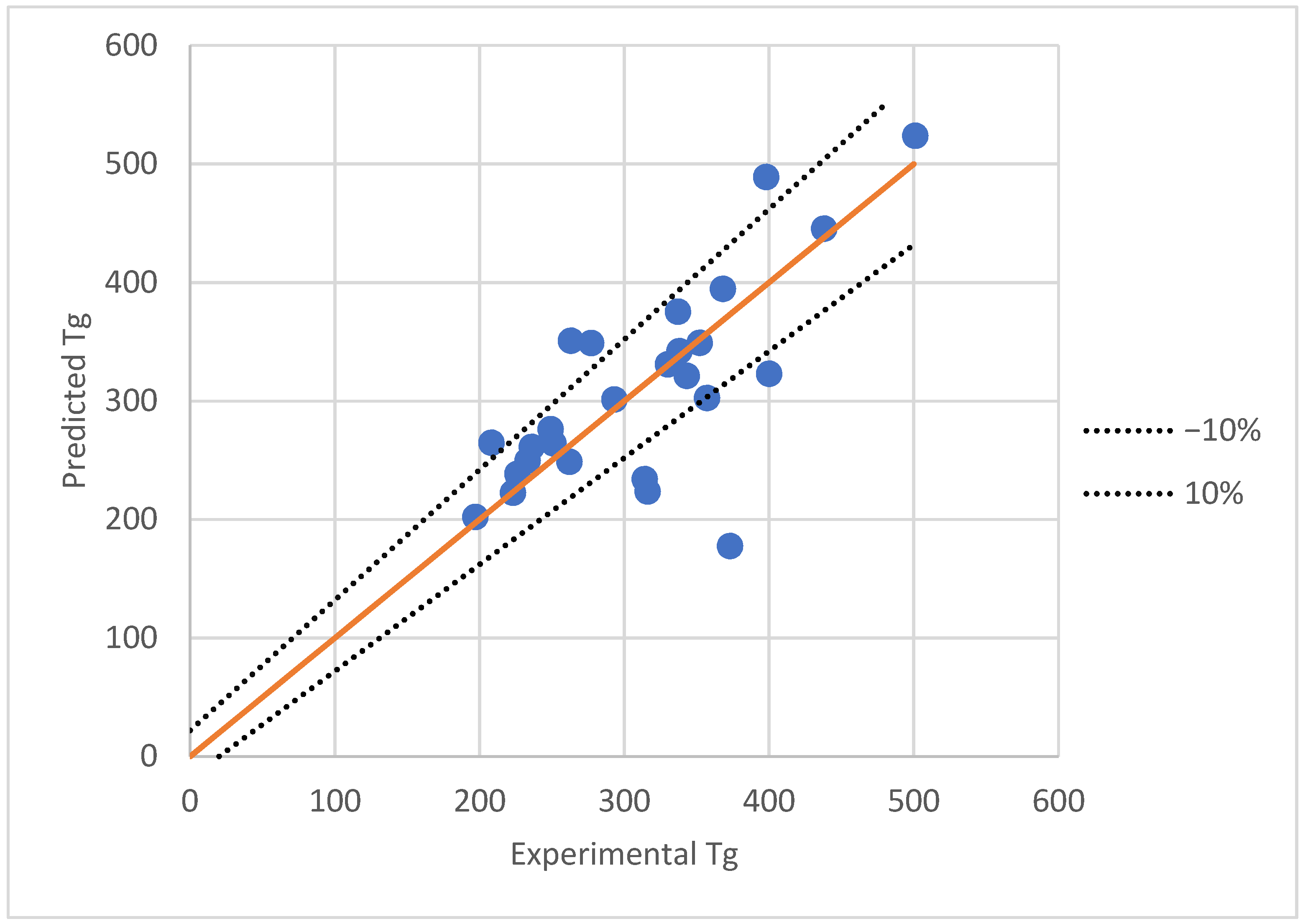
3.2. Artificial Neural Network Modeling
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wickramaarachchi, K.; Sundaram, M.M.; Henry, D.J.; Gao, X. Alginate biopolymer effect on the electrodeposition of manganese dioxide on electrodes for supercapacitors. ACS Appl. Energy Mater. 2021, 4, 7040–7051. [Google Scholar] [CrossRef]
- Sava, I.; Sacarescu, L.; Stoica, I.; Apostol, I.; Damian, V.; Hurduc, N. Photochromic properties of polyimide and polysiloxane azopolymers. Polym. Int. 2009, 58, 163–170. [Google Scholar] [CrossRef]
- Chiriac, A.P.; Rusu, A.G.; Nita, L.E.; Macsim, A.-M.; Tudorachi, N.; Rosca, I.; Stoica, I.; Tampu, D.; Aflori, M.; Doroftei, F. Synthesis of Poly (Ethylene Brassylate-Co-squaric Acid) as Potential Essential Oil Carrier. Pharmaceutics 2021, 13, 477. [Google Scholar] [CrossRef]
- Epure, E.-L.; Stoica, I.; Albu, R.M.; Hulubei, C.; Barzic, A.I. New Strategy for Inducing Surface Anisotropy in Polyimide Films for Nematics Orientation in Display Applications. Nanomaterials 2021, 11, 3107. [Google Scholar] [CrossRef]
- Yoshioka, A.; Tashiro, K. Solvent effect on the glass transition temperature of syndiotactic polystyrene viewed from time-resolved measurements of infrared spectra at the various temperatures and its simulation by molecular dynamics calculation. Macromolecules 2004, 37, 467–472. [Google Scholar] [CrossRef]
- Wu, C. Glass transition in single poly(ethylene oxide) chain: A molecular dynamics simulation study. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 178–188. [Google Scholar] [CrossRef]
- Li, C.; Coons, E.; Strachan, A. Material property prediction of thermoset polymers by molecular dynamics simulations. Acta Mech. 2014, 225, 1187–1196. [Google Scholar] [CrossRef]
- Ma, X.; Zheng, F.; van Sittert, C.G.; Lu, Q. Role of intrinsic factors of polyimides in glass transition temperature: An atomistic investigation. J. Phys. Chem. B 2019, 123, 8569–8579. [Google Scholar] [CrossRef]
- Wu, C. Re-examining the procedure for simulating polymer T g using molecular dynamics. J. Mol. Modeling 2017, 23, 270. [Google Scholar] [CrossRef]
- Hardian, R.; Liang, Z.; Zhang, X.; Szekely, G. Artificial intelligence: The silver bullet for sustainable materials development. Green Chem. 2020, 22, 7521–7528. [Google Scholar] [CrossRef]
- Ding, W.; Lu, Y.; Peng, X.-L.; Dong, H.; Chi, W.; Yuan, X.; Sun, Z.-Z.; He, H. Accelerating evaluation of the mobility of ionic liquids modulated PEDOT flexible electronics using machine learning. J. Mater. Chem. A 2021, 9, 25547–25557. [Google Scholar] [CrossRef]
- Yan, Y.; Mattisson, T.; Moldenhauer, P.; Anthony, E.J.; Clough, P.T. Applying machine learning algorithms in estimating the performance of heterogeneous, multi-component materials as oxygen carriers for chemical-looping processes. Chem. Eng. J. 2020, 387, 124072. [Google Scholar] [CrossRef]
- Kumar, S.; Ignacz, G.; Szekely, G. Synthesis of covalent organic frameworks using sustainable solvents and machine learning. Green Chem. 2021, 23, 8932–8939. [Google Scholar] [CrossRef]
- Cassar, D.R.; De Carvalho, A.C.; Zanotto, E.D. Predicting glass transition temperatures using neural networks. Acta Mater. 2018, 159, 249–256. [Google Scholar] [CrossRef]
- Valderrama, J.O.; Campusano, R.A.; Rojas, R.E. Glass transition temperature of ionic liquids using molecular descriptors and artificial neural networks. C. R. Chim. 2017, 20, 573–584. [Google Scholar] [CrossRef]
- Yu, X.; Huang, X. A quantitative relationship between Tgs and chain segment structures of polystyrenes. Polímeros 2017, 27, 68–74. [Google Scholar] [CrossRef][Green Version]
- Paolo, B.; Pingue, P. Glass Transition Temperature in Polystyrene Supported Thin Films: A SPM-based Investigation of the Role of Molecular Entanglement. J. Polym. Sci. Part B Polym. Phys. 2013, 51, 1149–1156. [Google Scholar]
- Lee, H.; Ahn, H.; Naidu, S.; Seong, B.S.; Ryu, D.Y.; Trombly, D.M.; Ganesan, V. Glass transition behavior of PS films on grafted PS substrates. Macromolecules 2010, 43, 9892–9898. [Google Scholar] [CrossRef]
- Kim, Y.S.; Kim, J.H.; Kim, J.S.; No, K.T. Prediction of glass transition temperature (T g) of some compounds in organic electroluminescent devices with their molecular properties. J. Chem. Inf. Comput. Sci. 2002, 42, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Hu, J.; Marrone, B.L.; Pilania, G.; Yu, X.B. A deep neural network for accurate and robust prediction of the glass transition temperature of polyhydroxyalkanoate homo-and copolymers. Materials 2020, 13, 5701. [Google Scholar] [CrossRef] [PubMed]
- Yu, X. Support vector machine-based QSPR for the prediction of glass transition temperatures of polymers. Fibers Polym. 2010, 11, 757–766. [Google Scholar] [CrossRef]
- Maul, T.H. Improving Neuroevolution with Complementarity-Based Selection Operators. Neural Process. Lett. 2016, 44, 887–911. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar]
- Zheng, S.; Jiang, A.; Yang, X.; Luo, G.; Pham, B.T. A New Reliability Rock Mass Classification Method Based on Least Squares Support Vector Machine Optimized by Bacterial Foraging Optimization Algorithm. Adv. Civ. Eng. 2020, 2020, 3897215. [Google Scholar] [CrossRef]
- Al-Kheraif, A.A.; Hashem, M.; Al Esawy, M.S.S. Developing Charcot–Marie–Tooth disease recognition system using bacterial foraging optimization algorithm based spiking neural network. J. Med. Syst. 2018, 42, 192. [Google Scholar] [CrossRef] [PubMed]
- Chouhan, S.S.; Kaul, A.; Singh, U.P.; Jain, S. Bacterial foraging optimization based radial basis function neural network (BRBFNN) for identification and classification of plant leaf diseases: An automatic approach towards plant pathology. IEEE Access 2018, 6, 8852–8863. [Google Scholar] [CrossRef]
- Teja, V.S.; Srinivas, C.; Radhika, P. Plant Disease Detection and Classification Using Bacteria Foraging Optimization Algorithm Through Convolution Neural Network. J. Comput. Theor. Nanosci. 2020, 17, 3567–3576. [Google Scholar] [CrossRef]
- Dhaliwal, B.S.; Pattnaik, S.S. BFO–ANN ensemble hybrid algorithm to design compact fractal antenna for rectenna system. Neural Comput. Appl. 2016, 28, 917–928. [Google Scholar] [CrossRef]
- Bicerano, J. Prediction of Polymer Properties; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Zhu, G.-Y.; Zhang, W.-B. Optimal foraging algorithm for global optimization. Appl. Soft Comput. 2017, 51, 294–313. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modeling, Control and International Conference on Intelligent Agents, Web Technologies and Internet Commerce, Vienna, Austria, 28 November 2005; pp. 695–701. [Google Scholar]
- Sharma, A.; Sharma, H.; Bhargava, A.; Sharma, N.; Bansal, J.C. Optimal placement and sizing of capacitor using Limaçon inspired spider monkey optimization algorithm. Memetic Comput. 2016, 9, 311–331. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S. Modern meta-heuristics based on nonlinear physics processes: A review of models and design procedures. Phys. Rep. 2016, 655, 1–70. [Google Scholar] [CrossRef]
- Islam, M.; Yao, X. Evolving Artificial Neural Network Ensembles. In Computational Intelligence: A Compendium; Fulcher, J., Jain, L., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; Volume 115, pp. 851–880. [Google Scholar]
- Yeung, D.S.; Cloete, I.; Shi, D.; Ng, W.W.Y. Sensitivity Analysis for Neural Networks; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Chen, G.Z.; Wang, J.Q.; Li, R.Z. Parameter Identification of the 2-Chlorophenol Oxidation Model Using Improved Differential Search Algorithm. J. Chem. 2015, 2015, 313105. [Google Scholar] [CrossRef]
- Montano, J.J.; Palmer, A. Numeric sensitivity analysis applied to feedforward neural networks. Neural Comput. Appl. 2003, 12, 119–125. [Google Scholar] [CrossRef]
- Gevrey, M.; Dimopoulos, I.; Lek, S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecol. Model. 2003, 160, 249–264. [Google Scholar] [CrossRef]
- Dragoi, E.-N.; Curteanu, S.; Galaction, A.-I.; Cascaval, D. Optimization methodology based on neural networks and self-adaptive differential evolution algorithm applied to an aerobic fermentation process. Appl. Soft Comput. 2013, 13, 222–238. [Google Scholar] [CrossRef]

| Case | Statistic Indicator | Fitness | MSE Training | MSE Testing | Correlation (R) Training | Correlation (R) Testing | Architecture |
|---|---|---|---|---|---|---|---|
| 1 | Best | 349.9282 | 0.002858 | 0.041977 | 0.976802 | 0.530663 | 18:13:01 |
| Worst | 150.3113 | 0.006653 | 0.087952 | 0.944351 | −0.15623 | 18:07:01 | |
| Average | 187.8869 | 0.00552 | 0.086771 | 0.954337 | −0.05816 | ||
| 2 | Best | 1125.606 | 0.000888 | 0.039731 | 0.988932 | 0.2676 | 15:08:01 |
| Worst | 213.079 | 0.00469 | 0.02958 | 0.93499 | 0.12272 | 15:04:01 | |
| Average | 813.29 | 0.001905 | 0.033154 | 0.974491 | 0.193581 | ||
| 3 | Best | 164.8208 | 0.006067 | 0.028287 | 0.920757 | 0.726176 | 21:07:01 |
| Worst | 116.8844 | 0.008555 | 0.058398 | 0.88678 | 0.539156 | 21:04:01 | |
| Average | 132.7765 | 0.007608 | 0.049029 | 0.899501 | 0.445961 |
| Order | Input | Sensitivity | Order | Input | Sensitivity |
|---|---|---|---|---|---|
| 1 | Cohesive energy | 10.238 | 12 | Molar volume, 1 K | 3.668 |
| 2 | H | 9.974 | 13 | Connectivity index 0χ | 3.479 |
| 3 | Density | 9.314 | 14 | ar CL | 3.102 |
| 4 | N | 9.183 | 15 | h CL | 3.074 |
| 5 | M CB | 8.023 | 16 | O | 2.920 |
| 6 | Linear | 5.185 | 17 | vdW volume | 2.386 |
| 7 | F | 5.060 | 18 | Molar volume, 298 K | 2.080 |
| 8 | cyc CL | 5.043 | 19 | M CB-H | 1.398 |
| 9 | C | 4.836 | 20 | h CB | 0.993 |
| 10 | Cl | 4.189 | 21 | Connectivity index 1χ | 0.951 |
| 11 | Entanglement molecular weight | 3.9295 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Epure, E.-L.; Oniciuc, S.D.; Hurduc, N.; Drăgoi, E.N. Artificial Neural Network Modeling of Glass Transition Temperatures for Some Homopolymers with Saturated Carbon Chain Backbone. Polymers 2021, 13, 4151. https://doi.org/10.3390/polym13234151
Epure E-L, Oniciuc SD, Hurduc N, Drăgoi EN. Artificial Neural Network Modeling of Glass Transition Temperatures for Some Homopolymers with Saturated Carbon Chain Backbone. Polymers. 2021; 13(23):4151. https://doi.org/10.3390/polym13234151
Chicago/Turabian StyleEpure, Elena-Luiza, Sîziana Diana Oniciuc, Nicolae Hurduc, and Elena Niculina Drăgoi. 2021. "Artificial Neural Network Modeling of Glass Transition Temperatures for Some Homopolymers with Saturated Carbon Chain Backbone" Polymers 13, no. 23: 4151. https://doi.org/10.3390/polym13234151
APA StyleEpure, E.-L., Oniciuc, S. D., Hurduc, N., & Drăgoi, E. N. (2021). Artificial Neural Network Modeling of Glass Transition Temperatures for Some Homopolymers with Saturated Carbon Chain Backbone. Polymers, 13(23), 4151. https://doi.org/10.3390/polym13234151