Effect of SiO2 Particles on the Relaxation Dynamics of Epoxidized Natural Rubber (ENR) in the Melt State by Time-Resolved Mechanical Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Processing
2.3. Characterizations
3. Results and Discussion
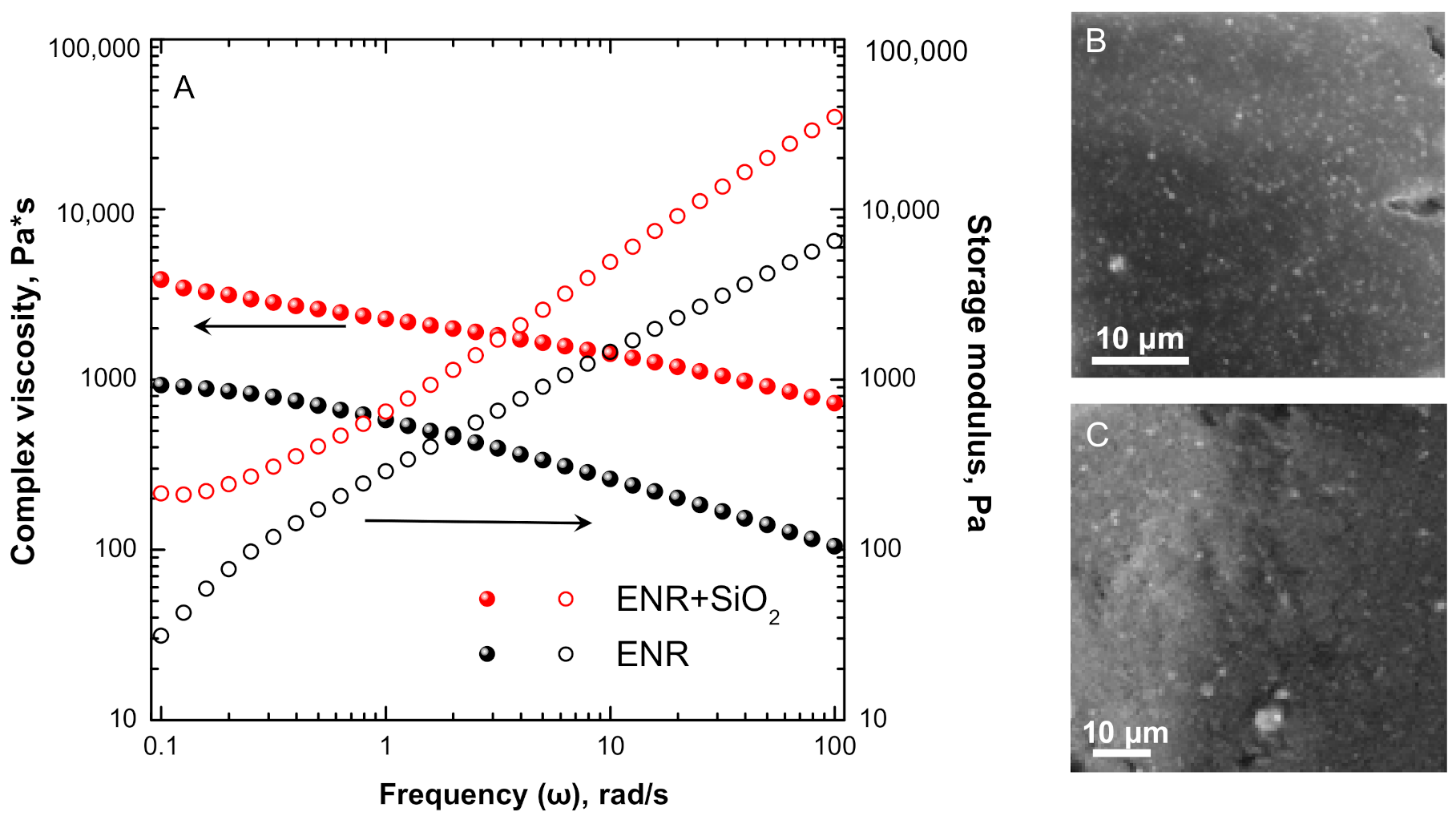
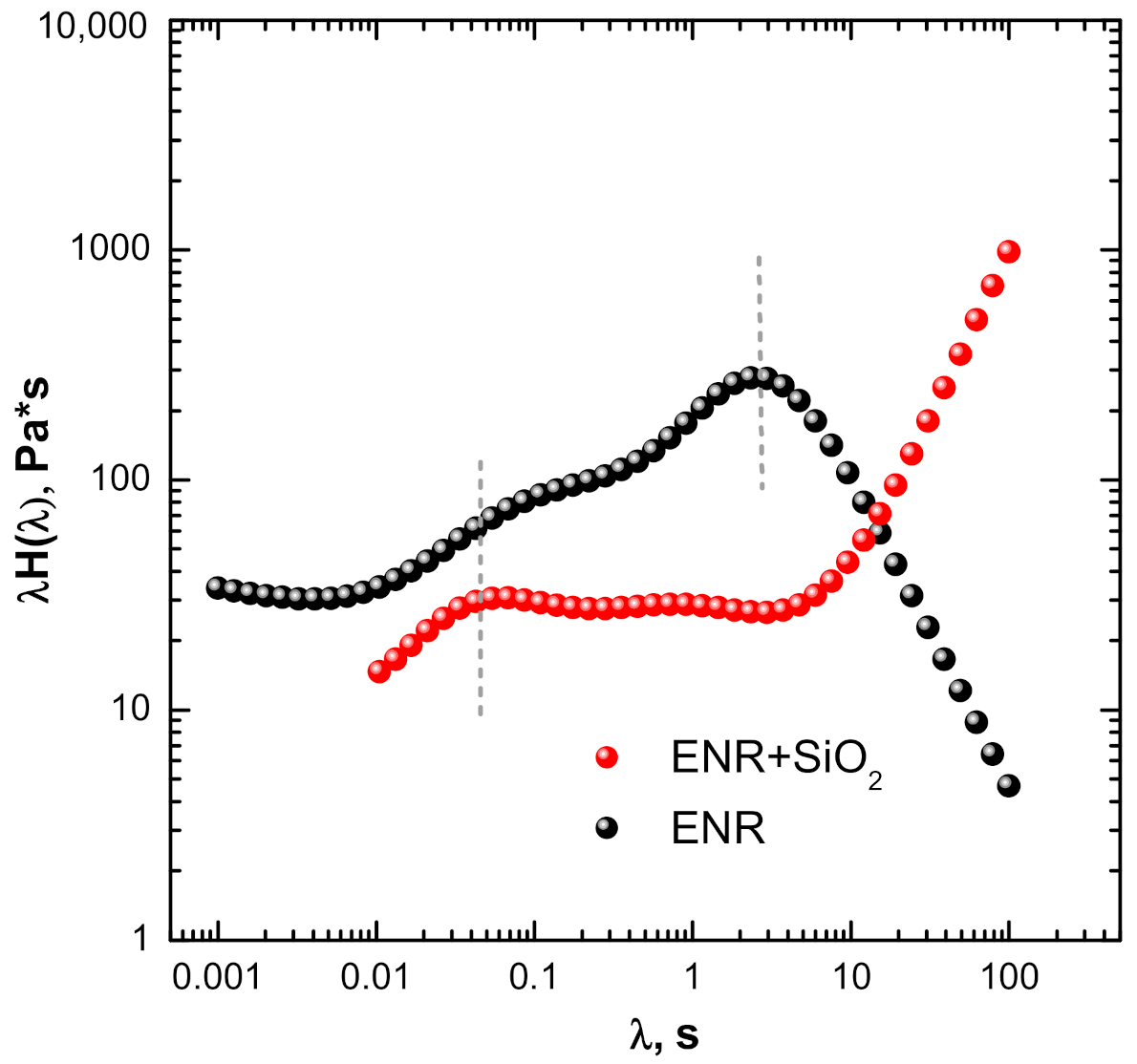
3.1. Linear Rheological Behavior
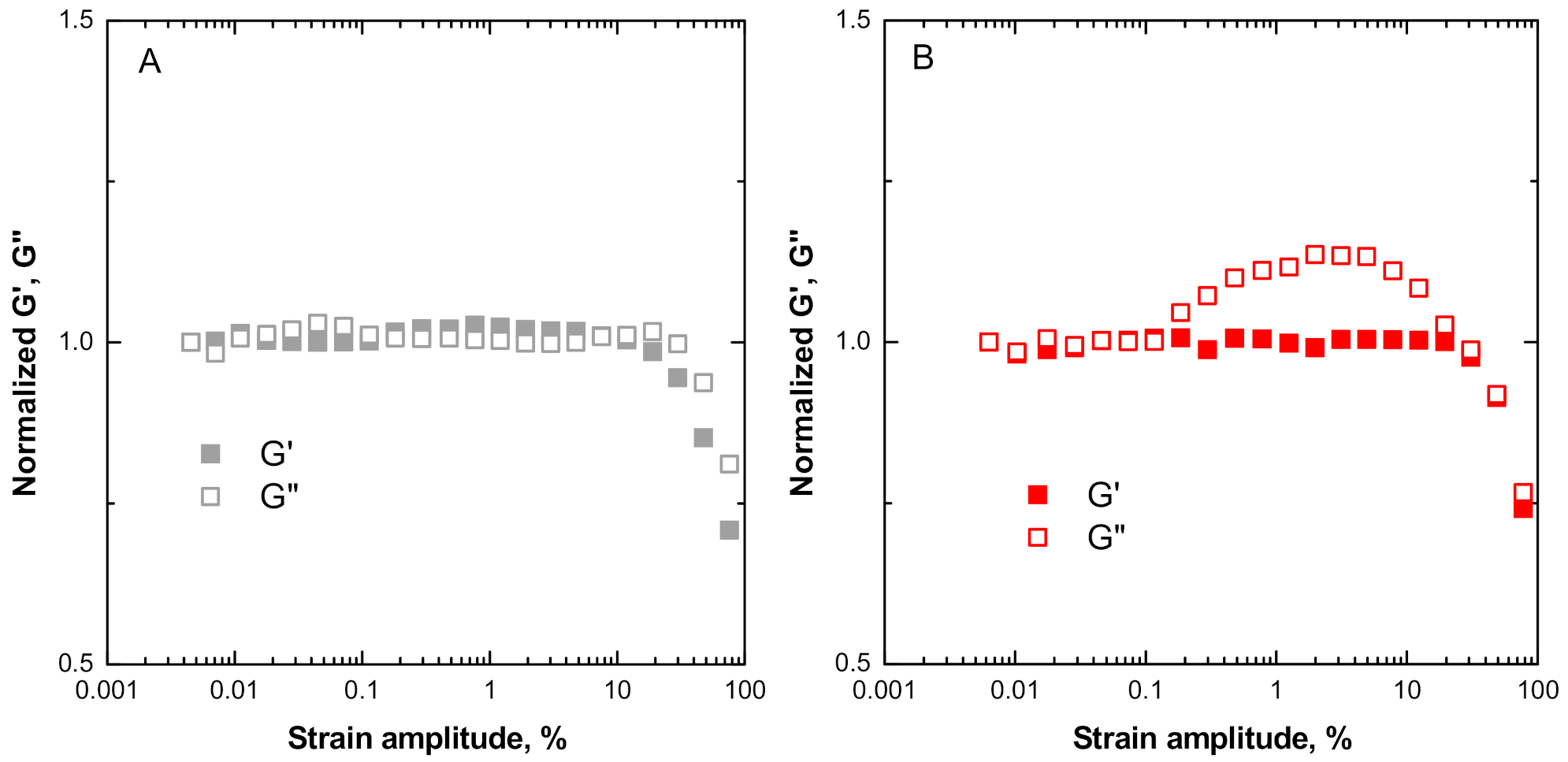
3.2. Non-Linear Rheological Behavior
3.3. Time-Resolved Mechanical Spectroscopy of ENR/SiO2 Composite
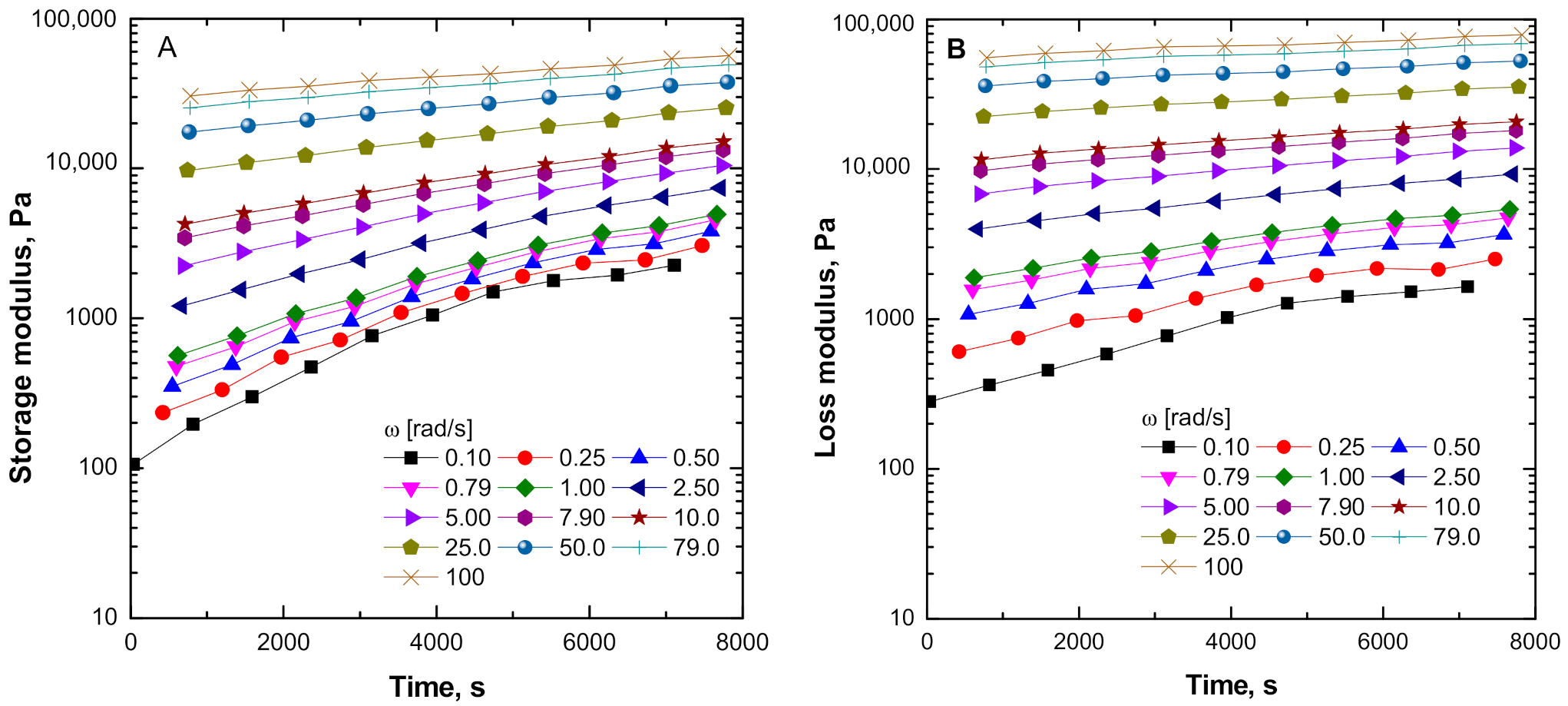
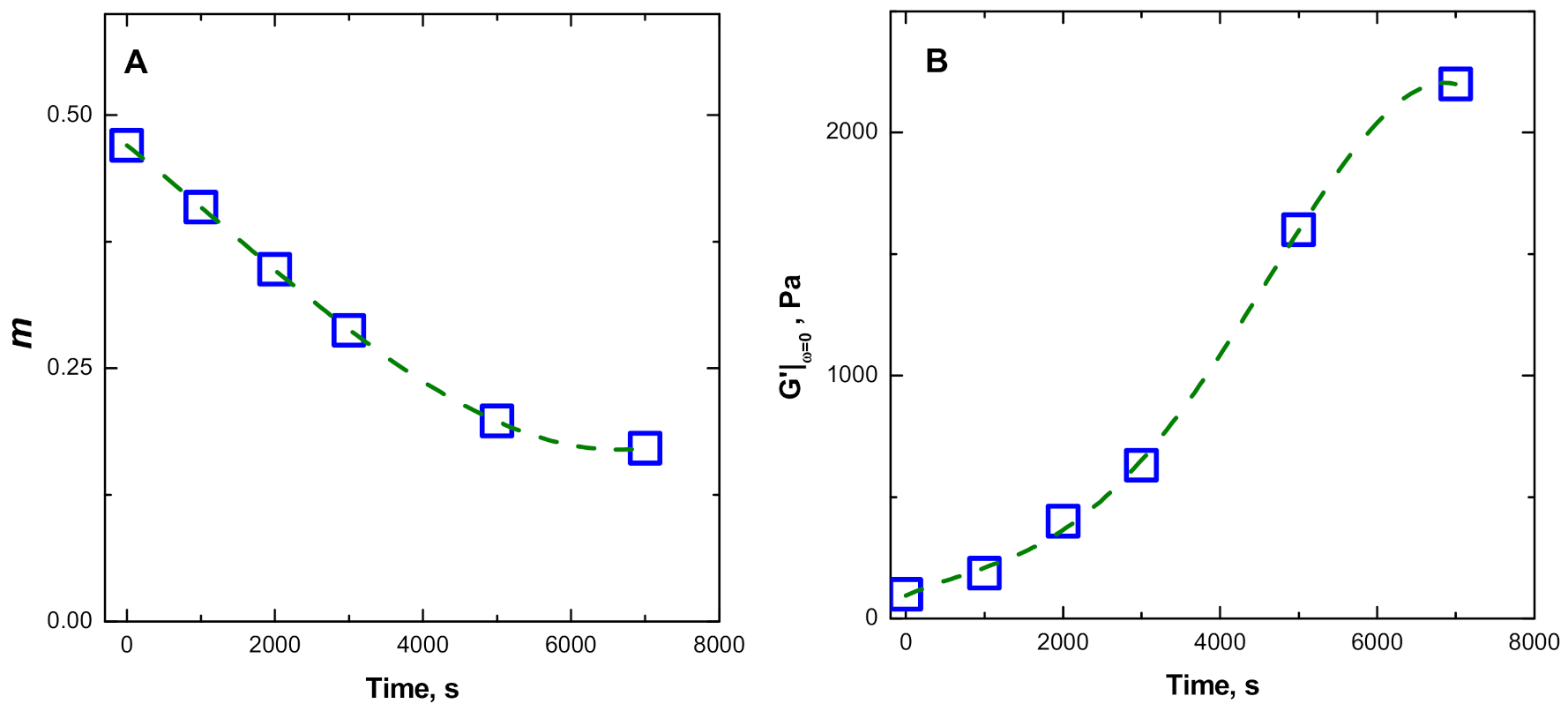
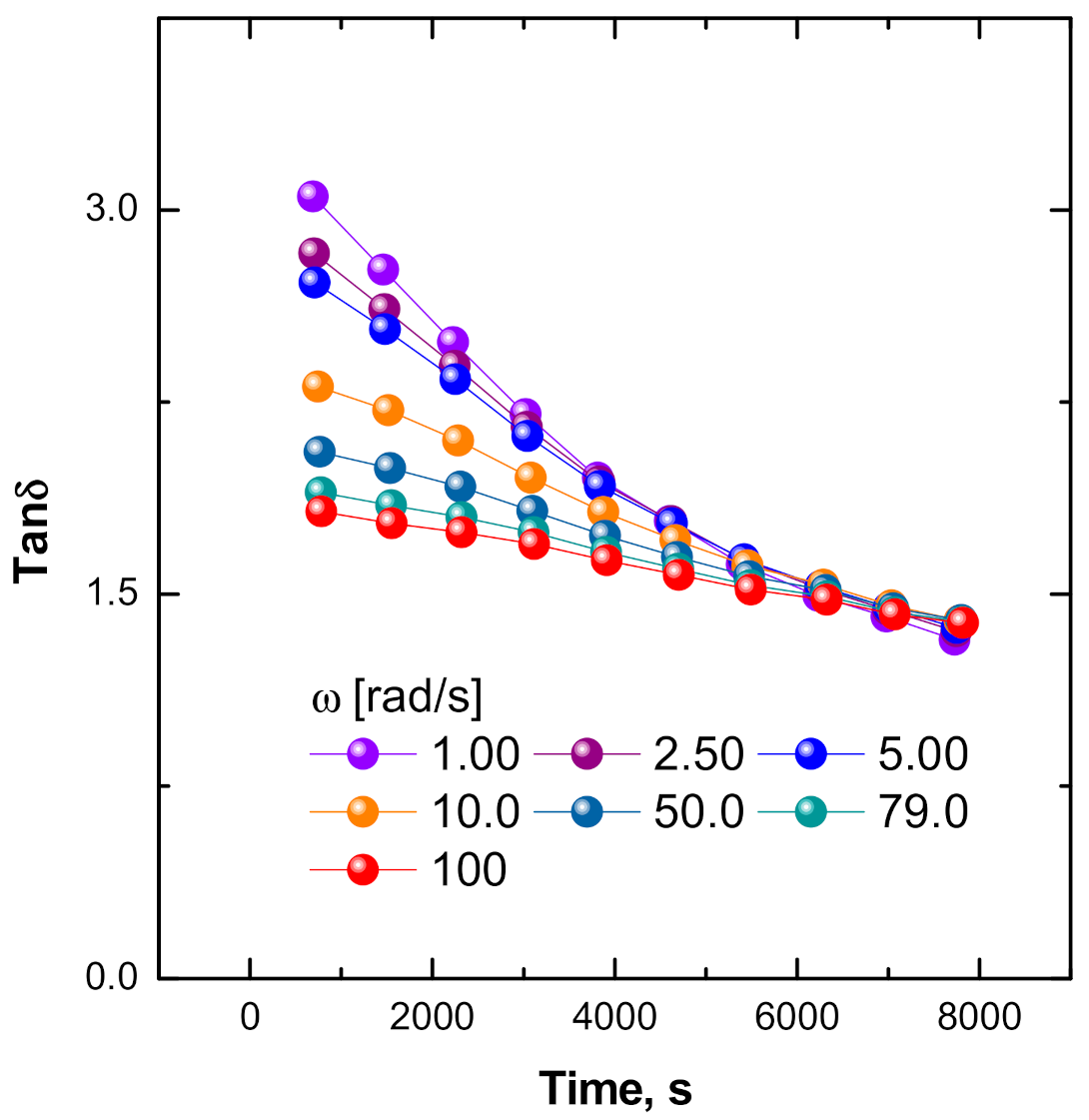
3.3.1. Evolution of the Dynamic Rheological Parameters of ENR + SiO2 Composite
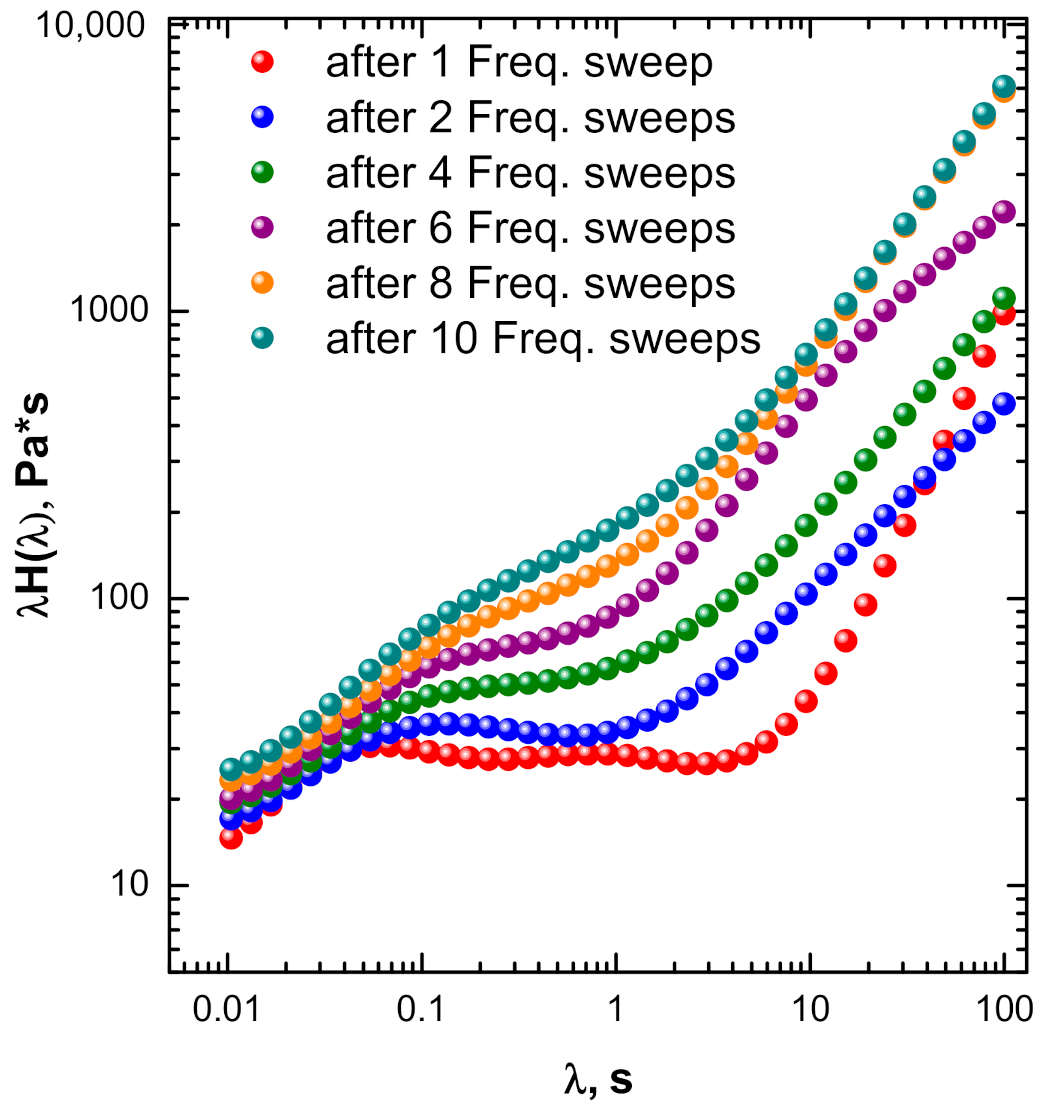
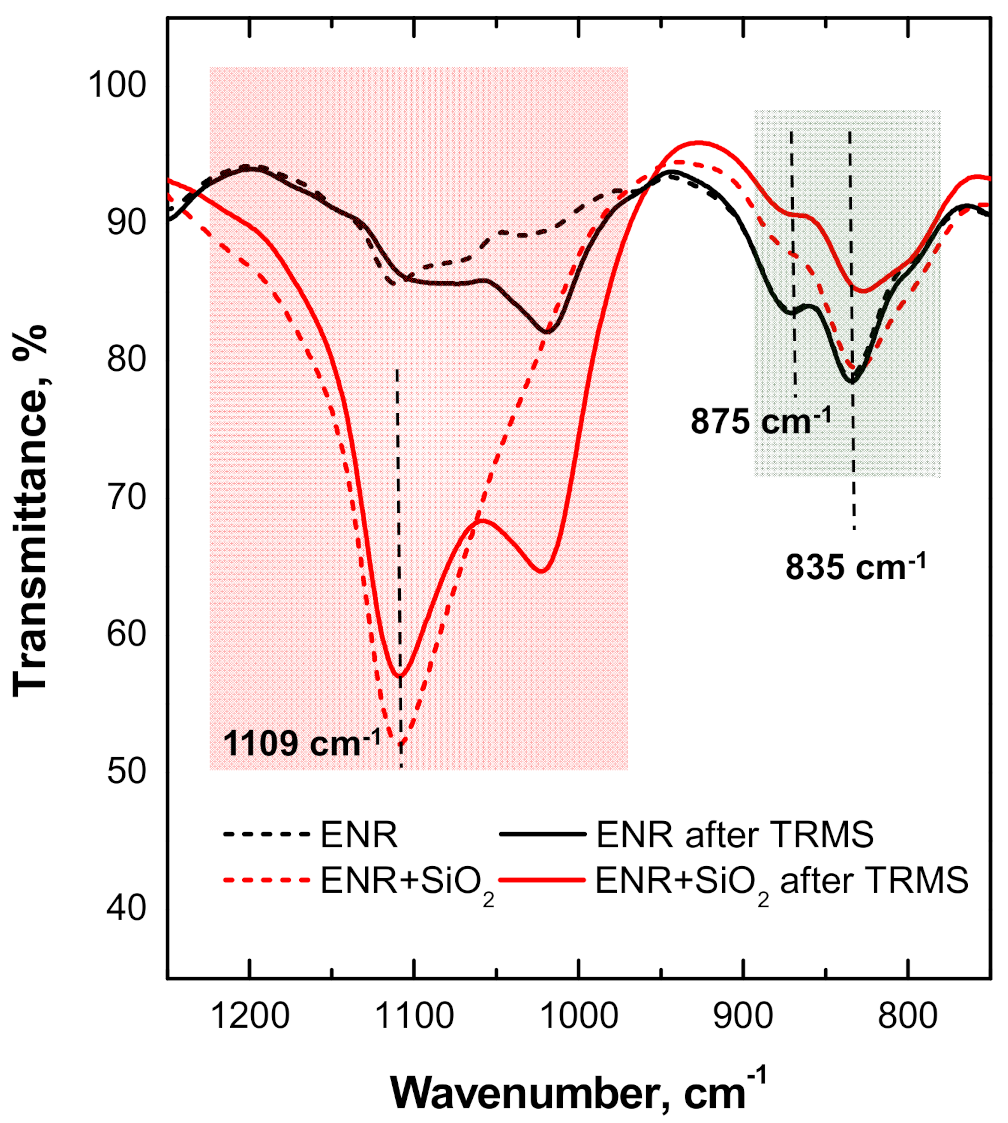
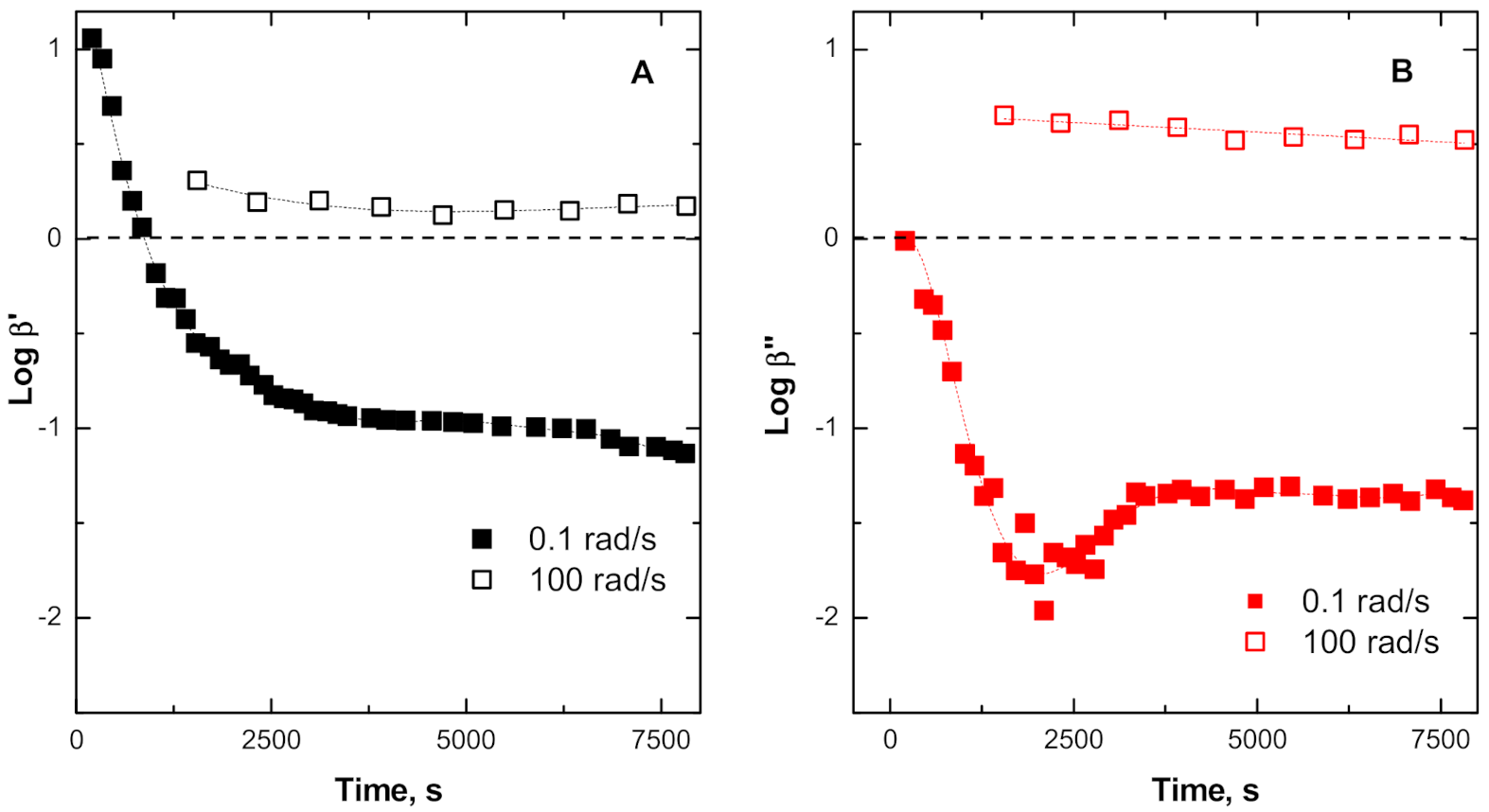
3.3.2. Insights into Phenomena Occurring During TRMS
3.3.3. Rheometric Analysis of the Relative Curing Kinetics of ENR + SiO2 Composite
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sankar Raman, V.; Das, A.; Stöckelhuber, K.W.; Eshwaran, S.B.; Chanda, J.; Malanin, M.; Reuter, U.; Leuteritz, A.; Boldt, R.; Wießner, S.; et al. Improvement of mechanical performance of solution styrene butadiene rubber by controlling the concentration and the size of in-situ derived sol-gel silica particles. RCS Adv. 2016, 6, 33643–33655. [Google Scholar]
- Thuong, N.T.; Dung, T.A.; Yusof, N.H.; Kawahara, S. Controlling the size of silica nanoparticles in filler nanomatrix structure of natural rubber. Polymer 2020, 195, 122444. [Google Scholar] [CrossRef]
- Liu, W.; Lv, L.; Yang, Z.; Zheng, Y.; Wang, H. The Effect of OMMT on the Properties of Vehicle Damping Carbon Black-Natural Rubber Composites. Polymers 2020, 12, 1983. [Google Scholar] [CrossRef] [PubMed]
- Sui, G.; Zhong, W.H.; Yang, X.P.; Yu, Y.H.; Zhao, S.H. Preparation and properties of natural rubber composites reinforced with pretreated carbon nanotubes. Polym. Adv. Technol. 2008, 19, 1543–1549. [Google Scholar] [CrossRef]
- Jarnthong, M.; Nakason, C.; Peng, Z.; Lopattananon, N. Influence of Surface Modification and Content of Nanosilica on Dynamic Mechanical Properties of Epoxidized Natural Rubber Nanocomposites. Adv. Mater. Res. 2013, 844, 289–292. [Google Scholar] [CrossRef]
- Phuhiangpa, N.; Ponloa, W.; Phongphanphanee, S.; Smitthipong, W. Performance of Nano- and Microcalcium Carbonate in Uncrosslinked Natural Rubber Composites: New Results of Structure–Properties Relationship. Polymers 2020, 12, 2002. [Google Scholar] [CrossRef]
- He, C.; She, X.; Peng, Z.; Zhong, J.; Liao, S.; Gong, W.; Liao, J.; Kong, L. Graphene Networks and Its Role on Free-Volume Properties of Graphene/Epoxidized Natural Rubber Composites with a Segregated Structure: Rheological and Positron Annihilation Studies. Phys. Chem. Chem. Phys. 2015, 17, 12175–12184. [Google Scholar] [CrossRef]
- Dintcheva, N.T.; Arrigo, R.; Catalanotto, F.; Morici, E. Improvement of the Photo-Stability of Polystyrene-block-Polybutadiene-block-Polystyrene through Carbon Nanotubes. Polym. Degrad. Stab. 2015, 118, 24–32. [Google Scholar] [CrossRef]
- Maria, H.J.; Lyczko, N.; Nzihou, A.; Joseph, K.; Mathew, K.; Thomas, S. Stress relaxation behavior of organically modified montmorillonite filled natural rubber/nitrile rubber nanocomposites. Appl. Clay Sci. 2014, 87, 20–128. [Google Scholar] [CrossRef]
- Shimizu, T.; Kishi, R.; Kobashi, K.; Morimoto, T.; Okazaki, T.; Yamada, T.; Hata, K. Improved thermal stability of silicone rubber nanocomposites with low filler content, achieved by well-dispersed carbon nanotubes. Compos. Comm. 2020, 22, 100482. [Google Scholar] [CrossRef]
- Song, P.; Song, J.; Zhang, Y. Stretchable conductor based on carbon nanotube/carbon black silicone rubber nanocomposites with highly mechanical, electrical properties and strain sensitivity. Compos. Part B Eng. 2020, 191, 107979. [Google Scholar] [CrossRef]
- Suchat, S.; Lanna, A.; Chotikhun, A.; Hiziroglu, S. Some Properties of Composite Drone Blades Made from Nanosilica Added Epoxidized Natural Rubber. Polymers 2020, 12, 1293. [Google Scholar] [CrossRef] [PubMed]
- Nematollahi, M.; Jalali-Arani, A.; Modarress, H. High-performance bio-based poly(lactic acid)/natural rubber/epoxidized natural rubber blends: Effect of epoxidized natural rubber on microstructure, toughness and static and dynamic mechanical properties. Polym. Int. 2019, 68, 439–446. [Google Scholar] [CrossRef]
- Sengloyluan, K.; Sahakaro, K.; Dierkes, W.K.; Noordermeer, J.W.M. Silica-reinforced tire tread compounds compatibilized by using epoxidized natural rubber. Eur. Polym. J. 2014, 51, 69–79. [Google Scholar] [CrossRef]
- Martin, P.J.; Brown, P.; Chapman, A.V.; Cook, S. Silica-reinforced epoxidized natural rubber tire treads-performance and durability. Rubber Chem. Technol. 2015, 88, 390–411. [Google Scholar] [CrossRef]
- Sarkawi, S.S.; Aziz, A.K.C.; Rahim, R.A.; Ghani, R.A.; Kamaruddin, A.N. Properties of Epoxidized Natural Rubber Tread Compound: The Hybrid Reinforcing Effect of Silica and Silane System. Polym. Polym. Compos. 2016, 24, 775–782. [Google Scholar] [CrossRef]
- Mora-Barrantes, I.; Ibarra, L.; Rodriguez, A.; Gonzalez, L.; Valentin, J.L. Elastomer composites based on improved fumed silica and carbon black. Advantages of mixed reinforcing systems. J. Mater. Chem. 2011, 21, 17526. [Google Scholar] [CrossRef]
- Leblanc, J.L. Rubber-filler interactions and rheological properties in filled compounds. Prog. Polym. Sci. 2002, 27, 627–687. [Google Scholar] [CrossRef]
- Zhu, Z.; Thompson, T.; Wang, S.Q.; von Meerwall, E.D.; Halasa, A. Investigating Linear and Nonlinear Viscoelastic Behavior Using Model Silica-Particle-Filled Polybutadiene. Macromolecules 2005, 38, 8816–8824. [Google Scholar] [CrossRef]
- Xu, H.; Xia, X.; Hussain, M.; Song, Y.; Zheng, Q. Linear and nonlinear rheological behaviors of silica filled nitrile butadiene rubber. Polymer 2018, 156, 222–227. [Google Scholar] [CrossRef]
- Song, Y.; Huang, D. Linear rheology of natural rubber compounds filled with silica, short nylon fiber or both. Polymer 2008, 134, 71–74. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, L.; Zhong, J.; He, D.; Xu, K.; Yang, C.; Luo, Y.; Peng, Z. The behavior of natural rubber–epoxidized natural rubber–silica composites based on wet masterbatch technique. J. Appl. Polym. Sci. 2016, 133, 43571. [Google Scholar] [CrossRef]
- Rueda, M.M.; Auscher, M.C.; Fulchiron, R.; Périé, T.; Martin, G.; Sonntag, P.; Cassagnau, P. Rheology and applications of highly filled polymers: A review of current understanding. Prog. Polym. Sci. 2017, 66, 22–53. [Google Scholar] [CrossRef]
- Domenech, T.; Zouari, R.; Vergnes, B.; Peuvrel-Disdier, E. Formation of Fractal-like Structure in Organoclay-Based Polypropylene Nanocomposites. Macromolecules 2014, 47, 3417–3427. [Google Scholar] [CrossRef]
- Filippone, G.; Carroccio, S.C.; Mendichi, R.; Gioiella, L.; Dintcheva, N.T.; Gambarotti, C. Time-resolved rheology as a tool to monitor the progress of polymer degradation in the melt state e Part I: Thermal and thermo-oxidative degradation of polyamide 11. Polymer 2015, 72, 134–141. [Google Scholar] [CrossRef]
- Gentile, G.; Ambrogi, V.; Cerruti, P.; Di Maio, R.; Nasti, G.; Carfagna, C. Pros and cons of melt annealing on the properties of MWCNT/polypropylene composites. Polym. Degrad. Stab. 2014, 110, 56–64. [Google Scholar] [CrossRef]
- Mours, M.; Winter, H.H. Time-resolved rheometry. Rheol. Acta 1994, 33, 385–397. [Google Scholar] [CrossRef]
- Kruse, M.; Wagner, M.H. Time-resolved rheometry of poly(ethylene terephthalate) during thermal and thermo-oxidative degradation. Rheol. Acta 2016, 55, 789–800. [Google Scholar] [CrossRef]
- Selahiyan, R.; Bandyopadhyay, J.; Sinha Ray, S. Mechanism of Thermal Degradation-Induced gel formation in Polyamide 6/Ethylene Vinyl Alcohol Blend Nanocomposites Studied by Time-Resolved Rheology and Hyphenated Termogravimetric Analyzer Fourier Transform Infrared Spectroscopy Mass Spectroscopy: Synergistic Role of Nanoparticles and Maleic-Grafted Polypropylene. ACS Omega 2019, 4, 9569–9582. [Google Scholar]
- Salehiyan, R.; Malwela, T.; Sinha Ray, S. Thermo-oxidative degradation study of melt-processed polyethylene and its blend with polyamide using time-resolved rheometry. Polym. Degrad. Stab. 2017, 139, 130–137. [Google Scholar] [CrossRef]
- Arrigo, R.; Mascia, L.; Clarke, J.; Malucelli, G. Structure evolution of Epoxidized Natural Rubber (ENR) in the melt state by Time-Resolved Mechanical Spectroscopy. Materials 2020, 13, 946. [Google Scholar] [CrossRef] [PubMed]
- Mascia, L.; Su, R.; Clarke, J.; Lou, Y.; Mele, E. Fibres from blends of epoxidized natural rubber and polylactic acid by the electrospinning process: Compatibilization and surface texture. Eur. Polym. J. 2017, 87, 241–254. [Google Scholar] [CrossRef]
- Mascia, L.; Russo, P.; Verdolotti, L.; Clarke, J.; Lavorgna, M.; Acierno, D. Probing the post-gelation reactions of epoxidized natural rubber cross-linked with dodecenyl succinic anhydride. Rubber Chem. Technol. 2015, 88, 560–573. [Google Scholar] [CrossRef]
- Xanthos, M. Modification of properties of functional fillers. In Functional Fillers for Plastics, 2nd ed.; Xanthos, M., Ed.; Willey-VCH, Verlag GmbH: Weinheim, Germany, 2010; pp. 19–39. [Google Scholar]
- Weese, J.; Honerkamp, L. A nonlinear regularization method for the calculation of relaxation spectra. Rheol. Acta 1993, 32, 65–73. [Google Scholar]
- Mascia, L. Thermoplastics Materials Engineering, 2nd ed.; Elsevier Science Publisher: London, UK, 1989. [Google Scholar]
- López-Barrón, C.R.; Macosko, C.W. Rheological and morphological study of cocontinuous polymer blends during coarsening. J. Rheol. 2012, 56, 1315. [Google Scholar] [CrossRef]
- Behbahani, A.F.; Rissanou, A.; Kritikos, G.; Doxastakis, M.; Burkhart, C.; Polińska, P.; Harmandaris, V.A. Conformations and Dynamics of Polymer Chains in Cis and Trans Polybutadiene/Silica Nanocomposites through Atomistic Simulations: From the Unentangled to the Entangled Regime. Macromolecules 2020, 53, 6173–6189. [Google Scholar] [CrossRef]
- Fan, X.; Xu, H.; Zhang, Q.; Di’e, X.; Song, Y.; Qiang, Z. Insight into the weak strain overshoot of carbon black filled natural rubber. Polymer 2019, 167, 109–117. [Google Scholar] [CrossRef]
- Fan, X.; Xu, H.; Wu, C.; Song, Y.; Zheng, Q. Influences of chemical crosslinking, physical associating, and filler filling on nonlinear rheological responses of polyisoprene. J. Rheol. 2020, 64, 775. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Soo Cho, K.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Progr. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Xu, T.; Jia, Z.; Wang, S.; Chen, Y.; Luo, Y.; Jia, D.; Peng, Z. Self-crosslinkable epoxidized natural rubber–silica hybrids. J. Appl. Polym. Sci. 2017, 134, 44605. [Google Scholar] [CrossRef]
- Rooshenass, P.; Yahya, R.; Gan, S.N. Comparison of three different degradation methods to produce liquid epoxidized natural rubber. Rubb. Chem. Technol. 2016, 89, 177–198. [Google Scholar] [CrossRef]
- Luo, Y.Y.; Wang, Y.Q.; Zhong, J.P.; He, C.Z.; Li, Y.Z.; Peng, Z. Interaction Between Fumed-Silica and Epoxidized Natural Rubber. J. Inorg. Organomet. Polym. 2011, 21, 777–783. [Google Scholar] [CrossRef]
- Chiou, B.S.; Raghavan, S.R.; Khan, S.A. Effect of Colloidal Fillers on the Cross-Linking of a UV-Curable Polymer: Gel Point Rheology and the Winter-Chambon Criterion. Macromolecules 2001, 34, 4526–4533. [Google Scholar] [CrossRef]
- Ono, S.; Kiuchi, Y.; Sawanobori, J.; Ito, M. Structure development in silica-filled rubber composites. Polym. Int. 1999, 48, 1035–1041. [Google Scholar] [CrossRef]
- Xu, H.; Liu, J.; Fang, L.; Wu, C. In situ Grafting onto Silica Surface with Epoxidized Natural Rubber via Solid State Method. J. Macromol. Sci. B 2007, 46, 693–703. [Google Scholar] [CrossRef]
- Mascia, L.; Clarke, J.; Ng, K.S.; Chua, K.S.; Russo, P. Curing efficiency of Dodecyl Succinic Anhydride as a Cross-Linking Agent for Elastomer Blends Based on Epoxidized Natural Rubber. J. Appl. Polym. Sci. 2015, 132, 41448. [Google Scholar] [CrossRef]
- Winter, H.H.; Chambon, F. Analysis of Linear Viscoelasticity of a Crosslinking Polymer at the Gel Point. J. Rheol. 1986, 30, 367. [Google Scholar] [CrossRef]
- Li, Z.; Kontopoulou, M. Evolution of Rheological Properties and Morphology Development during Crosslinking of Polyolefin Elastomers and their TPV Blends with Polypropylene. Polym. Eng. Sci. 2009, 49, 34–43. [Google Scholar] [CrossRef]
- Madbouly, S.A.; Otaigbe, J.U. Kinetic Analysis of Fractal Gel Formation in Waterborne Polyurethane Dispersions Undergoing High Deformation Flows. Macromolecules 2006, 39, 4144–4151. [Google Scholar] [CrossRef]
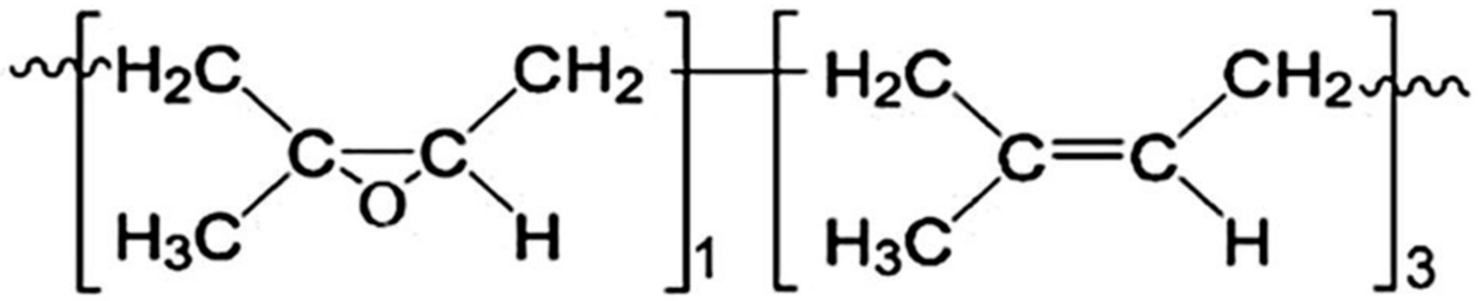

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arrigo, R.; Mascia, L.; Clarke, J.; Malucelli, G. Effect of SiO2 Particles on the Relaxation Dynamics of Epoxidized Natural Rubber (ENR) in the Melt State by Time-Resolved Mechanical Spectroscopy. Polymers 2021, 13, 276. https://doi.org/10.3390/polym13020276
Arrigo R, Mascia L, Clarke J, Malucelli G. Effect of SiO2 Particles on the Relaxation Dynamics of Epoxidized Natural Rubber (ENR) in the Melt State by Time-Resolved Mechanical Spectroscopy. Polymers. 2021; 13(2):276. https://doi.org/10.3390/polym13020276
Chicago/Turabian StyleArrigo, Rossella, Leno Mascia, Jane Clarke, and Giulio Malucelli. 2021. "Effect of SiO2 Particles on the Relaxation Dynamics of Epoxidized Natural Rubber (ENR) in the Melt State by Time-Resolved Mechanical Spectroscopy" Polymers 13, no. 2: 276. https://doi.org/10.3390/polym13020276
APA StyleArrigo, R., Mascia, L., Clarke, J., & Malucelli, G. (2021). Effect of SiO2 Particles on the Relaxation Dynamics of Epoxidized Natural Rubber (ENR) in the Melt State by Time-Resolved Mechanical Spectroscopy. Polymers, 13(2), 276. https://doi.org/10.3390/polym13020276






