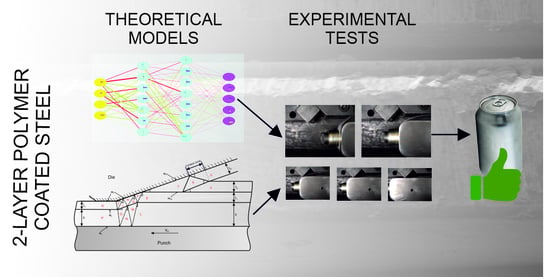
Use of a Novel Polymer-Coated Steel as an Alternative to Traditional Can Manufacturing in the Food Industry †
Abstract
1. Introduction
- Maximizing steel–polymer interface adhesion by appropriately selecting the polymer.
- Desired permeability can be implemented on the exterior surface, which can help in decoration.
- Formability can increase by modifying the mechanical properties of the polymer layers.
- Different design objectives are possible by altering the thickness of each layer.
2. Materials and Methods
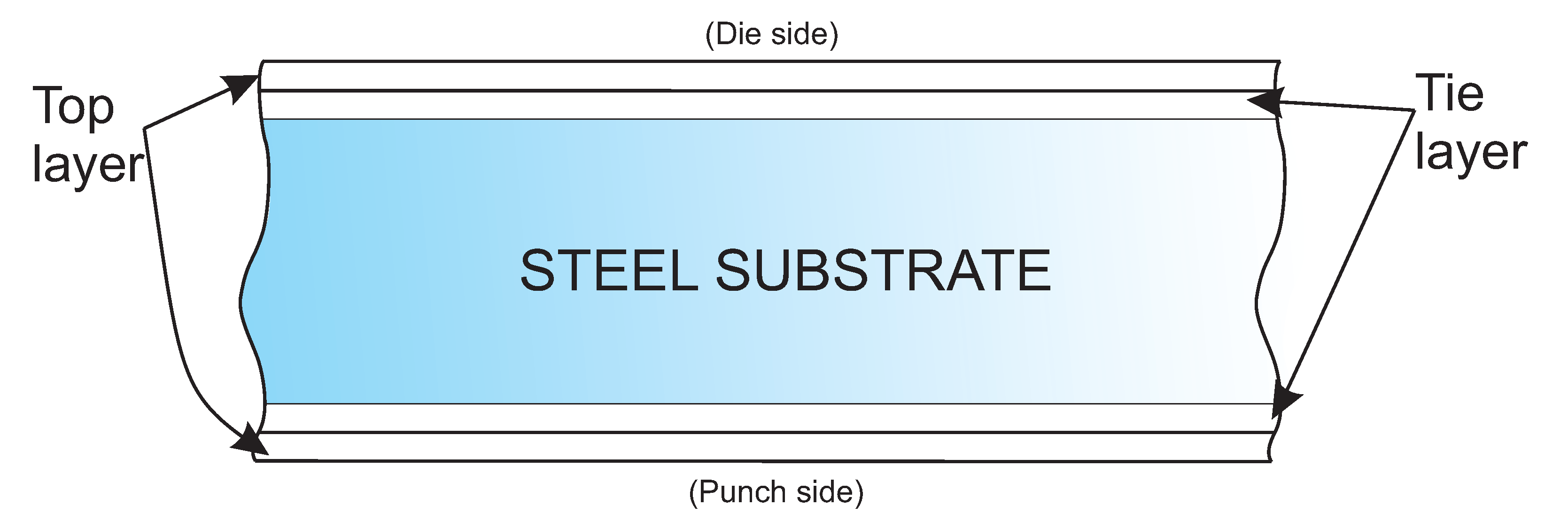
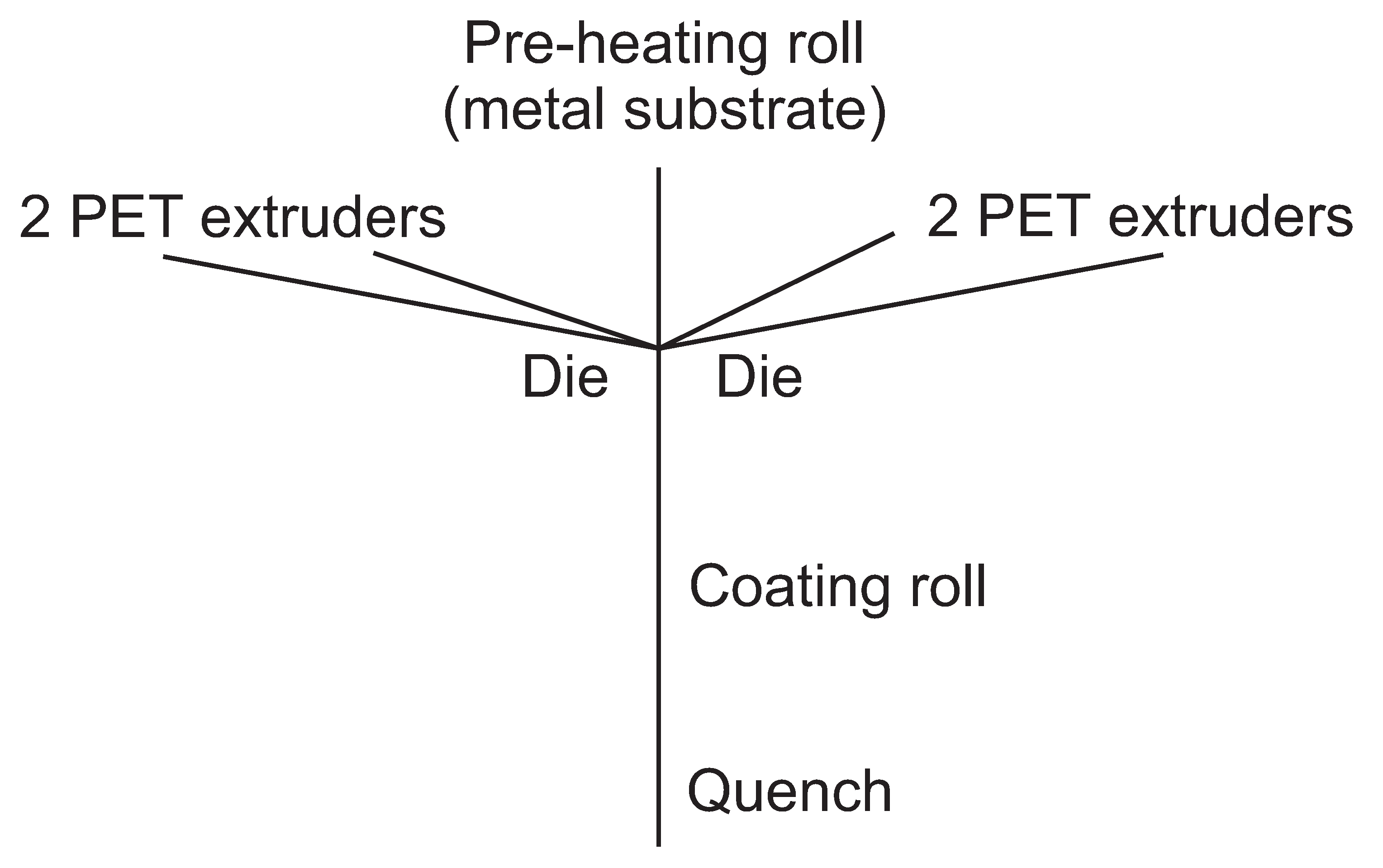
2.1. Material
2.2. Experimental Procedure
2.3. UBM Models
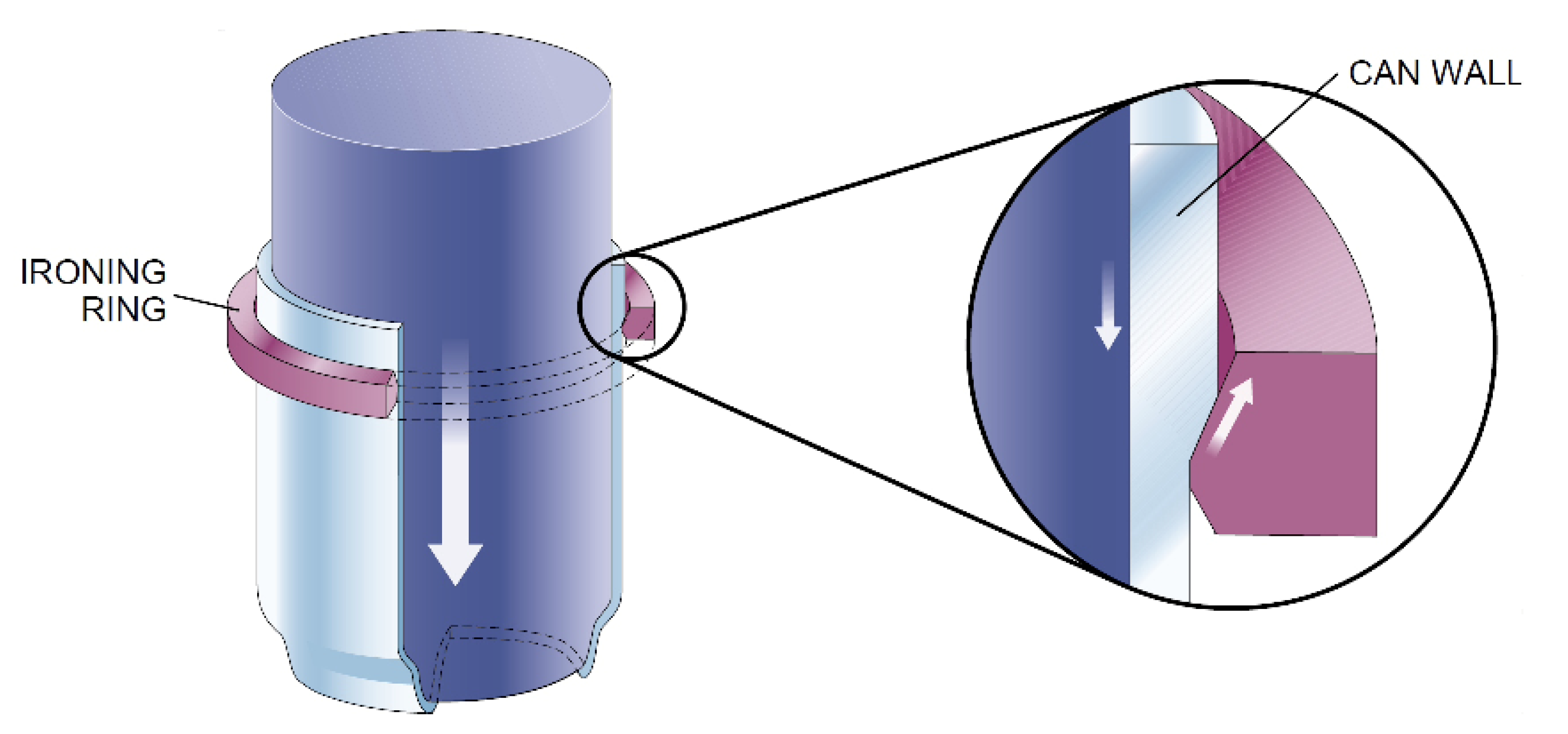
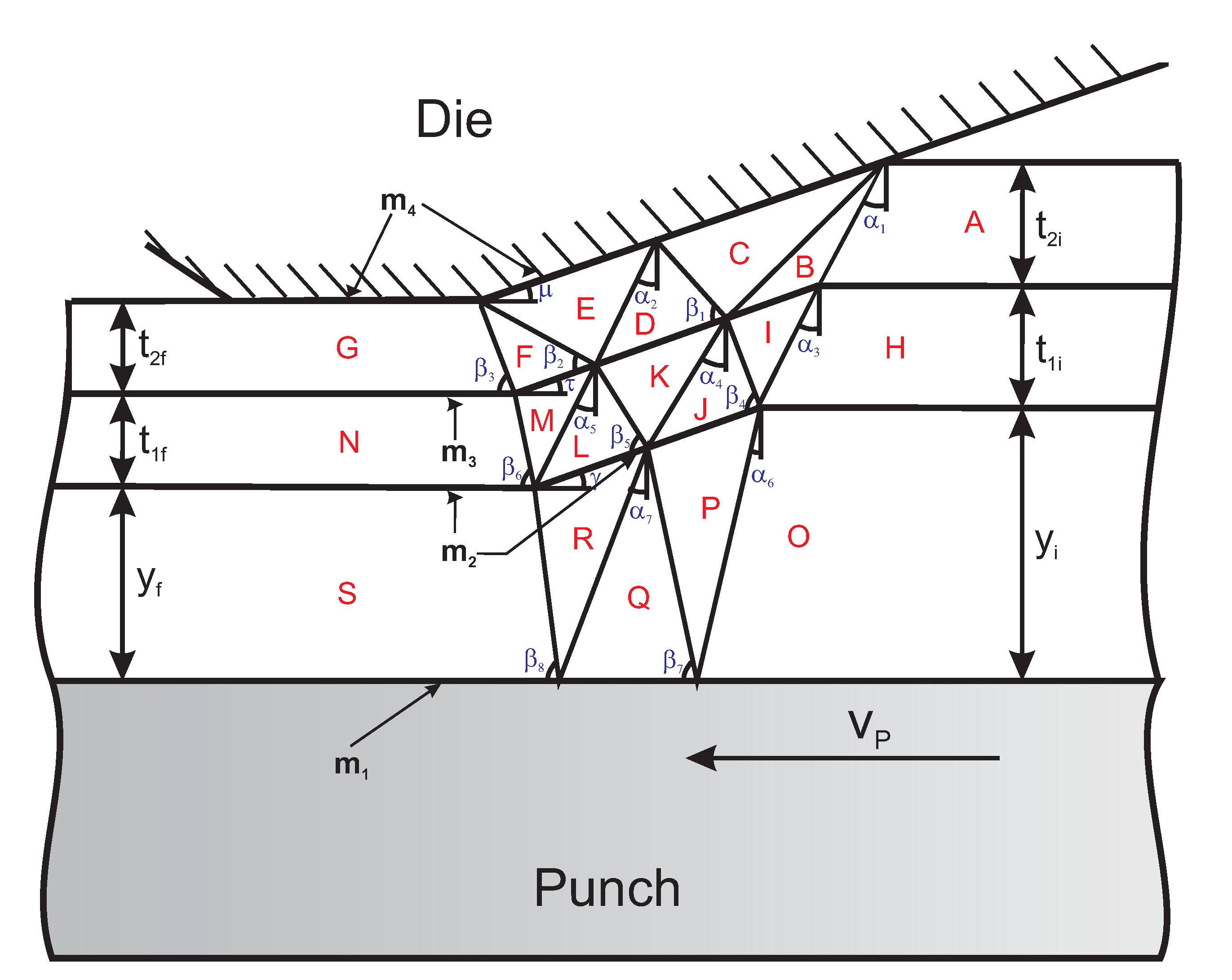
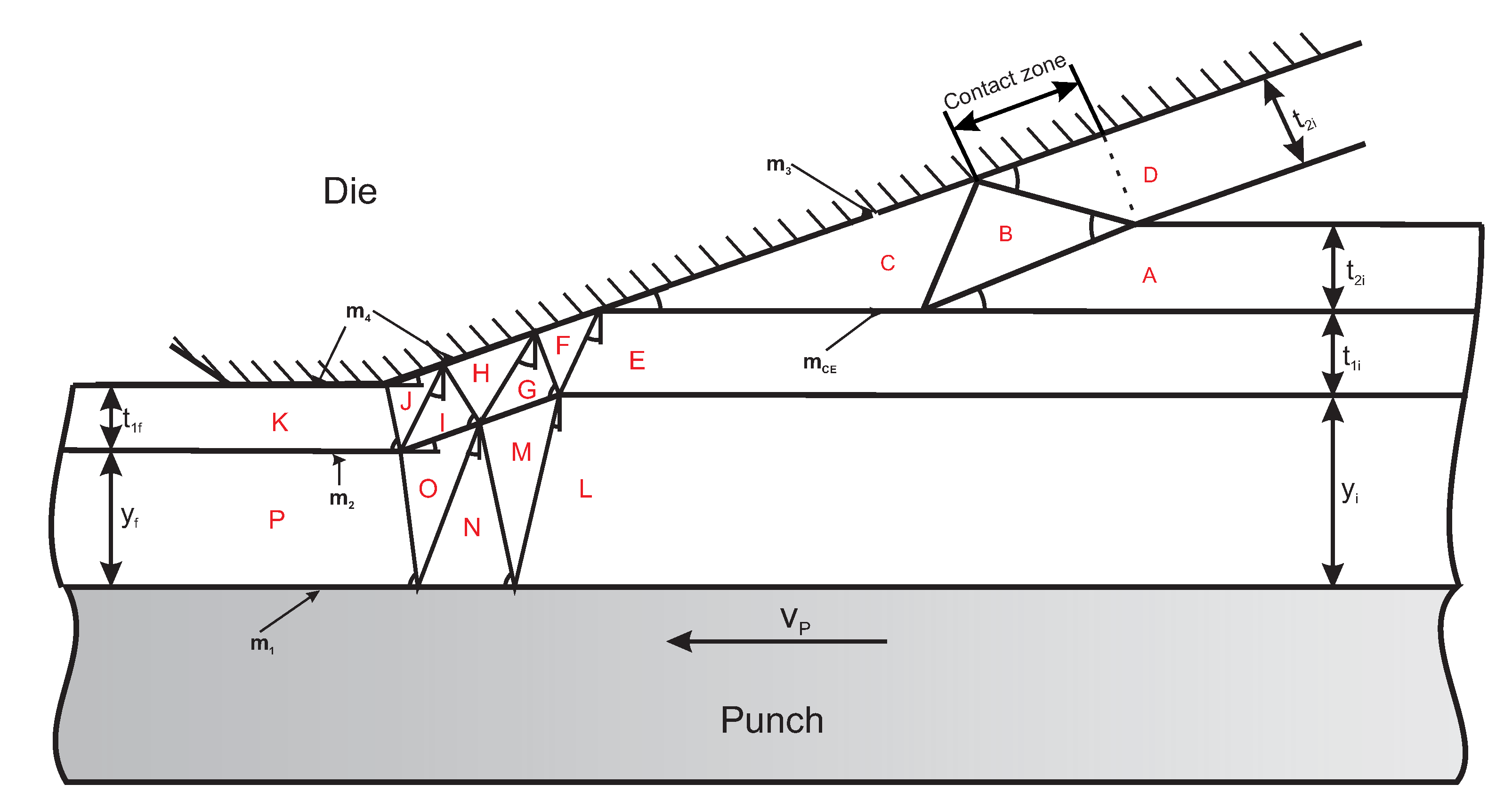
2.3.1. Model for Ironing
2.3.2. Model for Shaving
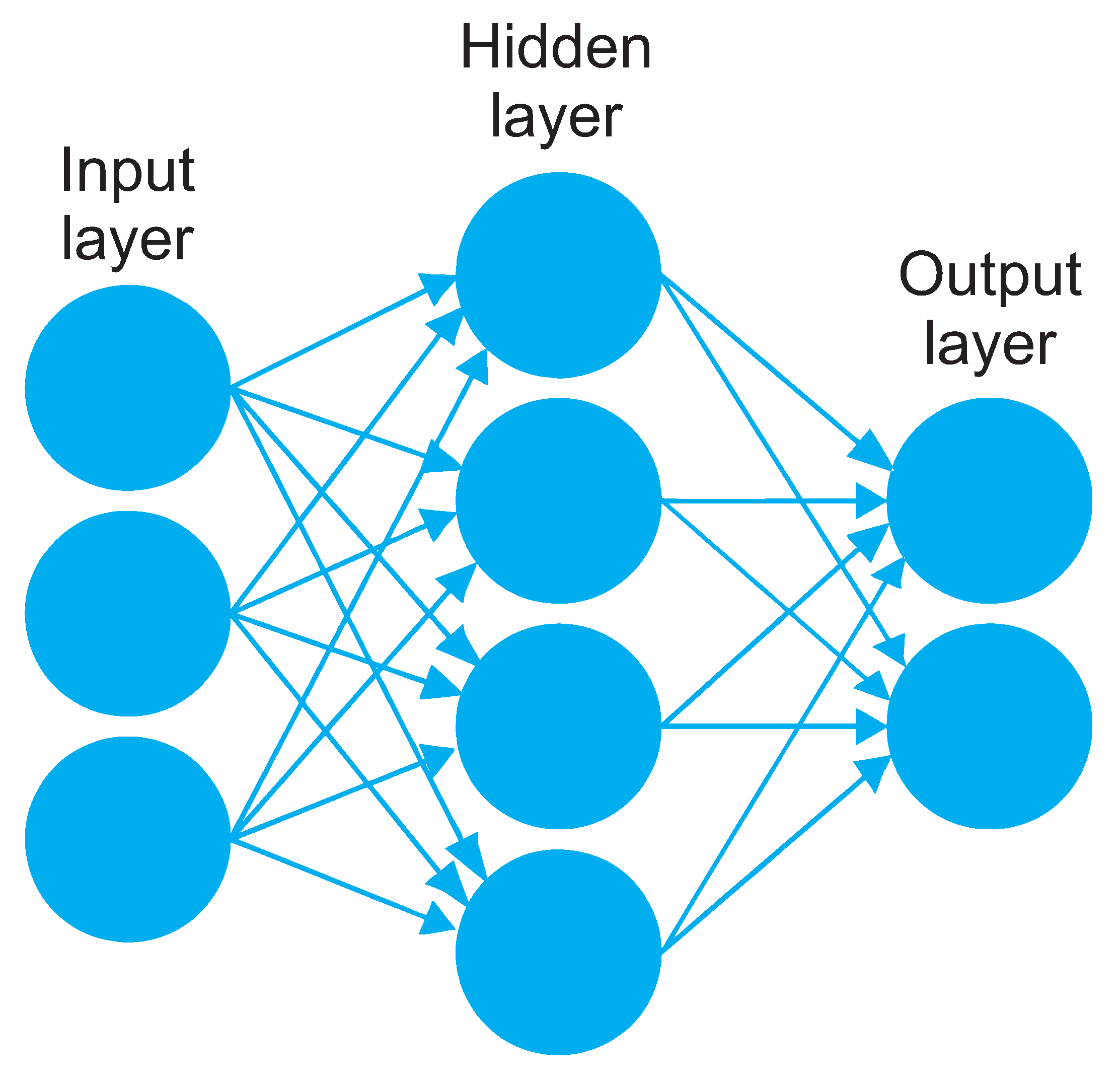
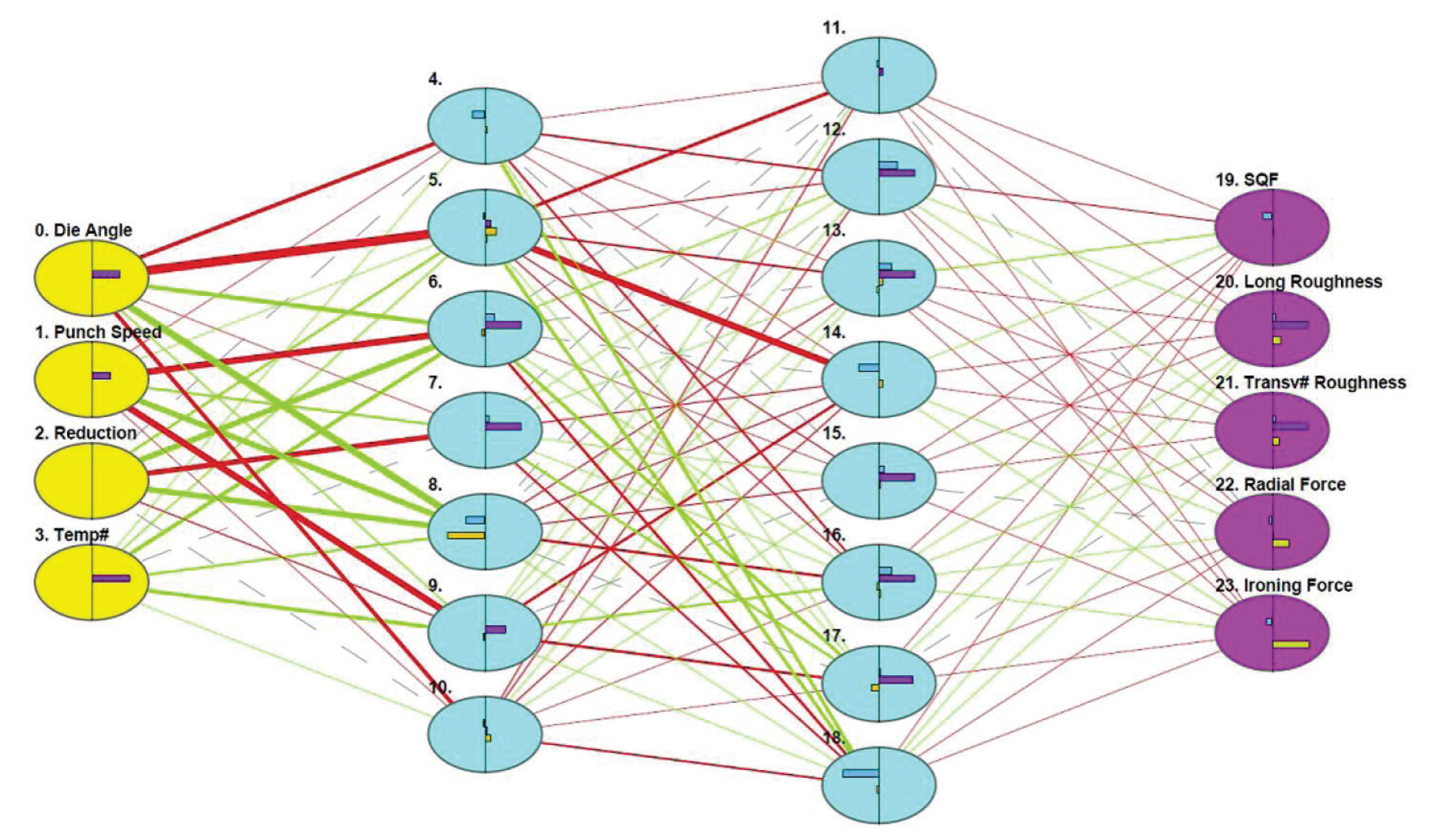
2.4. Artificial Neural Network (ANN)
3. Results
3.1. Theoretical Results
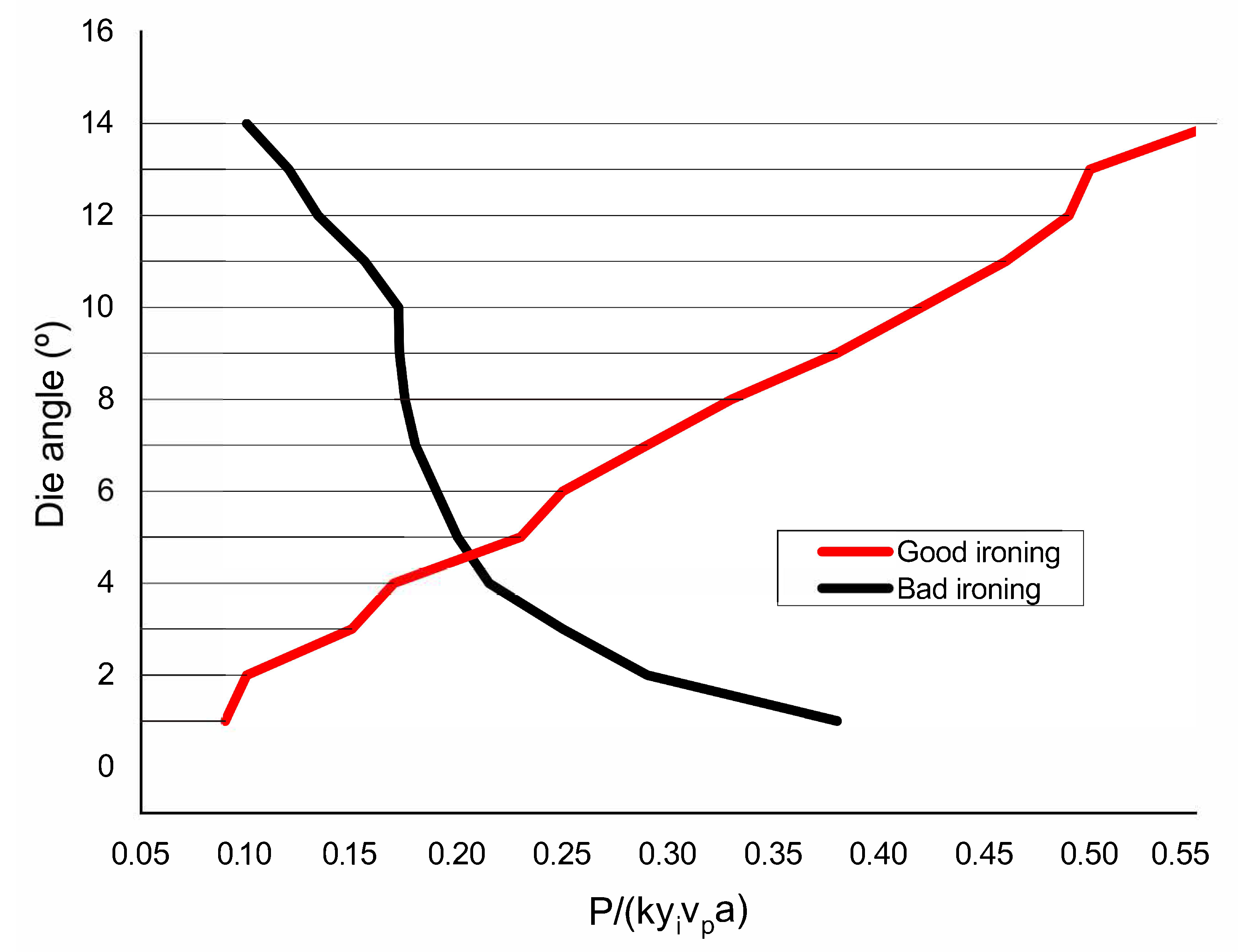
3.1.1. UBM Models Results
3.1.2. ANN Results
3.2. Experimental Results
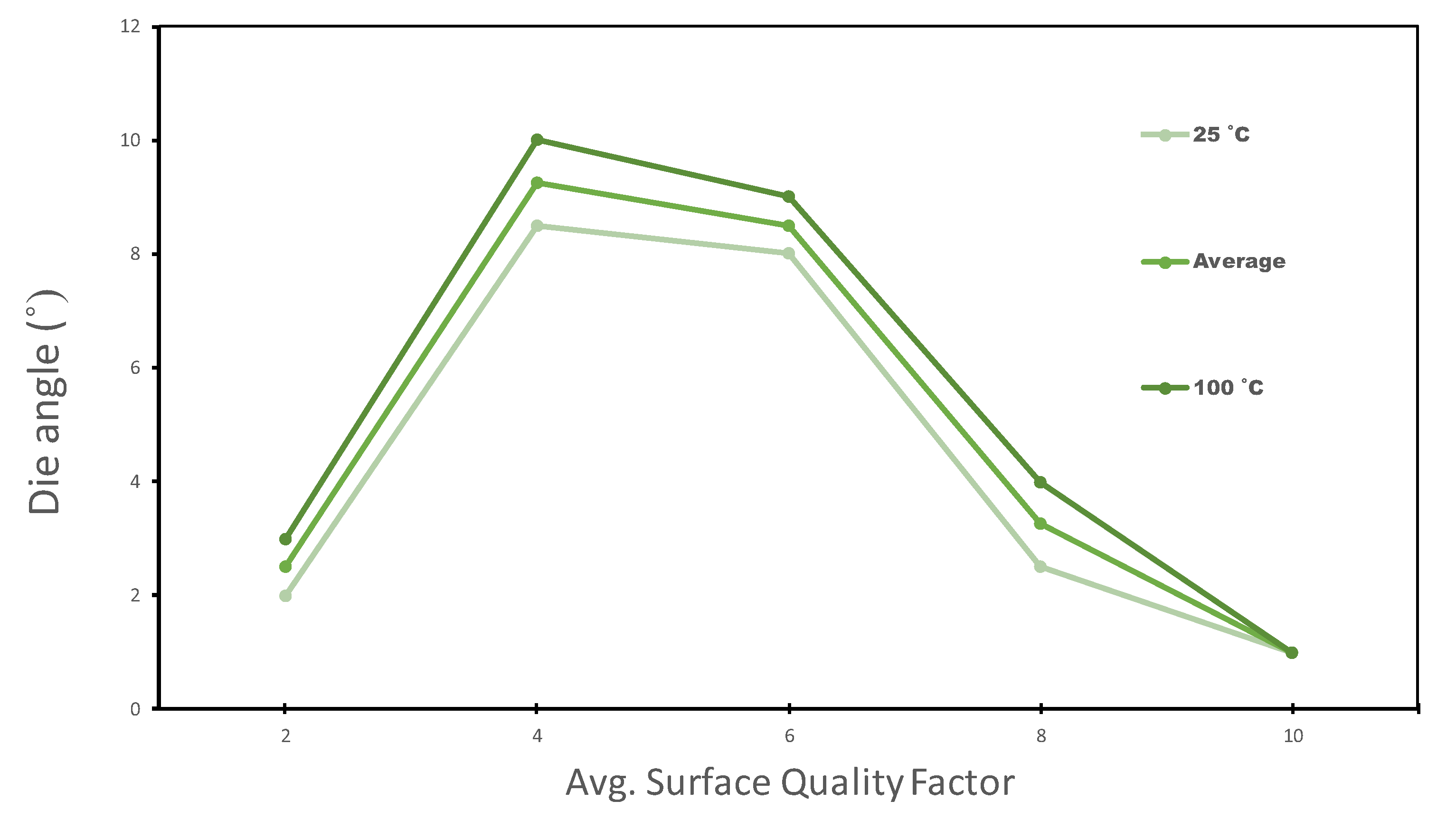
3.2.1. Surface Quality Factor
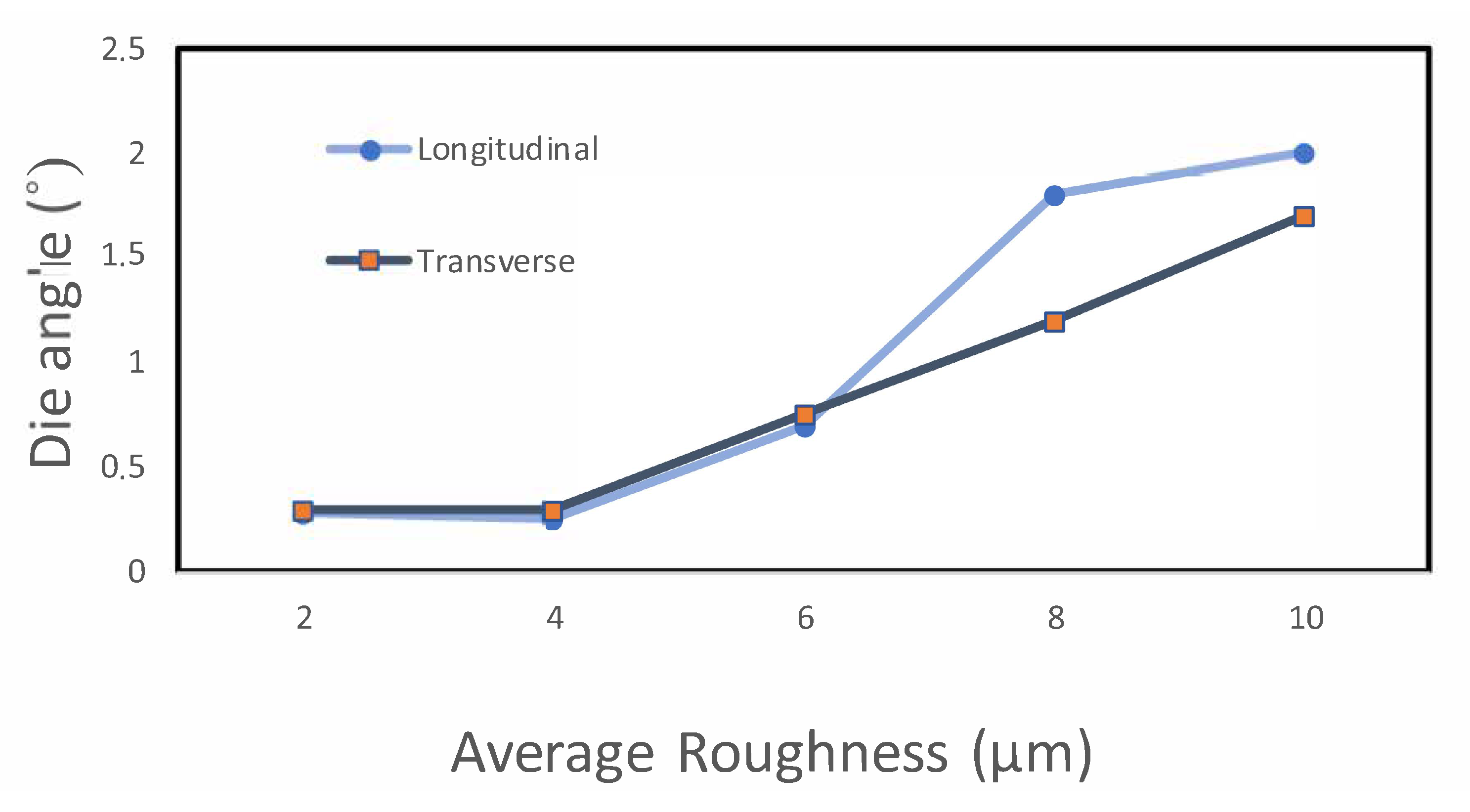
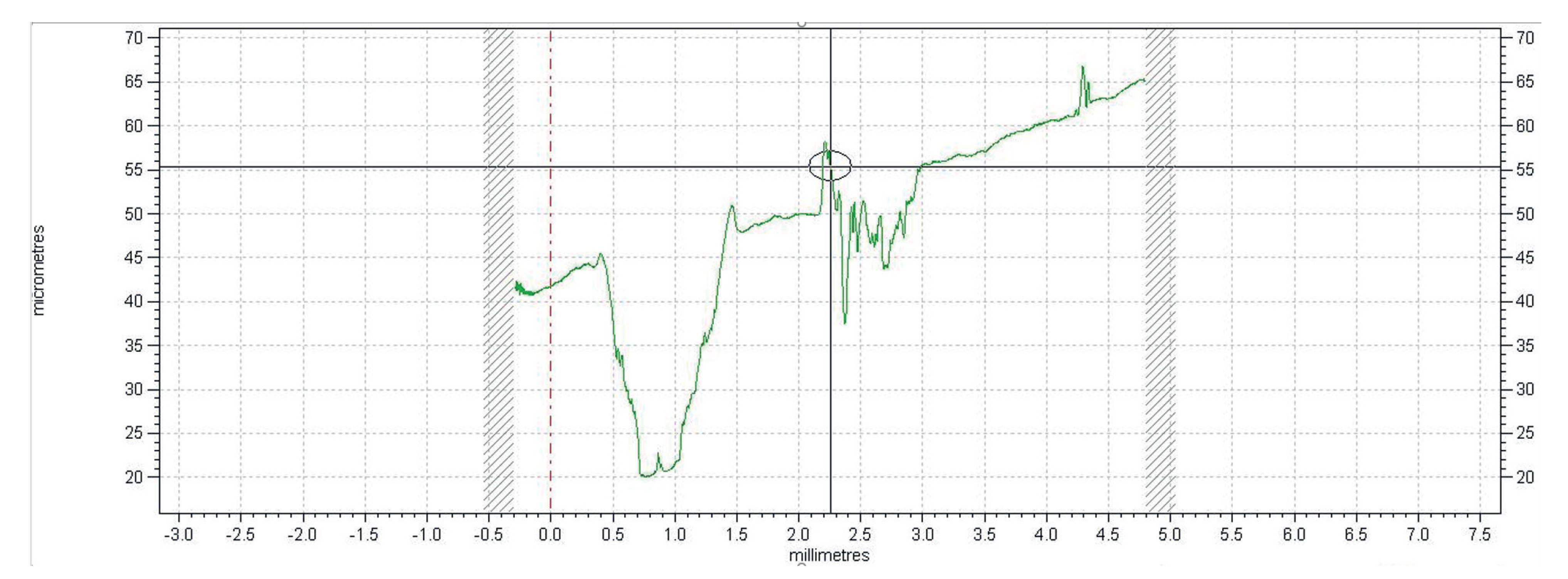
3.2.2. Roughness
3.2.3. Friction and Wear Volumes
3.2.4. Analysis of Variance (ANOVA)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, X.; Voigt, T. Implementation of the Manufacturing Execution System in the food and beverage industry. J. Food Eng. 2020, 278. [Google Scholar] [CrossRef]
- Aadil, R.; Madni, G.; Roobab, U.; Ur Rahman, U.; Zeng, X.A. Quality Control in Beverage Production: An Overview; Woodhead Publishing: Cambridge, UK, 2019; pp. 1–38. [Google Scholar] [CrossRef]
- Jaworski, J.A.; Schmid, S.R. Survivability of laminated polymer lubricant films in ironing. Tribol. Trans. 1999, 42, 32–38. [Google Scholar] [CrossRef]
- Selles, M.A.; Schmid, S.R.; Sanchez-Caballero, S.; Perez-Bernabeu, E.; Reig, M.J. Upper-bound modelization of an ironed three-layered polymer-coated steel strip. Int. J. Adv. Manuf. Technol. 2012, 60, 161–171. [Google Scholar] [CrossRef]
- Hosford, W.; Duncan, J. The aluminum beverage can. Sci. Am. 1994, 271, 48–53. [Google Scholar] [CrossRef]
- Jaworski, J.A.; Schmid, S.R.; Wang, J. An experimental investigation of the survivability and friction characteristics of tin-coated and polymer-laminated steels. J. Manuf. Sci. Eng. 1999, 121, 232–237. [Google Scholar] [CrossRef]
- Huang, C.H.; Schmid, S.R.; Wang, J.E. Thermal effects on polymer laminated steel formability in ironing. J. Manuf. Sci. Eng. 2001, 123, 225–230. [Google Scholar] [CrossRef]
- Van der Aa, M.; Schreurs, P.; Baaijens, F. Modelling of the wall ironing process of polymer coated sheet metal. Mech. Mater. 2001, 33, 555–572. [Google Scholar] [CrossRef]
- Wagner, J.; Moschakis, T.; Nelson, P.; Wedzicha, B. Development of a novel method to measure the film thickness of cured can coatings. J. Food Eng. 2011, 105, 530–536. [Google Scholar] [CrossRef]
- Van den Bosch, M.; Schreurs, P.; Geersa, M. On the prediction of delamination during deep-drawing of polymer coated metal sheet. J. Mater. Process. Technol. 2009, 209, 297–392. [Google Scholar] [CrossRef]
- Kampus, Z.; Nardin, B. Improving workability in ironing. J. Mater. Process. Technol. 2002, 130–131, 64–68. [Google Scholar] [CrossRef]
- Schünemann, M.; Ahmetoglu, M.; Altan, T. Prediction of process conditions in drawing and ironing of cans. J. Mater. Process. Technol. 1996, 59, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Dohda, K.; Jeong, Y. FEM simulation of surface smoothing in the ironing process. J. Mater. Process. Technol. 2001, 113, 705–709. [Google Scholar] [CrossRef]
- Chang, D.F. An analytical model of the ironing process including redundant work effect. J. Mater. Process. Technol. 1998, 75, 253–258. [Google Scholar] [CrossRef]
- Hosford, W.; Caddell, R. Metal Forming: Mechanics and Metallurgy, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Challen, J.; Mclean, L.; Oxley, L. Plastic deformation of a metal surface in sliding contact with a hard wedge: Its relation to friction and wear. Actas R. Soc. Lond. 1884, 394, 161–181. [Google Scholar]
- Wilson, W.; Halliday, K. An inlet zone analysis for the lubrication of a drawing process by a rigid-plastic solid. Wear 1977, 42, 135–148. [Google Scholar] [CrossRef]
- Cherukuri, H.; Perez-Bernabeu, E.; Selles, M.; Schmitz, T. Machining Chatter Prediction Using a Data Learning Model. J. Manuf. Mater. Process. 2019, 3, 45. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Wu, F.; Yu, L.; Ju, H.; Asempah, I.; Xu, J. Structural, mechanical and tribological properties of NbCN-Ag nanocomposite films deposited by reactive magnetron sputtering. Coatings 2018, 8, 50. [Google Scholar] [CrossRef]






| Input Variables | Units | Output Variables | Units |
|---|---|---|---|
| Surface Quality | SQF | ||
| Die angle | ° | Longitudinal roughness | um |
| Punch velocity | m/s | Transversal roughness | um |
| Reduction | % | Radial force | N |
| Temperature | °C | Ironing force | N |
| Input Variables | Units | Sensitivity |
|---|---|---|
| Die angle | ° | 0.132 |
| Punch velocity | m/s | 0.063 |
| Reduction | % | 0.005 |
| Temperature | C | 0.001 |
| Variables | Values | ||
|---|---|---|---|
| Loads (FN) | 2 N | 6 N | 10 N |
| Frequency (f) | 2 Hz | ||
| Sliding stroke | 10 mm | ||
| Sliding distance (cycle) | 500 m | (in 50,000 cycles) | |
| Input Variables | Sum of Squares |
|---|---|
| Die angle | 423.96 |
| Punch velocity | 15.20 |
| Reduction | 11.43 |
| Temperature | 16.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selles, M.A.; Schmid, S.R.; Sanchez-Caballero, S.; Ramezani, M.; Perez-Bernabeu, E. Use of a Novel Polymer-Coated Steel as an Alternative to Traditional Can Manufacturing in the Food Industry. Polymers 2021, 13, 222. https://doi.org/10.3390/polym13020222
Selles MA, Schmid SR, Sanchez-Caballero S, Ramezani M, Perez-Bernabeu E. Use of a Novel Polymer-Coated Steel as an Alternative to Traditional Can Manufacturing in the Food Industry. Polymers. 2021; 13(2):222. https://doi.org/10.3390/polym13020222
Chicago/Turabian StyleSelles, Miguel A., Steven R. Schmid, Samuel Sanchez-Caballero, Maziar Ramezani, and Elena Perez-Bernabeu. 2021. "Use of a Novel Polymer-Coated Steel as an Alternative to Traditional Can Manufacturing in the Food Industry" Polymers 13, no. 2: 222. https://doi.org/10.3390/polym13020222
APA StyleSelles, M. A., Schmid, S. R., Sanchez-Caballero, S., Ramezani, M., & Perez-Bernabeu, E. (2021). Use of a Novel Polymer-Coated Steel as an Alternative to Traditional Can Manufacturing in the Food Industry. Polymers, 13(2), 222. https://doi.org/10.3390/polym13020222