A Simulation-Data-Based Machine Learning Model for Predicting Basic Parameter Settings of the Plasticizing Process in Injection Molding
Abstract
:1. Introduction
2. Basics
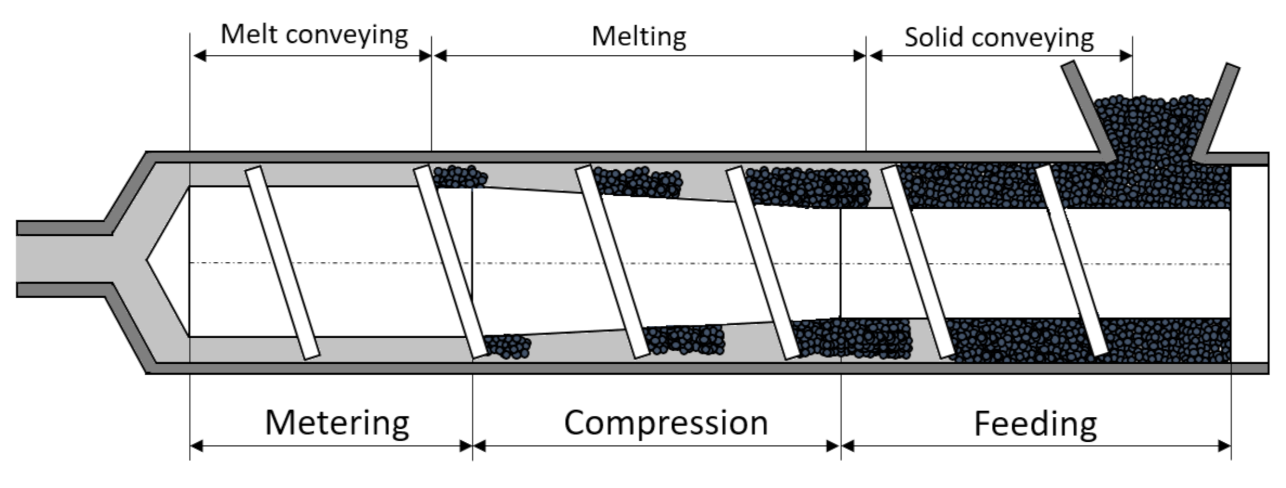
2.1. The Plasticizing Process and S3 Simulation Software
2.2. Artificial Neural Networks
3. Methods
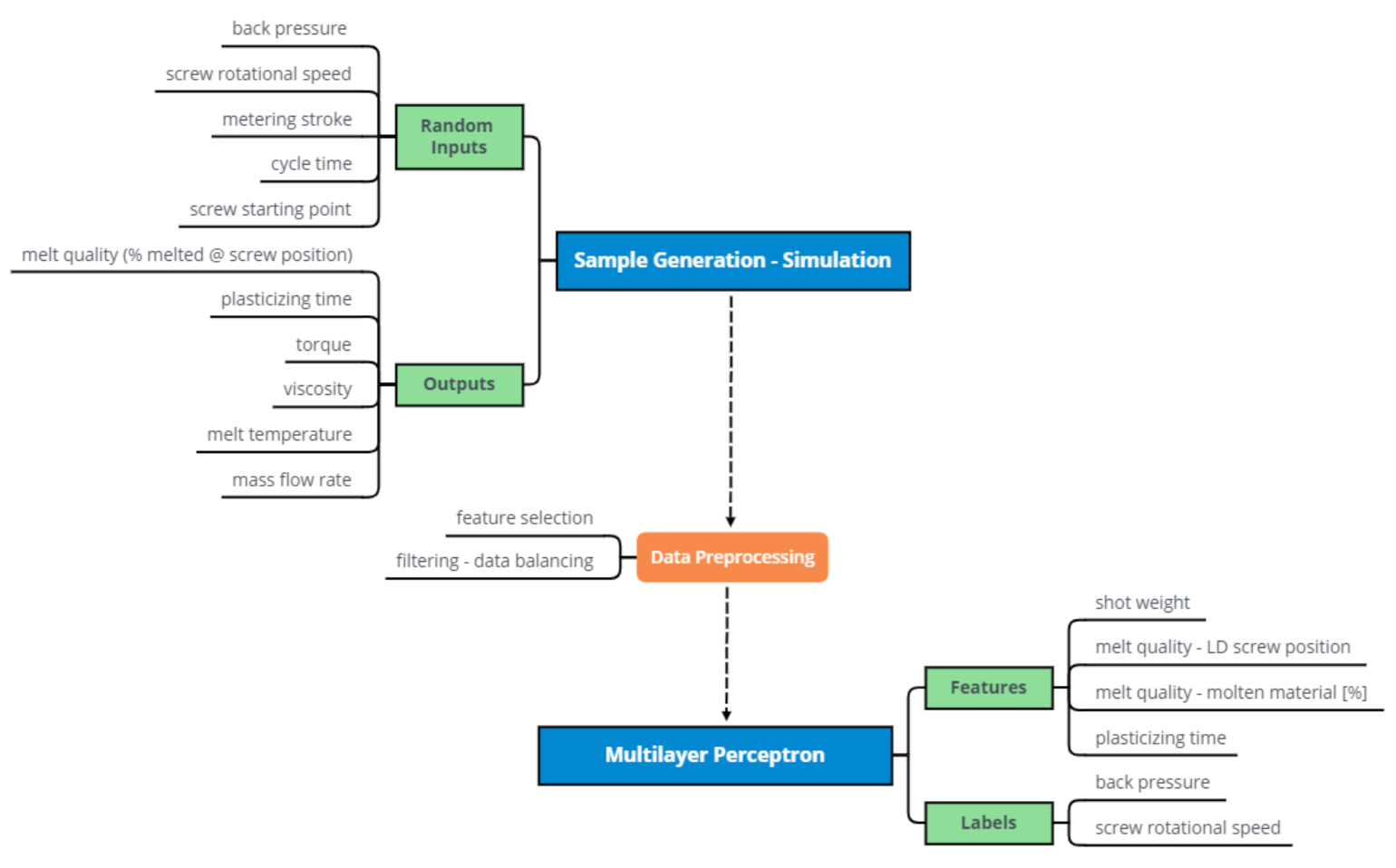
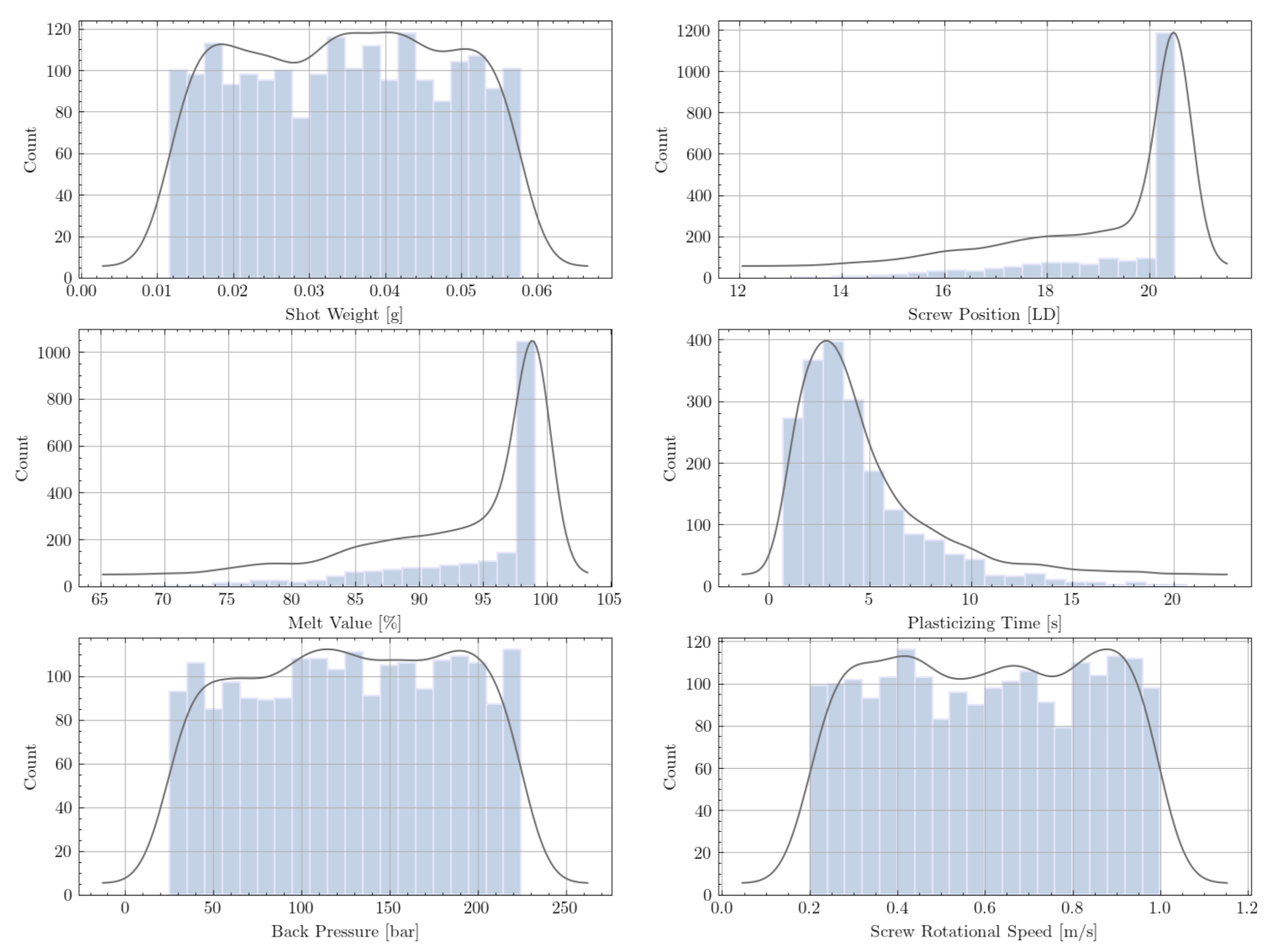
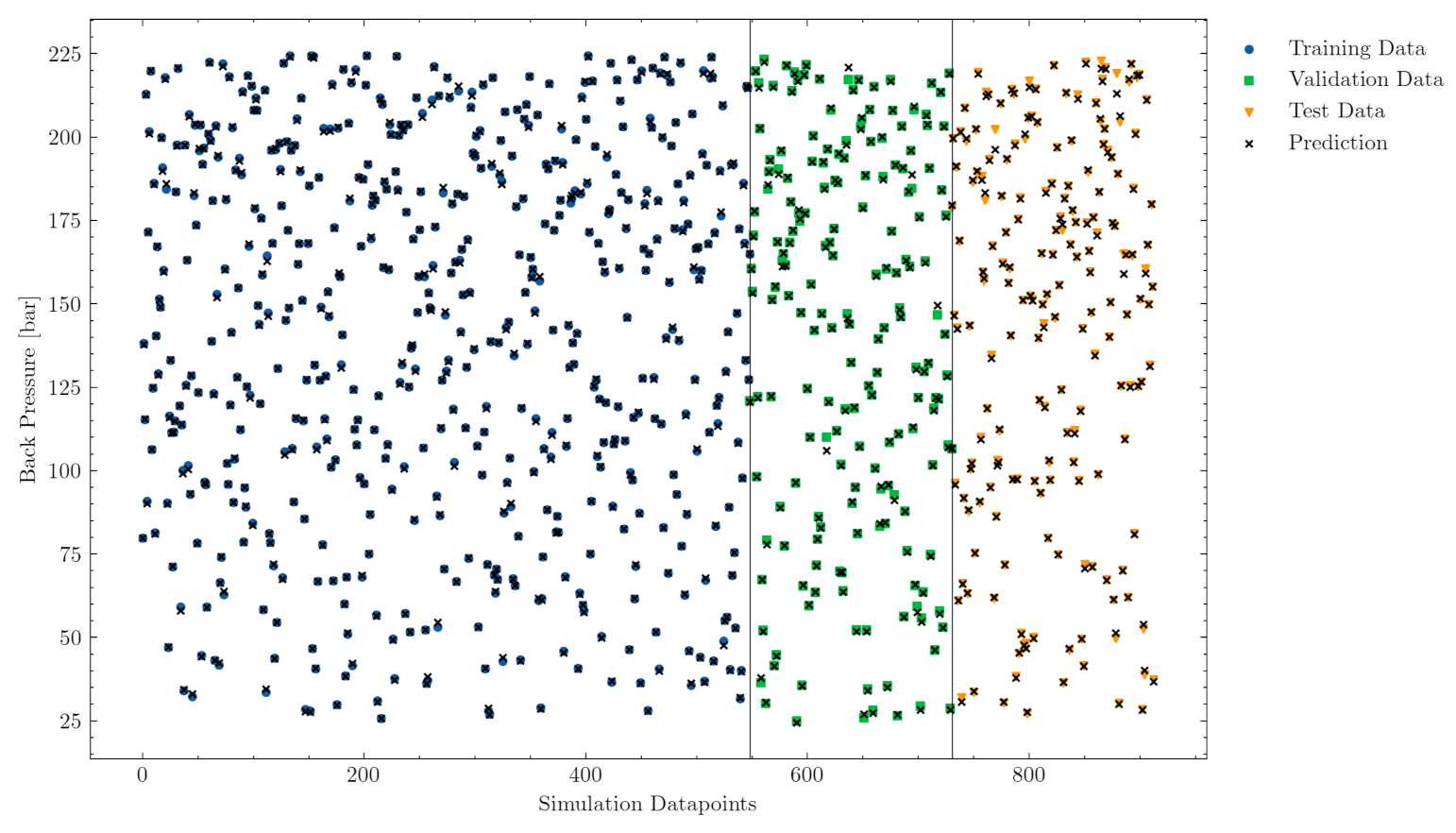
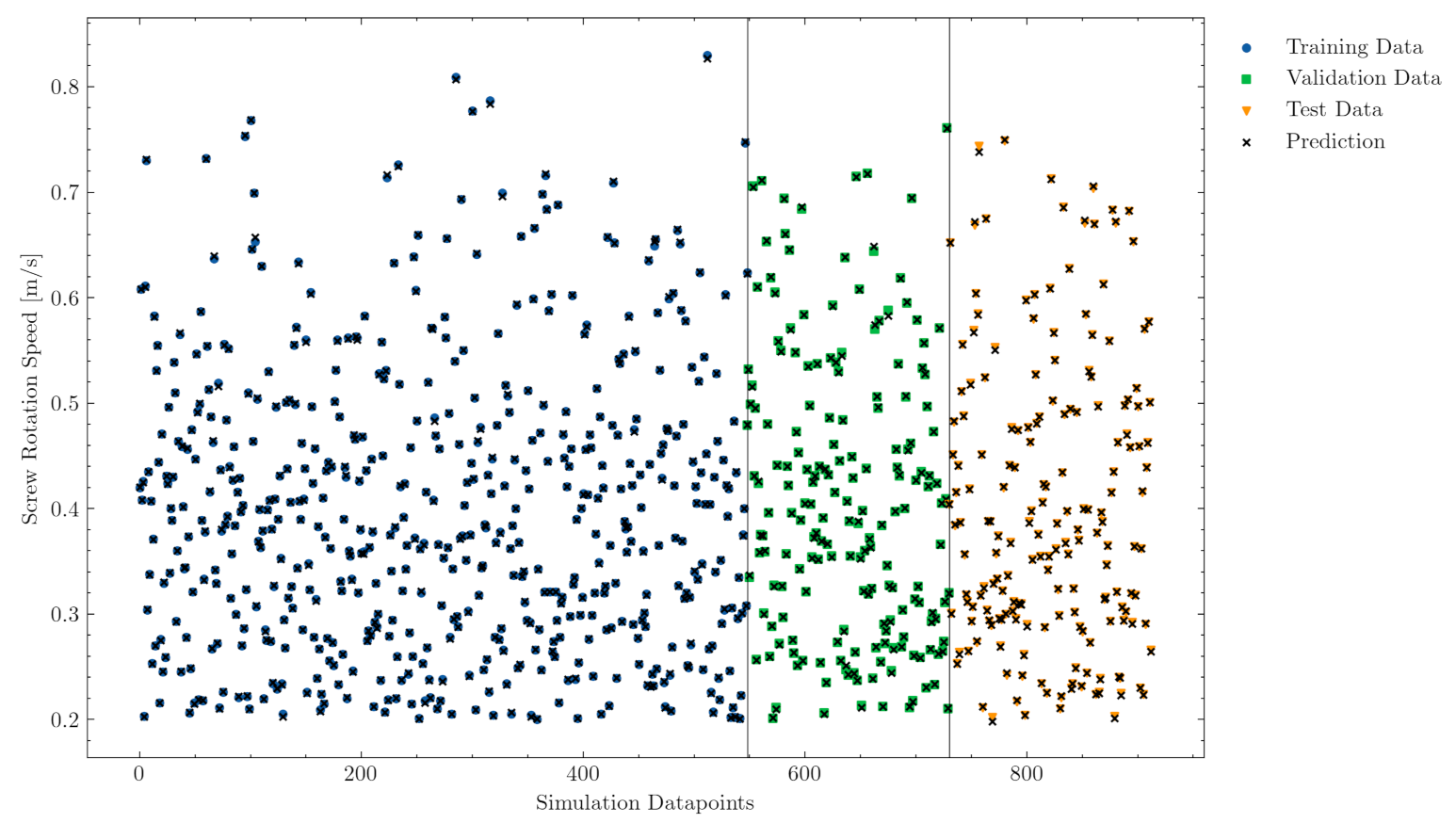
3.1. Data Generation and Preprocessing
- Which features (inputs) can be selected from the data in order to predict the desired labels?
- How can the model fulfill the requirement of good melt quality for the predictions?
- shot weight;
- melt quality—LD screw position;
- melt quality—molten material [%]; and
- plasticizing time.
3.2. Model Construction
- multilayer perceptron,
- Gaussian process regression,
- support vector regression,
- polynomial regression,
- random forest, and
- gradient boosting.
- Training set: 549 samples
- Validation set: 183 samples
- Test set: 183 samples
- Layer structure: 4 –> 50 –> 50 –> 30 –> 2
- Activation function: Tanh (for all layers)
- Optimizer: Pytorch Adam
- Loss function: Pytorch MSE
- Learning rate epoch 0–600:
- Learning rate epoch 600–1200:
- Learning rate epoch 1200–1500:
- Weight decay:
- Batch size: 32
- Epochs: 1500.
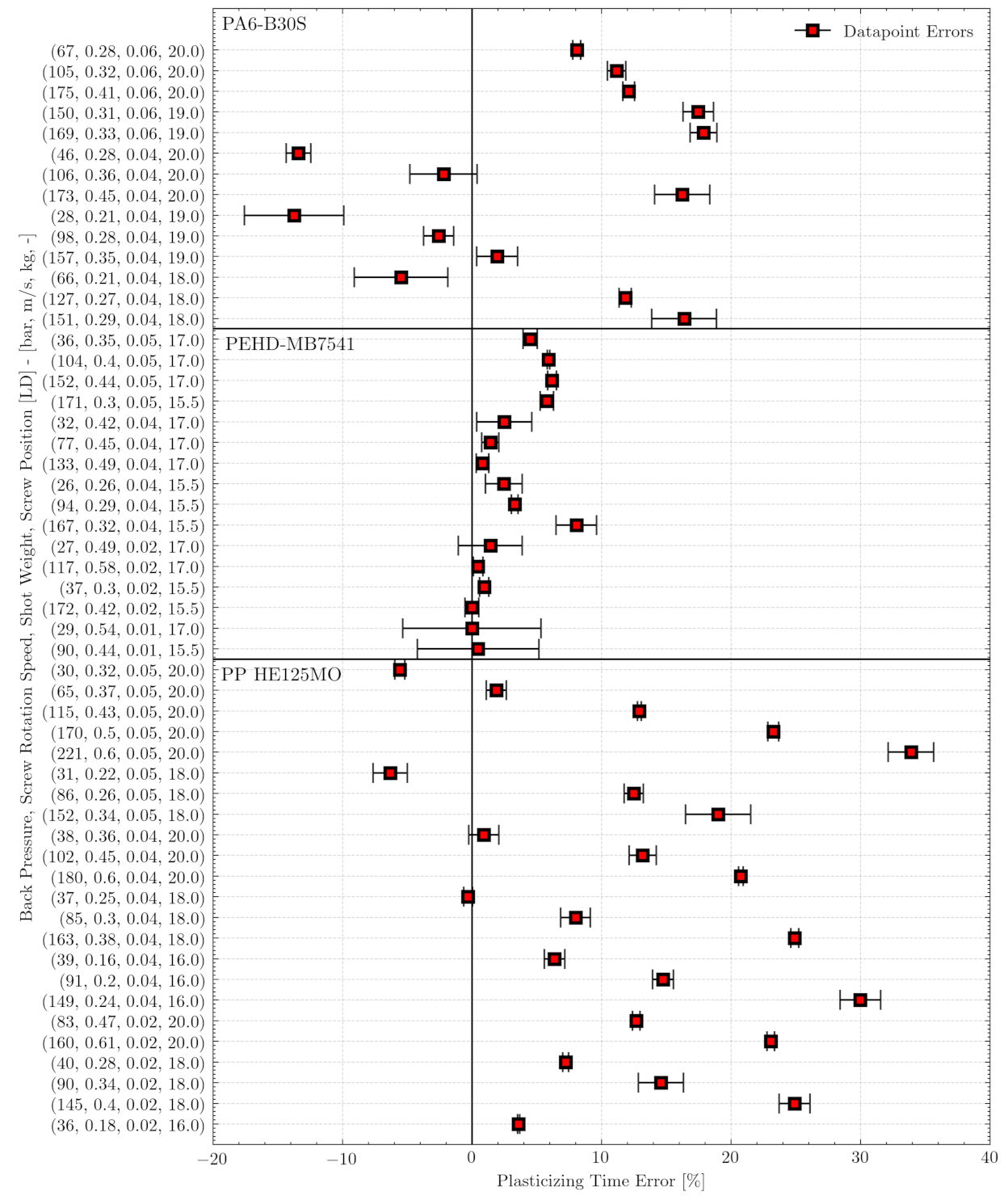
3.3. Experimental Evaluation of the Model
- melt value: 99% molten for each data point;
- screw Position (LD): 16, 18, 20;
- shot weight (kg): 0.02, 0.035, 0.05; and
- plasticizing time (s): 1–15.
4. Results
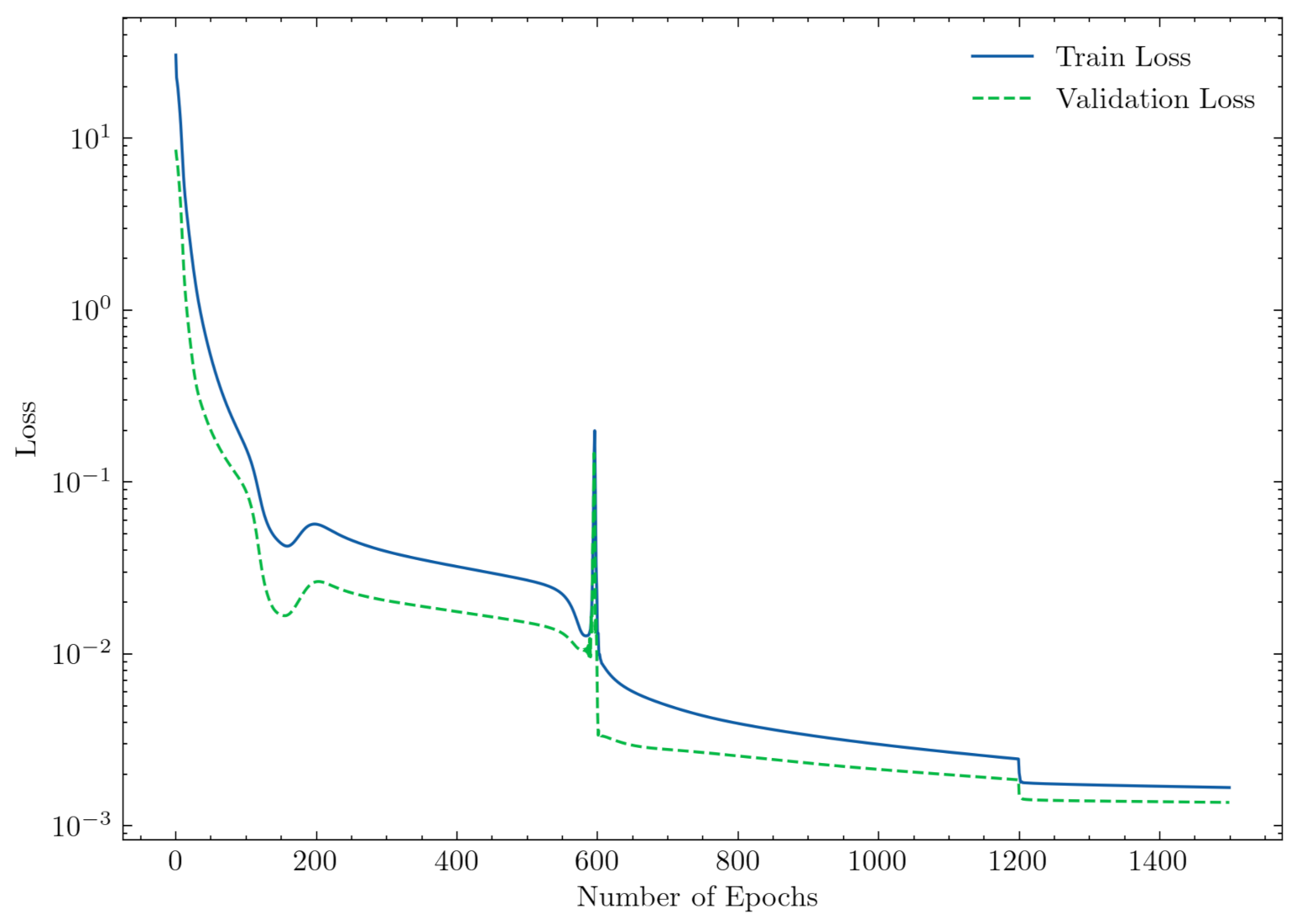
4.1. Results—Multilayer Perceptron Model
4.2. Results—Model vs. Experiment
4.3. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Nóbrega, J.M.; Gaspar-Cunha, A. Modeling of Plasticating Injection Molding—Experimental Assessment. Int. Polym. Process. 2014, 29, 558–569. [Google Scholar] [CrossRef]
- Subramanian, M.N. The Basics of Troubleshooting in Plastics Processing; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-0-470-62606-1. [Google Scholar]
- Singh, M.; Fuenmayor, E.; Hinchy, E.P.; Qiao, Y.; Murray, N.; Devine, D. Digital Twin: Origin to Future. ASI 2021, 4, 36. [Google Scholar] [CrossRef]
- Hopmann, C.H.; Theunissen, M.; Heinisch, J. Von der Simulation in die Maschine—Objektivierte Prozesseinrichtung durch Maschinelles Lernen; VDI Wissensforum GmbH (Hrsg.); Spritzgießen: Baden-Baden, Germany, 2018; pp. 29–42. [Google Scholar] [CrossRef]
- Lee, C.; Na, J.; Park, K.; Yu, H.; Kim, J.; Choi, K.; Park, D.; Park, S.; Rho, J.; Lee, S. Development of Artificial Neural Network System to Recommend Process Conditions of Injection Molding for Various Geometries. Adv. Intell. Syst. 2020, 2, 2000037. [Google Scholar] [CrossRef]
- Tercan, H.; Guajardo, A.; Heinisch, J.; Thiele, T.; Hopmann, C.; Meisen, T. Transfer-Learning: Bridging the Gap between Real and Simulation Data for Machine Learning in Injection Molding. Procedia CIRP 2018, 72, 185–190. [Google Scholar] [CrossRef]
- Limper, A. Verfahrenstechnik der Thermoplastextrusion; Carl Hanser Verlag: Munich, Germany, 2012; ISBN 978-3-446-41744-1. [Google Scholar]
- Altmann, D. Advanced Process Simulation for Single-Screw Plasticizing Units in Injection Molding. Ph.D. Thesis, Johannes Kepler University, Linz, Austria, 2019. [Google Scholar]
- Janssens, J. Data Science at the Command Line: Facing the Future with Time-Tested Tools; O’Reilly and Associates: Sebastopol, CA, USA, 2014; ISBN 978-1-491-94785-2. [Google Scholar]
- Marius, P.; Balas, V.E.; Perescu-Popescu, L.; Mastorakis, N.E. Multilayer perceptron and neural networks. WSEAS Trans. Circuits Syst. 2009, 8, 579–588. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: New York, NY, USA, 1995; ISBN 978-0-19-853864-6. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F.L., Jr. Python Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009; ISBN 978-1-4414-1269-0. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 2019, 32, 8024–8035. Available online: http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf (accessed on 28 April 2021).
- Wu, Y.; Liu, L.; Bae, J.; Chow, K.H.; Iyengar, A.; Pu, C.; Wei, W.; Yu, L.; Zhang, Q. Demystifying Learning Rate Policies for High Accuracy Training of Deep Neural Networks. arXiv 2019, arXiv:1908.06477. [Google Scholar]



| Back Pressure | Metering Stroke | Screw Rotational Speed | Cycle Time | |
|---|---|---|---|---|
| Min | 25 bar | 0.8 D | 0.2 | 10 s |
| Max | 225 bar | 4 D | 1 | 60 s |
| Screw Position [LD] | Plasticizing Time [s] | Back Pressure [bar] | Screw Rotational Speed [] |
|---|---|---|---|
| 16 | 9.62 | 148.7 | 0.24 |
| 16 | 11.05 | 90.9 | 0.20 |
| 16 | 12.13 | 38.7 | 0.16 |
| 18 | 6.03 | 163.2 | 0.38 |
| 18 | 7.10 | 84.9 | 0.30 |
| 18 | 7.82 | 37.1 | 0.25 |
| 20 | 3.87 | 180.4 | 0.60 |
| 20 | 4.59 | 102.2 | 0.45 |
| 20 | 5.31 | 38.1 | 0.36 |
| Method | Mean Error [%] | Std Error [%] | ||
|---|---|---|---|---|
| Train | Test | Train | Test | |
| Multilayer Perceptron | 0.21 | 0.27 | 0.26 | 0.37 |
| Gaussian Process Regression | 0.08 | 1.16 | 0.18 | 2.25 |
| Polynomial Regression | 0.34 | 1.27 | 0.55 | 4.98 |
| Support Vector Regression | 2.57 | 2.87 | 2.64 | 3.81 |
| Random Forest | 8.39 | 21.42 | 14.40 | 37.18 |
| Gradient Boosting | 18.44 | 24.34 | 31.44 | 43.54 |
| Label | RMSE Train | RMSE Test |
|---|---|---|
| Back Pressure [bar] | 0.41 | 0.61 |
| Screw Rotational Speed [m/s] | 0.0008 | 0.001 |
| PP-HE125MO | PEHD-MB7541 | PA6-B30S | |
|---|---|---|---|
| Mean | 14.4% | 2.8% | 10.8% |
| Std | 10% | 2% | 6% |
| Max | 34% | 8% | 18% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmid, M.; Altmann, D.; Steinbichler, G. A Simulation-Data-Based Machine Learning Model for Predicting Basic Parameter Settings of the Plasticizing Process in Injection Molding. Polymers 2021, 13, 2652. https://doi.org/10.3390/polym13162652
Schmid M, Altmann D, Steinbichler G. A Simulation-Data-Based Machine Learning Model for Predicting Basic Parameter Settings of the Plasticizing Process in Injection Molding. Polymers. 2021; 13(16):2652. https://doi.org/10.3390/polym13162652
Chicago/Turabian StyleSchmid, Matthias, Dominik Altmann, and Georg Steinbichler. 2021. "A Simulation-Data-Based Machine Learning Model for Predicting Basic Parameter Settings of the Plasticizing Process in Injection Molding" Polymers 13, no. 16: 2652. https://doi.org/10.3390/polym13162652
APA StyleSchmid, M., Altmann, D., & Steinbichler, G. (2021). A Simulation-Data-Based Machine Learning Model for Predicting Basic Parameter Settings of the Plasticizing Process in Injection Molding. Polymers, 13(16), 2652. https://doi.org/10.3390/polym13162652






