Predicting the Adsorption of Amoxicillin and Ibuprofen on Chitosan and Graphene Oxide Materials: A Density Functional Theory Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Molecular Models for Pharmaceuticals and Absorbent Structures
2.2. Pharmaceutical-Dimers Complexes
2.3. Electronic Transference, Conceptual Density Functional Theory and Molecular Interactions-Type (NBO Second-Order Perturbation Theory)
2.4. Energy Decomposition Analysis
3. Results
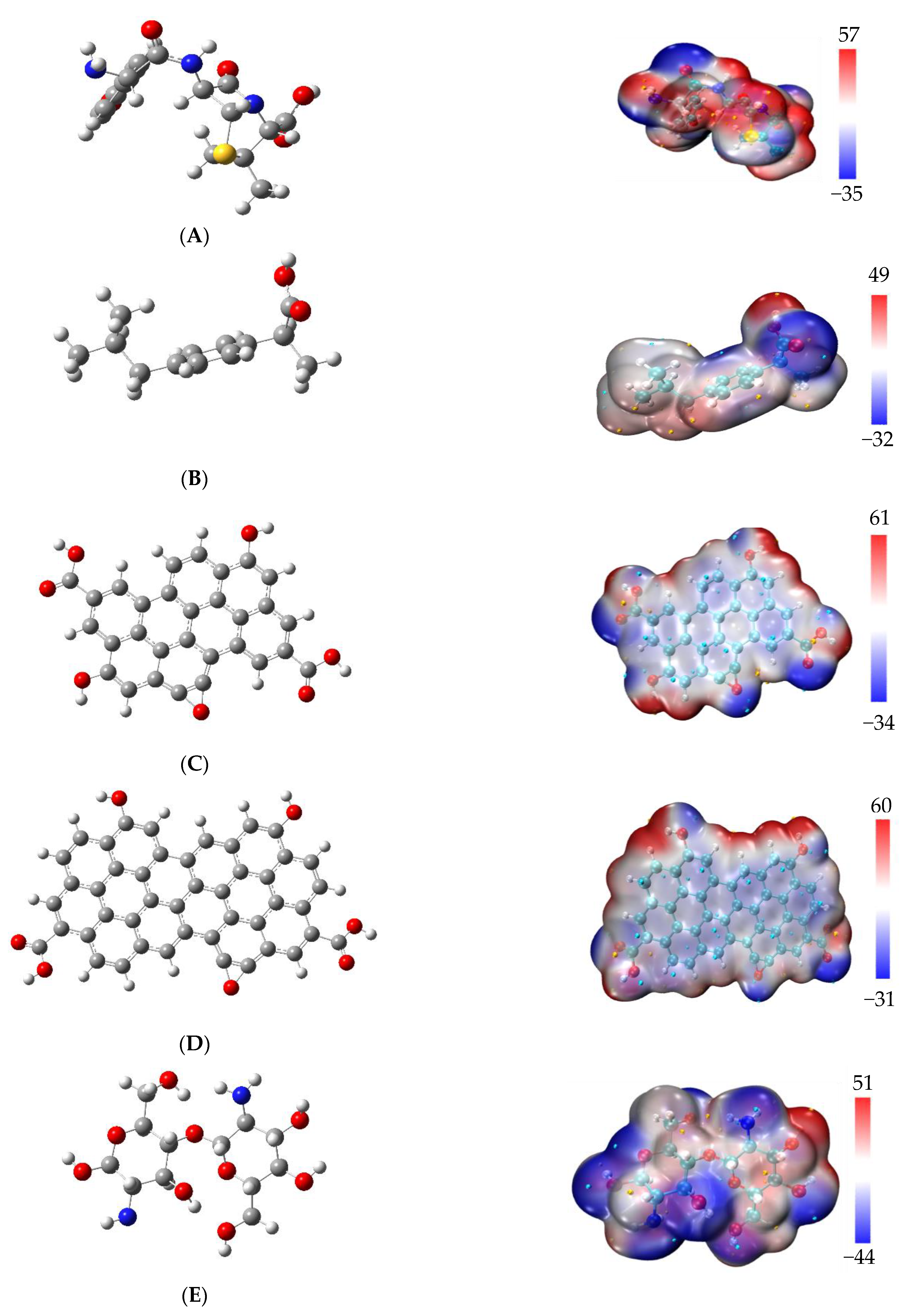
3.1. Minimum Molecular Structures
3.2. Complexes Structures of Amoxicillin and Ibuprofen, with Chitosan and Graphene-Oxides
3.3. Energetic and Thermodynamic Parameter for the Complex Formation
3.4. Electronic Transference, Conceptual Density Functional Theory and Molecular Interactions-Type (NBO Second-Order Perturbation Theory)
3.5. Energy Decomposition Analysis (EDA)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barker, K. Biosecure citizenship: Politicising symbiotic associations and the construction of biological threat. Trans. Inst. Br. Geogr. 2010, 35, 350–363. [Google Scholar] [CrossRef]
- Biermann, C.; Anderson, R.M. Conservation, biopolitics, and the governance of life and death. Geogr. Compass 2017, 11, e12329. [Google Scholar] [CrossRef]
- Dempsey, J. Enterprising Nature: Economics, Markets and Finance in Global Biodiversity Politics; Wiley Blackwell: Hoboken, NJ, USA, 2016; ISBN 9781118640517. [Google Scholar]
- Tortajada, C. Contributions of recycled wastewater to clean water and sanitation Sustainable Development Goals. NPJ Clean Water 2020, 3. [Google Scholar] [CrossRef]
- Bunke, D.; Moritz, S.; Brack, W.; Herráez, D.L.; Posthuma, L.; Nuss, M. Developments in society and implications for emerging pollutants in the aquatic environment. Environ. Sci. Eur. 2019, 31, 1–17. [Google Scholar] [CrossRef]
- Tang, Y.; Yin, M.; Yang, W.; Li, H.; Zhong, Y.; Mo, L.; Liang, Y.; Ma, X.; Sun, X. Emerging pollutants in water environment: Occurrence, monitoring, fate, and risk assessment. Water Environ. Res. 2019, 91, 984–991. [Google Scholar] [CrossRef]
- Fernandes, M.J.; Paíga, P.; Silva, A.; Llaguno, C.P.; Carvalho, M.; Vázquez, F.M.; Delerue-Matos, C. Antibiotics and antidepressants occurrence in surface waters and sediments collected in the north of Portugal. Chemosphere 2020, 239. [Google Scholar] [CrossRef]
- Khan, H.K.; Rehman, M.Y.A.; Malik, R.N. Fate and toxicity of pharmaceuticals in water environment: An insight on their occurrence in South Asia. J. Environ. Manag. 2020, 271. [Google Scholar] [CrossRef]
- Ngqwala, N.P.; Muchesa, P. Occurrence of pharmaceuticals in aquatic environments: A review and potential impacts in South Africa. S. Afr. J. Sci. 2020, 116. [Google Scholar] [CrossRef]
- Praveena, S.M.; Mohd Rashid, M.Z.; Mohd Nasir, F.A.; Sze Yee, W.; Aris, A.Z. Occurrence and potential human health risk of pharmaceutical residues in drinking water from Putrajaya (Malaysia). Ecotoxicol. Environ. Saf. 2019, 180, 549–556. [Google Scholar] [CrossRef]
- Ide, A.H.; Osawa, R.A.; Marcante, L.O.; da Costa Pereira, J.; de Azevedo, J.C.R. Occurrence of Pharmaceutical Products, Female Sex Hormones and Caffeine in a Subtropical Region in Brazil. CLEAN Soil Air Water 2017, 45, 1700334. [Google Scholar] [CrossRef]
- Sanganyado, E.; Lu, Z.; Fu, Q.; Schlenk, D.; Gan, J. Chiral pharmaceuticals: A review on their environmental occurrence and fate processes. Water Res. 2017, 124, 527–542. [Google Scholar] [CrossRef]
- Madikizela, L.M.; Tavengwa, N.T.; Chimuka, L. Status of pharmaceuticals in African water bodies: Occurrence, removal and analytical methods. J. Environ. Manag. 2017, 193, 211–220. [Google Scholar] [CrossRef]
- Kumar, A.; Pal, D. Antibiotic resistance and wastewater: Correlation, impact and critical human health challenges. J. Environ. Chem. Eng. 2018, 6, 52–58. [Google Scholar] [CrossRef]
- Tiedje, J.M.; Wang, F.; Manaia, C.M.; Virta, M.; Sheng, H.; Ma, L.; Zhang, T.; Topp, E. Antibiotic Resistance Genes in the Human-Impacted Environment: A One Health Perspective. Pedosphere 2019, 29, 273–282. [Google Scholar] [CrossRef]
- Sanganyado, E.; Gwenzi, W. Antibiotic resistance in drinking water systems: Occurrence, removal, and human health risks. Sci. Total Environ. 2019, 669, 785–797. [Google Scholar] [CrossRef]
- Zhang, J.; Li, W.; Chen, J.; Qi, W.; Wang, F.; Zhou, Y. Impact of biofilm formation and detachment on the transmission of bacterial antibiotic resistance in drinking water distribution systems. Chemosphere 2018, 203, 368–380. [Google Scholar] [CrossRef]
- Aus der Beek, T.; Weber, F.A.; Bergmann, A.; Hickmann, S.; Ebert, I.; Hein, A.; Küster, A. Pharmaceuticals in the environment-Global occurrences and perspectives. Environ. Toxicol. Chem. 2016, 35, 823–835. [Google Scholar] [CrossRef]
- Tyumina, E.A.; Bazhutin, G.A.; Cartagena Gómez, A.d.P.; Ivshina, I.B. Nonsteroidal Anti-inflammatory Drugs as Emerging Contaminants. Microbiology 2020, 89, 148–163. [Google Scholar] [CrossRef]
- Agunbiade, F.O.; Moodley, B. Occurrence and distribution pattern of acidic pharmaceuticals in surface water, wastewater, and sediment of the Msunduzi River, Kwazulu-Natal, South Africa. Environ. Toxicol. Chem. 2016, 35, 36–46. [Google Scholar] [CrossRef]
- Swan, G.E.; Cuthbert, R.; Quevedo, M.; Green, R.E.; Pain, D.J.; Bartels, P.; Cunningham, A.A.; Duncan, N.; Meharg, A.A.; Oaks, J.L.; et al. Toxicity of diclofenac to Gyps vultures. Biol. Lett. 2006, 2, 279–282. [Google Scholar] [CrossRef]
- Oaks, J.L.; Gilbert, M.; Virani, M.Z.; Watson, R.T.; Meteyer, C.U.; Rideout, B.A.; Shivaprasad, H.L.; Ahmed, S.; Chaudhry, M.J.I.; Arshad, M.; et al. Diclofenac residues as the cause of vulture population decline in Pakistan. Nature 2004, 427, 630–633. [Google Scholar] [CrossRef] [PubMed]
- Prakash, V.; Pain, D.J.; Cunningham, A.A.; Donald, P.F.; Prakash, N.; Verma, A.; Gargi, R.; Sivakumar, S.; Rahmani, A.R. Catastrophic collapse of indian white-backed Gyps bengalensis and long-billed Gyps indicus vulture populations. Biol. Conserv. 2003, 109, 381–390. [Google Scholar] [CrossRef]
- Kudrna, J.; Hnilicka, F.; Kubes, J.; Vachova, P.; Hnilickova, H.; Kuklova, M. Effect of Acetaminophen (APAP) on Physiological Indicators in Lactuca sativa. Life 2020, 10, 303. [Google Scholar] [CrossRef] [PubMed]
- Alkimin, G.D.; Daniel, D.; Frankenbach, S.; Serôdio, J.; Soares, A.M.V.M.; Barata, C.; Nunes, B. Evaluation of pharmaceutical toxic effects of non-standard endpoints on the macrophyte species Lemna minor and Lemna gibba. Sci. Total Environ. 2019, 657, 926–937. [Google Scholar] [CrossRef]
- Giménez, V.; Nunes, B. Effects of commonly used therapeutic drugs, paracetamol, and acetylsalicylic acid, on key physiological traits of the sea snail Gibbula umbilicalis. Environ. Sci. Pollut. Res. 2019, 26, 21858–21870. [Google Scholar] [CrossRef]
- Muga, H.E.; Mihelcic, J.R. Sustainability of wastewater treatment technologies. J. Environ. Manag. 2008, 88. [Google Scholar] [CrossRef]
- Alammar, A.; Park, S.H.; Ibrahim, I.; Deepak, A.; Holtzl, T.; Dumée, L.F.; Lim, H.N.; Szekely, G. Architecting neonicotinoid-scavenging nanocomposite hydrogels for environmental remediation. Appl. Mater. Today 2020, 21. [Google Scholar] [CrossRef]
- Benyekkou, N.; Ghezzar, M.R.; Abdelmalek, F.; Addou, A. Elimination of paracetamol from water by a spent coffee grounds biomaterial. Environ. Nanotechnol. Monit. Manag. 2020, 14. [Google Scholar] [CrossRef]
- Fotsing, P.N.; Woumfo, E.D.; Mezghich, S.; Mignot, M.; Mofaddel, N.; Le Derf, F.; Vieillard, J. Surface modification of biomaterials based on cocoa shell with improved nitrate and Cr(vi) removal. RSC Adv. 2020, 10. [Google Scholar] [CrossRef]
- Rangabhashiyam, S.; Suganya, E.; Selvaraju, N.; Varghese, L.A. Significance of exploiting non-living biomaterials for the biosorption of wastewater pollutants. World J. Microbiol. Biotechnol. 2014, 30, 1669–1689. [Google Scholar] [CrossRef]
- Peterson, J.W.; Petrasky, L.J.; Seymour, M.D.; Burkhart, R.S.; Schuiling, A.B. Adsorption and breakdown of penicillin antibiotic in the presence of titanium oxide nanoparticles in water. Chemosphere 2012, 87. [Google Scholar] [CrossRef]
- Liu, M.; Liu, Y.; Bao, D.; Zhu, G.; Yang, G.; Geng, J.; Li, H. Effective Removal of Tetracycline Antibiotics from Water using Hybrid Carbon Membranes. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Pap, S.; Taggart, M.A.; Shearer, L.; Li, Y.; Radovic, S.; Turk Sekulic, M. Removal behaviour of NSAIDs from wastewater using a P-functionalised microporous carbon. Chemosphere 2021, 264. [Google Scholar] [CrossRef]
- Phasuphan, W.; Praphairaksit, N.; Imyim, A. Removal of ibuprofen, diclofenac, and naproxen from water using chitosan-modified waste tire crumb rubber. J. Mol. Liq. 2019, 294. [Google Scholar] [CrossRef]
- Khan, N.A.; Khan, S.U.; Ahmed, S.; Farooqi, I.H.; Yousefi, M.; Mohammadi, A.A.; Changani, F. Recent trends in disposal and treatment technologies of emerging-pollutants- A critical review. TrAC Trends Anal. Chem. 2020, 122. [Google Scholar] [CrossRef]
- Checa, M.; Beltrán, F.J.; Rivas, F.J.; Cordero, E. On the role of a graphene oxide/titania catalyst, visible LED and ozone in removing mixtures of pharmaceutical contaminants from water and wastewater. Environ. Sci. Water Res. Technol. 2020, 6. [Google Scholar] [CrossRef]
- Zhang, Q.; Hou, Q.; Huang, G.; Fan, Q. Removal of heavy metals in aquatic environment by graphene oxide composites: A review. Environ. Sci. Pollut. Res. 2020, 27, 190–209. [Google Scholar] [CrossRef]
- Çalışkan Salihi, E.; Wang, J.; Kabacaoğlu, G.; Kırkulak, S.; Šiller, L. Graphene oxide as a new generation adsorbent for the removal of antibiotics from waters. Sep. Sci. Technol. 2021, 56. [Google Scholar] [CrossRef]
- Karimi-Maleh, H.; Ayati, A.; Davoodi, R.; Tanhaei, B.; Karimi, F.; Malekmohammadi, S.; Orooji, Y.; Fu, L.; Sillanpää, M. Recent advances in using of chitosan-based adsorbents for removal of pharmaceutical contaminants: A review. J. Clean. Prod. 2021, 291. [Google Scholar] [CrossRef]
- Costa, M.P.M.; Prates, L.M.; Baptista, L.; Cruz, M.T.M.; Ferreira, I.L.M. Interaction of polyelectrolyte complex between sodium alginate and chitosan dimers with a single glyphosate molecule: A DFT and NBO study. Carbohydr. Polym. 2018, 198. [Google Scholar] [CrossRef]
- Karimi-Maleh, H.; Shafieizadeh, M.; Taher, M.A.; Opoku, F.; Kiarii, E.M.; Govender, P.P.; Ranjbari, S.; Rezapour, M.; Orooji, Y. The role of magnetite/graphene oxide nano-composite as a high-efficiency adsorbent for removal of phenazopyridine residues from water samples, an experimental/theoretical investigation. J. Mol. Liq. 2020, 298. [Google Scholar] [CrossRef]
- Bahamon, D.; Vega, L.F. Molecular simulations of phenol and ibuprofen removal from water using multilayered graphene oxide membranes. Mol. Phys. 2019, 117. [Google Scholar] [CrossRef]
- Wazzan, N. Adsorption of non-steroidal anti-inflammatory drugs (NSAIDs) on nanographene surface: Density functional theory study. Arab. J. Chem. 2021, 14. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Wang, K.; Niu, Y.; Chen, H.; Bai, L.; Xue, Z. Removal of Ag(I) from aqueous solution by thiourea-functionalized silica gel: Experimental and theoretical study. Desalin. Water Treat. 2019, 151. [Google Scholar] [CrossRef]
- Plazinski, W.; Plazinska, A. Molecular dynamics study of the interactions between phenolic compounds and alginate/alginic acid chains. New J. Chem. 2011, 35. [Google Scholar] [CrossRef]
- Geerlings, P.; Chamorro, E.; Chattaraj, P.K.; De Proft, F.; Gázquez, J.L.; Liu, S.; Morell, C.; Toro-Labbé, A.; Vela, A.; Ayers, P. Conceptual density functional theory: Status, prospects, issues. Theor. Chem. Acc. 2020, 139. [Google Scholar] [CrossRef]
- Okoli, C.P.; Guo, Q.J.; Adewuyi, G.O. Application of quantum descriptors for predicting adsorption performance of starch and cyclodextrin adsorbents. Carbohydr. Polym. 2014, 101. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Chen, J.; Wei, X.; Hernandez Maldonado, A.J.; Chen, Z. Unveiling Adsorption Mechanisms of Organic Pollutants onto Carbon Nanomaterials by Density Functional Theory Computations and Linear Free Energy Relationship Modeling. Environ. Sci. Technol. 2017, 51. [Google Scholar] [CrossRef]
- Efremenko, I.; Sheintuch, M. Predicting solute adsorption on activated carbon: Phenol. Langmuir 2006, 22. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, W.; Peng, Y.; Chen, Z.; Chen, J.; Xiao, Z.; Zhao, X.; Qu, Y.; Li, J. Predicting the adsorption of organic pollutants on boron nitride nanosheets: Via in silico techniques: DFT computations and QSAR modeling. Environ. Sci. Nano 2021, 8. [Google Scholar] [CrossRef]
- Mishima, K.; Du, X.; Miyamoto, N.; Kano, N.; Imaizumi, H. Experimental and theoretical studies on the adsorption mechanisms of uranium (VI) ions on chitosan. J. Funct. Biomater. 2018, 9, 49. [Google Scholar] [CrossRef]
- Annadurai, G. Design of optimum response surface experiments for adsorption of direct dye on chitosan. Bioprocess Eng. 2000, 23. [Google Scholar] [CrossRef]
- Regti, A.; El Ayouchia, H.B.; Laamari, M.R.; Stiriba, S.E.; Anane, H.; El Haddad, M. Experimental and theoretical study using DFT method for the competitive adsorption of two cationic dyes from wastewaters. Appl. Surf. Sci. 2016, 390. [Google Scholar] [CrossRef]
- Dastani, N.; Arab, A.; Raissi, H. DFT computational study towards investigating Cladribine anticancer drug adsorption on the graphene and functionalized graphene. Struct. Chem. 2020, 31. [Google Scholar] [CrossRef]
- Parolini, M. Toxicity of the Non-Steroidal Anti-Inflammatory Drugs (NSAIDs) acetylsalicylic acid, paracetamol, diclofenac, ibuprofen and naproxen towards freshwater invertebrates: A review. Sci. Total Environ. 2020, 740. [Google Scholar] [CrossRef]
- Ogunbanwo, O.M.; Kay, P.; Boxall, A.B.; Wilkinson, J.; Sinclair, C.J.; Shabi, R.A.; Fasasi, A.E.; Lewis, G.A.; Amoda, O.A.; Brown, L.E. High Concentrations of Pharmaceuticals in a Nigerian River Catchment. Environ. Toxicol. Chem. 2020. [Google Scholar] [CrossRef]
- Bell, K.Y.; Wells, M.J.M.; Traexler, K.A.; Pellegrin, M.-L.; Morse, A.; Bandy, J. Emerging Pollutants. Water Environ. Res. 2011, 83. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, L.; Rysz, M.; Wang, Y.; Zhang, H.; Alvarez, P.J.J. Occurrence and Transport of Tetracycline, Sulfonamide, Quinolone, and Macrolide Antibiotics in the Haihe River Basin, China. Environ. Sci. Technol. 2011, 45. [Google Scholar] [CrossRef]
- Zhang, Q.-Q.; Ying, G.-G.; Pan, C.-G.; Liu, Y.-S.; Zhao, J.-L. Comprehensive Evaluation of Antibiotics Emission and Fate in the River Basins of China: Source Analysis, Multimedia Modeling, and Linkage to Bacterial Resistance. Environ. Sci. Technol. 2015, 49. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Li, N.; Zheng, H.; Lin, H. Occurrence and risk assessment of antibiotics in river water in Hong Kong. Ecotoxicol. Environ. Saf. 2016, 125. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Singh, A.P.; Kumar, S.; Giri, B.S.; Kim, K.-H. Antibiotic resistance in major rivers in the world: A systematic review on occurrence, emergence, and management strategies. J. Clean. Prod. 2019, 234. [Google Scholar] [CrossRef]
- Peña-Guzmán, C.; Ulloa-Sánchez, S.; Mora, K.; Helena-Bustos, R.; Lopez-Barrera, E.; Alvarez, J.; Rodriguez-Pinzón, M. Emerging pollutants in the urban water cycle in Latin America: A review of the current literature. J. Environ. Manag. 2019, 237. [Google Scholar] [CrossRef]
- Griffero, L.; Alcántara-Durán, J.; Alonso, C.; Rodríguez-Gallego, L.; Moreno-González, D.; García-Reyes, J.F.; Molina-Díaz, A.; Pérez-Parada, A. Basin-scale monitoring and risk assessment of emerging contaminants in South American Atlantic coastal lagoons. Sci. Total Environ. 2019, 697. [Google Scholar] [CrossRef]
- Serna-Galvis, E.A.; Botero-Coy, A.M.; Martínez-Pachón, D.; Moncayo-Lasso, A.; Ibáñez, M.; Hernández, F.; Torres-Palma, R.A. Degradation of seventeen contaminants of emerging concern in municipal wastewater effluents by sonochemical advanced oxidation processes. Water Res. 2019, 154. [Google Scholar] [CrossRef]
- Gallego-Álvarez, I.; García-Rubio, R.; Martínez-Ferrero, J. Environmental performance concerns in Latin America: Determinant factors and multivariate analysis. Rev. Contab. 2018, 21. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, L.; Bai, H.; Li, L. Graphene oxide-chitosan composite hydrogels as broad-spectrum adsorbents for water purification. J. Mater. Chem. A 2013, 1, 1992–2001. [Google Scholar] [CrossRef]
- Khan, A.; Wang, J.; Li, J.; Wang, X.; Chen, Z.; Alsaedi, A.; Hayat, T.; Chen, Y.; Wang, X. The role of graphene oxide and graphene oxide-based nanomaterials in the removal of pharmaceuticals from aqueous media: A review. Environ. Sci. Pollut. Res. 2017, 24. [Google Scholar] [CrossRef]
- Šponer, J.; Hobza, P.; Leszczynski, J. Computational Approaches to the Studies of the Interactions of Nucleic Acid Bases. Theor. Comput. Chem. 1999, 8, 85–117. [Google Scholar] [CrossRef]
- Hayes, I.C.; Stone, A.J. An intermolecular perturbation theory for the region of moderate overlap. Mol. Phys. 1984, 53. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeerschd, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView 2016; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision, D.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Bahamon, D.; Carro, L.; Guri, S.; Vega, L.F. Computational study of ibuprofen removal from water by adsorption in realistic activated carbons. J. Colloid Interface Sci. 2017, 498. [Google Scholar] [CrossRef]
- Juarez-Morales, L.A.; Hernandez-Cocoletzi, H.; Chigo-Anota, E.; Aguila-Almanza, E.; Tenorio-Arvide, M.G. Chitosan-Aflatoxins B1, M1 Interaction: A Computational Approach. Curr. Org. Chem. 2018, 21. [Google Scholar] [CrossRef]
- Mahmoud, E.-S.; Omar, A.; Bayoumy, A.M.; Ibrahim, M. Chitosan Ibuprofen Interaction: Modeling Approach. Sens. Lett. 2018, 16. [Google Scholar] [CrossRef]
- Aarab, N.; Laabd, M.; Eljazouli, H.; Lakhmiri, R.; Kabli, H.; Albourine, A. Experimental and DFT studies of the removal of pharmaceutical metronidazole from water using polypyrrole. Int. J. Ind. Chem. 2019, 10. [Google Scholar] [CrossRef]
- Kaczmarek-Kędziera, A. Gas Phase Computational Study of Diclofenac Adsorption on Chitosan Materials. Molecules 2020, 25, 2549. [Google Scholar] [CrossRef]
- Mora, J.R.; Lezama, J.; Márquez, E.; Escalante, L.; Córdova, T.; Chuchani, G. Theoretical study of neighboring carbonyl group participation in the elimination kinetics of chloroketones in the gas phase. J. Phys. Org. Chem. 2011, 24. [Google Scholar] [CrossRef]
- Luiggi, M.; Mora, J.R.; Loroño, M.; Marquez, E.; Lezama, J.; Cordova, T.; Chuchani, G. Theoretical calculations on the gas-phase thermal decomposition kinetics of selected thiomethyl chloroalkanes: A new insight of the mechanism. Comput. Theor. Chem. 2014, 1027. [Google Scholar] [CrossRef]
- Mora, J.; Cervantes, C.; Marquez, E. New Insight into the Chloroacetanilide Herbicide Degradation Mechanism through a Nucleophilic Attack of Hydrogen Sulfide. Int. J. Mol. Sci. 2018, 19, 2864. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Zhuang, T.; Zhang, Q.; Wang, W. Mechanistic studies on the dibenzofuran and dibenzo-p-dioxin formation reactions from anthracene. Sci. Total Environ. 2019, 662. [Google Scholar] [CrossRef] [PubMed]
- Liang, D.; Streefkerk, D.E.; Jordaan, D.; Wagemakers, J.; Baggerman, J.; Zuilhof, H. Silicon-Free SuFEx Reactions of Sulfonimidoyl Fluorides: Scope, Enantioselectivity, and Mechanism. Angew. Chem. 2020, 132. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y.; Donnelly, P.S.; Canty, A.J.; O’Hair, R.A.J. Desulfination versus decarboxylation as a means of generating three- and five-coordinate organopalladium complexes [(phen)nPd(C6H5)]+ (n = 1 and 2) to study their fundamental bimolecular reactivity. J. Organomet. Chem. 2019, 882. [Google Scholar] [CrossRef]
- Musher, J.I.; Salem, L. Energy of Interaction between Two Molecules. J. Chem. Phys. 1966, 44. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Baerends, E.J. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry. In Reviews in Computational Chemistry; Wiley-VCH: New York, NY, USA, 2007; Volume 15, pp. 1–86. [Google Scholar]
- Johnson, J.K.; Zollweg, J.A.; Gubbins, K.E. The lennard-jones equation of state revisited. Mol. Phys. 1993, 78, 591–618. [Google Scholar] [CrossRef]
- Glendening, E.D.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO Version 3.1; Gaussian Inc.: Pittsburgh, PA, USA, 1998. [Google Scholar]
- Fukui, K.; Koga, N.; Fujimoto, H. Interaction frontier orbitals. J. Am. Chem. Soc. 1981, 103. [Google Scholar] [CrossRef]
- Kumar, A.; Grewal, A.S.; Singh, V.; Narang, R.; Pandita, D.; Lather, V. Synthesis, Antimicrobial Activity and QSAR Studies of Some New Sparfloxacin Derivatives. Pharm. Chem. J. 2018, 52. [Google Scholar] [CrossRef]
- Malhotra, R.; Ravesh, A.; Singh, V. Synthesis, characterization, antimicrobial activities, and QSAR studies of organotin(IV) complexes. Phosphorus Sulfur Silicon Relat. Elem. 2017, 192. [Google Scholar] [CrossRef]
- Cortes, E.; Mora, J.; Márquez, E. Modelling the Anti-Methicillin-Resistant Staphylococcus Aureus (MRSA) Activity of Cannabinoids: A QSAR and Docking Study. Crystals 2020, 10, 692. [Google Scholar] [CrossRef]
- Flores, M.C.; Márquez, E.A.; Mora, J.R. Molecular modeling studies of bromopyrrole alkaloids as potential antimalarial compounds: A DFT approach. Med. Chem. Res. 2018, 27. [Google Scholar] [CrossRef]
- Alqahtani, F.; Aleanizy, F.; El Tahir, E.; Alhabib, H.; Alsaif, R.; Shazly, G.; AlQahtani, H.; Alsarra, I.; Mahdavi, J. Antibacterial Activity of Chitosan Nanoparticles Against Pathogenic, N. gonorrhoea. Int. J. Nanomed. 2020, 15. [Google Scholar] [CrossRef]
- Nooshkam, M.; Falah, F.; Zareie, Z.; Tabatabaei Yazdi, F.; Shahidi, F.; Mortazavi, S.A. Antioxidant potential and antimicrobial activity of chitosan–inulin conjugates obtained through the Maillard reaction. Food Sci. Biotechnol. 2019, 28. [Google Scholar] [CrossRef]
- Yildirim-Aksoy, M.; Beck, B.H. Antimicrobial activity of chitosan and a chitosan oligomer against bacterial pathogens of warmwater fish. J. Appl. Microbiol. 2017, 122. [Google Scholar] [CrossRef]
- Hunter, C.A.; Singh, J.; Thornton, J.M. π–π interactions: The geometry and energetics of phenylalanine-phenylalanine interactions in proteins. J. Mol. Biol. 1991, 218. [Google Scholar] [CrossRef]
- Zhou, R. Modeling of Nanotoxicity; Springer International Publishing: Cham, Switzerland, 2015; ISBN 978-3-319-15381-0. [Google Scholar]
- Tsuzuki, S.; Honda, K.; Uchimaru, T.; Mikami, M.; Tanabe, K. Origin of Attraction and Directionality of the π/π Interaction: Model Chemistry Calculations of Benzene Dimer Interaction. J. Am. Chem. Soc. 2002, 124. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, J.; Fu, W.; Jiang, D.; Lv, N.; Liu, H.; Li, H.; Zhu, W. Theoretical prediction of the SO2 absorption by hollow silica based porous ionic liquids. J. Mol. Graph. Model. 2021, 103. [Google Scholar] [CrossRef]
- Pramanik, B.; Ahmed, S.; Singha, N.; Das, B.K.; Dowari, P.; Das, D. Unorthodox Combination of Cation−π and Charge-Transfer Interactions within a Donor–Acceptor Pair. Langmuir 2019, 35. [Google Scholar] [CrossRef]
- Bhattacharyya, P.K. Exploring Cation−π Interaction in the Complexes with B≡B Triple Bond: A DFT Study. J. Phys. Chem. A 2017, 121. [Google Scholar] [CrossRef]
- Bronowska, K.A. Thermodynamics of Ligand-Protein Interactions: Implications for Molecular Design. In Thermodynamics—Interaction Studies—Solids, Liquids and Gases; IntechOpen: Rijeka, Croatia, 2011. [Google Scholar]
- Gupta, M.; da Silva, E.F.; Hartono, A.; Svendsen, H.F. Theoretical Study of Differential Enthalpy of Absorption of CO 2 with MEA and MDEA as a Function of Temperature. J. Phys. Chem. B 2013, 117. [Google Scholar] [CrossRef]
- Kim, I.; Hoff, K.A.; Hessen, E.T.; Haug-Warberg, T.; Svendsen, H.F. Enthalpy of absorption of CO2 with alkanolamine solutions predicted from reaction equilibrium constants. Chem. Eng. Sci. 2009, 64. [Google Scholar] [CrossRef]
- Al-Ghouti, M.A.; Da’ana, D.A. Guidelines for the use and interpretation of adsorption isotherm models: A review. J. Hazard. Mater. 2020, 393. [Google Scholar] [CrossRef] [PubMed]
- Piccini, G.; Alessio, M.; Sauer, J.; Zhi, Y.; Liu, Y.; Kolvenbach, R.; Jentys, A.; Lercher, J.A. Accurate Adsorption Thermodynamics of Small Alkanes in Zeolites. Ab initio Theory and Experiment for H-Chabazite. J. Phys. Chem. C 2015, 119. [Google Scholar] [CrossRef]
- Campbell, C.T.; Sellers, J.R.V. Enthalpies and Entropies of Adsorption on Well-Defined Oxide Surfaces: Experimental Measurements. Chem. Rev. 2013, 113. [Google Scholar] [CrossRef] [PubMed]
- Dauenhauer, P.J.; Abdelrahman, O.A. A Universal Descriptor for the Entropy of Adsorbed Molecules in Confined Spaces. ACS Cent. Sci. 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Li, Y.; Zhang, L.; Huang, H.; Hu, J.; Shah, S.M.; Su, X. Adsorption and removal of tetracycline antibiotics from aqueous solution by graphene oxide. J. Colloid Interface Sci. 2012, 368. [Google Scholar] [CrossRef]
- Feiner, A.S. The Nernst equation. J. Chem. Educ. 1994, 71, 493–494. [Google Scholar] [CrossRef]
- Anastopoulos, I.; Kyzas, G.Z. Are the thermodynamic parameters correctly estimated in liquid-phase adsorption phenomena? J. Mol. Liq. 2016, 218. [Google Scholar] [CrossRef]
- Beyhan, S.M.; Götz, A.W.; Visscher, L. Bond energy decomposition analysis for subsystem density functional theory. J. Chem. Phys. 2013, 138. [Google Scholar] [CrossRef]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22. [Google Scholar] [CrossRef]
- Morokuma, K. Molecular Orbital Studies of Hydrogen Bonds. III. C=O···H–O Hydrogen Bond in H2CO···H2O and H 2CO···2H2O. J. Chem. Phys. 1971, 55. [Google Scholar] [CrossRef]
- Phipps, M.J.S.; Fox, T.; Tautermann, C.S.; Skylaris, C.-K. Energy decomposition analysis approaches and their evaluation on prototypical protein–drug interaction patterns. Chem. Soc. Rev. 2015, 44. [Google Scholar] [CrossRef]

| Complex | ΔH (kcal/mol) | ΔS (cal/mol) | ΔG (kcal/mol) | ΔET (kcal/mol) |
|---|---|---|---|---|
| AMOX-CS | −42.53 | −61.78 | −24.11 | −25.36 |
| AMOX-GO-1 | −36.64 | −59.55 | −18.88 | −21.63 |
| AMOX-GO-2 | −39.65 | −79.53 | −15.93 | −24.71 |
| IBU-CS | −27.84 | −57.45 | −10.71 | −22.85 |
| IBU-GO-1 | −21.06 | −50.55 | −5.99 | −22.30 |
| IBU-GO-2 | −24.51 | −54.68 | −8.21 | −19.41 |
| Tetracycline-CS | −21.06 | −51.31 | −5.76 | −22.73 |
| Oxytetracycline-CS | −37.63 | −65.33 | −18.15 | −31.78 |
| doxycycline-CS | −22.98 | −52.94 | −7.20 | −23.78 |
| Tetracycline-GO-1 | −22.56 | −54.83 | −6.22 | −23.29 |
| Oxytetracycline-GO-1 | −20.26 | −48.71 | −5.74 | −22.95 |
| Doxycycline-GO-1 | −29.10 | −60.42 | −11.09 | −26.70 |
| Tetracycline-GO-2 | −18.56 | −50.83 | −3.41 | −18.09 |
| Oxytetracycline-GO-2 | −16.26 | −44.71 | −2.93 | −18.47 |
| Doxycycline-GO-2 | −27.10 | −56.42 | −10.28 | −26.03 |
| Molecular Descriptor | AMOX-CS | IBU-CS | AMOX-GO-1 | AMOX-GO-2 | IBU-GO-1 | IBU-GO-2 |
|---|---|---|---|---|---|---|
| HOMO | −188.77 | −196.17 | −159.85 | −155.27 | −161.78 | −156.46 |
| LUMO | 30.21 | 29.21 | −10.09 | −22.89 | −11.05 | −23.65 |
| µ global | −79.28 | −83.48 | −84.97 | −89.08 | −86.41 | −90.05 |
| η global | 109.49 | 112.69 | 74.88 | 66.19 | 75.36 | 66.40 |
| ΔN | −413.36 | −154.32 | −213.62 | −212.89 | −145.44 | −111.66 |
| Donator | Acceptor | Donator | Acceptor | ||
|---|---|---|---|---|---|
| Amoxcicillin-Chitosan | |||||
| BD C14-H18 | BD* O89-H90 | 0.29 | LP(2)O66 | BD* N33-H34 | 0.29 |
| BD N33-H34 | BD* N67-H68 | 0.56 | LP(2)O66 | BD* O31-H32 | 1.51 |
| LP O29 | BD* C48-H54 | 0.21 | LP(2)O66 | BD* N33-H34 | 0.29 |
| LP O31 | BD* C49-H55 | 0.86 | LP N67 | BD* C4-H8 | 0.23 |
| LP N33 | BD* N67-H68 | 17.25 | LP(1)O88 | BD* C2-H10 | 0.40 |
| LP O36 | BD* O89-H90 | 0.43 | LP(1)O88 | BD* C12-H15 | 0.69 |
| LP O33 | BD* O89-H90 | 25.72 | LP(2)O88 | BD* C12-H15 | 1.28 |
| BD C65-O66 | BD* O31-H32 | 4.54 | LP(1)O91 | BD* C1-H6 | 0.88 |
| BD C71-O91 | BD* C2-H10 | 0.34 | LP(1)O91 | BD* C4-H8 | 0.21 |
| BD C87-O88 | BD* C2-H10 | 0.63 | LP(2)O91 | BD* C4-H8 | 0.77 |
| BD C87-O88 | BD* C12-H15 | 0.23 | BD C8-C9 | BD* C70-C71 | 0.25 |
| BD O89-H90 | BD* C14-O36 | 0.49 | BD C13-C14 | BD* C72-C73 | 0.21 |
| LP(1)O66 | BD* O31-H32 | 4.77 | BD C15-C16 | LP*(1)C84 | 0.62 |
| LP(2)O66 | BD* O31-H32 | 1.51 | LP(1)O67 | BD* N88-H89 | 0.47 |
| Ibuprofen-Chitosan | |||||
| LP O27 | BD* O63-H64 | 1.50 | BD C49 - H55 | BD* C13-H16 | 0.23 |
| LP O27 | BD* O63-H 64 | 23.05 | BD C51 - C52 | BD* C5-H9 | 0.20 |
| LP O41 | BD* C 48-H 54 | 0.20 | BD C53 - C59 | RY* H7 | 0.55 |
| LP O41 | BD* C 48-H 54 | 0.75 | BD C61 - O62 | RY* H18 | 0.26 |
| BD C48-C49 | RY* H16 | 0.27 | BD C61 - O62 | BD* C14-H18 | 0.94 |
| BD C48-C53 | RY* H7 | 0.29 | BD O63 - H64 | BD* C24-O27 | 0.36 |
| BD C 48-C53 | BD* C3-H7 | 0.24 | LP O62 | BD* C14-H18 | 0.35 |
| LP O62 | BD* N43-H45 | 2.20 | LP O62 | BD* N43-H45 | 1.14 |
| Amoxicillin-GO-1 | |||||
| BD C7-C8 | BD* C50-C51 | 0.41 | BD C50-C51 | LP(1)C3 | 0.70 |
| BD C41-O42 | BD* N68-H69 | 1.24 | BD C50-C51 | LP*(1)C4 | 0.78 |
| BD C41-O42 | BD* C72-O77 | 1.11 | BD C64-O76 | BD* O47-H48 | 3.44 |
| BD O47-H48 | BD* C64-O76 | 0.34 | LP(1)O76 | BD* O47-H48 | 13.39 |
| BD O47-H48 | BD* C64-O76 | 0.60 | LP(1)O83 | BD* O43-H44 | 2.56 |
| LP(1)O42 | BD* N68-H69 | 3.63 | LP(2)O83 | BD* O43-H44 | 2.43 |
| LP(2)O42 | BD* N68-H69 | 3.74 | BD* C52-C53 | BD* C13-C14 | 0.26 |
| BD* C7-C8 | BD* C54-C55 | 0.67 | BD* C54-C55 | BD* C13-C14 | 0.53 |
| BD*C41-O42 | BD* N68-H69 | 0.29 | BD* C64-O76 | BD* O47-H48 | 1.60 |
| Amoxicillin-GO-2 | |||||
| BD C8-C9 | BD* C70-C71 | 0.25 | BD* C41-C42 | BD* C74-C75 | 0.55 |
| BD C13-C14 | BD* C72-C73 | 0.21 | BD C61-O62 | LP*(1)H105 | 3.46 |
| BD C15-C16 | LP*(1)C84 | 0.62 | LP(1)O62 | LP*(1)H105 | 2.53 |
| LP(1)O67 | BD* N88-H89 | 0.47 | LP(2)O62 | LP*(1)H105 | 4.90 |
| LP(2)O67 | BD* N88-H89 | 2.32 | BD* C61-O62 | LP*(1)H105 | 3.70 |
| BD* C11-C12 | BD* C70-C71 | 1.85 | BD* C41-C42 | BD* C74-C75 | 0.55 |
| IBU-GO-1 | |||||
| LP(1)O72 | BD* O47-H48 | 6.81 | BD C69-O70 | BD* O47-H48 | 0.22 |
| LP(2)O72 | BD* O47-H48 | 11.48 | BD C69-O72 | BD* C13-H15 | 0.42 |
| BD C22-C23 | BD* C79-H82 | 0.20 | BD C69-O72 | BD* O47-H48 | 0.40 |
| IBU-GO-2 | |||||
| LP(1)O62 | BD* O92-H91 | 8.38 | LP (1)O92 | LP*(1)C61 | 0.32 |
| BD C72-C73 | BD* C10-C27 | 0.22 | LP (2)O92 | LP*(1)C61 | 1.26 |
| BD C89-O92 | BD* C21-C22 | 0.38 | BD* C89-O92 | BD* C1-C6 | 0.26 |
| LP(2)O90 | BD* C21-C22 | 0.31 | BD* C89-O92 | BD* C21-C22 | 0.37 |
| Complex | ΔEelect (kcal/mol) | ΔEoi (kcal/mol) | ΔEPauli (kcal/mol) | ΔEint (kcal/mol) | ΔET (kcal/mol) | ΔEprep (kcal/mol) |
|---|---|---|---|---|---|---|
| AMOX-CS | −64.44 | −32.31 | 52.37 | −34.70 | −25.36 | 9.41 |
| AMOX-GO-1 | −26.79 | −21.06 | 7.39 | −33.21 | −21.63 | 11.62 |
| AMOX-GO-2 | −24.59 | −21.82 | 7.89 | −31.33 | −24.71 | 6.31 |
| IBU-CS | −30.23 | −19.79 | 17.26 | −25.50 | −22.85 | 2.62 |
| IBU-GO-1 | −13.29 | −11.95 | −3.47 | −24.41 | −22.30 | 2.10 |
| IBU-GO-2 | −22.32 | −12.00 | 7.24 | −23.21 | −19.41 | 3.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anchique, L.; Alcázar, J.J.; Ramos-Hernandez, A.; Méndez-López, M.; Mora, J.R.; Rangel, N.; Paz, J.L.; Márquez, E. Predicting the Adsorption of Amoxicillin and Ibuprofen on Chitosan and Graphene Oxide Materials: A Density Functional Theory Study. Polymers 2021, 13, 1620. https://doi.org/10.3390/polym13101620
Anchique L, Alcázar JJ, Ramos-Hernandez A, Méndez-López M, Mora JR, Rangel N, Paz JL, Márquez E. Predicting the Adsorption of Amoxicillin and Ibuprofen on Chitosan and Graphene Oxide Materials: A Density Functional Theory Study. Polymers. 2021; 13(10):1620. https://doi.org/10.3390/polym13101620
Chicago/Turabian StyleAnchique, Leonardo, Jackson J. Alcázar, Andrea Ramos-Hernandez, Maximiliano Méndez-López, José R. Mora, Norma Rangel, José Luis Paz, and Edgar Márquez. 2021. "Predicting the Adsorption of Amoxicillin and Ibuprofen on Chitosan and Graphene Oxide Materials: A Density Functional Theory Study" Polymers 13, no. 10: 1620. https://doi.org/10.3390/polym13101620
APA StyleAnchique, L., Alcázar, J. J., Ramos-Hernandez, A., Méndez-López, M., Mora, J. R., Rangel, N., Paz, J. L., & Márquez, E. (2021). Predicting the Adsorption of Amoxicillin and Ibuprofen on Chitosan and Graphene Oxide Materials: A Density Functional Theory Study. Polymers, 13(10), 1620. https://doi.org/10.3390/polym13101620







