A Novel Multiscale Methodology for Simulating Droplet Morphology Evolution during Injection Molding of Polymer Blends
Abstract
1. Introduction
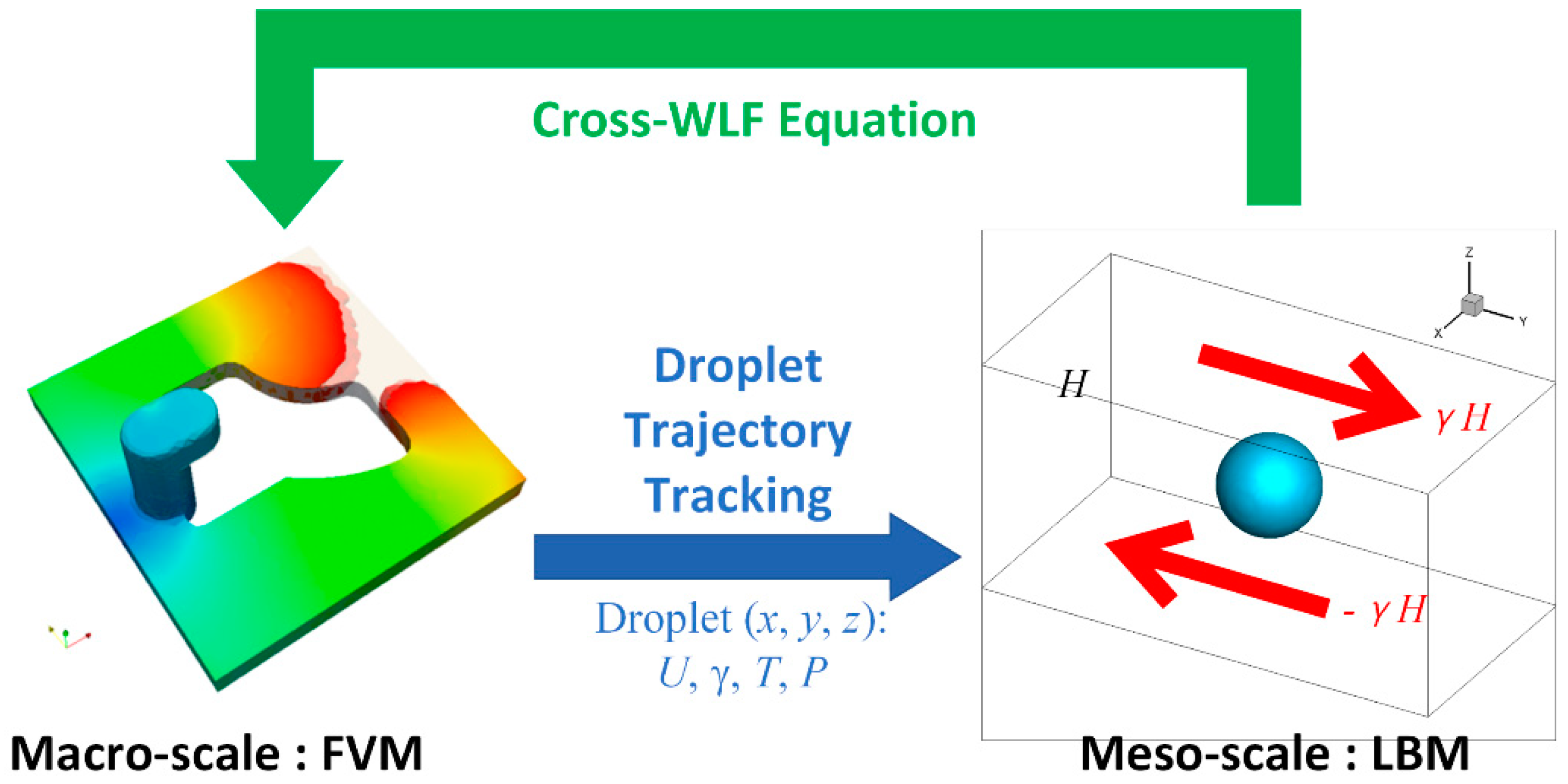
2. Multiscale Model
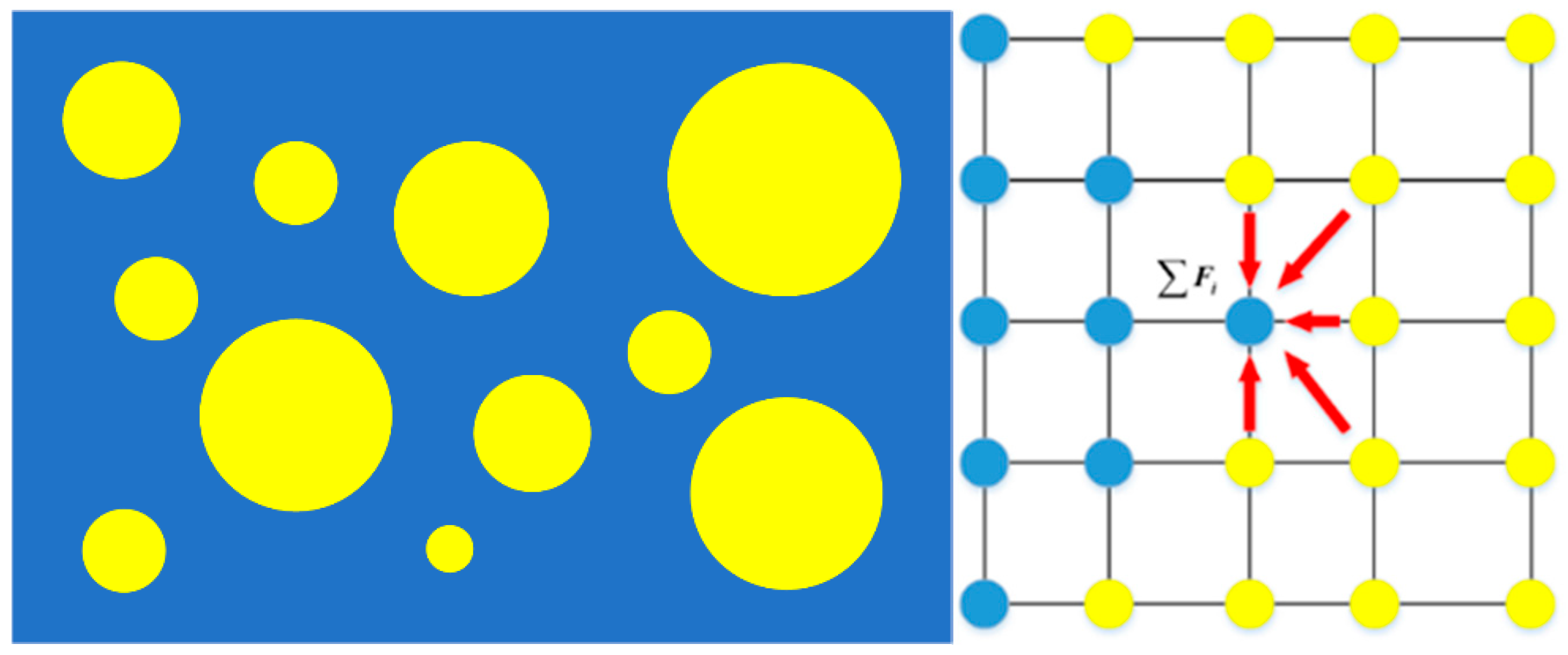
2.1. Macroscale Model for Mold Filling Flow of Polymer Melt
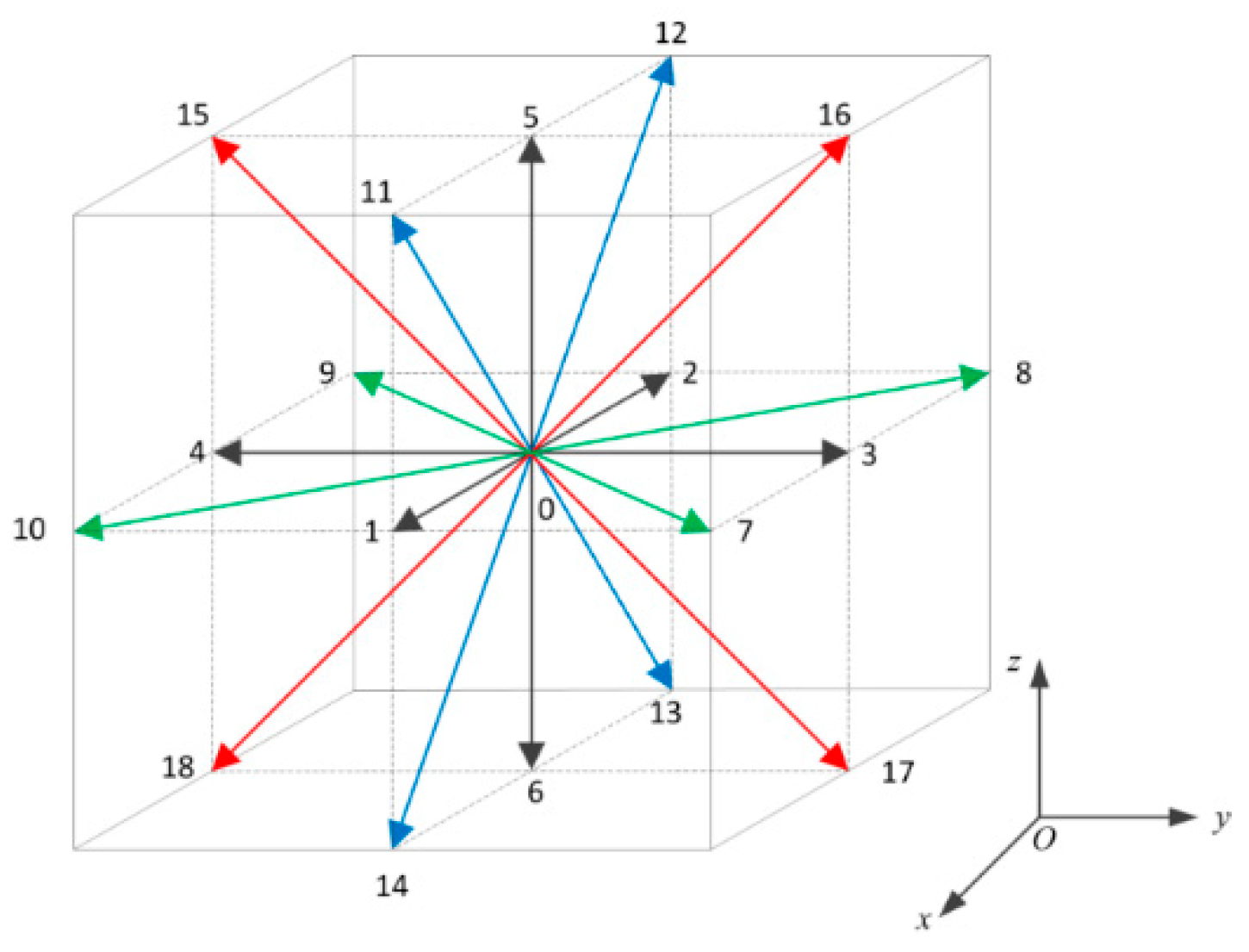
2.2. Mesoscale Droplet Morphology Evolution
2.3. Macro- and Meso-Scale Coupling
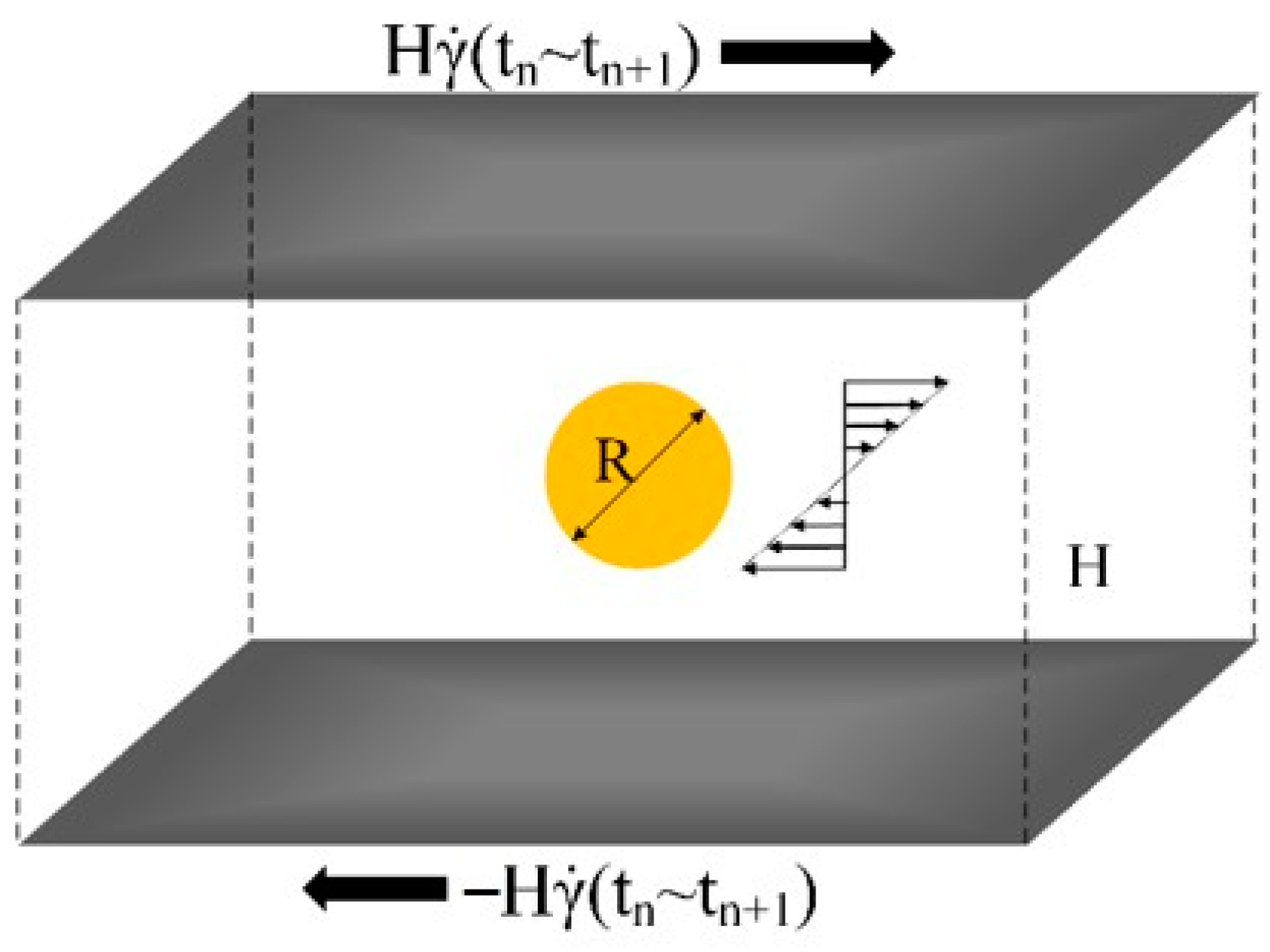
2.3.1. Droplet Trajectory Tracking
2.3.2. Model Set-Up for Droplet Morphology
2.3.3. Polymer Blends Constitutive Equation
2.4. Algorithm Summary
- (1)
- Given the initial macroscopic flow field of , and , the droplet morphology and coordinate at time ;
- (2)
- Calculate the shear rate on the droplet according to its coordinate ;
- (3)
- Solve Equations (1)–(4) to update the velocity, pressure and temperature to , and to time ;
- (4)
- Update the coordinate of the droplet to at time according Equations (23)–(25);
- (5)
- Calculate the shear rate on the droplet according to its coordinate ;
- (6)
- Solve Equations (15) and (27) to simulate the droplet morphology evolution during the timestep between and ;
- (7)
- Go back to step (2) until the mold filling ends.
3. Experimental Validation
3.1. Cavity Pressure Variation during Mold Filling
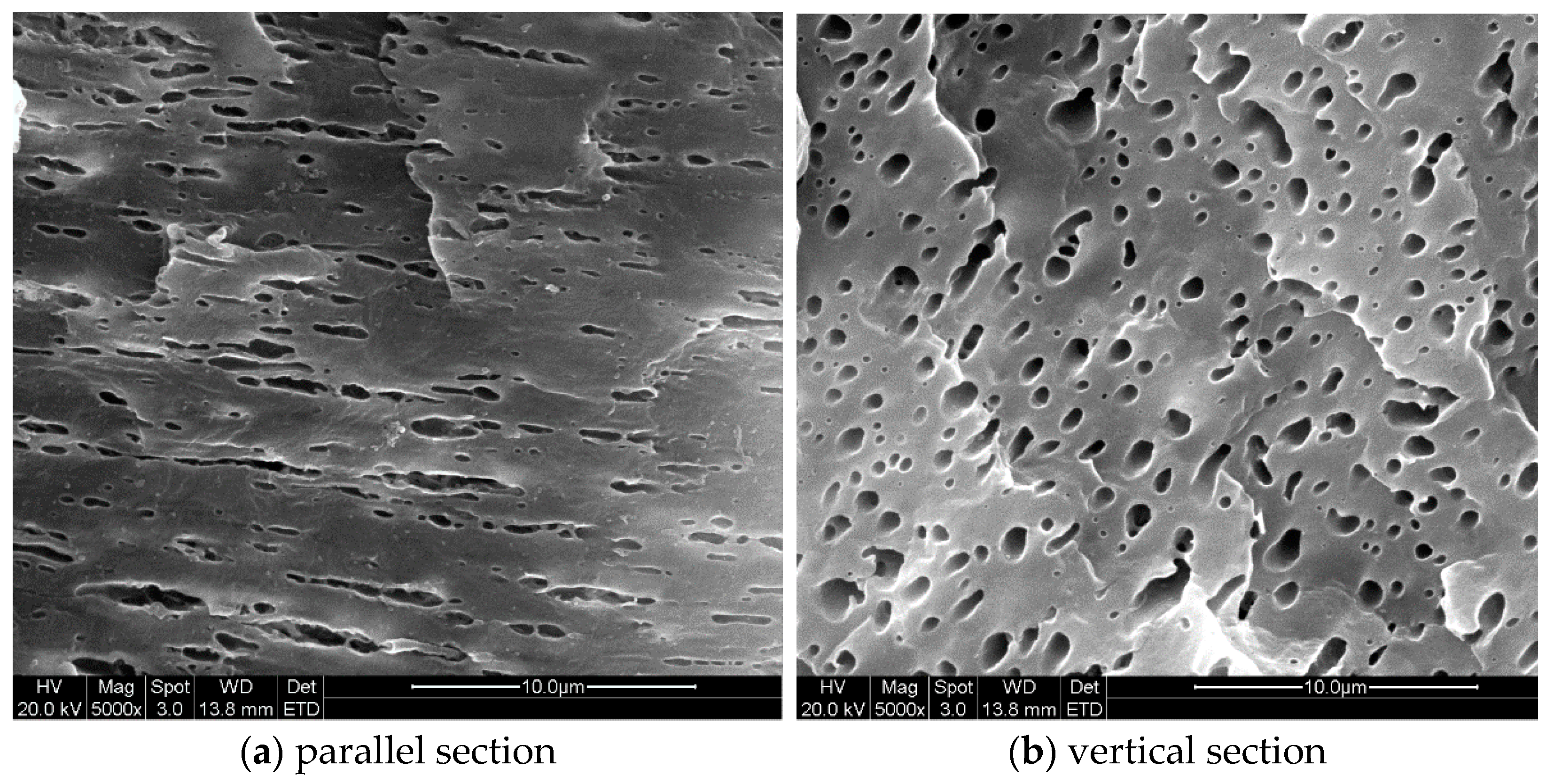
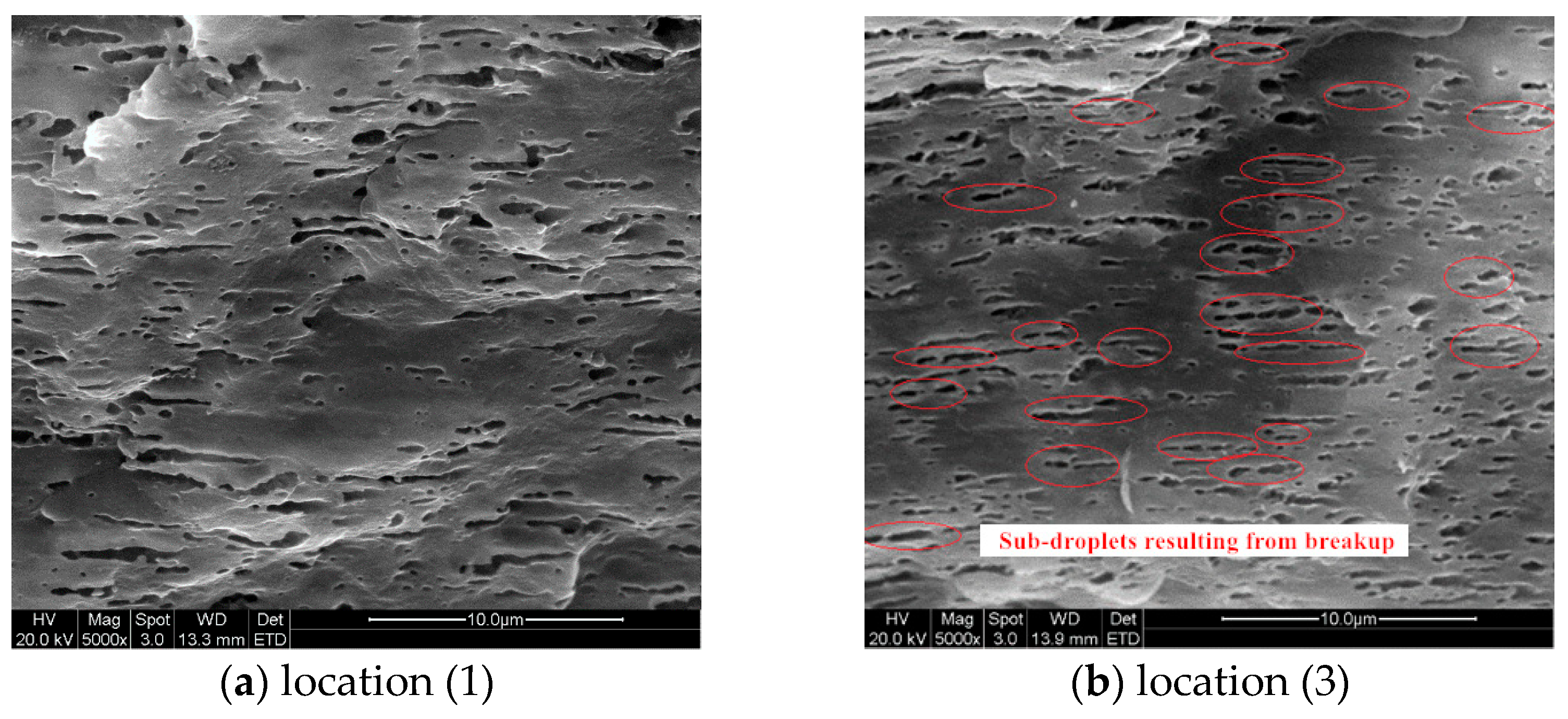
3.2. Droplet Morphology Evolution during Mold Filing
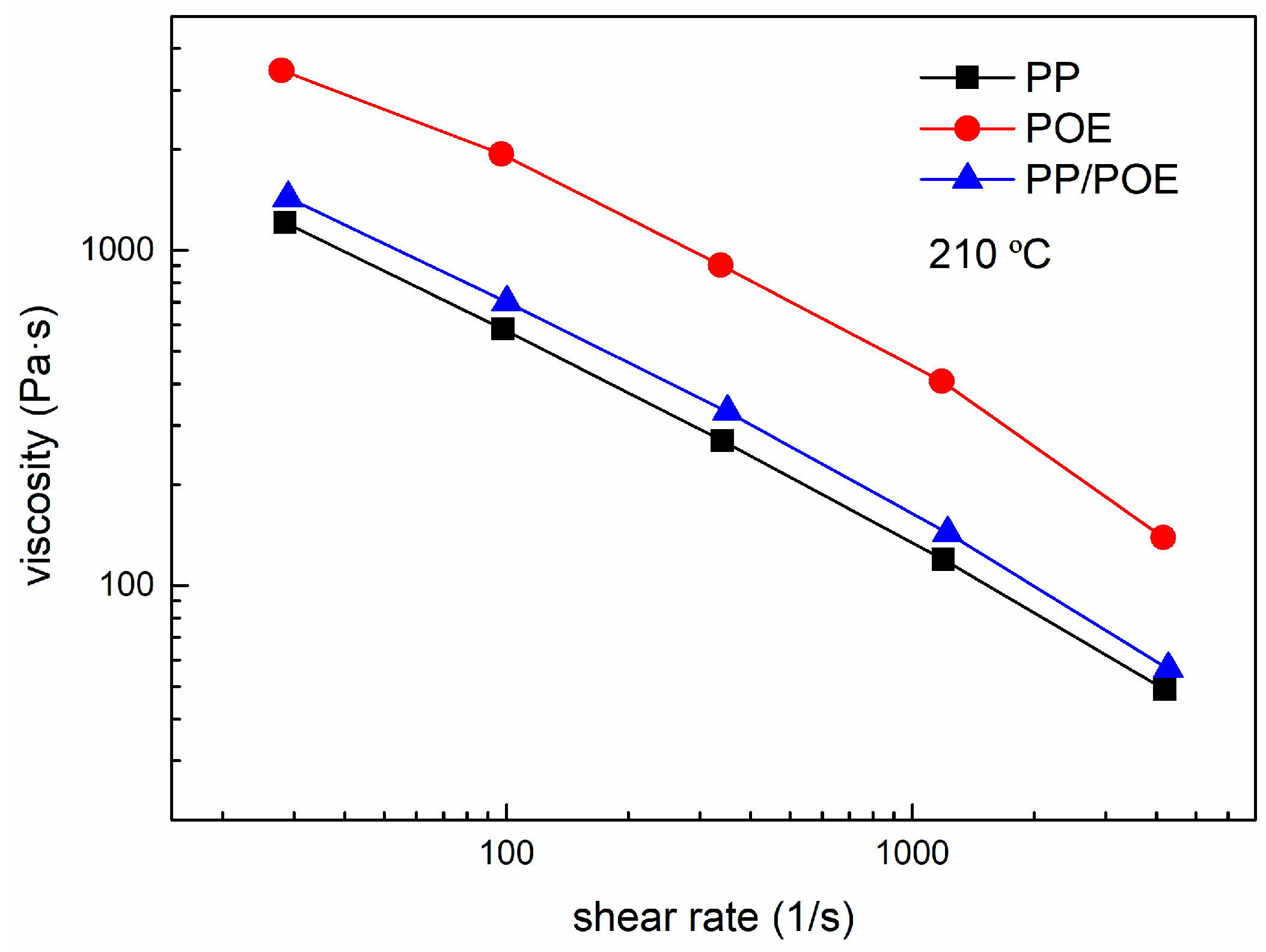
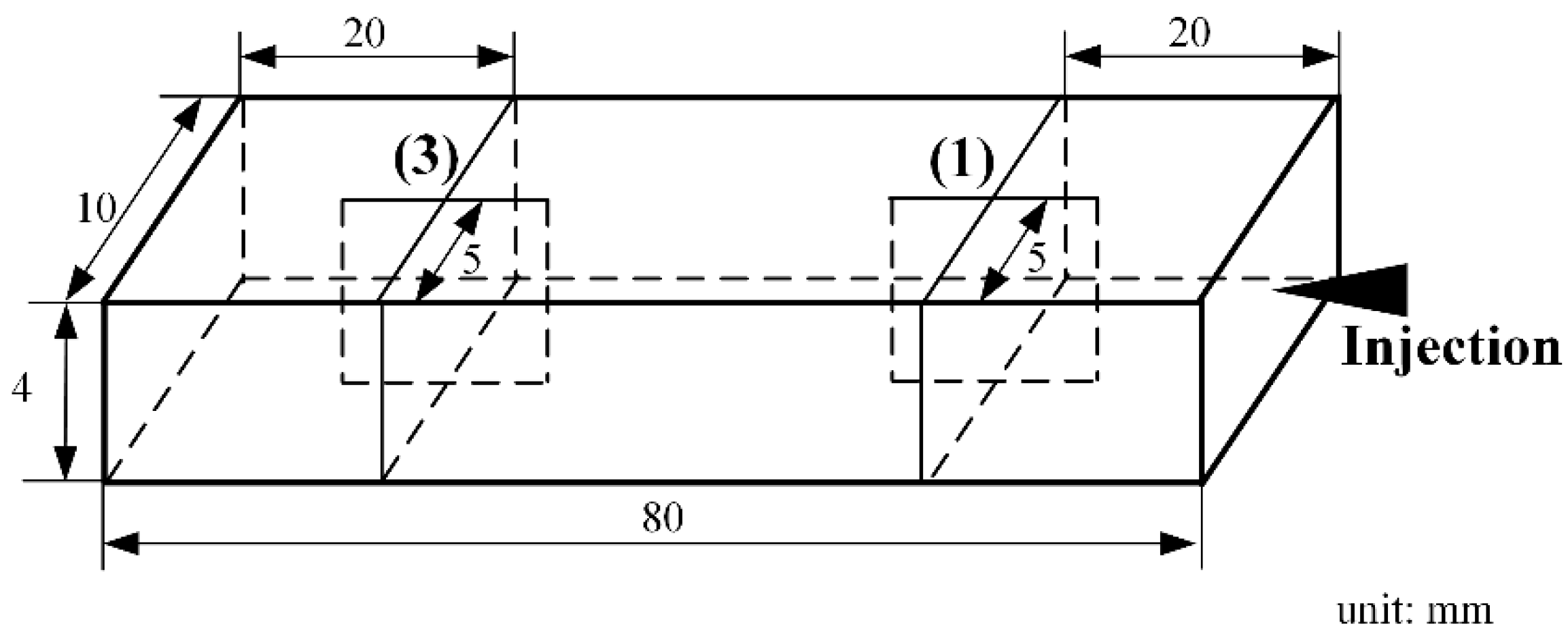
3.2.1. Experiments and Simulation Set-Up
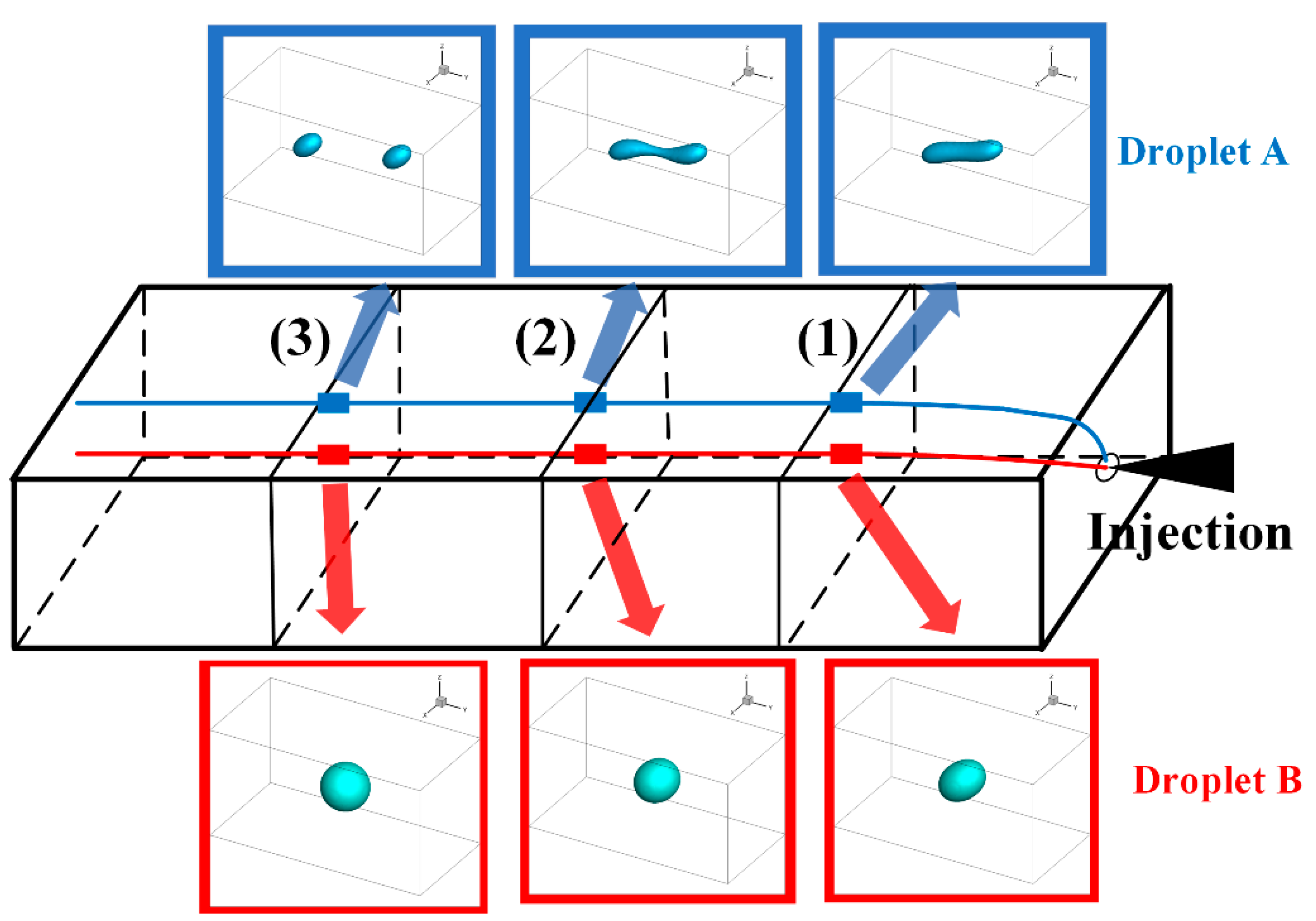
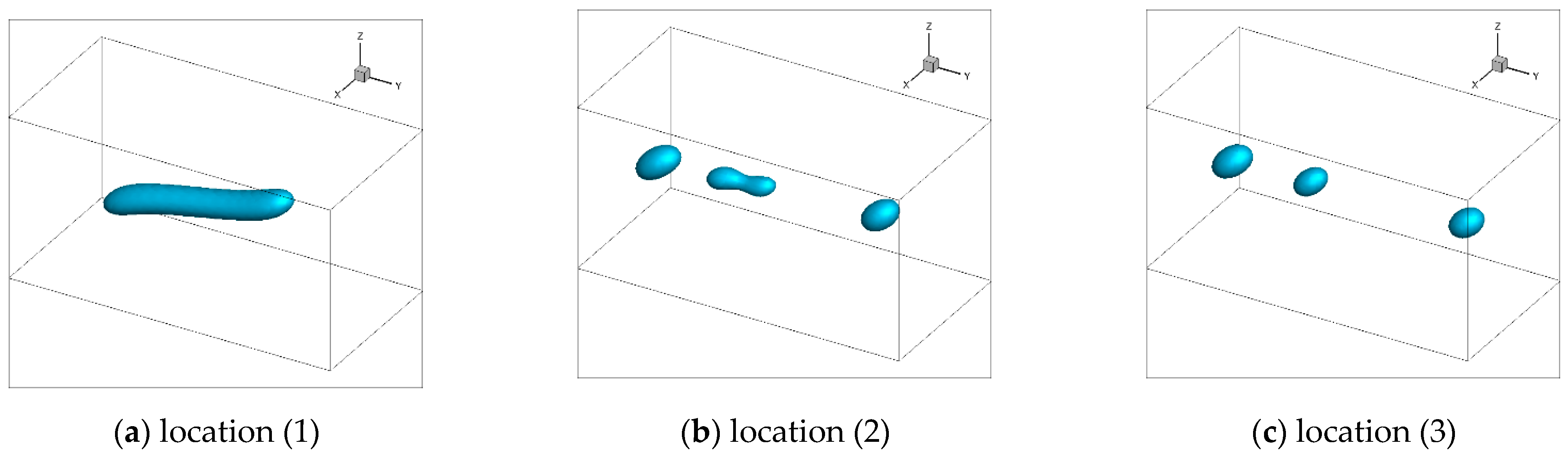
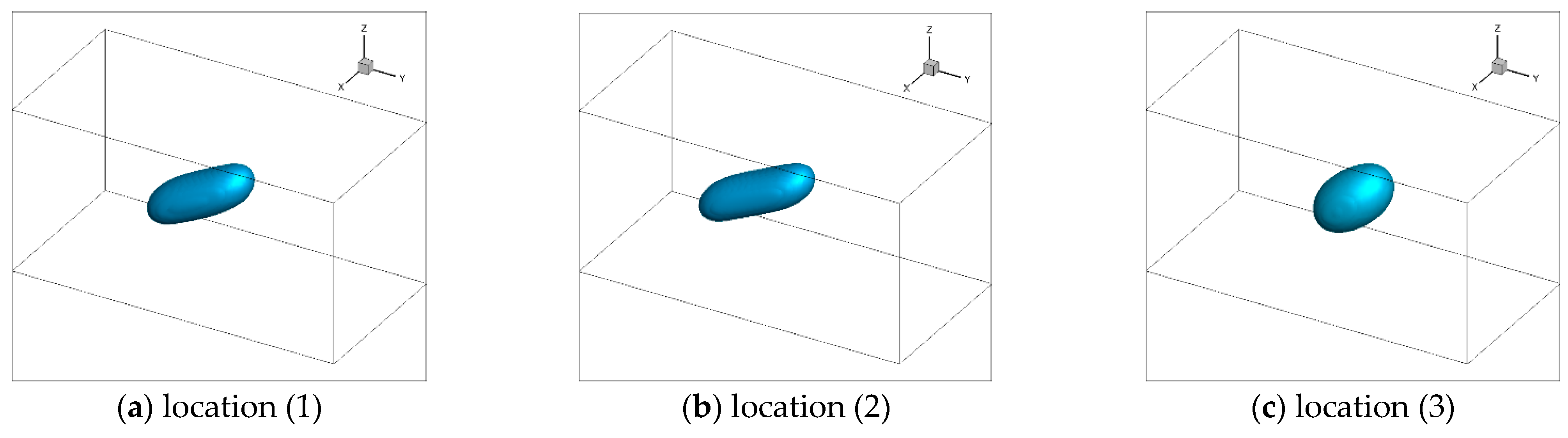
3.2.2. Numerical Validation
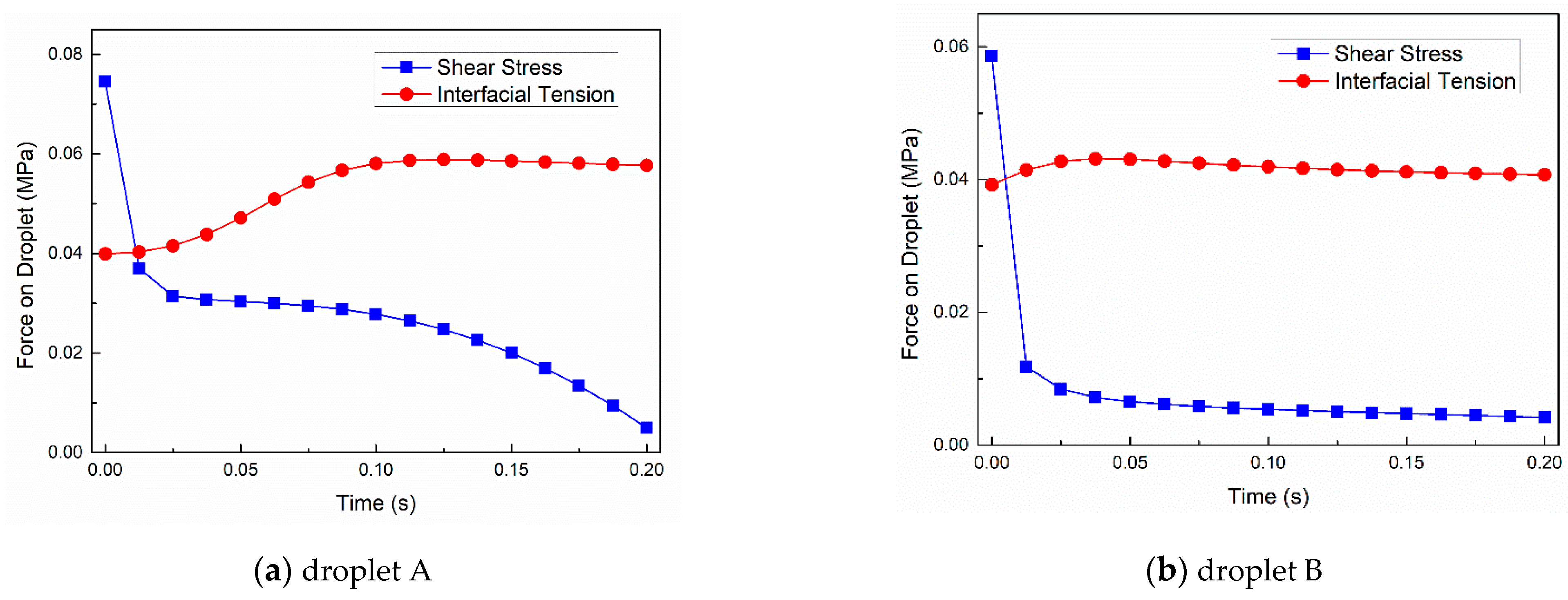
3.2.3. Force Analysis of Droplets
3.2.4. Effect of the Injection Rate
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Shen, Y.; Shen, Z.; Jiang, J.; Chen, L.; Nan, C.-W. Achieving High Energy Density in PVDF-Based Polymer Blends: Suppression of Early Polarization Saturation and Enhancement of Breakdown Strength. ACS Appl. Mater. Interfaces 2016, 8, 27236–27242. [Google Scholar] [CrossRef] [PubMed]
- Abtahi, A.; Johnson, S.; Park, S.M.; Luo, X.; Liang, Z.; Mei, J.; Graham, K.R. Designing π-conjugated polymer blends with improved thermoelectric power factors. J. Mater. Chem. A 2019, 7, 19774–19785. [Google Scholar] [CrossRef]
- Manson, J.A. Polymer Blends and Composites; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Iii, C.L.T.; Moldenaers, P. Microstructuralevolution Inpolymerblends. Annu. Rev. Fluid Mech. 2002, 34, 177–210. [Google Scholar] [CrossRef]
- Martuscelli, E. Polymer Blends: Processing, Morphology, and Properties; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Chen, S.; Zhang, Q.; Feng, J. 3D printing of tunable shape memory polymer blends. J. Mater. Chem. C 2017, 5, 8361–8365. [Google Scholar] [CrossRef]
- Bartczak, Z.; Galeski, A. Mechanical Properties of Polymer Blends. In Polymer Blends Handbook; Springer: Dordrecht, The Netherlands, 2014; pp. 1203–1297. [Google Scholar]
- Yamaguchi, M.; Lee, S.; Manaf, M.E.A.; Tsuji, M.; Yokohara, T. Modification of orientation birefringence of cellulose ester by addition of poly(lactic acid). Eur. Polym. J. 2010, 46, 2269–2274. [Google Scholar] [CrossRef]
- Doi, M.; Ohta, T. Dynamics and rheology of complex interfaces. I. J. Chem. Phys. 1991, 95, 1242–1248. [Google Scholar] [CrossRef]
- Lee, H.M.; Park, O.O. Rheology and dynamics of immiscible polymer blends. J. Rheol. 1994, 38, 1405–1425. [Google Scholar] [CrossRef]
- Grmela, M.; Ait-Kadi, A. Comments on the Doi-Ohta theory of blends. J. Non-Newton. Fluid Mech. 1994, 55, 191–195. [Google Scholar] [CrossRef]
- Lacroix, C.; Grmela, M.; Carreau, P. Relationships between rheology and morphology for immiscible molten blends of poly-propylene and ethylene copolymers under shear flow. J. Rheol. 1998, 42, 41–62. [Google Scholar] [CrossRef]
- Voit, A.; Krekhov, A.; Enge, W.; Kramer, L.; Köhler, W. Thermal Patterning of a Critical Polymer Blend. Phys. Rev. Lett. 2005, 94, 214501. [Google Scholar] [CrossRef]
- De Groot, S.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications Inc.: New York, NY, USA, 1984. [Google Scholar]
- Pincus, P. Dynamics of fluctuations and spinodal decomposition in polymer blends. II. J. Chem. Phys. 1981, 75, 1996–2000. [Google Scholar] [CrossRef]
- Prusty, M.; Keestra, B.; Goossens, H.; Anderson, P.P. Experimental and computational study on structure development of PMMA/SAN blends. Chem. Eng. Sci. 2007, 62, 1825–1837. [Google Scholar] [CrossRef]
- Tabatabaieyazdi, M.; Chan, P.K.; Wu, J. A computational study of long range surface-directed phase separation in polymer blends under a temperature gradient. Comput. Mater. Sci. 2016, 111, 387–394. [Google Scholar] [CrossRef]
- Forrest, B.M.; Toral, R. The phase diagram of the Flory-Huggins-de Gennes model of a binary polymer blend. J. Stat. Phys. 1994, 77, 473–489. [Google Scholar] [CrossRef]
- Maffettone, P.L.; Minale, M. Equation of change for ellipsoidal drops in viscous flow. J. Non-Newton. Fluid Mech. 1998, 78, 227–241. [Google Scholar] [CrossRef]
- Wetzel, E.D.; Tucker, C.L. Droplet deformation in dispersions with unequal viscosities and zero interfacial tension. J. Fluid Mech. 2001, 426, 199–228. [Google Scholar] [CrossRef]
- Jackson, N.E.; Tucker, C.L., III. A model for large deformation of an ellipsoidal droplet with interfacial tension. J. Rheol. 2003, 47, 659–682. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, C. Dynamics of droplet with viscoelastic interface. Soft Matter 2011, 7, 6337–6346. [Google Scholar] [CrossRef]
- Grmela, M.; Bousmina, M.; Palierne, J.-F. On the rheology of immiscible blends. Rheol. Acta 2001, 40, 560–569. [Google Scholar] [CrossRef]
- Minale, M. Models for the deformation of a single ellipsoidal drop: A review. Rheol. Acta 2010, 49, 789–806. [Google Scholar] [CrossRef]
- Van Puyvelde, P.; Vananroye, A.; Cardinaels, R.; Moldenaers, P. Review on morphology development of immiscible blends in confined shear flow. Polymer 2008, 49, 5363–5372. [Google Scholar] [CrossRef]
- Fortelný, I.; Jůza, J. Description of the Droplet Size Evolution in Flowing Immiscible Polymer Blends. Polymer 2019, 11, 761. [Google Scholar] [CrossRef] [PubMed]
- Laschet, G.; Spekowius, M.; Spina, R.; Hopmann, C. Multiscale simulation to predict microstructure dependent effective elastic proper-ties of an injection molded polypropylene component. Mech. Mater. 2017, 105, 123–137. [Google Scholar] [CrossRef]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A Review of Multiscale Computational Methods in Polymeric Materials. Polymer 2017, 9, 16. [Google Scholar] [CrossRef]
- Hua, S.; Zhang, S.; Cao, W.; Wang, Y.; Shao, C.; Liu, C.; Dong, B.; Shen, C. Simulation of Jetting in Injection Molding Using a Finite Volume Method. Polymer 2016, 8, 172. [Google Scholar] [CrossRef]
- Chang, R.-Y.; Yang, W.-H. Numerical simulation of mold filling in injection molding using a three-dimensional finite volume approach. Int. J. Numer. Methods Fluids 2001, 37, 125–148. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Mu, Y.; He, Y.-L.; Tao, W.-Q. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications. Int. J. Heat Mass Transf. 2014, 76, 210–236. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann Method for Complex Flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific Publishing: Singapore, Singapore, 2013. [Google Scholar]
- Zhou, J.; Turng, L.-S. Three-dimensional numerical simulation of injection mold filling with a finite-volume method and par-allel computing. Adv. Polym. Technol. 2006, 25, 247–258. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Kang, Q.J.; He, Y.L.; Chen, Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. [Google Scholar] [CrossRef]
- Shan, X.; Doolen, G. Multicomponent lattice-Boltzmann model with interparticle interaction. J. Stat. Phys. 1995, 81, 379–393. [Google Scholar] [CrossRef]
- Chen, S.; Wang, M.; Xia, Z. Multiscale Fluid Mechanics and Modeling. Procedia IUTAM 2014, 10, 100–114. [Google Scholar] [CrossRef]
- Ospald, F. Numerical Simulation of Injection Molding using OpenFOAM. PAMM 2014, 14, 673–674. [Google Scholar] [CrossRef]
- Özdemir, A.; Uluer, O.; Güldaş, A. Flow front advancement of molten thermoplastic materials during filling stage of a mold cavity. Polym. Test. 2004, 23, 957–966. [Google Scholar] [CrossRef]
- Wilkinson, A.N.; Ryan, A.J. Polymer Processing and Structure Development; Springer Science & Business Media: Berlin, Germany, 1998. [Google Scholar]
- Zhou, H. Computer Modeling for Injection Molding: Simulation, Optimization, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Zhou, Y.; Yu, F.; Deng, H.; Huang, Y.; Li, G.; Fu, Q. Morphology Evolution of Polymer Blends under Intense Shear During High Speed Thin-Wall Injection Molding. J. Phys. Chem. B 2017, 121, 6257–6270. [Google Scholar] [CrossRef] [PubMed]
- Na, B.; Zhang, Q.; Wang, Y.; Du, R.; Fu, Q. Three-dimensional phase morphologies in HDPE/EVA blends obtained via dynamic injection packing molding. Polymer 2003, 44, 5737–5747. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, F.; Huang, Z.; Xie, X.; Shan, B.; Zhou, H. Dispersed Phase Deformation Modeling of Immiscible Polymer Blends in Injection Molding. Adv. Polym. Technol. 2015, 34. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, C. A simple constitutive equation for immiscible blends. J. Rheol. 2007, 51, 179. [Google Scholar] [CrossRef]





| Variable | Meaning | Variable | Meaning |
|---|---|---|---|
| u | velocity | cp | specific heat |
| P | pressure | k | thermal conductivity |
| T | temperature | μ | viscosity |
| t | time | ρ | density |
| gravity | heat source |
| Equation | ϕ | Λ | Γ | Qϕ |
|---|---|---|---|---|
| Continuity | 1 | 1 | 0 | 0 |
| Momentum | ||||
| Energy |
| Processing Conditions | Parameters |
|---|---|
| Injection rate (cm3/s) | 25 |
| Mold temperature (°C) | 20 |
| Packing pressure (MPa) | 45 |
| Packing time (s) | 10 |
| Cooling time (s) | 10 |
| Melt temperature (°C) | 225 |
| Parameters | PP | POE |
|---|---|---|
| Melt density (g/cm3) | 0.738 | 0.776 |
| Thermal conductivity (J/(kg∙°C)) | 2755 | 2380 |
| Heat capacity (w/(m∙°C)) | 0.173 | 0.236 |
| Melt flow rate (g/10 min) | 3.5 | 1.0 |
| Melt index (10 g/min) | 3.6 | 0.50 |
| (Pa) | A1 | A2 (K) | D1 (Pa·s) | D2 (K) | D3 (K/Pa) | |
|---|---|---|---|---|---|---|
| 40,800.845 | 0.29 | 16.23 | 220.15 | 4.25 × 107 | 259 | 0 |
| Case I | Case II | Case III | |
|---|---|---|---|
| Injection rate (cm3/s) | 6 | 16 | 26 |
| Injection temperature (°C) | 225 | 225 | 225 |
| Mold wall temperature (°C) | 20 | 20 | 20 |
| Packing time (s) | 10 | 10 | 10 |
| Cooling time (s) | 10 | 10 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, L.; Fan, S.; Zhang, Y.; Huang, Z.; Jiang, S.; Li, J.; Zhou, H. A Novel Multiscale Methodology for Simulating Droplet Morphology Evolution during Injection Molding of Polymer Blends. Polymers 2021, 13, 133. https://doi.org/10.3390/polym13010133
Deng L, Fan S, Zhang Y, Huang Z, Jiang S, Li J, Zhou H. A Novel Multiscale Methodology for Simulating Droplet Morphology Evolution during Injection Molding of Polymer Blends. Polymers. 2021; 13(1):133. https://doi.org/10.3390/polym13010133
Chicago/Turabian StyleDeng, Lin, Suo Fan, Yun Zhang, Zhigao Huang, Shaofei Jiang, Jiquan Li, and Huamin Zhou. 2021. "A Novel Multiscale Methodology for Simulating Droplet Morphology Evolution during Injection Molding of Polymer Blends" Polymers 13, no. 1: 133. https://doi.org/10.3390/polym13010133
APA StyleDeng, L., Fan, S., Zhang, Y., Huang, Z., Jiang, S., Li, J., & Zhou, H. (2021). A Novel Multiscale Methodology for Simulating Droplet Morphology Evolution during Injection Molding of Polymer Blends. Polymers, 13(1), 133. https://doi.org/10.3390/polym13010133








