Characterization on Polyester Fibrous Panels and Their Homogeneity Assessment
Abstract
1. Introduction
2. Experiment
2.1. Materials
2.2. Direct Characterization
2.3. Acoustic Characterization
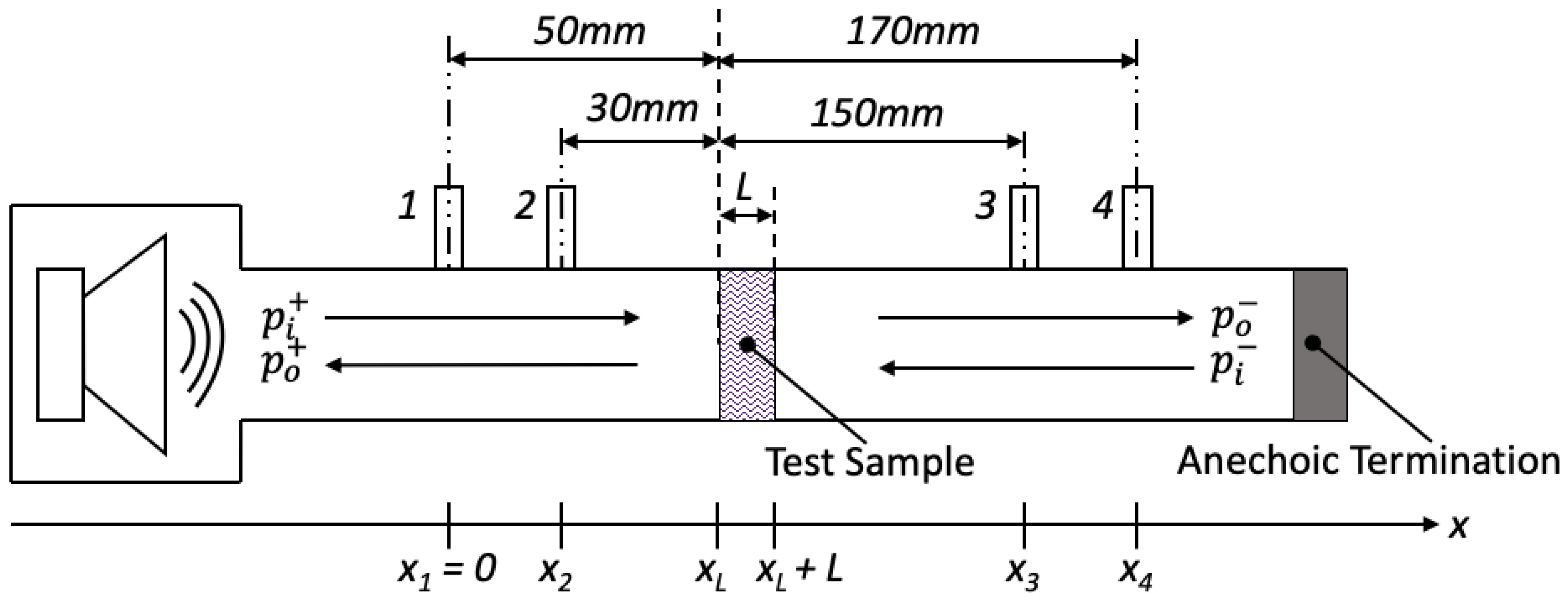
2.3.1. Impedance Tube Measurement
2.3.2. The Johnson-Champoux-Allard-Lafarge Model
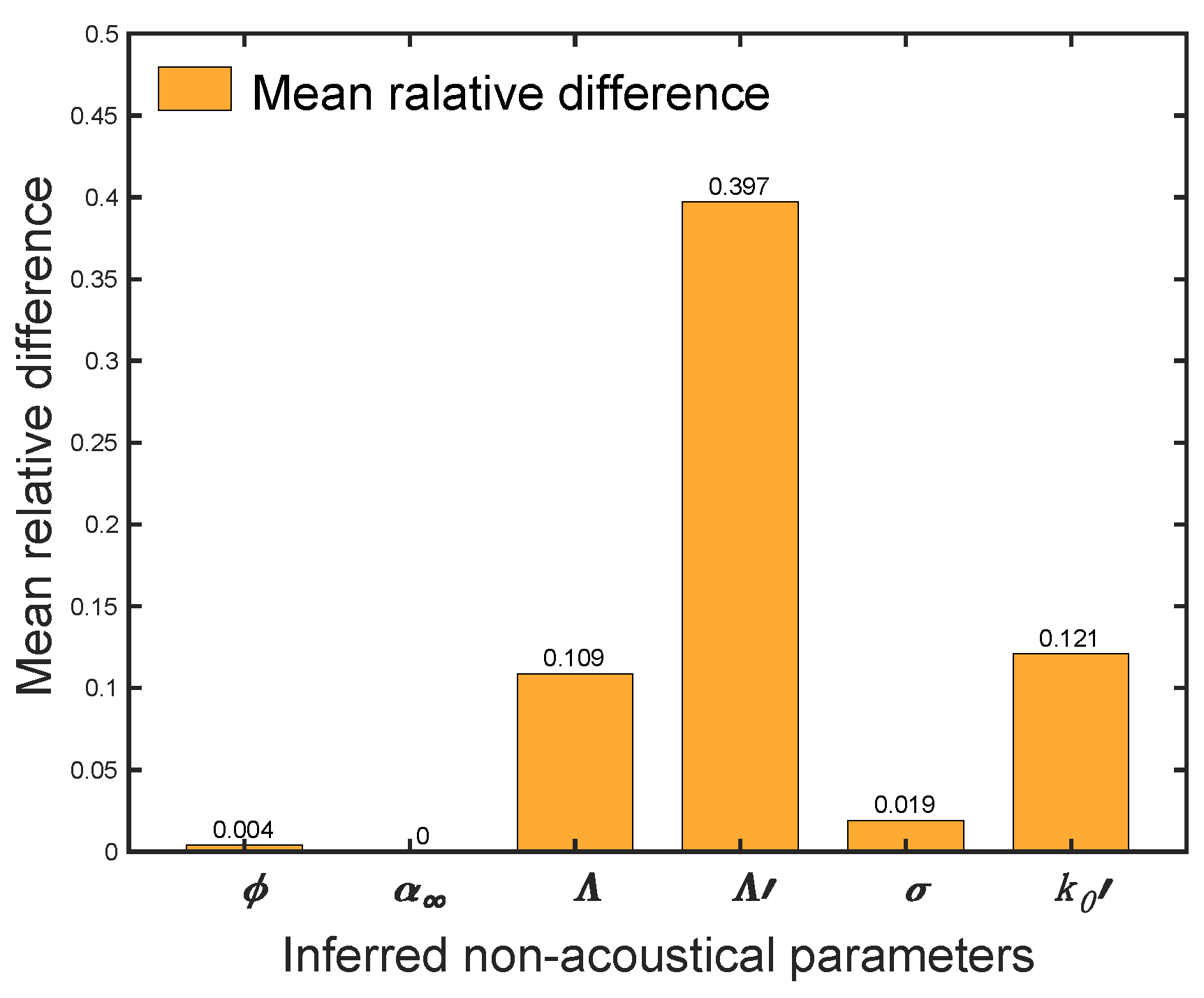
2.3.3. The Inversion Procedure
2.4. Homogeneity Assessment
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Narang, P.P. Material parameter selection in polyester fibre insulation for sound transmission and absorption. Appl. Acoust. 1995, 45, 335–358. [Google Scholar] [CrossRef]
- Kang, Y.A.; Lee, E.N.; Lee, K.C.; Choi, S.M.; Shin, E.J. Acoustic properties of sound-absorbing polyester fabrics woven with thick staple and thin draw textured yarn for use in interior decoration. J. Text. Inst. 2019, 110, 202–210. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, H. Sound Absorption Behavior of Knitted Spacer Fabrics. Text. Res. J. 2010, 80, 1949–1957. [Google Scholar]
- Arumugam, V.; Mishra, R.; Militky, J.; Novak, J. Thermo-acoustic behaviour of 3D knitted spacer fabrics. Fibers Polym. 2015, 16, 2467–2476. [Google Scholar] [CrossRef]
- Çelikel, D.C.; Babaarslan, O. Acoustic Insulation Behavior of Composite Nonwoven. In Engineered Fabrics; IntechOpen: London, UK, 2019. [Google Scholar]
- Arenas, J.P. Applications of Acoustic Textiles in Automotive/Transportation. In Acoustic Textiles; Springer: Singapore, 2016; pp. 143–163. [Google Scholar]
- Setunge, S.; Gamage, N. Application of acoustic materials in civil Engineering. In Acoustic Textiles; Springer: Singapore, 2016; pp. 165–183. [Google Scholar]
- Patnaik, A.; Mvubu, M.; Muniyasamy, S.; Botha, A.; Anandjiwala, R.D. Thermal and sound insulation materials from waste wool and recycled polyester fibers and their biodegradation studies. Energy Build. 2015, 92, 161–169. [Google Scholar] [CrossRef]
- Yang, T.; Saati, F.; Horoshenkov, K.V.; Xiong, X.; Yang, K.; Mishra, R.; Marburg, S.; Militký, J. Study on the sound absorption behavior of multi-component polyester nonwovens: Experimental and numerical methods. Text. Res. J. 2019, 89, 3342–3361. [Google Scholar] [CrossRef]
- Kino, N.; Ueno, T. Evaluation of acoustical and non-acoustical properties of sound absorbing materials made of polyester fibres of various cross-sectional shapes. Appl. Acoust. 2008, 69, 575–582. [Google Scholar] [CrossRef]
- Shoshani, Y.; Yakubov, Y. Numerical assessment of maximal absorption coefficients for nonwoven fiberwebs. Appl. Acoust. 2000, 59, 77–87. [Google Scholar] [CrossRef]
- Garai, M.; Pompoli, F. A simple empirical model of polyester fibre materials for acoustical applications. Appl. Acoust. 2005, 66, 1383–1398. [Google Scholar] [CrossRef]
- Azari, K.; Majidi, B.; Alamdari, H.; Ziegler, D.; Fafard, M. Characterization of Homogeneity of Green Anodes Through X-Ray Tomography and Image Analysis. In Light Metals; Grandfield, J., Ed.; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Suvari, F.; Ulcay, Y.; Pourdeyhimi, B. Sound absorption analysis of thermally bonded high-loft nonwovens. Text. Res. J. 2015, 86, 837–847. [Google Scholar] [CrossRef]
- Tascan, M.; Vaughn, E.A.; Stevens, K.A.; Brown, P.J. Effects of total surface area and fabric density on the acoustical behavior of traditional. J. Text. Inst. 2011, 102, 746–751. [Google Scholar] [CrossRef]
- Jirsák, O.; Wadsworth, L.C. Nonwoven Textiles; Carolina Academic Press: Durham, NC, USA, 1997. [Google Scholar]
- Xiong, X.; Mohanapriya, V.; Darina, J.; Tao, Y.; Rajesh, M.; Jiří, M.; Michal, P. An Experimental Evaluation of Convective Heat Transfer in Multi-Layered Fibrous Materials Composed by Different Middle Layer Structures. J. Ind. Text. 2019. [Google Scholar] [CrossRef]
- ASTM D1777-96. Standard method for Thickness of Textile Materials; American Society for Testing and Materials: West Conshohocken, PA, USA, 2019. [Google Scholar]
- ASTM C830-00. Standard Test Methods for Apparent Porosity, Liquid Absorption, Apparent Specific Gravity, and Bulk Density of Refractory Shapes by Vacuum Pressure; American Society for Testing and Materials: West Conshohocken, PA, USA, 2010. [Google Scholar]
- ISO 9053-1. Acoustics-Materials for Acoustical Applications-Determination of Airflow Resistance; International Organization for Standardization: Geneva, Switzerland, 2018. [Google Scholar]
- Xue, Y.; Bolton, J.S.; Gerdes, R.; Lee, S.; Herdtle, T. Prediction of airflow resistivity of fibrous acoustical media having two fiber components and a distribution of fiber radii. Appl. Acoust. 2018, 134, 145–153. [Google Scholar] [CrossRef]
- Yang, T.; Mishra, R.; Horoshenkov, K.V.; Hurrell, A.; Saati, F.; Xiong, X. A study of some airflow resistivity models for multi-component polyester fiber assembly. Appl. Acoust. 2018, 139, 75–81. [Google Scholar] [CrossRef]
- Gommes, C.J.; Bons, A.-J.; Blacher, S.; Dunsmuir, J.H.; Tsou, A.H. Practical Methods for Measuring the Tortuosity of Porous Materials from Binary or Gray-Tone Tomographic Reconstructions. AIChE J. 2014, 55, 2000–2012. [Google Scholar] [CrossRef]
- Maciel, D.O.R.; Ribeiro, C.G.D.; Ferreira, J.; Margem, F.M.; Monteiro, S.N. Characterization of Minerals, Metals, and Materials 2017. In The Minerals, Metals & Materials Series; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- McRae, J.D.; Naguib, H.E.; Atalla, N. Mechanical and acoustic performance of compression molded open cell polypropylene foams. Smart Mater. Adapt. Struct. Intell. Syst. 2008, 43314, 76–84. [Google Scholar]
- Horoshenkov, K.V. A review of acoustical methods for porous material characterization. Int. J. Acoust. Vib. 2017, 22, 92–103. [Google Scholar]
- Niskanen, M.; Groby, J.-P.; Duclos, A.; Dazel, O.; Le Roux, J.C.; Poulain, N.; Huttunen, T.; Lahivaara, T. Deterministic and statistical characterization of rigid frame porous materials from impedance tube measurements. J. Acoust. Soc. Am. 2017, 142, 2407–2418. [Google Scholar] [CrossRef]
- Groby, J.-P.; Ogam, E.; De Ryck, L.; Sebaa, N.; Lauriks, W. Analytical method for the ultrasonic characterization of homogeneous rigid porous materials from transmitted and reflected coefficients. J. Acoust. Soc. Am. 2010, 127, 764–772. [Google Scholar] [CrossRef]
- Smith, D.R.; Schultz, S.; Markoš, P.; Soukoulis, C.M. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B 2002, 65, 1–5. [Google Scholar] [CrossRef]
- Johnson, D.L.; Koplik, J.; Dashen, R. Theory of dynamic permeability and tortuosity in fluid saturated porous media. J. Fluid Mech. 1987, 176, 379–402. [Google Scholar] [CrossRef]
- Champoux, Y.; Allard, J.F. Dynamic tortuosity and bulk modulus in air-saturated porous media. J. Appl. Phys. 1991, 70, 1975–1979. [Google Scholar] [CrossRef]
- Lafarge, D.; Lemarinier, P.; Allard, J.F.; Tarnow, V. Dynamic compressibility of air in porous structures at audible frequencies. J. Acoust. Soc. Am. 1997, 102, 1995–2006. [Google Scholar] [CrossRef]
- Kino, N. A Comparison of Two Acoustical Methods for Estimating Parameters of Glass Fibre and Melamine Foam Materials. Appl. Acoust. 2012, 73, 590–603. [Google Scholar] [CrossRef]
- Fackler, C.J.; Xiang, N.; Horoshenkov, K.V. Bayesian acoustic analysis of multilayer porous media. J. Acoust. Soc. Am. 2018, 144, 3582–3592. [Google Scholar] [CrossRef]
- Chazot, J.-D.; Zhang, E.; Antoni, J. Acoustical and mechanical characterization of poroelastic materials using a Bayesian approach. J. Acoust. Soc. Am. 2012, 131, 4584–4595. [Google Scholar] [CrossRef]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure; Academic Press: San Diego, CA, USA, 1979; pp. 86–88. [Google Scholar]
- Cox, T.J.; D’Antonio, P. Acoustic Absorbers and Diffusers: Theory, Design and Application; CRC Press: Boca Raton, FL, USA, 2018; p. 205. [Google Scholar]
- Vallabh, R.; Banks-Lee, P.; Seyam, A.-F. New Approach for Determining Tortuosity in Fibrous Porous Media. J. Eng. Fibers Fabr. 2010, 5, 7–15. [Google Scholar] [CrossRef]
- Attenborough, K. Models for the acoustical characteristics of air filled granular materials. Acta Acust 1993, 1, 213–226. [Google Scholar]
- Berryman, J.G. Confirmation of Biot’s theory. Appl. Phys. Lett. 1980, 37, 382–384. [Google Scholar] [CrossRef]
- Pauwels, J.; Lamberty, A.; Schimmel, H. Homogeneity testing of reference materials. Accredit. Qual. Assur. 1998, 3, 51–55. [Google Scholar] [CrossRef]
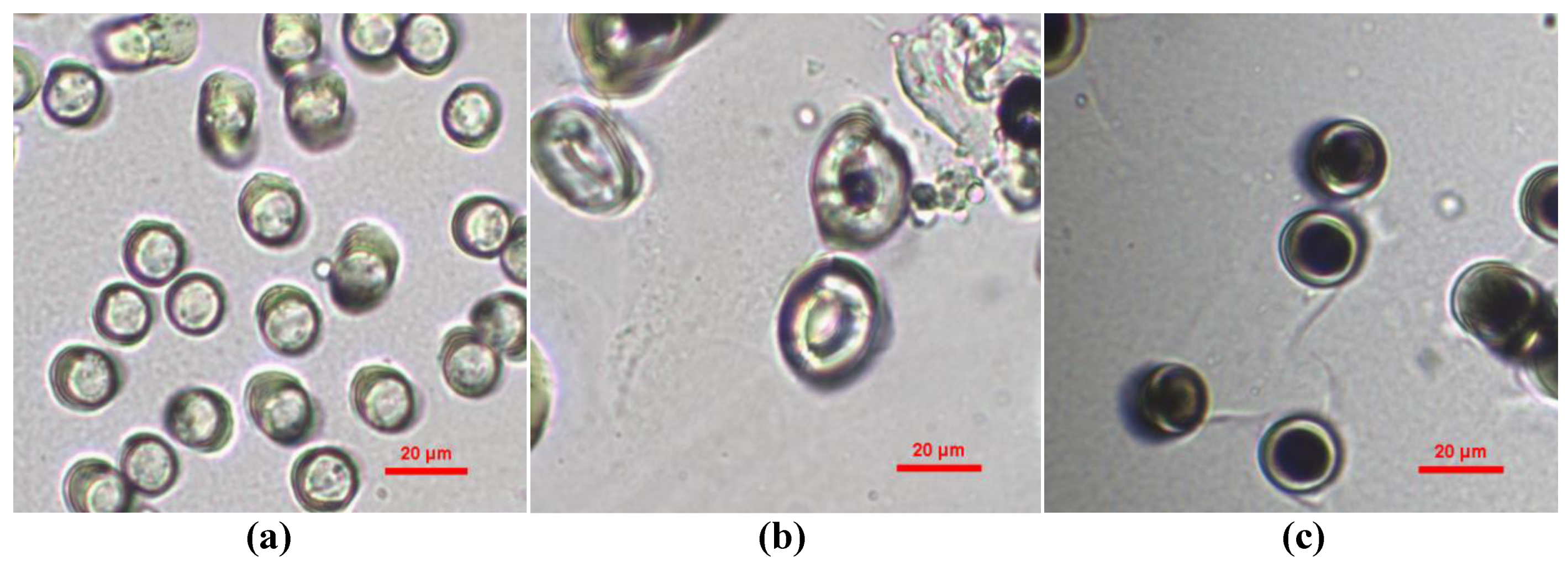





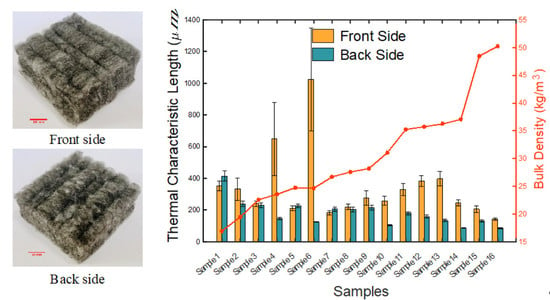
| Samples | Porosity (%) | Bulk Density (kg/m3) | Thickness (mm) | Airflow Resistivity (Pa·s/m²) |
|---|---|---|---|---|
| Sample 1 | 98.52 | 16.93 | 27.48 | 4108 ± 199 |
| Sample 2 | 98.29 | 19.49 | 23.87 | 5357 ± 217 |
| Sample 3 | 98.03 | 22.49 | 20.69 | 7029 ± 356 |
| Sample 4 | 97.94 | 23.54 | 20.32 | 7498 ± 333 |
| Sample 5 | 97.86 | 24.45 | 20.76 | 7319 ± 243 |
| Sample 6 | 97.85 | 24.54 | 19.49 | 10,978 ± 329 |
| Sample 7 | 97.66 | 26.71 | 19.00 | 7530 ± 408 |
| Sample 8 | 97.59 | 27.54 | 18.43 | 9829 ± 376 |
| Sample 9 | 97.58 | 27.61 | 16.85 | 10,181 ± 259 |
| Sample 10 | 97.29 | 30.94 | 15.46 | 13,397 ± 329 |
| Sample 11 | 96.94 | 34.95 | 13.31 | 12,868 ± 199 |
| Sample 12 | 96.89 | 35.56 | 14.27 | 14,989 ± 285 |
| Sample 13 | 96.86 | 35.87 | 14.15 | 15,414 ± 167 |
| Sample 14 | 96.59 | 38.98 | 12.27 | 19,751 ± 442 |
| Sample 15 | 96.09 | 44.60 | 10.43 | 20,474 ± 687 |
| Sample 16 | 96.01 | 45.56 | 11.14 | 19,733 ± 688 |
| Samples | Orientations | (%) | (μm) | (μm) | (Pa·s/m2) | (10−9 m2) | |
|---|---|---|---|---|---|---|---|
| Sample 1 | Direct | 99.8 (0.19) | 1(0.0017) | 184 (3.2) | 354(30.8) | 5225 | 6.98 (0.53) |
| Reverse | 99.8 (0.18) | 1(0.0017) | 187 (4.0) | 414(32.0) | 5202 | 6.95 (0.50) | |
| Sample 2 | Direct | 99.0 (0.86) | 1 (0.0026) | 146 (5.1) | 333(71.0) | 6527 | 4.56 (0.36) |
| Reverse | 99.8 (0.19) | 1 (0.0018) | 153 (3.3) | 239 (16.9) | 6638 | 4.81 (0.28) | |
| Sample 3 | Direct | 99.6 (0.30) | 1 (0.0027) | 123 (2.3) | 241 (16.7) | 8052 | 4.02 (0.24) |
| Reverse | 99.6 (0.35) | 1(0.0029) | 127 (2.6) | 231 (15.6) | 8129 | 3.83 (0.21) | |
| Sample 4 | Direct | 99.7 (0.27) | 1 (0.0027) | 110 (2.0) | 649 (230.0) | 9147 | 3.51 (0.15) |
| Reverse | 99.7 (0.18) | 1 (0.0016) | 131 (2.2) | 146 (7.7) | 9538 | 2.98 (0.18) | |
| Sample 5 | Direct | 99.8 (0.18) | 1 (0.0016) | 118 (1.8) | 211 (13.7) | 9650 | 4.27 (0.30) |
| Reverse | 99.8 (0.17) | 1(0.0012) | 114 (1.5) | 227 (12.2) | 9641 | 4.64 (0.33) | |
| Sample 6 | Direct | 98.9 (0.54) | 1 (0.0035) | 91 (1.8) | 1025 (325.0) | 10,754 | 4.07 (0.24) |
| Reverse | 100 (0.03) | 1 (0.0012) | 124 (2.0) | 125 (2.2) | 11,576 | 3.41 (0.30) | |
| Sample 7 | Direct | 99.8 (0.13) | 1 (0.0011) | 105 (1.6) | 184 (13.5) | 11,313 | 3.68 (0.18) |
| Reverse | 99.8 (0.14) | 1 (0.0014) | 103 (1.4) | 206 (12.9) | 11,213 | 3.77 (0.23) | |
| Sample 8 | Direct | 99.8 (0.18) | 1 (0.0012) | 98.7 (1.5) | 219 (17.4) | 12,283 | 3.97 (0.19) |
| Reverse | 99.8 (0.15) | 1 (0.0013) | 101 (1.3) | 204 (16.3) | 12,259 | 4.07 (0.35) | |
| Sample 9 | Direct | 97.0 (0.95) | 1 (0.0024) | 103 (3.4) | 276 (44.4) | 11,434 | 4.10 (0.31) |
| Reverse | 99.8 (0.25) | 1 (0.0022) | 107 (1.8) | 214 (15.3) | 11,491 | 4.00 (0.21) | |
| Sample 10 | Direct | 99.7 (0.24) | 1 (0.0020) | 76 (1.0) | 259 (28.9) | 14,528 | 3.13 (0.17) |
| Reverse | 99.8 (0.12) | 1 (0.0011) | 94 (1.4) | 104 (4.0) | 14,935 | 2.19 (0.14) | |
| Sample 11 | Direct | 99.7 (0.23) | 1 (0.0018) | 78 (0.9) | 330 (38.3) | 13,613 | 3.49 (0.18) |
| Reverse | 99.8 (0.18) | 1 (0.0012) | 83 (1.0) | 180 (8.9) | 13,763 | 3.18 (0.15) | |
| Sample 12 | Direct | 99.8 (0.13) | 1 (0.0013) | 76 (0.9) | 383 (34) | 14,535 | 4.03 (0.19) |
| Reverse | 99.8 (0.14) | 1 (0.0018) | 87 (1.3) | 159 (9.6) | 15,004 | 3.58 (0.20) | |
| Sample 13 | Direct | 99.8 (0.24) | 1 (0.0011) | 70 (0.9) | 398 (45) | 16,167 | 3.51 (0.14) |
| Reverse | 99.8 (0.15) | 1 (0.0020) | 79 (1.0) | 134 (7.6) | 16,567 | 2.95 (1.77) | |
| Sample 14 | Direct | 99.8 (0.16) | 1 (0.0017) | 68 (1.0) | 246 (19.4) | 17,734 | 3.24 (0.22) |
| Reverse | 99.9 (0.08) | 1 (0.0014) | 85 (1.4) | 86 (1.6) | 18,205 | 1.89 (0.95) | |
| Sample 15 | Direct | 98.3 (0.76) | 1 (0.0041) | 53 (1.1) | 206 (21.9) | 23,241 | 2.67 (0.18) |
| Reverse | 99.8 (0.16) | 1 (0.0016) | 56 (0.81) | 130 (6.9) | 23,432 | 2.60 (0.14) | |
| Sample 16 | Direct | 99.8 (0.14) | 1 (0.0020) | 66 (0.80) | 143 (8.0) | 20,712 | 2.43 (0.12) |
| Reverse | 99.8 (0.14) | 1(0.0017) | 72 (1.2) | 86 (4.1) | 20,619 | 1.81 (0.09) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Saati, F.; Groby, J.-P.; Xiong, X.; Petrů, M.; Mishra, R.; Militký, J.; Marburg, S. Characterization on Polyester Fibrous Panels and Their Homogeneity Assessment. Polymers 2020, 12, 2098. https://doi.org/10.3390/polym12092098
Yang T, Saati F, Groby J-P, Xiong X, Petrů M, Mishra R, Militký J, Marburg S. Characterization on Polyester Fibrous Panels and Their Homogeneity Assessment. Polymers. 2020; 12(9):2098. https://doi.org/10.3390/polym12092098
Chicago/Turabian StyleYang, Tao, Ferina Saati, Jean-Philippe Groby, Xiaoman Xiong, Michal Petrů, Rajesh Mishra, Jiří Militký, and Steffen Marburg. 2020. "Characterization on Polyester Fibrous Panels and Their Homogeneity Assessment" Polymers 12, no. 9: 2098. https://doi.org/10.3390/polym12092098
APA StyleYang, T., Saati, F., Groby, J.-P., Xiong, X., Petrů, M., Mishra, R., Militký, J., & Marburg, S. (2020). Characterization on Polyester Fibrous Panels and Their Homogeneity Assessment. Polymers, 12(9), 2098. https://doi.org/10.3390/polym12092098