A Microscopically Motivated Model for Particle Penetration into Swollen Biological Networks
Abstract
1. Introduction
2. The Mechanisms Behind Particle Penetration
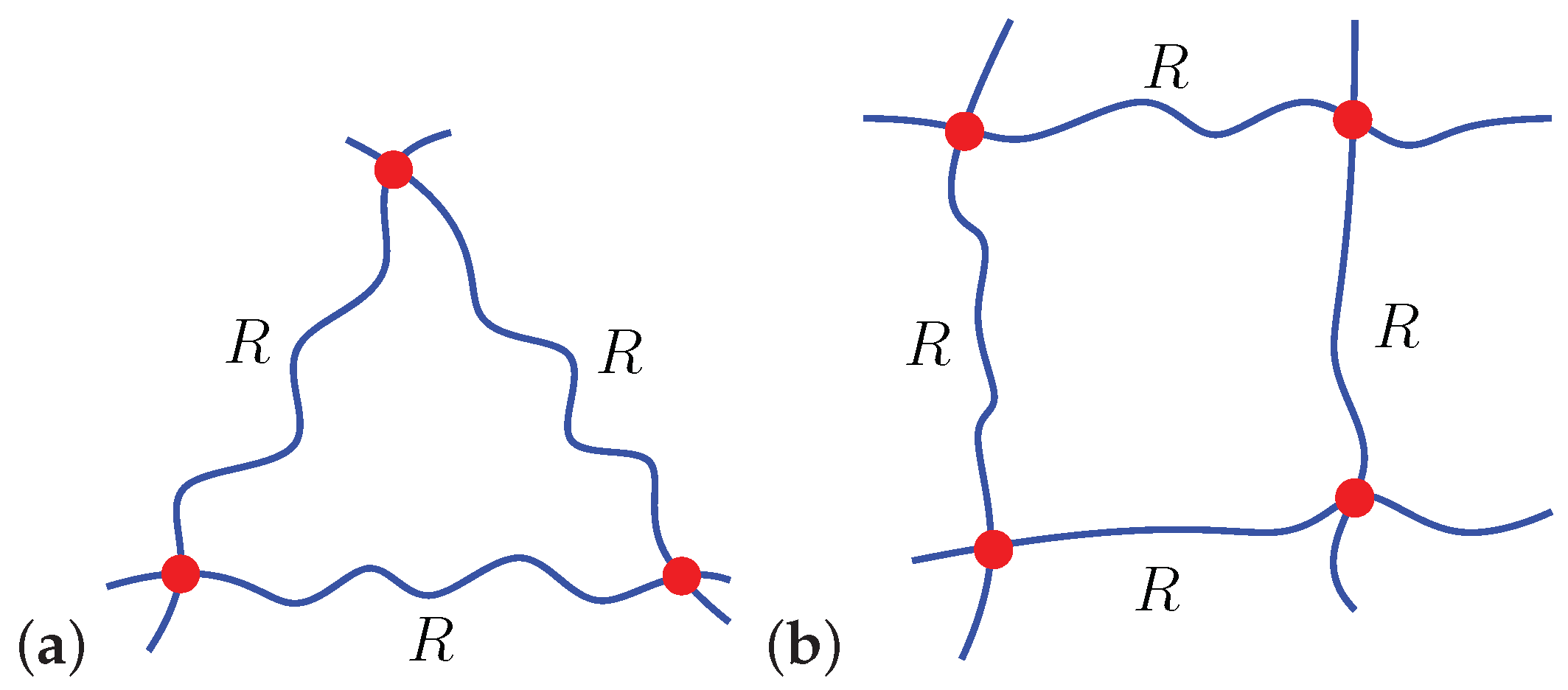
A Microscopically Motivated Model
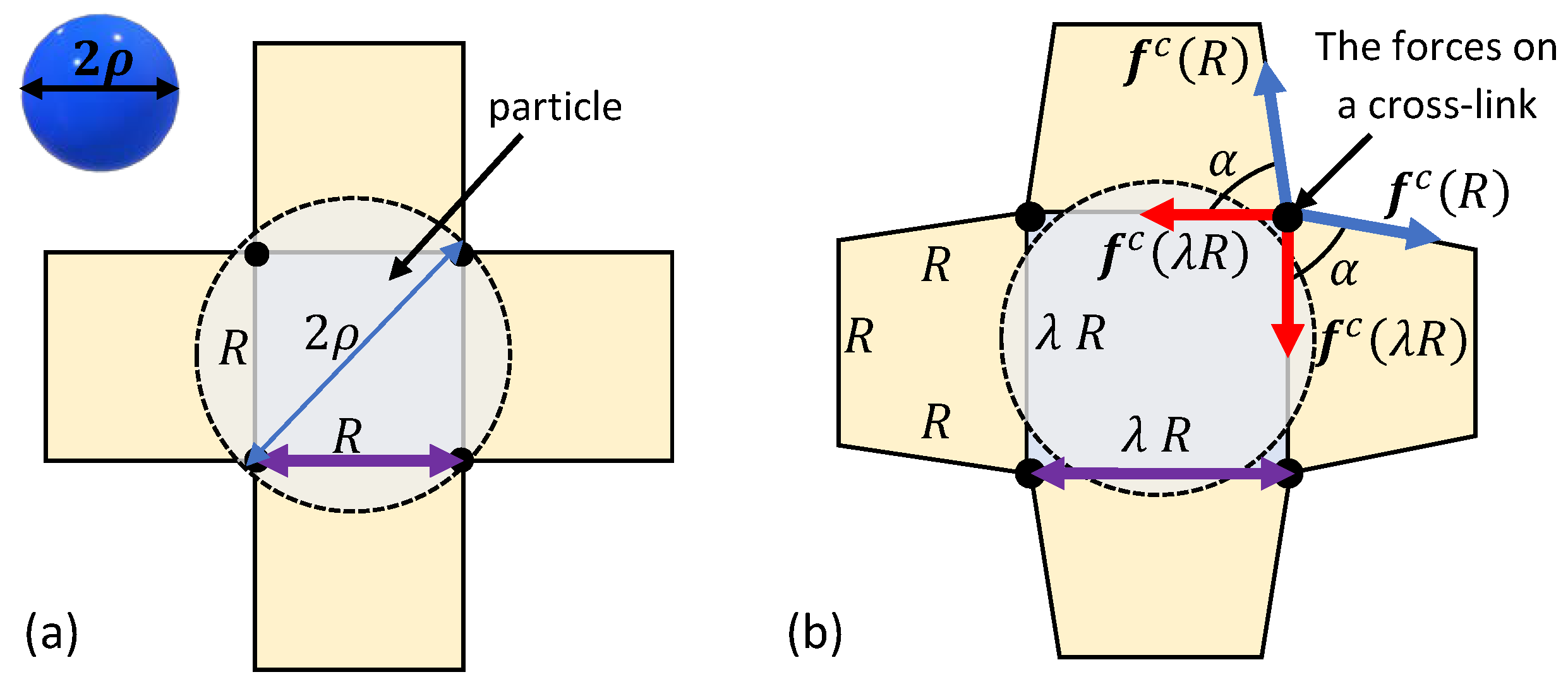
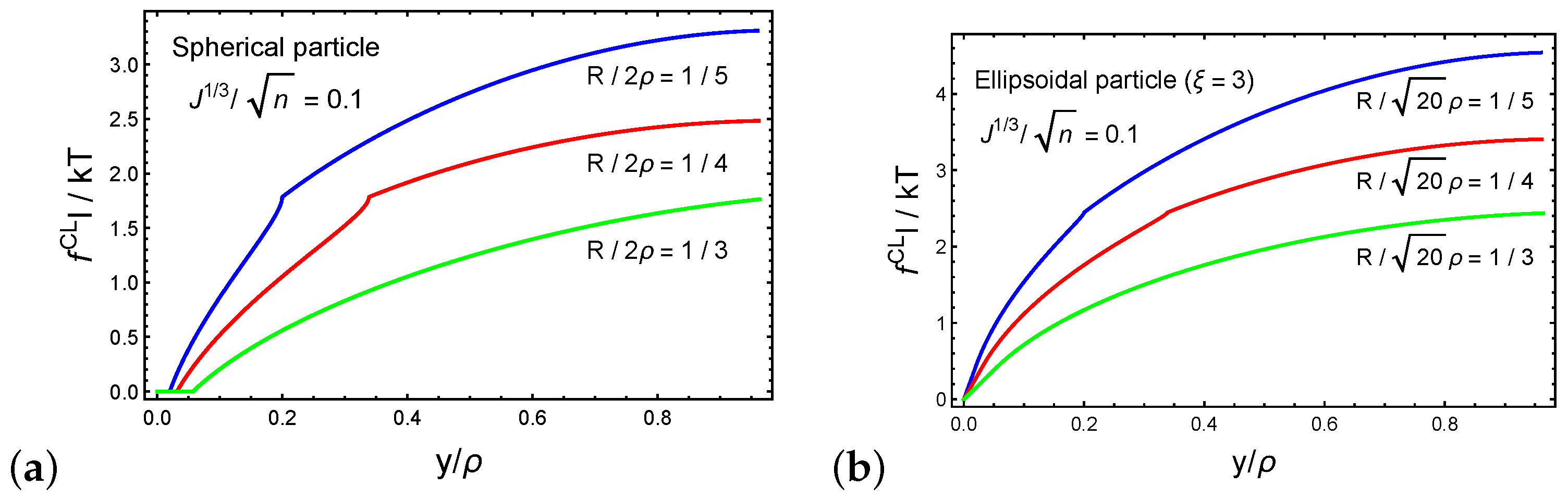
3. Spontaneous Particle Penetration
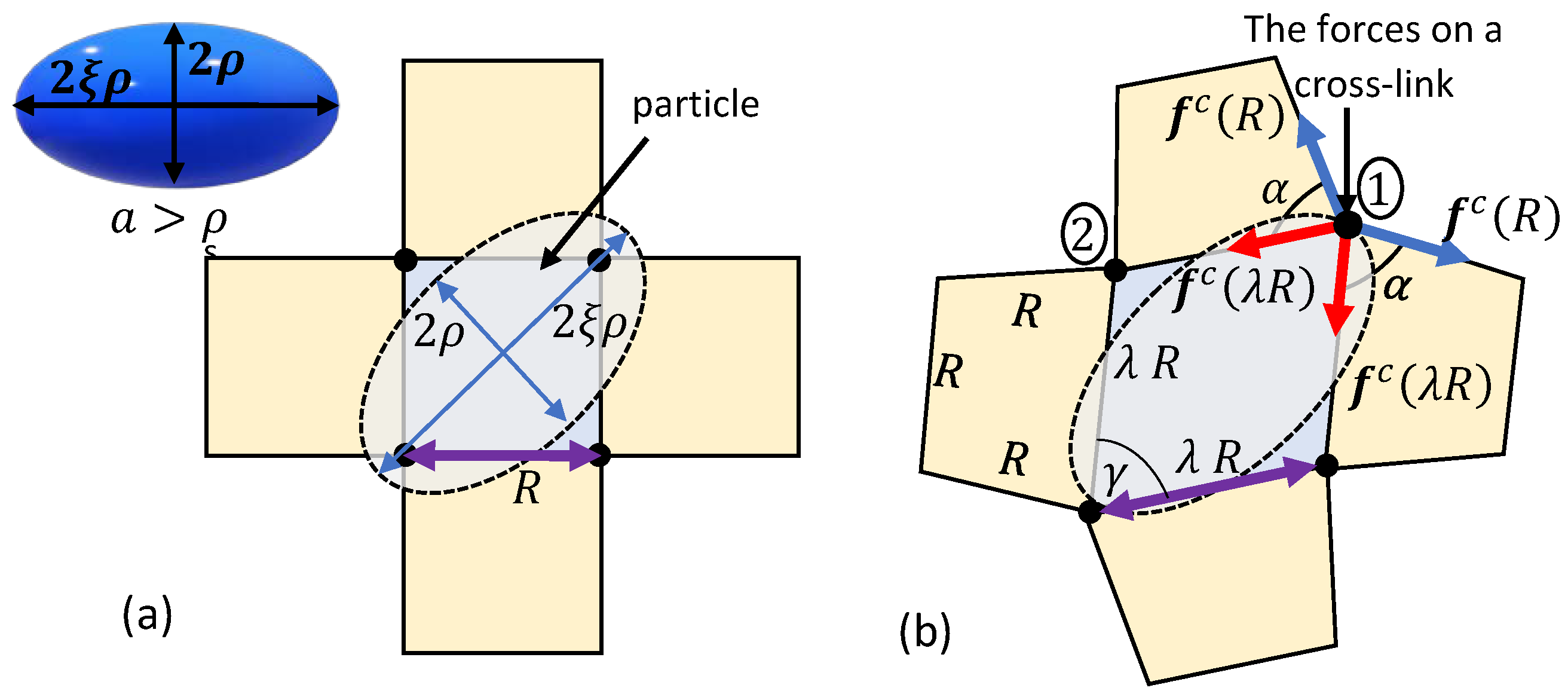
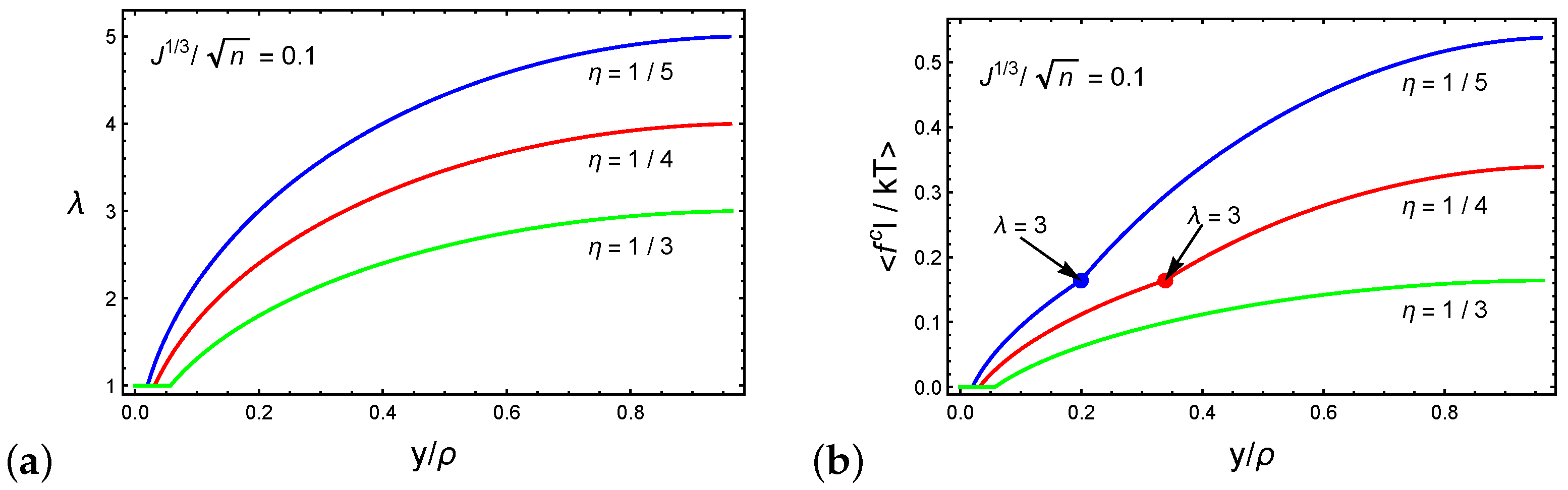
4. Forced Particle Penetration
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lieleg, O.; Ribbeck, K. Biological hydrogels as selective diffusion barriers. Trends Cell Biol. 2011, 21, 543–551. [Google Scholar] [CrossRef] [PubMed]
- Witten, J.; Ribbeck, K. The particle in the spider’s web: Transport through biological hydrogels. Nanoscale 2017, 9, 8080–8095. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Hansing, J.; Netz, R.R.; DeRouchey, J.E. Particle Transport through Hydrogels Is Charge Asymmetric. Biophys. J. 2015, 108, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Sanders, N.N.; Smedt, S.C.D.; Demeester, J. The Physical Properties of Biogels and their Permeability for Macromolecular Drugs and Colloidal Drug Carriers. J. Pharm. Sci. 2000, 89, 835–849. [Google Scholar] [CrossRef]
- Das Neves, J.; Sverdlov Arzi, R.; Sosnik, A. Molecular and cellular cues governing nanomaterial-mucosae interactions: From nanomedicine to nanotoxicology. Chem. Soc. Rev. 2020. [Google Scholar] [CrossRef]
- Birjiniuk, A.; Billings, N.; Nance, E.; Hanes, J.; Ribbeck, K.; Doyle, P.S. Single particle tracking reveals spatial and dynamic organization of the Escherichia coli biofilm matrix. New J. Phys. 2014, 16, 085014. [Google Scholar] [CrossRef]
- Wilking, J.N.; Zaburdaev, V.; Volder, M.D.; Losick, R.; Brenner, M.P.; Weitz, D.A. Liquid transport facilitated by channels in Bacillus subtilis biofilms. Proc. Natl. Acad. Sci. USA 2012, 110, 848–852. [Google Scholar] [CrossRef]
- Smart, J. The basics and underlying mechanisms of mucoadhesion. Adv. Drug Deliv. Rev. 2005, 57, 1556–1568. [Google Scholar] [CrossRef]
- Imperiale, J.C.; Nejamkin, P.; del Sole, M.J.; Lanusse, C.E.; Sosnik, A. Novel protease inhibitor-loaded Nanoparticle-in-Microparticle Delivery System leads to a dramatic improvement of the oral pharmacokinetics in dogs. Biomaterials 2015, 37, 383–394. [Google Scholar] [CrossRef]
- Biazar, E.; Majdi, A.; Zafari, M.; Avar, M.; Aminifard, S.; Zaeifi, D.; Jafarpour, M.; Montazeri, G. Nanotoxicology and nanoparticle safety in biomedical designs. Int. J. Nanomed. 2011, 6, 1117. [Google Scholar] [CrossRef]
- Traboulsi, H.; Guerrina, N.; Iu, M.; Maysinger, D.; Ariya, P.; Baglole, C. Inhaled Pollutants: The Molecular Scene behind Respiratory and Systemic Diseases Associated with Ultrafine Particulate Matter. Int. J. Mol. Sci. 2017, 18, 243. [Google Scholar] [CrossRef] [PubMed]
- Schraufnagel, D.E. The health effects of ultrafine particles. Exp. Mol. Med. 2020, 52, 311–317. [Google Scholar] [CrossRef] [PubMed]
- Ramasamy, M.; Lee, J. Recent nanotechnology approaches for prevention and treatment of biofilm-associated infections on medical devices. BioMed Res. Int. 2016, 2016, 1851242. [Google Scholar] [CrossRef] [PubMed]
- Flemstrom, G.; Hallgren, A.; Nylander, O.; Engstrand, L.; Wilander, E.; Allen, A. Adherent surface mucus gel restricts diffusion of macromolecules in rat duodenum in vivo. Am. J. Physiol. Gastrointest. Liver Physiol. 1999, 277, G375–G382. [Google Scholar] [CrossRef]
- Lai, S.K.; Wang, Y.Y.; Hida, K.; Cone, R.; Hanes, J. Nanoparticles reveal that human cervicovaginal mucus is riddled with pores larger than viruses. Proc. Natl. Acad. Sci. USA 2009, 107, 598–603. [Google Scholar] [CrossRef] [PubMed]
- Bajka, B.H.; Rigby, N.M.; Cross, K.L.; Macierzanka, A.; Mackie, A.R. The influence of small intestinal mucus structure on particle transport ex vivo. Colloids Surf. B Biointerfaces 2015, 135, 73–80. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.S.; Xu, Q.; Boylan, N.J.; Chisholm, J.; Tang, B.C.; Schuster, B.S.; Henning, A.; Ensign, L.M.; Lee, E.; Adstamongkonkul, P.; et al. Nanoparticles that do not adhere to mucus provide uniform and long-lasting drug delivery to airways following inhalation. Sci. Adv. 2017, 3, e1601556. [Google Scholar] [CrossRef] [PubMed]
- Yildiz, H.M.; McKelvey, C.A.; Marsac, P.J.; Carrier, R.L. Size selectivity of intestinal mucus to diffusing particulates is dependent on surface chemistry and exposure to lipids. J. Drug Target. 2015, 23, 768–774. [Google Scholar] [CrossRef]
- Cone, R.A. Barrier properties of mucus. Adv. Drug Deliv. Rev. 2009, 61, 75–85. [Google Scholar] [CrossRef]
- Sosnik, A.; das Neves, J.; Sarmento, B. Mucoadhesive polymers in the design of nano-drug delivery systems for administration by non-parenteral routes: A review. Prog. Polym. Sci. 2014, 39, 2030–2075. [Google Scholar] [CrossRef]
- Accili, D.; Menghi, G.; Bonacucina, G.; Martino, P.D.; Palmieri, G.F. Mucoadhesion dependence of pharmaceutical polymers on mucosa characteristics. Eur. J. Pharm. Sci. 2004, 22, 225–234. [Google Scholar] [CrossRef]
- Taherali, F.; Varum, F.; Basit, A.W. A slippery slope: On the origin, role and physiology of mucus. Adv. Drug Deliv. Rev. 2018, 124, 16–33. [Google Scholar] [CrossRef] [PubMed]
- Lai, S.K.; Wang, Y.Y.; Wirtz, D.; Hanes, J. Micro- and macrorheology of mucus. Adv. Drug Deliv. Rev. 2009, 61, 86–100. [Google Scholar] [CrossRef] [PubMed]
- Lai, S.K.; O’Hanlon, D.E.; Harrold, S.; Man, S.T.; Wang, Y.Y.; Cone, R.; Hanes, J. Rapid transport of large polymeric nanoparticles in fresh undiluted human mucus. Proc. Natl. Acad. Sci. USA 2007, 104, 1482–1487. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Cohen, N.; McMeeking, R.M. On the swelling induced microstructural evolution of polymer networks in gels. J. Mech. Phys. Solids 2019, 125, 666–680. [Google Scholar] [CrossRef]
- Cohen, N. Programming the equilibrium swelling response of heterogeneous polymeric gels. Int. J. Solids Struct. 2019, 178–179, 81–90. [Google Scholar] [CrossRef]
- Yi, X.; Shi, X.; Gao, H. Cellular Uptake of Elastic Nanoparticles. Phys. Rev. Lett. 2011, 107, 098101. [Google Scholar] [CrossRef]
- Li, Y.; Lian, Y.; Zhang, L.T.; Aldousari, S.M.; Hedia, H.S.; Asiri, S.A.; Liu, W.K. Cell and nanoparticle transport in tumour microvasculature: The role of size, shape and surface functionality of nanoparticles. Interface Focus 2016, 6, 20150086. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity; Oxford University Press: Oxford, MI, USA, 1975. [Google Scholar]
- Kuhn, W.; Grun, F. Beziehungen zwischen elastischen Konstanten und Dehnungsdoppelbrechung hochelastischer Stoffe. Kolloid Z. 1942, 101, 248–271. [Google Scholar] [CrossRef]
- Cohen, A. A Padé approximant to the inverse Langevin function. Rheol. Acta 1991, 30, 270–273. [Google Scholar] [CrossRef]
- Cohen, N.; Eisenbach, C.D. A microscopically motivated model for the swelling-induced drastic softening of hydrogen-bond dominated biopolymer networks. Acta Biomater. 2019, 96, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Cu, Y.; Saltzman, W.M. Mathematical modeling of molecular diffusion through mucus. Adv. Drug Deliv. Rev. 2009, 61, 101–114. [Google Scholar] [CrossRef] [PubMed]
- Backstrom, M.; Ambort, D.; Thomsson, E.; Johansson, M.E.V.; Hansson, G.C. Increased Understanding of the Biochemistry and Biosynthesis of MUC2 and Other Gel-Forming Mucins Through the Recombinant Expression of Their Protein Domains. Mol. Biotechnol. 2013, 54, 250–256. [Google Scholar] [CrossRef]
- Ambort, D.; van der Post, S.; Johansson, M.E.; MacKenzie, J.; Thomsson, E.; Krengel, U.; Hansson, G.C. Function of the CysD domain of the gel-forming MUC2 mucin. Biochem. J. 2011, 436, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Bansil, R.; Celli, J.P.; Hardcastle, J.M.; Turner, B.S. The Influence of Mucus Microstructure and Rheology in Helicobacter pylori Infection. Front. Immunol. 2013, 4, 310. [Google Scholar] [CrossRef]
- Hamed, G.R. Molecular Aspects of the Fatigue and Fracture of Rubber. Rubber Chem. Technol. 1994, 67, 529–536. [Google Scholar] [CrossRef]
- Mohammadi, N.; Klein, A.; Sperling, L.H. Polymer chain rupture and the fracture behavior of glassy polystyrene. Macromolecules 1993, 26, 1019–1026. [Google Scholar] [CrossRef]
- Schuster, B.S.; Suk, J.S.; Woodworth, G.F.; Hanes, J. Nanoparticle diffusion in respiratory mucus from humans without lung disease. Biomaterials 2013, 34, 3439–3446. [Google Scholar] [CrossRef]
- Murgia, X.; Pawelzyk, P.; Schaefer, U.F.; Wagner, C.; Willenbacher, N.; Lehr, C.M. Size-Limited Penetration of Nanoparticles into Porcine Respiratory Mucus after Aerosol Deposition. Biomacromolecules 2016, 17, 1536–1542. [Google Scholar] [CrossRef]
- Dawson, M.; Wirtz, D.; Hanes, J. Enhanced Viscoelasticity of Human Cystic Fibrotic Sputum Correlates with Increasing Microheterogeneity in Particle Transport. J. Biol. Chem. 2003, 278, 50393–50401. [Google Scholar] [CrossRef]
- Suk, J.S.; Lai, S.K.; Wang, Y.Y.; Ensign, L.M.; Zeitlin, P.L.; Boyle, M.P.; Hanes, J. The penetration of fresh undiluted sputum expectorated by cystic fibrosis patients by non-adhesive polymer nanoparticles. Biomaterials 2009, 30, 2591–2597. [Google Scholar] [CrossRef] [PubMed]
- Abdulkarim, M.; Agulló, N.; Cattoz, B.; Griffiths, P.; Bernkop-Schnürch, A.; Borros, S.G.; Gumbleton, M. Nanoparticle diffusion within intestinal mucus: Three-dimensional response analysis dissecting the impact of particle surface charge, size and heterogeneity across polyelectrolyte, pegylated and viral particles. Eur. J. Pharm. Biopharm. 2015, 97, 230–238. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Y.; Lai, S.; Suk, J.; Pace, A.; Cone, R.; Hanes, J. Addressing the PEG Mucoadhesivity Paradox to Engineer Nanoparticles that “Slip” through the Human Mucus Barrier. Angew. Chem. Int. Ed. 2008, 47, 9726–9729. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, J.W. Water binding in biofilms. Water Sci. Technol. 1999, 39, 77–82. [Google Scholar] [CrossRef]
- Peulen, T.O.; Wilkinson, K.J. Diffusion of Nanoparticles in a Biofilm. Environ. Sci. Technol. 2011, 45, 3367–3373. [Google Scholar] [CrossRef]
- Fahs, A.; Quiles, F.; Jamal, D.; Humbert, F.; Francius, G. In-Situ Analysis of Bacterial Extracellular Polymeric Substances from Pseudomonas fluorescens Biofilm by Combined Vibrational and Single Molecule Force Spectroscopies. J. Phys. Chem. B 2014, 118, 6702–6713. [Google Scholar] [CrossRef]
- Ehret, A.E.; Böl, M. Modelling mechanical characteristics of microbial biofilms by network theory. J. R. Soc. Interface 2013, 10, 20120676. [Google Scholar] [CrossRef]
- Marszalek, P.E.; Oberhauser, A.F.; Pang, Y.P.; Fernandez, J.M. Polysaccharide elasticity governed by chair–boat transitions of the glucopyranose ring. Nature 1998, 396, 661–664. [Google Scholar] [CrossRef]
- Savidge, T. Microbial Imaging; Elsevier Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2005. [Google Scholar]
- Marcotte, L.; Therien-Aubin, H.; Sandt, C.; Barbeau, J.; Lafleur, M. Solute Size Effects on the Diffusion in Biofilms ofStreptococcus mutans. Biofouling 2004, 20, 189–201. [Google Scholar] [CrossRef]
- Georgiades, P.; di Cola, E.; Heenan, R.K.; Pudney, P.D.A.; Thornton, D.J.; Waigh, T.A. A combined small-angle X-ray and neutron scattering study of the structure of purified soluble gastrointestinal mucins. Biopolymers 2014, 101, 1154–1164. [Google Scholar] [CrossRef]
- Abe, Y.; Polyakov, P.; Skali-Lami, S.; Francius, G. Elasticity and physico-chemical properties during drinking water biofilm formation. Biofouling 2011, 27, 739–750. [Google Scholar] [CrossRef] [PubMed]
- Francius, G.; Alsteens, D.; Dupres, V.; Lebeer, S.; Keersmaecker, S.D.; Vanderleyden, J.; Gruber, H.J.; Dufrêne, Y.F. Stretching polysaccharides on live cells using single molecule force spectroscopy. Nat. Protoc. 2009, 4, 939–946. [Google Scholar] [CrossRef]
- Lai, S.K.; Hanes, J. Real-Time Multiple Particle Tracking of Gene Nanocarriers in Complex Biological Environments. In Gene Therapy Protocols; Humana Press: Totowa, NJ, USA, 2008; pp. 81–97. [Google Scholar] [CrossRef]
- Su, C.; Padra, M.; Constantino, M.A.; Sharba, S.; Thorell, A.; Lindén, S.K.; Bansil, R. Influence of the viscosity of healthy and diseased human mucins on the motility of Helicobacter pylori. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Shoulders, M.D.; Raines, R.T. Collagen Structure and Stability. Annu. Rev. Biochem. 2009, 78, 929–958. [Google Scholar] [CrossRef] [PubMed]
- Wichterle, O.; Lim, D. Hydrophilic Gels for Biological Use. Nature 1960, 185, 117–118. [Google Scholar] [CrossRef]
- Hobbs, S.K.; Monsky, W.L.; Yuan, F.; Roberts, W.G.; Griffith, L.; Torchilin, V.P.; Jain, R.K. Regulation of transport pathways in tumor vessels: Role of tumor type and microenvironment. Proc. Natl. Acad. Sci. USA 1998, 95, 4607–4612. [Google Scholar] [CrossRef]
- Stylianopoulos, T.; Diop-Frimpong, B.; Munn, L.L.; Jain, R.K. Diffusion Anisotropy in Collagen Gels and Tumors: The Effect of Fiber Network Orientation. Biophys. J. 2010, 99, 3119–3128. [Google Scholar] [CrossRef]
- Occhipinti, P.; Griffiths, P.C. Quantifying diffusion in mucosal systems by pulsed-gradient spin-echo NMR. Adv. Drug Deliv. Rev. 2008, 60, 1570–1582. [Google Scholar] [CrossRef]
- Nguyen, K.T.H.; Mathias, E.V.; Porter, E.; Ba, Y. Diffusions of beta-cyclodextrins in mucus studied by 19F diffusion. J. Incl. Phenom. Macrocycl. Chem. 2016, 86, 273–282. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Xu, X.; Bertrand, N.; Pridgen, E.; Swami, A.; Farokhzad, O.C. Interactions of nanomaterials and biological systems: Implications to personalized nanomedicine. Adv. Drug Deliv. Rev. 2012, 64, 1363–1384. [Google Scholar] [CrossRef]
- Gamboa, J.M.; Leong, K.W. In vitro and in vivo models for the study of oral delivery of nanoparticles. Adv. Drug Deliv. Rev. 2013, 65, 800–810. [Google Scholar] [CrossRef] [PubMed]
- DeSesso, J.; Jacobson, C. Anatomical and physiological parameters affecting gastrointestinal absorption in humans and rats. Food Chem. Toxicol. 2001, 39, 209–228. [Google Scholar] [CrossRef]
- Khanvilkar, K. Drug transfer through mucus. Adv. Drug Deliv. Rev. 2001, 48, 173–193. [Google Scholar] [CrossRef]
- Liu, X.Q.; Tang, R.Z. Biological responses to nanomaterials: Understanding nano-bio effects on cell behaviors. Drug Deliv. 2017, 24, 1–15. [Google Scholar] [CrossRef]
- Murphy, C.J.; Vartanian, A.M.; Geiger, F.M.; Hamers, R.J.; Pedersen, J.; Cui, Q.; Haynes, C.L.; Carlson, E.E.; Hernandez, R.; Klaper, R.D.; et al. Biological Responses to Engineered Nanomaterials: Needs for the Next Decade. ACS Cent. Sci. 2015, 1, 117–123. [Google Scholar] [CrossRef]

| Source | Reported Particle Diameter Size Range | Reported Average Particle Diameter | References | |||
|---|---|---|---|---|---|---|
| Mucus gel | ||||||
| Respiratory mucus | 60–300 nm | 140 nm | 95% | [17,22,41,42,43,44] | ||
| Intestinal mucus | 20–500 nm | 210 nm | 95% | [16,18,45] | ||
| Cervicovaginal mucus | 50–1800 nm | 340 nm | 95% | [15,24,46] | ||
| Biofilms | ||||||
| Pseudomonas fluorescens | 10–50 nm | 30 nm | 87–99% | [47,48,49,50,51,52] | ||
| Streptococcus mutans | 0.2–2.5 nm | 2.0 nm | 87–99% | [51,52,53] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arzi, R.S.; Sosnik, A.; Cohen, N. A Microscopically Motivated Model for Particle Penetration into Swollen Biological Networks. Polymers 2020, 12, 1912. https://doi.org/10.3390/polym12091912
Arzi RS, Sosnik A, Cohen N. A Microscopically Motivated Model for Particle Penetration into Swollen Biological Networks. Polymers. 2020; 12(9):1912. https://doi.org/10.3390/polym12091912
Chicago/Turabian StyleArzi, Roni Sverdlov, Alejandro Sosnik, and Noy Cohen. 2020. "A Microscopically Motivated Model for Particle Penetration into Swollen Biological Networks" Polymers 12, no. 9: 1912. https://doi.org/10.3390/polym12091912
APA StyleArzi, R. S., Sosnik, A., & Cohen, N. (2020). A Microscopically Motivated Model for Particle Penetration into Swollen Biological Networks. Polymers, 12(9), 1912. https://doi.org/10.3390/polym12091912






