Improving the Sensory Properties of Layered Phospholipid-Graphene Films Due to the Curvature of Graphene Layers
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
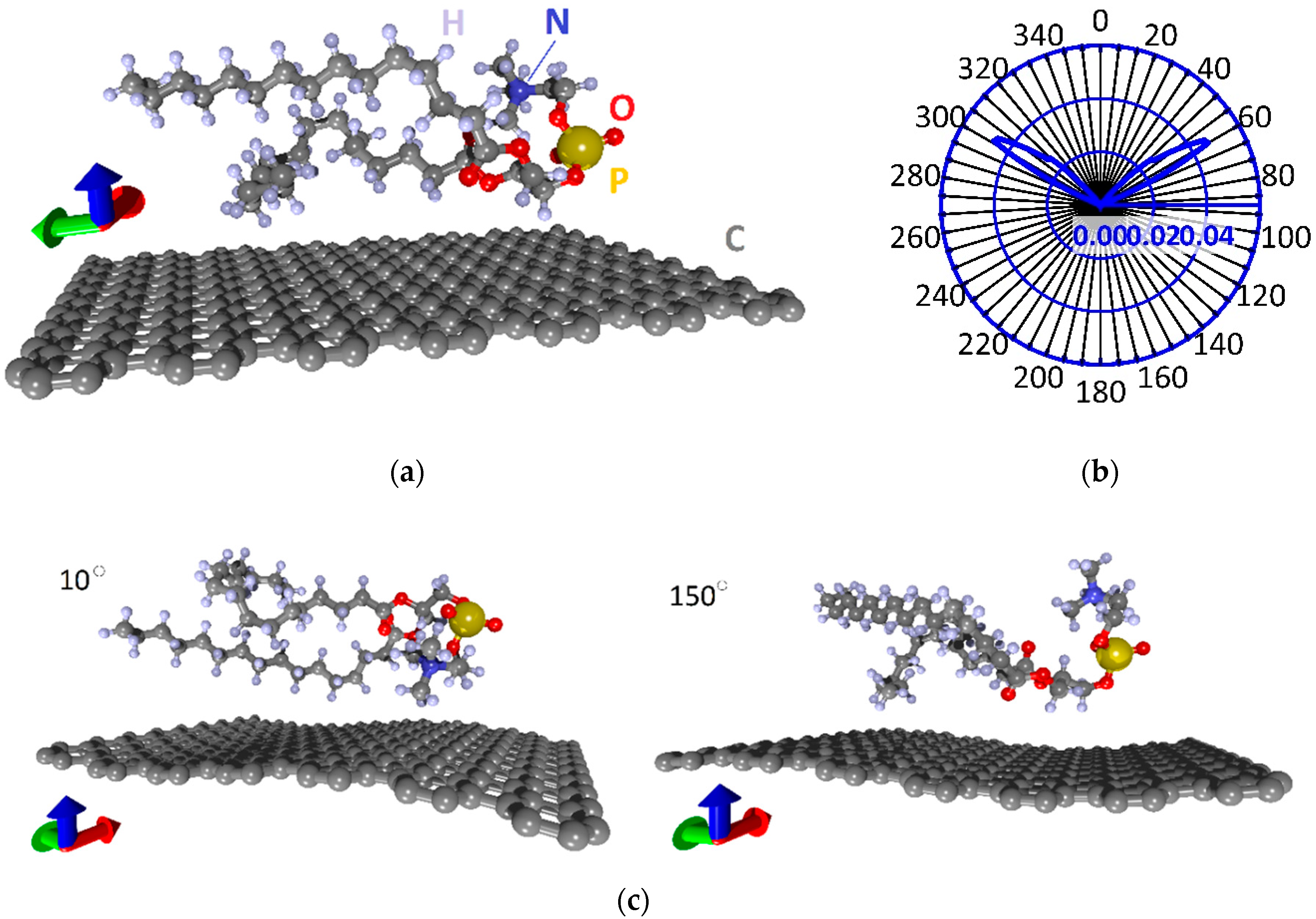
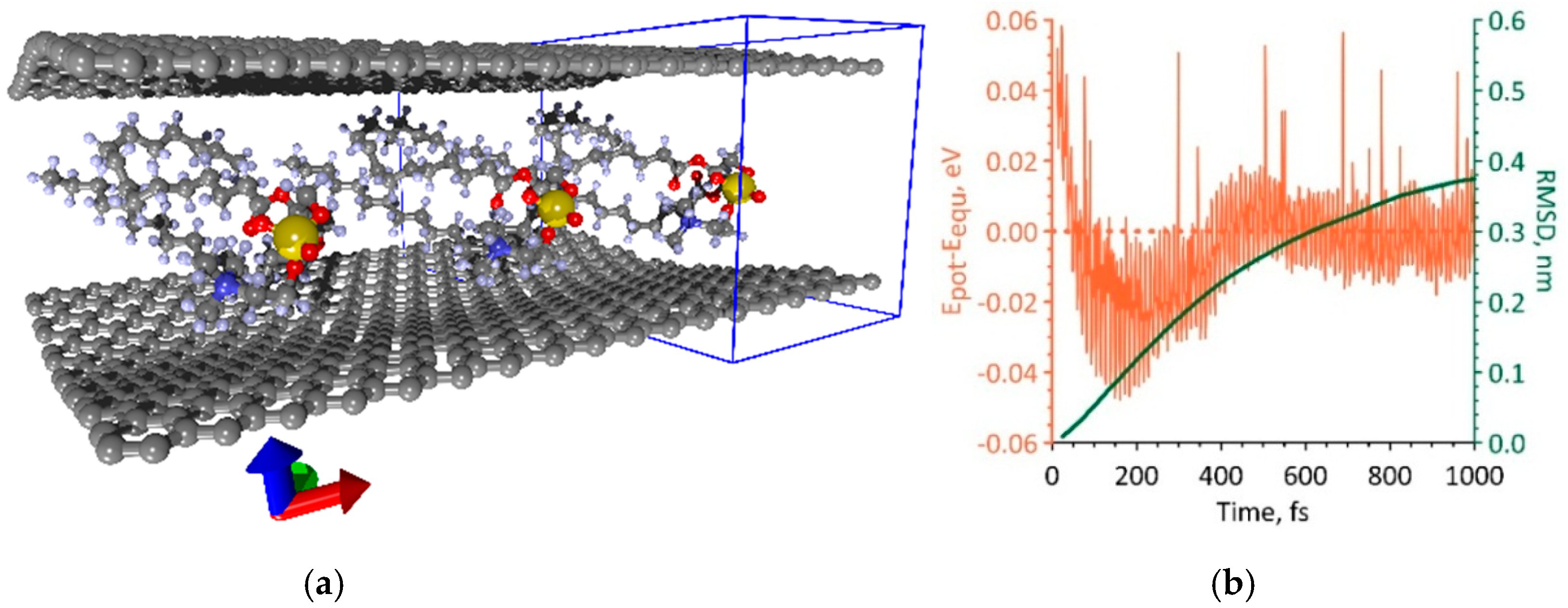
3.1. Atomistic Models and Electron Properties of Monolayer Phospholipid-Graphene Films
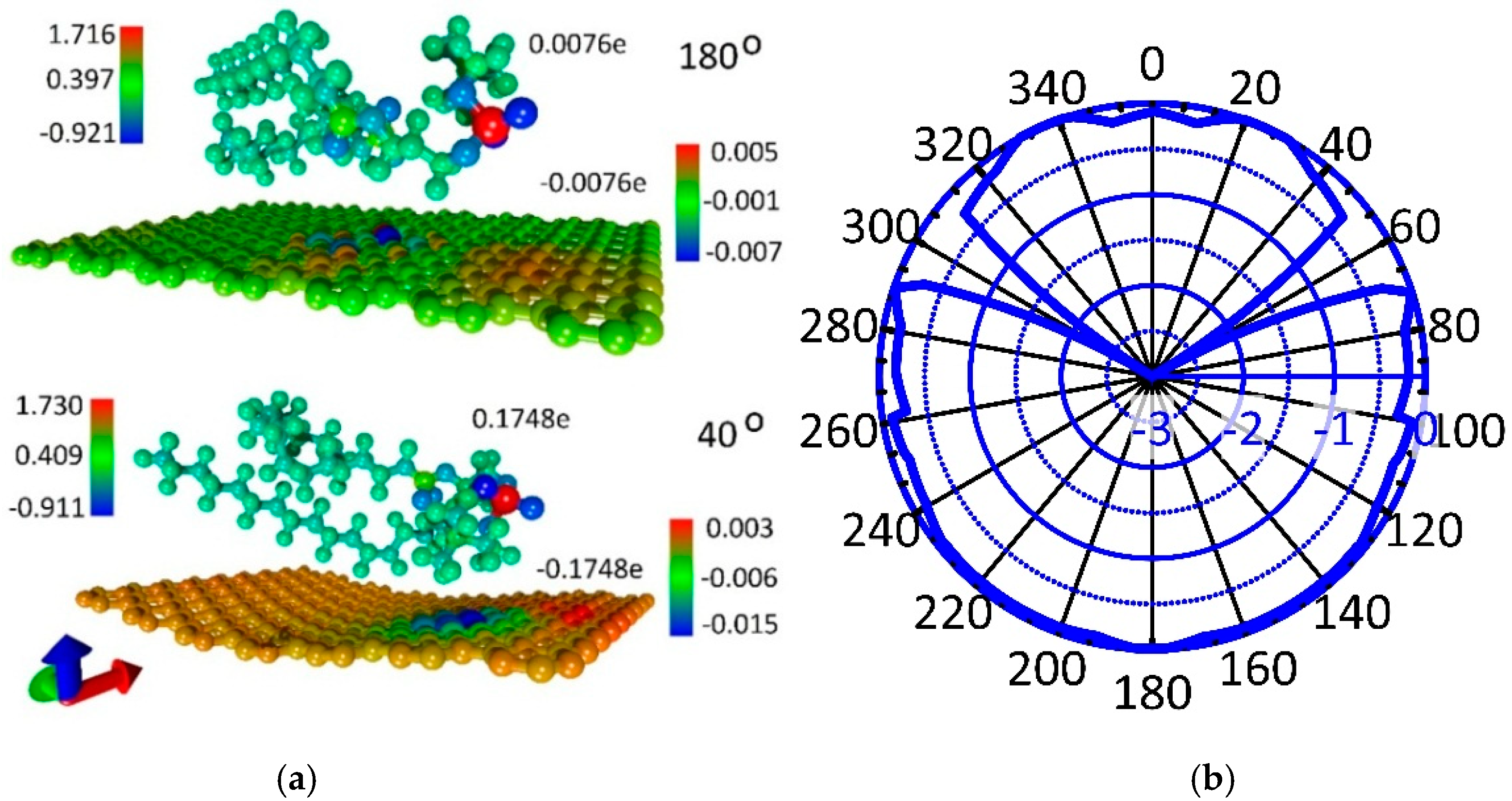
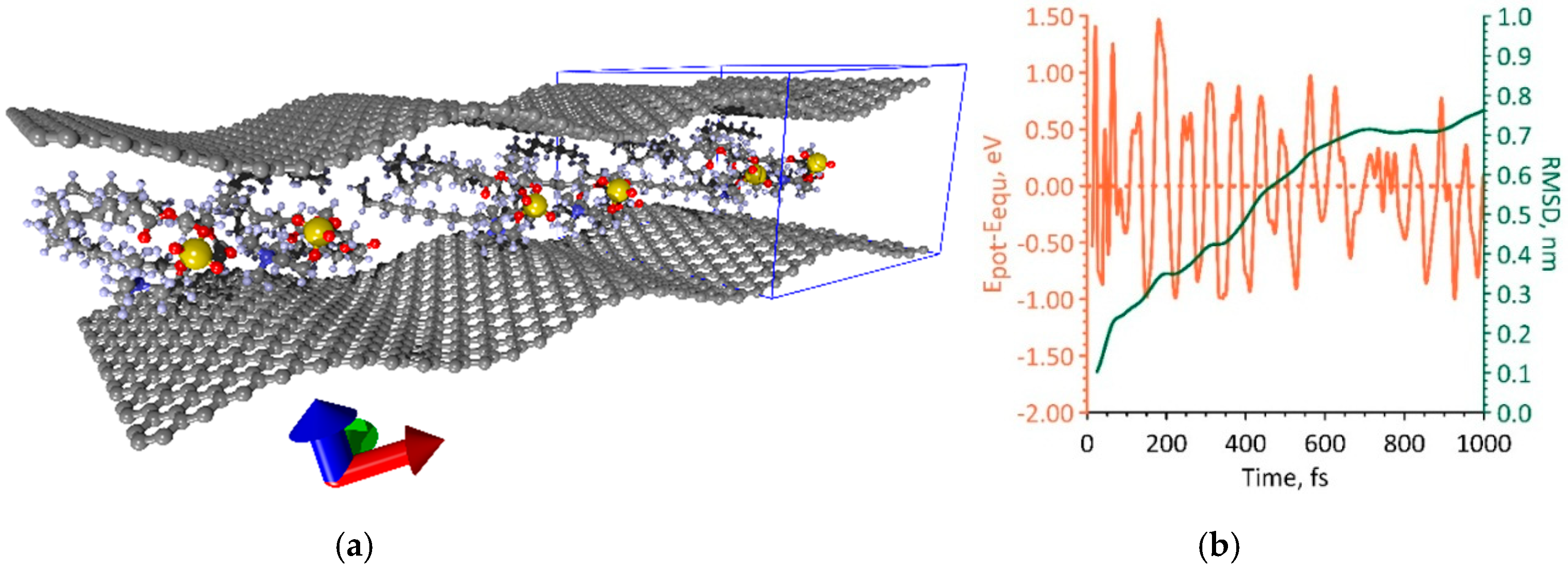
3.2. Atomistic Models and Electron Properties of Bilayer Phospholipid-Graphene Films
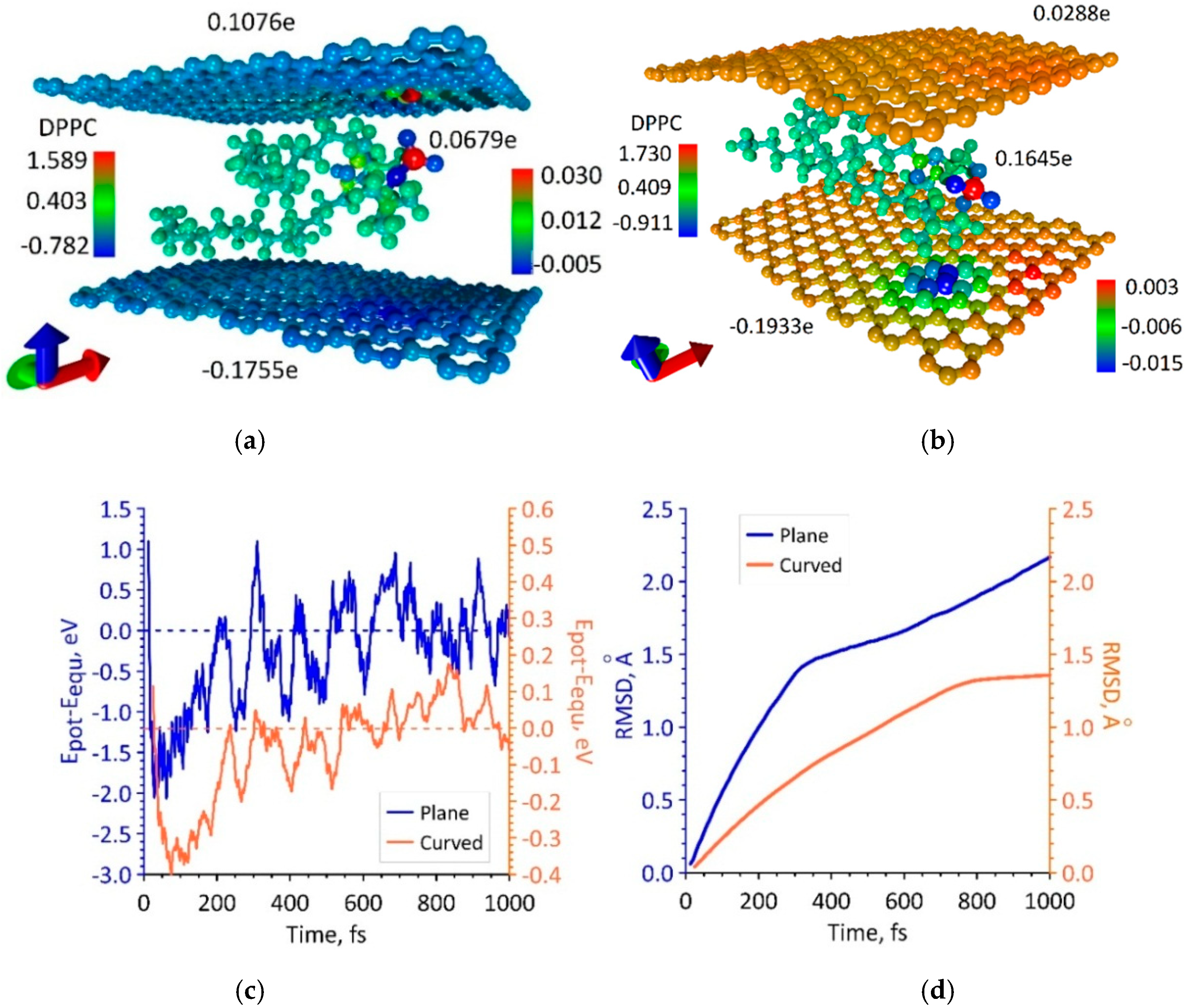
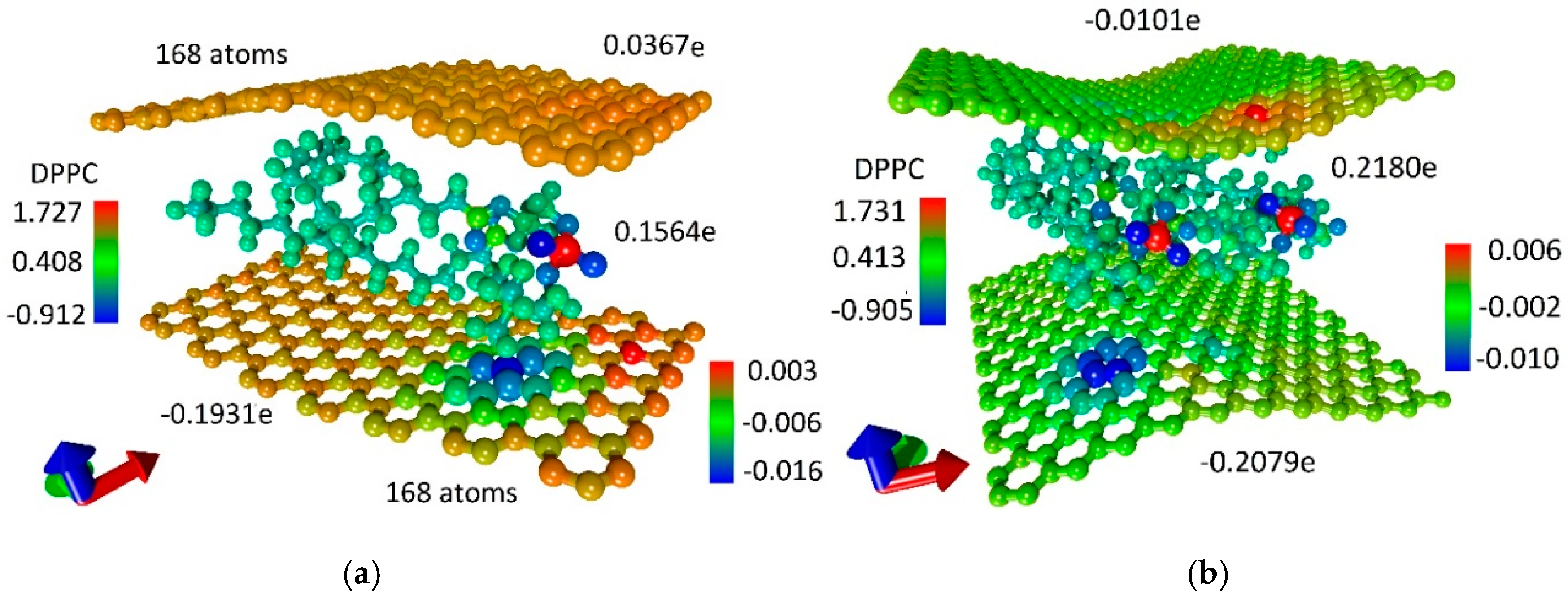
3.3. Phospholipid-Graphene Bilayer Films with Curved Graphene Providing Close Packing of DPPC Molecules and Charge Transfer
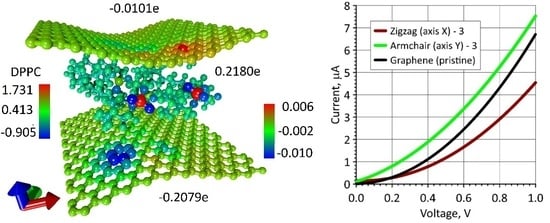
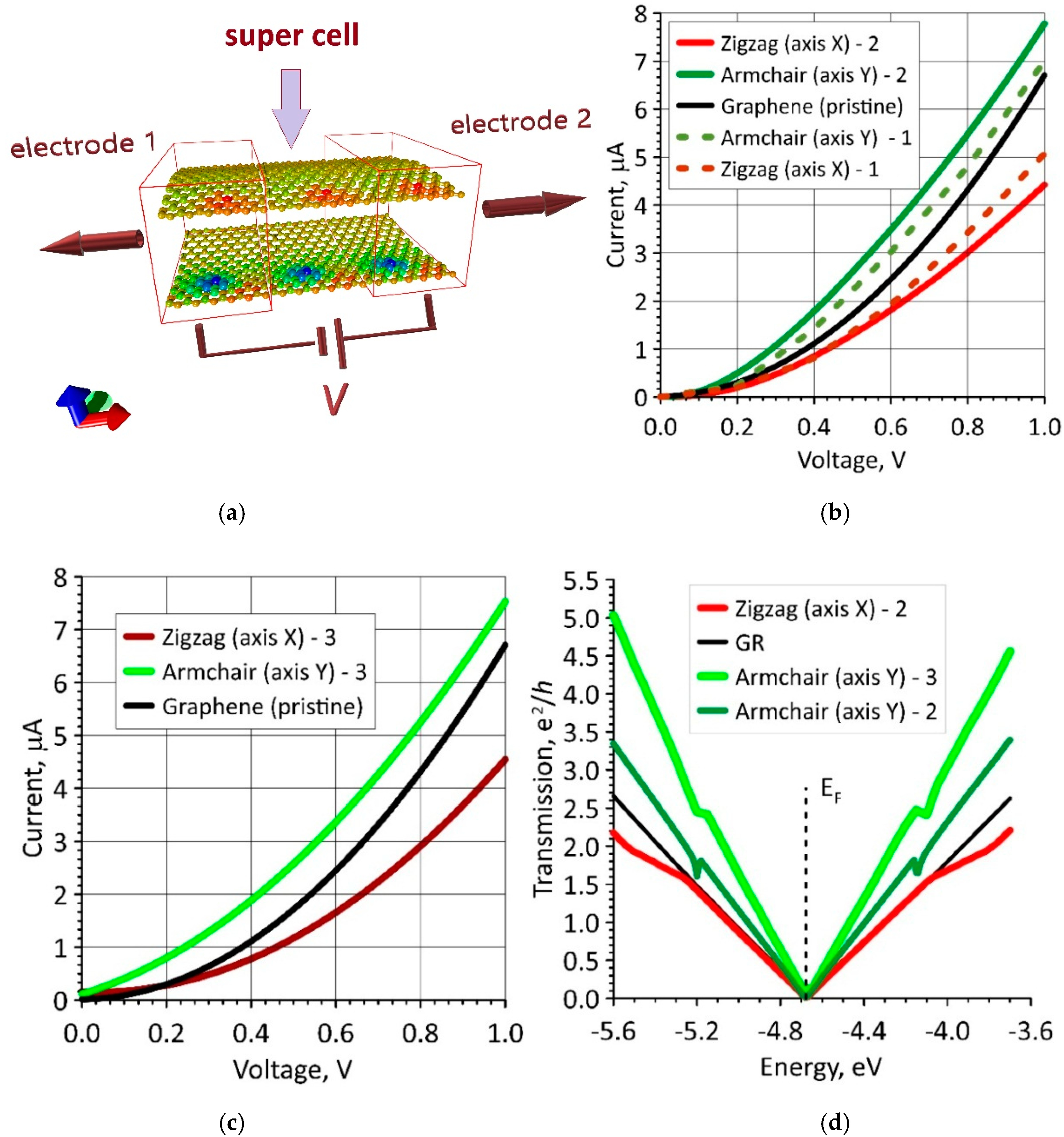
3.4. The Electrical Conductivity of Graphene Layers in Bilayer Phospholipid-Graphene Films with Curved Graphene and the Effect of Curvature on the Sensory Ability of Films
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mohan, V.B.; Lau, K.E.; Hui, D.C.; Bhattacharyya, D. Graphene-based materials and their composites: A review on production, applications and product limitations. Compos. B Eng. 2018, 142, 200–220. [Google Scholar] [CrossRef]
- Yang, Y.; Asiri, A.M.; Tang, Z.; Du, D.; Lin, Y. Graphene based materials for biomedical applications. Mater. Today 2013, 16, 365–373. [Google Scholar] [CrossRef]
- Dsouza, P.; Swetha, P.; Manisha, H.; Sudhakaraprasad, K. Graphene and graphene-based materials in biomedical science. Part. Part. Syst. Char. 2018, 35, 1800105. [Google Scholar]
- Li, D.; Zhang, W.; Yu, X.; Wang, Z.; Su, Z.; Wei, G. When biomolecules meet graphene: From molecular level interactions to material design and applications. Nanoscale 2016, 8, 19491–19509. [Google Scholar] [CrossRef]
- Rivel, T.; Yesylevskyy, S.O.; Ramseyer, C. Structures of single, double and triple layers of lipids adsorbed on graphene: Insights from all-atom molecular dynamics simulations. Carbon 2017, 118, 358–369. [Google Scholar] [CrossRef]
- Lima, L.M.C.; Fu, W.; Jiang, L.; Kros, A.; Schneider, G.F. Graphene-stabilized lipid monolayer heterostructures: A novel biomembrane superstructure. Nanoscale 2016, 8, 18646–18653. [Google Scholar] [CrossRef]
- Li, W.; Chung, J.K.; Lee, Y.K.; Groves, J.T. Graphene-templated supported lipid bilayer nanochannels. Nano Lett. 2016, 16, 5022–5026. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, Y.; Tsuzuki, K.; Iwasa, S.; Ishikawa, R.; Sandhu, A.; Tero, R. Fabrication of supported lipid bilayer on graphene oxide. J. Phys. Conf. Ser. 2012, 352, 012017. [Google Scholar] [CrossRef]
- Pykal, M.; Šafářová, K.; Machalová Šišková, K.; Jurečka, P.; Bourlinos, A.B.; Zbořil, R.; Otyepka, M. Lipid enhanced exfoliation for production of graphene nanosheets. J. Phys. Chem. C 2013, 117, 11800–11803. [Google Scholar] [CrossRef]
- Williams, A.T.; Donno, R.; Tirelli, N.; Dryfe, R.A.W. Phospholipid-mediated exfoliation as a facile preparation method for graphene suspensions. RSC Adv. 2018, 8, 19220–19225. [Google Scholar] [CrossRef]
- Frost, R.; Jönsson, G.E.; Chakarov, D.; Svedhem, S.; Kasemo, B. Graphene oxide and lipid membranes: Interactions and nanocomposite structures. Nano Lett. 2012, 12, 3356–3362. [Google Scholar] [CrossRef] [PubMed]
- Frost, R.; Svedhem, S.; Langhammer, C.; Kasemo, B. Graphene oxide and lipid membranes: Size-dependent interactions. Langmuir 2016, 32, 2708–2717. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Lei, H.; Zhang, X.; Zhang, Y. Strong hydrophobic interaction between graphene oxide and supported lipid bilayers revealed by AFM. Microsc. Res. Tech. 2016, 79, 721–726. [Google Scholar] [CrossRef] [PubMed]
- Phan, A.D.; Woods, L.M.; Hoang, T.X.; Phan, T.L. Repulsive interactions of a lipid membrane with graphene in composite materials. J. Chem. Phys. 2013, 139, 184703. [Google Scholar] [CrossRef] [PubMed]
- Yue, T.; Wang, X.; Zhang, X.; Huang, F. Molecular modeling of interaction between lipid monolayer and graphene nanosheets: Implications for pulmonary nanotoxicity and pulmonary drug delivery. RSC Adv. 2015, 5, 30092–30106. [Google Scholar] [CrossRef]
- Moore, T.C.; Yang, A.H.; Ogungbesan, O.; Hartkamp, R.; Iacovella, C.R.; Zhang, Q.; McCabe, C. Influence of single-stranded DNA coatings on the interaction between graphene nanoflakes and lipid bilayers. J. Phys. Chem. B 2019, 123, 7711–7721. [Google Scholar] [CrossRef]
- Dallavalle, M.; Bottoni, A.; Calvaresi, M.; Zerbetto, F. Functionalization pattern of graphene oxide sheets controls entry or produces lipid turmoil in phospholipid membranes. ACS Appl. Mater. Interfaces 2018, 10, 15487–15493. [Google Scholar] [CrossRef]
- Monasterio, B.G.; Alonso, B.; Sot, J.; Garcia-Arribas, A.B.; Gil-Carton, D.; Valle, M.; Zurutuza, A.; Goni, F.M. Coating graphene oxide with lipid bilayers greatly decreases its hemolytic properties. Langmuir 2017, 33, 8181–8191. [Google Scholar] [CrossRef]
- Singh, S.P.; Li, Y.; Be’er, A.; Oren, Y.; Tour, J.M.; Arnusch, C.J. Laser-induced graphene layers and electrodes prevents microbial fouling and exerts antimicrobial action. ACS Appl. Mater. Interfaces 2017, 9, 18238–18247. [Google Scholar] [CrossRef]
- Durso, M.; Borrachero-Conejo, A.I.; Bettini, C.; Treossi, E.; Scidà, A.; Saracino, E.; Gazzano, M.; Christian, M.; Morandi, V.; Tuci, G.; et al. Biomimetic graphene for enhanced interaction with the external membrane of astrocytes. J. Mater. Chem. B 2018, 6, 5335–5342. [Google Scholar] [CrossRef]
- Glukhova, O.E.; Kolesnikova, A.S.; Slepchenkov, M.M. New approach to manipulate the phospholipid molecules on graphene. J. Phys. Chem. C 2015, 119, 11941–11946. [Google Scholar] [CrossRef]
- Hirtz, M.; Oikonomou, A.; Georgiou, T.; Fuchs, H.; Vijayaraghavan, A. Multiplexed biomimetic lipid membranes on graphene by dip-pen nanolithography. Nat. Commun. 2013, 4, 2591. [Google Scholar] [CrossRef] [PubMed]
- Hai, L.; He, D.; He, X.; Wang, K.; Yang, X.; Liu, J.; Cheng, H.; Huang, X.; Shangguan, J. Facile fabrication of a resveratrol loaded phospholipid@reduced graphene oxide nanoassembly for targeted and near-infrared laser-triggered chemo/photothermal synergistic therapy of cancer in vivo. J. Mater. Chem. B 2017, 5, 5783–5792. [Google Scholar] [CrossRef] [PubMed]
- Willems, N.; Urtizberea, A.; Verre, A.F.; Iliut, M.; Lelimousin, M.; Hirtz, M.; Vijayaraghavan, A.; Sansom, M.S. Biomimetic phospholipid membrane organization on graphene and graphene oxide surfaces: A molecular dynamics simulation study. ACS Nano 2017, 11, 1613–1625. [Google Scholar] [CrossRef]
- Rui, L.; Liu, J.; Li, J.; Weng, Y.; Dou, Y.; Yuan, B.; Yang, K.; Ma, Y. Reduced graphene oxide directed self-assembly of phospholipid monolayers in liquid and gel phases. Biochim. Biophys. Acta 2015, 1848, 1203–1211. [Google Scholar] [CrossRef]
- Tsang, D.K.H.; Lieberthal, T.J.; Watts, C.; Dunlop, E.L.; Ramadan, S.; Hernandez, A.E.D.R.; Klien, N. Chemically functionalised graphene FET biosensor for the label-free sensing of exosomes. Sci. Rep. 2019, 9, 1–10. [Google Scholar]
- Kuo, C.J.; Chiang, H.C.; Tseng, C.A.; Chang, C.F.; Ulaganathan, R.K.; Ling, T.T.; Chang, Y.J.; Chen, C.C.; Chen, Y.R.; Chen, Y.T. Lipid-modified graphene-transistor biosensor for monitoring amyloid-β aggregation. ACS Appl. Mater. Interfaces 2018, 10, 12311–12316. [Google Scholar] [CrossRef]
- Blaschke, B.M.; Böhm, P.; Drieschner, S.; Nickel, B.; Garrido, J.A. Lipid monolayer formation and lipid exchange monitored by a graphene field-effect transistor. Langmuir 2018, 34, 4224–4233. [Google Scholar] [CrossRef]
- Khvedelidze, M.; Mdzinarashvili, T.; Shekiladze, E.; Schneider, M.; Moersdorf, D.; Bernhardt, I. Structure of drug delivery DPPA and DPPC liposomes with ligands and their permeability through cells. J. Liposome Res. 2015, 25, 20–31. [Google Scholar] [CrossRef]
- Kenaan, A.; Cheng, J.; Qi, D.; Chen, D.; Cui, D.; Song, J. Physicochemical analysis of DPPC and photopolymerizable liposomal binary mixture for spatiotemporal drug release. Anal. Chem. 2018, 90, 9487–9494. [Google Scholar] [CrossRef]
- Glukhova, O.E.; Prytkova, T.R.; Savostyanov, G.V. Simulation of high density lipoprotein behavior on a few layer graphene undergoing non-uniform mechanical load. J. Phys. Chem. B 2016, 120, 3593–3600. [Google Scholar] [CrossRef] [PubMed]
- De Morais, F.; Gonçalves, R.S.; Vilsinski, B.H.; de Oliveira, É.L.; Rocha, N.L.; Hioka, N.; Caetano, W. Hypericin photodynamic activity in DPPC liposome. PART I: Biomimetism of loading, location, interactions and thermodynamic properties. J. Photochem. Photobiol. B. 2019, 190, 118–127. [Google Scholar] [CrossRef] [PubMed]
- de Morais, F.; Gonçalves, R.S.; Vilsinski, B.H.; Lazarin-Bidóia, D.; Balbinot, R.B.; Tsubone, T.M.; Brunaldi, K.; Vatatu Nakamura, C.; Hioka, N.; Caetano, W. Hypericin photodynamic activity in DPPC liposomes—Part II: Stability and application in melanoma B16-F10 cancer cells. Photochem. Photobiol. Sci. 2020, 19, 620–630. [Google Scholar] [CrossRef] [PubMed]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Elstner, M. The SCC-DFTB method and its application to biological systems. Theor. Chem. Acc. 2006, 116, 316–325. [Google Scholar] [CrossRef]
- Aradi, B.; Hourahine, B.; Frauenheim, T. DFTB+, a Sparse Matrix-Based Implementation of the DFTB Method. J. Phys. Chem. A 2007, 111, 5678–5684. [Google Scholar] [CrossRef]
- Glukhova, O.E. Molecular dynamics as the tool for investigation of carbon nanostructures properties. In Thermal Transport in Carbon-Based Nanomaterials, 1st ed.; Zhang, G., Ed.; Elsevier: Oxford, UK, 2017; pp. 267–289. [Google Scholar]
- Kvazar-Mizar Programs. Available online: http://nanokvazar.ru (accessed on 10 February 2020).
- Mulliken, R.S. Electronic population analysis on LCAO-MO molecular wave functions. I. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef]
- Datta, S. Quantum Transport.: Atom. to Transistor, 2nd ed.; Cambridge University Press: New York, NY, USA, 2005; pp. 217–251. [Google Scholar]
- Keldysh, L.V. Diagram technique for nonequilibrium processes. JETP 1965, 20, 1018–1026. [Google Scholar]
- Glukhova, O.E.; Shmygin, D.S. The electrical conductivity of CNT/graphene composites: A new method for accelerating transmission function calculations. Beilstein. J. Nanotechnol. 2018, 9, 1254–1262. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slepchenkov, M.M.; Glukhova, O.E. Improving the Sensory Properties of Layered Phospholipid-Graphene Films Due to the Curvature of Graphene Layers. Polymers 2020, 12, 1710. https://doi.org/10.3390/polym12081710
Slepchenkov MM, Glukhova OE. Improving the Sensory Properties of Layered Phospholipid-Graphene Films Due to the Curvature of Graphene Layers. Polymers. 2020; 12(8):1710. https://doi.org/10.3390/polym12081710
Chicago/Turabian StyleSlepchenkov, Michael M., and Olga E. Glukhova. 2020. "Improving the Sensory Properties of Layered Phospholipid-Graphene Films Due to the Curvature of Graphene Layers" Polymers 12, no. 8: 1710. https://doi.org/10.3390/polym12081710
APA StyleSlepchenkov, M. M., & Glukhova, O. E. (2020). Improving the Sensory Properties of Layered Phospholipid-Graphene Films Due to the Curvature of Graphene Layers. Polymers, 12(8), 1710. https://doi.org/10.3390/polym12081710