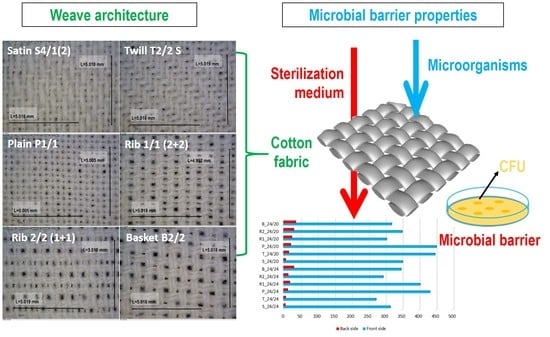
Microbial Barrier Properties of Cotton Fabric—Influence of Weave Architecture
Abstract
1. Introduction
1.1. Woven Fabrics in Function of Medical Textiles
1.2. Structural and Permeability Properties of Woven Fabrics
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. The Yarn Linear Density
2.2.2. Warp and Weft Density (i.e., Number of Threads Per Unit Length)
2.2.3. Woven Fabric Mass Per Unit Area
2.2.4. Woven Fabrics Thickness
2.2.5. Air Permeability
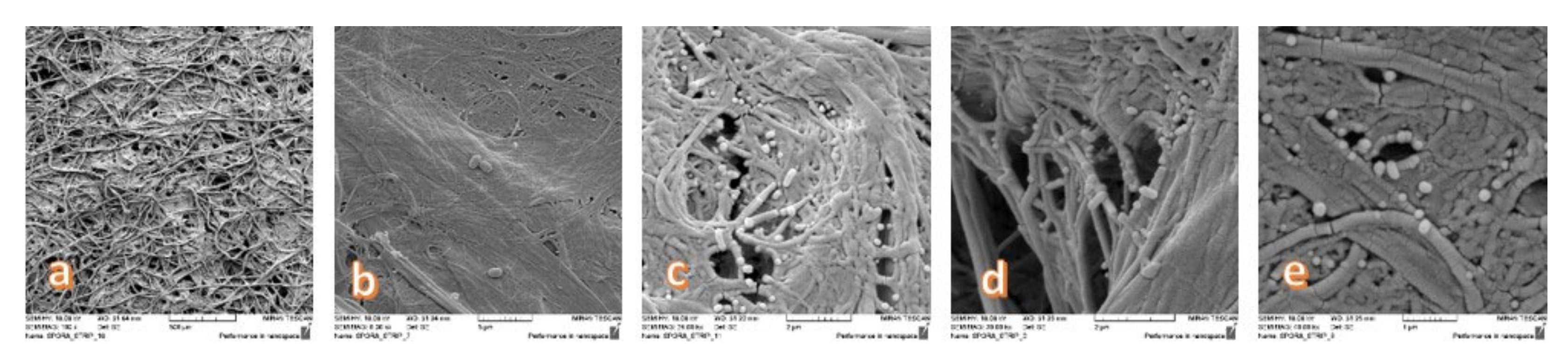
2.2.6. Microbial Barrier Properties
3. Results and Discussion
4. Conclusions
- The investigation results of microbial barrier permeability with respect to fabric weave pattern after extreme contamination with bacterial spores of Geobacillus Stearothermophilus and Bacillus Atrophaeus showed a significant influence of weave pattern on permeability of microorganisms. It was found that the difference between permeability of less bacteria permeable fabric (satin) and the most permeable fabric (basket) was in range of six to seven times. The assessment of the other fabrics put them in the same order regarding bacteria permeability.
- The correlation among the structural and physical characteristics and obtained results of microbial permeability confirmed that neither sample had a predominant influence. The most influential element of weave on permeability is corrected number of pores, their size and floating of warp and weft yarns. As expected, the number of pores and the number of floating yarns correlated positively and equivalent average size correlated negatively with CFU.
- Multiple linear regression of pore numbers, equivalent average pore diameter and floating threads produced equations which correspond in 99% to the measuring results for densities 24/24 and 24/20, and more than 98% when both densities of the set were taken into consideration. It gives the possibility to predict bacteria penetration through woven fabrics without significant differences in densities of warp and weft—woven structures near to square woven fabrics (up to ratio density of weft/ density of warp = 0.8).
- It was found that the floating threads have significant influence on the permeability of microorganisms. Without the effect of floating threads, such high correlation between multiple regression results and CFU could not be recognized.
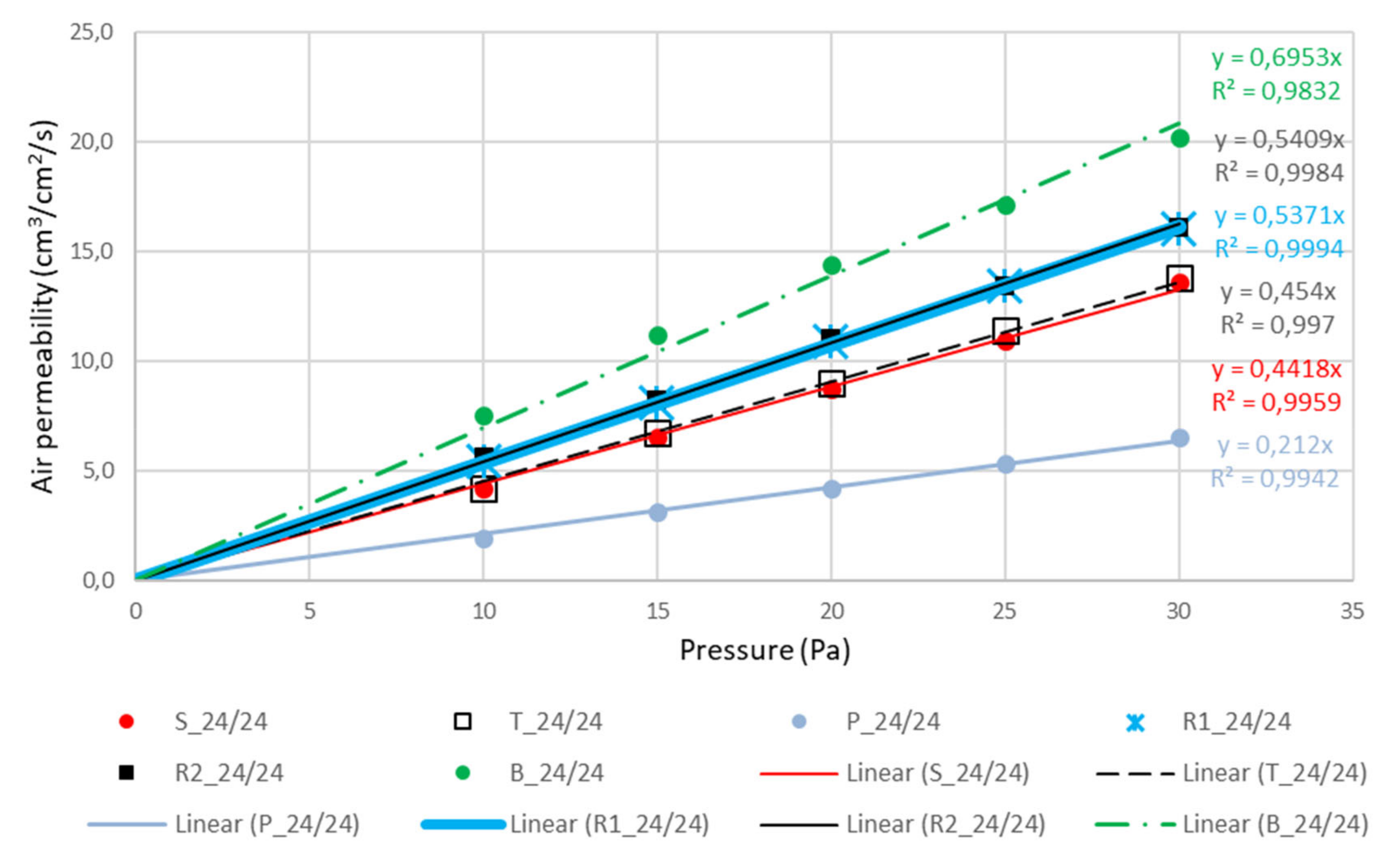
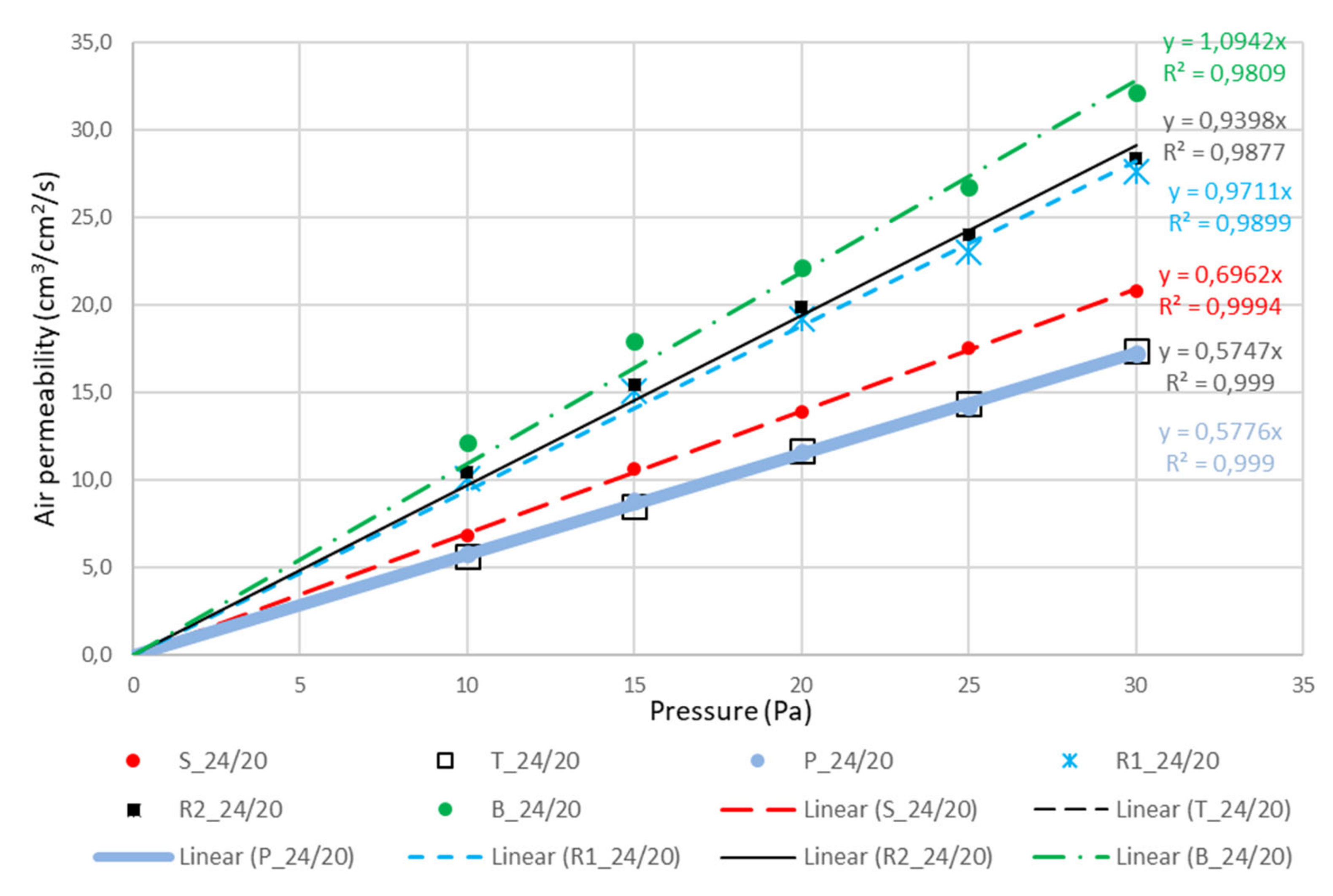
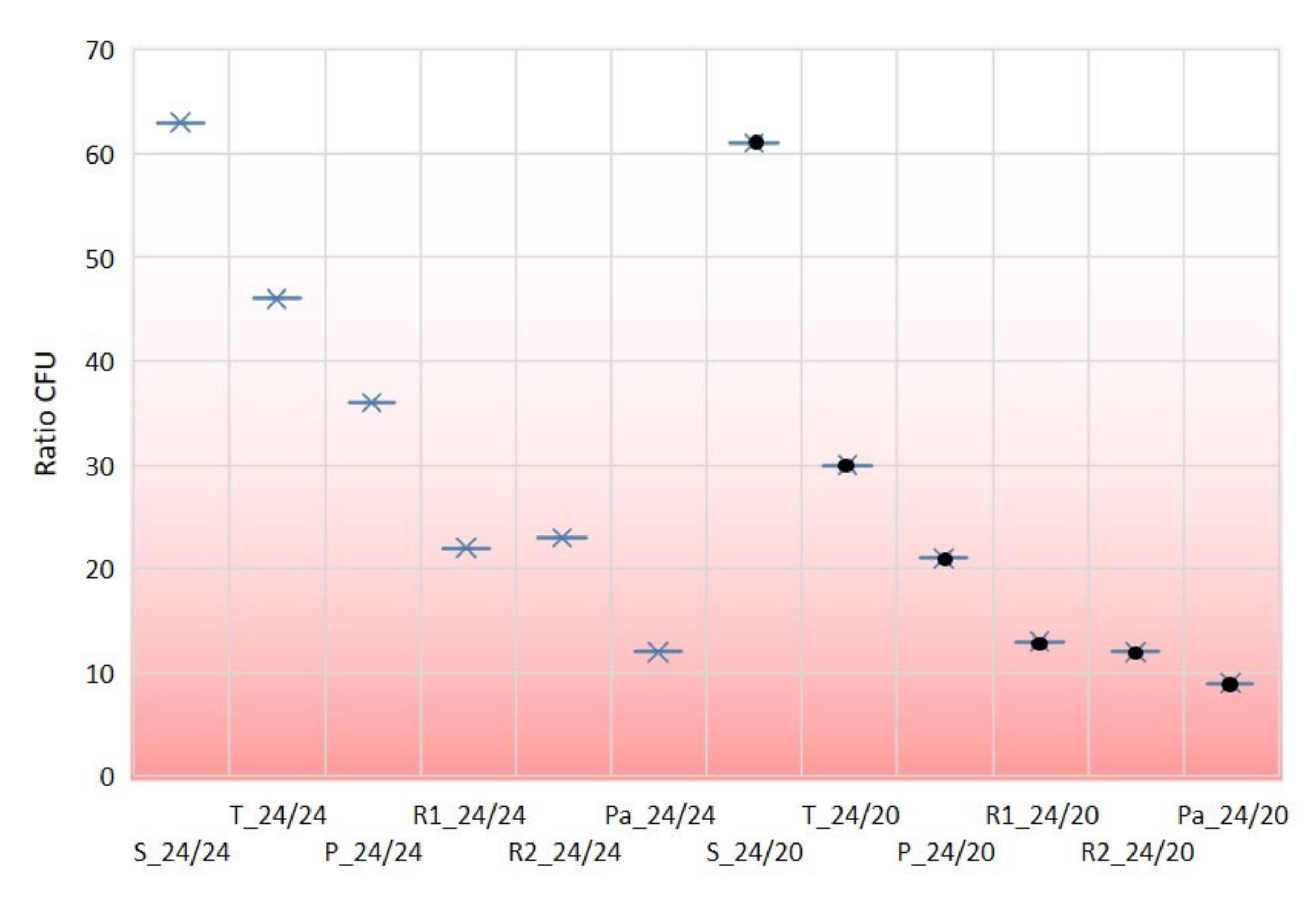
- With both thread densities (24/24 and 24/20) the sequence of permeability per weave patterns was the same: satin, twill, plain, rib (R1, R2), and basket.
- The accuracy of the results is confirmed by behavior of rib weaves (R1 and R2) which are the same structure but turned by 90° and gave almost identical results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rieber, G.; Jiang, J.; Deter, N.; Chen, N.; Mitschang, P. Influence of textile parameters on the in-plane Permeability. Compos. Part A Appl. Sci. Manuf. 2013, 52, 89–98. [Google Scholar] [CrossRef]
- Rahnev, I.; Rimini, G. Isotropy equilibrium of the double woven fabric with cotton face and wool reverse fibrous compositions. IOP Conf. Ser. Mater. Sci. Eng. 2017, 254, 1–9. [Google Scholar] [CrossRef]
- Malnick, S.; Bardenstein, R.; Huszar, M.; Gabbay, J.; Borkow, G. Pyjamas and sheets as a potential source of nosocomial pathogens. J. Hosp. Infect 2008, 70, 89–92. [Google Scholar] [CrossRef] [PubMed]
- O’Hanlon, S.J.; Enright, M.C. A novel bactericidal fabric coating with potent in vitro activity against meticillin-resistant Staphylococcus aureus (MRSA). Int. J. Antimicrob. Agents 2009, 33, 427–431. [Google Scholar] [CrossRef] [PubMed]
- Borkow, G.; Gabbay, J. Biocidal textiles can help fight nosocomial infections. Med. Hypotheses 2008, 70, 990–994. [Google Scholar] [CrossRef]
- Stephens-Borg, K. Surgical dressings and turbulent years of cotton industry. J. Perioper. Pract. 2008, 18, 305–306. [Google Scholar] [CrossRef]
- Leonas, K.K. Effect of laundering on the barrier properties of reusable surgical gown fabrics. Am. J. Infect. Control 1998, 26, 495–501. [Google Scholar] [CrossRef]
- Rutala, W.A.; Weber, D.J. A Review of Single Use and Reusable Gowns and Drapers in Health Care. Infect. Control Hosp. Epidemiol. 2001, 22, 248–257. [Google Scholar] [CrossRef]
- Rogina-Car, B.; Budimir, A.; Turcic, V.; Katović, D. Do multi-use cellulosic textiles provide safe protection against contamination of sterilized items? Cellulose 2014, 21, 2101–2109. [Google Scholar] [CrossRef]
- Sattar, S.A.; Gallant, M.; Nair, R.C.; Scott, E.; Kain, J. Transfer of bacteria from fabrics to hands and other fabrics: Development and application of a quantitative method using Staphylococcus aureus as a model. J. Appl. Microbiol. 2001, 90, 962–970. [Google Scholar] [CrossRef]
- Burden, M.; Cervantes, L.; Weed, D.; Keniston, A.; Price, C.S.; Albert, R.K. Newly cleaned physician uniforms and infrequently washed white coats have similar rates of bacterial contamination after an 8 hour workday: A randomized controlled trial. J. Hops. Med. 2011, 6, 177–182. [Google Scholar] [CrossRef] [PubMed]
- Wiener-Well, Y.; Margalit Galuty, R.N.; Rudensky, B.; Schlesinger, Y.; Attias, D.; Yinnon, A.M. Nursing and physician attire as possible source of nosocomial infections. Am. J. Infect. Control 2011, 39, 555–559. [Google Scholar] [CrossRef]
- Rogina-Car, B. Microbial Barrier Properties of Medical Textiles. Ph.D. Thesis, Faculty of Textile Technology, University of Zagreb, Zagreb, Croatia, 2014. [Google Scholar]
- Rogina-Car, B.; Budimir, A.; Katovic, D. Microbial barrier properties of healthcare professional uniforms. Text. Res. J. 2017, 87, 1860–1868. [Google Scholar] [CrossRef]
- Rogina-Car, B.; Budimir, A.; Turcic, V.; Katović, D. New method for determination of barrier properties of medical textiles. Tekstil 2014, 62, 403–408. [Google Scholar]
- Rogina-Car, B.; Budimir, A.; Turcic, V.; Katović, D. Cellulosic Textiles as Wrapping Material in Medical Sterilization. In Cellulose and Cellulose Composites: Modification, Characterization and Applications; Nova Science Publishers, Inc.: New York, NY, USA, 2015; pp. 415–444. [Google Scholar]
- HRN EN ISO 22612:2008. Clothing for Protection Against Infectious Agents—Test Method for Resistance to Dry Microbial Penetration; (ISO 22612:2005; EN ISO 22612:2005). Available online: http://31.45.242.218/HZN/Todb.nsf/wFrameset2?OpenFrameSet&Frame=Down&Src=%2FHZN%2FTodb.nsf%2Fcd07510acb630f47c1256d2c006ec863%2F225767f844df0602c12570a0002d0ebf%3FOpenDocument%26AutoFramed (accessed on 15 July 2020).
- Enko, M.T. Sterile Supply Packaging; WFHSS-ÖGSV Basic Script: Brussels, Belgium, 2009. [Google Scholar]
- Bojić-Turčić, V. Sterilization and Disinfection in Medicine; Medicinska naklada, Medicom: Zagreb, Croatia, 1994. [Google Scholar]
- Jeng-Jong, L. Prediction of Elastic Properties of Plain Weave Fabric Using Geometrical Modeling. In Woven Fabric Engineering; Dubrovski, P.D., Ed.; IntechOpen: Rijeka, Croatia, 2010; pp. 135–154. ISBN 978-953-307-194-7. [Google Scholar]
- Saville, B.P. Physical Testing of Textiles; Woodhead Publishing Limited: Cambridge, UK, 2004. [Google Scholar]
- Daukantiene, V.; Skarulskiene, A. Wear and hygienic properties of cotton velvet fabrics light industry-Fibrous materials. In Proceedings of the Radom International Scientific Conference, Radom, Poland, 3 June 2005; pp. 355–358. [Google Scholar]
- Więcek, B.; Danych, R.; Kowalski, K. Air and water vapour permeability in double-layered knitted fabrics with different raw materials. Fabr. Text. East. Eur. 2006, 14, 77–80. [Google Scholar]
- Havlová, M. Model of Vertical Porosity Occurring in Woven Fabrics and its Effect on Air Permeability. Fibers Text. East. Eur. 2014, 22, 58–63. [Google Scholar]
- Lu, W.M.; Tung, K.L.; Hwang, K.J. Fluid Flow Through Basic Weaves of Monofilament Filter. Cloth. Text. Res. J. 1996, 66, 311–323. [Google Scholar] [CrossRef]
- Zupin, Ž.; Hladnik, A.; Dimitrovski, K. Prediction of one-layer woven fabric air permeability using porosity parameters. Text. Res. J. 2011, 82, 117–128. [Google Scholar] [CrossRef]
- Fatahi, I.; Yazdi, A.A. Predicting Air Permeability from the Parameters of Weave Structure. Fibers Text. East. Eur. 2012, 3, 78–81. [Google Scholar]
- Milašius, R.; Milašius, V. Investigation of Unevenness of Some Fabric CrossSection Parameters. Fibres Text. East. Eur. 2002, 10, 47–49. [Google Scholar]
- Milašius, R.; Rukuižiene, Ž. Investigation of Correlation of Fabric Inequality in Width with Fabric Shrinkage. Fibers Text. East. Eur. 2003, 11, 42–45. [Google Scholar]
- Hoerner, S.F. Aerodynamic Properties of Screens and Fabric. Text. Res. J. 1952, 274–280. [Google Scholar] [CrossRef]
- Gooijer, H.; Warmoeskerken, M.M.C.G.; Groot Wassink, J. Flow Resistance of Textile Materials-Part I: Monofilament Fabrics. Text. Res. J. 2003, 73, 437–443. [Google Scholar] [CrossRef]
- Havrdová, M. Air Permeability and a Structure of Woven Fabrics. Vlákna Text. 2003, 10, 86–90. [Google Scholar]
- Owczarek, M. Morphometrical structural analysis of inter-thread pores in woven fabrics with the use of computer image analysis. Text. Res. J. 2019, 89, 4858–4874. [Google Scholar] [CrossRef]
- Malik, S.A.; Kocaman, R.T.; Gereke, T.; Aibibu, D.; Cherif, C. Prediction of the Porosity of Barrier Woven Fabrics with Respect to Material, Construction and Processing Parameters and Its Relation with Air Permeability. Fibers Text. East. Eur. 2018, 26, 71–79. [Google Scholar] [CrossRef]
- ISO 2060:2008. Textiles-Yarn from Packages-Determination of Linear Density (Mass per Unit Length) by the Skein Method; ICS: London, UK, 2008. [Google Scholar]
- HRN ISO 7211-5:2003. Textiles-Woven Fabrics-Construction-Methods of Analysis-Part 5: Determination of Linear Density of Yarn Removed from Fabric; ICS: London, UK, 2003. [Google Scholar]
- HRN EN ISO 1049-2:2003. Textiles-Woven fabrics-Construction-Methods of analysis-Part 2: Determination of Number of Threads per Unit Length; ISO 7211-2:1984 modified; EN 1049-2:1993; ICS: London, UK, 2003. [Google Scholar]
- HRN ISO 3801:2003. Textil-Woven Fabrics-Determination of Mass per Unit Length and Mass per Unit Area; ISO 3801:1977; ICS: London, UK, 2003. [Google Scholar]
- Kostajnšek, K.; Dimitrovski, K. Multilayer Cotton Fabric Porosity and its Influence on Permeability Properties. Tekstilec 2018, 61, 254–264. [Google Scholar] [CrossRef]
- HRN EN ISO 5084:2003. Textiles-Determination of Thickness of Woven and Knitted Fabrics (other than Textile Floor Coverings); ICS: London, UK, 2003. [Google Scholar]
- ISO 9237:1995. Textiles-Determination of the Permeability of Fabrics to Air; ICS: London, UK, 1995. [Google Scholar]
- Dobnik Dubrovski, P. Volume porosity of woven fabrics. Text. Res. J. 2000, 70, 915–919. [Google Scholar] [CrossRef]
- Xiao, X.; Zeng, X.; Long, A.; Lin, H.; Clifford, M.; Saldaeva, E.; Lee, K.; Watson, S. An analytical model for through-thickness permeability of woven fabric. Text. Res. J. 2012, 82, 492–501. [Google Scholar] [CrossRef]
- Dimitrovski, K. Equivalent average diameter of Pores–Definition and determination. In Book of Proceedings–12th International Scientific-Professional Symposium Textile Science & Economy 2019 French-Croatian Forum; Ivan, N., Ed.; University of Zagreb Faculty of Textile Technology: Zagreb, Croatia, 2019; pp. 115–122. [Google Scholar]
- Rogina-Car, B.; Rogina, J.; Govorčin Bajsić, E.; Budimir, A. Propolis-Eco-friendly natural antibacterial finish for nonwoven fabrics for medical application. J. Ind. Text. 2020, 49, 1100–1119. [Google Scholar] [CrossRef]
- Schwarz, I.; Rogina-Car, B.; Brunsek, R. Woven Military Fabrics from the Aspect of the Microbial Barrier Permeability. In Functional Textiles and Clothing; Abhijit, M., Deepti, G., Sanjay, G., Eds.; Springer: Singapore, 2019; pp. 11–19. [Google Scholar]




| Degree of Influence on Pore Size | Source of Influence | |||
|---|---|---|---|---|
| Yarn Fineness (tex) | Filament Fineness (dtex) | Yarn Density (Threads/cm) | Weave Type | |
| Micro pores (<10−3 m) | + | +++ | ++ | + |
| Meso pores (10−3–10−2 m) | +++ | + | +++ | +++ |
| Sample | Label | Mass per Area (g/m2) | Thickness (mm) | Linear Density (tex) | Fabric Density (Threads/cm) | |||
|---|---|---|---|---|---|---|---|---|
| Warp | Weft | Warp | Weft | |||||
| Satin S4/1(2) | S_24/24 | Mean | 177.1 | 0.398 | 34.5 | 35.6 | 24.6 | 23.9 |
| SD | 1.1 | 0 | 1.6 | 1.9 | 0.8 | 0.6 | ||
| CV (%) | 0.6 | 1.2 | 4.8 | 5.4 | 3.4 | 2.4 | ||
| Twill T2/2 S | T_24/24 | Mean | 182.3 | 0.362 | 34.2 | 35.8 | 24.8 | 24.1 |
| SD | 2.5 | 0 | 2.1 | 1.8 | 0.4 | 0.3 | ||
| CV (%) | 1.4 | 1.2 | 6.1 | 5.0 | 1.7 | 1.3 | ||
| Plain P1/1 | P_24/24 | Mean | 186.7 | 0.332 | 34.2 | 36.5 | 24.2 | 24.0 |
| SD | 0.2 | 0 | 0.7 | 0.9 | 0.4 | 0 | ||
| CV (%) | 0.1 | 1.1 | 2.1 | 2.6 | 1.7 | 0 | ||
| Rib 1/1 (2+2) | R1_24/24 | Mean | 177.1 | 0.377 | 35.1 | 36.7 | 24.5 | 24.0 |
| SD | 1.2 | 0 | 1.0 | 0.8 | 0.5 | 0.8 | ||
| CV (%) | 0.7 | 0.9 | 2.8 | 2.3 | 2.2 | 3.4 | ||
| Rib 2/2 (1+1) | R2_24/24 | Mean | 178.1 | 0.376 | 35.9 | 35.6 | 24.40 | 24.3 |
| SD | 1.6 | 0 | 1.1 | 1.0 | 0.5 | 0.5 | ||
| CV (%) | 0.9 | 1.2 | 3.2 | 2.9 | 2.1 | 2.0 | ||
| Basket B2/2 | B_24/24 | Mean | 178.8 | 0.379 | 35.3 | 36.3 | 24.3 | 23.7 |
| SD | 1.1 | 0 | 1.6 | 1.1 | 0.5 | 0.5 | ||
| CV (%) | 0.6 | 0.9 | 4.4 | 3.1 | 2.0 | 2.0 | ||
| Sample | Label | Mass per Area (g/m2) | Thickness (mm) | Linear Density (tex) | Fabric Density (Threads/cm) | |||
|---|---|---|---|---|---|---|---|---|
| Warp | Weft | Warp | Weft | |||||
| Satin S4/1(2) | S_24/20 | Mean | 161.2 | 0.370 | 34.7 | 36.0 | 24.3 | 19.7 |
| SD | 1.6 | 0 | 1.2 | 1.3 | 0.5 | 0.5 | ||
| CV (%) | 1.0 | 0.8 | 3.4 | 3.7 | 2.0 | 2.5 | ||
| Twill T2/2 S | T_24/20 | Mean | 162.0 | 0.357 | 34.7 | 35.3 | 24.4 | 19.9 |
| SD | 2.0 | 0 | 2.4 | 1.7 | 0.5 | 0.6 | ||
| CV (%) | 1.2 | 0.6 | 6.8 | 4.7 | 2.1 | 2.9 | ||
| Plain P1/1 | P_24/20 | Mean | 165.8 | 0.333 | 35.7 | 35.6 | 24.3 | 20.3 |
| SD | 0.5 | 0 | 1.5 | 1.2 | 0.5 | 0.5 | ||
| CV (%) | 0.3 | 1.1 | 4.3 | 3.3 | 2.0 | 2.4 | ||
| Rib 1/1 (2+2) | R1_24/20 | Mean | 162.9 | 0.364 | 34.0 | 36.3 | 24.4 | 19.6 |
| SD | 1.3 | 0 | 1.3 | 1.4 | 0.5 | 0.5 | ||
| CV (%) | 0.8 | 1.3 | 3.9 | 3.8 | 2.1 | 2.6 | ||
| Rib 2/2 (1+1) | R2_24/20 | Mean | 160.4 | 0.363 | 35.3 | 36.6 | 23.5 | 19.9 |
| SD | 0.8 | 0 | 1.5 | 1.7 | 0.5 | 0.3 | ||
| CV (%) | 0.5 | 1.9 | 4.2 | 4.6 | 2.2 | 1.6 | ||
| Basket B2/2 | B_24/20 | Mean | 161.3 | 0.364 | 34.1 | 36.0 | 24.4 | 19.6 |
| SD | 0.6 | 0 | 2.3 | 2.1 | 0.5 | 0.7 | ||
| CV (%) | 0.4 | 1.6 | 6.7 | 5.9 | 2.1 | 3.6 | ||
| Sample | Specific Density (ρfabric, g/cm3) 1 | Fabric Porosity (P, %) 2 | Set Number of Pores (n) | Actual Number of Pores (n) 3 | Corrected Number of Pores (n) | EAD Diameter of Pores 1 (μm) | EAD Diameter of Pores 2 (µm) |
|---|---|---|---|---|---|---|---|
| S_24/24 | 0.445 | 70.7 | 576 | 588 | 588 | 122.20 | 122.20 |
| T_24/24 | 0.504 | 66.9 | 576 | 598 | 598 | 119.70 | 119.70 |
| P_24/24 | 0.562 | 63.0 | 576 | 581 | 581 | 97.50 | 97.50 |
| R1_24/24 | 0.470 | 69.1 | 576 | 588 | 294 | 126.70 | 150.50 |
| R2_24/24 | 0.474 | 68.8 | 576 | 593 | 297 | 126.50 | 150.40 |
| B_24/24 | 0.472 | 69.0 | 576 | 576 | 144 | 135.90 | 192.14 |
| S_24/20 | 0.436 | 71.3 | 480 | 479 | 479 | 141.50 | 141.50 |
| T_24/20 | 0.454 | 70.1 | 480 | 486 | 486 | 133.90 | 133.90 |
| P_24/20 | 0.498 | 67.2 | 480 | 493 | 493 | 130.45 | 130.45 |
| R1_24/20 | 0.448 | 70.6 | 480 | 478 | 239 | 152.01 | 180.77 |
| R2_24/20 | 0.442 | 70.9 | 480 | 468 | 234 | 154.13 | 183.29 |
| B_24/20 | 0.443 | 70.8 | 480 | 478 | 120 | 157.90 | 223.30 |
| Sample | Air Permeability (cm3/s, cm2)–Measurement Area 50 cm2 | Values of Coefficient A in Equation (3) | |||||
|---|---|---|---|---|---|---|---|
| Pressure (Pa) | |||||||
| 10 Pa | 15 Pa | 20 Pa | 25 Pa | 30 Pa | 100 Pa | ||
| S_24/24 | 4.2 | 6.5 | 8.7 | 10.9 | 13.6 | 41.77 | 0.4418 |
| T_24/24 | 4.2 | 6.7 | 9.0 | 11.4 | 13.8 | 38.71 | 0.4540 |
| P_24/24 | 1.9 | 3.1 | 4.2 | 5.3 | 6.5 | 21.77 | 0.2120 |
| R1_24/24 | 5.4 | 8.1 | 10.9 | 13.4 | 16.0 | 44.14 | 0.5371 |
| R2_24/24 | 5.6 | 8.2 | 11.0 | 13.4 | 16.1 | 42.93 | 0.5409 |
| B_24/24 | 7.5 | 11.2 | 14.4 | 17.1 | 20.2 | 51.51 | 0.6953 |
| S_24/20 | 6.8 | 10.6 | 13.9 | 17.5 | 20.8 | 60.88 | 0.6962 |
| T_24/20 | 5.6 | 8.5 | 11.7 | 14.4 | 17.4 | 52.09 | 0.5776 |
| P_24/20 | 5.8 | 8.8 | 11.6 | 14.2 | 17.2 | 45.52 | 0.5747 |
| R1_24/20 | 10.1 | 15.1 | 19.2 | 23.0 | 27.6 | 76.49 | 0.9398 |
| R2_24/20 | 10.4 | 15.4 | 19.9 | 24.0 | 28.4 | 73.29 | 0.9711 |
| B_24/20 | 12.1 | 17.9 | 22.1 | 26.7 | 32.1 | 78.33 | 1.0942 |
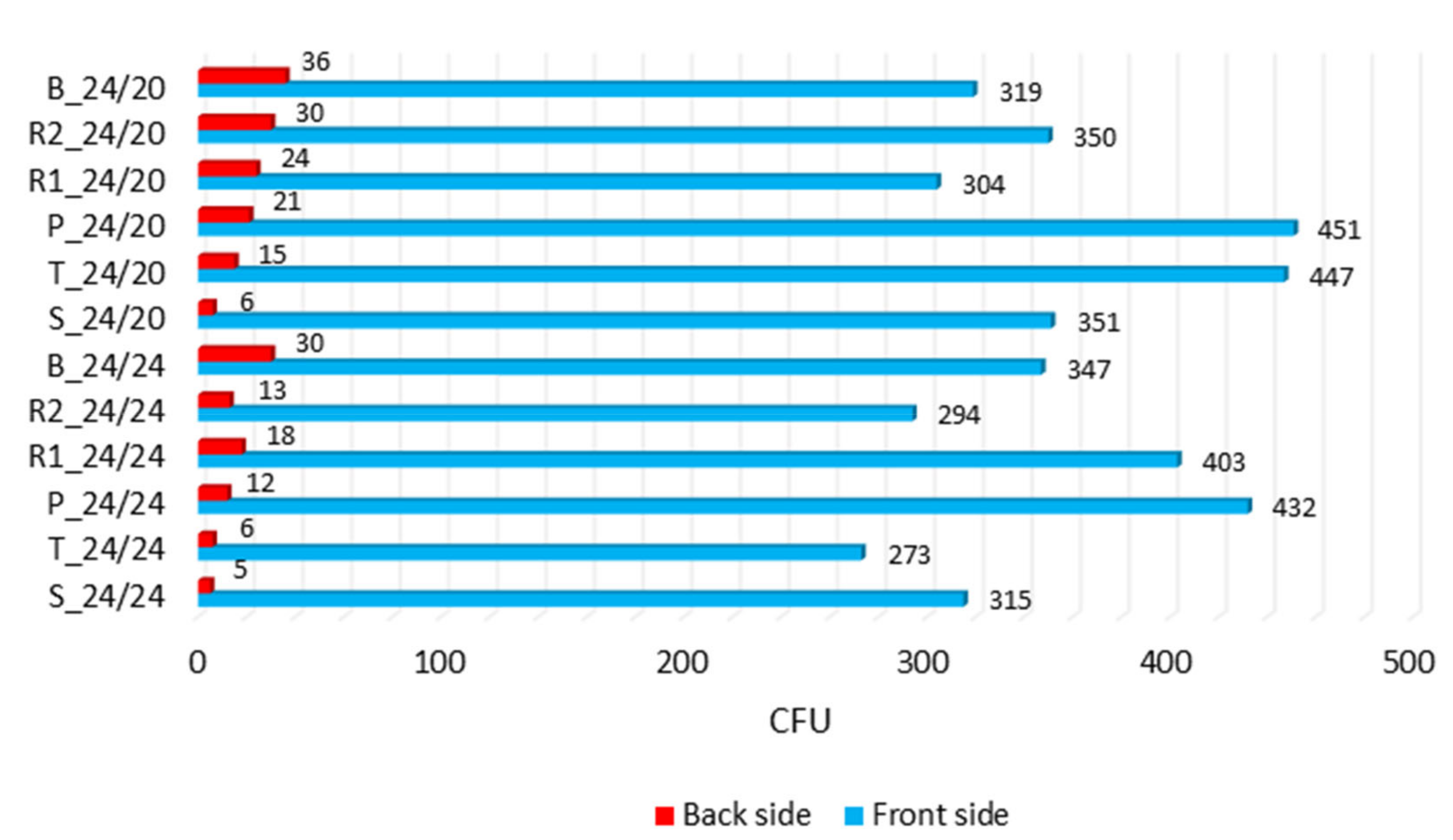
| Sample | Number of Isolates | Colonies of the Back Side/Plate Mean ± SD (range) | The Average Number of Colonies on the Front Side | Ratio CFU (on the Front Side and on the Back Side) |
|---|---|---|---|---|
| S_24/24 | 12 | 5 ± 3.0 (1–8) | 315 | 63:1 |
| T_24/24 | 12 | 6 ± 2.3 (3–10) | 273 | 46:1 |
| P_24/24 | 12 | 12 ± 8.9 (5–28) | 432 | 36:1 |
| R1_24/24 | 12 | 18 ± 8.3 (9–25) | 403 | 22:1 |
| R2_24/24 | 12 | 13 ± 3.3 (7–22) | 294 | 23:1 |
| B_24/24 | 12 | 30 ± 24.9 (9–56) | 347 | 12:1 |
| S_24/20 | 12 | 6 ± 8.2 (1–18) | 351 | 61:1 |
| T_24/20 | 12 | 15 ± 6.0 (9–21) | 447 | 30:1 |
| P_24/20 | 12 | 21 ± 10.6 (10–31) | 451 | 21:1 |
| R1_24/20 | 12 | 24 ± 21.6 (4–47) | 304 | 13:1 |
| R2_24/20 | 12 | 30 ± 21.1 (8–50) | 350 | 12:1 |
| B_24/20 | 12 | 36 ± 22.7 (17–61) | 319 | 9:1 |
| Sample | Actual Number of Pores (n)3 | Corrected Number of Pores (n) | EAD Diameter of Pores 1 (μm) | EAD Diameter of Pores 2 (de2, µm) | Fabric Porosity (P, %) | Thickness (mm) | Floating (yarns) | Air Permeability (cm3/s, cm2) | CFU |
|---|---|---|---|---|---|---|---|---|---|
| S_24/24 | 588 | 588 | 122.20 | 122.20 | 70.7 | 0.40 | 8 | 41.77 | 63 |
| T_24/24 | 598 | 598 | 119.70 | 119.70 | 66.9 | 0.36 | 4 | 38.71 | 46 |
| P_24/24 | 581 | 581 | 97.50 | 97.50 | 63.0 | 0.33 | 2 | 21.77 | 36 |
| R1_24/24 | 577 | 294 | 126.70 | 150.50 | 68.8 | 0.38 | 3 | 44.14 | 22 |
| R2_24/24 | 588 | 297 | 126.50 | 150.40 | 69.0 | 0.38 | 3 | 42.93 | 23 |
| B_24/24 | 593 | 144 | 135.90 | 192.14 | 69.1 | 0.38 | 4 | 51.51 | 12 |
| S_24/20 | 479 | 479 | 141.50 | 141.50 | 71.3 | 0.37 | 8 | 60.88 | 61 |
| T_24/20 | 486 | 486 | 133.90 | 133.90 | 70.1 | 0.36 | 4 | 52.09 | 30 |
| P_24/20 | 493 | 493 | 130.45 | 130.45 | 67.2 | 0.33 | 2 | 45.52 | 21 |
| R1_24/20 | 478 | 239 | 152.01 | 180.77 | 70.9 | 0.36 | 3 | 76.49 | 13 |
| R2_24/20 | 466 | 234 | 154.13 | 183.29 | 70.8 | 0.36 | 3 | 73.29 | 12 |
| B_24/20 | 478 | 120 | 157.90 | 223.30 | 70.6 | 0.36 | 4 | 78.33 | 9 |
| corr; 1-6; 7-12 | −0.05477 | 0.99859 | 0.87163 | 0.97863 | 0.97403 | 0.97272 | 1 | 0.85553 | 0.95338 |
| corr; 1-6; CFU 1-6 | 0.17785 | 0.88813 | −0.40059 | −0.72543 | 0.04035 | 0.14203 | 0.69053 | −0.36169 | |
| corr; 7-12; CFU 7-12 | 0.20376 | 0.70413 | −0.40990 | −0.62224 | 0.19370 | 0.23062 | 0.86498 | −0.44411 | |
| corr; 1-12; CFU 1-12 | 0.28234 | 0.80833 | -0.41593 | -0.69669 | -0.04881 | 0.24264 | 0.75298 | -0.45598 |
| Sample | Corrected Number of Pores (ncorr) | EAD Diameter of Pores 2 (de2, µm) | Number of Float (yarns) | CFU | Calculated *CFU | Error |
|---|---|---|---|---|---|---|
| S_24/24 | 588 | 122.20 | 8 | 63 | 63.22 | 0.22 |
| T_24/24 | 598 | 119.70 | 4 | 46 | 45.04 | 0.96 |
| P_24/24 | 581 | 97.50 | 2 | 36 | 37.52 | 1.52 |
| R1_24/24 | 294 | 150.50 | 3 | 22 | 21.34 | 0.66 |
| R2_24/24 | 297 | 150.40 | 3 | 23 | 21.50 | 1.50 |
| B_24/24 | 144 | 192.14 | 4 | 12 | 13.58 | 1.38 |
| Sample | Corrected Number of Pores (ncorr) | EAD Diameter of Pores 2 (de2, µm) | Number of Float (yarns) | CFU | Calculated *CFU | Error |
|---|---|---|---|---|---|---|
| S_24/20 | 479 | 141.50 | 8 | 61 | 60.05 | 0.95 |
| T_24/20 | 486 | 133.90 | 4 | 30 | 32.84 | 2.84 |
| P_24/20 | 493 | 130.45 | 2 | 21 | 19.18 | 1.82 |
| R1_24/20 | 239 | 180.77 | 3 | 13 | 12.73 | 0.27 |
| R2_24/20 | 234 | 183.29 | 3 | 12 | 12.10 | 0.10 |
| B_24/20 | 120 | 223.30 | 4 | 9 | 9.10 | 0.10 |
| Sample | Corrected Number of Pores (ncorr) | EAD Diameter of Pores 2 (de2, µm) | Number of Float (yarns) | CFU | Calculated *CFU | Error |
|---|---|---|---|---|---|---|
| S_24/24 | 588 | 122.20 | 8 | 63 | 65.44 | 2.44 |
| T_24/24 | 598 | 119.70 | 4 | 46 | 41.57 | 4.43 |
| P_24/24 | 581 | 97.50 | 2 | 36 | 33.75 | 2.25 |
| R1_24/24 | 294 | 150.50 | 3 | 22 | 21.11 | 0.89 |
| R2_24/24 | 297 | 150.40 | 3 | 23 | 21.20 | 1.80 |
| B_24/24 | 144 | 192.14 | 4 | 12 | 14.34 | 2.34 |
| S_24/20 | 479 | 141.50 | 8 | 61 | 58.48 | 2.52 |
| T_24/20 | 486 | 133.90 | 4 | 30 | 35.67 | 5.67 |
| P_24/20 | 493 | 130.45 | 2 | 21 | 24.27 | 3.27 |
| R1_24/20 | 239 | 180.77 | 3 | 13 | 13.02 | 0.02 |
| R2_24/20 | 234 | 183.29 | 3 | 12 | 12.34 | 0.34 |
| B_24/20 | 120 | 223.30 | 4 | 9 | 6.82 | 2.18 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogina-Car, B.; Kovačević, S.; Schwarz, I.; Dimitrovski, K. Microbial Barrier Properties of Cotton Fabric—Influence of Weave Architecture. Polymers 2020, 12, 1570. https://doi.org/10.3390/polym12071570
Rogina-Car B, Kovačević S, Schwarz I, Dimitrovski K. Microbial Barrier Properties of Cotton Fabric—Influence of Weave Architecture. Polymers. 2020; 12(7):1570. https://doi.org/10.3390/polym12071570
Chicago/Turabian StyleRogina-Car, Beti, Stana Kovačević, Ivana Schwarz, and Krste Dimitrovski. 2020. "Microbial Barrier Properties of Cotton Fabric—Influence of Weave Architecture" Polymers 12, no. 7: 1570. https://doi.org/10.3390/polym12071570
APA StyleRogina-Car, B., Kovačević, S., Schwarz, I., & Dimitrovski, K. (2020). Microbial Barrier Properties of Cotton Fabric—Influence of Weave Architecture. Polymers, 12(7), 1570. https://doi.org/10.3390/polym12071570