Study of the Sound Absorption Properties of 3D-Printed Open-Porous ABS Material Structures
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
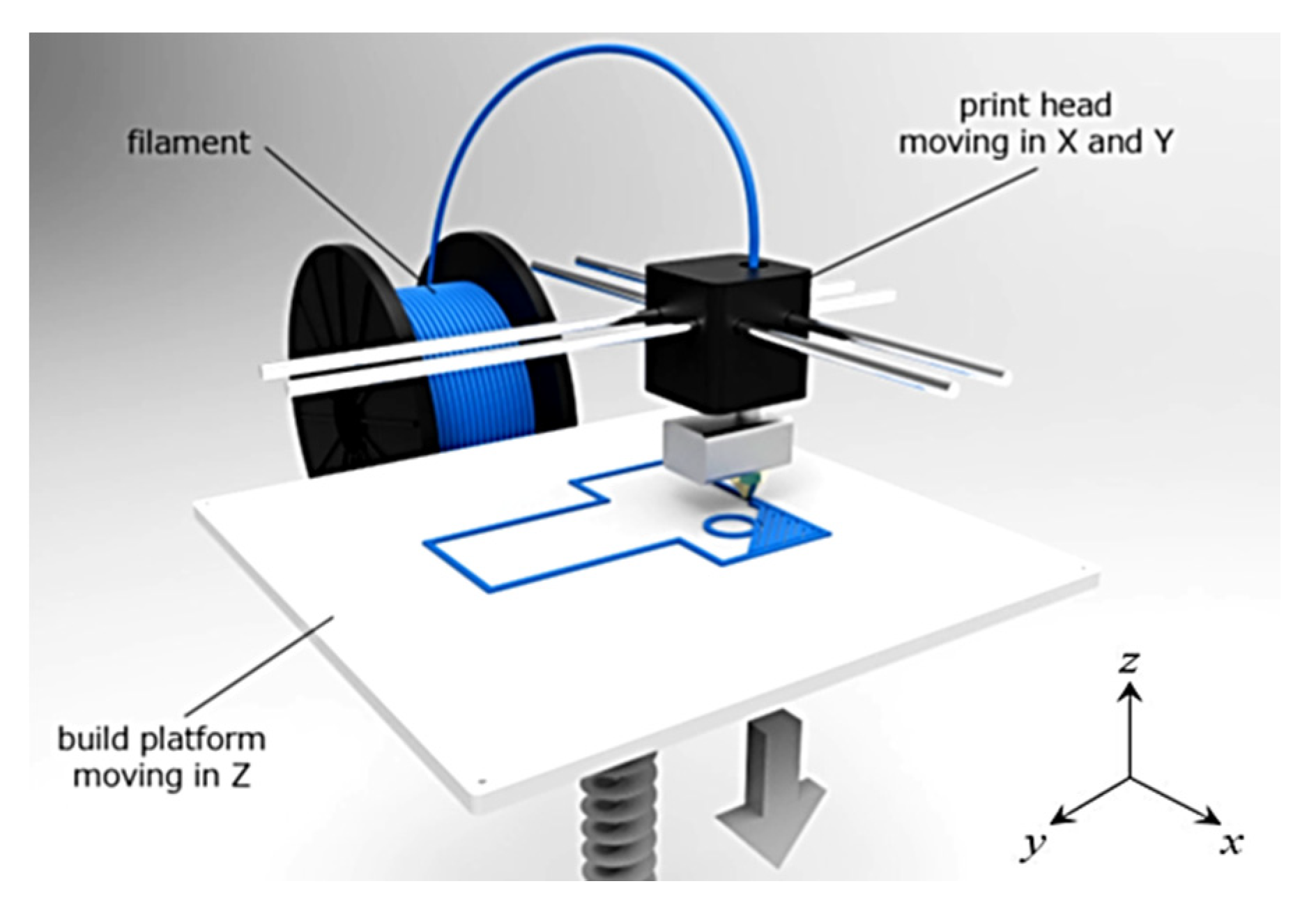
2.2. Samples Production
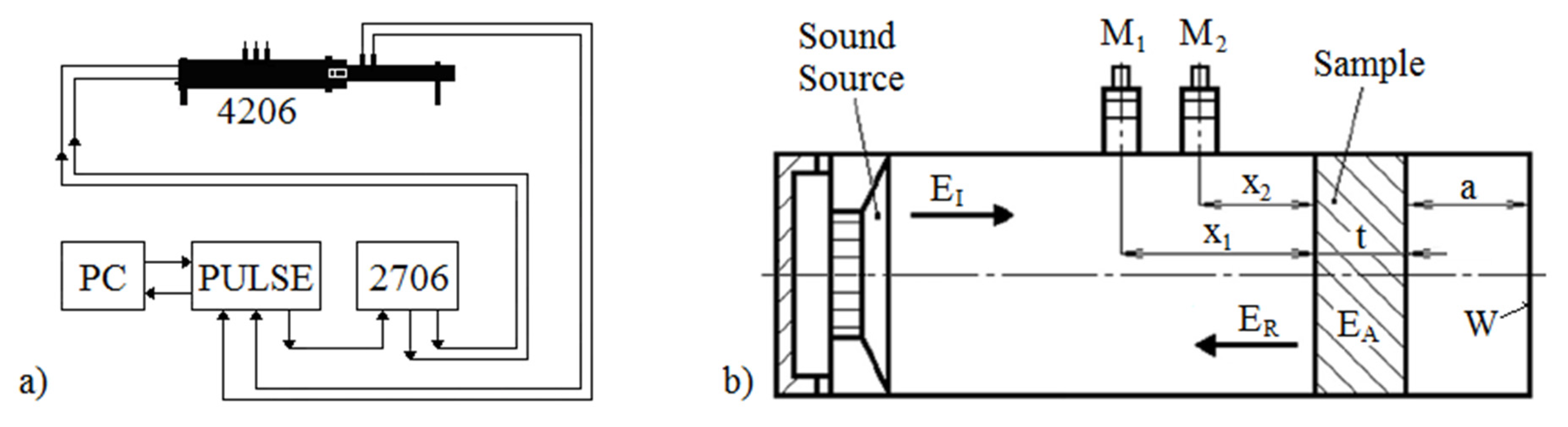
2.3. Measurement Methodology
2.3.1. Sound Absorption Coefficient
2.3.2. Noise Reduction Coefficient
2.3.3. Sound Absorption Properties
3. Results and Discussion
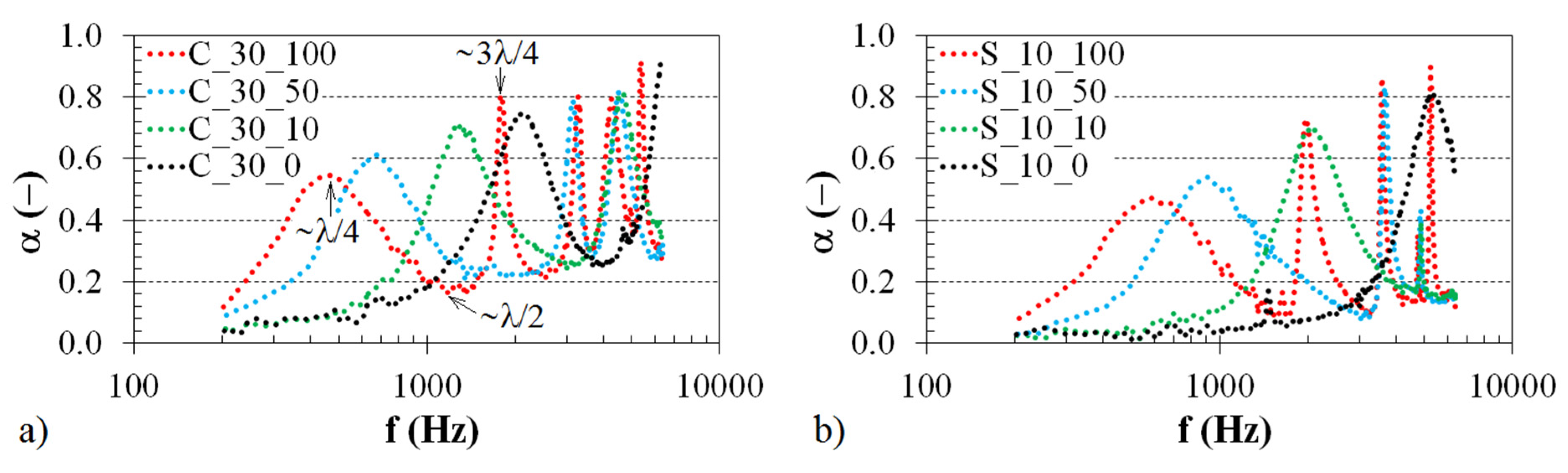
3.1. Frequency Dependencies of the Sound Absorption Coefficient
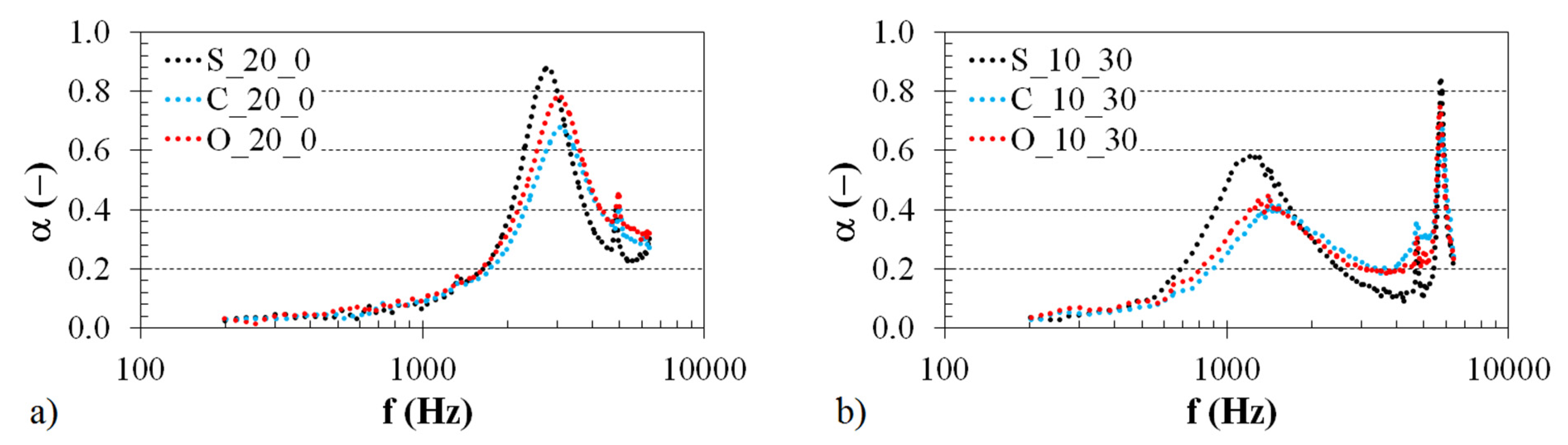
3.1.1. Effect of Structure Type
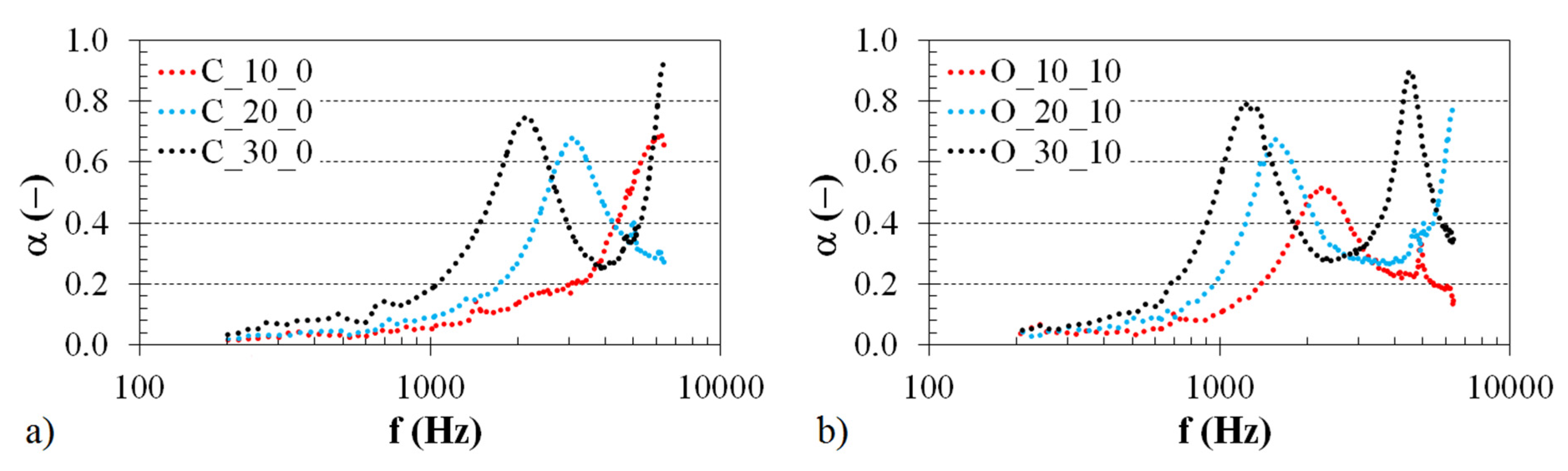
3.1.2. Effect of Material Thickness
3.1.3. Effect of the Air Gap Size
3.1.4. Effect of Excitation Frequency
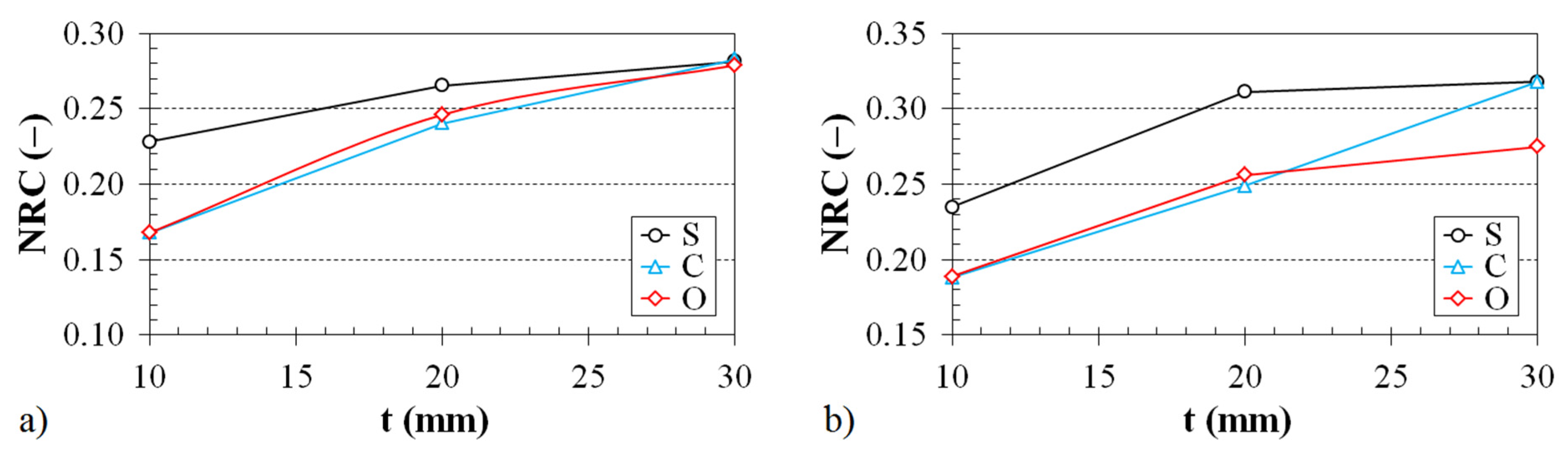
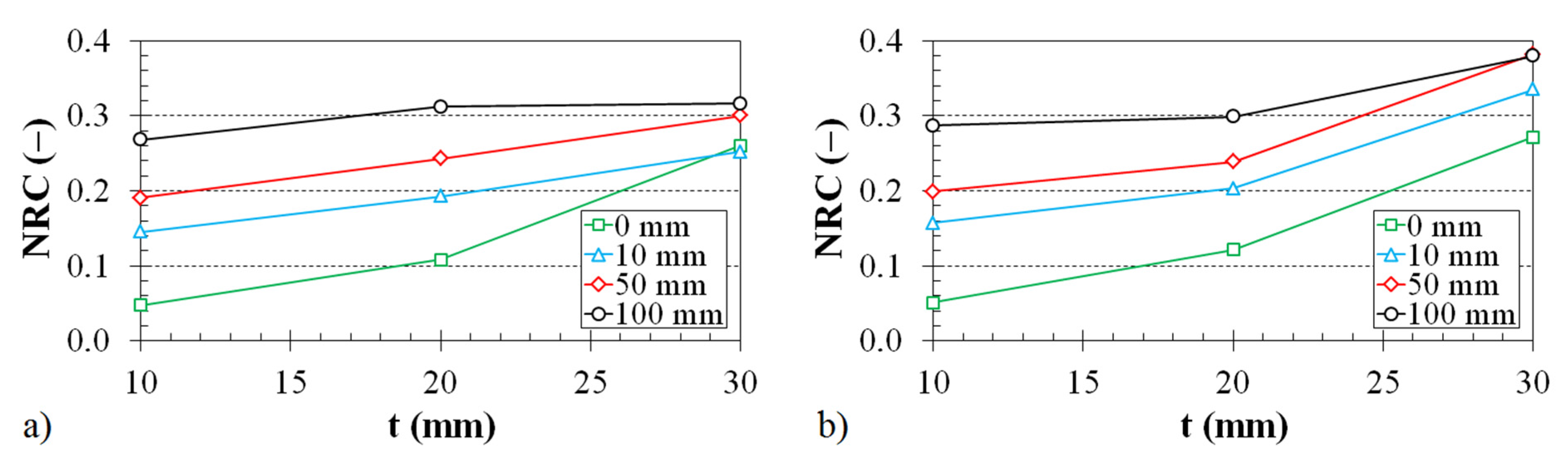
3.2. Noise Reduction Coefficient
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, W.D.; Li, Y. Sound absorption performance of natural fibers and their composites. Sci. China Technol. Sci. 2012, 55, 2278–2283. [Google Scholar] [CrossRef]
- Gan, W.S.; Kuo, S.M. An integrated audio and active noise control headsets. IEEE Trans. Consum. Electron. 2002, 48, 242–247. [Google Scholar] [CrossRef]
- Luo, L.; Sun, J.W.; Huang, B.Y. A novel feedback active noise control for broadband chaotic noise and random noise. Appl. Acoust. 2017, 116, 229–237. [Google Scholar] [CrossRef]
- Chang, C.Y. Simple Approaches to Improve the Performance of Noise Cancellation. JVC/J. Vib. Control 2009, 15, 1875–1883. [Google Scholar] [CrossRef]
- Kuo, S.M.; Mitra, S.; Gan, W.S. Active Noise control System for Headphone Applications. IEEE Trans. Control Syst. Technol. 2006, 14, 331–335. [Google Scholar] [CrossRef]
- Chang, C.Y. Efficient active noise controller using a fixed-point DSP. Signal Process. 2009, 89, 843–850. [Google Scholar] [CrossRef]
- Utsuno, H.; Tanaka, T.; Fujikawa, T.; Seibert, A.F. Transfer-function method for measuring characteristic impedance and propagation constant of porous materials. J. Acoust. Soc. Am. 1989, 86, 637–643. [Google Scholar] [CrossRef]
- Fakrul, M.; Che, S.; Putra, A.; Kassim, D.H.; Alkahari, M.R. 3D-printed lattice structure as sound absorber. Proc. Mech. Eng. Res. Day 2019, 2019, 287–288. [Google Scholar]
- Sim, S.; Kwon, O.M.; Ahn, K.H.; Lee, H.R.; Kang, Y.J.; Cho, E.B. Preparation of polycarbonate/poly(acrylonitrile-butadiene-styrene)/mesoporous silica nanocomposite films and its rheological, mechanical, and sound absorption properties. J. Appl. Polym. Sci. 2018, 135, 1–14. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Daynes, S.; Zhang, H.; Feih, S.; Wang, M.Y. Design of graded lattice structure with optimized mesostructures for additive manufacturing. Mater. Des. 2018, 142, 114–123. [Google Scholar] [CrossRef]
- Cao, L.; Fu, Q.; Si, Y.; Ding, B.; Yu, J. Porous materials for sound absorption. Compos. Commun. 2018, 10, 25–35. [Google Scholar] [CrossRef]
- Gulia, P.; Gupta, A. Sound attenuation in triple panel using locally resonant sonic crystal and porous material. Appl. Acoust. 2019, 156, 113–119. [Google Scholar] [CrossRef]
- Yoon, W.U.; Park, J.H.; Lee, J.S.; Kim, Y.Y. Topology optimization design for total sound absorption in porous media. Comput. Methods Appl. Mech. Eng. 2020, 360, 112723. [Google Scholar] [CrossRef]
- Rosli, N.A.; Hasan, R.; Alkahari, M.R.; Tokoroyama, T. Effect of process parameters on the geometrical quality of ABS polymer lattice structure. Proc. SAKURA Symp. Mech. Sci. Eng. 2017, 2017, 3–5. [Google Scholar]
- Kim, B.S.; Kwon, S.; Jeong, S.; Park, J. Semi-active control of smart porous structure for sound absorption enhancement. J. Intell. Mater. Syst. Struct. 2019, 30, 2575–2580. [Google Scholar] [CrossRef]
- Jimbo, K.; Tateno, T. Design of isotropic-tensile-strength lattice structure fabricated by AMAMによる製作を想定した引張強度に関して等方性を有する格子構造の設計. Trans. JSME 2019, 85, 18-00098. (In Japanese) [Google Scholar]
- Salomons, E.M.; Lohman, W.J.A.; Zhou, H. Simulation of sound waves using the lattice Boltzmann method for fluid flow: Benchmark cases for outdoor sound propagation. PLoS ONE 2016, 11, e0147206. [Google Scholar] [CrossRef]
- Zvolensky, P.; Grencik, J.; Kasiar, L.; Stuchly, V. Simulation of sound transmission through the porous material, determining the parameters of acoustic absorption and sound reduction. MATEC Web Conf. 2018, 157, 2058. [Google Scholar] [CrossRef]
- Chen, M.; Jiang, H.; Zhang, H.; Li, D.; Wang, Y. Design of an acoustic superlens using single-phase metamaterials with a star-shaped lattice structure. Sci. Rep. 2018, 8, 2–9. [Google Scholar] [CrossRef]
- Stansbury, J.W.; Idacavage, M.J. 3D printing with polymers: Challenges among expanding options and opportunities. Dent. Mater. 2016, 32, 54. [Google Scholar] [CrossRef]
- Bourell, D.; Pierre, J.; Leu, M.; Levy, G.; Rosen, D.; Beese, A.M.; Clare, A. Materials for additive manufacturing. CIRP Ann. 2017, 66, 659–681. [Google Scholar] [CrossRef]
- Pantazopoulos, G.A. A Short Review on Fracture Mechanisms of Mechanical Components Operated under Industrial Process Conditions: Fractographic Analysis and Selected Prevention Strategies. Metals 2019, 9, 148. [Google Scholar] [CrossRef]
- Brenne, F.; Niendorf, T.; Maier, H.J. Additively manufactured cellular structures: Impact of microstructure and local strains on the monotonic and cyclic behavior under uniaxial and bending load. J. Mater. Process. Technol. 2013, 213, 1558–1564. [Google Scholar] [CrossRef]
- Koizumi, T.; Tsujiuchi, N.; Adachi, A. The development of sound absorbing materials using natural bamboo fibers. High Perform. Struct. Mater. 2002, 4, 157–166. [Google Scholar]
- Borlea, A.; Rusu, T.; Ionescu, S.; Cretu, M.; Innescu, A. Acoustical materials—Sound absoring materials made of pine sawdust. Rom. J. Acoust. Vib. 2011, 8, 95–98. [Google Scholar]
- Tiwari, W.; Shukla, A.; Bose, A. Acoustic properties of cenosphere reinforced cement and asphalt concrete. Appl. Acoust. 2004, 65, 263–275. [Google Scholar] [CrossRef]
- Buratti, C. Indoor noise reduction index with an open window (Part II). Appl. Acoust. 2006, 67, 383–401. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 10534-2, Acoustics-Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes-Part 2: Transfer-Function Method; ISO/TC 43/SC2 Building Acoustics; CEN, European Committee for Standardization: Brussels, Belgium, 1998; pp. 10534–10542. [Google Scholar]
- Han, F.S.; Seiffert, G.; Zhao, Y.Y.; Gibbs, B. Acoustic absorption behaviour of an open-celled alluminium foam. J. Phys. D Appl. Phys. 2003, 36, 294–302. [Google Scholar] [CrossRef]
- Cheerier, O.; Pommier-Budinger, V.; Simon, F. Panel of resonators with variable resonance frequency for noise control. Appl. Acoust. 2012, 73, 781–790. [Google Scholar] [CrossRef]
- Doutres, O.; Atalla, N.; Dong, K. Effect of the microstructure closed pore content on the acoustic behavior of polyurethane foams. J. Appl. Phys. 2011, 110, 064901. [Google Scholar] [CrossRef]
- Zhai, W.; Yu, X.; Song, X.; Ang, L.Y.L.; Cui, F.; Lee, H.P.; Li, T. Microstructure-based experimental and numerical investigations on the sound absorption property of open-cell metallic foams manufactured by a template replication technique. Mater. Des. 2018, 137, 108–116. [Google Scholar] [CrossRef]
- Baich, L.; Monogharan, G.; Marie, H. Study of infill print design on production cost-time of 3D printed ABS parts. Int. J. Rapid Manuf. 2015, 5, 308–319. [Google Scholar] [CrossRef]
- Derossi, A.; Caporizzi, R.; Azzollini, D.; Severini, C. Application of 3D printing for customized food. A case on the development of a fruit-based snack for children. J. Food Eng. 2018, 220, 65–75. [Google Scholar] [CrossRef]
- Everest, F.A. Absorption of sound. In Master Handbook of Acoustics, 4th ed.; McGraw-Hill: New York, NY, USA, 2001; pp. 179–233. [Google Scholar]
- Lim, Z.Y.; Putra, A.; Nor, M.J.M.; Yaakob, M.Y. Sound absorption performance of natural kenaf fibres. Appl. Acoust. 2018, 130, 107–114. [Google Scholar] [CrossRef]
- Putra, A.; Or, K.H.; Selamat, M.Z.; Nor, M.J.M.; Hassan, M.H.; Prasetiyo, I. Sound absorption of extracted pineapple-leaf fibres. Appl. Acoust. 2018, 136, 9–15. [Google Scholar] [CrossRef]



| Structure Type | Volume ratio (%) | Label | Front View | Strut Diameter | Cell Sizes (mm) |
|---|---|---|---|---|---|
| Cartesian | 57 | C_57 |  | 1.4 | x = 5 |
| y = 5 | |||||
| z = 5 | |||||
| Starlit | 57 | S_57 |  | 1.4 | x = 9 |
| y = 9 | |||||
| z = 5 | |||||
| Octagonal | 57 | O_57 |  | 1.4 | x = 7 |
| y = 7 | |||||
| z = 5 |
| Structure Type | t (mm) | a (mm) | fmax1 (Hz) | αmax1 (−) | fmin1 (Hz) | αmin1 (−) |
|---|---|---|---|---|---|---|
| Cartesian | 30 | 0 | 2096 | 0.76 | 4184 | 0.25 |
| 10 | 1304 | 0.73 | 3000 | 0.23 | ||
| 50 | 656 | 0.63 | 1864 | 0.22 | ||
| 100 | 432 | 0.55 | 1136 | 0.17 | ||
| Starlit | 10 | 0 | 5328 | 0.81 | - | - |
| 10 | 2064 | 0.71 | 5912 | 0.15 | ||
| 50 | 904 | 0.55 | 2992 | 0.08 | ||
| 100 | 552 | 0.48 | 1312 | 0.09 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasina, M.; Monkova, K.; Monka, P.P.; Kozak, D.; Tkac, J. Study of the Sound Absorption Properties of 3D-Printed Open-Porous ABS Material Structures. Polymers 2020, 12, 1062. https://doi.org/10.3390/polym12051062
Vasina M, Monkova K, Monka PP, Kozak D, Tkac J. Study of the Sound Absorption Properties of 3D-Printed Open-Porous ABS Material Structures. Polymers. 2020; 12(5):1062. https://doi.org/10.3390/polym12051062
Chicago/Turabian StyleVasina, Martin, Katarina Monkova, Peter Pavol Monka, Drazan Kozak, and Jozef Tkac. 2020. "Study of the Sound Absorption Properties of 3D-Printed Open-Porous ABS Material Structures" Polymers 12, no. 5: 1062. https://doi.org/10.3390/polym12051062
APA StyleVasina, M., Monkova, K., Monka, P. P., Kozak, D., & Tkac, J. (2020). Study of the Sound Absorption Properties of 3D-Printed Open-Porous ABS Material Structures. Polymers, 12(5), 1062. https://doi.org/10.3390/polym12051062










