A Sacrificial Route for Soft Porous Polymers Synthesized via Frontal Photo-Polymerization
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Photo-Polymerization
2.3. Microfluidics and Soft-Embossing
3. Results
3.1. Optimized Formulation
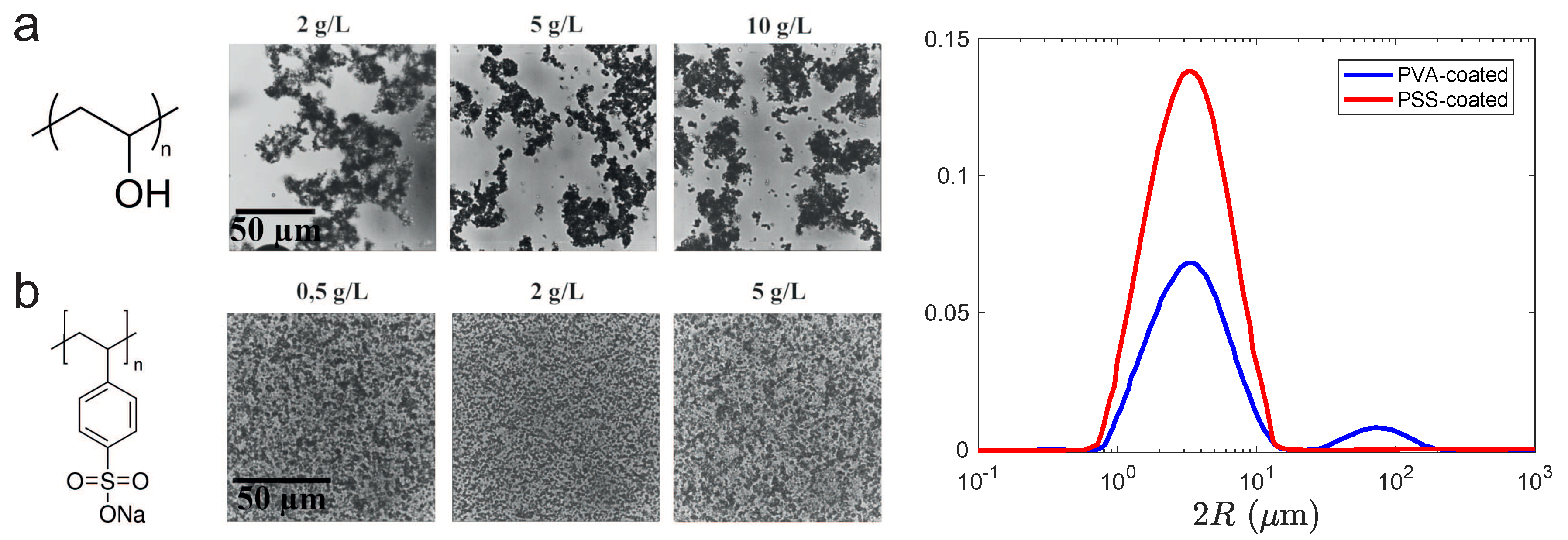
3.2. Preparation and Characterization of Porous Polymeric Monoliths
3.2.1. Frontal Photo-Polymerization in the Presence of Calcite
3.2.2. Characterization of Soft Porous Polymer
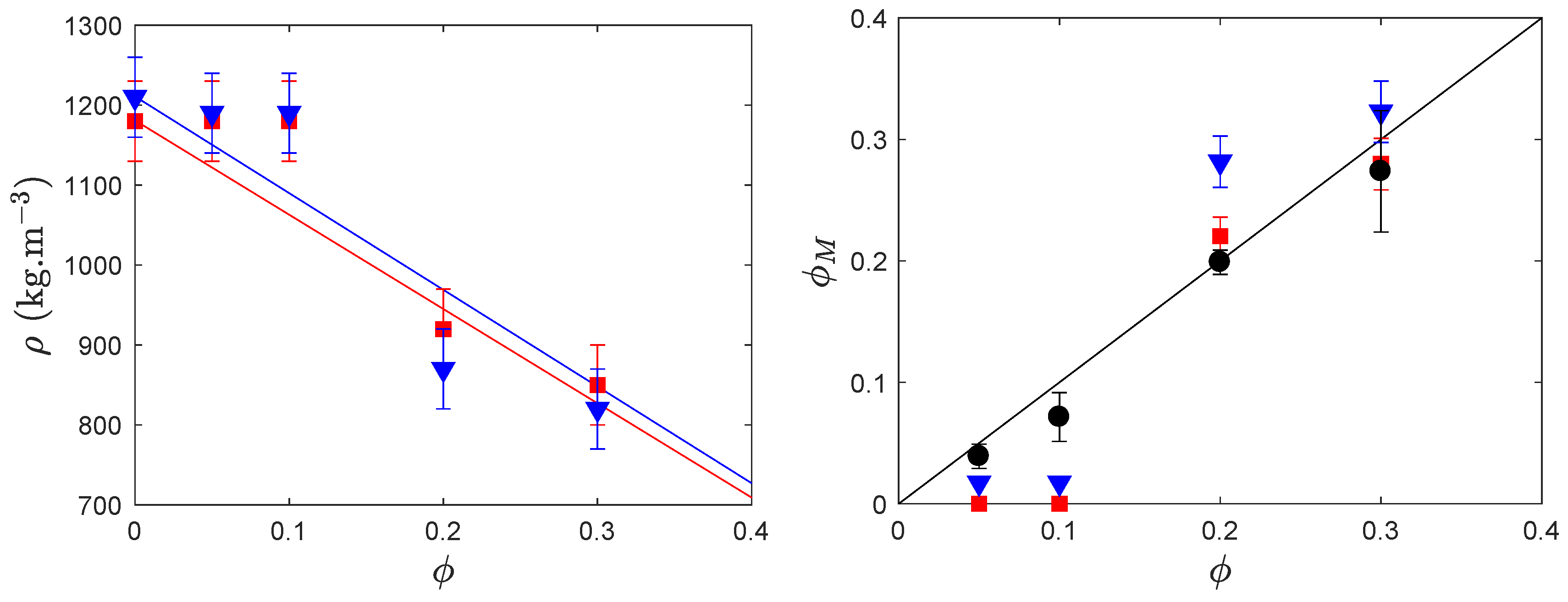
3.2.2.1. Porosity Measured by Density Measurements
3.2.2.2. Porosity Measured by Image Analysis
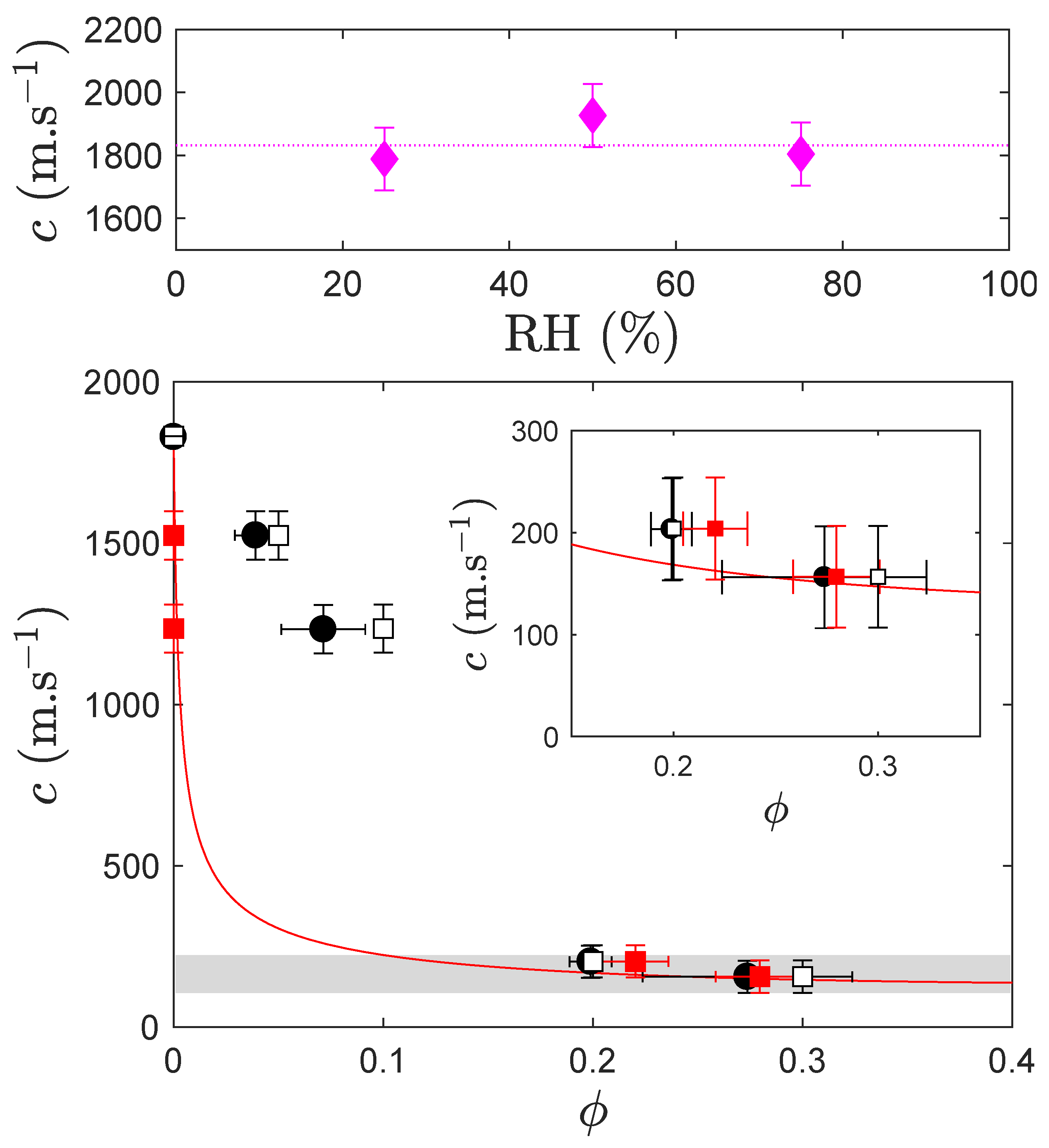
3.2.2.3. Porosity and Sound Speed
4. Advanced Material Forming
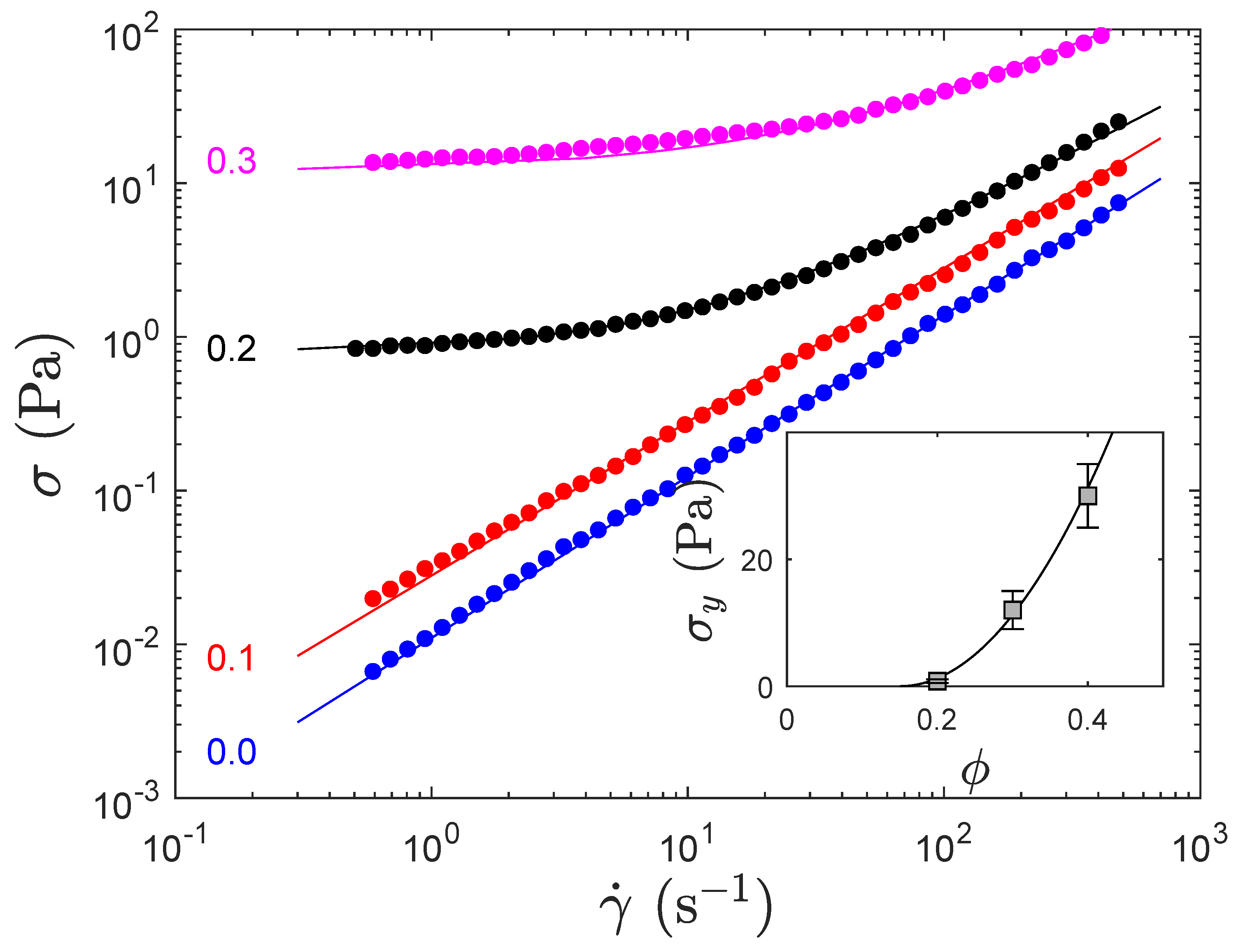
4.1. Porous Particles out of Emulsions
4.1.1. Batch Emulsions
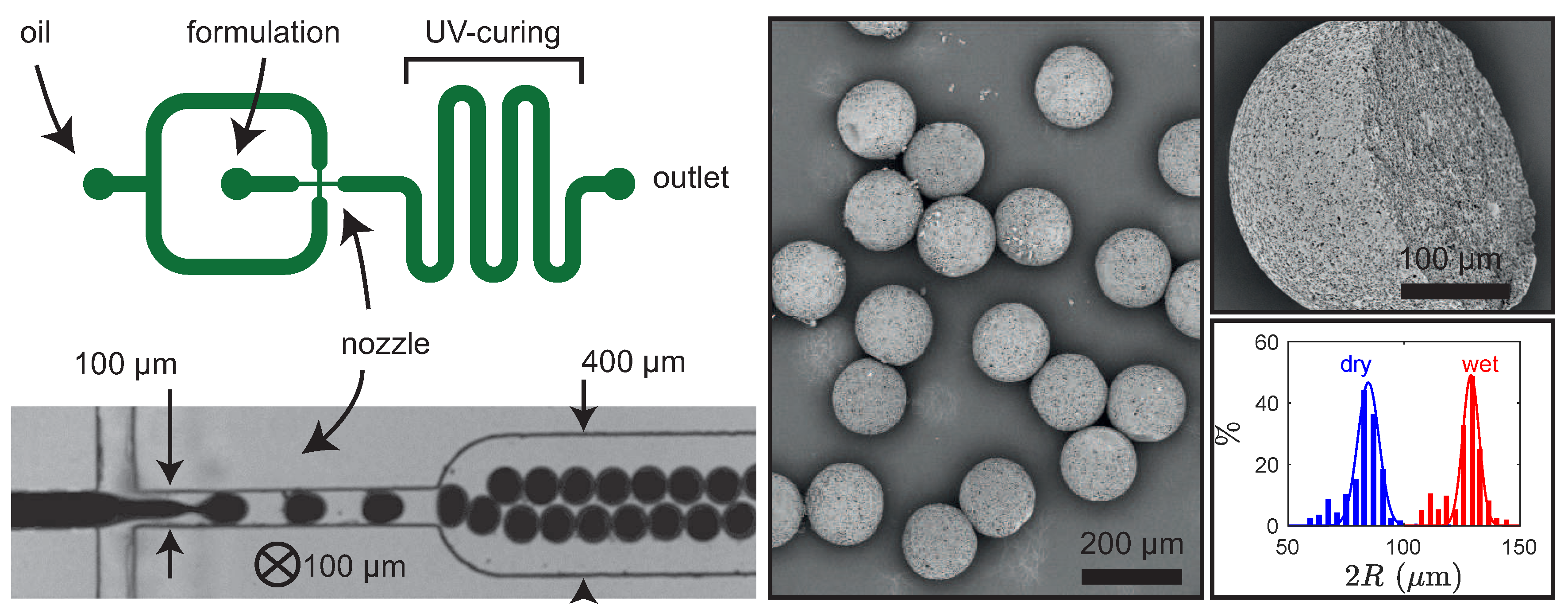
4.1.2. Microfluidic Engineered Emulsions
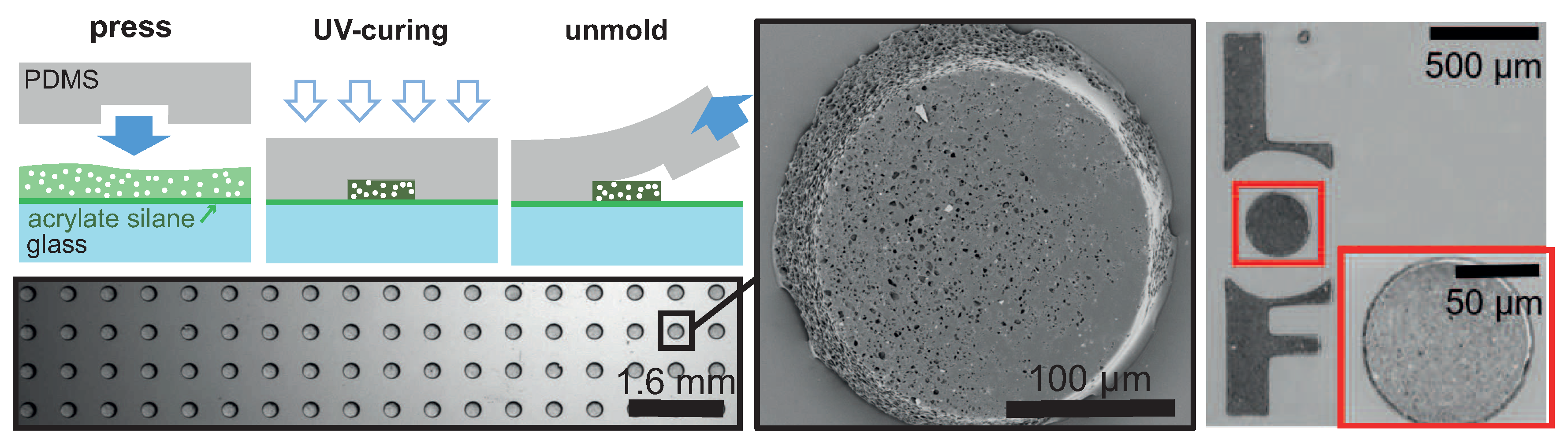
4.2. Soft Embossing
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Okay, O. Macroporous copolymer networks. Prog. Polym. Sci. 2000, 25, 711–779. [Google Scholar] [CrossRef]
- Gama, N.V.; Ferreira, A.; Barros-Timmons, A. Polyurethane foams: Past, present, and future. Materials 2018, 11, 1841. [Google Scholar] [CrossRef] [PubMed]
- Silverstein, M.S. PolyHIPEs: Recent advances in emulsion-templated porous polymers. Prog. Polym. Sci. 2014, 39, 199–234. [Google Scholar] [CrossRef]
- Turani-i Belloto, A.; Meunier, N.; Lopez, P.; Leng, J. Diffusion-limited dissolution of calcium carbonate in a hydrogel. Soft Matter 2019, 15, 2942–2949. [Google Scholar] [CrossRef]
- Gokmen, M.T.; Du Prez, F.E. Porous polymer particles—A comprehensive guide to synthesis, characterization, functionalization and applications. Prog. Polym. Sci. 2012, 37, 365–405. [Google Scholar] [CrossRef]
- Chung, B.G.; Lee, K.H.; Khademhosseini, A.; Lee, S.H. Microfluidic fabrication of microengineered hydrogels and their application in tissue engineering. Lab Chip 2012, 12, 45–59. [Google Scholar] [CrossRef]
- Truby, R.L.; Lewis, J.A. Printing soft matter in three dimensions. Nature 2016, 540, 371–378. [Google Scholar] [CrossRef]
- Wang, C.; He, C.; Tong, Z.; Liu, X.; Ren, B.; Zeng, F. Combination of adsorption by porous CaCO3 microparticles and encapsulation by polyelectrolyte multilayer films for sustained drug delivery. Int. J. Pharm. 2006, 308, 160–167. [Google Scholar] [CrossRef]
- Yi, J.; Wangcai, L.; Jiarong, W.; Jianghua, F.; Haoqi, G. (Protamine/dextran sulfate) microcapules templated on biocompatible calcium carbonate microspheres. Colloids Surf. A Physicochem. Eng. Asp. 2009, 342, 40–45. [Google Scholar]
- Kim, H.M.; Noh, Y.J.; Yu, J.; Kim, S.Y.; Youn, J.R. Silica aerogel/polyvinyl alcohol (PVA) insulation composites with preserved aerogel pores using interfaces between the superhydrophobic aerogel and hydrophilic PVA solution. Compos. Part A Appl. Sci. Manuf. 2015, 75, 39. [Google Scholar] [CrossRef]
- Vitale, A.; Hennessy, M.G.; Matar, O.K.; Cabral, J.T. A Unified Approach for Patterning via Frontal Photopolymerization. Adv. Mater. 2015, 27, 6118–6124. [Google Scholar] [CrossRef] [PubMed]
- Kynch, G.J. A Theory of Sedimentation. Trans. Faraday Soc. 1952, 48, 166–176. [Google Scholar] [CrossRef]
- Dendukuri, D.; Panda, P.; Haghgooie, R.; Kim, J.M.; Hatton, T.A.; Doyle, P.S. Modeling of oxygen-inhibited free radical photopolymerization in a PDMS microfluidic device. Macromolecules 2008, 41, 8547–8556. [Google Scholar] [CrossRef]
- Halloran, J.W.; Tomeckova, V.; Gentry, S.; Das, S.; Cilino, P.; Yuan, D.; Guo, R.; Rudraraju, A.; Shao, P.; Wu, T.; et al. Photopolymerization of powder suspensions for shaping ceramics. J. Eur. Ceram. Soc. 2011, 31, 2613–2619. [Google Scholar] [CrossRef]
- Dendukuri, D.; Doyle, P.S. The Synthesis and Assembly of Polymeric Microparticles Using Microfluidics. Adv. Mater. 2009, 21, 4071–4086. [Google Scholar] [CrossRef]
- Cabral, J.T.; Hudson, S.D.; Harrison, C.; Douglas, J.F. Frontal photopolymerization for microfluidic applications. Langmuir 2004, 20, 10020–10029. [Google Scholar] [CrossRef]
- Vitale, A.; Hennessy, M.G.; Matar, O.K.; Cabral, J.T. Interfacial profile and propagation of frontal photopolymerization waves. Macromolecules 2015, 48, 198–205. [Google Scholar] [CrossRef]
- Wu, K.C.; Seefeldt, K.F.; Solomon, M.J.; Halloran, J.W. Prediction of ceramic stereolithography resin sensitivity from theory and measurement of diffusive photon transport. J. Appl. Phys. 2005, 98, 0249902. [Google Scholar] [CrossRef]
- Chartier, T.; Dupas, C.; Lasgorceix, M.; Brie, J.; Champion, E.; Delhote, N.; Chaput, C. Additive Manufacturing to Produce Complex 3D Ceramic Parts. J. Ceram. Sci. Technol. 2015, 6, 95–104. [Google Scholar]
- Griffith, M.L.; Halloran, J.W. Scattering of Ultraviolet Radiation in Turbid Suspensions. J. Appl. Phys. 1997, 81, 2538–2546. [Google Scholar] [CrossRef]
- Kovalenko, A.; Fauquignon, M.; Brunet, T.; Mondain-Monval, O. Tuning the sound speed in macroporous polymers with a hard or soft matrix. Soft Matter 2017, 13, 4526–4532. [Google Scholar] [CrossRef] [PubMed]
- Zimny, K.; Merlin, A.; Ba, A.; Aristégui, C.; Brunet, T.; Mondain-Monval, O. Soft Porous Silicone Rubbers as Key Elements for the Realization of Acoustic Metamaterials. Langmuir 2015, 31, 3215–3221. [Google Scholar] [CrossRef] [PubMed]
- Kovalenko, A.; Zimny, K.; Mascaro, B.; Brunet, T.; Mondain-Monval, O. Tailoring of the porous structure of soft emulsion-templated polymer materials. Soft Matter 2016, 12, 5154–5163. [Google Scholar] [CrossRef] [PubMed]
- Ba, A.; Kovalenko, A.; Aristégui, C.; Mondain-Monval, O.; Brunet, T. Soft porous silicone rubbers with ultra-low sound speeds in acoustic metamaterials. Sci. Rep. 2017, 7, 40106. [Google Scholar] [CrossRef] [PubMed]
- Mason, T.G.; Bibette, J. Emulsification in Viscoelastic Media. Phys. Rev. Lett. 1996, 77, 3481–3484. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Howes, P.; deMello, A. Recent Advances in Droplet Microfluidics. Anal. Chem. 2020, 92, 132–149. [Google Scholar] [CrossRef]
- Daly, A.C.; Riley, L.; Segura, T.; Burdick, J.A. Hydrogel microparticles for biomedical applications. Nat. Rev. Mater. 2020, 5, 20–43. [Google Scholar] [CrossRef]
- Liang, D.Y.; Tentori, A.M.; Dimov, I.K.; Lee, L.P. Systematic characterization of degas-driven flow for poly(dimethylsiloxane) microfluidic devices. Biomicrofluidics 2011, 5, 024108. [Google Scholar] [CrossRef]
- Leroy, V.; Strybulevych, A.; Lanoy, M.; Lemoult, F.; Tourin, A.; Page, J.H. Superabsorption of acoustic waves with bubble metascreens. Phys. Rev. B 2015, 91, 020301(R). [Google Scholar] [CrossRef]
- Gkantzounis, G.; Amoah, T.; Florescu, M. Hyperuniform disordered phononic structures. Phys. Rev. B 2017, 95, 094120. [Google Scholar] [CrossRef]
- Jin, Y.; Kumar, R.; Poncelet, O.; Mondain-Monval, O.; Brunet, T. Flat acoustics with soft gradient-index metasurfaces. Nat. Commun. 2019, 10, 143. [Google Scholar] [CrossRef]
- Brunet, T.; Leng, J.; Mondain-Monval, O. Soft acoustic metamaterials. Science 2013, 342, 323–324. [Google Scholar] [CrossRef]
- Brunet, T.; Merlin, A.; Mascaro, B.; Zimny, K.; Leng, J.; Poncelet, O.; Aristégui, C.; Mondain-Monval, O. Soft 3D acoustic metamaterial with negative index. Nat. Mater. 2014, 14, 1–5. [Google Scholar] [CrossRef]
- Raffy, S.; Mascaro, B.; Brunet, T.; Mondain-Monval, O.; Leng, J. A Soft 3D Acoustic Metafluid with Dual-Band Negative Refractive Index. Adv. Mater. 2016, 28, 1760–1764. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Vijayavenkataraman, S.; Lu, W.F.; Fuh, J.Y. A review on the use of computational methods to characterize, design, and optimize tissue engineering scaffolds, with a potential in 3D printing fabrication. J. Biomed. Mater. Res. Part B Appl. Biomater. 2019, 107, 1329–1351. [Google Scholar] [CrossRef] [PubMed]
- Choi, A.; Seo, K.D.; Kim, D.W.; Kim, B.C.; Kim, D.S. Recent advances in engineering microparticles and their nascent utilization in biomedical delivery and diagnostic applications. Lab Chip 2017, 17, 591–613. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Singh, A.K.; Shepodd, T.J.; Kirby, B.J. Microchip Dialysis of Proteins Using in Situ Photopatterned Nanoporous Polymer Membranes. Anal. Chem. 2004, 76, 2367–2373. [Google Scholar] [CrossRef]
- Decock, J.; Schlenk, M.; Salmon, J.-B. In situ photo-patterning of pressure-resistant hydrogel membranes with controlled permeabilities in PEGDA microfluidic channels. Lab Chip 2018, 18, 1075–1083. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turani-i-Belloto, A.; Brunet, T.; Khaldi, A.; Leng, J. A Sacrificial Route for Soft Porous Polymers Synthesized via Frontal Photo-Polymerization. Polymers 2020, 12, 1008. https://doi.org/10.3390/polym12051008
Turani-i-Belloto A, Brunet T, Khaldi A, Leng J. A Sacrificial Route for Soft Porous Polymers Synthesized via Frontal Photo-Polymerization. Polymers. 2020; 12(5):1008. https://doi.org/10.3390/polym12051008
Chicago/Turabian StyleTurani-i-Belloto, Alexandre, Thomas Brunet, Alexandre Khaldi, and Jacques Leng. 2020. "A Sacrificial Route for Soft Porous Polymers Synthesized via Frontal Photo-Polymerization" Polymers 12, no. 5: 1008. https://doi.org/10.3390/polym12051008
APA StyleTurani-i-Belloto, A., Brunet, T., Khaldi, A., & Leng, J. (2020). A Sacrificial Route for Soft Porous Polymers Synthesized via Frontal Photo-Polymerization. Polymers, 12(5), 1008. https://doi.org/10.3390/polym12051008







