Small and Medium Amplitude Oscillatory Shear Rheology of Model Branched Polystyrene (PS) Melts
Abstract
1. Introduction
2. Definition of MAOS Material Functions
3. Materials and Methods
3.1. Materials
3.2. Rheological Measurements
4. Results and Discussion
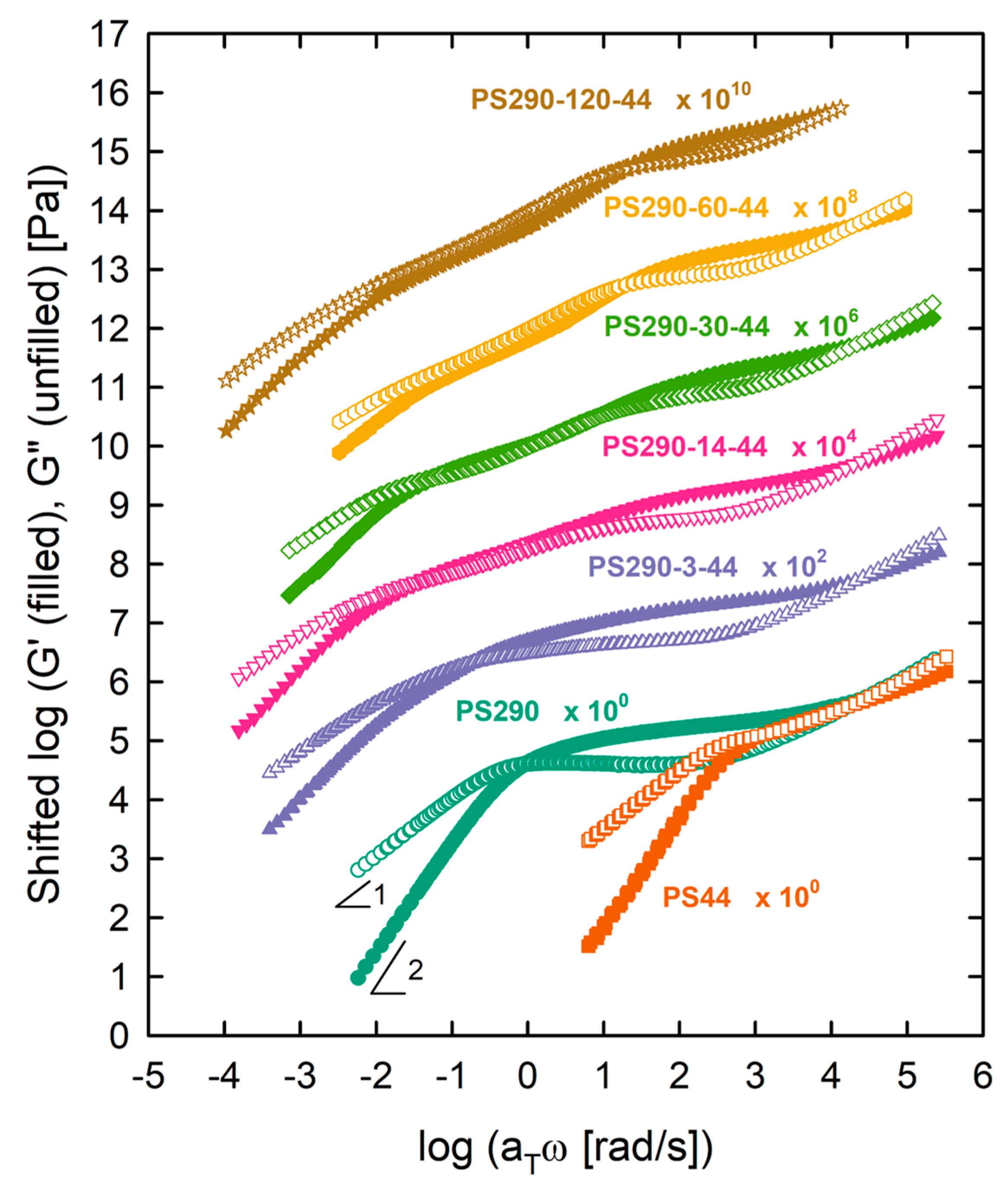
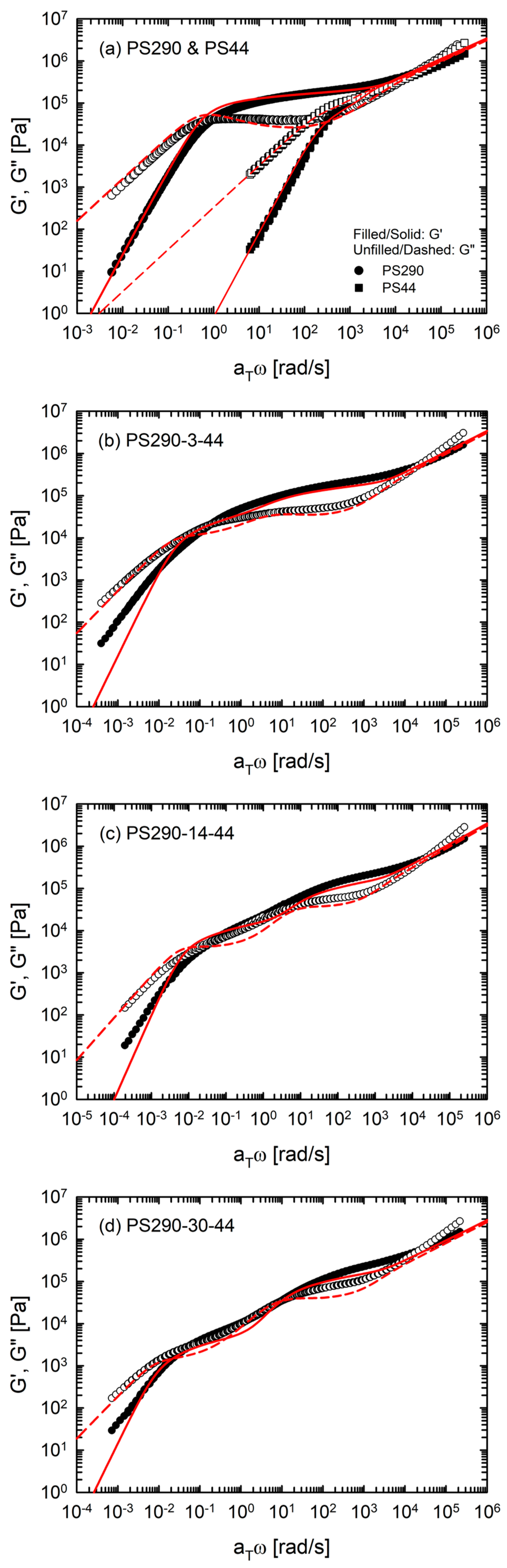
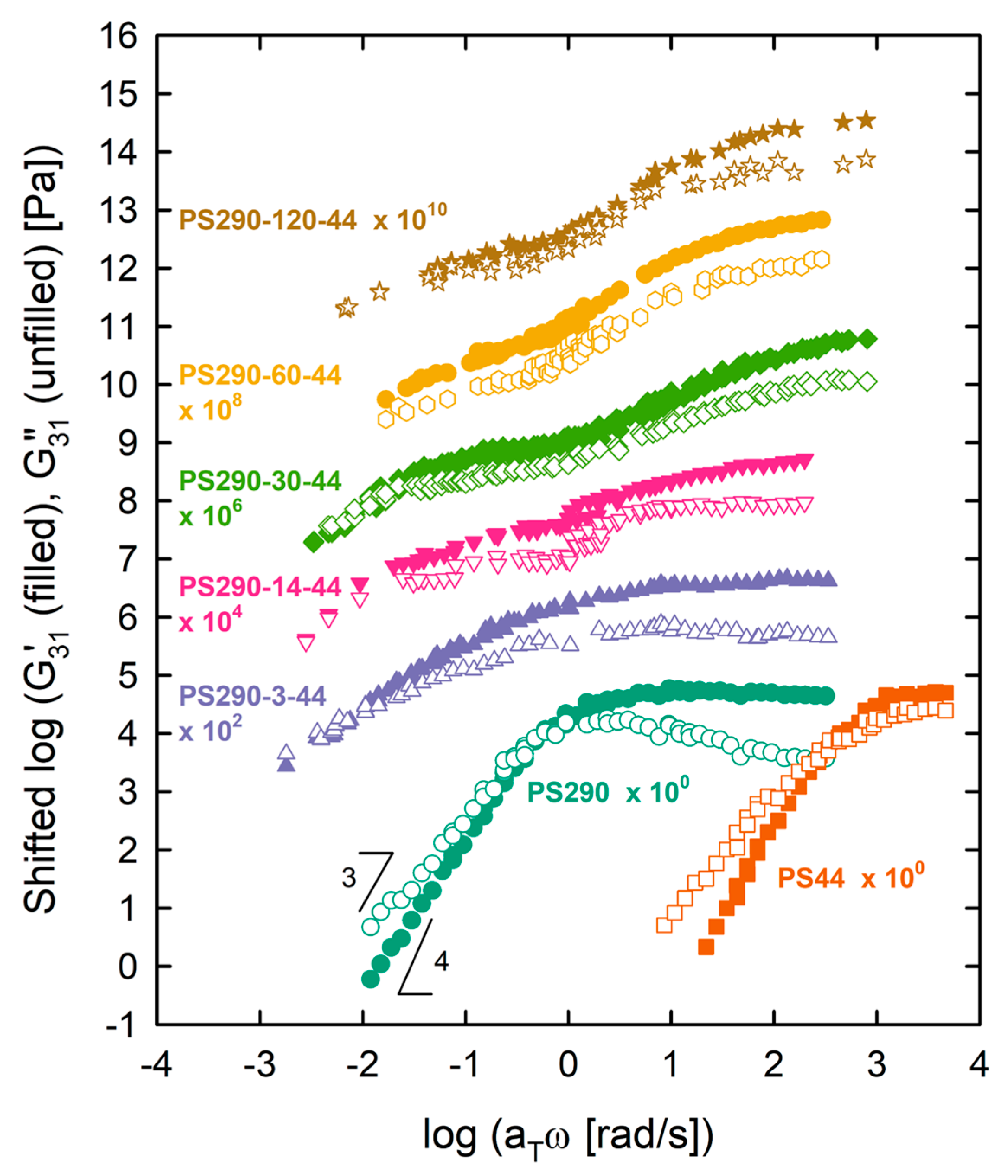
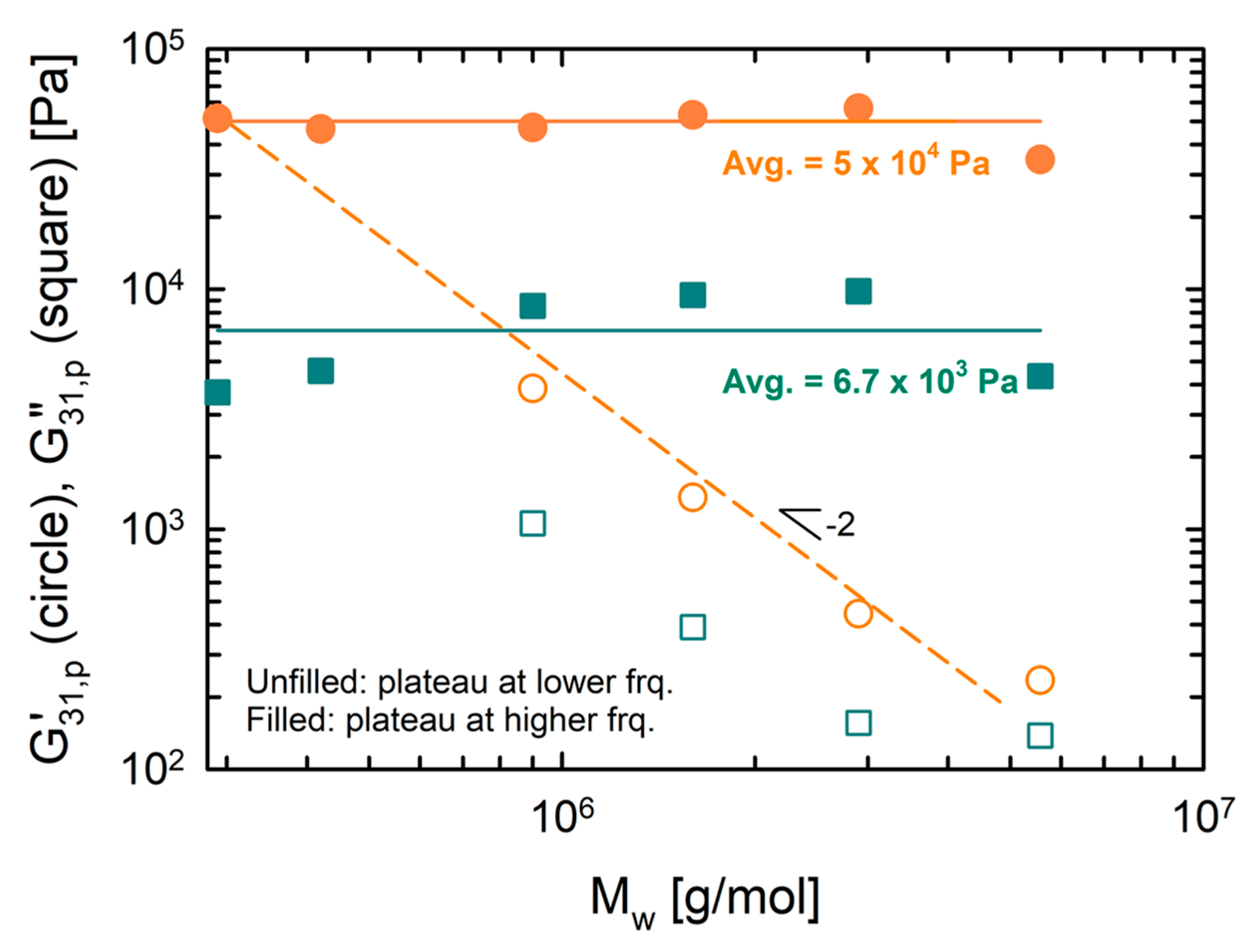
4.1. SAOS Results
4.2. Hierarchical Modeling
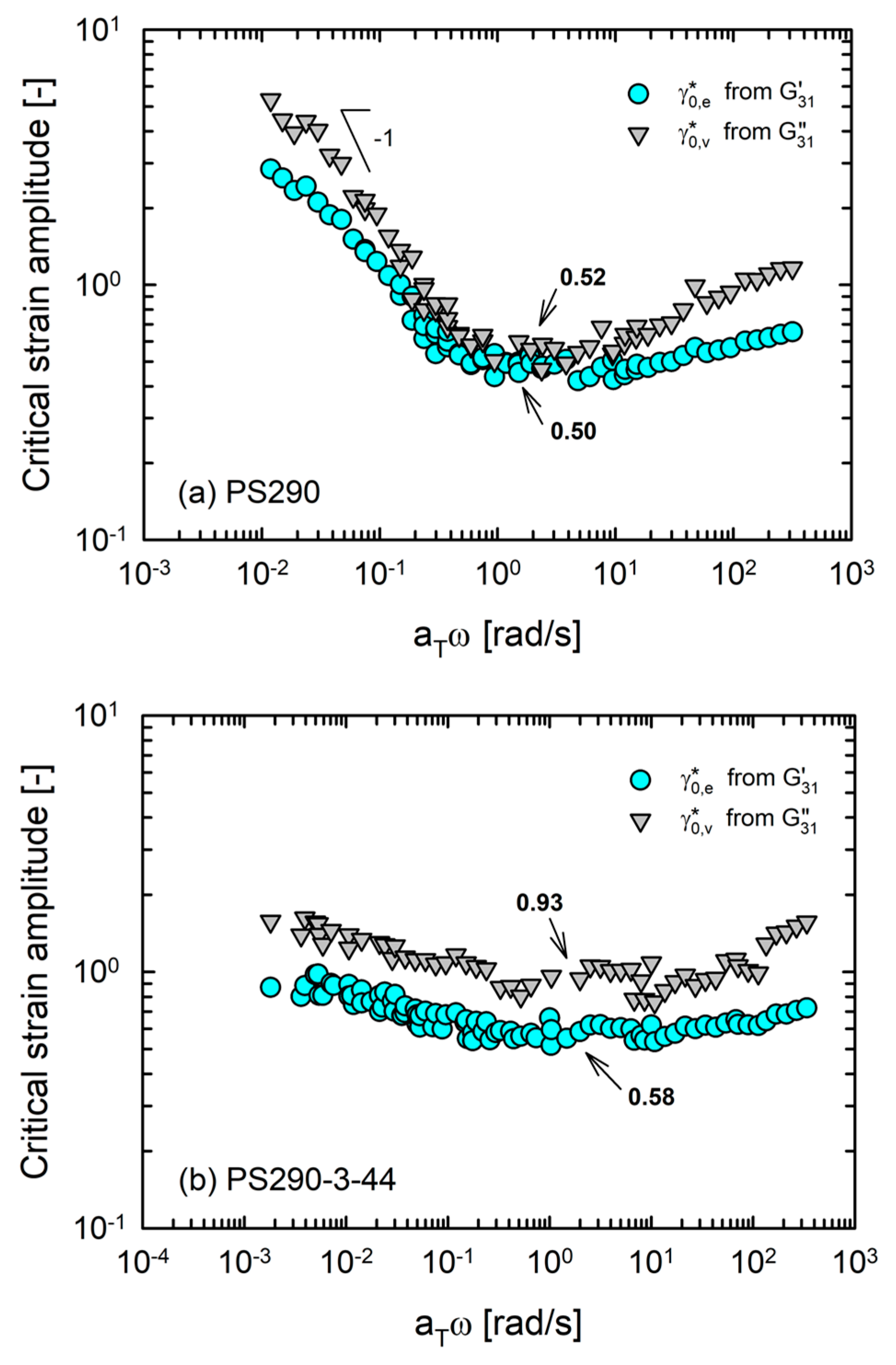
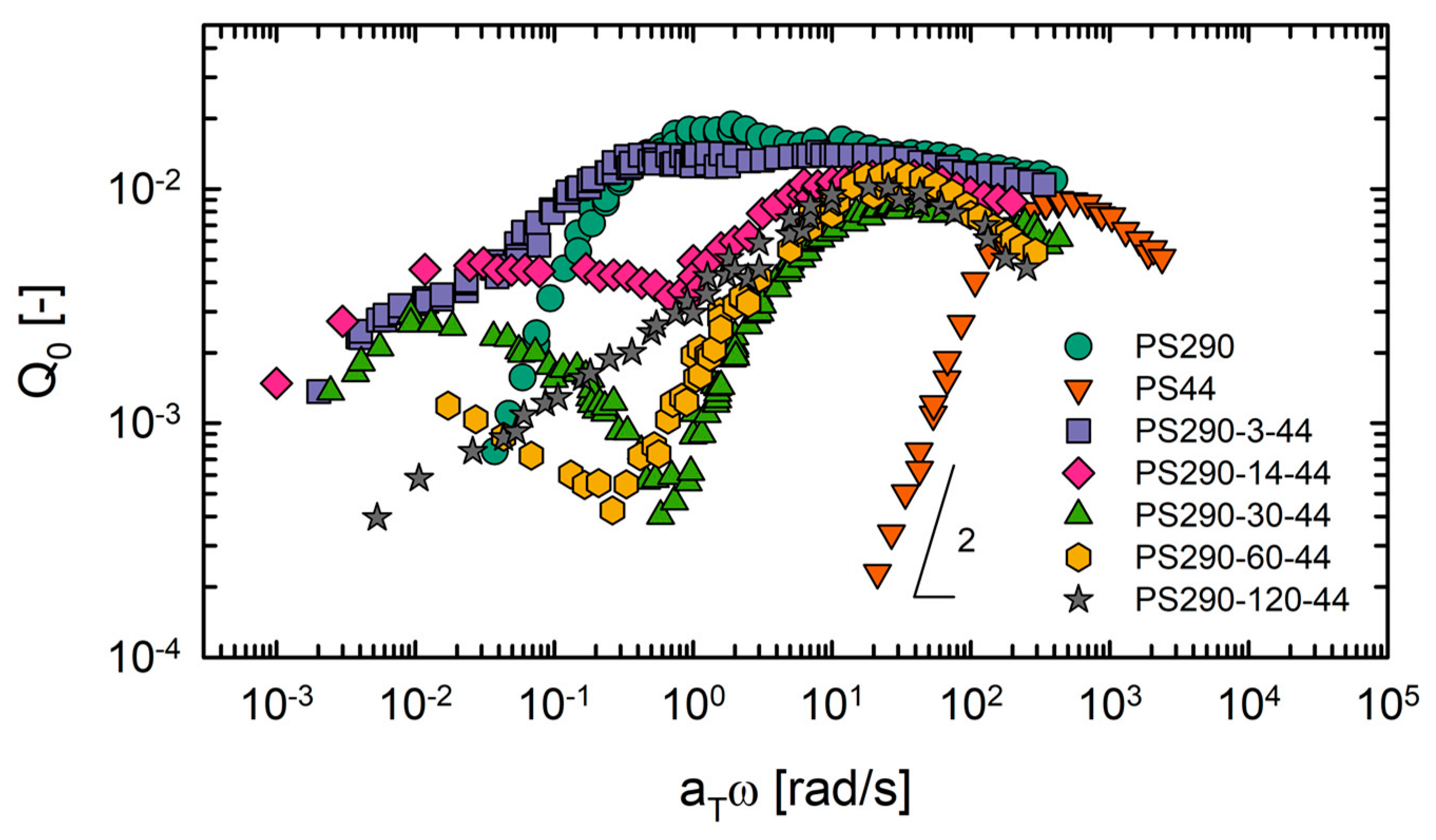
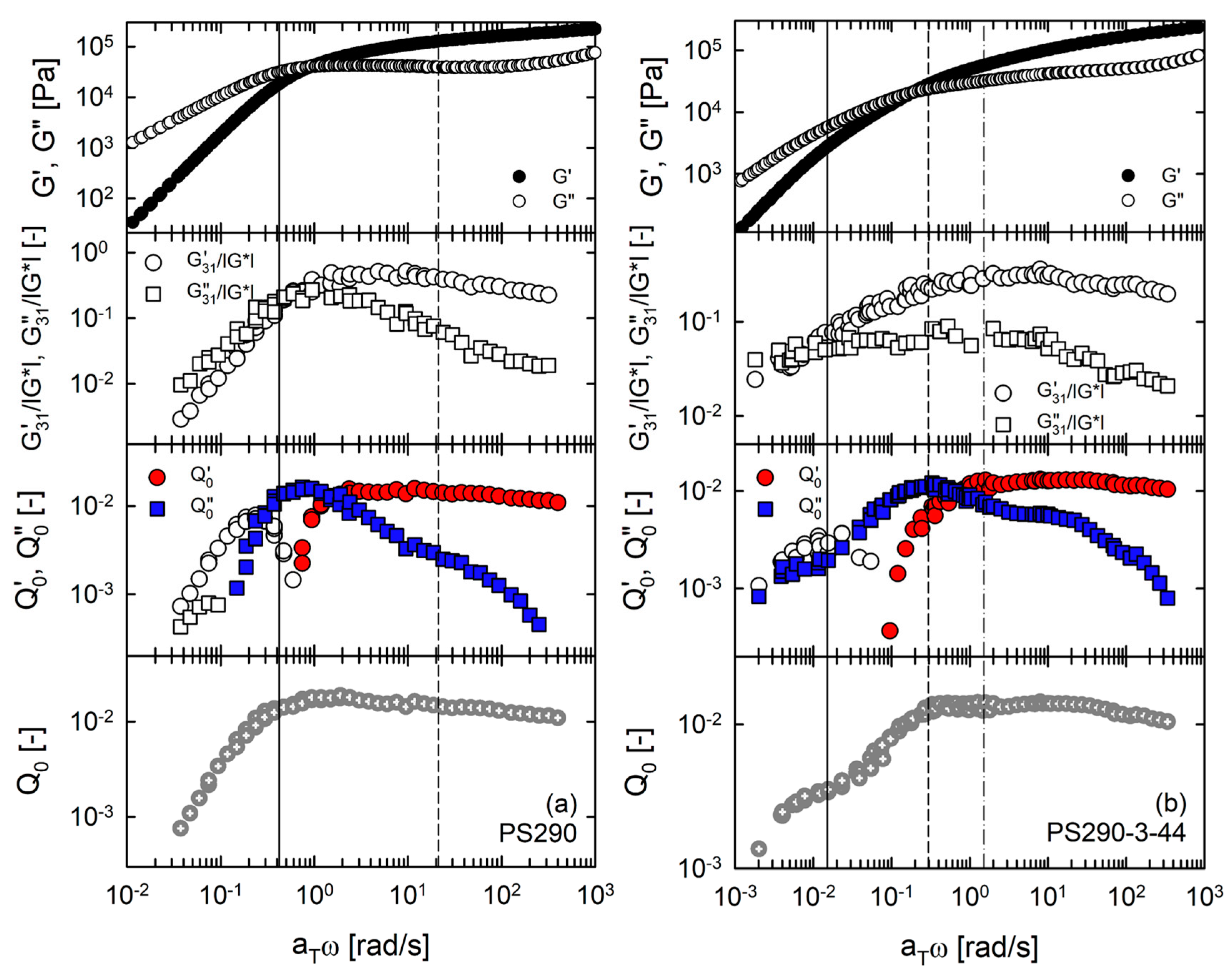
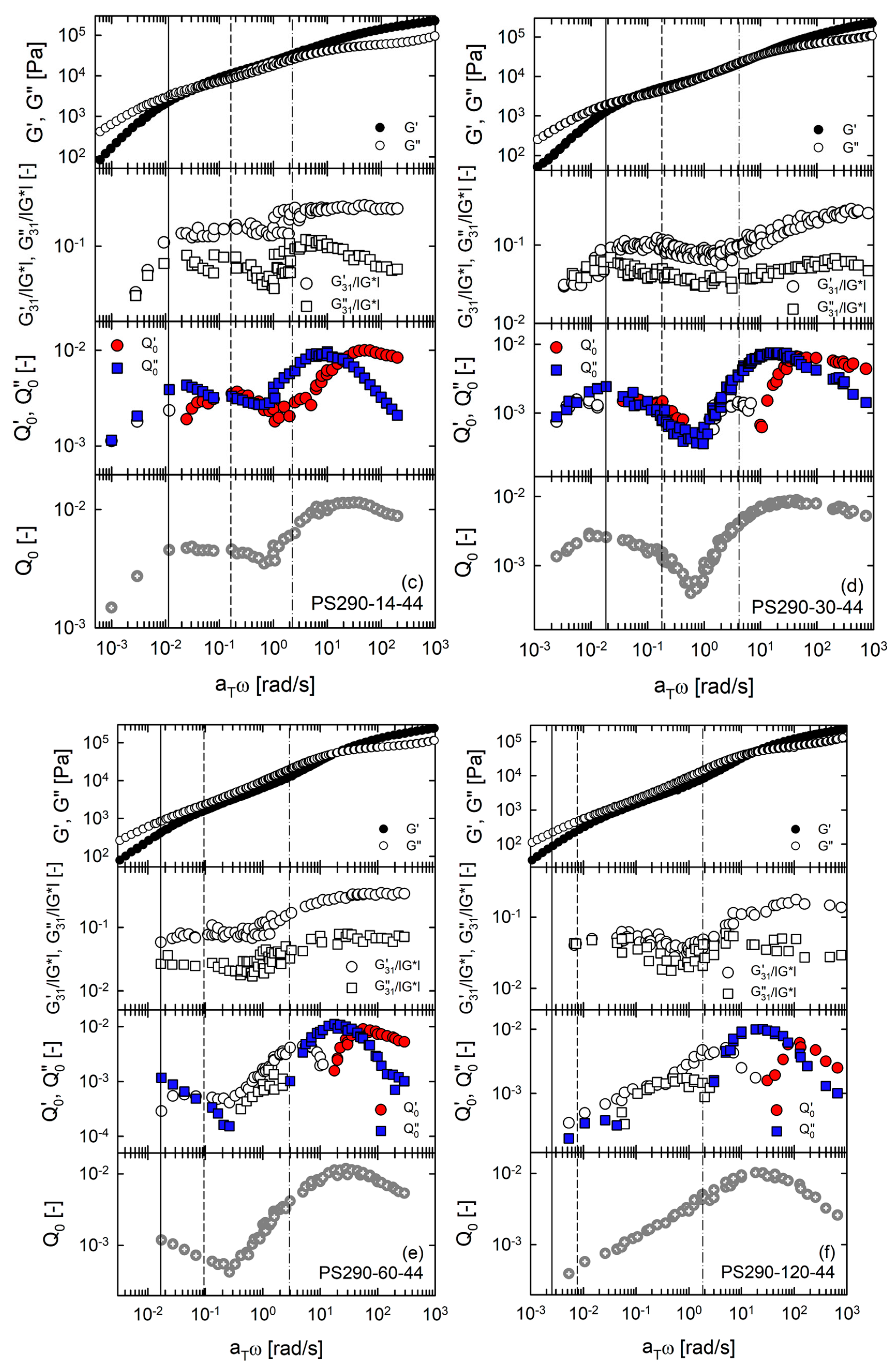
4.3. MAOS Results
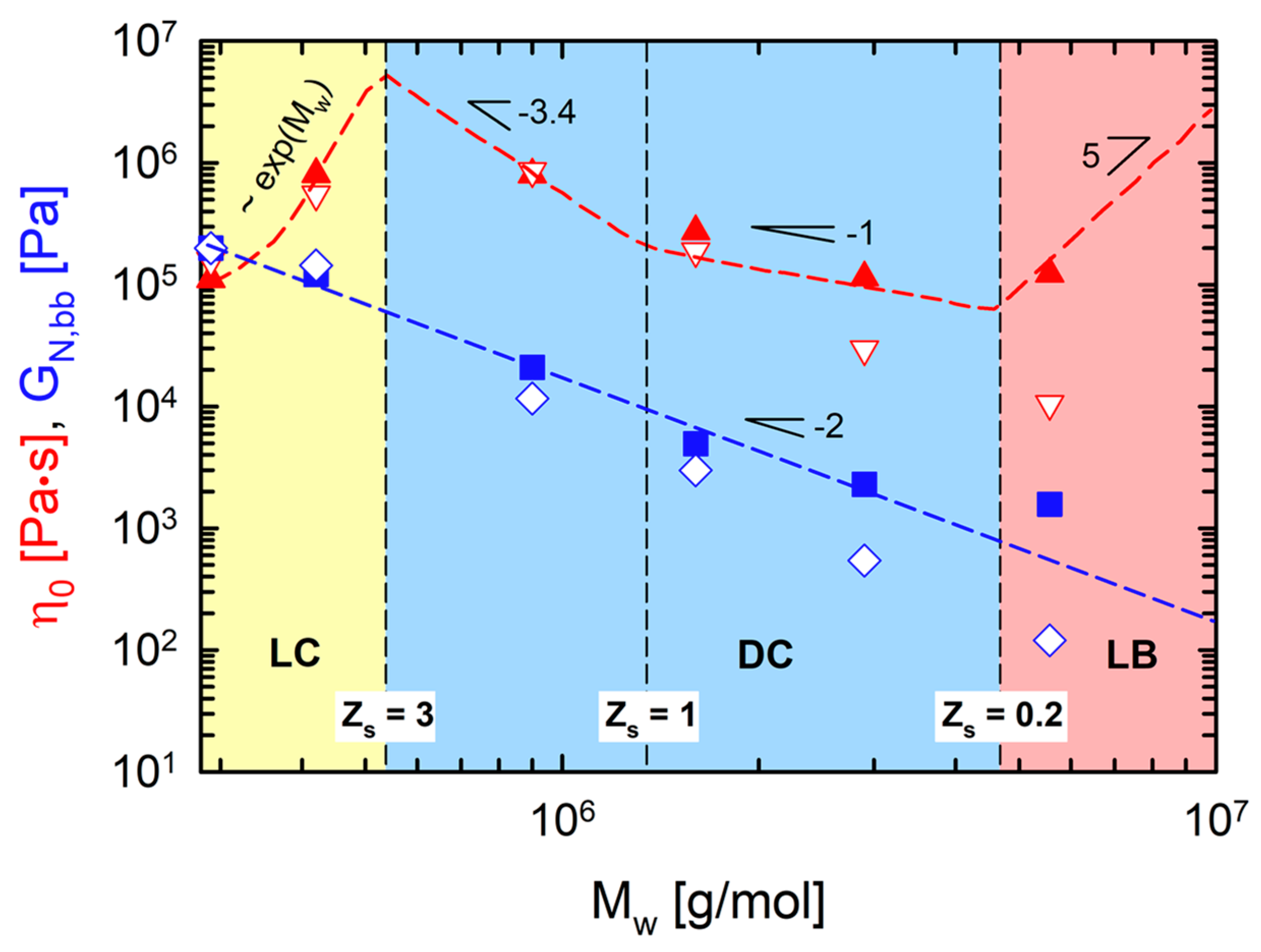
4.4. Comparison of Rheological Parameters with Characteristic Relaxation Times
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dealy, J.M.; Larson, R.G. Structure and Rheology of Molten Polymers: From Structure to Flow Behavior and Back Again, 1st ed.; Carl Hanser Verlag: Munich, Germany, 2006. [Google Scholar]
- Wood-Adams, P.M.; Dealy, J.M.; deGroot, A.W.; Redwine, O.D. Effect of molecular structure on the linear viscoelastic behavior of polyethylene. Macromolecules 2000, 33, 7489–7499. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G. Long chain branching and polydispersity effects on the rheological properties of polyethylenes. Polym. Eng. Sci. 2000, 40, 2279–2287. [Google Scholar] [CrossRef]
- Abbasi, M.; Ebrahimi, N.G.; Nadali, M.; Esfahani, M.K. Elongational viscosity of LDPE with various structures: Employing a new evolution equation in MSF theory. Rheol. Acta 2012, 51, 163–177. [Google Scholar] [CrossRef]
- Lentzakis, H.; Das, C.; Vlassopoulos, D.; Read, D.J. Pom-pom-like constitutive equations for comb polymers. J. Rheol. 2014, 58, 1855–1875. [Google Scholar] [CrossRef]
- Snijkers, F.; Pasquino, R.; Olmsted, P.; Vlassopoulos, D. Perspectives on the viscoelasticity and flow behavior of entangled linear and branched polymers. J. Phys. Condens. Mat. 2015, 27, 473002. [Google Scholar] [CrossRef] [PubMed]
- Larson, R.G. Combinatorial rheology of branched polymer melts. Macromolecules 2001, 34, 4556–4571. [Google Scholar] [CrossRef]
- Fetters, L.J.; Kiss, A.D.; Pearson, D.S.; Quack, G.F.; Vitus, F.J. Rheological behavior of star-shaped polymers. Macromolecules 1993, 26, 647–654. [Google Scholar] [CrossRef]
- van Ruymbeke, E.; Kapnistos, M.; Vlassopoulos, D.; Huang, T.; Knauss, D.M. Linear melt rheology of pom-pom polystyrenes with unentangled branches. Macromolecules 2007, 40, 1713–1719. [Google Scholar] [CrossRef]
- Lentzakis, H.; Vlassopoulos, D.; Read, D.J.; Lee, H.; Chang, T.; Driva, P.; Hadjichristidis, N. Uniaxial extensional rheology of well-characterized comb polymers. J. Rheol. 2013, 57, 605–625. [Google Scholar] [CrossRef]
- Lee, J.H.; Orfanou, K.; Driva, P.; Iatrou, H.; Hadjichristidis, N.; Lohse, D.J. Linear and nonlinear rheology of dendritic star polymers: Experiment. Macromolecules 2008, 41, 9165–9178. [Google Scholar] [CrossRef]
- Roovers, J. Synthesis and dilute solution characterization of comb polystyrenes. Polymer 1979, 20, 843–849. [Google Scholar] [CrossRef]
- Stadler, F.J.; Arikan-Conley, B.; Kaschta, J.; Kaminsky, W.; Münstedt, H. Synthesis and characterization of novel ethylene-graft-ethylene/propylene copolymers. Macromolecules 2011, 44, 5053–5063. [Google Scholar] [CrossRef]
- Kapnistos, M.; Vlassopoulos, D.; Roovers, J.; Leal, L.G. Linear rheology of architecturally complex macromolecules: Comb polymers with linear backbones. Macromolecules 2005, 38, 7852–7862. [Google Scholar] [CrossRef]
- Snijkers, F.; Vlassopoulos, D.; Ianniruberto, G.; Marrucci, G.; Lee, H.; Yang, J.; Chang, T. Double stress overshoot in start-up of simple shear flow of entangled comb polymers. ACS Macro Lett. 2013, 2, 601–604. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M. Establishing a new mechanical nonlinear coefficient Q from FT-rheology: First investigation of entangled linear and comb polymer model systems. Macromolecules 2009, 42, 411–422. [Google Scholar] [CrossRef]
- Paturej, J.; Sheiko, S.S.; Panyukov, S.; Rubinstein, M. Molecular structure of bottlebrush polymers in melts. Sci. Adv. 2016, 2, e1601478. [Google Scholar] [CrossRef]
- Daniel, W.F.M.; Burdyńska, J.; Vatankhah-Varnoosfaderani, M.; Matyjaszewski, K.; Paturej, J.; Rubinstein, M.; Dobrynin, A.V.; Sheiko, S.S. Solvent-free, supersoft and superelastic bottlebrush melts and networks. Nat. Mater. 2016, 15, 183–189. [Google Scholar] [CrossRef]
- Liang, H.; Morgan, B.J.; Xie, G.; Martinez, M.R.; Zhulina, E.B.; Matyjaszewski, K.; Sheiko, S.S.; Dobrynin, A.V. Universality of the entanglement plateau modulus of comb and bottlebrush polymer melts. Macromolecules 2018, 51, 10028–10039. [Google Scholar] [CrossRef]
- Dalsin, S.J.; Hillmyer, M.A.; Bates, F.S. Linear rheology of polyolefin-based bottlebrush polymers. Macromolecules 2015, 48, 4680–4691. [Google Scholar] [CrossRef]
- Abbasi, M.; Faust, L.; Riazi, K.; Wilhelm, M. Linear and extensional rheology of model branched polystyrenes: From loosely grafted combs to bottlebrushes. Macromolecules 2017, 50, 5964–5977. [Google Scholar] [CrossRef]
- Abbasi, M.; Faust, L.; Wilhelm, M. Comb and bottlebrush polymers with superior rheological and mechanical properties. Adv. Mater. 2019, 31, 1806484. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Xia, Y.; McKenna, G.B.; Kornfield, J.A.; Grubbs, R.H. Linear rheological response of a series of densely branched brush polymers. Macromolecules 2011, 44, 6935–6943. [Google Scholar] [CrossRef]
- Haugan, I.N.; Maher, M.J.; Chang, A.B.; Lin, T.-P.; Grubbs, R.H.; Hillmyer, M.A.; Bates, F.S. Consequences of grafting density on the linear viscoelastic behavior of graft polymers. ACS Macro Lett. 2018, 7, 525–530. [Google Scholar] [CrossRef]
- López-Barrón, C.R.; Shivokhin, M.E. Extensional strain hardening in highly entangled molecular bottlebrushes. Phys. Rev. Lett. 2019, 122, 037801. [Google Scholar] [CrossRef] [PubMed]
- López-Barrón, C.R.; Shivokhin, M.E.; Hagadorn, J.R. Extensional rheology of highly-entangled α-olefin molecular bottlebrushes. J. Rheol. 2019, 63, 917–926. [Google Scholar] [CrossRef]
- Cziep, M.A.; Abbasi, M.; Heck, M.; Arens, L.; Wilhelm, M. Effect of molecular weight, polydispersity and monomer of linear homopolymer melts on the intrinsic mechanical nonlinearity 3Q0(ω) in MAOS. Macromolecules 2016, 49, 3566–3579. [Google Scholar] [CrossRef]
- Song, H.Y.; Park, S.J.; Hyun, K. Characterization of dilution effect of semidilute polymer solution on intrinsic nonlinearity Q0 via FT rheology. Macromolecules 2017, 50, 6238–6254. [Google Scholar] [CrossRef]
- Song, H.Y.; Nnyigide, O.S.; Salehiyan, R.; Hyun, K. Investigation of nonlinear rheological behavior of linear and 3-arm star 1,4-cis-polyisoprene (PI) under medium amplitude oscillatory shear (MAOS) flow via ft-rheology. Polymer 2016, 104, 268–278. [Google Scholar] [CrossRef]
- Kempf, M.; Ahirwal, D.; Cziep, M.; Wilhelm, M. Synthesis and linear and nonlinear melt rheology of well-defined comb architectures of PS and PpMS with a low and controlled degree of long-chain branching. Macromolecules 2013, 46, 4978–4994. [Google Scholar] [CrossRef]
- Wilhelm, M. Fourier-transform rheology. Macromol. Mater. Eng. 2002, 287, 83–105. [Google Scholar] [CrossRef]
- Giacomin, A.J.; Dealy, J.M. Large-amplitude oscillatory shear. In Techniques in Rheological Measurement; Collyer, A.A., Ed.; Chapman & Hall: London, UK; New York, NY, USA, 1993; pp. 99–121. [Google Scholar]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Pearson, D.S.; Rochefort, W.E. Behavior of concentrated polystyrene solutions in large-amplitude oscillating shear fields. J. Polym. Sci. Polym. Phys. Ed. 1982, 20, 83–98. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; Bharadwaj, N.A. Low-dimensional intrinsic material functions for nonlinear viscoelasticity. Rheol. Acta 2013, 52, 201–219. [Google Scholar] [CrossRef]
- Song, H.Y.; Hyun, K. First-harmonic intrinsic nonlinearity of model polymer solutions in medium amplitude oscillatory shear (MAOS). Korea-Aust. Rheol. J. 2019, 31, 1–13. [Google Scholar] [CrossRef]
- Song, H.Y.; Hyun, K. Decomposition of Q0 from FT-rheology into elastic and viscous parts: Intrinsic-nonlinear master curves for polymer solutions. J. Rheol. 2018, 62, 919–939. [Google Scholar] [CrossRef]
- Song, H.Y.; Hyun, K. Nonlinear material functions under medium amplitude oscillatory shear (MAOS) flow. Korea-Aust. Rheol. J. 2019, 31, 267–284. [Google Scholar] [CrossRef]
- Song, H.Y.; Salehiyan, R.; Li, X.; Lee, S.H.; Hyun, K. A comparative study of the effects of cone-plate and parallel-plate geometries on rheological properties under oscillatory shear flow. Korea-Aust. Rheol. J. 2017, 29, 281–294. [Google Scholar] [CrossRef]
- Park, S.J.; Shanbhag, S.; Larson, R.G. A hierarchical algorithm for predicting the linear viscoelastic properties of polymer melts with long-chain branching. Rheol. Acta 2005, 44, 319–330. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, X.; Larson, R.G. Comparing tube models for predicting the linear rheology of branched polymer melts. J. Rheol. 2010, 54, 223–260. [Google Scholar] [CrossRef]
- Das, C.; Inkson, N.J.; Read, D.J.; Kelmanson, M.A.; McLeish, T.C.B. Computational linear rheology of general branch-on-branch polymers. J. Rheol. 2006, 50, 207–234. [Google Scholar] [CrossRef]
- Ahmadi, M.; Bailly, C.; Keunings, R.; Nekoomanesh, M.; Arabi, H.; van Ruymbeke, E. Time marching algorithm for predicting the linear rheology of monodisperse comb polymer melts. Macromolecules 2011, 44, 647–659. [Google Scholar] [CrossRef]
- Chen, X.; Larson, R.G. Effect of branch point position on the linear rheology of asymmetric star polymers. Macromolecules 2008, 41, 6871–6872. [Google Scholar] [CrossRef]
- Hyun, K.; Kim, S.H.; Ahn, K.H.; Lee, S.J. Large amplitude oscillatory shear as a way to classify the complex fluids. J. Non-Newtonian Fluid Mech. 2002, 107, 51–65. [Google Scholar] [CrossRef]
- Bharadwaj, N.A.; Ewoldt, R.H. The general low-frequency prediction for asymptotically nonlinear material functions in oscillatory shear. J. Rheol. 2014, 58, 891–910. [Google Scholar] [CrossRef]
- Kirkwood, K.M.; Leal, L.G.; Vlassopoulos, D.; Driva, P.; Hadjichristidis, N. Stress relaxation of comb polymers with short branches. Macromolecules 2009, 42, 9592–9608. [Google Scholar] [CrossRef]


| Name a | Mw,bbb (kg/mol) | PDIbb b (-) | Mw,brb (kg/mol) | PDIbr b (-) | Mwb (kg/mol) | PDI b (-) | Zsc (-) | Nbrc (-) | Topology d |
|---|---|---|---|---|---|---|---|---|---|
| PS290 | 290 | 1.07 | 290 | 1.07 | 20 | 0 | Linear | ||
| PS44 | 43 | 1.03 | 43 | 1.03 | 3.03 | 0 | Linear | ||
| PS290-3-44 | 290 | 1.10 | 45 | 1.07 | 420 | 1.11 | 5.06 | 3 | LC |
| PS290-14-44 | 290 | 1.10 | 45 | 1.07 | 900 | 1.08 | 1.36 | 14 | DC |
| PS290-30-44 | 290 | 1.10 | 43 | 1.03 | 1600 | 1.03 | 0.65 | 30 | DC |
| PS290-60-44 | 290 | 1.10 | 44 | 1.05 | 2900 | 1.03 | 0.33 | 60 | DC |
| PS290-120-44 | 290 | 1.10 | 44 | 1.05 | 5570 | 1.11 | 0.17 | 120 | LB |
| Samples | # of Regimes | ||
|---|---|---|---|
| PS290 | 1 | 1 | 3 |
| PS44 | 1 | 1 | 3 |
| PS290-3-44 | 1 | 1 | 3 |
| PS290-14-44 | 1 | 1 | 3 |
| PS290-30-44 | 3 | 1 | 5 |
| PS290-60-44 | 1 | 3 | 5 |
| PS290-120-44 | 1 | 3 | 5 |
| Samples | τLa (s) | (-) | τR,bbd (s) | τbre (s) |
|---|---|---|---|---|
| PS290 | 2.37 × 100 | 20.14 b | 3.91 × 10−2 | - |
| PS44 | 2.34 × 10−3 | 3.06 b | 2.55 × 10−4 | - |
| PS290-3-44 | 6.63 × 101 | 6.54 c | 3.38 × 100 | 6.58 × 10−1 |
| PS290-14-44 | 8.81 × 101 | 4.80 c | 6.12 × 100 | 4.42 × 10−1 |
| PS290-30-44 | 5.46 × 101 | 3.25 c | 5.60 × 100 | 2.40 × 10−1 |
| PS290-60-44 | 5.96 × 101 | 1.88 c | 1.06 × 101 | 3.47 × 10−1 |
| PS290-120-44 | 3.96 × 102 | 1.01 c | 1.30 × 102 | 5.44 × 10−1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.Y.; Faust, L.; Son, J.; Kim, M.; Park, S.J.; Ahn, S.-k.; Wilhelm, M.; Hyun, K. Small and Medium Amplitude Oscillatory Shear Rheology of Model Branched Polystyrene (PS) Melts. Polymers 2020, 12, 365. https://doi.org/10.3390/polym12020365
Song HY, Faust L, Son J, Kim M, Park SJ, Ahn S-k, Wilhelm M, Hyun K. Small and Medium Amplitude Oscillatory Shear Rheology of Model Branched Polystyrene (PS) Melts. Polymers. 2020; 12(2):365. https://doi.org/10.3390/polym12020365
Chicago/Turabian StyleSong, Hyeong Yong, Lorenz Faust, Jinha Son, Mingeun Kim, Seung Joon Park, Suk-kyun Ahn, Manfred Wilhelm, and Kyu Hyun. 2020. "Small and Medium Amplitude Oscillatory Shear Rheology of Model Branched Polystyrene (PS) Melts" Polymers 12, no. 2: 365. https://doi.org/10.3390/polym12020365
APA StyleSong, H. Y., Faust, L., Son, J., Kim, M., Park, S. J., Ahn, S.-k., Wilhelm, M., & Hyun, K. (2020). Small and Medium Amplitude Oscillatory Shear Rheology of Model Branched Polystyrene (PS) Melts. Polymers, 12(2), 365. https://doi.org/10.3390/polym12020365





