Dielectric Response Spectroscopy as Means to Investigate Interfacial Effects for Ultra-Thin Film Polymer-Based High NA EUV Lithography
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Differential Scanning Calorimetry
2.2.2. Dielectric Response Spectroscopy
2.2.3. EUV Exposure and Characterization
3. Results and Discussion
3.1. Influence of Platform with Different Protecting Groups on the Tg
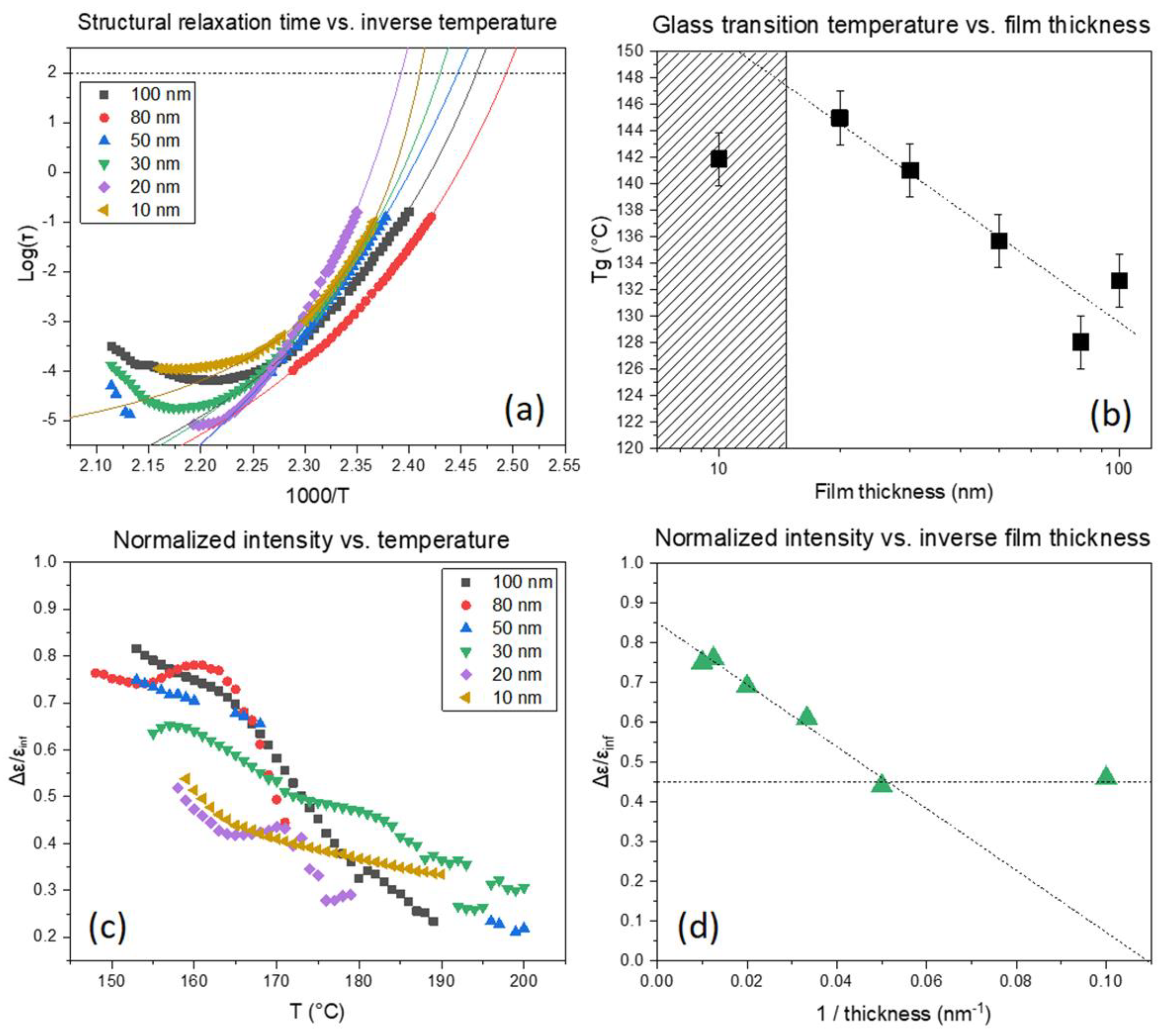
3.2. Influence of Film Thickness and the Tg
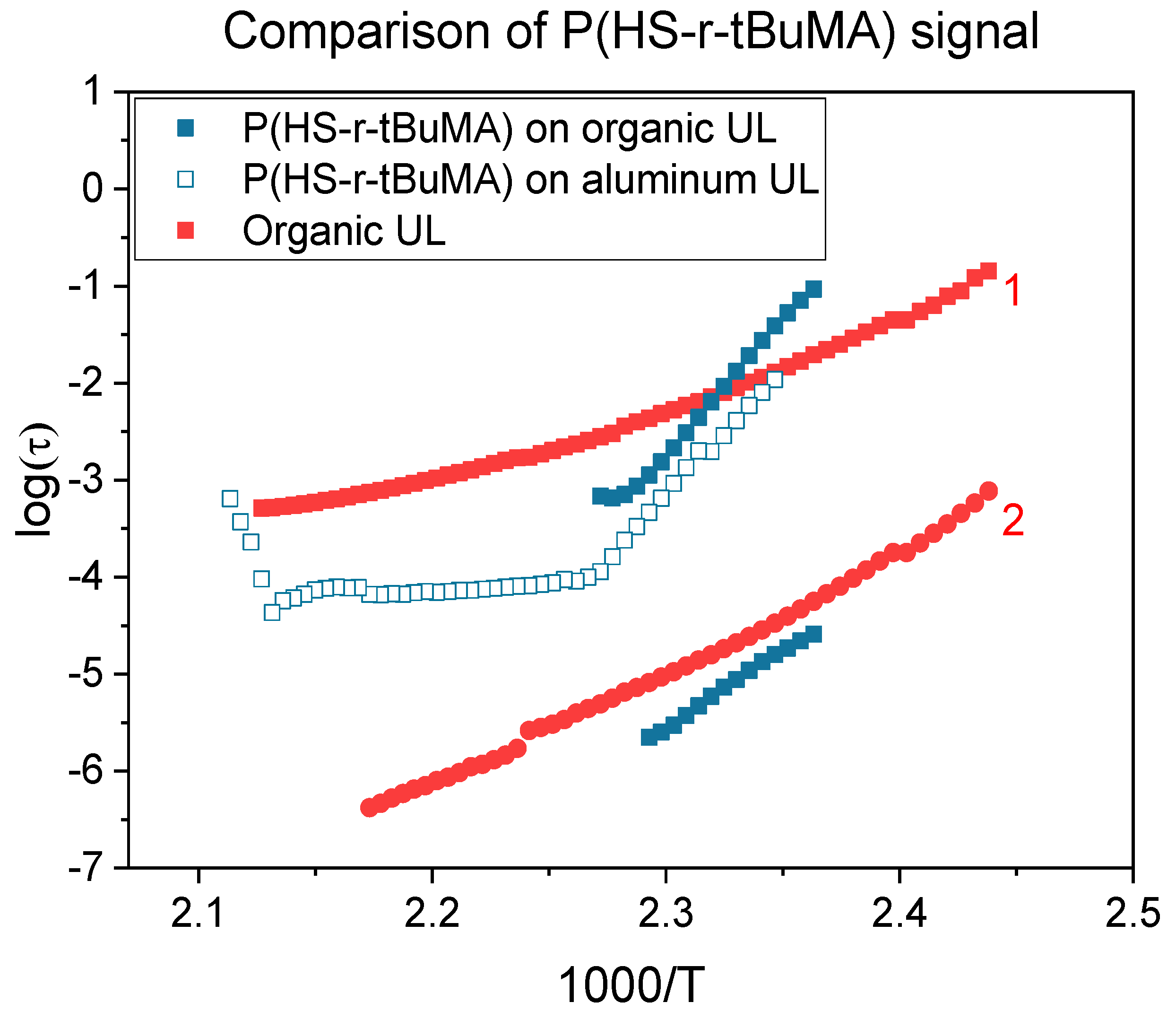
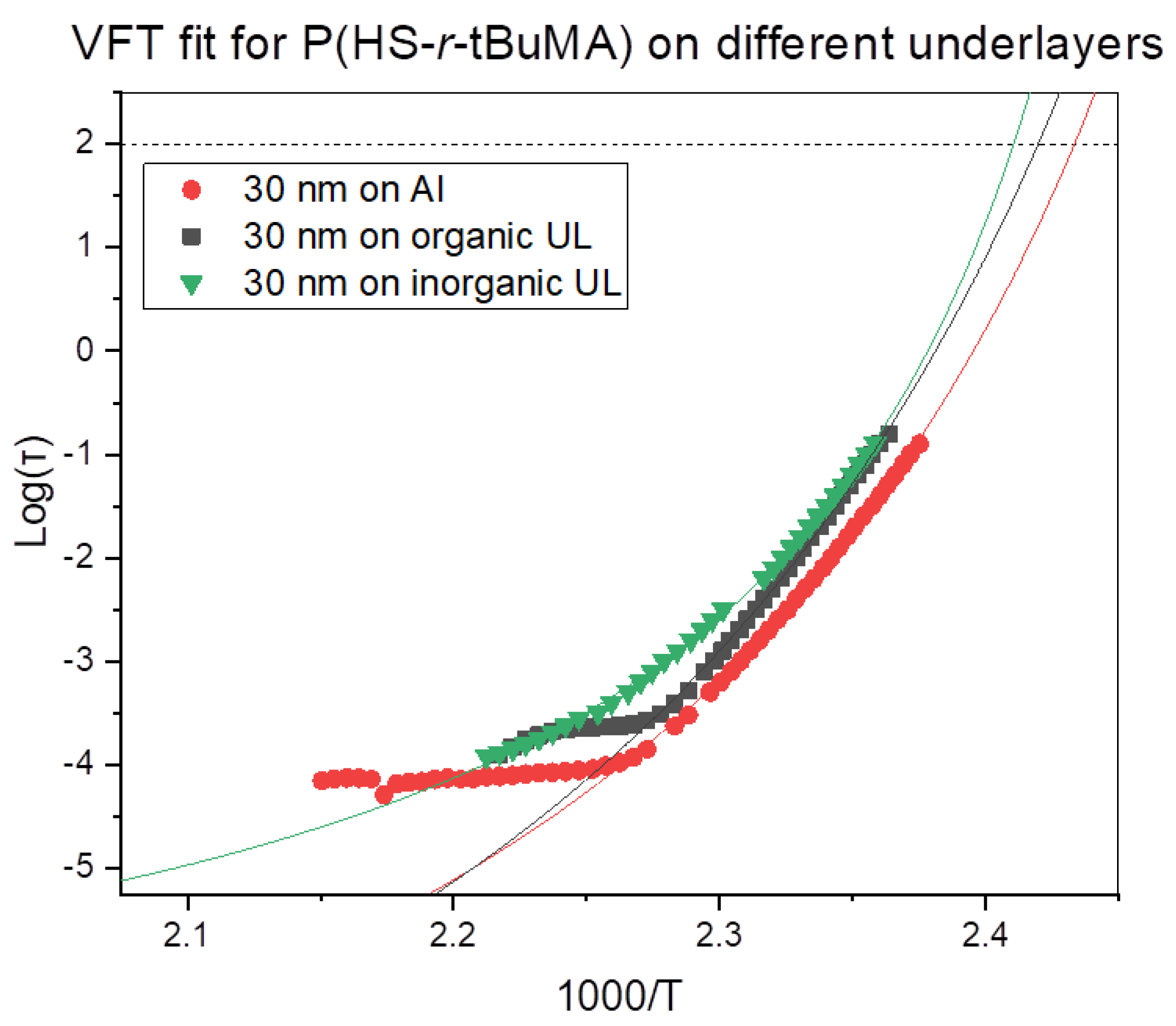
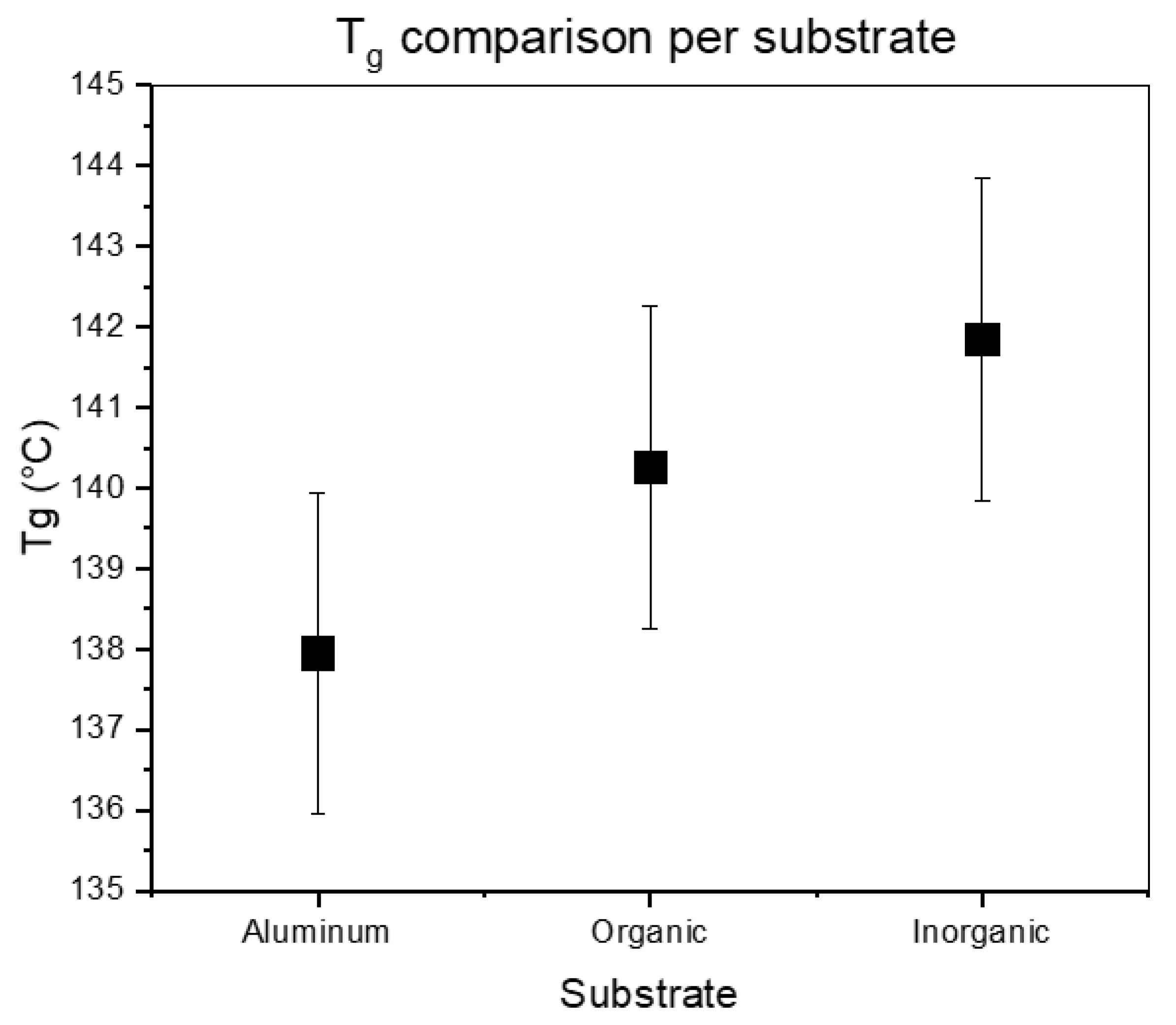
3.3. Influence of Underlayers on the Tg
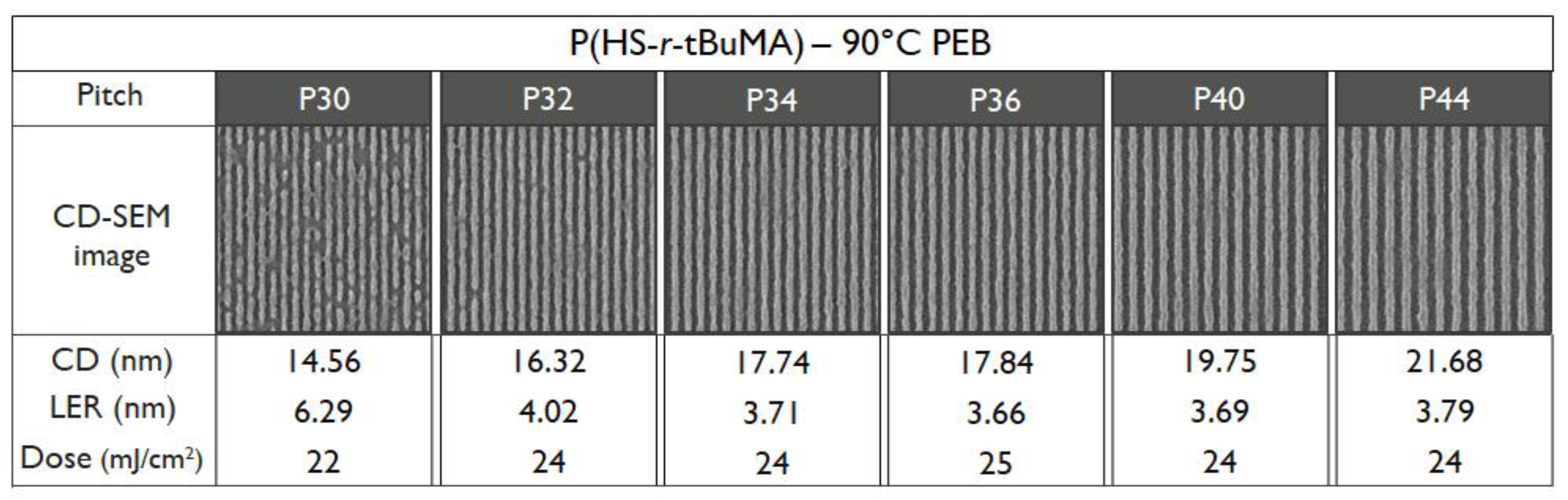
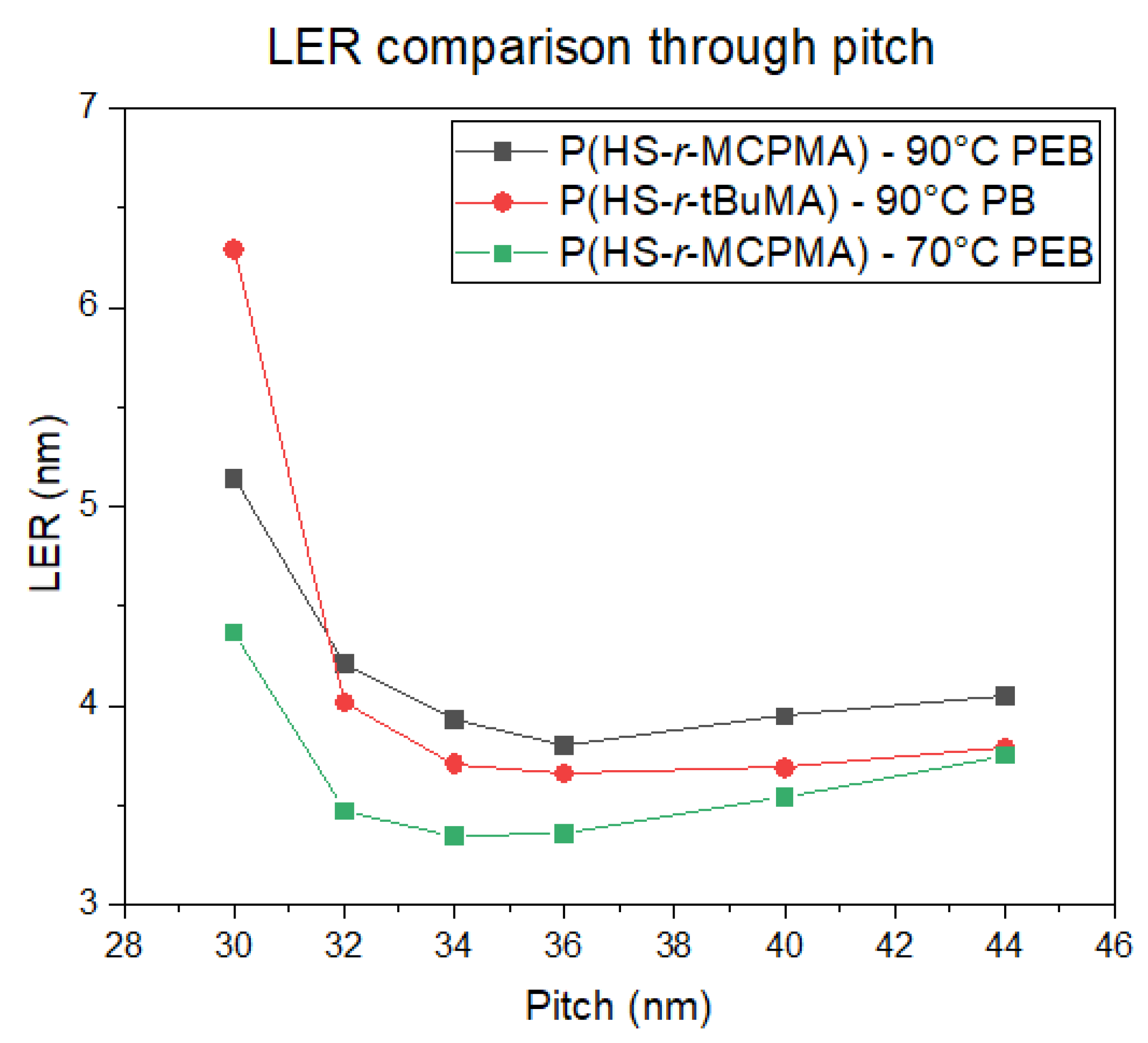
3.4. EUV Patterning Performance of the Full Resist Formulation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Samsung Electronics Begins Mass Production at New EUV Manufacturing Line. Available online: https://news.samsung.com/global/samsung-electronics-begins-mass-production-at-new-euv-manufacturing-line (accessed on 25 January 2020).
- Halfacree, G. TSMC’s EUV N7+ Node Hits Volume Production. Available online: https://bit-tech.net/news/tech/cpus/tsmcs-euv-n7-node-hits-volume-production/1/ (accessed on 25 January 2020).
- Van Schoot, J.; Zahlten, C.; Gräupner, P.; Kürz, P.; Stoeldraijer, J.; Kaiser, W. High-NA EUV lithography pushing the limits. Proc. SPIE 2019, 11177, 111770B. [Google Scholar] [CrossRef]
- Lio, A. EUV resists: What’s next? Proc. SPIE 2016, 9776, 97760V. [Google Scholar] [CrossRef]
- Chini, S.F.; Amirfazli, A. Understanding Pattern Collapse in Photolithography Process Due to Capillary Forces. Langmuir 2010, 26, 13707–13714. [Google Scholar] [CrossRef] [PubMed]
- Silva, D.; De Silva, A.; Dutta, A.; Meli, L.; Yao, Y.; Mignot, Y.; De Silva, A.; Dutta, A.; Meli, L.; Yao, Y.; et al. Inorganic hardmask development for EUV patterning. Proc. SPIE 2020, 10583, 105830V. [Google Scholar] [CrossRef]
- Vanelderen, P.; De Simone, D.; Spampinato, V.; Franquet, A.; Vandenberghe, G. The Role of Underlayers in EUVL. J. Photopolym. Sci. Technol. 2018, 31, 209–214. [Google Scholar] [CrossRef] [Green Version]
- Jablonski, E.L.; Prabhu, V.M.; Sambasivan, S.; Fischer, D.A.; Lin, E.K.; Goldfarb, D.L.; Angelopoulos, M.; Ito, H. Surface and bulk chemistry of chemically amplified photoresists: Segregation in thin films and environmental stability issues. Proc. SPIE 2004, 5376, 302–311. [Google Scholar] [CrossRef]
- Malik, S.; Eisele, J.; Whewell, A.; Ferreira, L.; Holt, T.; Bowden, M. Post-Exposure Bake Temperature Considerations for High Activation Energy Resist Systems. J. Photopolym. Sci. Technol. 2000, 13, 513–518. [Google Scholar] [CrossRef]
- Forrest, J.A.; Dalnoki-Veress, K.; Stevens, J.R.; Dutcher, J.R. Effect of free surfaces on the glass transition temperature of thin polymer films. Phys. Rev. Lett. 1996, 77, 2002–2005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Z.; Clough, A.; Lam, C.H.; Tsui, O.K.C. Glass transition dynamics and surface mobility of entangled polystyrene films at equilibrium. Macromolecules 2011, 44, 8294–8300. [Google Scholar] [CrossRef]
- Callen, H.B.; Welton, T.A. Irreversibility and Generalized Noise. Phys. Rev. 1951, 83, 34–40. [Google Scholar] [CrossRef]
- Napolitano, S.; Glynos, E.; Tito, N.B. Glass transition of polymers in bulk, confined geometries, and near interfaces. Reports Prog. Phys. 2017, 80, 036602. [Google Scholar] [CrossRef] [PubMed]
- Nakamichi, T. Glass Transition Temperature and Free Volume (I). J. Jpn. Soc. Colour Mater. 1995, 68, 41–51. [Google Scholar] [CrossRef] [Green Version]
- Uematsu, I. Crystallization and Glass Transition (Second Order Transition) of Polymers. J. Jpn. Soc. Colour Mater. 1957, 30, 944–954. [Google Scholar]
- Park, J.; Lee, S.-G.; Vesters, Y.; Severi, J.; Kim, M.; De Simone, D.; Oh, H.-K.; Hur, S.-M. Molecular Modeling of EUV Photoresist Revealing the Effect of Chain Conformation on Line-Edge Roughness Formation. Polymers 2019, 11, 1923. [Google Scholar] [CrossRef] [PubMed] [Green Version]
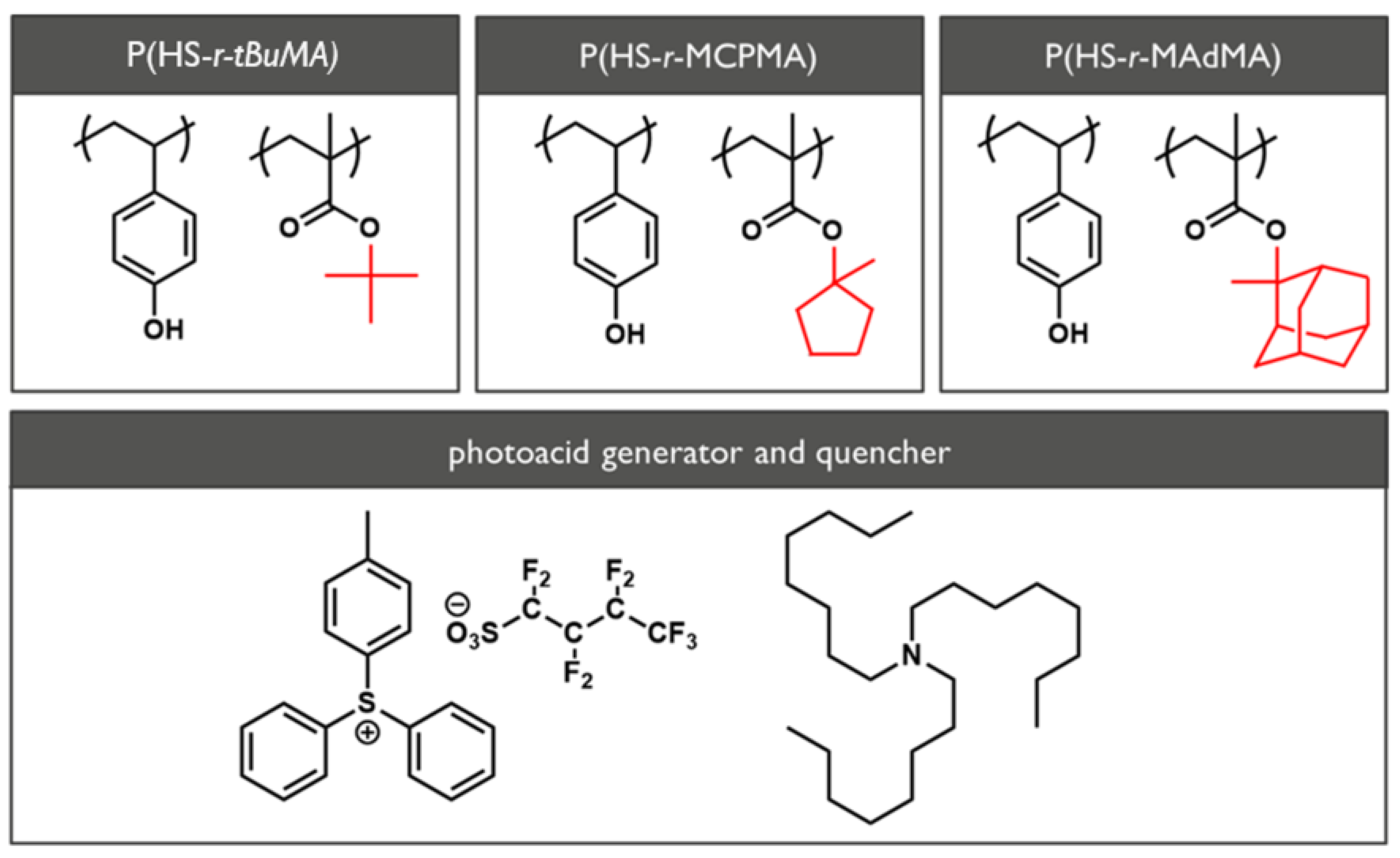

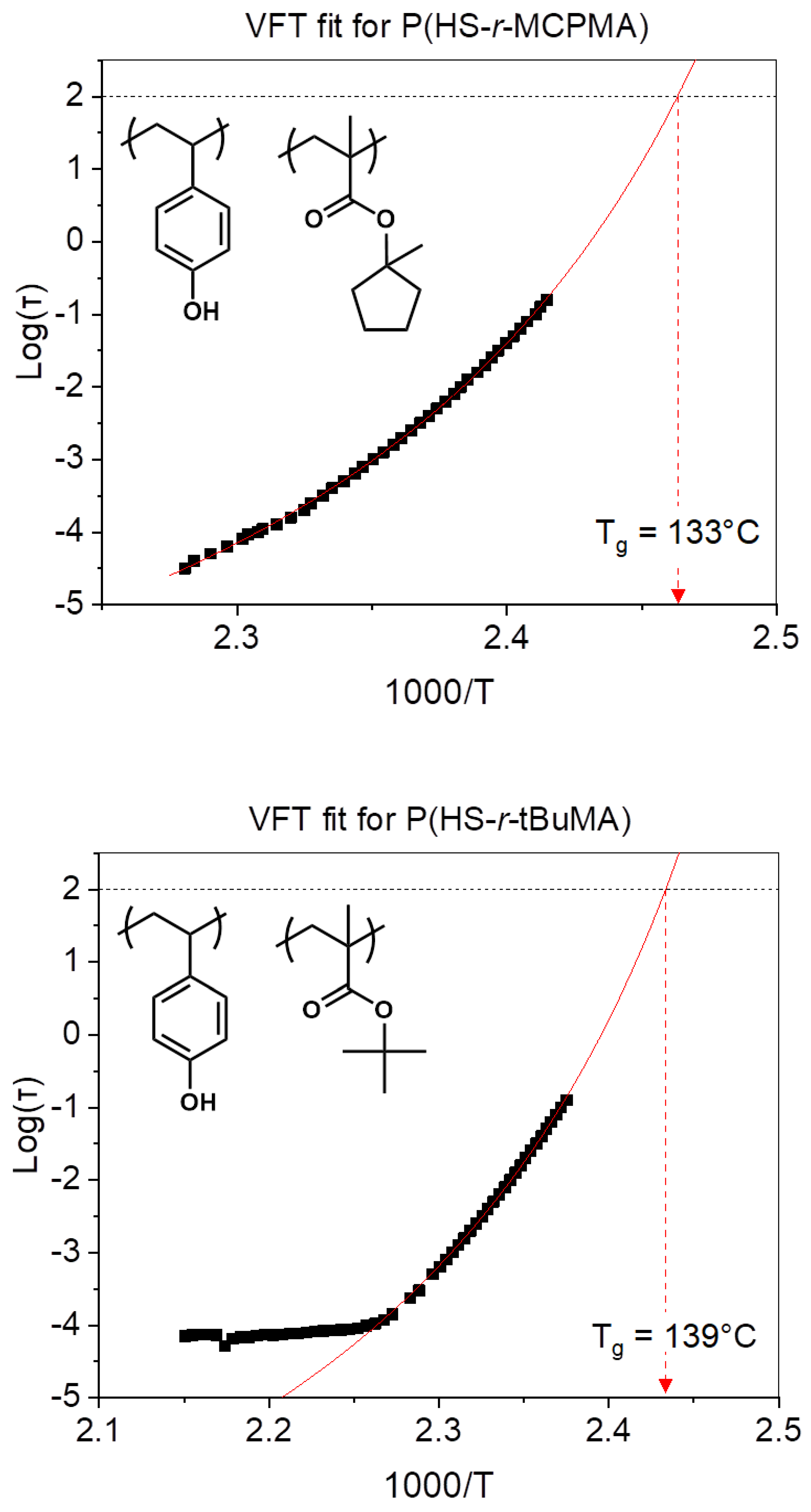
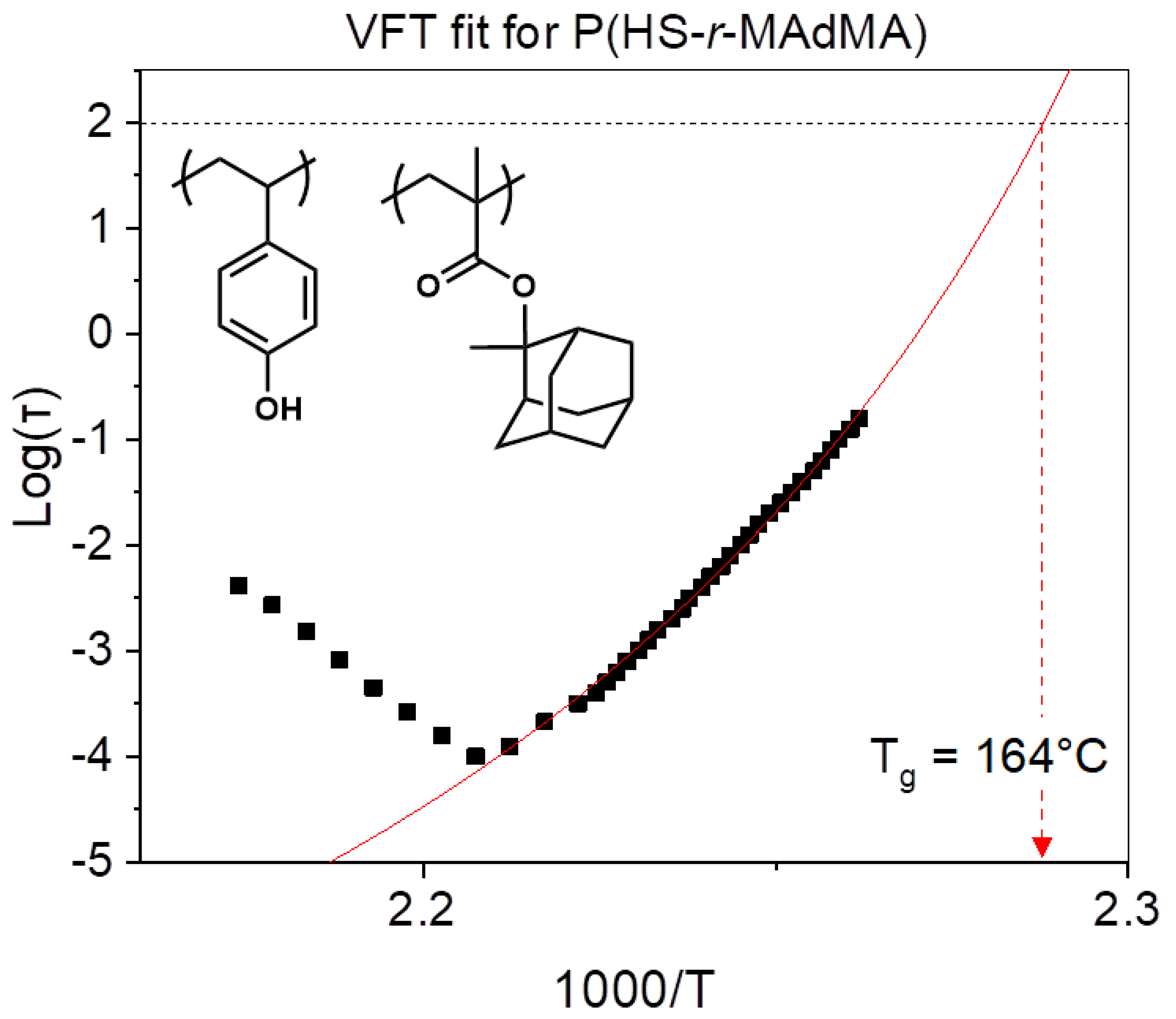





| Polymer | Tg (DSC) | Tg (DRS) |
|---|---|---|
| P(HS-r-MCPMA | 79 °C | 133 ± 2 °C |
| P(HS-r-tBuMA) | 98 °C | 139 ± 2 °C |
| P(HS-r-MAdMA | 133 °C | 164 ± 2 °C |
| Underlayer | Tg (DRS) |
|---|---|
| Aluminum | 138 ± 2 °C |
| Organic | 140 ± 2 °C |
| Inorganic | 142 ± 2 °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Severi, J.; De Simone, D.; De Gendt, S. Dielectric Response Spectroscopy as Means to Investigate Interfacial Effects for Ultra-Thin Film Polymer-Based High NA EUV Lithography. Polymers 2020, 12, 2971. https://doi.org/10.3390/polym12122971
Severi J, De Simone D, De Gendt S. Dielectric Response Spectroscopy as Means to Investigate Interfacial Effects for Ultra-Thin Film Polymer-Based High NA EUV Lithography. Polymers. 2020; 12(12):2971. https://doi.org/10.3390/polym12122971
Chicago/Turabian StyleSeveri, Joren, Danilo De Simone, and Stefan De Gendt. 2020. "Dielectric Response Spectroscopy as Means to Investigate Interfacial Effects for Ultra-Thin Film Polymer-Based High NA EUV Lithography" Polymers 12, no. 12: 2971. https://doi.org/10.3390/polym12122971
APA StyleSeveri, J., De Simone, D., & De Gendt, S. (2020). Dielectric Response Spectroscopy as Means to Investigate Interfacial Effects for Ultra-Thin Film Polymer-Based High NA EUV Lithography. Polymers, 12(12), 2971. https://doi.org/10.3390/polym12122971






