Large-Scale Shape Transformations of a Sphere Made of a Magnetoactive Elastomer
Abstract
:1. Introduction
1.1. Field-Induced Striction in Magnetoactive Elastomers
1.2. MAE Objects and Dense Ferrofluid Droplets: Resemblances and Differences
2. MAE Sphere under a Uniform Field. Qualitative Analysis
3. MAE Sphere under a Uniform Field: A Coupled Magnetoelastic Problem
3.1. Finite Deformations Approach
3.2. Elasticity Energy
3.3. Magnetic Energy
4. Method of Solution
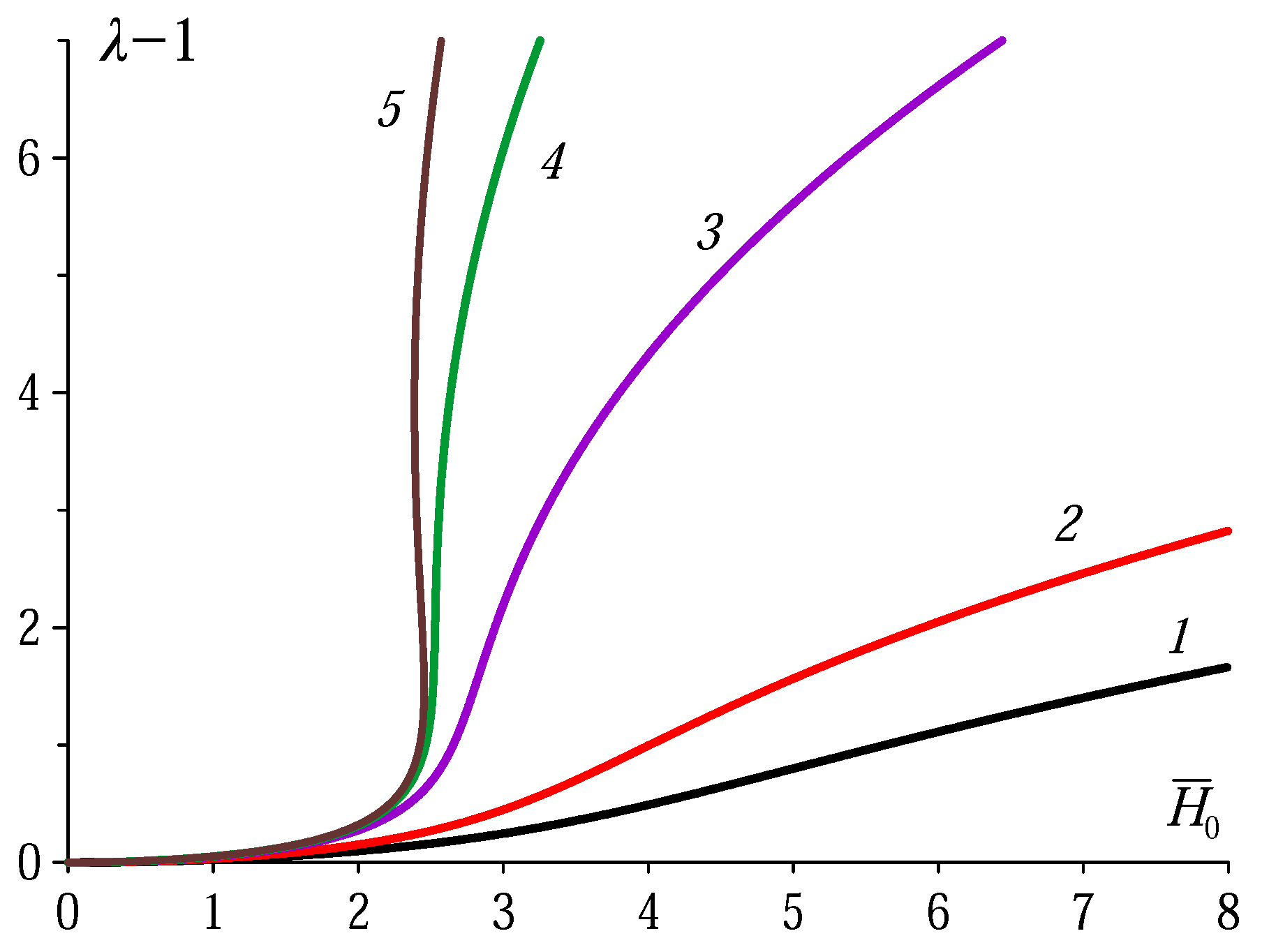
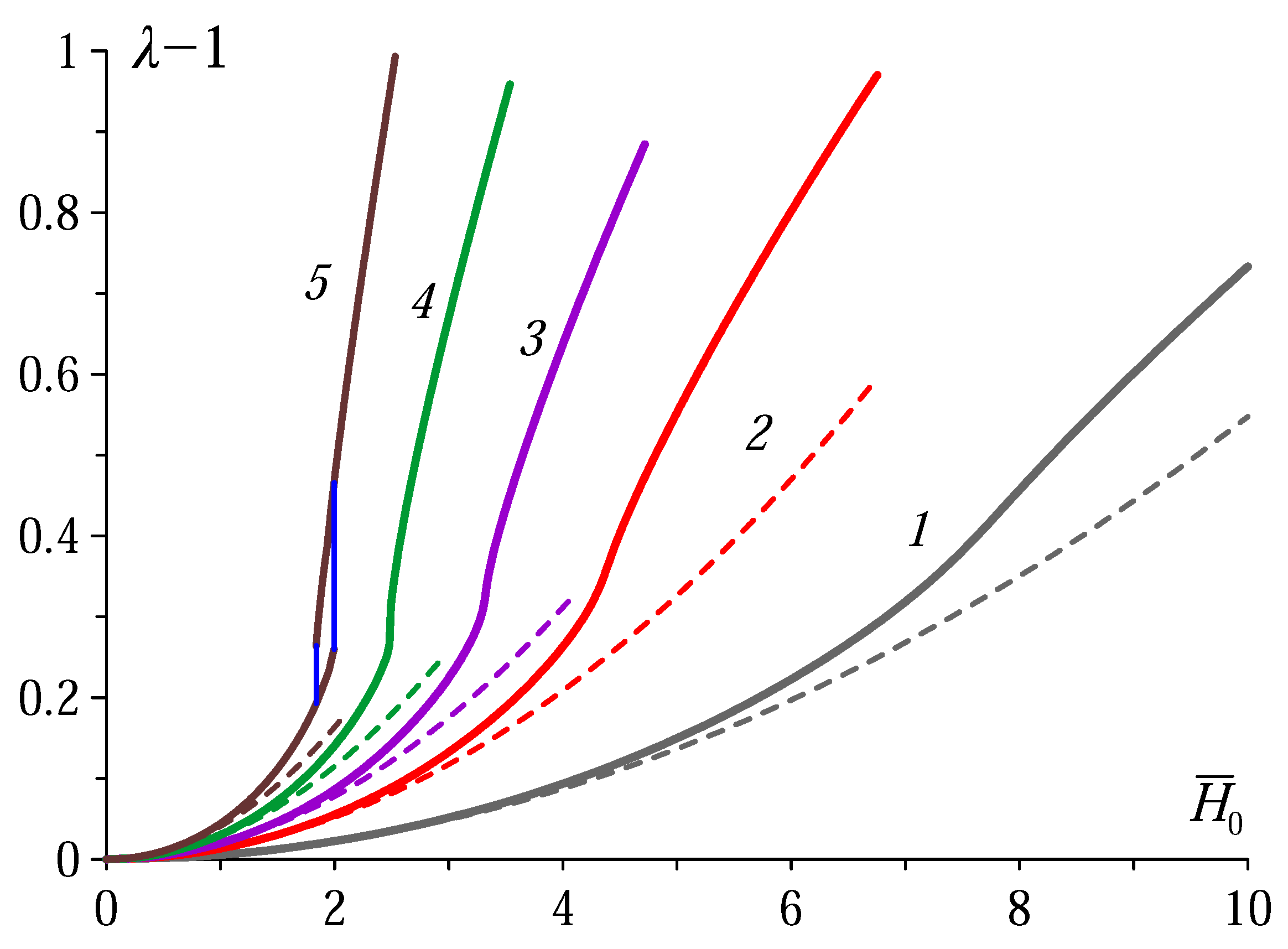
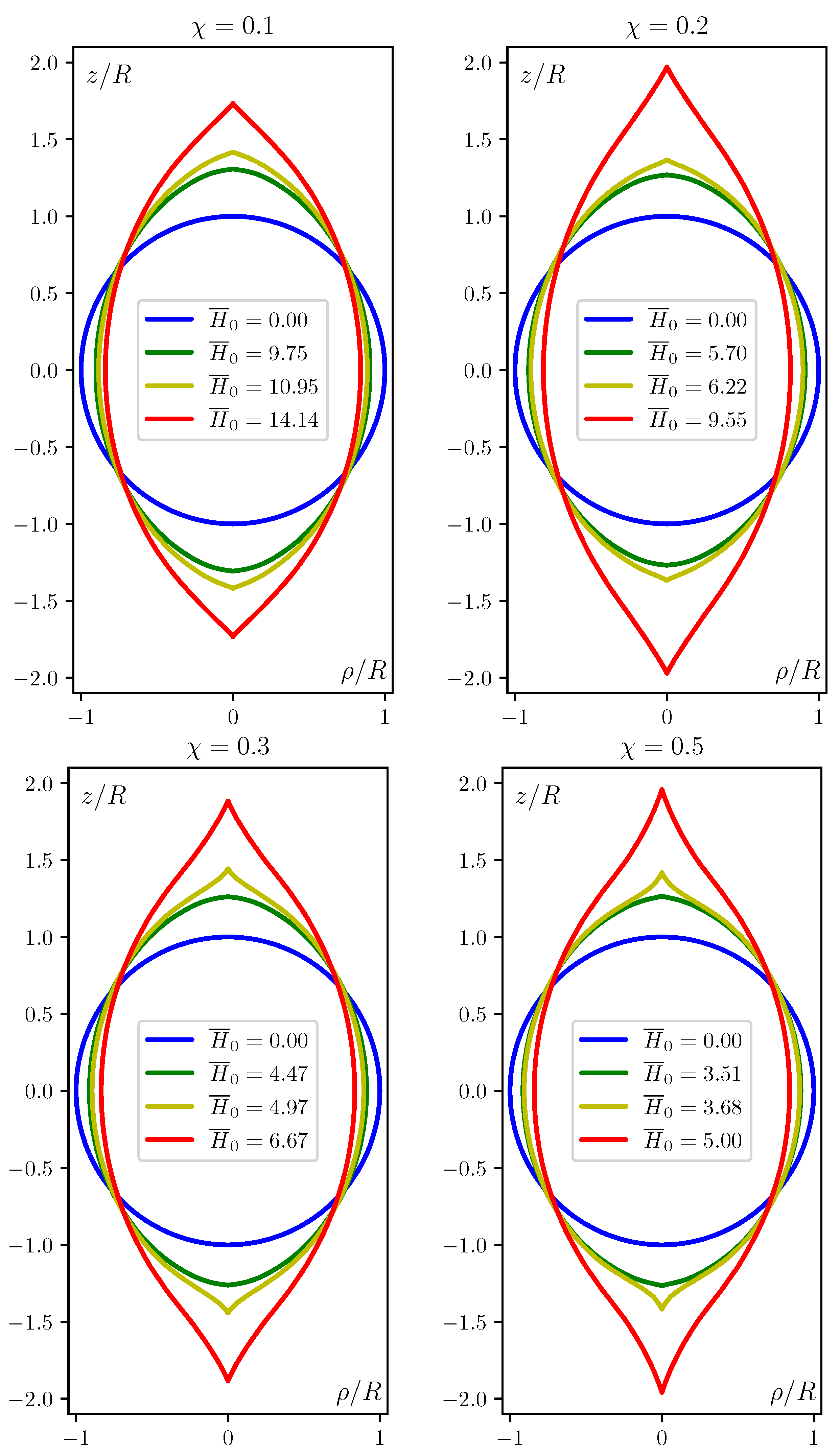
5. Results and Discussion
6. Conclusions
- Theoretical evidence is presented that magnetostriction effect in free-standing MAE samples—sphere is a test object—could be understood and studied adequately only with the aid of a detailed magnetomechanical description. The basic cause for that is that only the finite-element or alike methods are able to account for the virtually infinite number of degrees of freedom of a deformable elastic body.
- As soon as a powerful numerical tool is applied, it turns out that the estimates obtained with ‘spheroidal’ approximation could be used exclusively for qualitative analysis and have no quantitative validity. The here obtained solution refutes the former prediction of virtual impossibility to observe magnetomechanical hysteresis of MAE samples and moves the appropriate parameter interval to a real range.
- Even if the magnetic susceptibility of a MAE is not high enough to ensure a real jump of the stretch ratio , function signals on the proximity of the hysteresis regime by a characteristic inflexion. Besides that, and contrary to the case of ferrofluid droplets, in MAE objects the effect has no size limitations and may well occur at macroscopic scale.
- The model that we use is adequate for the problem solved but is limited to statics and linearly magnetiable MAEs. A first step forward, utterly necessary and not extremely laborious, should be its extension for a nonlinear magnetization law since magnetic saturation is a fundamental feature of MAEs; such an improvement would bring theoretical predictions closer to real situation.
- In our view, for further advances the model should be developed along the following lines:
- –
- it should allow for re-distribution of the filler particles, which, albeit elastically impeded by the MAE matrix, possess some translational freedom that is the greater the softer the elastomer. Due to geometry reasons, the internal field gradients in the tips exceed those in the middle section of the body, so that the magnetic forces urge the particles to the tips. The augmented particle concentration enhances the local magnetic susceptibility of the tip, and this, in turn, affects its geometry. At present, the net effect of this interplay is unknown.
- –
- it should be extended to have a dynamic formulation. This would give an opportunity to estimate the response time of a MAE sphere shape morphing that, obviously, would strongly depend on the object size. Besides that, a large number of cases where MAE objects of various shapes may undergo field-controlled motion and locomotion would become accessible for reliable predcitions. Evidently, this class of problems is very interesting from a great many of applicational viewpoints.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yu, K.; Fang, N.X.; Huang, G.; Wang, Q. Magnetoactive acoustic metamaterials. Adv. Mater. 2018, 30, 1706348. [Google Scholar] [CrossRef] [PubMed]
- Behrooz, M.; Gordaninejad, F. A flexible microfluid transport system featuring magnetorheological elastomer. Smart Mater. Struct. 2016, 25, 025011. [Google Scholar] [CrossRef]
- Yuan, Y.; Yalikun, Y.; Ota, N.; Tanaka, Y. Property investigation of replaceable PDMS membrane as an actuator in microfluidic device. Actuators 2018, 7, 68. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Alekhina, Y.A.; Makarova, L.A.; Kostrov, S.A.; Stepanov, G.V.; Kazimirova, E.G.; Perov, N.S.; Kramarenko, E.Y. Development of magnetoactive elastomers for sealing eye retina detachments. J. Appl. Polym. Sci. 2019, 136, 47452. [Google Scholar] [CrossRef]
- Alapan, Y.; Karacakol, A.C.; Guzelhan, S.N.; Isik, I.; Sitti, M. Reprogrammable shape morphing of magnetic soft machines. Sci. Adv. 2020, 6, eabc6414. [Google Scholar] [CrossRef]
- Zhalmuratova, D.; Chung, H.-J. Reinforced gels and elastomers for biomedical and soft robotics applications. ACS Appl. Polym. Mater. 2020, 2, 1073–1091. [Google Scholar] [CrossRef]
- Stepanov, G.V.; Borin, D.Y.; Raikher, Y.L.; Melenev, P.V.; Perov, N.S. Motion of ferroparticles inside the polymeric matrix in magnetoactive elastomers. J. Phys. Condens. Matter 2008, 20, 204121. [Google Scholar] [CrossRef]
- Biller, A.M.; Stolbov, O.V.; Raikher, Y.L. Modeling of particle interactions in magnetorheological elastomers. J. Appl. Phys. 2014, 116, 114904. [Google Scholar] [CrossRef]
- Stolbov, O.V.; Raikher, Y.L.; Balasoiu, M. Modelling of magnetodipolar striction in soft magnetic elastomers. Soft Matter 2011, 7, 8484–8487. [Google Scholar] [CrossRef]
- Gong, X.; Liao, G.; Xuan, S. Full-field deformation of magnetorheological elastomer under uniform magnetic field. Appl. Phys. Lett. 2012, 100, 211909. [Google Scholar] [CrossRef] [Green Version]
- Menzel, A. Bridging from particle to macroscopic scales in uniaxial magnetic gels. J. Chem. Phys. 2014, 141, 194907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pessot, G.; Weeber, R.; Holm, C.; Löwen, H.; Menzel, A. Towards a scale-bridging description of ferrogels. J. Phys. Condens. Matter 2015, 27, 325105. [Google Scholar] [CrossRef] [Green Version]
- Fischer, L.; Menzel, A. Magnetostriction in magnetic gels and elastomers as a function of the internal structure and particle distribution. J. Chem. Phys. 2019, 151, 114906. [Google Scholar] [CrossRef]
- Ginder, J.M.; Clark, S.M.; Schlotter, W.F.; Nichols, M.E. Magnetostrictive phenomena in magnetorheological elastomers. Int. J. Mod. Phys. B 2002, 16, 2412–2418. [Google Scholar] [CrossRef]
- Gollwitzer, C.; Turanov, A.; Krekhova, M.; Lattermann, G.; Rehberg, I.; Richter, R. Measuring the deformation of a ferrogel sphere in a homogeneous magnetic field. J. Chem. Phys. 2008, 128, 164709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guan, X.; Dong, X.; Ou, J. Magnetostrictive effect of magnetorheological elastomer. J. Magn. Magn. Mater. 2008, 320, 158–163. [Google Scholar] [CrossRef]
- Filipcsei, G.; Zrínyi, M. Magnetodeformation effects and the swelling of ferrogels in a uniform magnetic field. J. Phys. Condens. Matter 2010, 22, 276001. [Google Scholar] [CrossRef]
- Diguet, G.; Beaugnon, E.; Cavaillé, J.Y. Shape effect in the magnetostriction of ferromagnetic composite. J. Magn. Magn. Mater. 2010, 322, 3337–3341. [Google Scholar] [CrossRef]
- Andriuschenko, P.; Nefedev, K.; Stepanov, G. Calculations of magnetoactive elastomer reactions in a uniform external magnetic field. Eur. Phys. J. B 2014, 87, 11. [Google Scholar] [CrossRef]
- Saveliev, D.V.; Belyaeva, I.A.; Chashin, D.V.; Fetisov, L.Y.; Romeis, D.; Kettl, W.; Kramarenko, E.Y.; Saphiannikova, M.; Stepanov, G.V.; Shamonin, M. Giant extensional strain of magnetoactive elastomeric cylinders in uniform magnetic fields. Materials 2020, 13, 3297. [Google Scholar] [CrossRef] [PubMed]
- Romeis, D.; Kostrov, S.A.; Kramarenko, E.Y.; Stepanov, G.V.; Shamonin, M.; Saphiannikova, M. Magnetic-field-induced stress in confined magnetoactive elastomers. Soft Matter 2020, 16, 9047–9058. [Google Scholar] [CrossRef]
- Raikher, Y.L.; Stolbov, O.V. Magnetodeformational effect in a ferroelastic material. Tech. Phys. Lett. 2000, 26, 156–158. [Google Scholar] [CrossRef]
- Raikher, Y.L.; Stolbov, O.V. Deformation of an ellipsoidal ferrogel sample in a uniform magnetic field. J. Appl. Mech. Tech. Phys. 2005, 46, 434–443. [Google Scholar] [CrossRef]
- Raikher, Y.L.; Stolbov, O.V. Numerical modeling of large field-induced strains in ferroelastic bodies: A continuum approach. J. Phys. Condens. Matter 2008, 20, 204126. [Google Scholar] [CrossRef]
- Morozov, K.; Shliomis, M.; Yamaguchi, H. Magnetic deformation of ferrogel bodies: Procrustes effect. Phys. Rev. E 2009, 79, 040801. [Google Scholar] [CrossRef]
- Ivaneyko, D.; Toshchevikov, V.; Saphiannikova, M.; Heinrich, G. Mechanical properties of magneto-sensitive elastomers: Unification of the continuum-mechanics and microscopic theoretical approaches. Soft Matter 2014, 10, 2213–2227. [Google Scholar] [CrossRef] [Green Version]
- Zubarev, A.Y.; Borin, D.Y. Effect of particle concentration on ferrogel magnetodeformation. J. Magn. Magn. Mater. 2015, 377, 373–377. [Google Scholar] [CrossRef]
- Romeis, D.; Metsch, P.; Kästner, M.; Saphiannikova, M. Modeling and simulation of magnetorheological elastomers: A comparison of continuum and dipole approaches. Phys. Rev. E 2017, 95, 042501. [Google Scholar] [CrossRef]
- Arkhipenko, V.I.; Barkov, Y.D.; Bashtovoi, V.G. Study of a magnetized fluid drop shape in a homogeneous magnetic field. Magnetohydrodynamics 1978, 14, 373–375. [Google Scholar]
- Drozdova, V.I.; Skrobotova, T.V.; Chekanov, V.V. Experimental study of the hydrostatics of the interphase surface of a ferrofluid. Magnetohydrodynamics 1979, 15, 12–14. [Google Scholar]
- Bacri, J.-C.; Salin, D.; Massart, R. Study of the deformation of ferrofluid droplets in a magnetic field. J. Phys. Lett. 1982, 43, 179–185. [Google Scholar] [CrossRef]
- Bacri, J.-C.; Salin, D. Instability of ferrofluid magnetic drops under magnetic field. J. Phys. Lett. 1982, 43, 649–654. [Google Scholar] [CrossRef]
- Cebers, A. Virial method of investigation of statics and dynamics of magnetizable liquids. Magnetohydrodynamics 1985, 21, 19–27. [Google Scholar]
- Afkhami, S.; Tyler, A.J.; Renardy, Y.; Renardy, M.; St. Pierre, T.G.; Woodward, R.C.; Riffle, J.S. Deformation of a hydrophobic ferrofluid droplet suspended in a viscous medium under uniform magnetic fields. J. Fluid Mech. 2010, 663, 358–384. [Google Scholar] [CrossRef] [Green Version]
- Misra, K. Magnetic (electric) drop deformation in uniform external fields: Volume averaged methods and formation of static and dynamic conical tips. Phys. Fluids 2020, 32, 107104. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P. Electrodynamics of Continuous Media, 2nd ed.; Pergamon Press: Oxford, UK, 1984. [Google Scholar]
- Peng, S.T.J.; Landel, R.F. Stored energy function and compressibility of compressible rubberlike materials under large strain. J. Appl. Phys. 1975, 46, 2599–2604. [Google Scholar] [CrossRef]
- Naletova, V.A.; Pelevina, D.A.; Merkulov, D.I.; Zeidis, I.; Zimmermann, K. Bi-stability of the deformation of a body with a magnetizable elastomer in a magnetic field. Magnetohydrodynamics 2016, 52, 287–298. [Google Scholar] [CrossRef]
- Lurie, A.I. Nonlinear Theory of Elasticity; North-Holland: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Alnæs, M.S.; Blechta, J.; Hake, J.; Johansson, A.; Kehlet, B.; Logg, A.; Richardson, C.; Ring, J.; Rognes, M.E.; Wells, G.N. The FEniCS project version 1.5. Arch. Numer. Softw. 2015, 3, 9–23. [Google Scholar] [CrossRef]
- FEniCS Project. Available online: https://fenicsproject.org (accessed on 15 September 2020).
- Kashima, S.; Myasaka, F.; Hirata, K. Novel soft actuator using magnetorheological elastomer. IEEE Trans. Magn. 2012, 48, 1649–1652. [Google Scholar] [CrossRef]
- Mitsumata, T.; Ohori, S.; Honds, A.; Kawai, M. Magnetism and viscoelasticity of magnetic elastomers with wide range modulation of dynamic modulus. Soft Matter 2013, 9, 904–912. [Google Scholar] [CrossRef]
- Zrínyi, M.; Barsi, L.; Szabó, L.; Kilian, H.-G. Direct observation of abrupt shape transition in ferrogels induced by nonuniform magnetic field. J. Chem. Phys. 1997, 106, 5685–5692. [Google Scholar] [CrossRef]
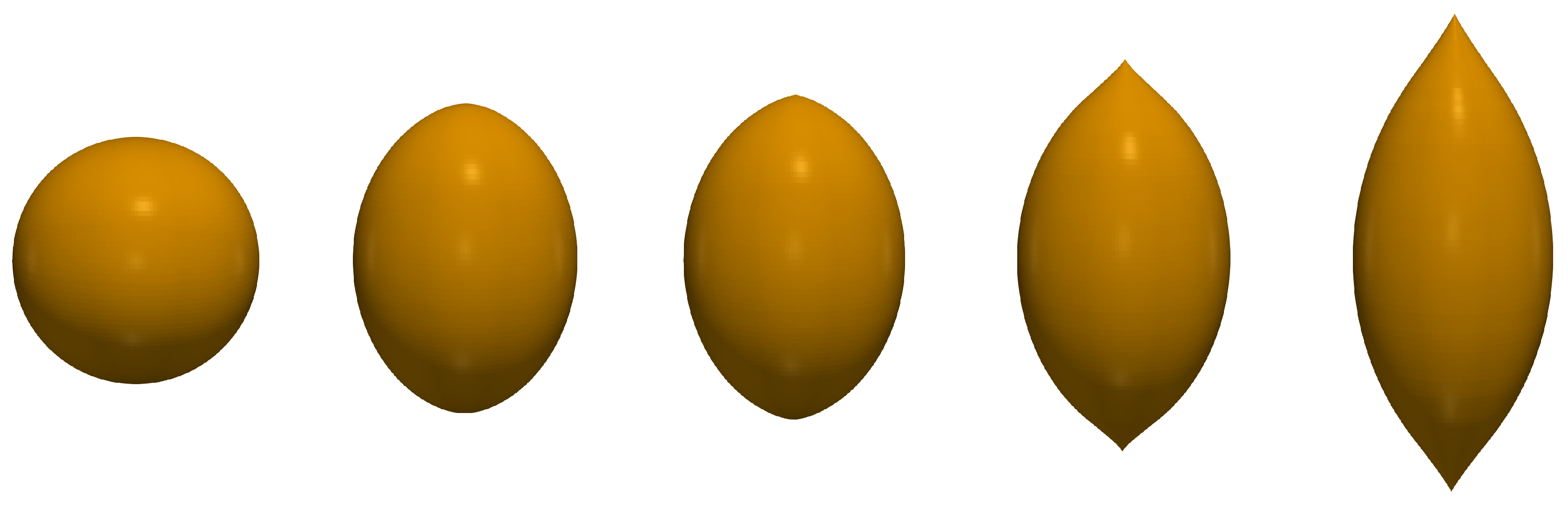
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stolbov, O.; Raikher, Y. Large-Scale Shape Transformations of a Sphere Made of a Magnetoactive Elastomer. Polymers 2020, 12, 2933. https://doi.org/10.3390/polym12122933
Stolbov O, Raikher Y. Large-Scale Shape Transformations of a Sphere Made of a Magnetoactive Elastomer. Polymers. 2020; 12(12):2933. https://doi.org/10.3390/polym12122933
Chicago/Turabian StyleStolbov, Oleg, and Yuriy Raikher. 2020. "Large-Scale Shape Transformations of a Sphere Made of a Magnetoactive Elastomer" Polymers 12, no. 12: 2933. https://doi.org/10.3390/polym12122933




