Pore-Scale Modeling of the Effect of Wettability on Two-Phase Flow Properties for Newtonian and Non-Newtonian Fluids
Abstract
1. Introduction
2. Governing Equations and Methodology
2.1. Two-Phase Flow Governing Equations
2.2. Fluid Rheology: Shear-Thinning Fluid
2.3. Dynamic Contact Angle and Hysteresis Modeling: Fluid-Solid Matrix Interaction
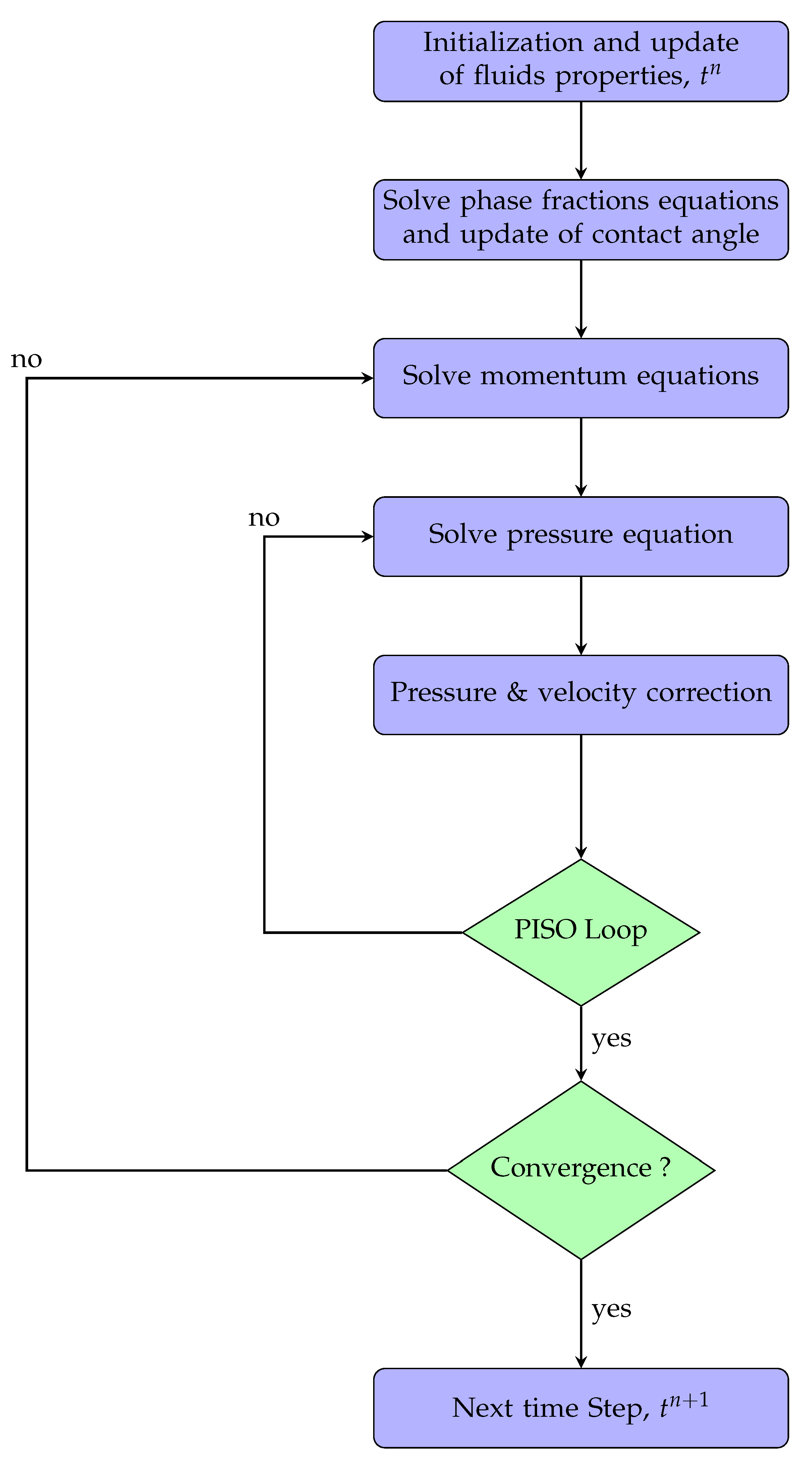
2.4. Numerical Methods
3. Results and Discussion
3.1. Model Validation
3.1.1. Single Phase Flow and 3D Rocks: Absolute Permeability
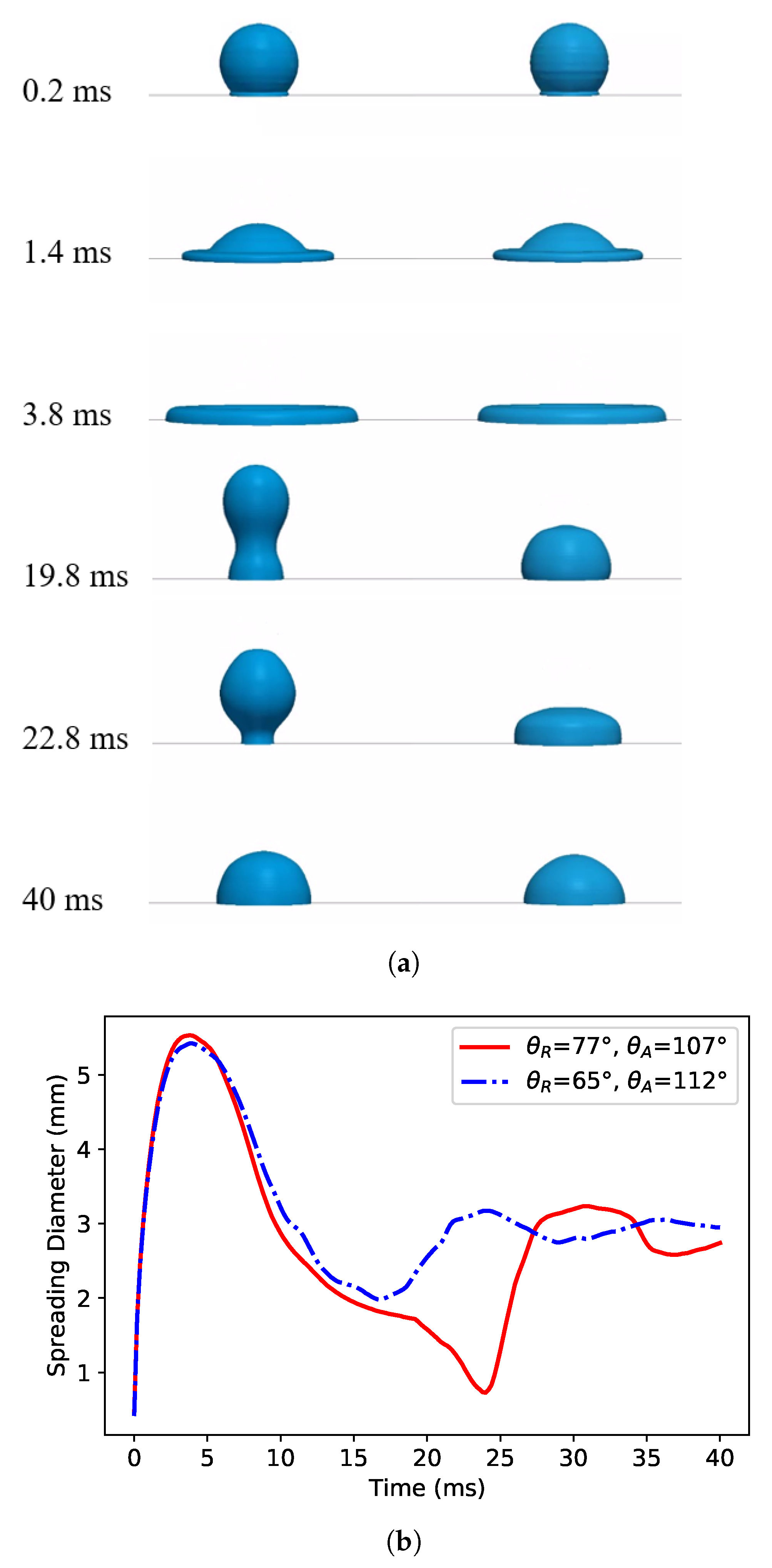
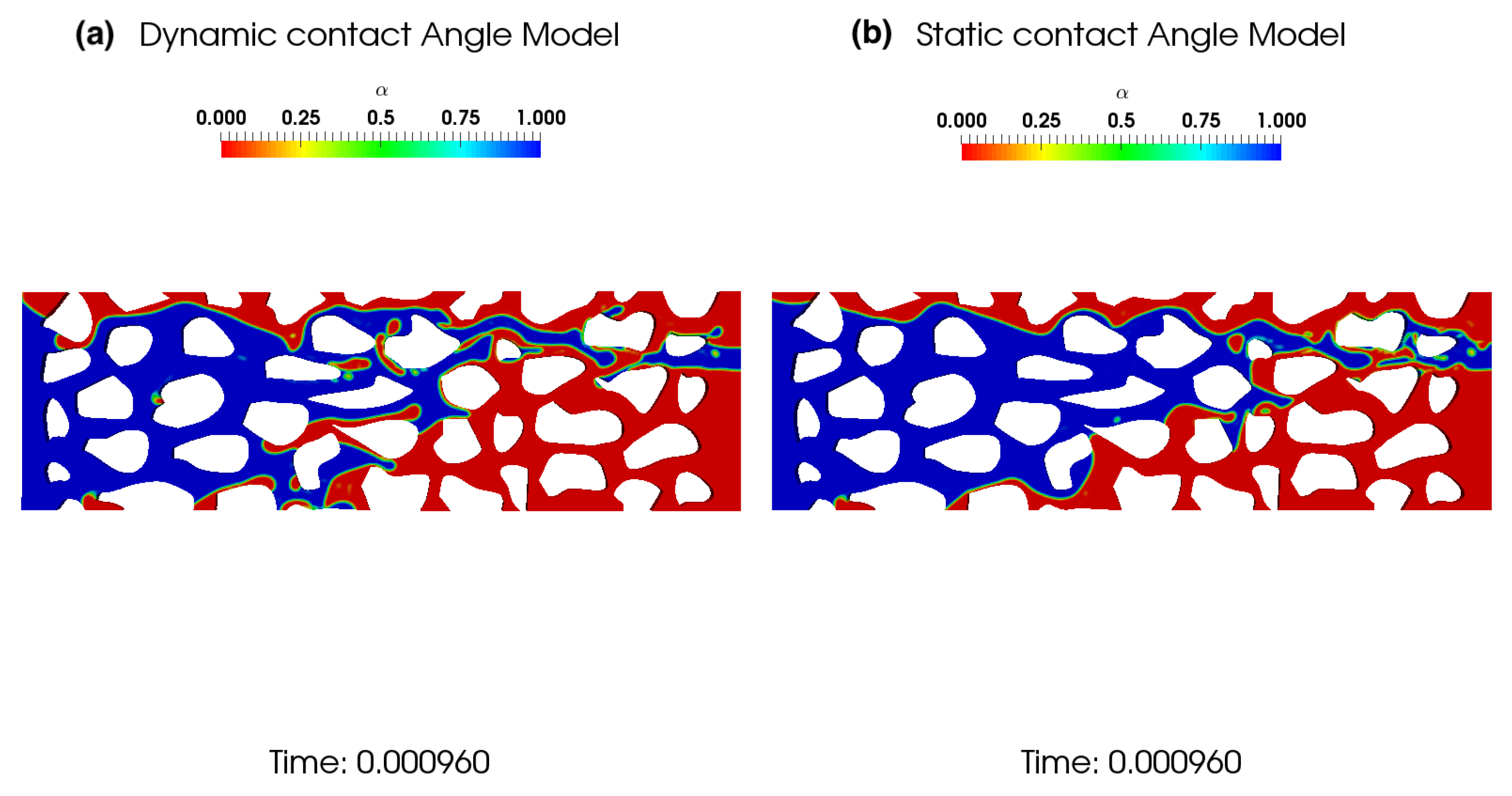
3.1.2. The Relevance of Dynamic Contact Angle in Two-Phase Flow Modeling
3.2. Two-Phase Flow in Porous Media with Hysteresis Effect
3.2.1. Newtonian Fluid
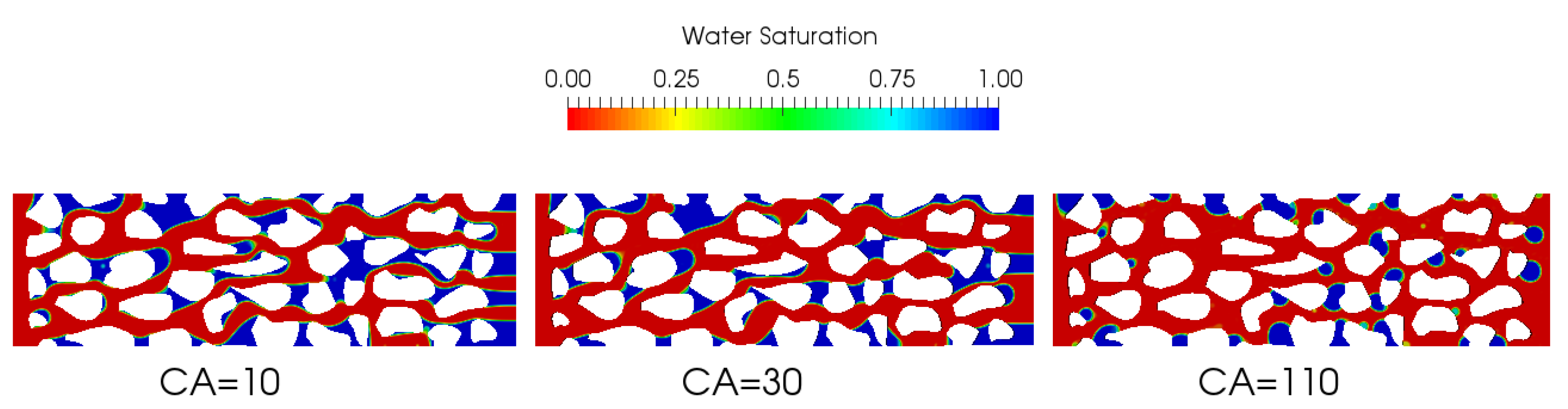
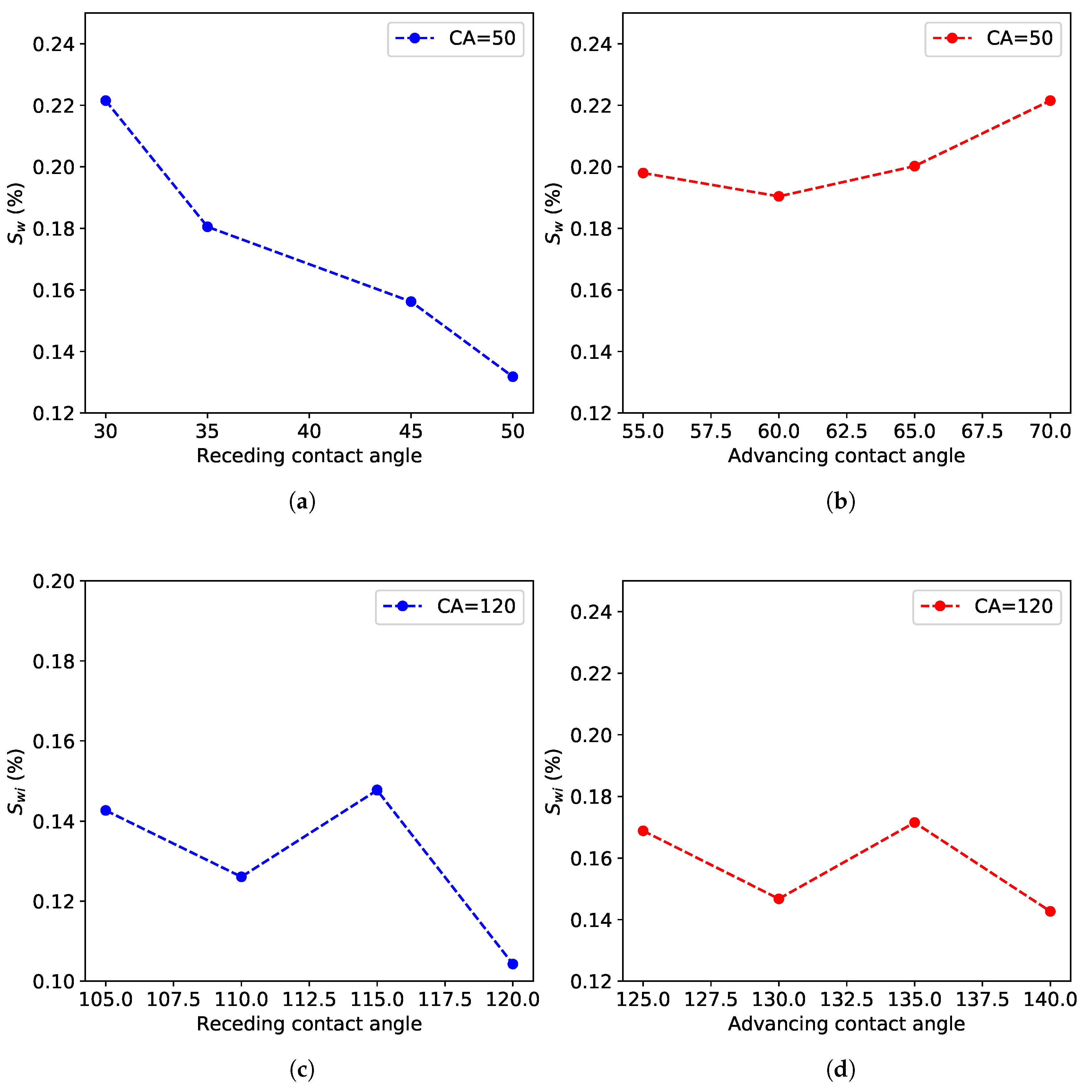
Effect of the Contact Angle Models
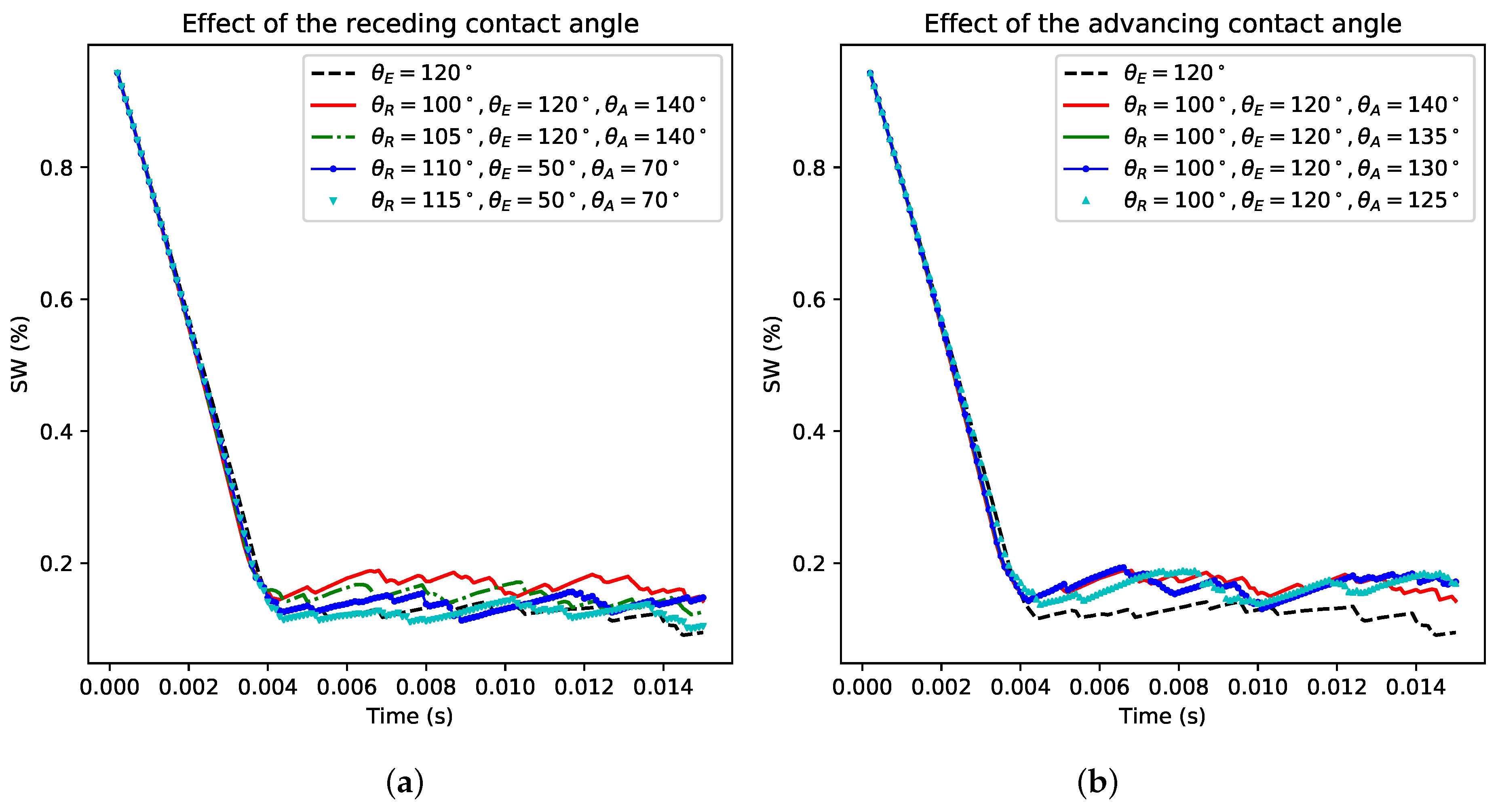
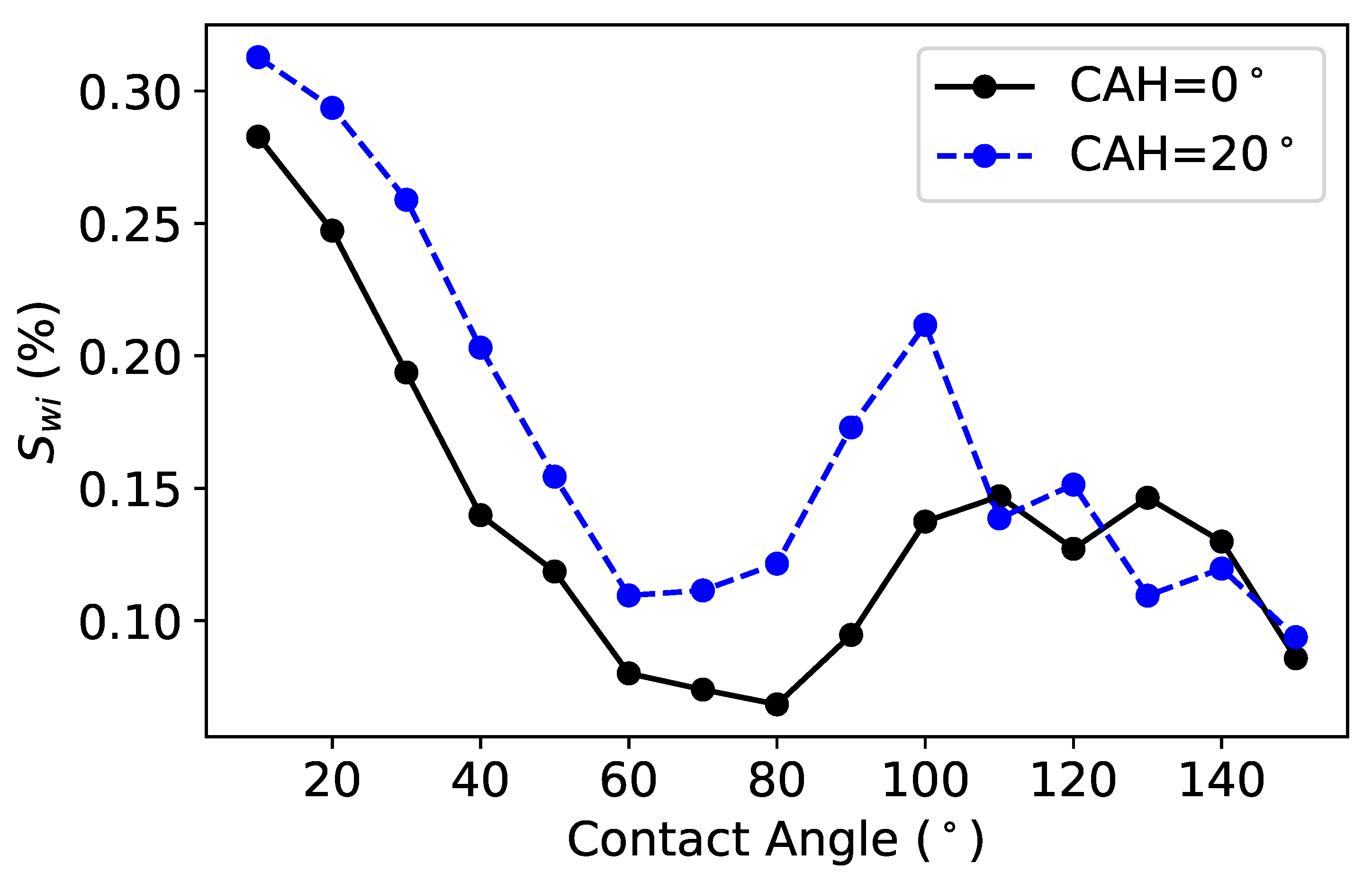
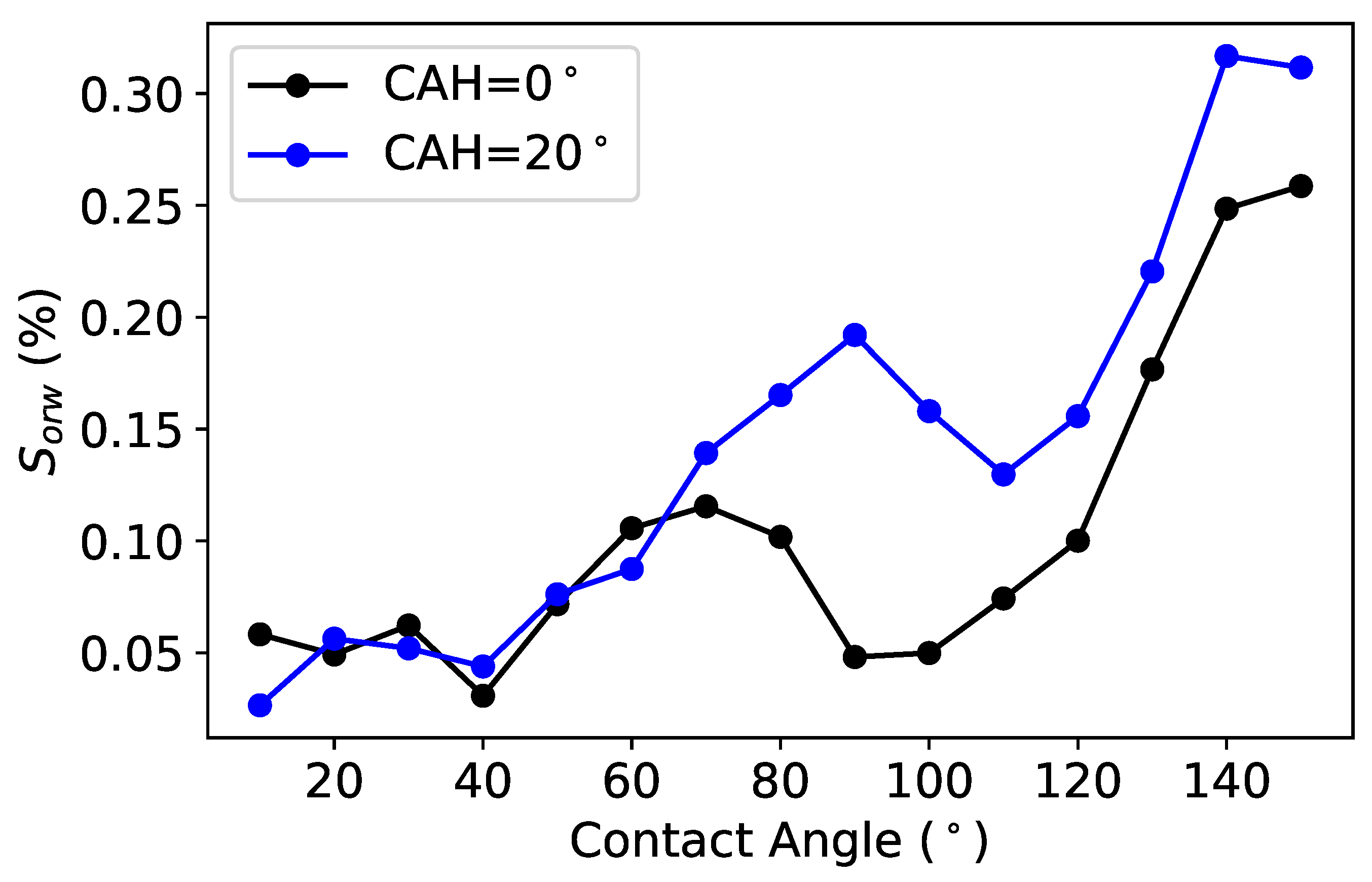
Effect of the Contact Angle Hysteresis
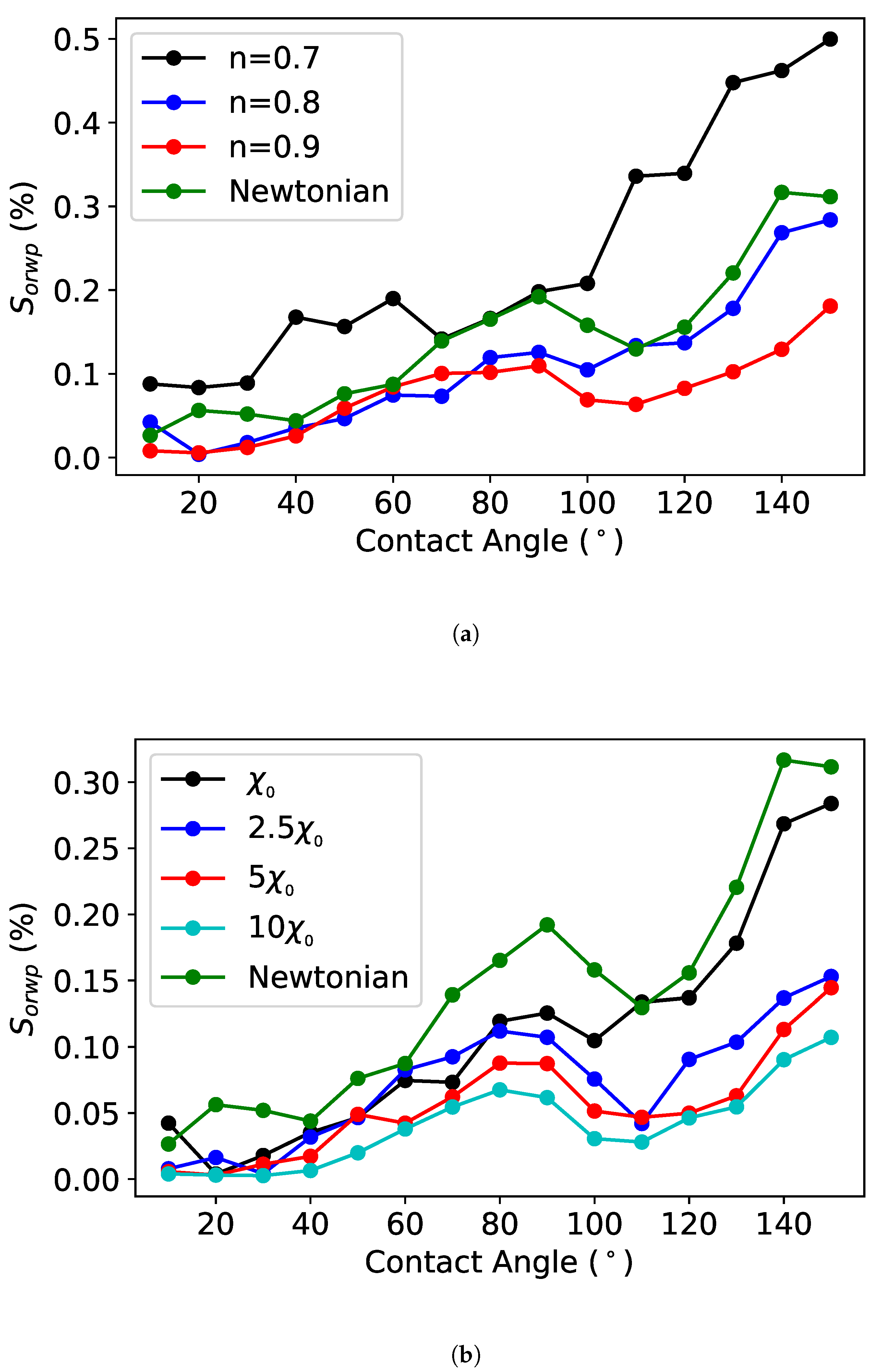
Effect of the Dynamic Contact Angle on and
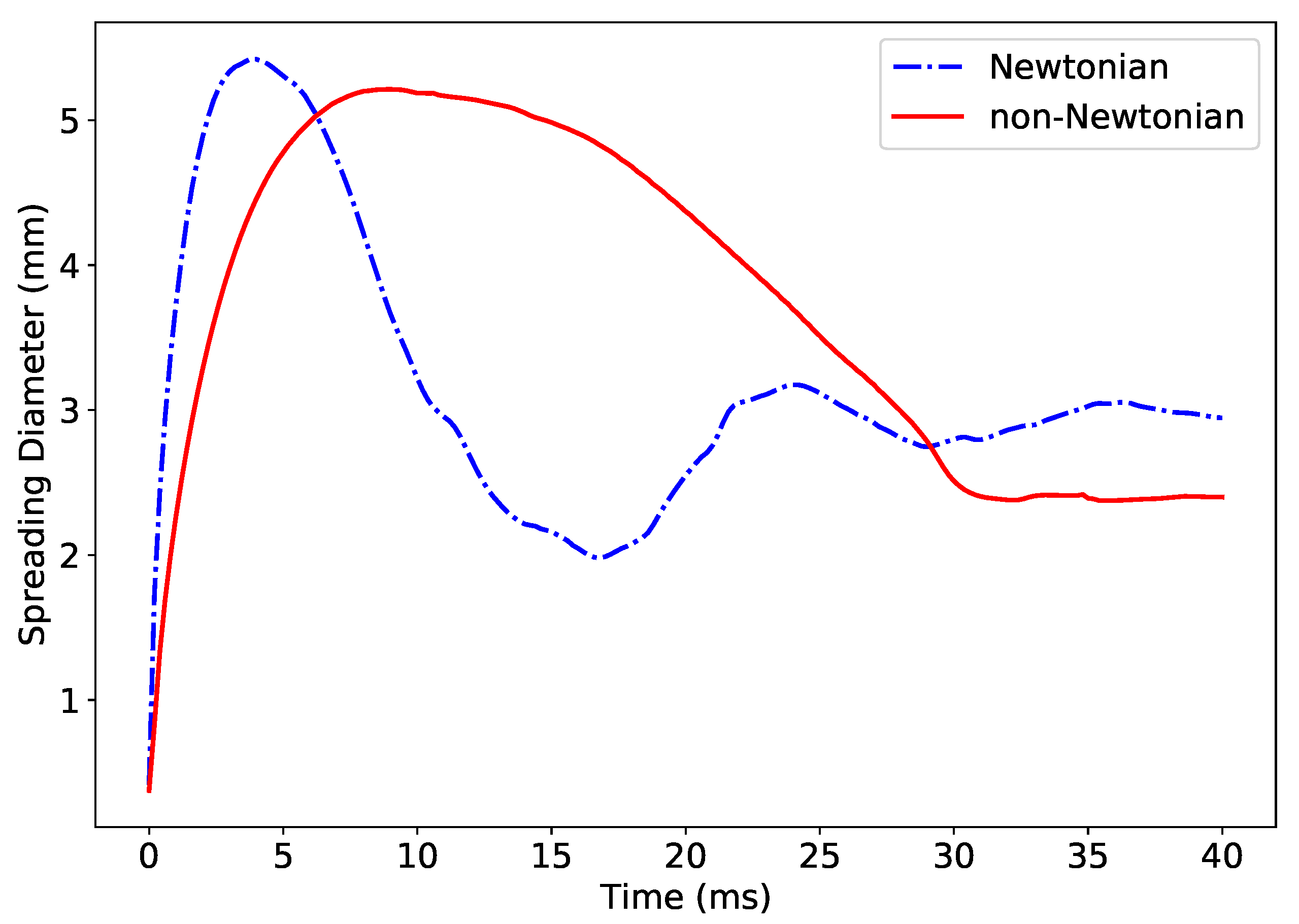
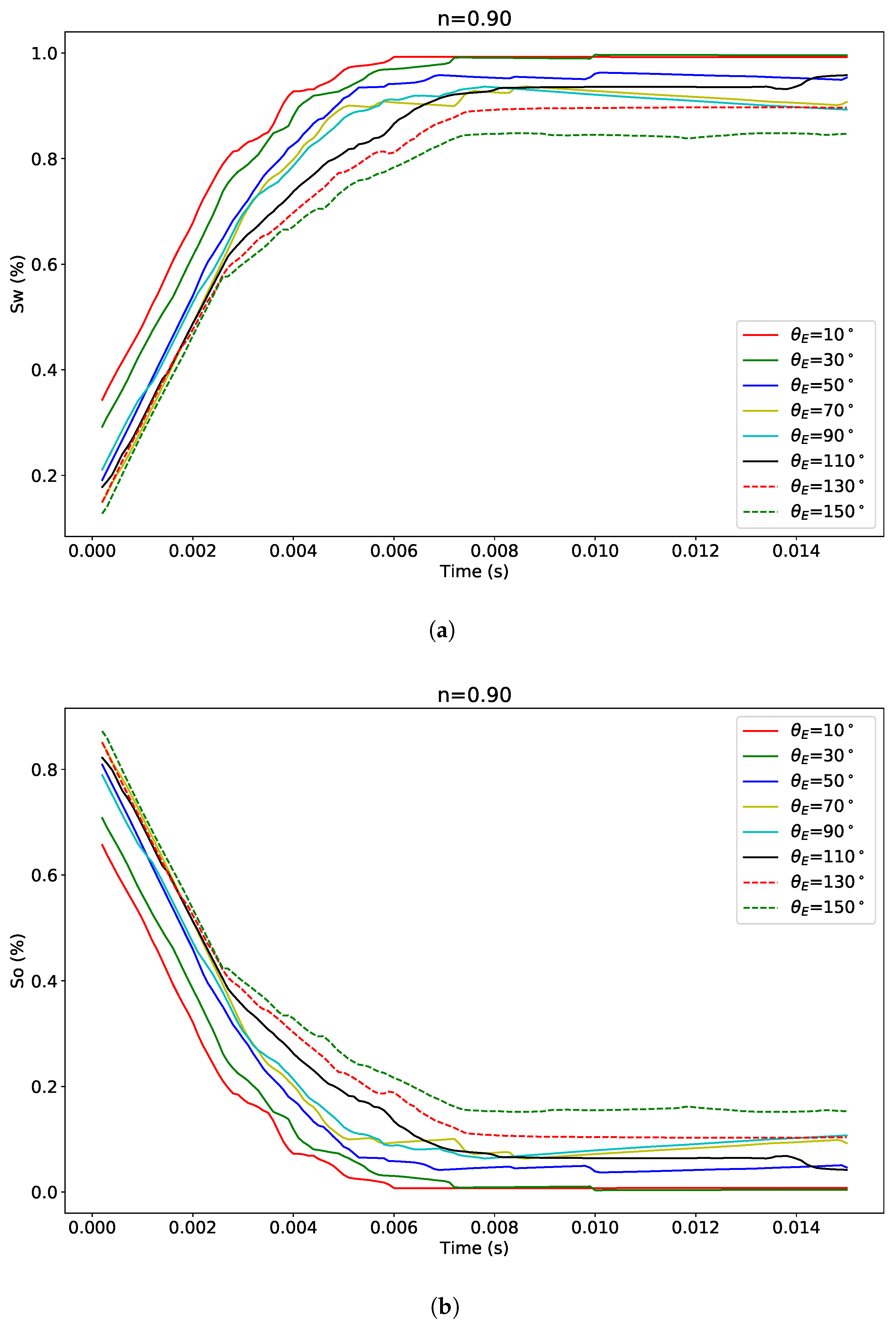
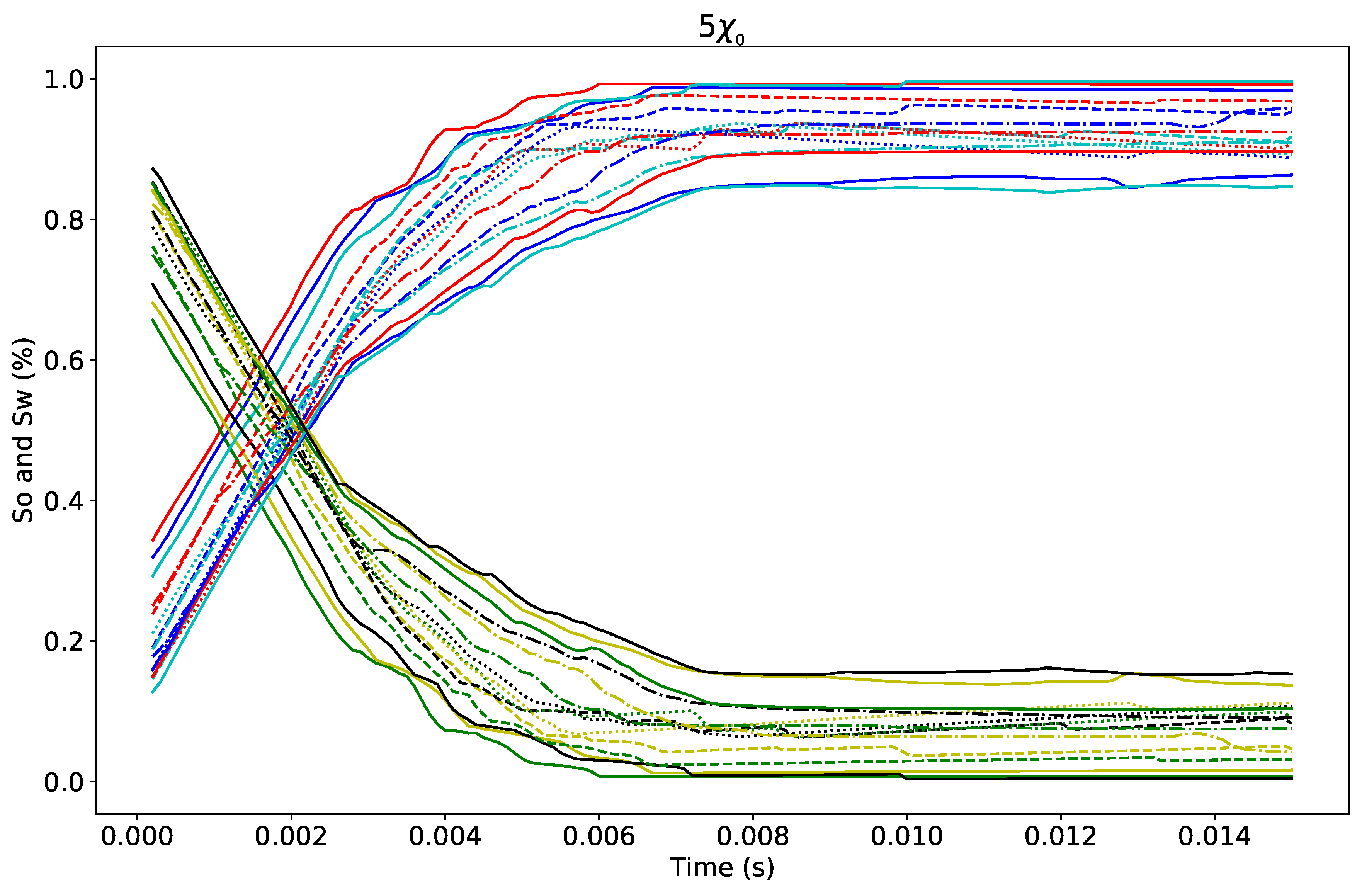
3.2.2. Non-Newtonian Fluid
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-scale imaging and modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef]
- Andrä, H.; Combaret, N.; Dvorkin, J.; Glatt, E.; Han, J.; Kabel, M.; Keehm, Y.; Krzikalla, F.; Lee, M.; Madonna, C.; et al. Digital rock physics benchmarks-Part I: Imaging and segmentation. Comput. Geosci. 2013, 50, 25–32. [Google Scholar] [CrossRef]
- Jouini, M.S.; Vega, S. Simulation of Elastic Properties in Carbonates. Leading Edge 2011, 30, 1400–1407. [Google Scholar] [CrossRef]
- Islam, A.; Faisal, T.F.; Chevalier, S.; Jouini, M.S.; Sassi, M. Multi-scale experimental and numerical simulation workflow of absolute permeability in heterogeneous carbonates. J. Pet. Sci. Eng. 2019, 173, 326–338. [Google Scholar] [CrossRef]
- Jadhunandan, P.P.; Morrow, N.R. Effect of wettability on waterflood recovery for crude-oil/brine/rock systems. SPE Reserv. Eng. (Soc. Pet. Eng.) 1995, 10, 40–46. [Google Scholar] [CrossRef]
- Deng, X.; Kamal, M.S.; Patil, S.; Hussain, S.M.S.; Zhou, X. A Review on Wettability Alteration in Carbonate Rocks: Wettability Modifiers. Energy Fuels 2020, 34, 31–54. [Google Scholar] [CrossRef]
- Dong, H.; Blunt, M.J. Pore-network extraction from micro-computerized-tomography images. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2009, 80, 1–11. [Google Scholar] [CrossRef]
- Mostaghimi, P.; Blunt, M.J.; Bijeljic, B. Computations of Absolute Permeability on Micro-CT Images. Math. Geosci. 2013, 45, 103–125. [Google Scholar] [CrossRef]
- Andrä, H.; Combaret, N.; Dvorkin, J.; Glatt, E.; Han, J.; Kabel, M.; Keehm, Y.; Krzikalla, F.; Lee, M.; Madonna, C.; et al. Digital rock physics benchmarks-part II: Computing effective properties. Comput. Geosci. 2013, 50, 33–43. [Google Scholar] [CrossRef]
- Guibert, R.; Nazarova, M.; Horgue, P.; Hamon, G.; Creux, P.; Debenest, G. Computational Permeability Determination from Pore-Scale Imaging: Sample Size, Mesh and Method Sensitivities. Transp. Porous Media 2015, 107, 641–656. [Google Scholar] [CrossRef]
- Tembely, M.; AlSumaiti, A.M.; Jouini, M.S.; Rahimov, K. The effect of heat transfer and polymer concentration on non-Newtonian fluid from pore-scale simulation of rock X-ray micro-CT. Polymers 2017, 9, 509. [Google Scholar] [CrossRef] [PubMed]
- Tembely, M.; AlSumaiti, A.M.; Alameri, W. A deep learning perspective on predicting permeability in porous media from network modeling to direct simulation. Comput. Geosci. 2020, 24, 1541–1556. [Google Scholar] [CrossRef]
- Jackson, M.D.; Valvatne, P.H.; Blunt, M.J. Prediction of wettability variation and its impact on flow using pore- to reservoir-scale simulations. J. Pet. Sci. Eng. 2003, 39, 231–246. [Google Scholar] [CrossRef]
- Sochi, T. Non-Newtonian flow in porous media. Polymer 2010, 51, 5007–5023. [Google Scholar] [CrossRef]
- Valvatne, P.H.; Piri, M.; Lopez, X.; Blunt, M.J. Predictive pore-scale modeling of single and multiphase flow. Transp. Porous Media 2005, 58, 23–41. [Google Scholar] [CrossRef]
- Eichheimer, P.; Thielmann, M.; Popov, A.; Golabek, G.J.; Fujita, W.; Kottwitz, M.O.; Kaus, B.J. Pore-scale permeability prediction for Newtonian and non-Newtonian fluids. Solid Earth 2019, 10, 1717–1731. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Direct simulations of two-phase flow on micro-CT images of porous media and upscaling of pore-scale forces. Adv. Water Resour. 2014, 74, 116–126. [Google Scholar] [CrossRef]
- Alhammadi, A.M.; Alratrout, A.; Singh, K.; Bijeljic, B.; Blunt, M.J. In situ characterization of mixed-wettability in a reservoir rock at subsurface conditions. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, J.; Bertola, V.; Wang, M. Lattice Boltzmann modeling for multiphase viscoplastic fluid flow. J. Non-Newton. Fluid Mech. 2016, 234, 118–128. [Google Scholar] [CrossRef]
- Xie, C.; Lv, W.; Wang, M. Shear-thinning or shear-thickening fluid for better EOR? — A direct pore-scale study. J. Pet. Sci. Eng. 2018, 161, 683–691. [Google Scholar] [CrossRef]
- Voinov, O.V. Hydrodynamics of wetting. Fluid Dyn. 1976, 11, 714–721. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College London (University of London), London, UK, 2002. [Google Scholar]
- Tembely, M.; Attarzadeh, R.; Dolatabadi, A. On the numerical modeling of supercooled micro-droplet impact and freezing on superhydrophobic surfaces. Int. J. Heat Mass Transf. 2018, 127, 193–202. [Google Scholar] [CrossRef]
- Roisman, I.V.; Opfer, L.; Tropea, C.; Raessi, M.; Mostaghimi, J.; Chandra, S. Drop impact onto a dry surface: Role of the dynamic contact angle. Colloids Surfaces Physicochem. Eng. Asp. 2008, 322, 183–191. [Google Scholar] [CrossRef]
- Berberovic, E. Investigation of Free-Surface Flow Associated with Drop Impact: Numerical Simulations and Theoretical Modeling. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2010. [Google Scholar]
- Habla, F.; Marschall, H.; Hinrichsen, O.; Dietsche, L.; Jasak, H.; Favero, J.L. Numerical Simulation of Viscoelastic Two-Phase Flows Using openFOAM®. Chem. Eng. Sci. 2011, 66, 5487–5496. [Google Scholar] [CrossRef]
- Popinet, S. An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 2009, 228, 5838–5866. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow: Computational Methods in Mechanics and Thermal Science; Hemisphere Publication Corporation: Washington, DC, USA, 1980; pp. 1–197. [Google Scholar]
- Tembely, M.; Vadillo, D.; Soucemarianadin, A.; Dolatabadi, A. Numerical simulations of polymer solution droplet impact on surfaces of different wettabilities. Processes 2019, 7, 798. [Google Scholar] [CrossRef]
- Kistler, S.F. “Hydrodynamics of Wetting" in Wettability. In “Hydrodynamics of Wetting" in Wettability; Berg, J.C., Ed.; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Thompson, R.L.; Soares, E.J. Motion of a power-law long drop in a capillary tube filled by a Newtonian fluid. Chem. Eng. Sci. 2012, 72, 126–141. [Google Scholar] [CrossRef]
- Yokoi, K.; Vadillo, D.; Hinch, J.; Hutchings, I. Numerical studies of the influence of the dynamic contact angle on a droplet impacting on a dry surface. Phys. Fluids 2009, 21. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Tembely, M.; Jadidi, M.; Esmail, N.; Dolatabadi, A. Shear driven droplet shedding and coalescence on a superhydrophobic surface. Phys. Fluids 2015, 27, 32106. [Google Scholar] [CrossRef]
- Vadillo, D.C.; Soucemarianadin, A.; Delattre, C.; Roux, D.C. Dynamic contact angle effects onto the maximum drop impact spreading on solid surfaces. Phys. Fluids 2009, 21, 1–8. [Google Scholar] [CrossRef]
- Antonini, C.; Villa, F.; Bernagozzi, I.; Amirfazli, A.; Marengo, M. Drop rebound after impact: The role of the receding contact angle. Langmuir 2013, 29, 16045–16050. [Google Scholar] [CrossRef] [PubMed]



| Boundaries | Pressures | Velocity | Phase Fraction () |
|---|---|---|---|
| Inlet | normal gradient, = 0 | fixed valued, V | fixed value, |
| Outlet | fixed value, p = 0 Pa | normal gradient, = 0 | normal gradient, = 0 |
| Sides | normal gradient, = 0 | fixed valued, V = 0 | normal gradient, = 0 |
| liquid-solid interface | normal gradient, = 0 | No-slip, V = 0 | contact angle enforced through Equation (14) |
| Sample Name | Voxel Size (μm) | Image Size (X × Y × Z) | PNM | FVM | LBM |
|---|---|---|---|---|---|
| Sandstone | 7.5 | 288 × 288 × 300 | 1353 | 1614 | 1610 |
| Carbonate | 2.02 | 400 × 400 × 400 | 205 | 217 | 214 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tembely, M.; Alameri, W.S.; AlSumaiti, A.M.; Jouini, M.S. Pore-Scale Modeling of the Effect of Wettability on Two-Phase Flow Properties for Newtonian and Non-Newtonian Fluids. Polymers 2020, 12, 2832. https://doi.org/10.3390/polym12122832
Tembely M, Alameri WS, AlSumaiti AM, Jouini MS. Pore-Scale Modeling of the Effect of Wettability on Two-Phase Flow Properties for Newtonian and Non-Newtonian Fluids. Polymers. 2020; 12(12):2832. https://doi.org/10.3390/polym12122832
Chicago/Turabian StyleTembely, Moussa, Waleed S. Alameri, Ali M. AlSumaiti, and Mohamed S. Jouini. 2020. "Pore-Scale Modeling of the Effect of Wettability on Two-Phase Flow Properties for Newtonian and Non-Newtonian Fluids" Polymers 12, no. 12: 2832. https://doi.org/10.3390/polym12122832
APA StyleTembely, M., Alameri, W. S., AlSumaiti, A. M., & Jouini, M. S. (2020). Pore-Scale Modeling of the Effect of Wettability on Two-Phase Flow Properties for Newtonian and Non-Newtonian Fluids. Polymers, 12(12), 2832. https://doi.org/10.3390/polym12122832






