Phase Diagrams of n-Type Low Bandgap Naphthalenediimide-Bithiophene Copolymer Solutions and Blends
Abstract
1. Introduction
2. Experimental and Calculation Methods
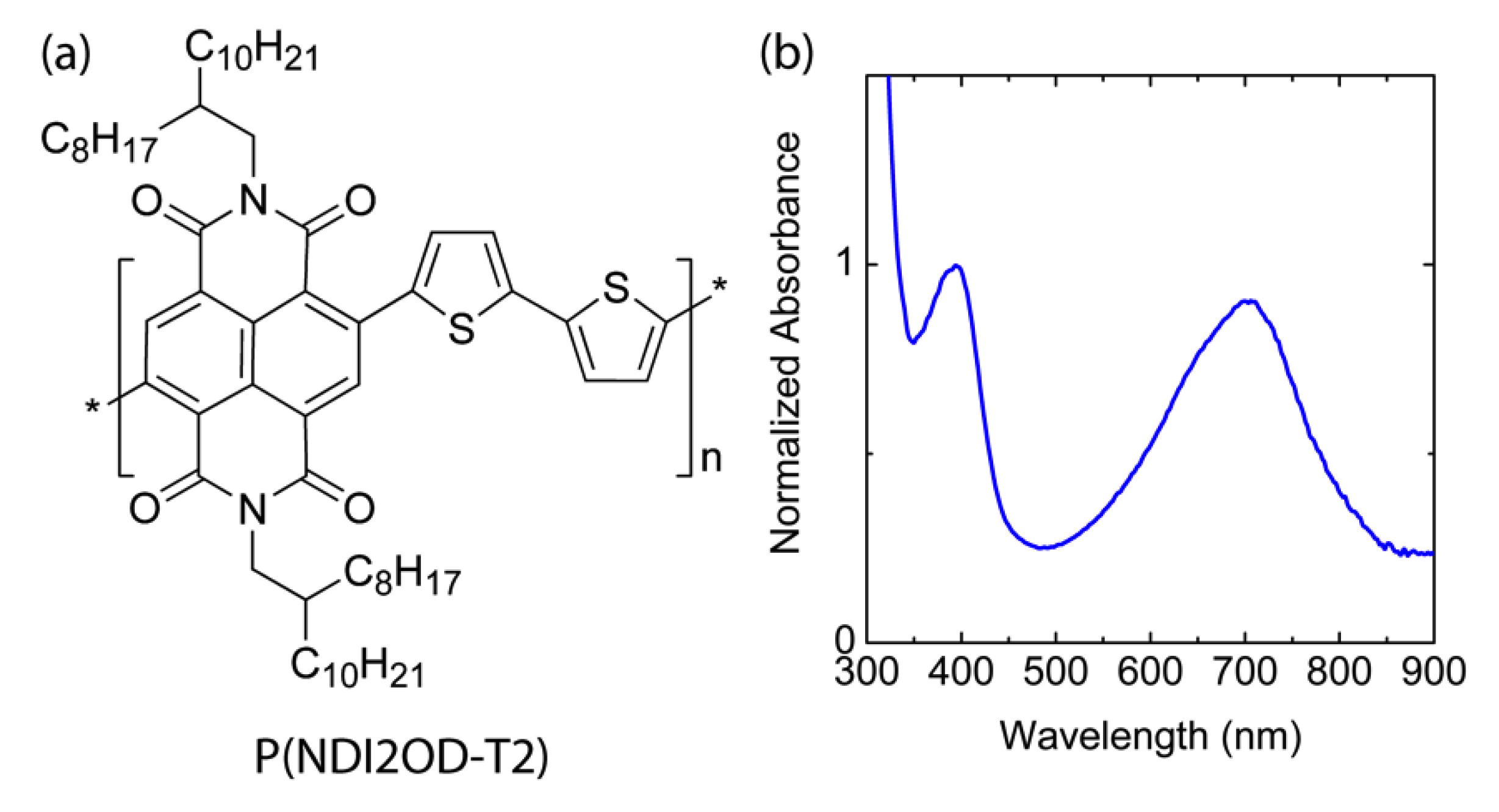
2.1. Materials
2.2. Contact Angle Measurement
2.3. Solubility Parameter Calculation
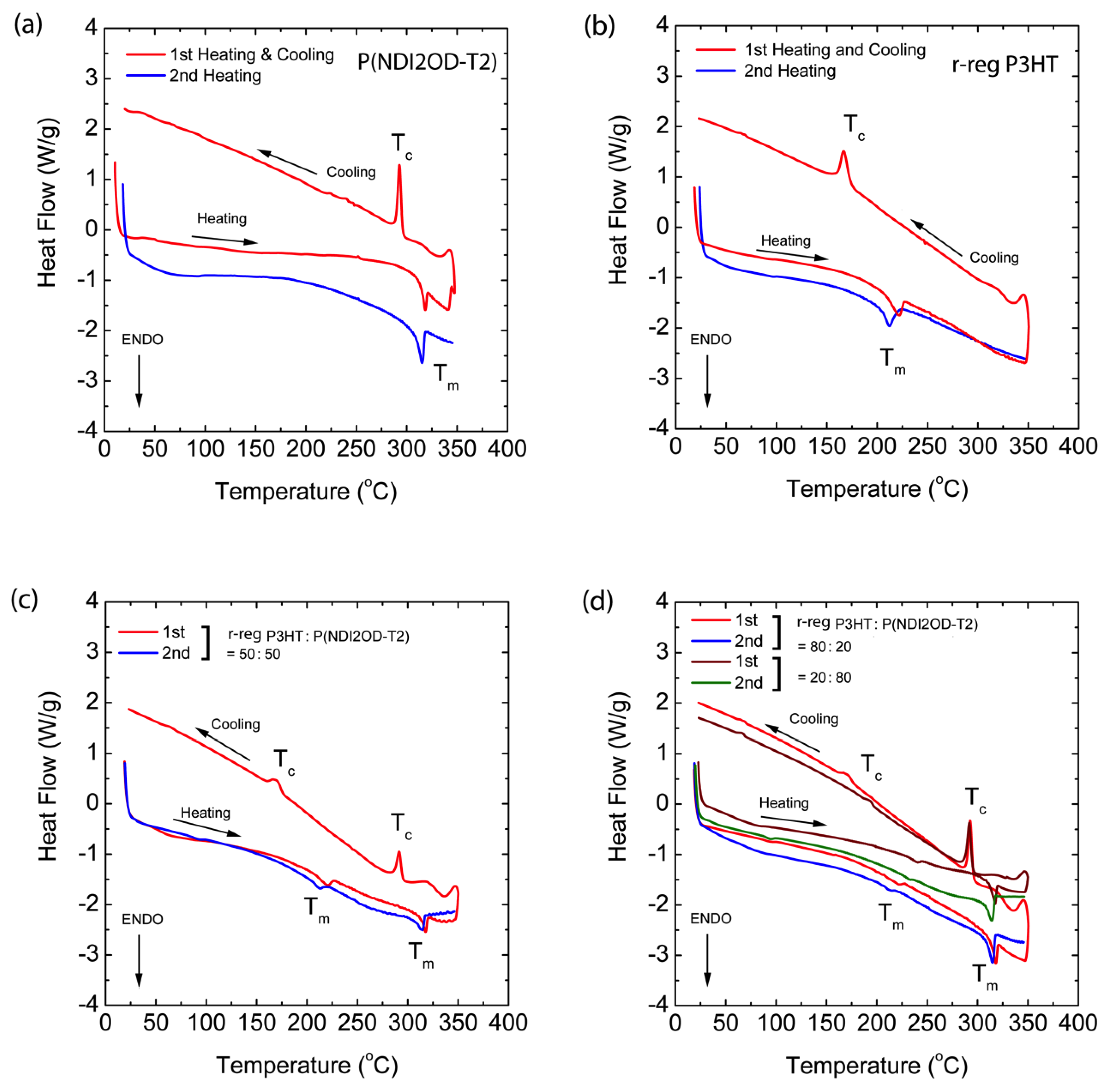
2.4. Thermal Characterization
3. Results and Discussion
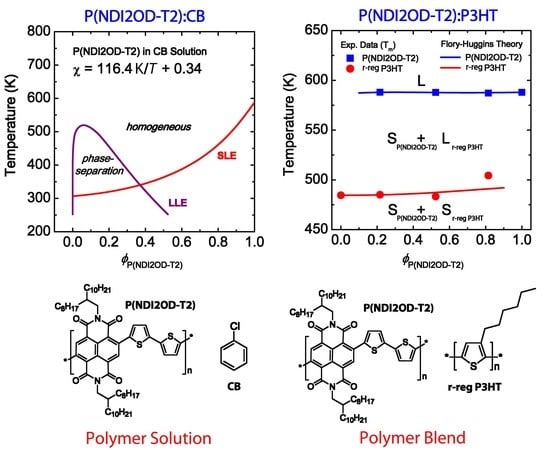
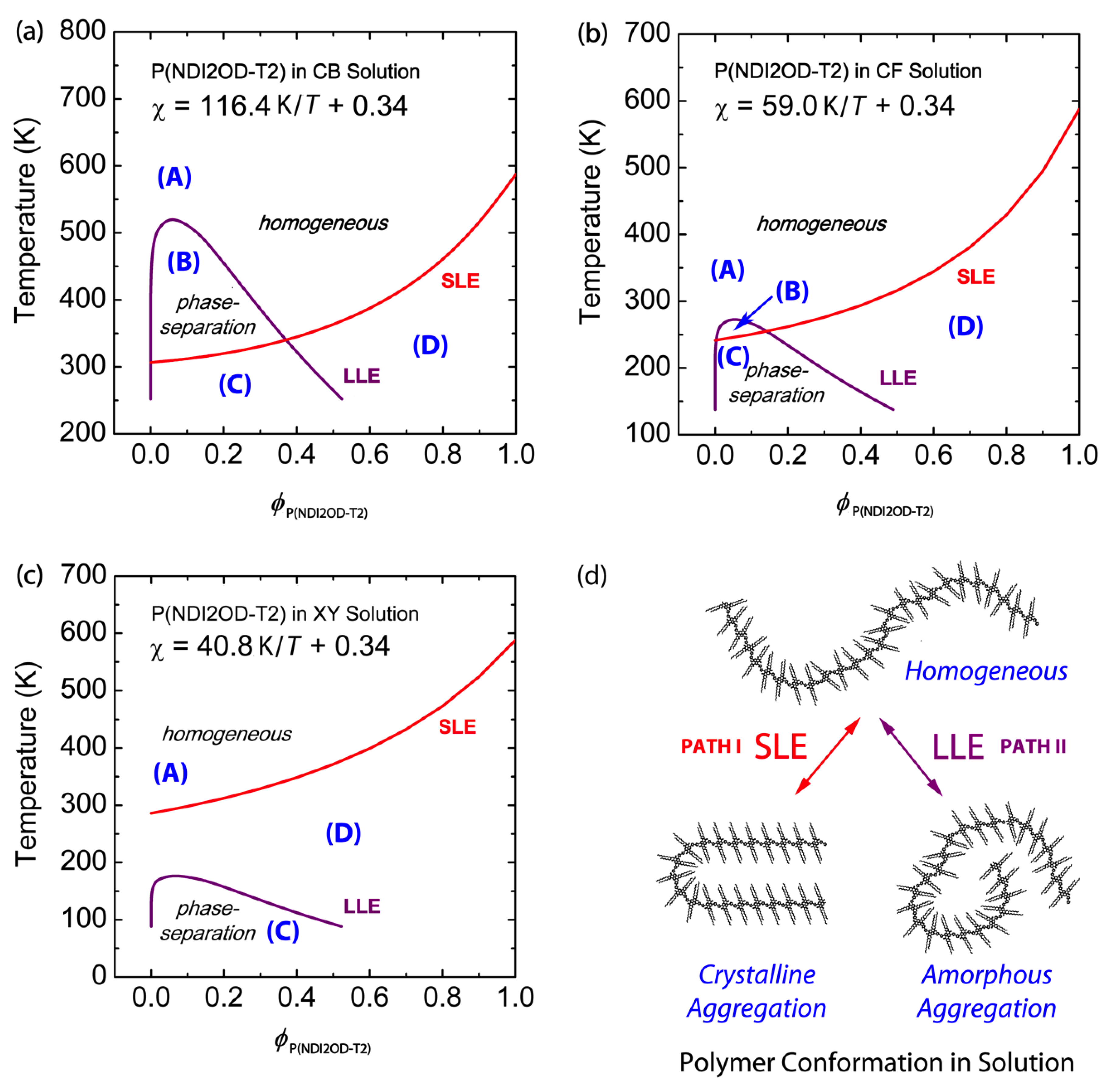
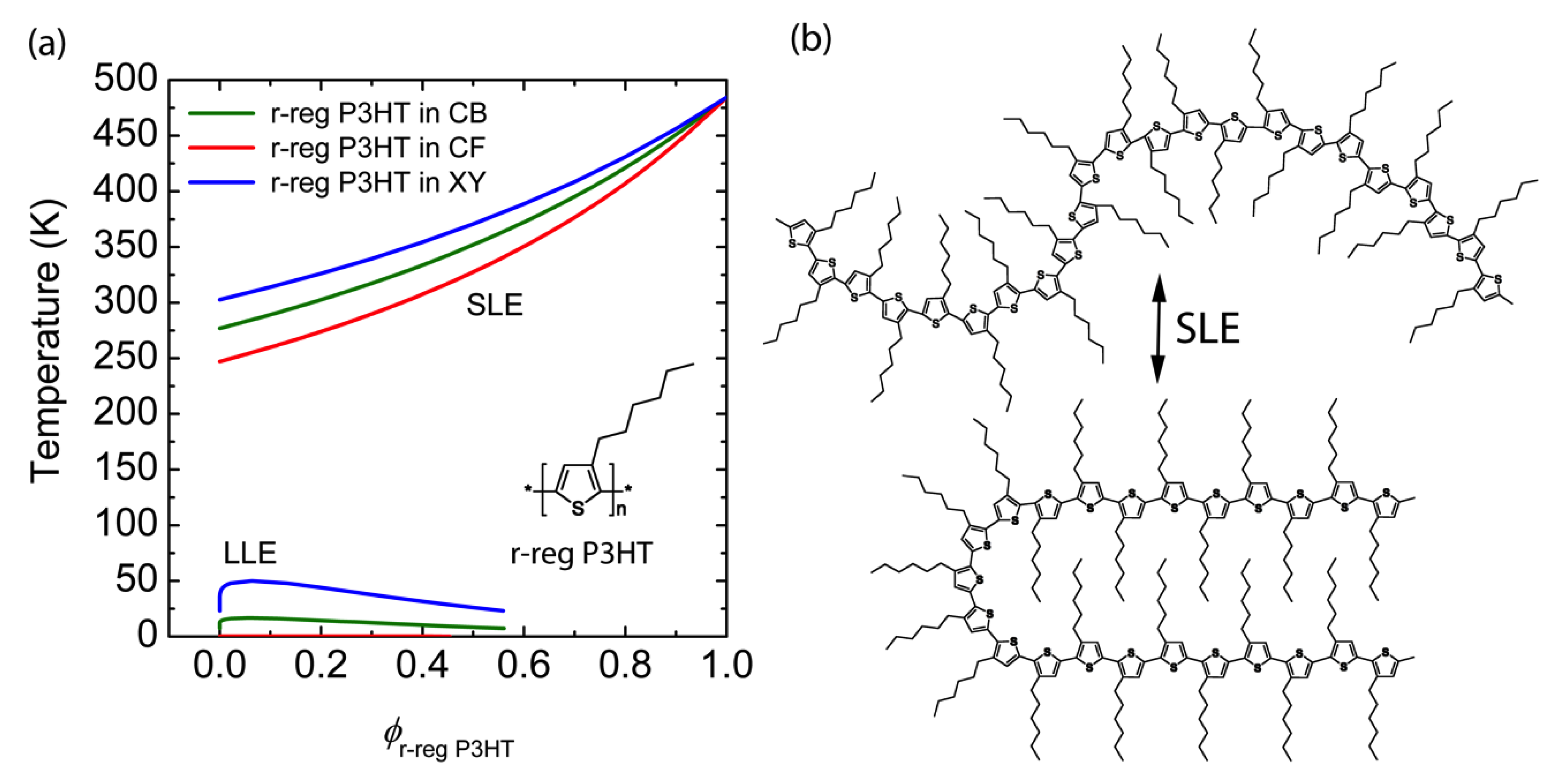
3.1. Binary Polymer–Solvent Mixture
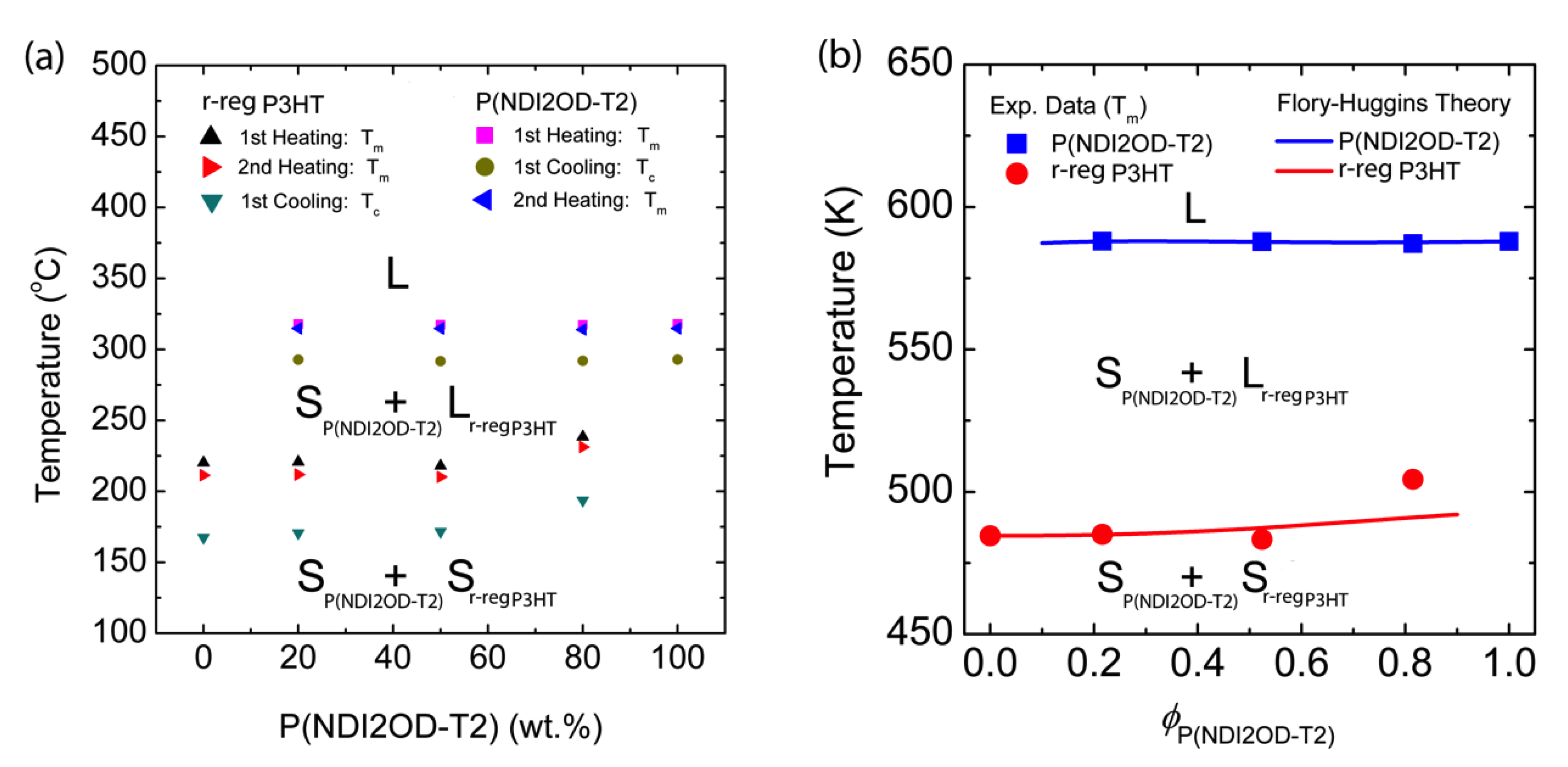
3.2. Binary Polymer–Polymer Mixture
4. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Kim, J.Y. Order-Disorder Phase Equilibria of Regioregular Poly(3-hexylthiophene-2,5,diyl) Solution. Macromolecules 2018, 51, 9026–9034. [Google Scholar] [CrossRef]
- Kim, J.Y. Phase Diagrams of Binary Low Bandgap Conjugated Polymer Solutions and Blends. Macromolecules 2019, 52, 4317. [Google Scholar] [CrossRef]
- Cahn, J.W. Phase Separation by Spinodal Decomposition in Isotropic Systems. J. Chem. Phys. 1965, 42, 93–99. [Google Scholar] [CrossRef]
- Bates, F.S. Polymer-Polymer Phase Behavior. Science 1991, 251, 898. [Google Scholar] [CrossRef] [PubMed]
- McNeill, C.R.; Greenham, N.C. Conjugated-Polymer Blends for Optoelectronics. Adv. Mater. 2009, 21, 3840. [Google Scholar] [CrossRef]
- Binder, K. Collective Diffusion, Nucleation, and Spinodal Decomposition in Polymer Mixtures. J. Chem. Phys. 1983, 79, 6387–6409. [Google Scholar] [CrossRef]
- Favvas, E.P.; Mitropoulos, A.C. What is spinodal decomposition? J. Eng. Sci. Technol. Rev. 2008, 1, 25–37. [Google Scholar] [CrossRef]
- Vaynzof, Y.; Kabra, D.; Zhao, L.; Chua, L.L.; Steiner, U.; Friend, R.H. Surface-Directed Spinodal Decomposition in Poly[3 -hexylthiophene] and C61-Butyric Acid Methyl Ester Blends. ACS Nano 2011, 5, 329–336. [Google Scholar] [CrossRef]
- Whitesides, G.M.; Grzybowski, B. Self-Assembly at All Scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef]
- Whitesides, G.M.; Boncheva, M. Beyond Molecules: Self-Assembly of Mesoscopic and Macroscopic Compounds. PNAS 2002, 99, 4769–4774. [Google Scholar] [CrossRef]
- Wang, G.; Melkonyan, F.S.; Facchetti, A.; Marks, T.J. All-Polymer Solar Cells: Recent Progress, Challenges, and Prospects. Angew. Chem. 2019, 58, 4129–4142. [Google Scholar] [CrossRef] [PubMed]
- Fan, B.; Ying, L.; Zhu, P.; Pan, F.; Liu, F.; Chen, J.; Huang, F.; Cao, Y. All-Polymer Solar Cells Based on a Conjugated Polymer Containing Siloxane-Functionalized Side Chains with Efficiency over 10%. Adv. Mater. 2017, 29, 1703906. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Xu, X.; Zhang, W.; Meng, X.; Genene, Z.; Ma, W.; Mammo, W.; Yartsev, A.; Andersson, M.R.; Janssen, R.A.J.; et al. 9.0% power conversion efficiency from ternary all-polymer solar cells. Energy Environ. Sci. 2017, 10, 2212–2221. [Google Scholar] [CrossRef]
- Li, Z.; Ying, L.; Xie, R.; Zhu, P.; Li, N.; Zhong, W.; Huang, F.; Cao, Y. Designing ternary blend all-polymer solar cells with an efficiency of over 10% and a fill factor of 78%. Nano Energy 2018, 51, 434–441. [Google Scholar] [CrossRef]
- Kolhe, N.B.; Lee, H.; Kuzuhara, D.; Yoshimoto, N.; Koganezawa, T.; Jenekhe, S.A. All-Polymer Solar Cells with 9.4% Efficiency from Naphthalene Diimide-Biselenophene Copolymer Acceptor. Chem. Mater. 2018, 30, 6540–6548. [Google Scholar] [CrossRef]
- Tański, T.; Matysiak, W.; Hajduk, B. Manufacturing and investigation of physical properties of polyacrylonitrile nanofibre composites with SiO2, TiO2 and Bi2O3 nanoparticles. Beilstein J. Nanotechnol. 2016, 7, 1141–1155. [Google Scholar] [CrossRef]
- Matysiak, W.; Tański, T.; Zaborowska, M. Analysis of the Optical Properties of PVP/ZnO Composite Nanofibers. In Properties and Characterization of Modern Materials; Öchsner, A., Altenbach, H., Eds.; Springer: Singapore, 2017; Volume 33. [Google Scholar]
- Tański, T.; Jarka, P.; Szindler, M.; Drygała, A.; Matysiak, W.; Libera, M. Study of dye sensitized solar cells photoelectrodes consisting of nanostructures. Appl. Surf. Sci. 2019, 491, 807. [Google Scholar] [CrossRef]
- Liu, Z.; Zeng, D.; Gao, X.; Li, P.; Zhang, Q.; Peng, X. Non-fullerene polymer acceptors based on perylene diimides in all-polymer solar cells. Solar Energ. Mat. Sol. C. 2019, 189, 103–117. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, Y.; Zhang, Q.; Gao, X. Non-fullerene small molecule acceptors based on perylene diimides. J. Mater. Chem. A 2016, 4, 17604–17622. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Y.; Dong, J.; Yang, M.; Liu, M.; Zhang, Y.; Wen, J.; Ma, H.; Gao, X.; Chen, W.; et al. Chlorinated Wide-Bandgap Donor Polymer Enabling Annealing Free Nonfullerene Solar Cells with the Efficiency of 11.5%. J. Phys. Chem. Lett. 2018, 9, 6955–6962. [Google Scholar] [CrossRef]
- Wen, S.; Yu, Y.; Wang, Y.; Li, Y.; Liu, L.; Jiang, H.; Liu, Z.; Yang, R. Pyran-Bridged Indacenodithiophene as a Building Block for Constructing Efficient A–D–A-Type Nonfullerene Acceptors for Polymer Solar Cells. ChemSusChem 2018, 11, 360–366. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, L.; Shao, M.; Wu, Y.; Zeng, D.; Cai, X.; Duan, J.; Zhang, X.; Gao, X. Fine-Tuning the Quasi-3D Geometry: Enabling Efficient Nonfullerene Organic Solar Cells Based on Perylene Diimides. ACS Appl. Mater. Interfaces 2018, 10, 762–768. [Google Scholar] [CrossRef] [PubMed]
- Yao, H.; Bai, F.; Hu, H.; Arunagiri, L.; Zhang, J.; Chen, Y.; Yu, H.; Chen, S.; Liu, T.; Lai, J.Y.L.; et al. Efficient All-Polymer Solar Cells based on a New Polymer Acceptor Achieving 10.3% Power Conversion Efficiency. ACS Energy Lett. 2019, 4, 417–422. [Google Scholar] [CrossRef]
- Fan, B.; Zhang, D.; Li, M.; Zhong, W.; Zeng, Z.; Ying, L.; Huang, F.; Cao, Y. Achieving over 16% efficiency for single-junction organic solar cells. Sci. China Chem. 2019, 62, 405. [Google Scholar] [CrossRef]
- Yan, H.; Chen, Z.; Zheng, Y.; Newman, C.; Quinn, J.R.; Dotz, F.; Kastler, M.; Faccetti, A. A high-mobility electron-transporting polymer for printed transistors. Nature 2009, 457, 679. [Google Scholar] [CrossRef]
- Moore, J.R.; Albert-Seifried, A.; Rao, A.; Massip, S.; Watts, B.; Morgan, D.J.; Friend, R.H.; McNeill, C.R.; Sirringhaus, H. Polymer Blend Solar Cells Based on a High-Mobility Naphthalenediimide-Based Polymer Acceptor: Device Physics, Photophysics and Morphology. Adv. Energy Mater. 2011, 1, 230–240. [Google Scholar] [CrossRef]
- Fabiano, S.; Chen, Z.; Vahedi, S.; Facchetti, A.; Pignataro, B.; Loi, M.A. Role of photoactive layer morphology in high fill factor all-polymer bulk heterojunction solar cells. J. Mater. Chem. 2011, 21, 5891–5896. [Google Scholar] [CrossRef]
- Schuettfort, T.; Huettner, S.; Lilliu, S.; Macdonald, J.E.; Thomsen, L.; McNeill, C.R. Surface and Bulk Structural Characterization of a High-Mobility Electron-Transporting Polymer. Macromolecules 2011, 44, 1530–1539. [Google Scholar] [CrossRef]
- Steyrleuthner, R.; Schubert, M.; Howard, I.; Klaumunzer, B.; Schilling, K.; Chen, Z.; Saalfrank, P.; Laquai, F.; Facchetti, A.; Neher, D. Aggregation in a High-Mobility n-Type Low-Bandgap Copolymer with Implications on Semicrystalline Morphology. J. Am. Chem. Soc. 2012, 134, 18303–18317. [Google Scholar] [CrossRef]
- Schubert, M.; Dolfen, D.; Frisch, J.; Roland, S.; Steyrleuthner, R.; Stiller, B.; Chen, Z.; Scherf, U.; Koch, N.; Facchetti, A.; et al. Influence of Aggregation on the Performance of All-Polymer Solar Cells Containing Low-Bandgap Naphthalenediimide Copolymers. Adv. Energy Mater. 2012, 2, 369–380. [Google Scholar] [CrossRef]
- Yan, H.; Collins, B.A.; Gann, E.; Wang, C.; Ade, H.; McNeill, C.R. Correlating the Efficiency and Nanomorphology of Polymer Blend Solar Cells Utilizing Resonant Soft X-ray Scattering. ACS Nano 2012, 6, 677–688. [Google Scholar] [CrossRef] [PubMed]
- Mori, D.; Benten, H.; Okada, I.; Ohkita, H.; Ito, S. Highly efficient charge-carrier generation and collection in polymer/polymer blend solar cells with a power conversion efficiency of 5.7%. Energy Environ. Sci. 2014, 7, 2939–2943. [Google Scholar] [CrossRef]
- Zhou, K.; Zhang, R.; Jiu, J.; Li, M.; Yu, X.; Xing, R.; Han, Y. Donor/Acceptor Molecular Orientation-Dependent Photovoltaic Performance in All-Polymer Solar Cells. ACS Appl. Mater. Interfaces 2015, 7, 25352–25361. [Google Scholar] [CrossRef] [PubMed]
- Zerson, M.; Neumann, M.; Steyrleuthner, R.; Neher, D.; Magerle, R. Surface Structure of Semicrystalline Naphthalene Diimide–Bithiophene Copolymer Films Studied with Atomic Force Microscopy. Macromolecules 2016, 49, 6549–6557. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, H.; Zhou, K.; Zhang, J.; Yu, X.; Liu, J.; Han, Y. Molecular Orientation and Phase Separation by Controlling Chain Segment and Molecule Movement in P3HT/N2200 Blends. Macromolecules 2016, 49, 6987–6996. [Google Scholar] [CrossRef]
- Pope, M.; Swenberg, C.E. Electronic Processes in Organic Crystals and Polymers, 2nd ed.; Oxford Science Publications: New York, NY, USA, 1999. [Google Scholar]
- Gregg, B.A.; Hanna, M.C. Comparing organic to inorganic photovoltaic cells: Theory, experiment, and simulation. J. Appl. Phys. 2003, 93, 3605–3614. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of High Polymer Solutions. J. Chem. Phys. 1942, 10, 51–61. [Google Scholar] [CrossRef]
- Huggins, M.L. Some Properties of Solutions of Long-chain Compounds. J. Phys. Chem. 1942, 46, 151–158. [Google Scholar] [CrossRef]
- Li, D.; Neumann, A.W. A Reformulation of the Equation of State for Interfacial Tensions. J. Colloid Interface Sci. 1990, 137, 304–307. [Google Scholar] [CrossRef]
- Li, D.; Neumann, A.W. Contact Angles on Hydrophobic Solid Surfaces and Their Interpretation. J. Colloid Interface Sci. 1992, 148, 190–200. [Google Scholar] [CrossRef]
- Belmares, M.; Blanco, M.; Goddard, W.A., III; Ross, R.B.; Caldwell, G.; Chou, S.-H.; Pham, J.; Olofson, P.M.; Thomas, C. Hildebrand and Hansen solubility parameters from Molecular Dynamics with applications to electronic nose polymer sensors. J. Comput. Chem. 2004, 25, 1814–1826. [Google Scholar] [CrossRef] [PubMed]
- Patterson, D. Free Volume and Polymer Solubility. A Qualitative View. Macromolecules 1969, 2, 672–677. [Google Scholar] [CrossRef]
- Koningsveld, R.; Staverman, A.J. Liquid–liquid phase separation in multicomponent polymer solutions. II. The critical state. J. Polym. Sci. Part A-2: Polym. Phys. 1968, 6, 325. [Google Scholar] [CrossRef]
- Riedl, B.; Prud’Homme, R.E. Thermodynamics of miscible polymer blends using a concentration-dependent χ parameter. J. Polym. Sci. B Polym. Phys. 1988, 26, 1769–1780. [Google Scholar] [CrossRef]
- Qian, C.; Mumby, S.J.; Eichinger, B.E. Phase Diagrams of Binary Polymer Solutions and Blends. Macromolecules 1991, 24, 1655–1661. [Google Scholar] [CrossRef]
- Takacs, C.J.; Treat, N.D.; Kramer, S.; Chen, Z.; Facchetti, A.; Chabinyc, M.L.; Heeger, A.J. Remarkable Order of a High-Performance Polymer. Nano Lett. 2013, 13, 2522–2527. [Google Scholar] [CrossRef] [PubMed]
- Clark, J.; Chang, J.-F.; Spano, F.C.; Friend, R.H.; Silva, C. Determining exciton bandwidth and film microstructure in polythiophene films using linear absorption spectroscopy. Appl. Phys. Lett. 2009, 94, 163306. [Google Scholar] [CrossRef]
- Richards, R.B. The phase equilibria between a crystalline polymer and solvents. Trans. Faraday Soc. 1946, 42, 10–28. [Google Scholar] [CrossRef]
- Flory, P.J.; Mandelkern, L.; Hall, H.K. Crystallization in High Polymers. VII. Heat of Fusion of Poly-(N,N′-sebacoylpiperazine) and its Interaction with Diluents. J. Am. Chem. Soc. 1951, 73, 2532–2538. [Google Scholar] [CrossRef]
- Dereje, M.M.; Ji, D.; Kang, S.-H.; Yang, C.D.; Noh, Y.-Y. Effect of pre-aggregation in conjugated polymer solution on performance of diketopyrrolopyrrole-based organic field-effect transistors. Dyes Pigments 2017, 145, 270–276. [Google Scholar] [CrossRef]
- Hiemenz, P.C.; Lodge, T.P. Polymer Chemistry, 2nd ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2007. [Google Scholar]
- Kim, J.Y.; Frisbie, C.D. Correlation of Phase Behavior and Charge Transport in Conjugated Polymer/Fullerene Blends. J. Phys. Chem. C 2008, 112, 17726. [Google Scholar] [CrossRef]
- Ye, L.; Hu, H.; Ghasemi, M.; Wang, T.; Collins, B.A.; Kim, J.H.; Jiang, K.; Carpenter, J.H.; Li, H.; Li, Z.; et al. Quantitative Relations Between Interaction Parameter, Miscibility and Function in Organic Solar Cells. Nat. Mater. 2018, 17, 253. [Google Scholar] [CrossRef] [PubMed]
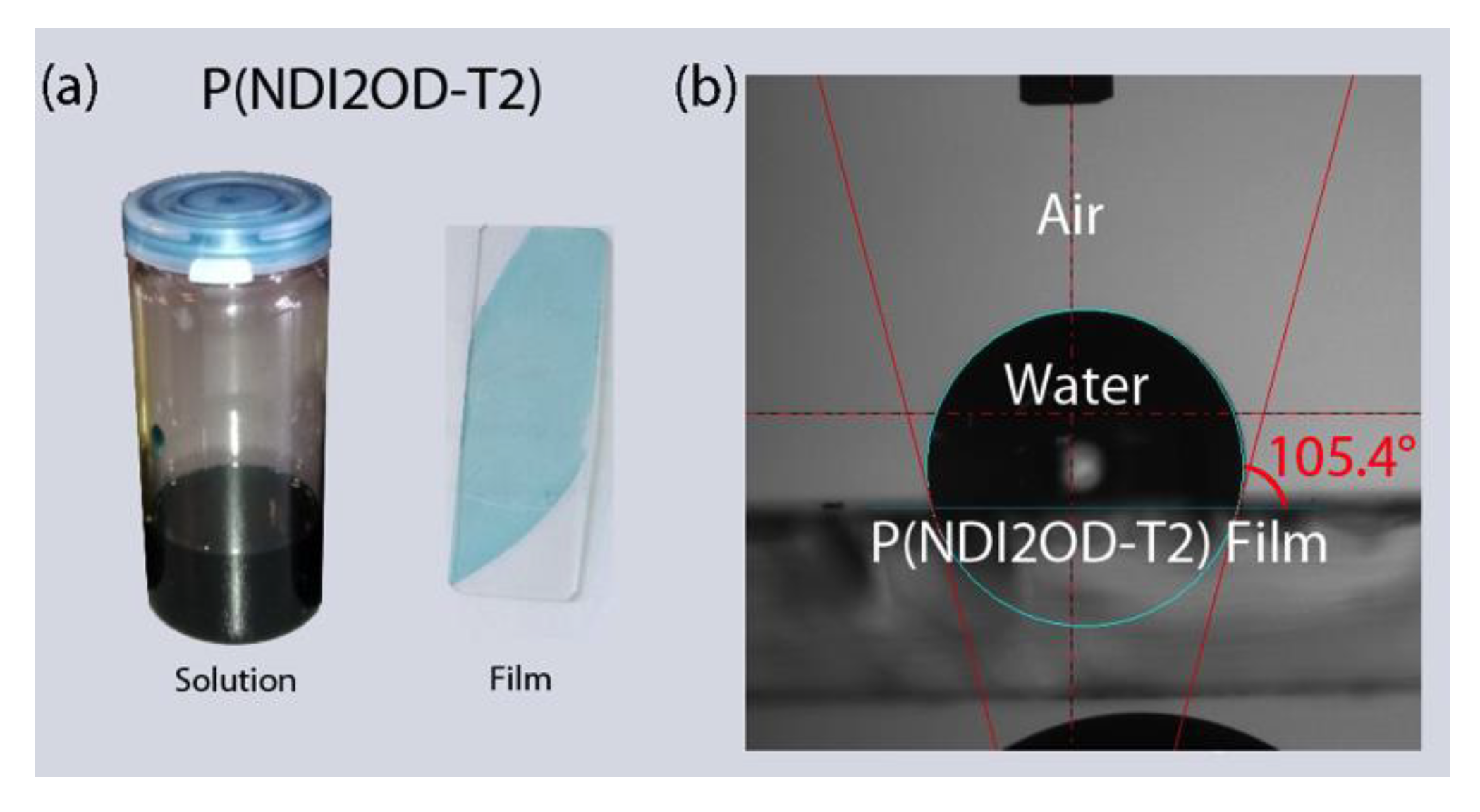
| Materials | Contact Angle (°) | Surface Energy (mJ/m2) | Solubility Parameter (cal/cm3)1/2 |
|---|---|---|---|
| P(NDI2OD-T2) | 105.40 | 19.07 | 7.99 |
| r-reg P3HT | 94.90 | 25.48 | 9.23 |
| Solvent | Solubility Parameter (cal/cm3)1/2 | Molecular Weight (g/mol) | Molar Volume (cm3/mol) | Density (g/cm3) | Boiling Point (°C) | Radius of Lattice Site Volume (nm) |
|---|---|---|---|---|---|---|
| CB | 9.5 | 112.56 | 101.41 | 1.11 | 132 | 0.34 |
| CF | 9.2 | 119.38 | 80.12 | 1.49 | 61 | 0.31 |
| XY | 8.8 | 106.16 | 123.44 | 0.86 | 138 | 0.36 |
| Solvent | P(NDI2OD-T2)/Solvent Mixture | R-reg P3HT/Solvent Mixture | ||
|---|---|---|---|---|
| CB | 288 | 116.4 K/T + 0.34 | 265 | 3.72 K/T + 0.34 |
| CF | 364 | 59.0 K/T + 0.34 | 336 | 0.04 K/T + 0.34 |
| XY | 236 | 40.8 K/T + 0.34 | 218 | 11.49 K/T + 0.34 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fanta, G.M.; Jarka, P.; Szeluga, U.; Tański, T.; Kim, J.Y. Phase Diagrams of n-Type Low Bandgap Naphthalenediimide-Bithiophene Copolymer Solutions and Blends. Polymers 2019, 11, 1474. https://doi.org/10.3390/polym11091474
Fanta GM, Jarka P, Szeluga U, Tański T, Kim JY. Phase Diagrams of n-Type Low Bandgap Naphthalenediimide-Bithiophene Copolymer Solutions and Blends. Polymers. 2019; 11(9):1474. https://doi.org/10.3390/polym11091474
Chicago/Turabian StyleFanta, Gada Muleta, Pawel Jarka, Urszula Szeluga, Tomasz Tański, and Jung Yong Kim. 2019. "Phase Diagrams of n-Type Low Bandgap Naphthalenediimide-Bithiophene Copolymer Solutions and Blends" Polymers 11, no. 9: 1474. https://doi.org/10.3390/polym11091474
APA StyleFanta, G. M., Jarka, P., Szeluga, U., Tański, T., & Kim, J. Y. (2019). Phase Diagrams of n-Type Low Bandgap Naphthalenediimide-Bithiophene Copolymer Solutions and Blends. Polymers, 11(9), 1474. https://doi.org/10.3390/polym11091474