Computational Investigations on Soundproof Applications of Foam-Formed Cellulose Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Background Approaches
2.2. Materials
2.3. Methods
2.3.1. Foam Forming Methods
2.3.2. Microscopic Studies and Structural Analysis
2.3.3. Acoustics Evaluation
2.3.4. Geometrical Properties
2.3.5. Transport Properties
3. Results
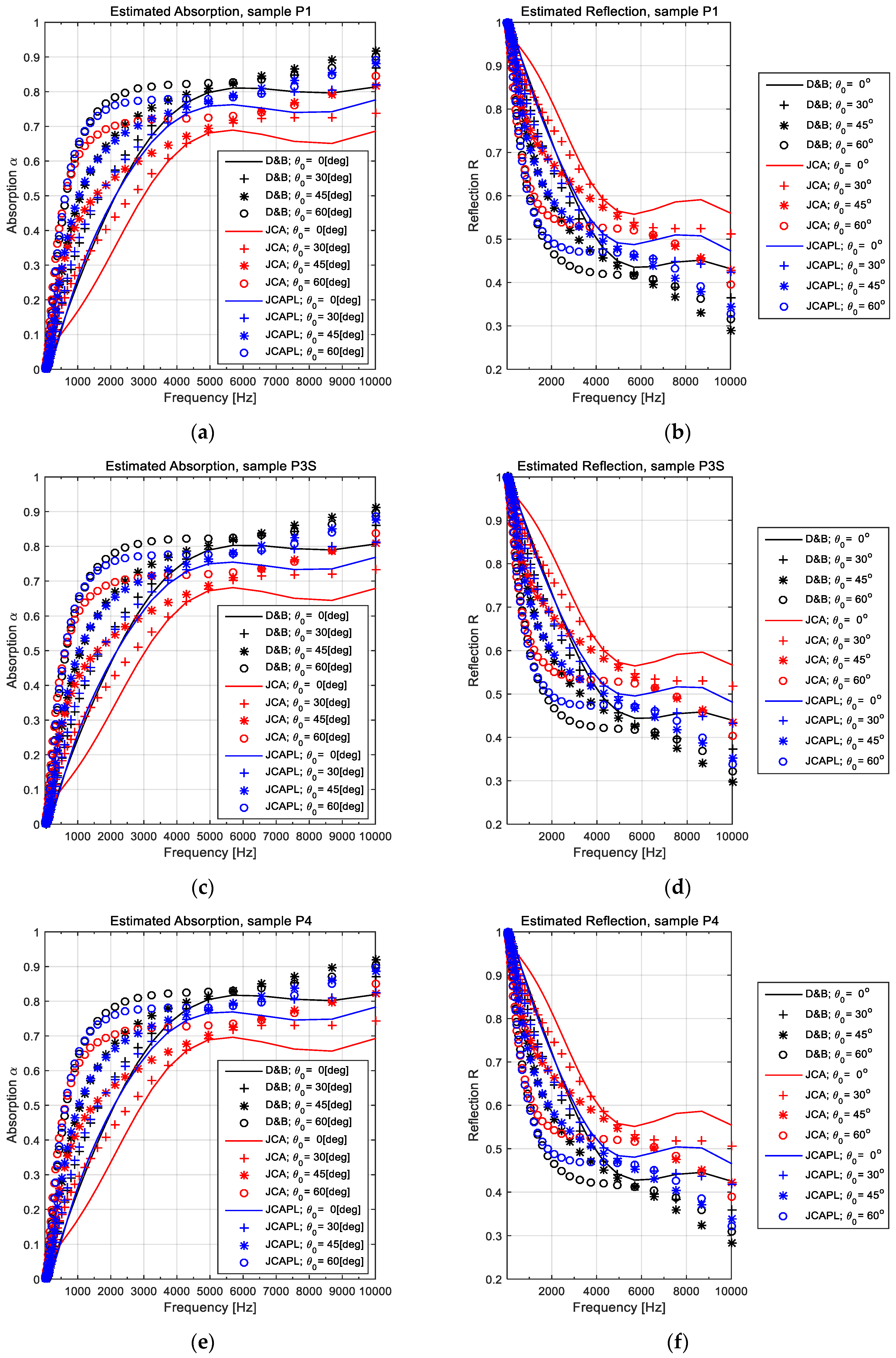
3.1. Comparison Between Experiments and Computational Approaches
3.2. Extended Computational Investigations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ottenhall, A.; Seppänen, T.; Ek, M. Water-stable cellulose fiber foam with antimicrobial properties for bio based low-density materials. Cellulose 2018, 25, 2599–2613. [Google Scholar] [CrossRef]
- Klemm, D.; Heublein, B.; Fink, H.P.; Bohn, A. Cellulose: Fascinating biopolymer and sustainable raw material. Angew. Chem. Int. Ed. 2005, 44, 3358–3393. [Google Scholar] [CrossRef] [PubMed]
- Filpponen, I.; Kontturi, E.; Nummelin, S.; Rosilo, H.; Kolehmainen, E.; Ikkala, O.; Laine, J. Generic method for modular surface modification of cellulosic materials in aqueous medium by sequential “click” reaction and adsorption. Biomacromolecules 2012, 13, 736–742. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Fu, Q.; Si, Y.; Ding, B.; Yu, J. Porous materials for sound absorption. Compos. Commun. 2018, 10, 25–35. [Google Scholar] [CrossRef]
- Li, R.; Du, J.; Zheng, Y.; When, Y.; Zhang, X.; Yang, W.; Lue, A.; Zhang, L. Ultra-lightweight cellulose foam material: Preparation and properties. Cellulose 2017, 24, 1417–1426. [Google Scholar] [CrossRef]
- Madani, A.; Zeinoddini, S.; Varahmi, S.; Turnbull, H.; Phillion, A.B.; Olson, J.A.; Martinez, D.M. Ultra-lightweight paper foams: Processing and properties. Cellulose 2014, 21, 2023–2031. [Google Scholar] [CrossRef]
- Poranen, J.; Kiiskinen, H.; Salmela, J.; Asikainen, J.; Keränen, J.T.; Pääkkönen, E. Breakthrough in papermaking resource efficiency with foam forming. In Proceedings of the TAPPI PaperCon, Atlanta, GA, USA, 28 April–1 May 2013. [Google Scholar]
- Bernardin, L.J. Process of Forming Absorbent Paper from a Mixture of Cellulosic Fibers and Partially Crosslinked Cellulosic Fibers and Paper Thereof. U.S. Patent 3,434,918, 3 March 1969. [Google Scholar]
- Chung, R. Method of Controlling the Orientation of Fibers in a Foam Formed Sheet. U.S. Patent 3,837,999, 24 September 1974. [Google Scholar]
- Radvan, B.; Gatward, A.P.J. The Formation of Wet-Laid Webs by a Foaming Process. Tappi 1972, 55, 748. [Google Scholar]
- Kidner, T. The Radfoam Process for Fine Papers. Pap. Technol. 1974, 15, 346–351. [Google Scholar]
- Poranen, J. Resource Efficiency with Foam Forming. FIBIC’s EffFibre & Effnet Seminar. 22 November 2012. Available online: http://fibic.fi/other/efffibre-effnet-seminarpresentations (accessed on 1 July 2019).
- Punton, V.W. Fibre Distribution in Foam and Foamlaid Paper. In Proceedings of the International Paper Physics Conference, Ellenville, NY, USA, 21–25 September 1975; pp. 135–139. [Google Scholar]
- Jahangiri, P.; Korehei, R.; Zeinoddini, S.S.; Madani, A.; Sharma, Y.; Phillion, A.; Martinez, D.M.; Olson, J.A. On filtration and heat insulation properties of foam formed cellulose based materials. Nord. Pulp. Pap. Res. J. 2014, 29, 584–591. [Google Scholar] [CrossRef]
- Samsudin, E.M.; Ismail, L.H.; Kadir, A.A. A review on physical factors influencing absorption performance of fibrous sound absorption material from natural fibers. J. Eng. Appl. Sci. 2016, 11, 3703–3711. [Google Scholar]
- Luu, H.T.; Perrot, C.; Panneton, R. Influence of Porosity, Fiber Radius and Fiber Orientation on the Transportand Acoustic Properties of Random Fiber Structures. Acta Acust. United Acust. 2017, 103, 1050–1063. [Google Scholar] [CrossRef]
- Alsayednoor, J. Modelling and Characterisation of Porous Materials. Ph.D. Thesis, School of Engineering, University of Glasgow, Glasgow, Scotland, October 2013. [Google Scholar]
- Chen, Z.; Wang, X.; Giuliani, F.; Atkinson, A. Microstructural characteristics and elastic modulus of porous solids. Acta Mater. 2015, 89, 268–277. [Google Scholar] [CrossRef]
- Berardi, U.; Iannace, G. Predicting the sound absorption of natural materials: Best-fit inverse laws for the acoustic impedance and the propagation constant. Appl. Acoust. 2017, 115, 131–138. [Google Scholar] [CrossRef]
- Peyrega, C.; Jeulin, D. Effects of the Microstructure of Fibrous Media on their Acoustic Properties. In Proceedings of the COMSOL International Conference, Versailles, France, 17–19 November 2010. [Google Scholar]
- Wang, C.N.; Torng, J.H. Experimental study of the absorption characteristics of some porous fibrous materials. Appl. Acoust. 2001, 62, 447–459. [Google Scholar] [CrossRef]
- Nedeff, F.M.; Bârsan, N.; Fînaru, A.L. Studies and research concerning the use of some recyclable absorbent materials for increasing acoustic comfort into a room designed for speaking. Chem. Chem. Eng. 2017, 18, 329–338. [Google Scholar]
- Kuczmarski, M.A.; Johnston, J.C. Acoustic Absorption in Porous Materials. NASA Technical Reports NASA/TM—2011-216995. Available online: https://ntrs.nasa.gov/archive/.../20110011143.pdf (accessed on 20 May 2019).
- Arenas, J.P.; Crocker, M.J. Recent Trends in Porous Sound-Absorbing Materials. Sound Vib. 2010, 44, 12–17. [Google Scholar]
- Hu, Y.; Galland, M.A.; Chen, K. Acoustic transmission performance of double wall active sound packages in a tube: Numerical/experimental validations. Appl. Acoust. 2012, 73, 323–337. [Google Scholar] [CrossRef]
- Dib, L.; Bouhedja, S.; Amrani, H. Mechanical Parameters Effects on Acoustic Absorption at Polymer Foam. Adv. Mater. Sci. Eng. 2015. [Google Scholar] [CrossRef]
- Jones, P.W. Prediction of the acoustic performance of small poroelastic foam filled mufflers: A case study. Acoust. Aust. 2010, 38, 69–75. [Google Scholar]
- Luu, H.T.; Perrot, C.; Monchiet, V.; Panneton, R. Sound waves and angular orientation in fibrous materials. In Proceedings of the International Conference on Noise and Vibration Engineering (ISMA 2016), Leuven, Belgium, 19–21 September 2016. [Google Scholar]
- Zhu, X.; Kim, B.J.; Wang, Q.; Wu, Q. Recent Advances in the sound insulation properties of bio-based materials. BioResources 2014, 9, 1764–1786. [Google Scholar] [CrossRef]
- Egab, L.; Wang, X.; Fard, M. Acoustical characterisation of porous sound absorbing materials: A review. Int. J. Veh. Noise Vib. 2014, 10, 129–149. [Google Scholar] [CrossRef]
- Trematerra, A.; Lombardi, I. Acoustic Properties of Cellulose. IOP Conf. Ser. Mater. Sci. Eng. 2017, 225, 012082. [Google Scholar] [CrossRef]
- Karademir, A.; Aydemir, C.; Yenidoğan, S. Sound absorption and print density properties of recycled sheets made from waste paper and agricultural plant fibres. Afr. J. Agric. Res. 2011, 6, 6073–6081. [Google Scholar] [CrossRef]
- Sambu, M.; Yahya, M.N.; Latif, H.A.; Hatta, M.N.H.; Ghazali, M.I.B. Preliminary study on acoustical and physical charachteristics of kenaf (hibiscus cannabinus) using natural rubber as binder. J. Eng. Appl. Sci. 2016, 11, 2467–2474. [Google Scholar]
- Ramis, J.; Rey, R.; Alba, J.; Godinho, L.; Carbajo, J. A model for acoustic absorbent materials derived from coconut fiber. Mater. Constr. 2014, 64. [Google Scholar] [CrossRef]
- Arenas, J.P.; Rebolledo, J.; Rey, R.; Alba, J. Sound Absorption properties of unbleached cellulose loose-fill insulation material. BioResources 2014, 9, 6227–6240. [Google Scholar] [CrossRef]
- Nechita, P.; Nastac, S. Foam-formed cellulose composite materials with potential applications in sound insulation. J. Compos. Mater. 2018, 52, 747–754. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, Y. Sound Absorption Characterization of Natural Materials and Sandwich Structure Composites. Aerospace 2018, 5, 75. [Google Scholar] [CrossRef]
- Mamtaz, H.; Fouladi, M.H.; Atabi, M.A.; Namasivayam, S.N. Acoustic Absorption of Natural Fiber Composites. J. Eng. 2016. [Google Scholar] [CrossRef]
- Taraldsen, G. The Delany-Bazley Impedance Model and Darcy’s Law. Acta Acust. United Acust. 2005, 91, 41–50. [Google Scholar]
- Delany, M.E.; Bazley, E.N. Acoustical properties of fibrous absorbent materials. Appl. Acoust. 1970, 3, 105–116. [Google Scholar] [CrossRef]
- Taban, E.; Khavanin, A.; Faridan, M.; Samaei, S.E.; Samimi, K.; Rashidi, R. Comparison of acoustic absorption characteristics of coir and date palm fibers: Experimental and analytical study of green composites. Int. J. Environ. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Chazot, J.D.; Zhang, E.; Antoni, J. Acoustical and mechanical characterization of poroelastic materials using a Bayesian approach. J. Acoust. Soc. Am. 2012, 131, 4584–4595. [Google Scholar] [CrossRef] [PubMed]
- Maderuelo-Sanz, R.; Barrigón Morillas, J.M.; Martín-Castizo, M.; Gómez Escobar, V.; Rey Gozalo, G. Acoustical performance of porous absorber made from recycled rubber and polyurethane resin. Lat. Am. J. Solids Struct. 2013, 10, 585–600. [Google Scholar] [CrossRef]
- Herdtle, T.; Xue, Y.; Bolton, J.S. Numerical Modeling of the Acoustics of Low Density Fibrous Media Having a Distribution of Fiber Sizes; Ray W. Herrick Laboratories: Tippecanoe County, IN, USA, 2017; p. 167. Available online: http://docs.lib.purdue.edu/herrick/167 (accessed on 10 February 2019).
- Zampolli, M.; Malm, N.; Tesei, A. Improved Perfectly Matched Layers for Acoustic Radiation and Scattering Problems. In Proceedings of the COMSOL International Conference, Hannover, Germany, 4–6 November 2008. [Google Scholar]
- Semeniuk, B.P.; Göransson, P. Modelling the Dynamic Viscous and Thermal Dissipation Mechanisms in a Fibrous Porous Material. In Proceedings of the COMSOL International Conference, Lausanne, Switzerland, 22–24 October 2018. [Google Scholar]
- Brennan, M.; Dossi, M.; Moesen, M. A Multi-Physics Study of the Wave Propagation Problem in Open Cell Polyurethane Foams. In Proceedings of the COMSOL International Conference, Rotterdam, The Netherlands, 18–20 October 2017. [Google Scholar]
- Zielinski, T.G. Multiphysics Modelling of Sound Absorption in Rigid Porous Media Based on Periodic Representations of Their Microstructural Geometry. In Proceedings of the COMSOL International Conference, Rotterdam, The Netherlands, 23–25 October 2013. [Google Scholar]
- Zielinski, T.G. Multiphysics Modelling of Sound Absorption Fibrous and Porous Materials. In Proceedings of the COMSOL International Conference, Grenoble, France, 14–16 October 2015. [Google Scholar]
- Mills, N.J.; Lyn, G. Modelling of Air Flow in Impacted Polyurethane Foam. Cell. Polym. 2002, 21, 343–368. [Google Scholar] [CrossRef]
- Mills, N.J. Finite Element Models for the Viscoelasticity of Open-Cell Polyurethane foam. Cell. Polym. 2006, 25, 293–316. [Google Scholar] [CrossRef]
- Schrodt, M.; Benderoth, G.; Kühhorn, A.; Silber, G. Hyperelastic Description of Polymer Soft Foams at Finite Deformations. Technischemechanik 2005, 25, 162–173. [Google Scholar]
- Weaire, D.; Hutzler, W. The Physics of Foams; Clarendon Press: Oxford, UK, 1999; pp. 1–55. [Google Scholar]
- Cantat, I.; Cohen-Addad, S.; Elias, F.; Graner, F.; Höhler, R.; Pitois, O.; Rouyer, F.; Saint-Jalmes, A. Foams: Structure and Dynamics; Oxford University Press: Oxford, UK, 2013; p. 265. [Google Scholar]
- Exerowa, D.; Kruglyakov, P.M. Foam and Foam Films: Theory, Experiment, Application; Elsevier: Amsterdam, The Netherlands, 1998; p. 773. [Google Scholar]
- Korehei, R.; Jahangiri, P.; Nikbakht, A.; Martinez, M.; Olson, J. Effects of drying strategies and microfibrillated cellulose fiber content on the properties of foam-formed paper. J. Wood Chem. Technol. 2016, 36, 235–249. [Google Scholar] [CrossRef]
- Rwawiire, S.; Tomkova, B.; Militky, J.; Hes, L.; Kale, B.M. Acoustic and thermal properties of a cellulose nonwoven natural fabric (barkcloth). Appl. Acoust. 2017, 116, 177–183. [Google Scholar] [CrossRef]
- Cox, T.J.; D’Antonio, P. Acoustic Absorbers and Diffusers Theory, Design and Application; Taylor & Francis Group: London, UK; New York, NY, USA, 2004; pp. 129–155. [Google Scholar]
- Horoshenkov, K.V. A Review of Acoustical Methods for Porous Material Characterisation. IJAV 2017, 22, 92–103. [Google Scholar] [CrossRef]


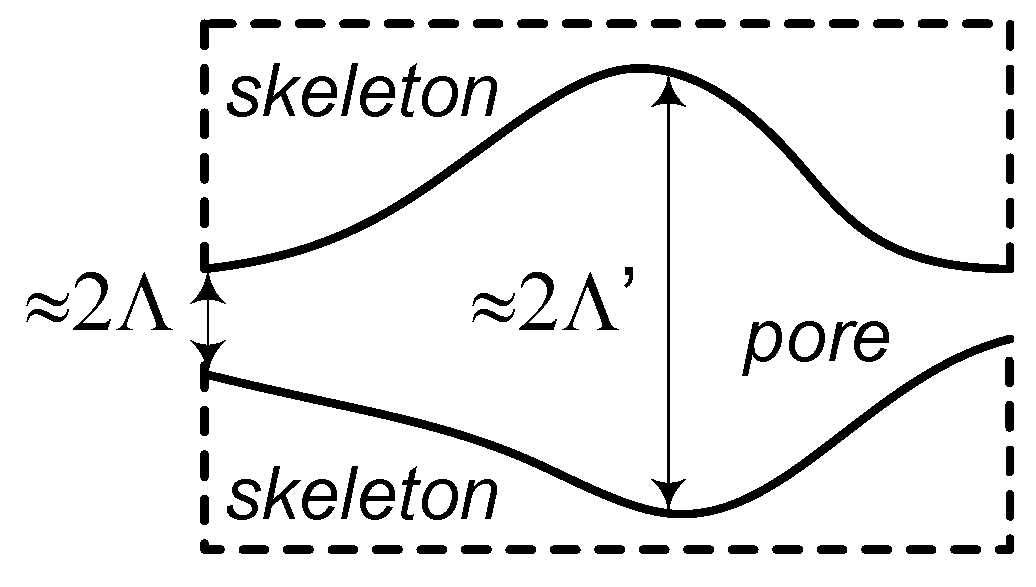
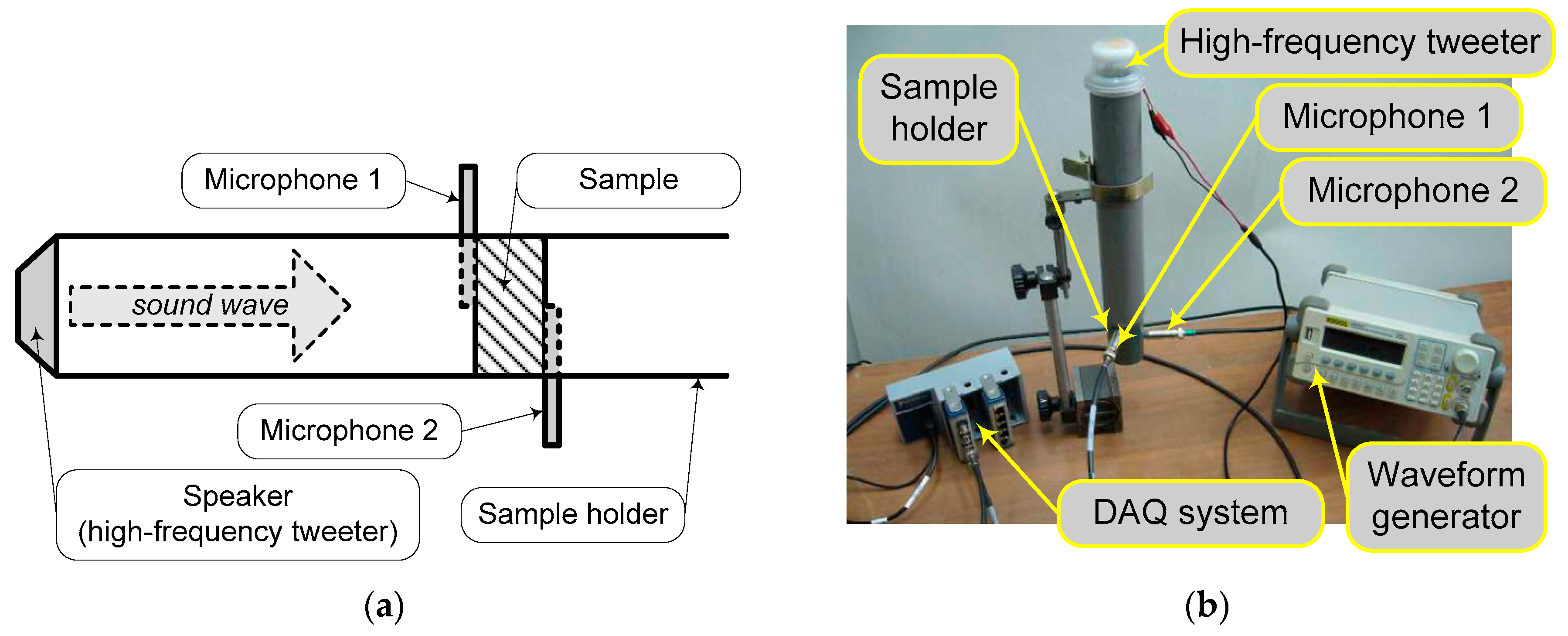
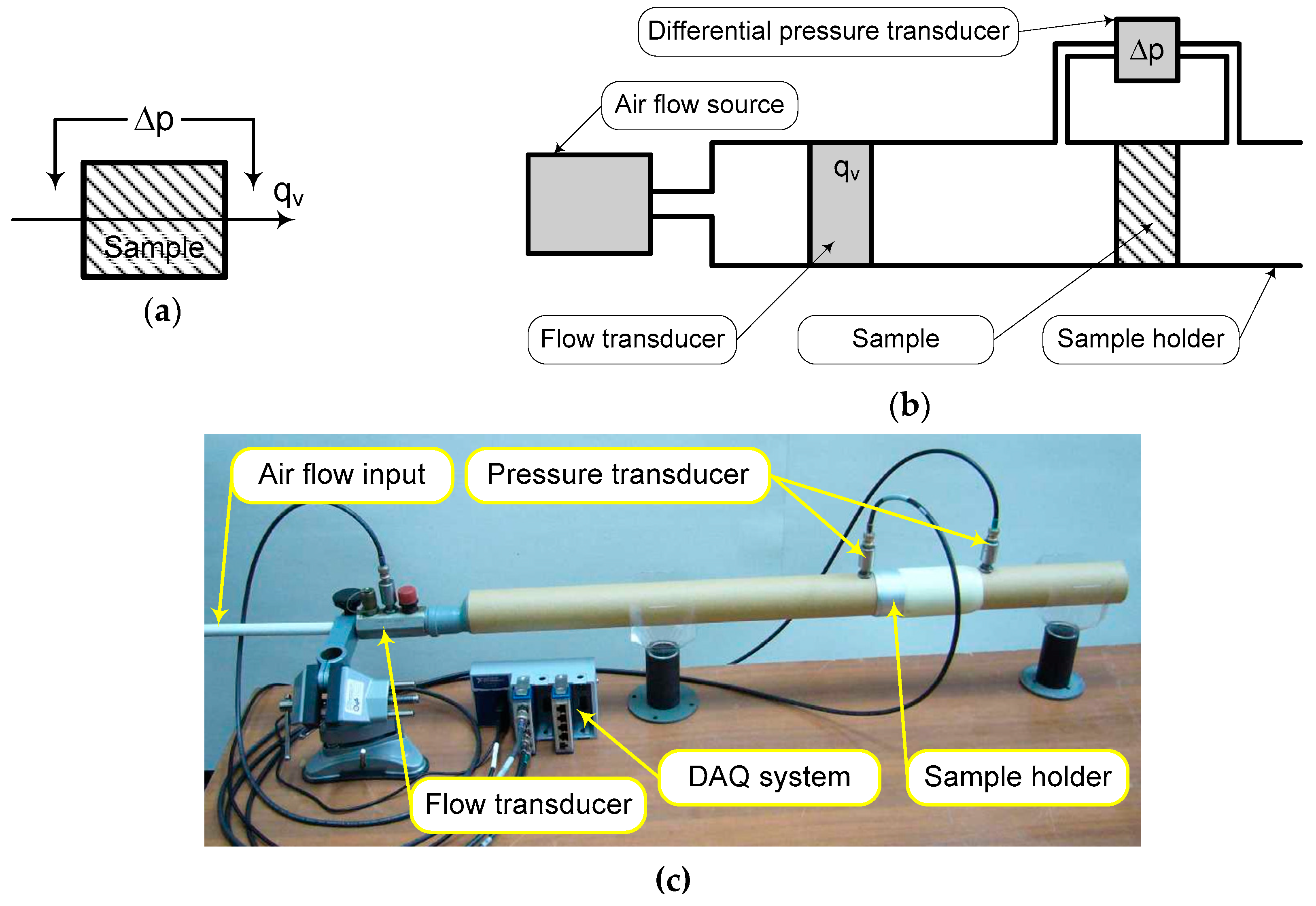
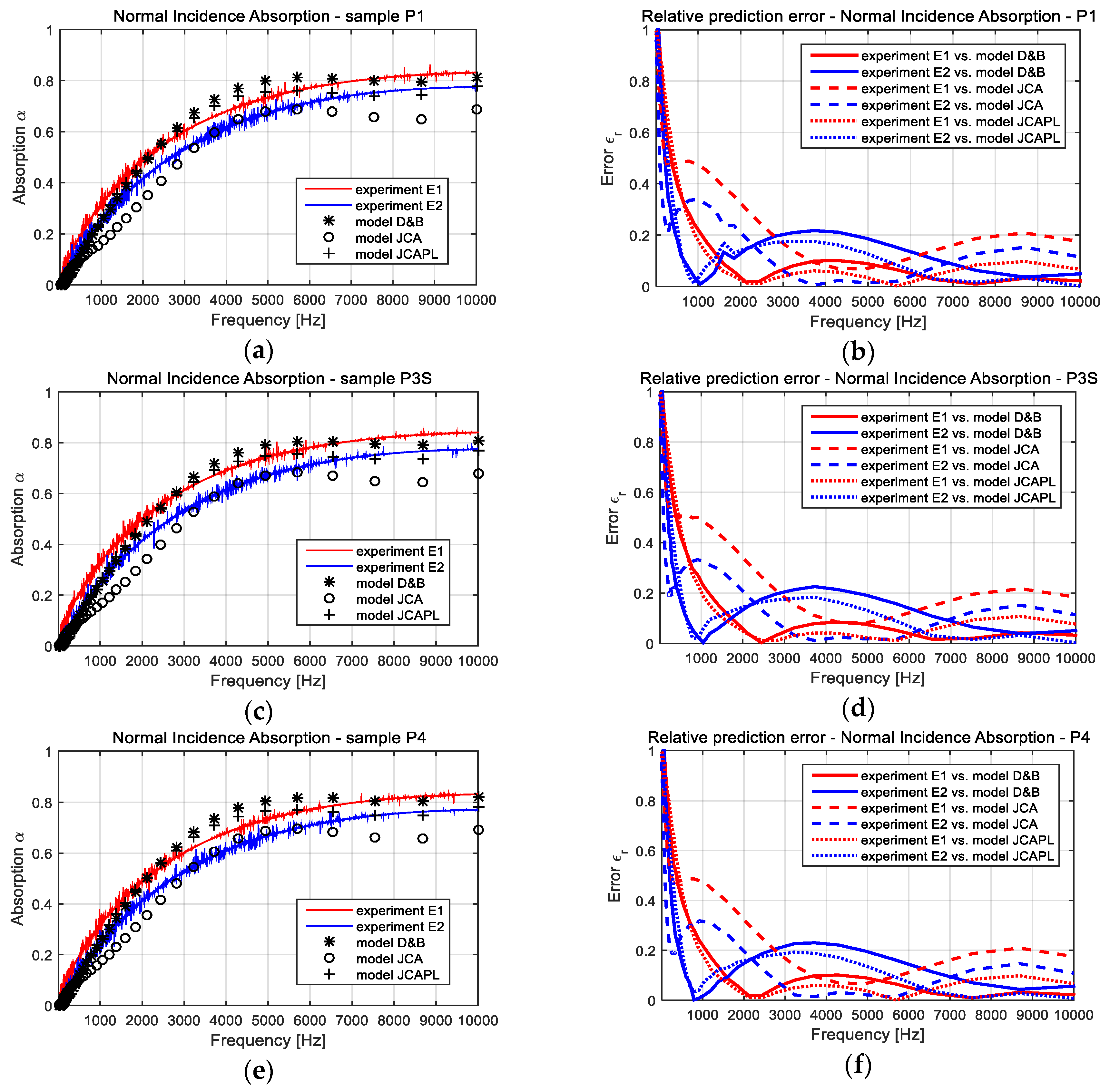

| FCM Sample Codes | Composition |
|---|---|
| P1 | 100% (BHCF) |
| P3S | 100% (RCF) |
| P4 | 50% (BHCF) + 50% (RCF) |
| Material Type | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
|---|---|---|---|---|---|---|---|---|
| material 1 | 0.0571 | 0.745 | 0.087 | 0.732 | 0.0978 | 0.700 | 0.189 | 0.595 |
| material 2 | 0.078 | 0.623 | 0.074 | 0.660 | 0.159 | 0.571 | 0.121 | 0.530 |
| material 3 | 0.114 | 0.369 | 0.0985 | 0.758 | 0.168 | 0.715 | 0.136 | 0.491 |
| material 4 | 0.212 | 0.455 | 0.105 | 0.607 | 0.163 | 0.592 | 0.188 | 0.544 |
| Tortuosity | Sample P1 | Sample P3S | Sample P4 |
|---|---|---|---|
| theoretical | 1.008097 | 1.007585 | 1.00861 |
| experimental (averaged values) | 1.04721428 | 1.036407 | 1.049156122 |
| Airflow Resistivity [Pa s m−2] | Sample P1 | Sample P3S | Sample P4 | |
|---|---|---|---|---|
| Theoretical estimation—Equation (29) | 5936.869 | 5685.805 | 6161.118 | |
| Theoretical estimation—Equation (30) | 5179.872 | 4538.770 | 5865.454 | |
| Experimental investigation (averaged values) | 6104.445 | 5849.473 | 6332.070 | |
| Average value per sample | 5740.395 | 5358.016 | 6119.547 | |
| Relative error [%] of experimental value related to | Equation (29) | 2.75 | 2.80 | 2.70 |
| Equation (30) | 15.15 | 22.41 | 7.37 | |
| Relative error [%] of average value related to | Experiment | 5.96 | 8.40 | 3.36 |
| Equation (29) | 3.31 | 5.77 | 0.67 | |
| Equation (30) | 10.82 | 18.05 | 4.33 | |
| Parameter | Sample P1 | Sample P3S | Sample P4 |
|---|---|---|---|
| Bulk density [kg m−3] | 37.3 | 36.3 | 38.18 |
| Foam porosity [-] | 0.984 | 0.985 | 0.983 |
| Flow resistivity [Pa s m−2] | 6000 | 5770 | 6200 |
| Tortuosity [-] | 1.0081 | 1.0076 | 1.00861 |
| Static viscous tortuosity [-] | 1.3441 | 1.3435 | 1.3448 |
| Static thermal tortuosity [-] | 1.3333 | 1.3333 | 1.3333 |
| Viscous characteristic length [m] | 157.24 × 10−6 | 160.22 × 10−6 | 154.80 × 10−6 |
| Thermal characteristic length [m] | 314.48 × 10−6 | 320.44 × 10−6 | 309.60 × 10−6 |
| Static thermal permeability [m2] | 3.02 × 10−9 | 3.14 × 10−9 | 2.92 × 10−9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Debeleac, C.; Nechita, P.; Nastac, S. Computational Investigations on Soundproof Applications of Foam-Formed Cellulose Materials. Polymers 2019, 11, 1223. https://doi.org/10.3390/polym11071223
Debeleac C, Nechita P, Nastac S. Computational Investigations on Soundproof Applications of Foam-Formed Cellulose Materials. Polymers. 2019; 11(7):1223. https://doi.org/10.3390/polym11071223
Chicago/Turabian StyleDebeleac, Carmen, Petronela Nechita, and Silviu Nastac. 2019. "Computational Investigations on Soundproof Applications of Foam-Formed Cellulose Materials" Polymers 11, no. 7: 1223. https://doi.org/10.3390/polym11071223
APA StyleDebeleac, C., Nechita, P., & Nastac, S. (2019). Computational Investigations on Soundproof Applications of Foam-Formed Cellulose Materials. Polymers, 11(7), 1223. https://doi.org/10.3390/polym11071223







