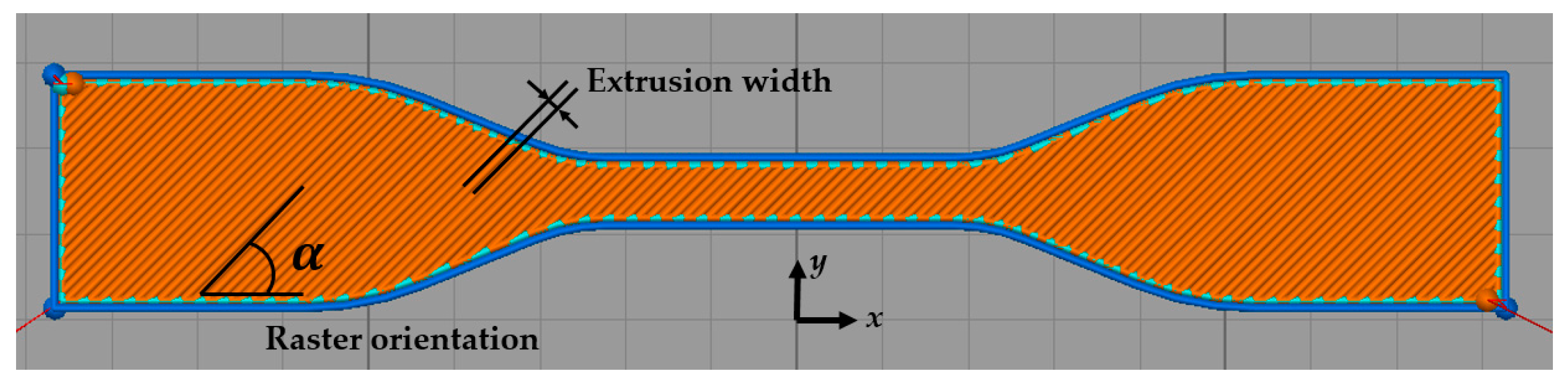
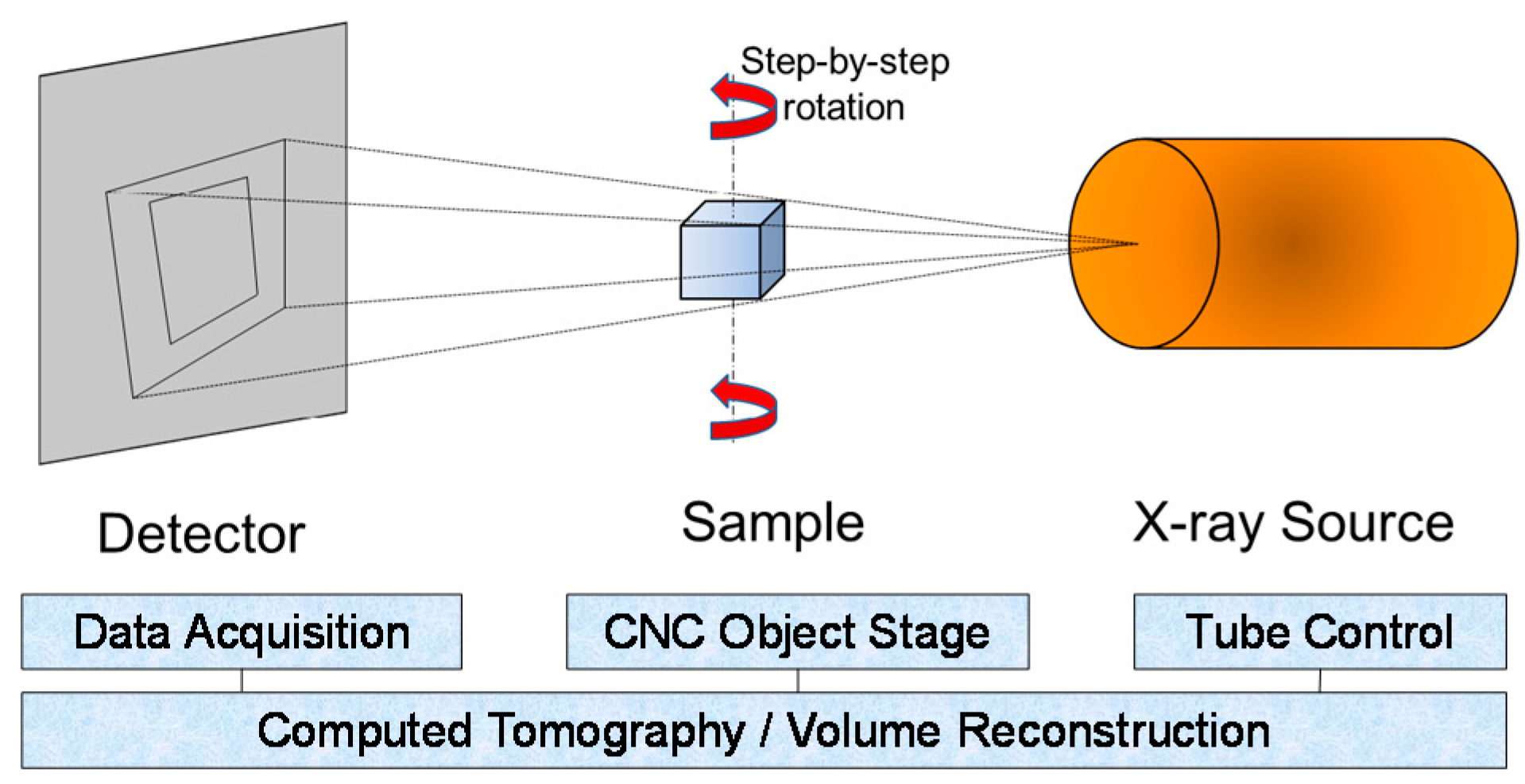
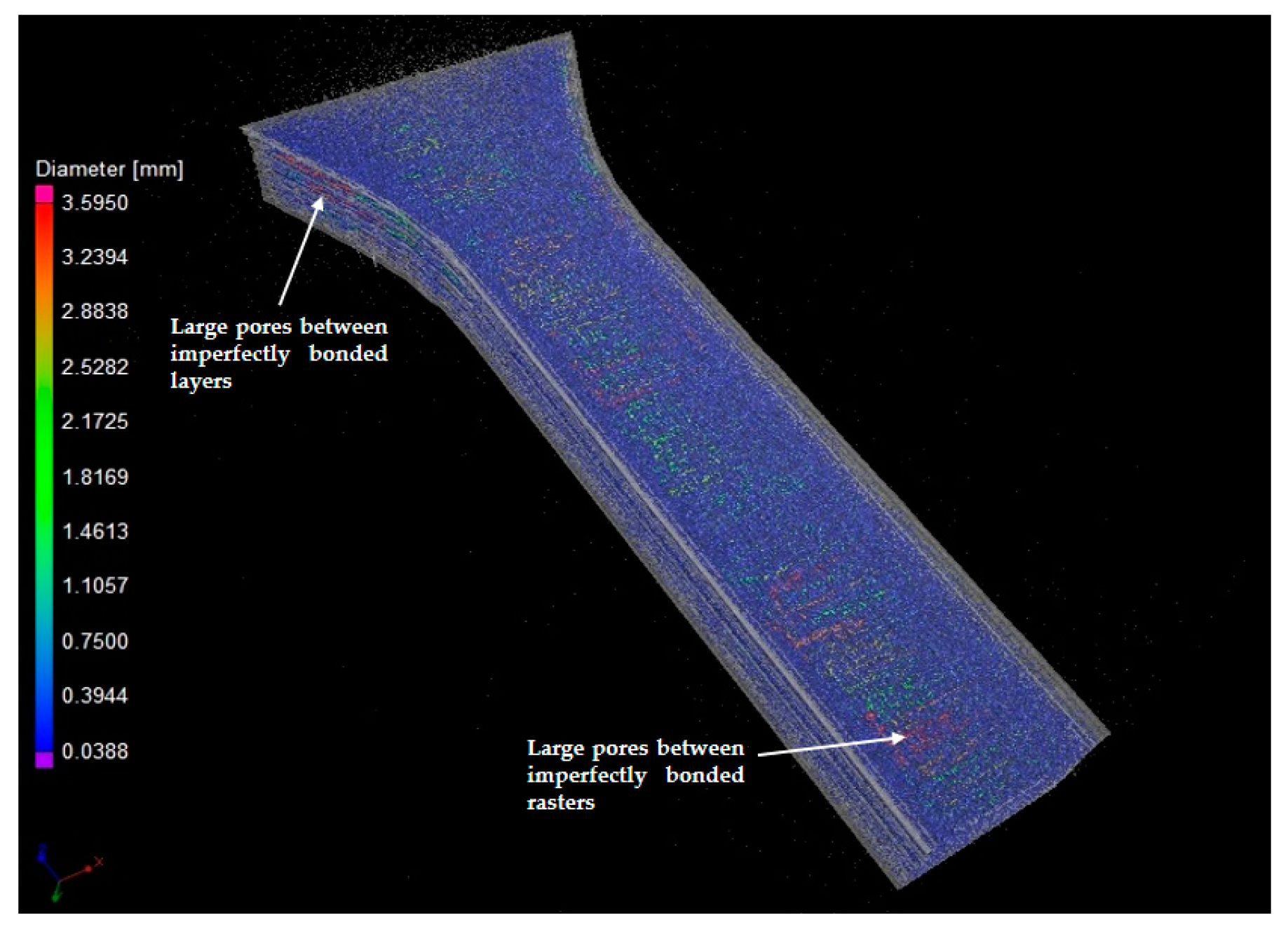
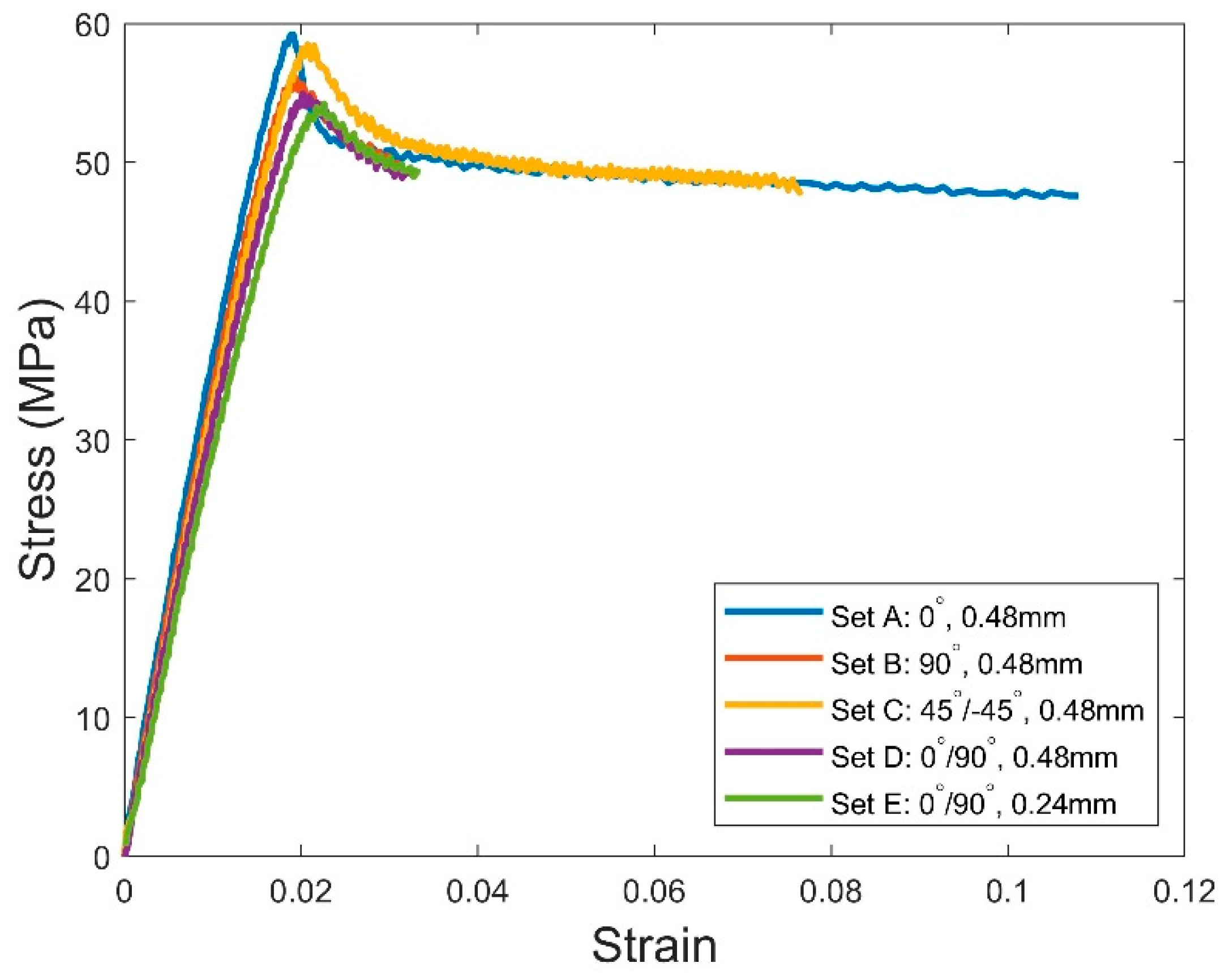
A micromechanical finite element model is proposed in this section to predict the elastic properties of 3D printed PLA material based on the actual microscopic details of the pores characterized by XCT. The model was developed through an two dimensional analysis of a periodic representative volume element (RVE), a micromechanical technique widely used in the literature for estimating the macroscopic behavior of composites which consist of a matrix containing microscale inhomogeneities, such as pores or fibers [
10,
29,
30]. The identification of such a composite material into an RVE is not unique. One popular identification method is to assume that the inhomogeneities are uniformly distributed in the matrix and have the same geometry [
31,
32]. This method is easy to implement but clearly not adequate for quantifying the size distribution and the spatial location of pores in FDM processed materials.
Here we propose an identification methodology based on the internal structures of the 3D printed PLA material, as illustrated in
Figure 11, where the RVE was modeled as a square elastic matrix containing
N pores whose sizes were determined according to the actual pore sizes characterized by XCT. The pores were assumed to have circular shapes since the actual pore sizes were quantified in the XCT analysis by measuring the diameter for the circumscribed sphere of each pore. After determining the pore sizes, the
N pores were randomly positioned within the RVE provided that the pores were not overlapping each other. A MATLAB script was used for generating the geometry of the RVE. For such a RVE, the porosity is calculated as the total pore area divided by the RVE area.
Since the 3D printed PLA material is considered as a periodic array of the RVEs, periodic boundary conditions were applied to the RVE model. This implies that each RVE is a continuous body and two continuities must be satisfied: (a) The shape at the two opposite boundaries must remain the same, such that no separation or overlap occurs between the neighboring RVEs under deformation; and (b) the tractions at the two opposite boundaries must be continuous [
30,
31].
To evaluate the elastic properties, a uniaxial tension was applied to the x direction on the RVE for a finite element analysis using a commercial finite element analysis package (ABAQUS, Simulia, Providence, RI), where a Python script was developed to implement the periodic boundary conditions on the RVE. The Young’s modulus for the RVE matrix was selected as 3500MPa which was given in the material data sheet for the PLA filament used for the printing. However, the data sheet did not provide any information on the Poisson’s ratio of the PLA filament. Considering that Poisson’s ratio is approximately equal to 0.33, almost independent of the process parameters and porosity from the experimental data in
Table 7, here we selected Poisson’s ratio as 0.33 for the matrix to investigate whether the macroscopic Poisson’s ratio would be dependent on the porosity in the RVE analysis. The pores in the RVE were modeled as very weak solid material, that is, Young’s modulus and Poisson’s ratio were selected respectively as 0.000001 MPa and 0.000001. The RVE were meshed using six-node plane stress elements CPS6M, and mesh convergence analysis was carried out by using seed size 0.015, 0.03, and 0.06 and checking the homogenized stresses and strains over the whole RVE, which were calculated respectively by
and
where
and
denote respectively the homogenized stresses and strains in the macroscale,
and
denote respectively the microscopic stresses and strains in the RVE, and
is the total volume of the RVE. After obtaining the homogenized stresses and strains, the effective elastic properties in the macroscale, that is, the predicted elastic properties for the 3D printed PLA material, can be computed by simply using
and
where
is the macroscopic stress component along
x axis and
and
are respectively the macroscopic strain components along the
x and
y directions.
3.3.1. Statistical Simulations
To simulate the statistical studies for the 3D printed PLA material as given in
Section 2.4, a statistical approach was adopted to generate the RVEs as follows.
To construct an RVE, the sizes for the
N pores were determined based on the actual pore size distributions for the specimens given in
Table 6. The ranges of the
N pore sizes were selected to be the same with the actual pore size ranges, that is, from 0.0388 to 1 mm. To simulate the actual pore size distribution, the sizes of the
N pores were selectively distributed in the five size ranges in
Table 6 in such a manner that most of the pores had a pore size below 0.2 mm, a medium number of pores fell into the size range between 0.2 and 0.6 mm, and the pore size larger than 0.8 mm was kept very rare. One example of such a pore size distribution pattern is given in
Table 8, where the number of pores in the RVE was selected between 5 and 100. For a fixed value of
N, within each size range, the sizes of the pores in the RVE were randomly selected from the large population of the actual pore sizes characterized by XCT.
Once the sizes of the pores were determined, the size of RVE can be calculated for a given porosity. To create a more general model, we selected the porosity values between 3% and 50% for the micromechanical modeling, which allows the RVE to predict the elastic properties for the specimens tested in our study as well as the other materials of larger porosity provided that the pore size distributions for the material also fall in the range of between 0.038 mm to 1 mm, which is determined by the upper and lower pore size limit in XCT characterizations. Once the size of the RVE was determined, the N pores were randomly distributed in the RVE as discussed. Three RVEs were generated for fixed values of N and the porosity to capture the variations of elastic properties.
3.3.2. Number of Pores Required for Homogenizing the Elastic Properties of the 3D Printed PLA Material
To predict the elastic properties using the proposed micromechanical model, the first step is to check the minimum number of pores for homogenizing the effective Young’s modulus and Poisson’s ratio of the RVE. More specifically, the pores in the RVE should be sufficient for representing the microscopic details in the 3D printed PLA material; however, the number of pores should be as small as possible to ensure an economic computation.
To determine the minimum number of pores in each RVE, statistical simulations were conducted using the pore size distributions following
Table 8 to evaluate the elastic properties for the specimens with the selected porosity between 3% and 50% and the number of pores between 5 and 100.
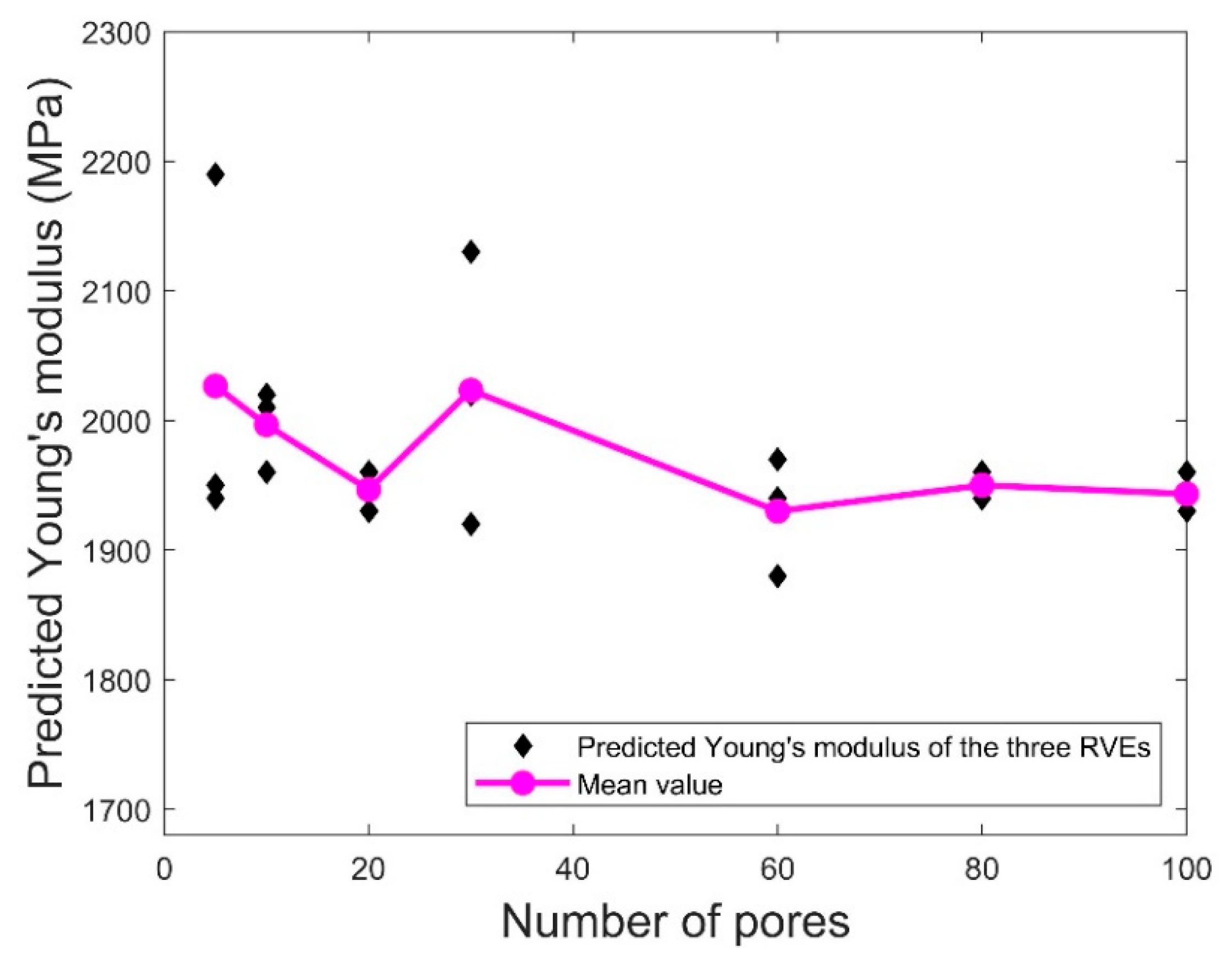
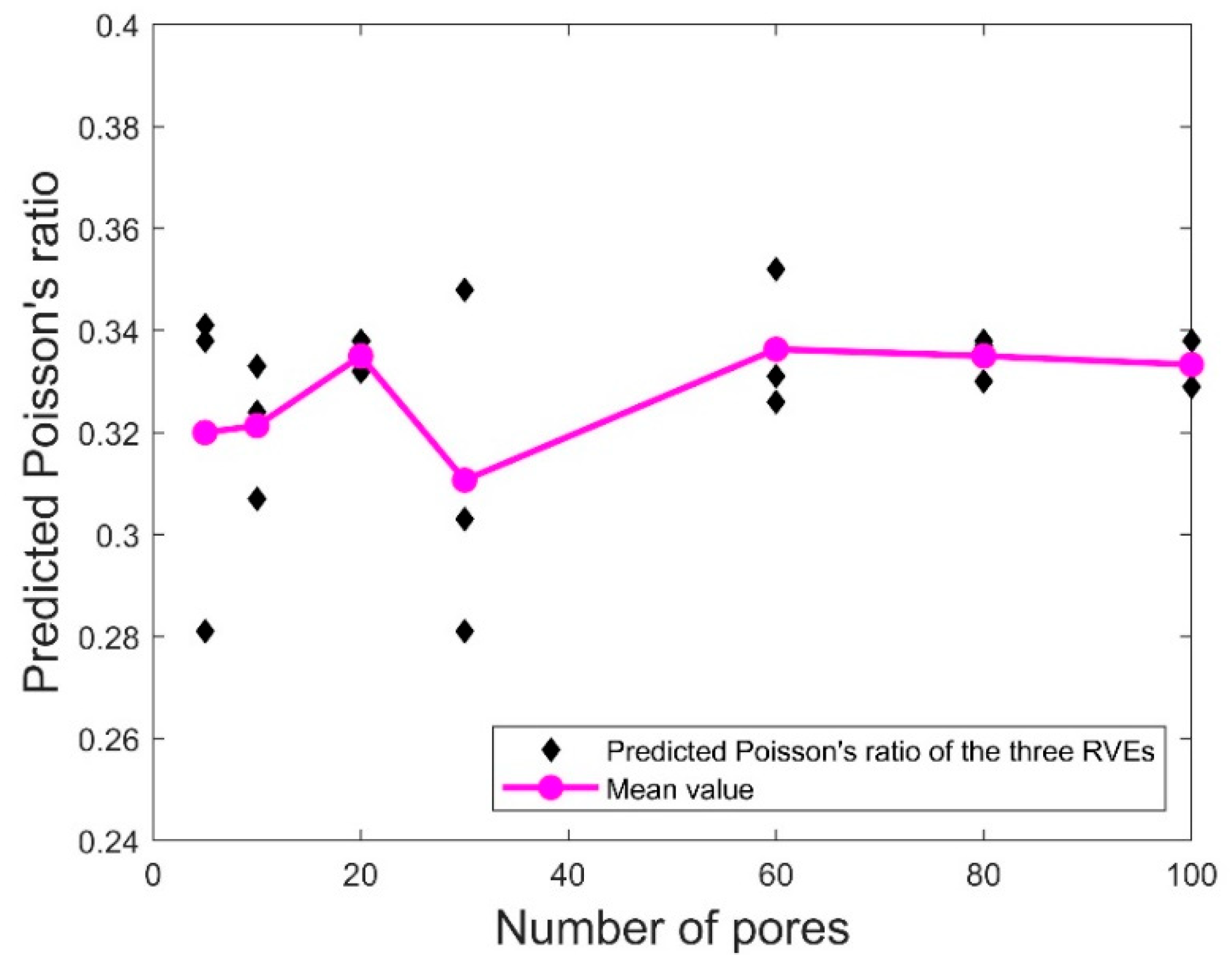
Figure 12 and
Figure 13, respectively, show the variations of the representative predicted Young’s modulus and Poisson’s ratio of the three RVEs in set A for different numbers of pores and porosity = 20%. Also included are the mean values of the elastic properties of the three RVEs for each value of
N. It was observed that the mean values of both elastic properties did not change very much as the number of pores reached 80. Moreover, for the number of pores below 80, the variation of the elastic properties for the three RVEs was much more serious compared to the corresponding data for
N = 80 and 100. This indicates that 80 pores in the RVE may be sufficient for homogenizing the predicted Young’s modulus and Poisson’s ratio. For the following results, we use
N = 80 in the RVE to predict the elastic properties.
For
N = 80 and 100, it was also found that the mean values of the elastic properties predicted by using the pore size data for the five sets of specimens were very close to each other with a percentage difference up to 1.8%. This is not surprising due to the following reasons. As shown in
Table 6, for the test specimens with different porosities, the pore size ranges are the same and the size distributions are highly similar. Considering the number of pores
N in the RVE is a much smaller number compared to the number of pores in the real population (ranges from 464,653 to 712,525 for porosities between 4.05% and 6.32%), it is expected that adopting the pore size data from any specimen in the five sets will lead to very similar prediction results. Thus in the following sections, we select the pore size distributions of set A for predicting the elastic properties of the 3D printed PLA materials.
3.3.3. Comparison with the Existing Models
In this section, the predicted elastic properties by the proposed micromechanical model are compared with two existing classical numerical works widely used for benchmarking elasticity problems involving porosity effects [
33,
34]. In the first model, [
35] investigated a zig-zag array of circular holes with uniform sizes in an infinite matrix by assuming complex stress potentials in the form of Laurent series expansions. Specifically, the effective Young’s modulus for two specially decoupled arrays of the holes, the square array and the equilateral triangular array, are explicitly given as functions of the fraction of the holes (which can be considered as porosity) up to 50% in terms of power series fitted to the numerical results.
The second numerical model [
36] applied periodic boundary conditions on an RVE to analyze the effective Young’s modulus of three patterns of circular holds, also with uniform sizes, as a function of the porosity. The three patterns included non-overlapping periodically centered holes on (a) a honeycomb lattice, (b) a triangular lattice, and(c) overlapping-allowed, randomly centered circular holes.
For our micromechanical model, the predicted elastic properties are expected to depend on the porosity as well as the pore size distributions [
37]. Thus, apart from the pore size distributions described in
Section 3.3.1, here we consider one more distribution of the pore sizes in the RVE for a more comprehensive study. As indicated in
Table 6, over 99% of pore sizes fell into the range below 0.2 mm. To capture the large population of the smaller pores, we assumed all of the 80 pores in the RVE to have sizes between 0.0388 and 0.2 mm. The prediction results were compared with the RVE analysis using the full range of the pore sizes (between 0.0388 and 1 mm) selected as in
Table 8 as well as the two existing numerical works. As before, three RVEs were generated for each type of pore size distribution and each porosity for
N = 80.
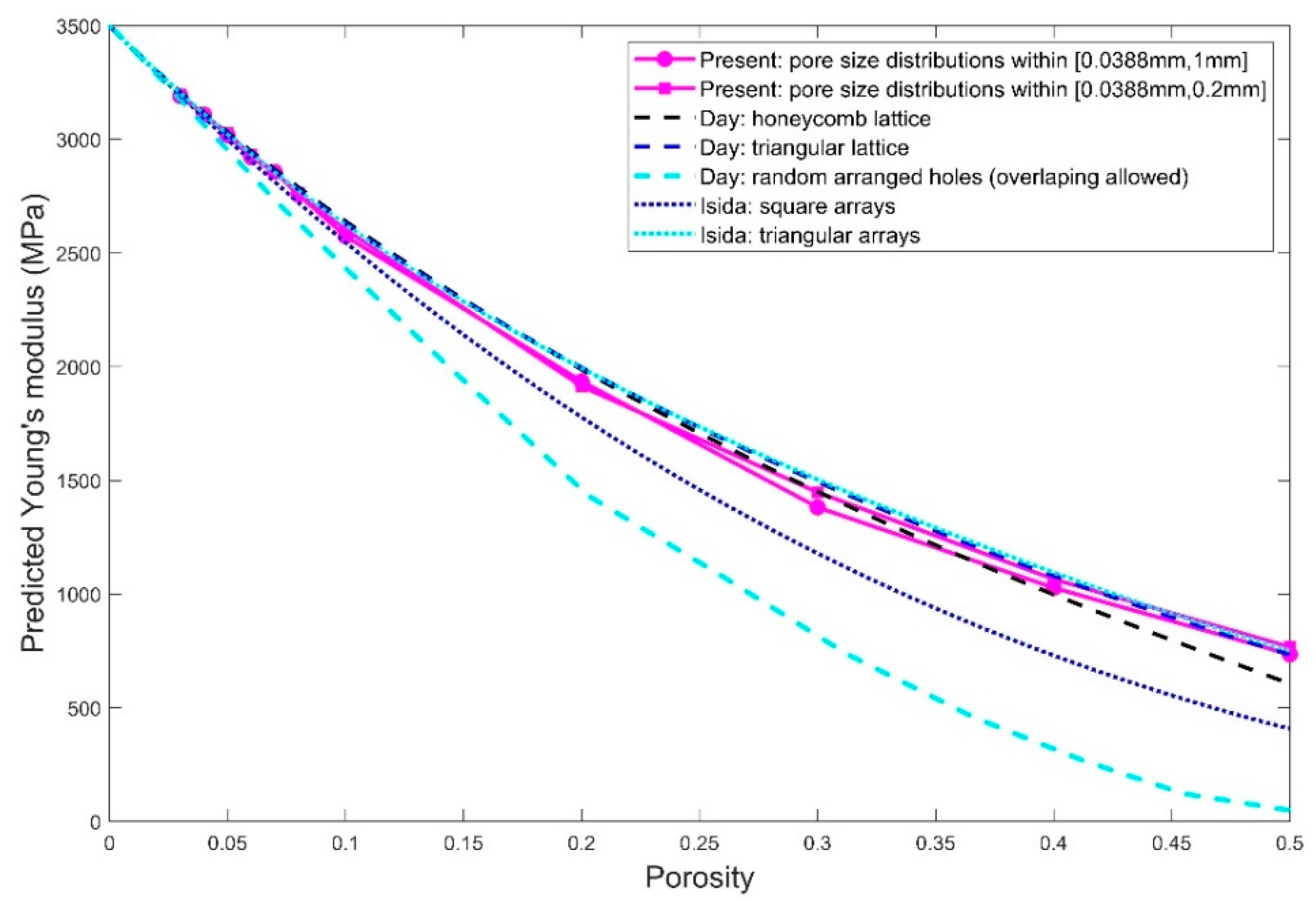
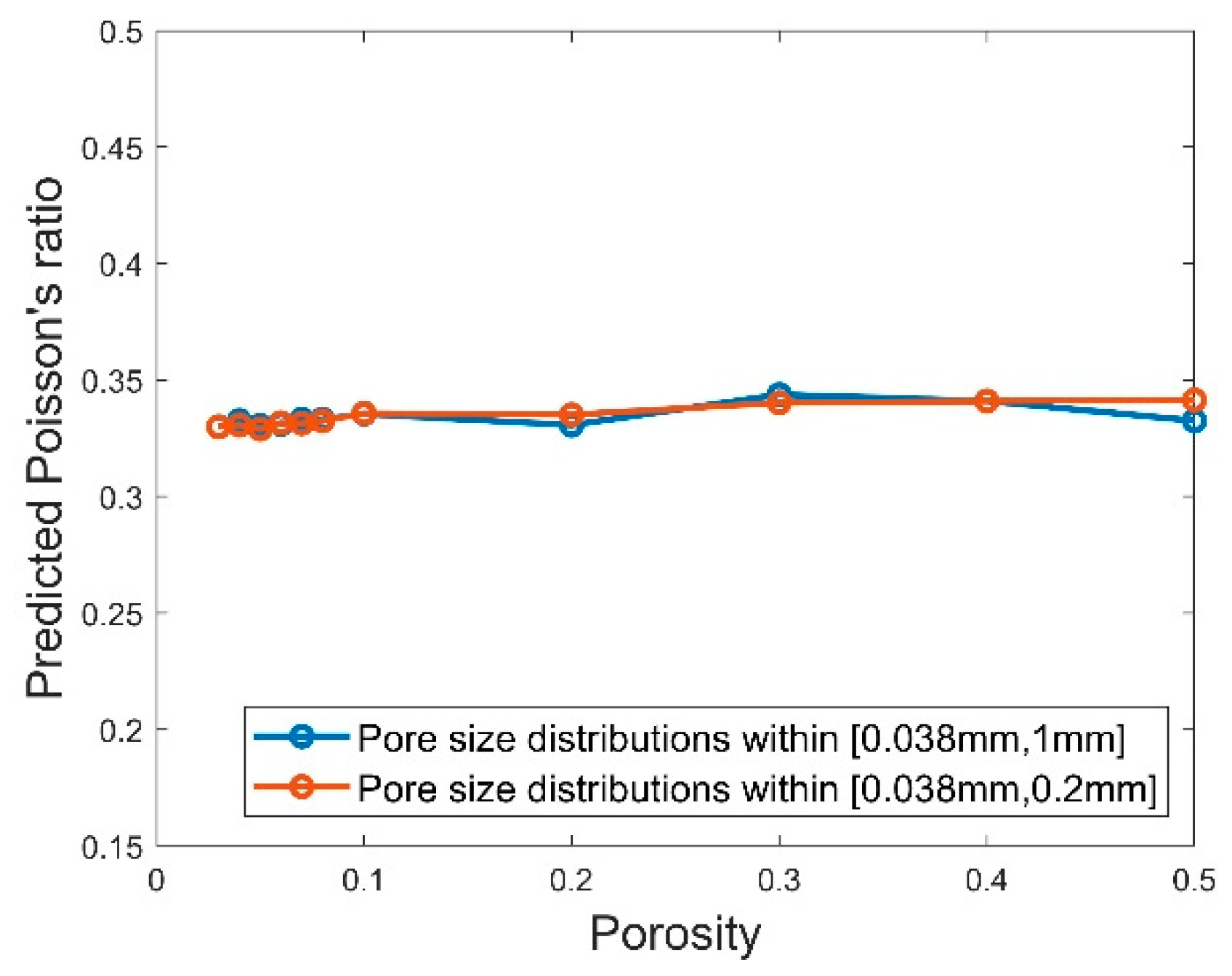
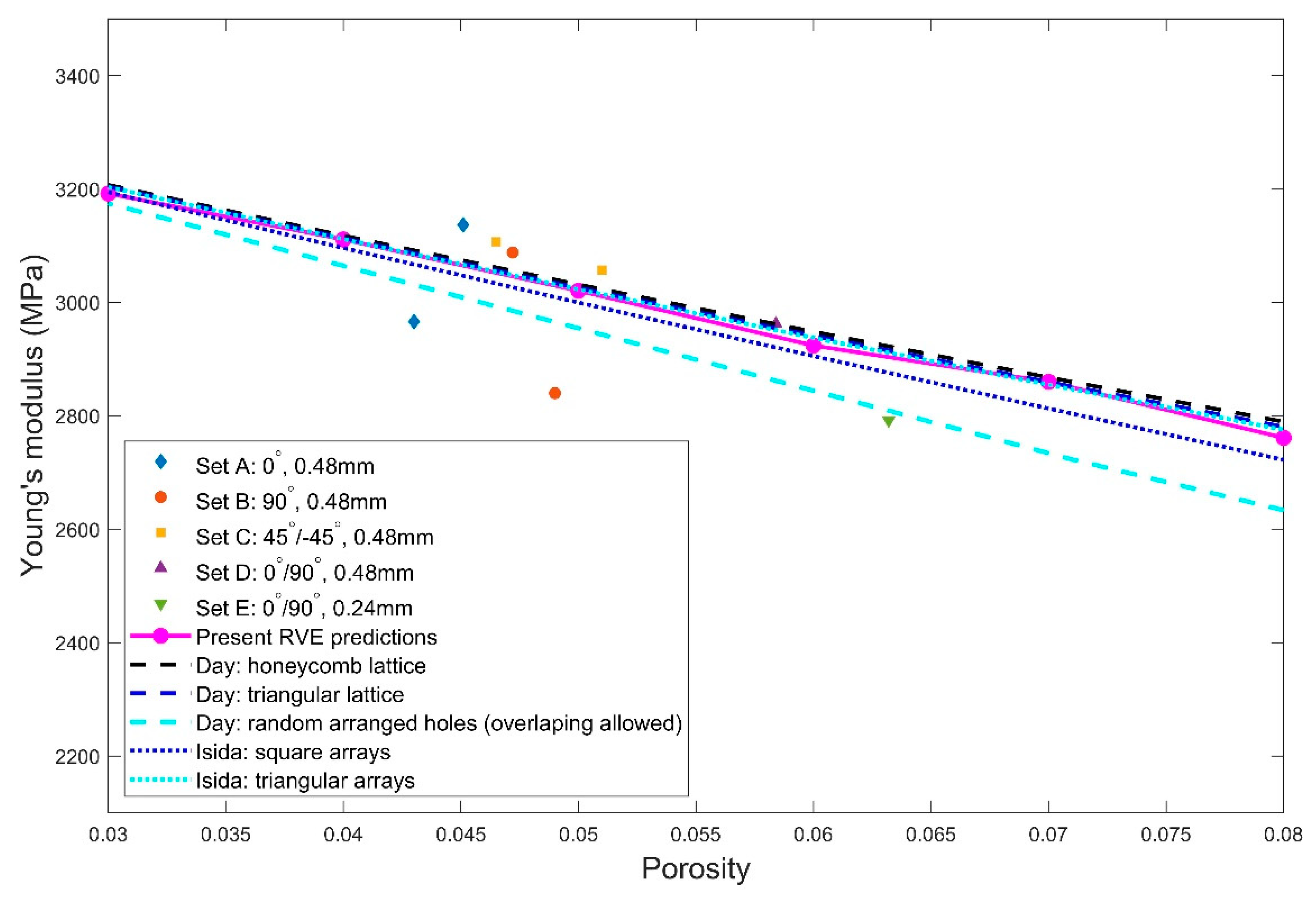
For the porosity between 3% and 50%, the prediction results of Young’s modulus and Poisson’s ratio are respectively given in
Figure 14 and
Figure 15 for the cases using the pore sizes in the full range (that is, from 0.038 to 1 mm) as well as only small pore sizes below 0.2 mm. The presented data were obtained by averaging the elastic properties calculated for the three RVEs with the randomly positioned pores. Also included are the Young’s modulus predicted by the existing models [
35,
36]. It is observed that the elastic properties predicted using the two pore size distributions do not differ too much, having a percentage difference up to 6.5% for larger porosity between 10% and 50% and a percentage difference up to 1.2% for smaller porosity below 10%. The prediction results using the pore sizes between 0.0388 and 0.2 mm are slightly larger compared to the ones using the full range of pore sizes. It appears that the larger pores with sizes ranging from 0.2 to 1 mm do not affect the prediction results very much, since the main contribution comes from the large population of the smaller pores (below 0.2 mm).
When it cames to the comparison with the existing models in [
35,
36], our predictions were generally close to the effective Young’s modulus estimated by the cases of the centered holes in honeycomb and triangular lattices in [
36] as well as the case of periodic holes in triangular arrays in [
35], especially for porosity lower than 40%. The predicted Young’s modulus for both pore size distributions falls between the triangular and square array of holds proposed by [
35]. Compared to the pore size distributions involving the large pores (the full range of pore sizes), the RVEs using only smaller pores below 0.2 mm gave rise to predicted Young’s modulus closer to the case with the holes centered in a triangular lattice in [
36] and the holes in triangular arrays in [
35]. This may be as expected since [
35] and [
36] assume the holes to have uniform diameters and our pore size selected within 0.0388 to 0.2 mm gave rise to more uniform-like sizes compared to the other case with the pore sizes selected up to 1mm. Moreover, it is not surprising from
Figure 14 that the cases with the randomly arranged holes from [
36] provide Young’s modulus that is much deviated from our prediction results if we take into account that overlapped holes are allowed in [
36] but strictly not allowed in our micromechanical model.
For Poisson’s ratio, it is observed from
Figure 15 that the predicted values for the different values of porosity and both pore size distributions are all approximately equal to 0.33 which is the Poisson’s ratio which we used as the material property of the matrix in the micromechanical simulations. This also matches one of the conclusions in [
36], which pointed out that the effective Poisson’s ratio should be approximately equal to 1/3 if the Poisson’s ratio for the matrix is taken as 1/3.