Effect of Chitin Whiskers on the Molecular Dynamics of Carrageenan-Based Nanocomposites
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Preparation of Films
2.2. Dielectric Relaxation Spectroscopy (DRS) Characterization
3. Results
4. Conclusions
- i.
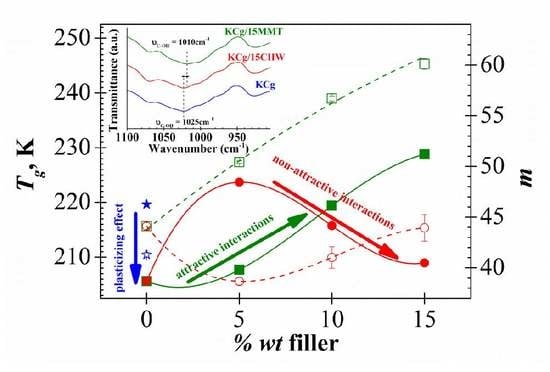
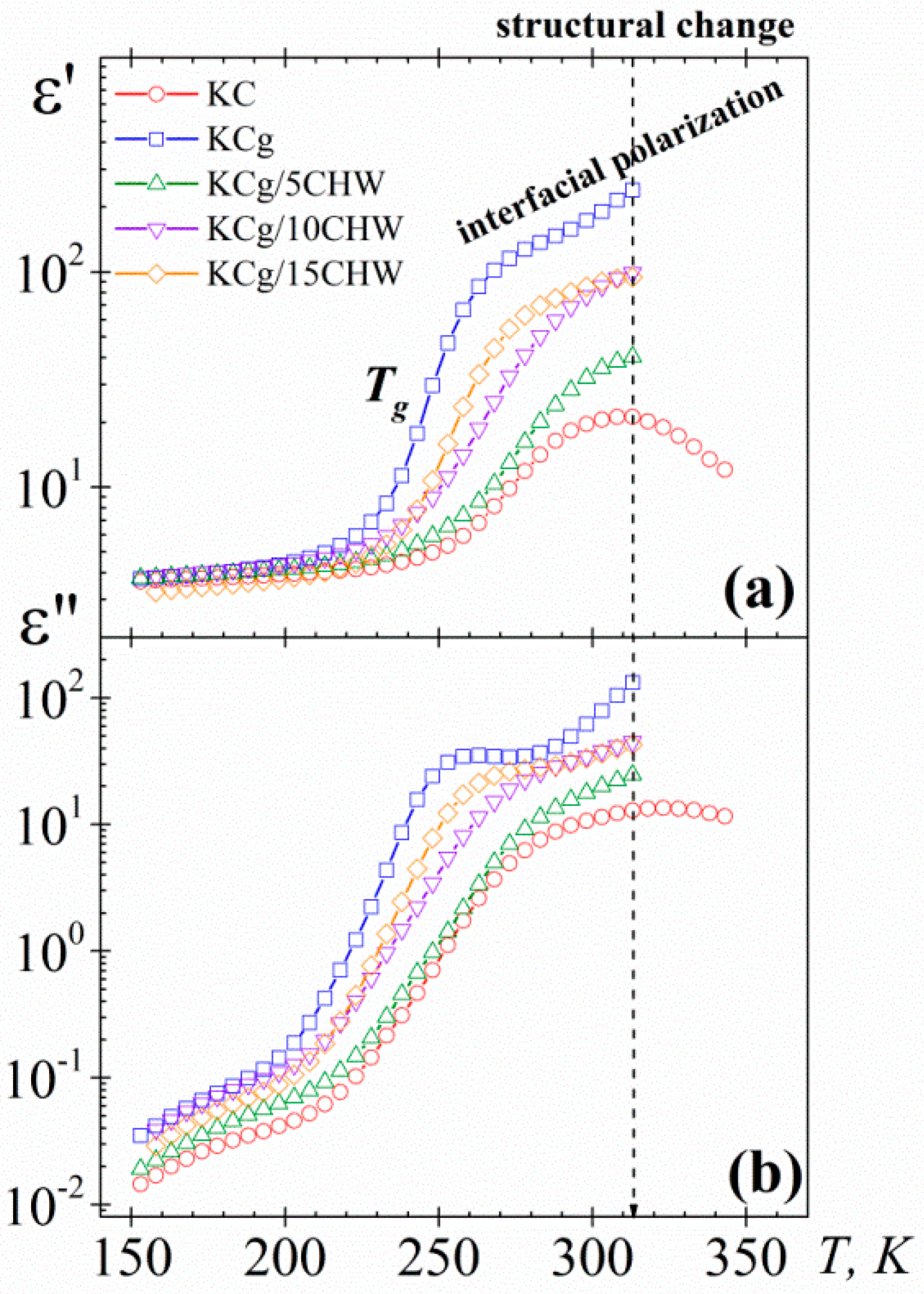
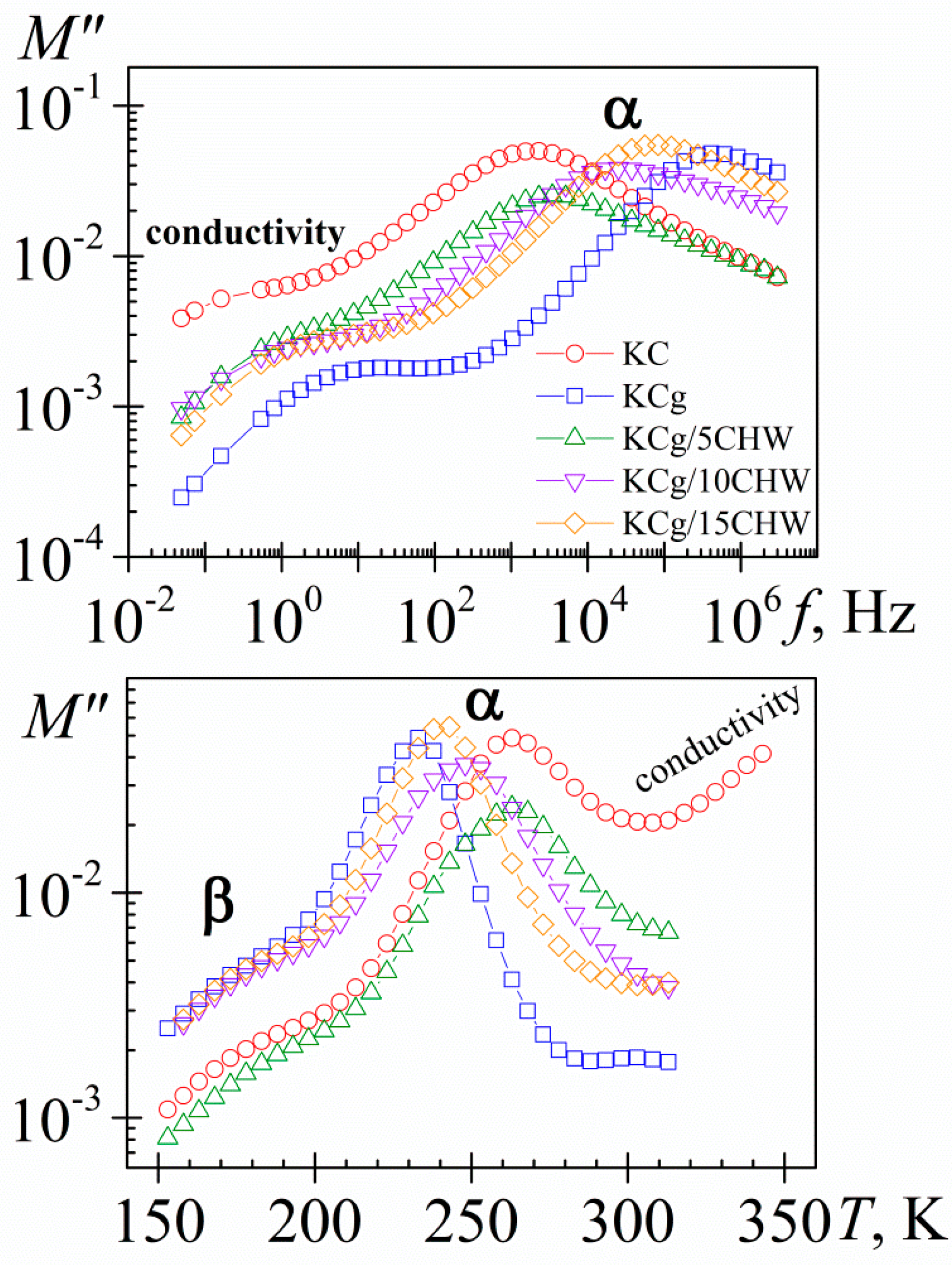
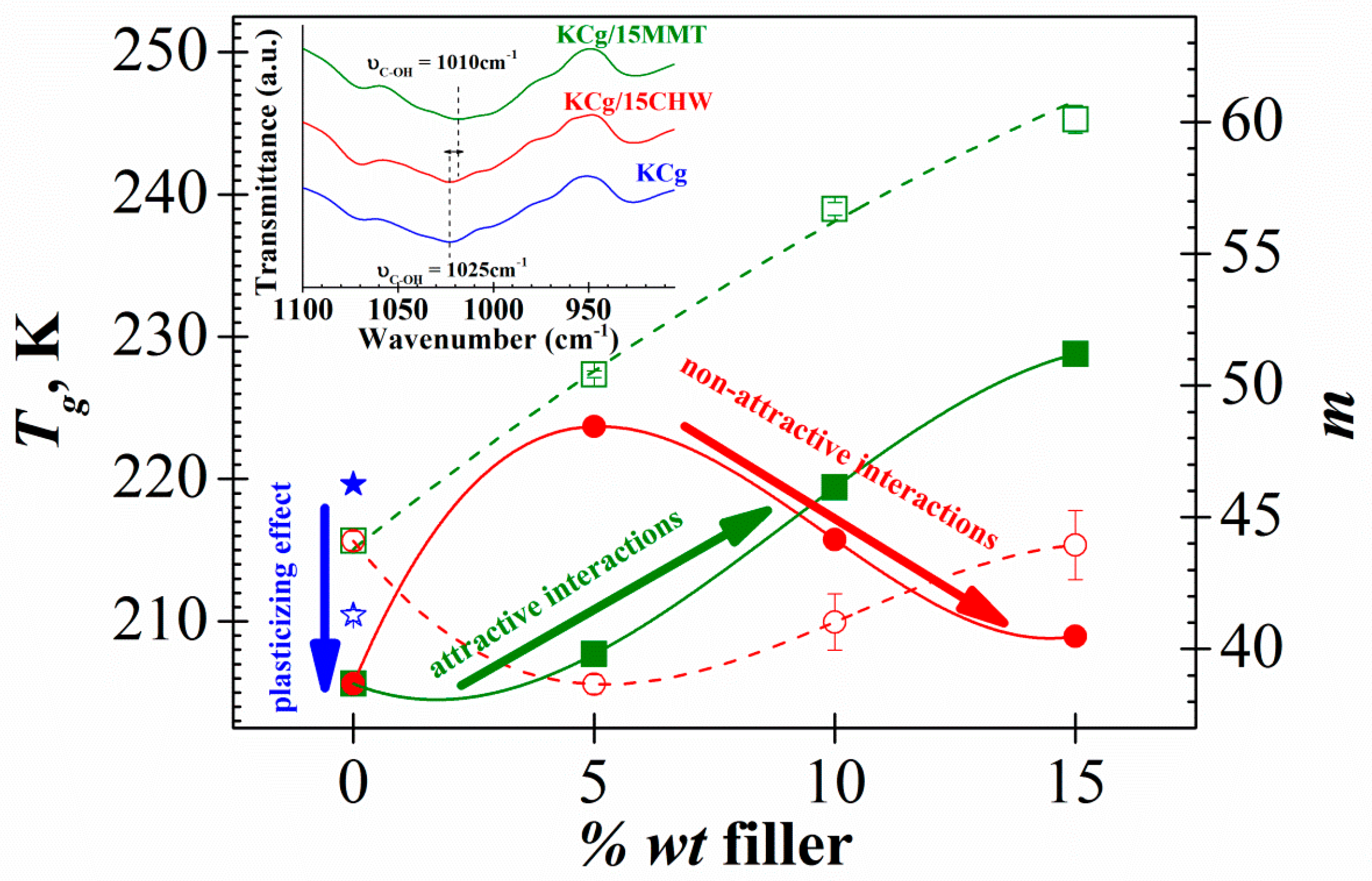
- By addition of CHW filler, the relaxation process was shifted to lower frequencies, up to two orders of magnitude compared to the unfilled polymer, and to higher temperatures. Like this, the Tg evaluated from DRS measurements increases from 205.4 K (KCg) to 223.7 K with the incorporation of a 5% wt of CHW, but as the CHW content increases, a decrease of the Tg to 209 K for a 15 wt % was observed. These trends indicate a decrease and increase, respectively, of molecular mobility by modifying the CHW content.
- ii.
- As the content of CHW filler increased, the height of the peak decreased. Thus, the CHW incorporation restricted the movement of the polymer molecules near the nanowhiskers surface. Consequently, the number of polymer chains that participate in the process was reduced.
- iii.
- The broadness of the α-relaxation increased slightly with the addition of the CHW filler to the KCg matrix. This tendency is related to the fact that polymer chain mobility near CHW is not the same as the mobility of the pure polymer.
- iv.
- A reduction of the fragility index m was obtained with the filler CHW addition to the KCg matrix. The lower value was obtained when a 5% of CHW was added to the KCg matrix, increasing the fragility index m as the CHW content rose.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zheng, Y.; Monty, J.; Linhardt, R.J. Polysaccharide-based nanocomposites and their applications. Carbohydr. Res. 2015, 405, 23–32. [Google Scholar] [CrossRef]
- Jamróz, E.; Kulawik, P.; Kopel, P. The Effect of Nanofillers on the Functional Properties of Biopolymer-Based Films: A Review. Polymers 2019, 11, 675. [Google Scholar] [CrossRef]
- Park, S.B.; Lih, E.; Park, K.S.; Joung, Y.K.; Han, D.K. Biopolymer-based functional composites for medical applications. Prog. Polym. Sci. 2017, 68, 77–105. [Google Scholar] [CrossRef]
- Xie, F.; Pollet, E.; Halley, P.J.; Averous, L. Starch-based nano-biocomposites. Prog. Polym. Sci. 2013, 38, 1590–1628. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, X.; Wang, J.; Cheng, M. Synthesis and Characterization of Konjac Glucomannan/Carrageenan/Nano-silica Films for the Preservation of Postharvest White Mushrooms. Polymers 2019, 11, 6. [Google Scholar] [CrossRef] [PubMed]
- Rhim, J.W.; Park, H.M.; Ha, C.S. Bio-nanocomposites for food packaging applications. Prog. Polym. Sci. 2013, 38, 1629–1652. [Google Scholar] [CrossRef]
- Müller, K.; Bugnicourt, E.; Latorre, M.; Jorda, M.; Echegoyen Sanz, Y.; Lagaron, J.; Miesbauer, O.; Bianchin, A.; Hankin, S.; Bölz, U.; et al. Review on the Processing and Properties of Polymer Nanocomposites and Nanocoatings and Their Applications in the Packaging, Automotive and Solar Energy Fields. Nanomaterials 2017, 7, 74. [Google Scholar] [CrossRef] [PubMed]
- Shankar, S.; Reddy, J.P.; Rhim, J.; Kim, H. Preparation, characterization, and antimicrobial activity of chitin nanofibrils reinforced carrageenan nanocomposite films. Carbohydr. Polym. 2015, 117, 468–475. [Google Scholar] [CrossRef] [PubMed]
- Corvaglia, S.; Rodriguez, S.; Bardi, G.; Torres, F.G.; Lopez, D. Chitin whiskers reinforced carrageenan films as low adhesion cell substrates. Int. J. Polym. Mater. Polym. Biomater. 2016, 65, 574–580. [Google Scholar] [CrossRef]
- Shojaee-Aliabadi, S.; Mohammadifar, M.A.; Hosseini, H.; Mohammadi, A.; Ghasemlou, M.; Hosseini, S.M.; Khaksar, R. Characterization of nanobiocomposite kappa-carrageenan film with Zataria multiflora essential oil and nanoclay. Int. J. Biol. Macromol. 2014, 69, 282–289. [Google Scholar] [CrossRef] [PubMed]
- Reddy, M.M.; Vivekanandhan, S.; Misra, M.; Bhatia, S.K.; Mohanty, A.K. Biobased plastics and bionanocomposites: Current status and future opportunities. Prog. Polym. Sci. 2013, 38, 1653–1689. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, X.; Lv, Y.; Li, M.; Liu, X.; Li, G.; Yu, G. Structural and compositional characteristics of hybrid carrageenans from red algae Chondracanthus chamissoi. Carbohydr. Polym. 2012, 89, 914–919. [Google Scholar] [CrossRef] [PubMed]
- Byankina, A.O.; Sokolova, E.V.; Anastyuk, S.D.; Isakov, V.V.; Glazunov, V.P.; Volod’ko, A.V.; Yakovleva, I.M.; Solov’eva, T.F.; Yermak, I.M. Polysaccharide structure of tetrasporic red seaweed Tichocarpus crinitus. Carbohydr. Polym. 2013, 98, 26–35. [Google Scholar] [CrossRef] [PubMed]
- Stortz, C.A.; Cerezo, A.S. The 13C NMR spectroscopy of carrageenans: Calculation of chemical shifts and computer-aided structural determination. Carbohydr. Polym. 1992, 18, 237–242. [Google Scholar] [CrossRef]
- Rodriguez, S.A.; Weese, E.; Nakamatsu, J.; Torres, F. Development of Biopolymer Nanocomposites Based on Polysaccharides Obtained from Red Algae Chondracanthus chamissoi Reinforced with Chitin Whiskers and Montmorillonite. Polym. Plast. Technol. Eng. 2016, 55, 1557–1564. [Google Scholar] [CrossRef]
- Mitsuiki, M.; Yamamoto, Y.; Mizuno, A.; Motoki, M. Glass transition properties as a function of water content for various low-moisture galactans. J. Agric. Food Chem. 1998, 46, 3528–3534. [Google Scholar] [CrossRef]
- Picker, K.M. The use of carrageenan in mixture with microcrystalline cellulose and its functionality for making tablets. Eur. J. Pharm. Biopharm. 1999, 48, 27–36. [Google Scholar] [CrossRef]
- Kasapis, S.; Mitchell, J.R. Definition of the rheological glass transition temperature in association with the concept of iso-free-volume. Int. J. Biol. Macromol. 2001, 29, 315–321. [Google Scholar] [CrossRef]
- Fouda, M.M.; El-Aassar, M.R.; El Fawal, G.F.; Hafez, E.E.; Masry, S.H.; Abdel-Megeed, A. k-Carrageenan/poly vinyl pyrollidone/polyethylene glycol/silver nanoparticles film for biomedical application. Int. J. Biol. Macromol. 2015, 74, 179–184. [Google Scholar] [CrossRef]
- Arof, A.K.; Shuhaimi, N.E.A.; Alias, N.A.; Kufian, M.Z.; Majid, S.R. Application of chitosan/iota-carrageenan polymer electrolytes in electrical double layer capacitor (EDLC). J. Solid State Electrochem. 2010, 14, 2145–2152. [Google Scholar] [CrossRef]
- Rescignano, N.; Fortunati, E.; Armentano, I.; Hernandez, R.; Mijangos, C.; Pasquino, R.; Kenny, J.M. Use of alginate, chitosan and cellulose nanocrystals as emulsion stabilizers in the synthesis of biodegradable polymeric nanoparticles. J. Colloid Interface Sci. 2015, 445, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Mincea, M.; Negrulescu, A.; Ostafe, V. Preparation, modification, and applications of chitin nanowhiskers: A review. Rev. Adv. Mater. Sci. 2012, 30, 225–242. [Google Scholar]
- Chang, P.R.; Jian, R.; Yu, J.; Ma, X. Starch-based composites reinforced with novel chitin nanoparticles. Carbohydr. Polym. 2010, 80, 420–425. [Google Scholar] [CrossRef]
- Blackwell, J. Chitin. In Biopolymers; Walton, A.G., Blackwell, J., Eds.; Academic Press: New York, NY, USA, 1973; pp. 474–489. [Google Scholar]
- Zeng, J.-B.; He, Y.-S.; Li, S.-L.; Wang, Y.-Z. Chitin Whiskers: An Overview. Biomacromolecules 2012, 13, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Villanueva, M.E.; Salinas, A.; Díaz, L.E.; Copello, G.J. Chitin nanowhiskers as alternative antimicrobial controlled release carriers. New J. Chem. 2015, 39, 614–620. [Google Scholar] [CrossRef]
- Kameda, T.; Miyazawa, M.; Ono, H.; Yoshida, M. Hydrogen Bonding Structure and Stability of α-Chitin Studied by 13C Solid-State NMR. Macromol. Biosci. 2005, 5, 103–106. [Google Scholar] [CrossRef] [PubMed]
- Marchessault, R.H.; Morehead, F.F.; Walter, N.M. Liquid crystal systems from fibrillar polysaccharides. Nature 1959, 184, 632–633. [Google Scholar] [CrossRef]
- Paillet, M.; Dufresne, A. Chitin whisker reinforced thermoplastic nanocomposites. Macromolecules 2001, 34, 6527–6530. [Google Scholar] [CrossRef]
- Gopalan Nair, K.; Dufresne, A. Crab shell chitin whisker reinforced natural rubber nanocomposites. 1. Processing and swelling behavior. Biomacromolecules 2003, 4, 657–665. [Google Scholar] [CrossRef]
- Huang, Y.; Yao, M.; Zheng, X.; Liang, X.; Su, X.; Zhang, Y.; Zhang, L. Effects of chitin whiskers on physical properties and osteoblast culture of alginate-based nanocomposite hydrogels. Biomacromolecules 2015, 16, 3499–3507. [Google Scholar] [CrossRef]
- Morin, A.; Dufresne, A. Nanocomposites of chitin whiskers from Riftia tubes and poly (caprolactone). Macromolecules 2002, 35, 2190–2199. [Google Scholar] [CrossRef]
- Watthanaphanit, A.; Supaphol, P.; Tamura, H.; Tokura, S.; Rujiravanit, R. Fabrication structure, and properties of chitin whisker-reinforced alginate nanocomposite fibers. J. Appl. Polym. Sci. 2008, 110, 890–899. [Google Scholar] [CrossRef]
- Salaberria, A.M.; Diaz, R.H.; Labidi, J.; Fernandes, S.C.M. Preparing valuable renewable nanocomposite films based exclusively on oceanic Biomass—Chitin nanofillers and chitosan. React. Funct. Polym. 2015, 89, 31–39. [Google Scholar] [CrossRef]
- Rodríguez, S.; Gatto, F.; Pesce, L.; Canale, C.; Pompa, P.P.; Bardi, G.; Torres, F.G. Monitoring cell substrate interactions in exopolysaccharide-based films reinforced with chitin whiskers and starch nanoparticles used as cell substrates. Int. J. Polym. Mater. Polym. Biomater. 2017, 7, 333–339. [Google Scholar] [CrossRef]
- Pazmiño Betancourt, B.A.; Douglas Francis, J.F.; Starr, W. Fragility and cooperative motion in a glass-forming polymer–nanoparticle composite. Carbohydr. Res. 2013, 9, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Kremer, F.; Schönhals, A. Broadband Dielectric Spectroscopy; Springer: Berlin, Germany, 2003. [Google Scholar]
- Sanchis, M.J.; Carsí, M.; Culebras, M.; Gómez, C.M.; Rodriguez, S.; Torres, F.G. Molecular dynamics of carrageenan composites reinforced with Cloisite Na+ montmorillonite nanoclay. Carbohydr. Polym. 2017, 176, 117–126. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhang, K.; Girpuard, N.; Meredith, J. Facile Route to Produce Chitin Nanofibers as Precursors for Flexible and Transparent Gas Barrier Materials. Biomacromolecules 2014, 15, 4614–4620. [Google Scholar] [CrossRef] [PubMed]
- Sauti, G.; McLachlan, D.S.J. Impedance and modulus spectra of the percolation system silicon-polyester resin and their analysis using the two-exponent phenomenological percolation equation. J. Mater. Sci. 2007, 42, 6477–6488. [Google Scholar] [CrossRef]
- Johari, G.P.; Kim, S.; Shanker, R.M. Dielectric Relaxation and Crystallization of Ultraviscous Melt and Glassy States of Aspirin, Ibuprofen, Progesterone, and Quinidine. J. Pharm. Sci. 2007, 96, 1159–1175. [Google Scholar] [CrossRef]
- Anastasiadis, S.H.; Karatasos, K.; Vlachos, G.; Manias, E.; Giannelis, E.P. Nanoscopic-Confinement Effects on Local Dynamics. Phys. Rev. Lett. 2000, 84, 915. [Google Scholar] [CrossRef]
- Böhning, M.; Goering, H.; Fritz, A.; Brzezinka, K.-W.; Turky, G.; Schönhals, A.; Schartel, B. Dielectric study of molecular mobility in poly(propylene-graft-maleicanhydride)/Clay nanocomposites. Macromolecules 2005, 38, 2764–2774. [Google Scholar] [CrossRef]
- Hodge, I.M.; Ngai, K.L.; Moynihan, C.T. Comments on the electric modulus function. J. Non-Cryst. Solids 2005, 351, 104. [Google Scholar] [CrossRef]
- Havriliak, S.F.; Havriliak, J.S. Dielectric and Mechanical Relaxation in Materials; Hanser: Munich, Germany, 1997. [Google Scholar]
- Havriliak, S.; Negami, S. A complex plane analysis of α-dispersions in some polymer systems. J. Polym. Sci. Polym. Symp. 1966, 14, 99–117. [Google Scholar] [CrossRef]
- Tsangaris, G.M.; Psarras, G.C.; Kouloumbi, N. Electric modulus and interfacial polarization in composite polymeric systems. J. Mater. Sci. 1998, 33, 2027–2037. [Google Scholar] [CrossRef]
- Vogel, H. The law of the relationship between viscosity of liquids and the temperature. Phys. Z. 1921, 22, 645–646. [Google Scholar]
- Fulcher, G.S. Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 1925, 8, 339–340. [Google Scholar] [CrossRef]
- Tamman, G.; Hesse, W. Die Abhängigkeit der Viscosität von der Temperatur bie unterkühlten Flüssigkeiten. Z. Anorg. Allg. Chem. 1926, 156, 245–247. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Pissis, P.; Bokobza, L. Glass transition and molecular dynamics in poly(dimethylsiloxane)/silica nanocomposites. Polymer 2005, 46, 6001–6008. [Google Scholar] [CrossRef]
- Rittigstein, P.; Torkelson, J.M. Polymer–Nanoparticle Interfacial Interactions in Polymer Nanocomposites: Confinement Effects on Glass Transition Temperature and Suppression of Physical Aging. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 2935–2943. [Google Scholar] [CrossRef]
- Oh, H.; Green, P.F. Polymer chain dynamics and glass transition in a thermal polymer/nanoparticle mixture. Nat. Mater. 2009, 8, 139–143. [Google Scholar] [CrossRef]
- Riggleman, R.A.; Yoshimoto, K.; Douglas, J.F.; de Pablo, J.J. Influence of confinement on the fragility of antiplasticized and pure polymer films. Phys. Rev. Lett. 2006, 97, 045502. [Google Scholar] [CrossRef]
- Doolittle, A.K. Studies in newtonian flow. II. The dependence of the viscosity of liquids on free-Space. J. Appl. Phys. 1951, 22, 1471. [Google Scholar] [CrossRef]
- Doolittle, A.K. Studies in newtonian flow. III. The dependence of the viscosity of liquids on molecular weight and free space (in homologous series). J. Appl. Phys. 1952, 23, 236. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 2nd ed.; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Angell, C.A. Strong and fragile liquids. In Relaxations in Complex Systems; Ngai, K.L., Wright, G.B., Eds.; NRL: Washington, DC, USA, 1985; pp. 3–11. [Google Scholar]
- Plazek, D.J.; Ngai, K.L. Correlation of polymer segmental chain dynamics with temperature-dependent time-scale shifts. Macromolecules 1991, 24, 1222–1224. [Google Scholar] [CrossRef]
- Merino, E.G.; Atlas, S.; Raihane, M.; Belfkira, A.; Lahcini, M.; Hult, A.; Dionísio, M.; Correia, N.T. Molecular dynamics of poly(ATRIF) homopolymer and poly(AN-co-ATRIF) copolymer investigated by dielectric relaxation spectroscopy. Eur. Polym. J. 2011, 47, 1429–1446. [Google Scholar] [CrossRef]
- Bohmer, R.; Ngai, K.L.; Angell, C.A.; Plazek, D.J. Nonexponential relaxations in strong and fragile glass formers. J. Chem. Phys. 1993, 99, 4201. [Google Scholar] [CrossRef]
- Roland, C.M.; Ngai, K.L. Segmental relaxation and molecular structure in polybutadienes and polyisoprene. Macromolecules 1991, 24, 5315–5319. [Google Scholar] [CrossRef]
- Roland, C.M.; Ngai, K.L. Corrections Segmental relaxation and molecular structure in polybutadienes and polyisoprene. Macromolecules 1992, 25, 1844. [Google Scholar] [CrossRef]
- Ngai, K.L.; Roland, C.M. Chemical structure and intermolecular cooperativity: Dielectric relaxation results. Macromolecules 1993, 26, 6824–6830. [Google Scholar] [CrossRef]
- Roland, C.M. Terminal and segmental relaxations in epoxidized polyisoprene. Macromolecules 1992, 25, 7031–7036. [Google Scholar] [CrossRef]
- Angell, C.A.; Poole, P.H.; Shao, J. Glass-forming liquids, anomalous liquids, and polyamorphism in liquids and biopolymers. Nuovo Cim. D 1994, 16, 993–1025. [Google Scholar] [CrossRef]
- Roland, C.M.; Ngai, K.L. The anomalous Debye-Waller factor and the fragility of glasses. J. Chem. Phys. 1996, 104, 2967–2970. [Google Scholar] [CrossRef]
- Hodge, I.M. Effects of Annealing and Prior History on Enthalpy Relaxation in Glassy Polymers. 6. Adam—Gibbs Formulation of Nonlinearity. Macromolecules 1987, 20, 2897–2907. [Google Scholar] [CrossRef]
- Hodge, I.M. Influence of the glass network on the vibrational energy transfer from H2O impurities in the Ge-As-Se glass series. J. Non-Cryst. Solids 1996, 202, 164–172. [Google Scholar] [CrossRef]
- Roland, C.M.; Ngai, K.L. Commentary on ‘Strong and fragile liquids—A brief critique’. J. Non-Cryst. Solids 1997, 212, 74–76. [Google Scholar] [CrossRef]
- Angell, C.A. Why C1 = 16 − 17 in the WLF equation is physical and the fragility of polymers. Polymer 1997, 38, 6261–6266. [Google Scholar] [CrossRef]
- Angell, C.A. Formation of Glasses from Liquids and Biopolymers. Science 1995, 267, 1924–1935. [Google Scholar] [CrossRef]
- Angell, C.A. Relaxation in liquids, polymers and plastic crystals- strong/fragile patterns and problems. J. Non-Cryst. Solids 1991, 131–133, 13–31. [Google Scholar] [CrossRef]
- Kunal, K.; Robertson, C.G.; Pawlus, S.; Hahn, S.F.; Sokolov, A.P. Role of Chemical Structure in Fragility of Polymers: A Qualitative Picture. Macromolecules 2008, 41, 7232–7238. [Google Scholar] [CrossRef]
- Sokolov, A.P.; Novikov, V.N.; Ding, Y. Why many polymers are so fragile. J. Phys. Condens. Matter 2007, 19. [Google Scholar] [CrossRef]
- Sanchis, M.J.; Domínguez-Espinosa, G.; Díaz-Calleja, R.; Guzmán, J.; Riande, E. Influence of structural chemical characteristics on polymer chain dynamics. J. Chem. Phys. 2008, 129, 054903. [Google Scholar] [CrossRef] [PubMed]


| Sample Code | KC | KCg | KCg/5CHW | KCg/10 CHW | KCg/15 CHW |
|---|---|---|---|---|---|
| wt % CHW | 0 | 0 | 5 | 10 | 15 |
| τ0 (s) | 10−8.6 ± 100.3 | 10−12.1 ± 100.1 | 10−11.4 ± 100.2 | 10−11.9 ± 101.8 | 10−11.1 ± 101.8 |
| M(K) | 1390.6 ± 12.2 | 2119.3 ± 22.4 | 1786.0 ± 21.3 | 1799.8 ± 20.2 | 672.8 ± 20.3 |
| Tv(K) | 162.9 ± 4.6 | 140.1 ± 0.6 | 156.7 ± 0.7 | 151.6 ± 6.1 | 150.2 ± 6.5 |
| TgDRS (K) (τ = 100 s) | 219.6 | 205.4 | 223.7 | 215.7 | 209.0 |
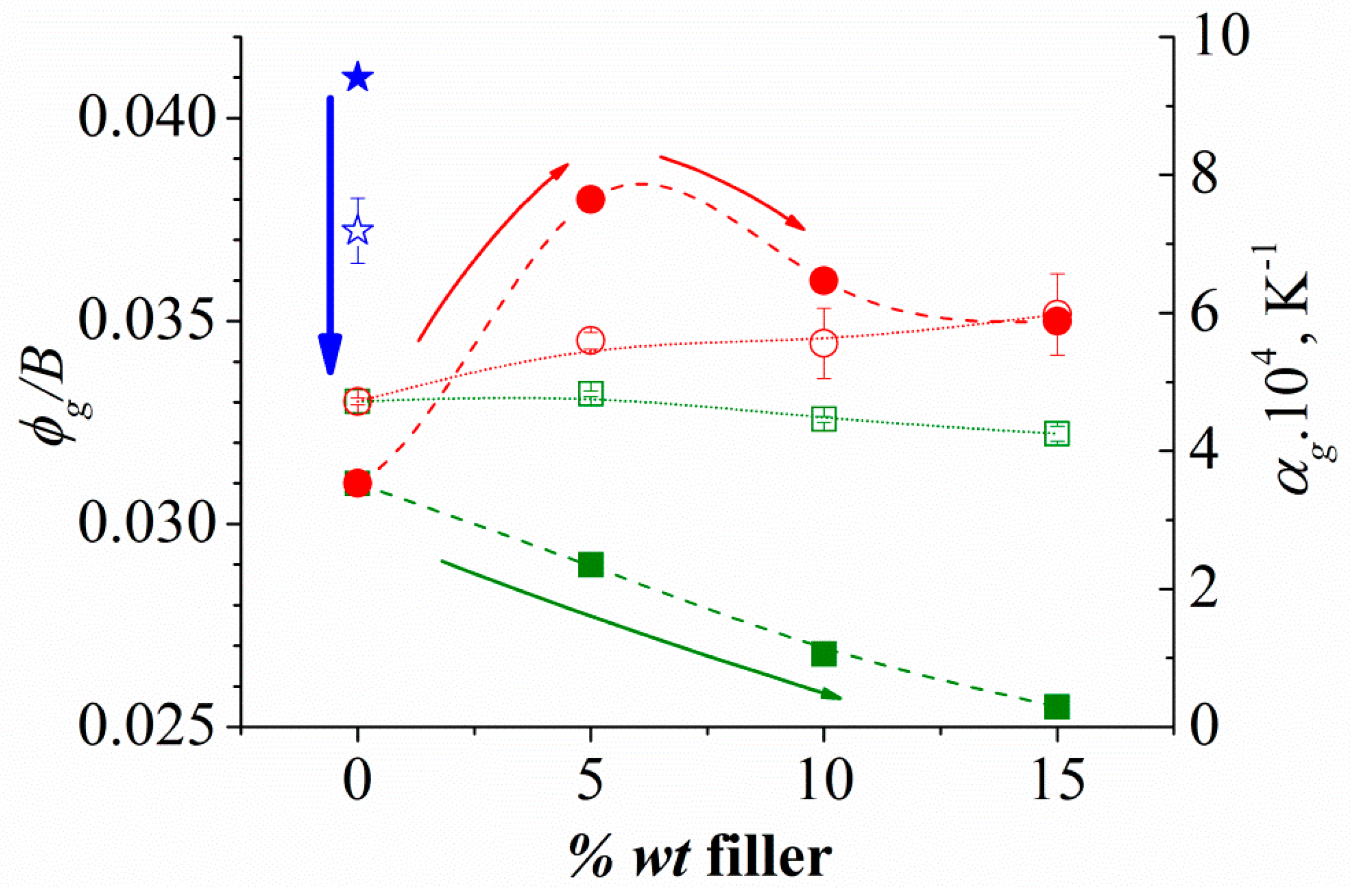
| ϕg/B | 0.041 ± 0.002 | 0.031 ± 0.002 | 0.038 ± 0.003 | 0.036 ± 0.003 | 0.035 ± 0.003 |
| αg⋅104, K−1 | 7.19 ± 0.47 | 4.72 ± 0.09 | 5.60 ± 0.12 | 5.56 ± 0.51 | 5.98 ± 0.59 |
| m | 41.3 ± 2.2 | 44.1 ± 0.3 | 38.7 ± 0.4 | 41.0 ± 2.7 | 43.9 ± 3.1 |
| Ea(Tg), kJ mol−1 | 173.6 ± 3.4 | 173.6 ± 3.8 | 165.6 ± 4.3 | 169.5 ± 38.9 | 175.8 ± 46.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carsi, M.; Sanchis, M.J.; Gómez, C.M.; Rodriguez, S.; G. Torres, F. Effect of Chitin Whiskers on the Molecular Dynamics of Carrageenan-Based Nanocomposites. Polymers 2019, 11, 1083. https://doi.org/10.3390/polym11061083
Carsi M, Sanchis MJ, Gómez CM, Rodriguez S, G. Torres F. Effect of Chitin Whiskers on the Molecular Dynamics of Carrageenan-Based Nanocomposites. Polymers. 2019; 11(6):1083. https://doi.org/10.3390/polym11061083
Chicago/Turabian StyleCarsi, Marta, Maria J. Sanchis, Clara M. Gómez, Sol Rodriguez, and Fernando G. Torres. 2019. "Effect of Chitin Whiskers on the Molecular Dynamics of Carrageenan-Based Nanocomposites" Polymers 11, no. 6: 1083. https://doi.org/10.3390/polym11061083
APA StyleCarsi, M., Sanchis, M. J., Gómez, C. M., Rodriguez, S., & G. Torres, F. (2019). Effect of Chitin Whiskers on the Molecular Dynamics of Carrageenan-Based Nanocomposites. Polymers, 11(6), 1083. https://doi.org/10.3390/polym11061083