Tethered Semiflexible Polymer under Large Amplitude Oscillatory Shear
Abstract
1. Introduction
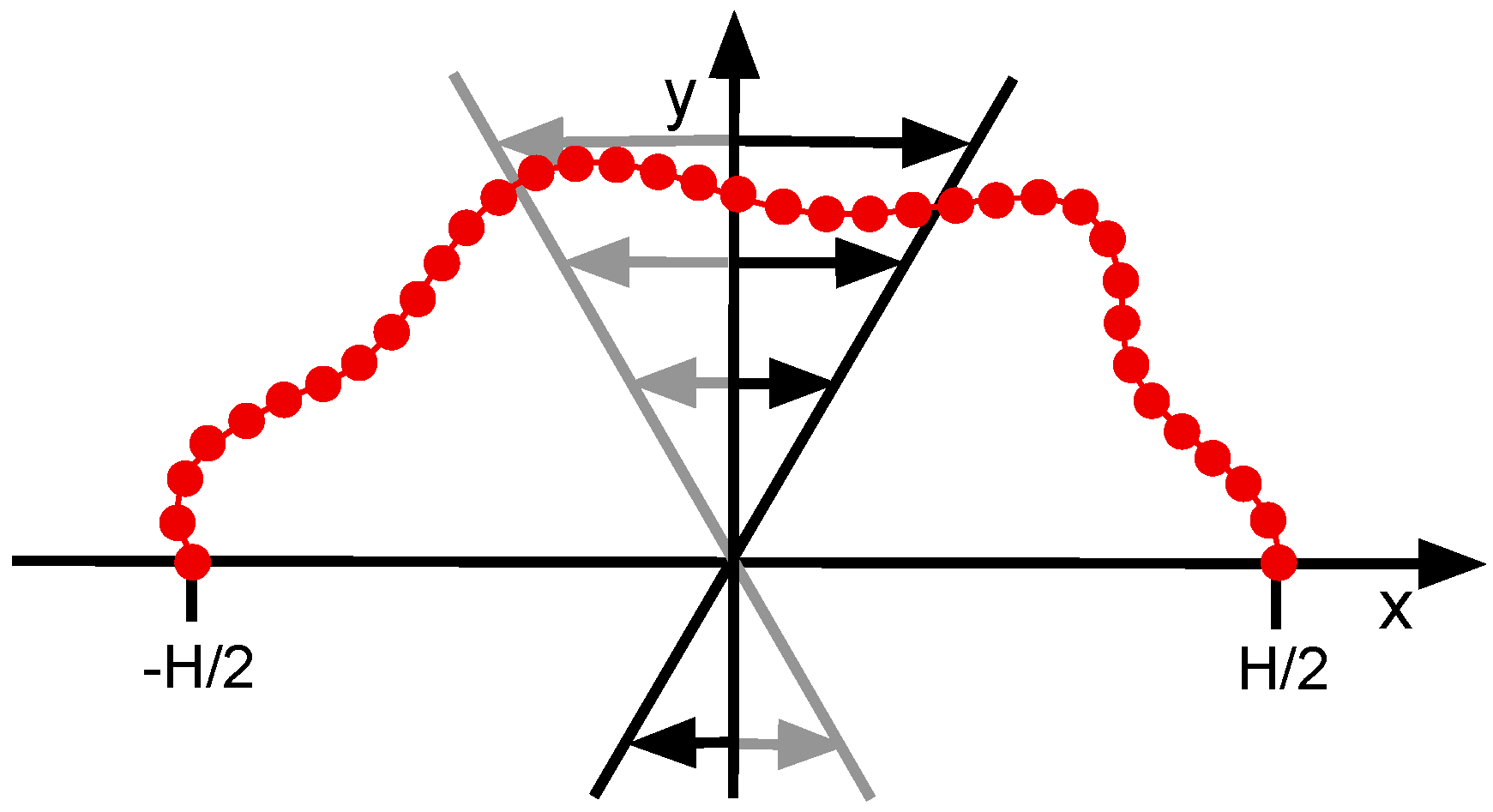
2. Model and Method
3. Results
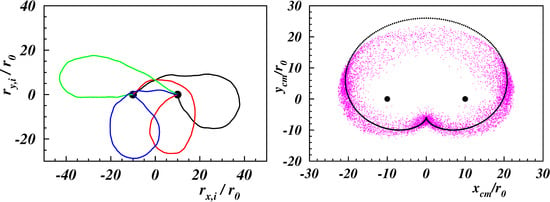
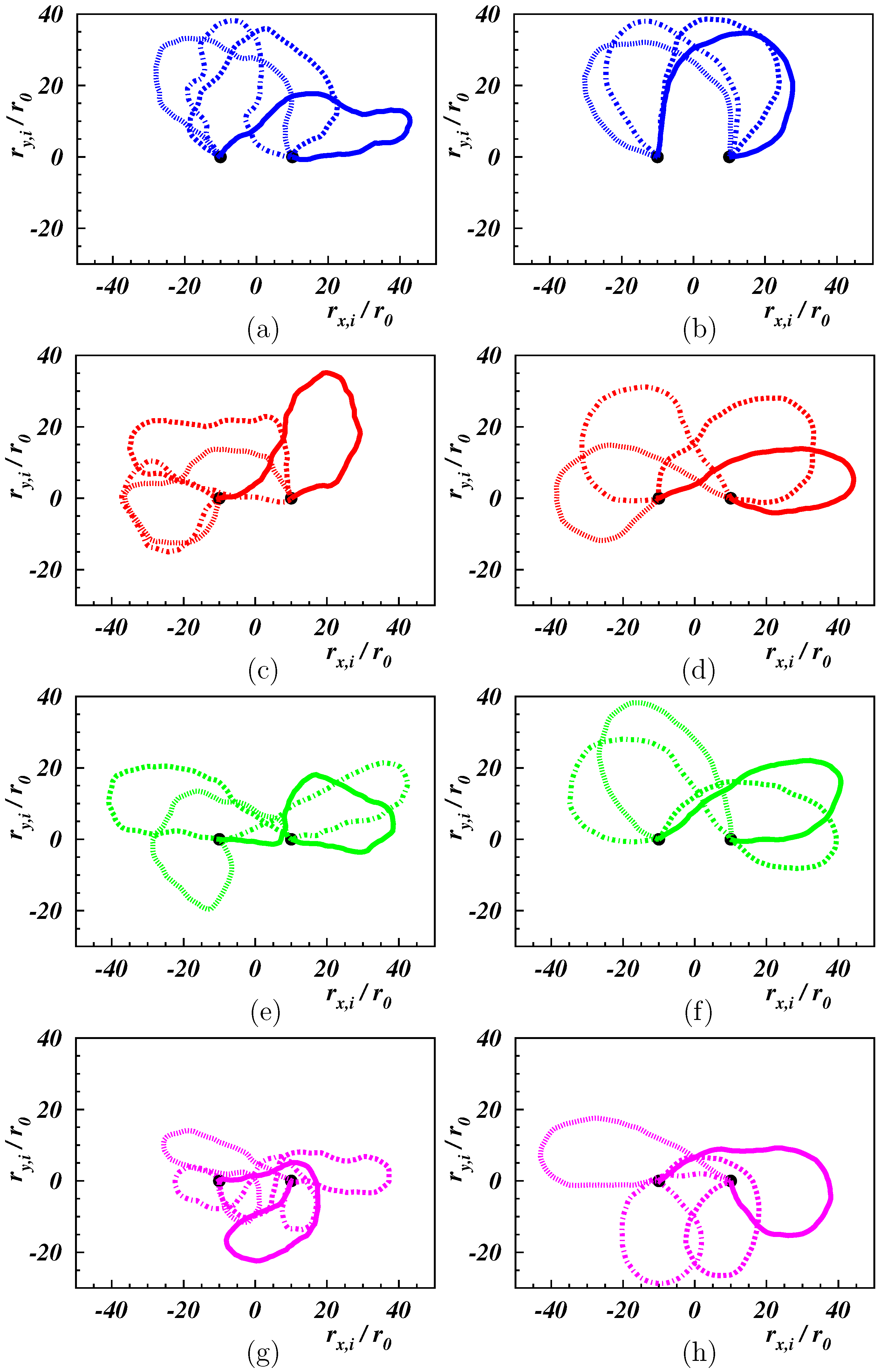
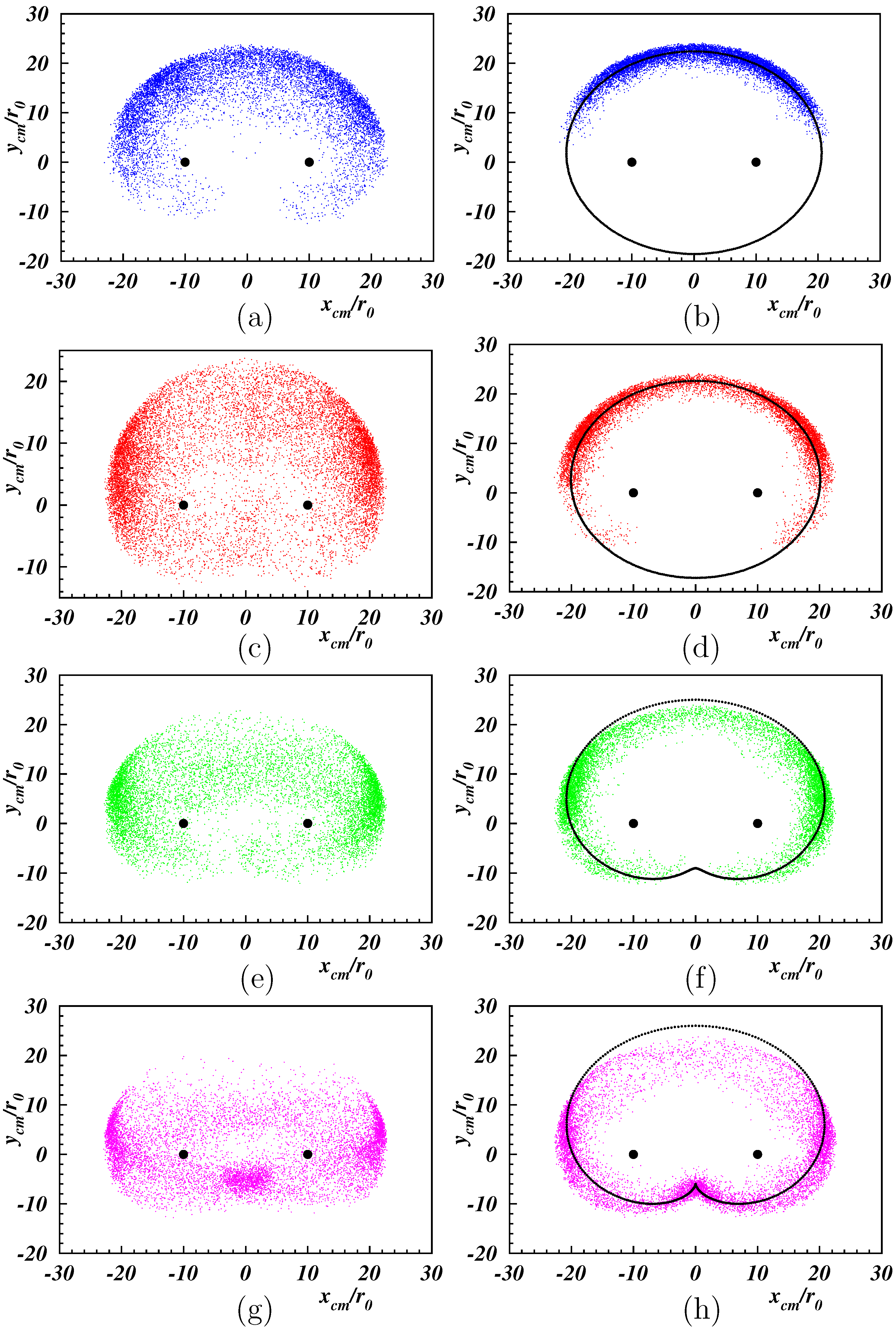
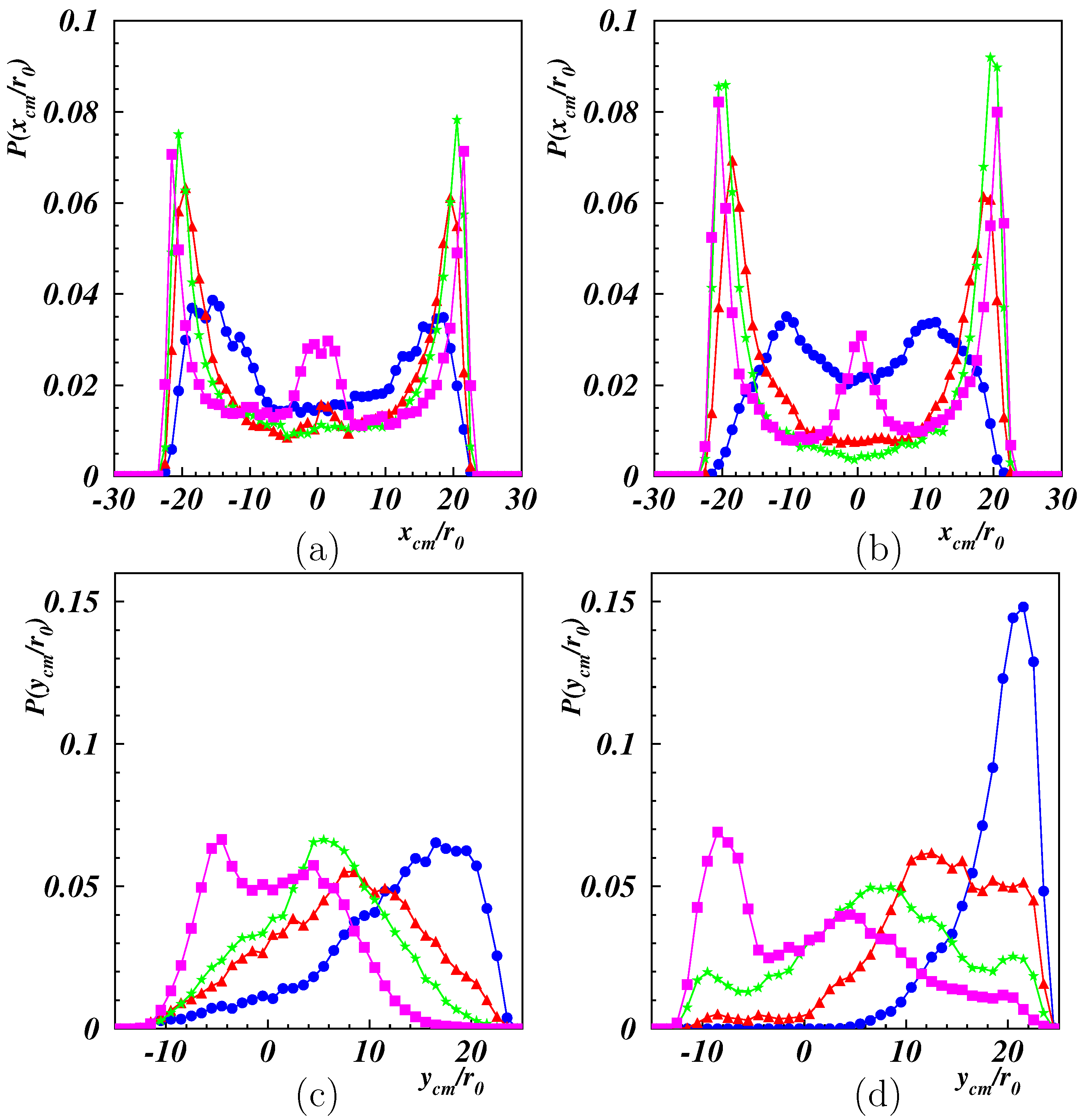
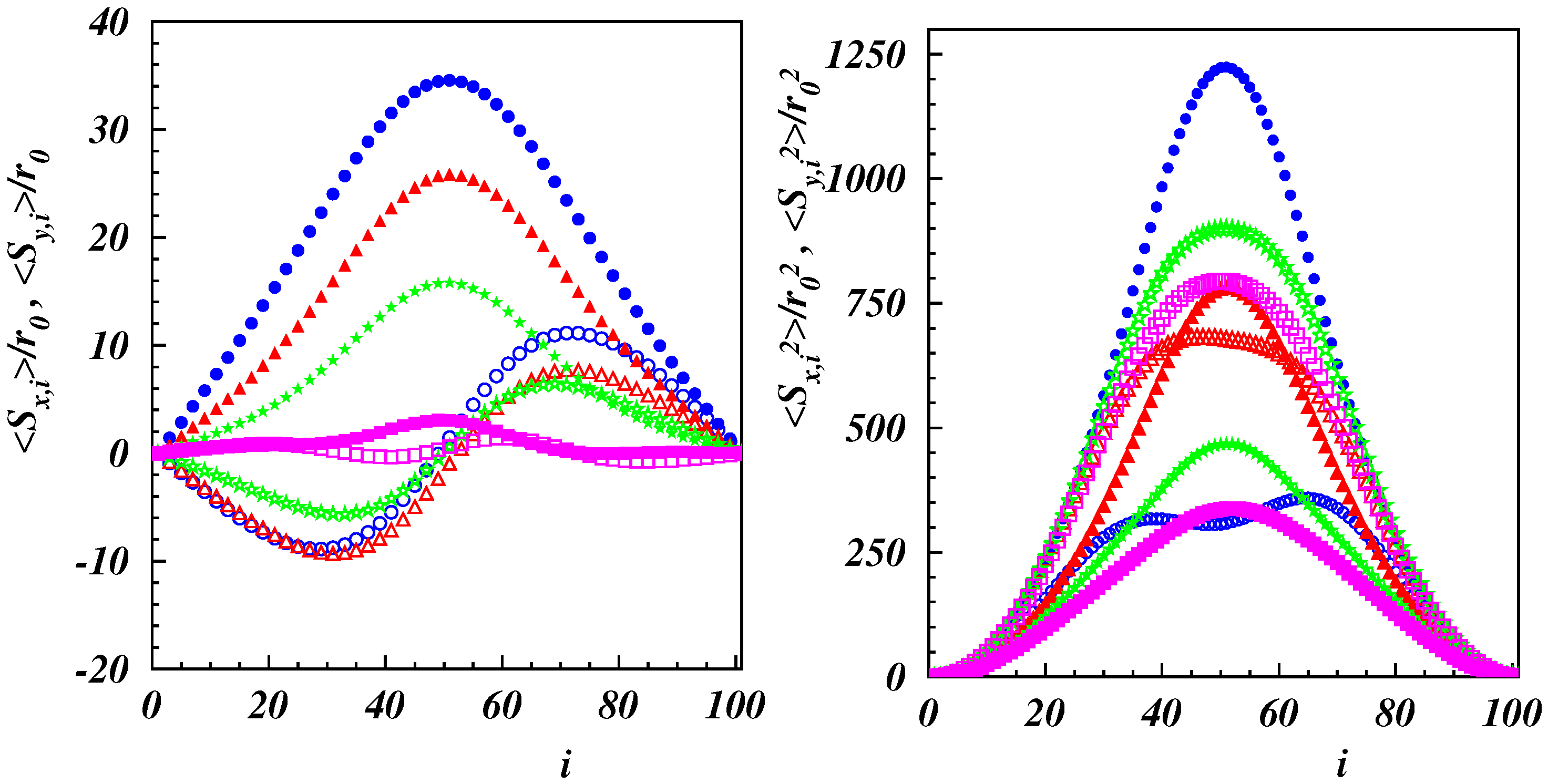
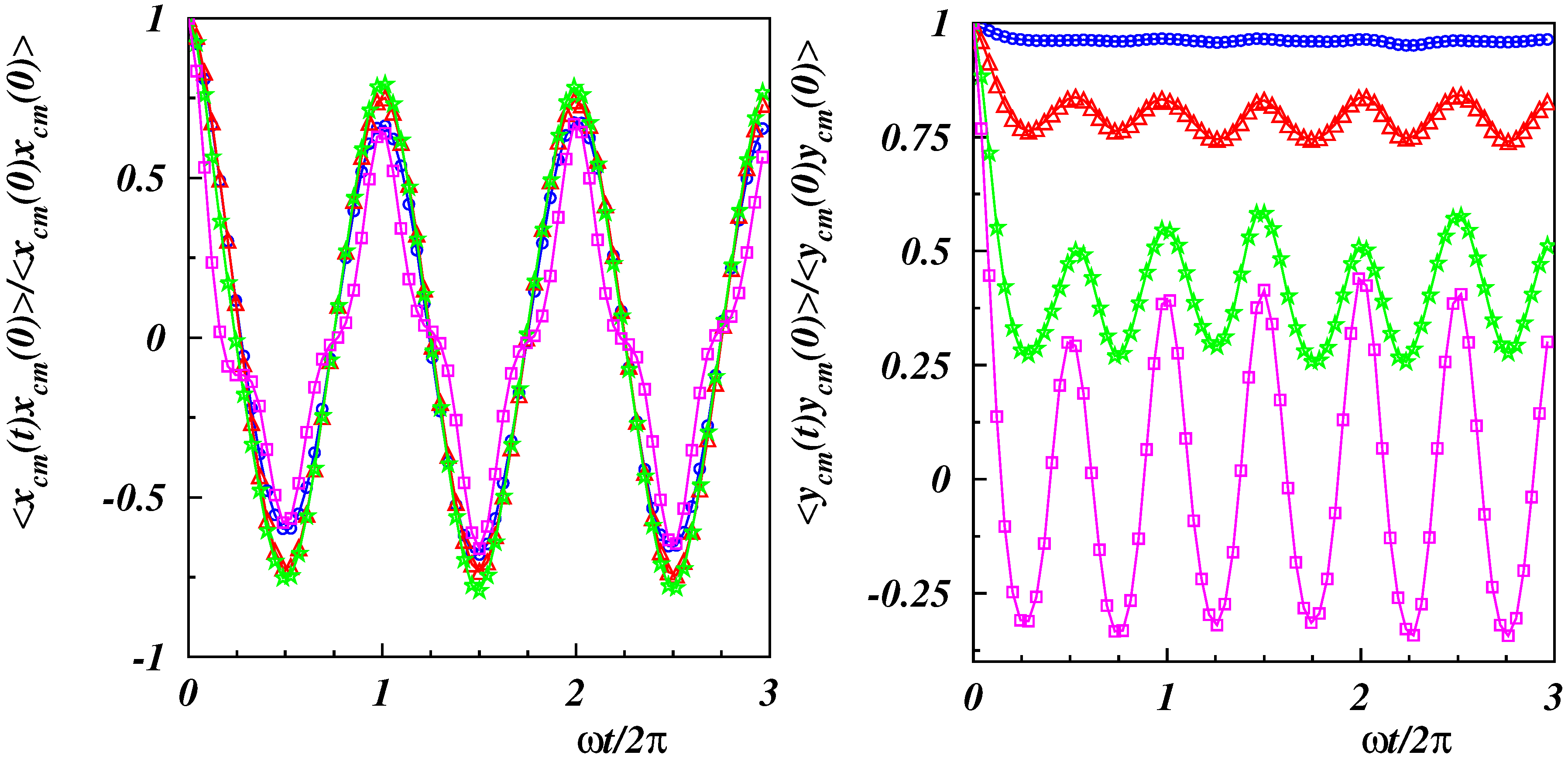
3.1. Center-of-Mass Properties
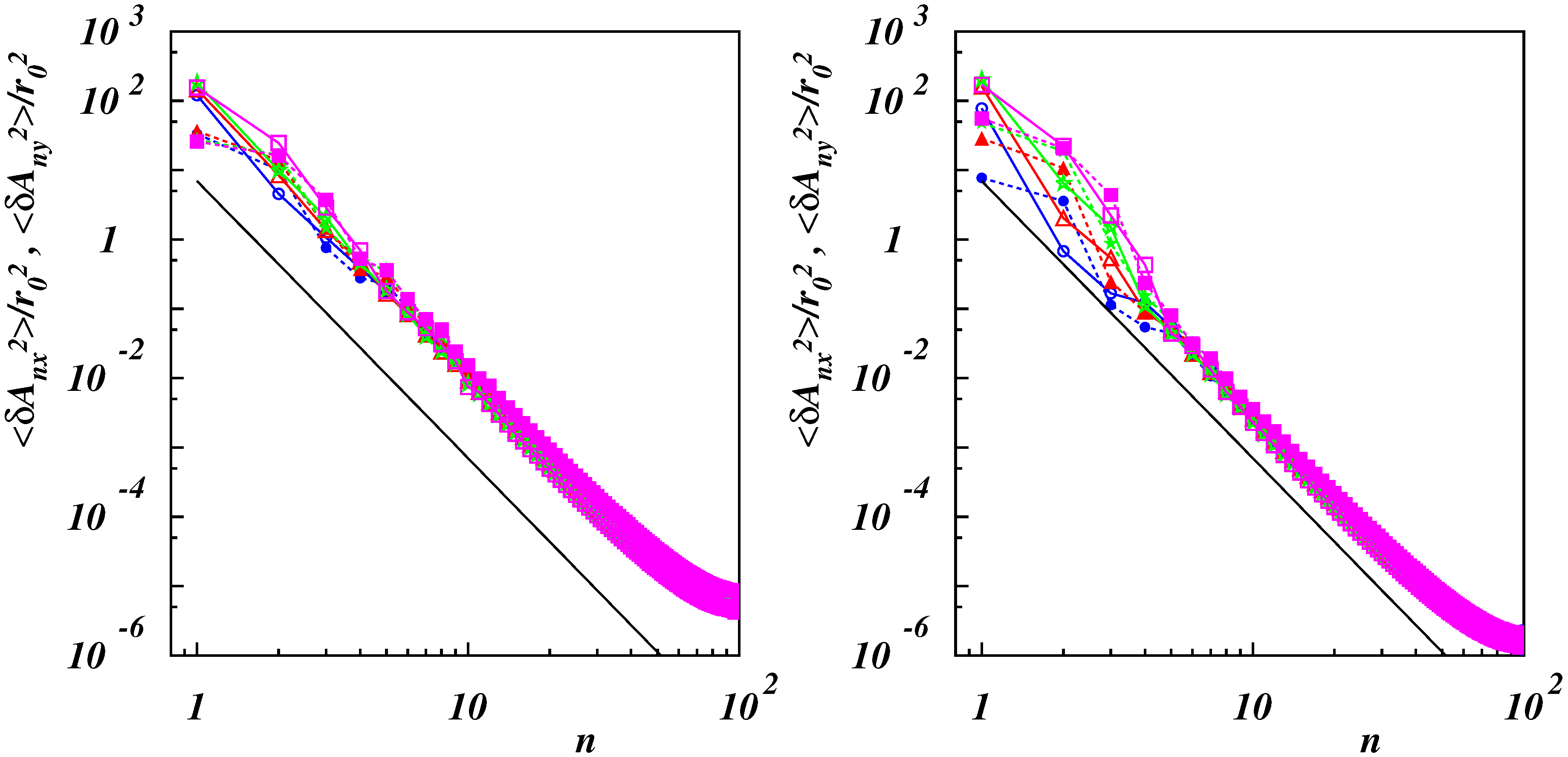
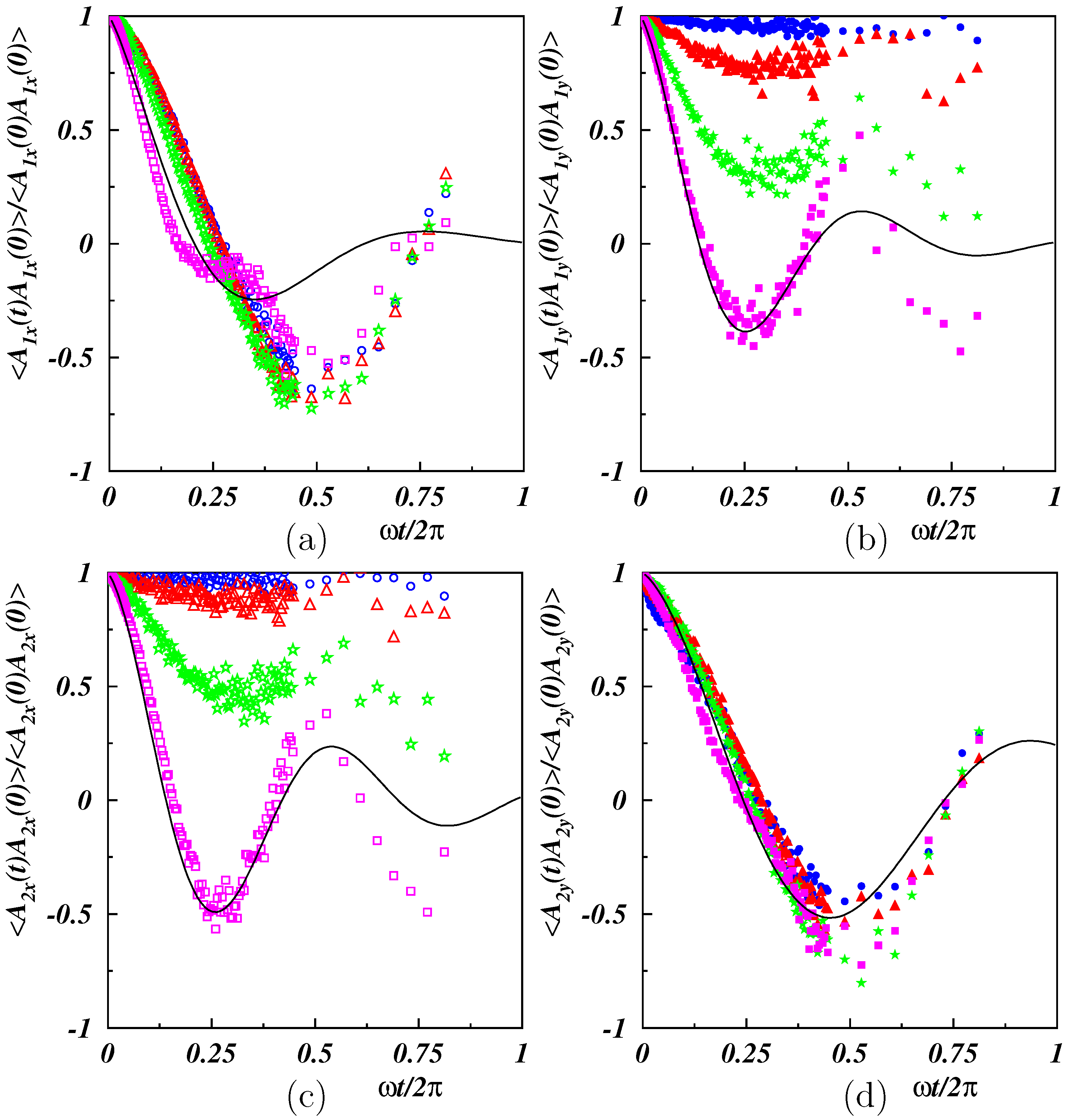
3.2. Conformational Properties
3.2.1. Normal Mode Expansion
3.2.2. Dynamical Properties
4. Summary and Conclusions
Author Contributions
Conflicts of Interest
References
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymer Liquids; John Wiley & Sons: New York, NY, USA, 1987; Volume 1. [Google Scholar]
- Rubinstein, M.; Colby, R.C. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Larson, R.G.; Desai, P.S. Modeling the rheology of polymer melts and solutions. Ann. Rev. Fluid Mech. 2015, 47, 47–65. [Google Scholar] [CrossRef]
- Shaw, M.T.; MacKnight, W.J. Introduction to Polymer Viscoelasticity; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Schroeder, C.M. Single polymer dynamics for molecular rheology. J. Rheol. 2018, 62, 371–403. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymer Liquids; John Wiley & Sons: New York, NY, USA, 1987; Volume 2. [Google Scholar]
- Öttinger, H.C. Stochastic Processes in Polymeric Fluids; Springer: Berlin, Germany, 1996. [Google Scholar]
- Prakash, J.R. Rouse chains with excluded volume interactions: Linear viscoelasticity. Macromolecules 2001, 34, 3396–3411. [Google Scholar] [CrossRef][Green Version]
- Huang, C.C.; Winkler, R.G.; Sutmann, G.; Gompper, G. Semidilute polymer solutions at equilibrium and under shear flow. Macromolecules 2010, 43, 10107–10116. [Google Scholar] [CrossRef]
- Winkler, R.G. Conformational and rheological properties of semiflexible polymers in shear flow. J. Chem. Phys. 2010, 133, 164905. [Google Scholar] [CrossRef]
- Smith, D.E.; Babcock, H.P.; Chu, S. Single-Polymer Dynamics in Steady Shear Flow. Science 1999, 283, 1724–1727. [Google Scholar] [CrossRef] [PubMed]
- Schroeder, C.M.; Teixeira, R.E.; Shaqfeh, E.S.G.; Chu, S. Characteristic Periodic Motion of Polymers in Shear Flow. Phys. Rev. Lett. 2005, 95, 018301. [Google Scholar] [CrossRef]
- Teixeira, R.E.; Babcock, H.P.; Shaqfeh, E.S.G.; Chu, S. Shear Thinning and Tumbling Dynamics of Single Polymers in the Flow-Gradient Plane. Macromolecules 2005, 38, 581–592. [Google Scholar] [CrossRef]
- Schroeder, C.M.; Teixeira, R.E.; Shaqfeh, E.S.G.; Chu, S. Dynamics of DNA in the flow-gradient plane of steady shear flow: Observations and simulations. Macromolecules 2005, 38, 1967–1978. [Google Scholar] [CrossRef]
- Doyle, P.S.; Ladoux, B.; Viovy, J.L. Dynamics of a tethered polymer in shear flow. Phys. Rev. Lett. 2000, 84, 4769. [Google Scholar] [CrossRef] [PubMed]
- Ladoux, B.; Doyle, P.S. Stretching tethered DNA chains in shear flow. Europhys. Lett. 2000, 52, 511. [Google Scholar] [CrossRef]
- Gerashchenko, S.; Steinberg, V. Statistics of Tumbling of a Single Polymer Molecule in Shear Flow. Phys. Rev. Lett. 2006, 96, 038304. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Schroeder, C.M. Single polymer dynamics under large amplitude oscillatory extension. Phys. Rev. Fluid 2016, 1, 053301. [Google Scholar] [CrossRef]
- Liu, T. Flexible polymer chain dynamics and rheological properties in steady flows. J. Chem. Phys. 1989, 90, 5826–5842. [Google Scholar] [CrossRef]
- Delgado-Buscalioni, R. Cyclic Motion of a Grafted Polymer under Shear Flow. Phys. Rev. Lett. 2006, 96, 088303. [Google Scholar] [CrossRef]
- Hur, J.S.; Shaqfeh, E.S.G.; Larson, R.G. Brownian dynamics simulations of single DNA molecules in shear flow. J. Rheol. 2000, 44, 713–742. [Google Scholar] [CrossRef]
- Jose, P.P.; Szamel, G. Single-chain dynamics in a semidilute polymer solution under steady shear. J. Chem. Phys. 2008, 128, 224910. [Google Scholar] [CrossRef] [PubMed]
- He, G.L.; Messina, R.; Löwen, H.; Kiriy, A.; Bocharova, V.; Stamm, M. Shear-induced stretching of adsorbed polymer chains. Soft Matter 2009, 5, 3014–3017. [Google Scholar] [CrossRef]
- Knudsen, K.D.; de la Torre, J.G.; Elgsaeter, A. Gaussian chains with excluded volume and hydrodynamic interaction: shear rate dependence of radius of gyration, intrinsic viscosity and flow birefringence. Polymer 1996, 37, 1317–1322. [Google Scholar] [CrossRef]
- Lyulin, A.V.; Adolf, D.B.; Davies, G.R. Brownian dynamics simulations of linear polymers under shear flow. J. Chem. Phys. 1999, 111, 758–771. [Google Scholar] [CrossRef]
- Petera, D.; Muthukumar, M. Brownian dynamics simulation of bead–rod chains under shear with hydrodynamic interaction. J. Chem. Phys. 1999, 111, 7614–7623. [Google Scholar] [CrossRef]
- Jendrejack, R.M.; de Pablo, J.J.; Graham, M.D. Stochastic simulations of DNA in flow: Dynamics and the effects of hydrodynamic interactions. J. Chem. Phys. 2002, 116, 7752–7759. [Google Scholar] [CrossRef]
- Hsieh, C.C.; Larson, R.G. Modelling hydrodynamic interaction in Brownian dynamics: Simulation of extensional and shear flows of dilute solutions of high molecular weight polystyrene. J. Rheol. 2004, 48, 995–1021. [Google Scholar] [CrossRef]
- Liu, S.; Ashok, B.; Muthukumar, M. Brownian dynamics simulations of bead-rod-chain in simple shear flow and elongational flow. Polymer 2004, 45, 1383–1389. [Google Scholar] [CrossRef]
- Pamies, R.; Martinez, M.C.L.; Cifre, J.G.H.; de la Torre, J.G. Non-Newtonian viscosity of dilute polymer solutions. Macromolecules 2005, 38, 1371–1377. [Google Scholar] [CrossRef]
- Sendner, C.; Netz, R.R. Shear-induced repulsion of a semiflexible polymer from a wall. EPL 2008, 81, 54006. [Google Scholar] [CrossRef]
- Pierleoni, C.; Ryckaert, J.P. Deformation and orientation of flexible polymers in solution under shear flow: A new picture of intermediate reduced shear rates. Macromolecules 1995, 28, 5097–5108. [Google Scholar] [CrossRef]
- Aust, C.; Kröger, M.; Hess, S. Structure and dynamics of dilute polymer solutions under shear flow via nonequilibrium molecular dynamics. Macromolecules 1999, 32, 5660–5672. [Google Scholar] [CrossRef]
- Gratton, Y.; Slater, G.W. Molecular dynamics study of tethered polymers in shear flow. Eur. Phys. J. E 2005, 17, 455–465. [Google Scholar] [CrossRef]
- Zhang, Y.; Donev, A.; Weisgraber, T.; Alder, B.J.; Graham, M.G.; de Pablo, J.J. Tethered DNA dynamics in shear flow. J. Chem. Phys. 2009, 130, 234902. [Google Scholar] [CrossRef]
- Ryder, J.F.; Yeomans, J.M. Shear thinning in dilute polymer solutions. J. Chem. Phys. 2006, 125, 194906. [Google Scholar] [CrossRef]
- Ripoll, M.; Winkler, R.G.; Gompper, G. Star polymers in shear flow. Phys. Rev. Lett. 2006, 96, 188302. [Google Scholar] [CrossRef]
- Kobayashi, H.; Yamamoto, R. Tumbling motion of a single chain in shear flow: A crossover from Brownian to non-Brownian behavior. Phys. Rev. E 2010, 81, 041807. [Google Scholar] [CrossRef]
- Lamura, A.; Winkler, R.G. Semiflexible polymers under external fields confined to two dimensions. J. Chem. Phys. 2012, 137, 244909. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.G.; Fedosov, D.A.; Gompper, G. Dynamical and rheological properties of soft colloid suspensions. Curr. Opin. Colloid Interface Sci. 2014, 19, 594–610. [Google Scholar] [CrossRef]
- Cannavacciuolo, L.; Winkler, R.G.; Gompper, G. Mesoscale simulation of polymer dynamics in microchannel flows. EPL 2008, 83, 34007. [Google Scholar] [CrossRef][Green Version]
- Chelakkot, R.; Winkler, R.G.; Gompper, G. Migration of semiflexible polymers in microcapillary flow. EPL 2010, 91, 14001. [Google Scholar] [CrossRef]
- Chelakkot, R.; Winkler, R.G.; Gompper, G. Flow-Induced Helical Coiling of Semiflexible Polymers in Structured Microchannels. Phys. Rev. Lett. 2012, 109, 178101. [Google Scholar] [CrossRef] [PubMed]
- Bogie, K.; Harris, J. An experimental analysis of the Weissenberg rheogoniometer. Rheol. Acta 1966, 5, 212–215. [Google Scholar] [CrossRef]
- Philippoff, W. Vibrational Measurements with Large Amplitudes. Trans. Soc. Rheol. 1966, 10, 317–334. [Google Scholar] [CrossRef]
- Giacomin, A.J.; Dealy, J.M. Large-amplitude oscillatory shear. In Techniques in Rheological Measurement; Collyer, A.A., Ed.; Springer: Dordrecht, The Netherland, 1993; pp. 99–121. [Google Scholar]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Poly. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Ripoll, M.; Winkler, R.G.; Gompper, G. Hydrodynamic screening of star polymers in shear flow. Eur. Phys. J. E 2007, 23, 349–354. [Google Scholar] [CrossRef]
- Gompper, G.; Ihle, T.; Kroll, D.M.; Winkler, R.G. Multi-Particle Collision Dynamics: A particle-based mesoscale simulation approach to the hydrodynamics of complex Fluids. Adv. Polym. Sci. 2009, 221, 1. [Google Scholar]
- Kikuchi, N.; Gent, A.; Yeomans, J.M. Polymer collapse in the presence of hydrodynamic interactions. Eur. Phys. J. E 2002, 9, 63–66. [Google Scholar] [CrossRef] [PubMed]
- Kapral, R. Multiparticle Collision Dynamics: Simulations of complex systems on mesoscale. Adv. Chem. Phys. 2008, 140, 89–146. [Google Scholar]
- Ihle, T.; Kroll, D.M. Stochastic rotation dynamics: A Galilean-invariant mesoscopic model for fluid flow. Phys. Rev. E 2001, 63, 020201(R). [Google Scholar] [CrossRef]
- Lamura, A.; Gompper, G.; Ihle, T.; Kroll, D.M. Multiparticle collision dynamics: Flow around a circular and a square cylinder. Europhys. Lett. 2001, 56, 319–325. [Google Scholar] [CrossRef]
- Bronshtein, I.N.; Semendyayev, K.A. A Guide Book to Mathematics: Fundamental Formulas· Tables· Graphs· Methods; Springer: Berlin, Germany, 1973. [Google Scholar]
- Winkler, R.G. Analytical Calculation of the Relaxation Dynamics of Partially Stretched Flexible Chain Molecules: Necessity of a Wormlike Chain Description. Phys. Rev. Lett. 1999, 82, 1843. [Google Scholar] [CrossRef]
- Harnau, L.; Winkler, R.G.; Reineker, P. Dynamic properties of molecular chains with variable stiffness. J. Chem. Phys. 1995, 102, 7750–7757. [Google Scholar] [CrossRef]
- Aragón, S.R.; Pecora, R. Dynamics of wormlike chains. Macromolecules 1985, 18, 1868–1875. [Google Scholar] [CrossRef]
- Winkler, R.G.; Keller, S.; Rädler, J.O. Intramolecular Dynamics of Linear Macromolecules by Fluorescence Correlation Spectroscopy. Phys. Rev. E 2006, 73, 041919. [Google Scholar] [CrossRef] [PubMed]
- Harnau, L.; Winkler, R.G.; Reineker, P. Dynamic Structure Factor of Semiflexible Macromolecules in Dilute Solution. J. Chem. Phys. 1996, 104, 6355–6368. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamura, A.; Winkler, R.G. Tethered Semiflexible Polymer under Large Amplitude Oscillatory Shear. Polymers 2019, 11, 737. https://doi.org/10.3390/polym11040737
Lamura A, Winkler RG. Tethered Semiflexible Polymer under Large Amplitude Oscillatory Shear. Polymers. 2019; 11(4):737. https://doi.org/10.3390/polym11040737
Chicago/Turabian StyleLamura, Antonio, and Roland G. Winkler. 2019. "Tethered Semiflexible Polymer under Large Amplitude Oscillatory Shear" Polymers 11, no. 4: 737. https://doi.org/10.3390/polym11040737
APA StyleLamura, A., & Winkler, R. G. (2019). Tethered Semiflexible Polymer under Large Amplitude Oscillatory Shear. Polymers, 11(4), 737. https://doi.org/10.3390/polym11040737