NMR Analysis of Poly(Lactic Acid) via Statistical Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
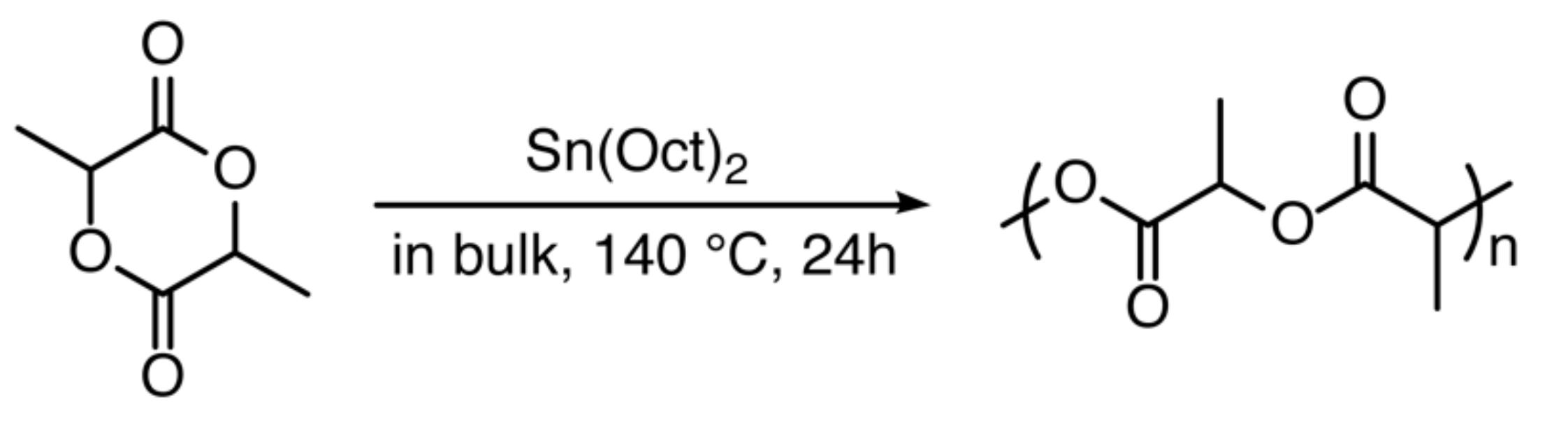
2.2. Synthesis of PLA
2.3. NMR Analysis
3. Results and Discussion
3.1. Preparation of the PLA Samples
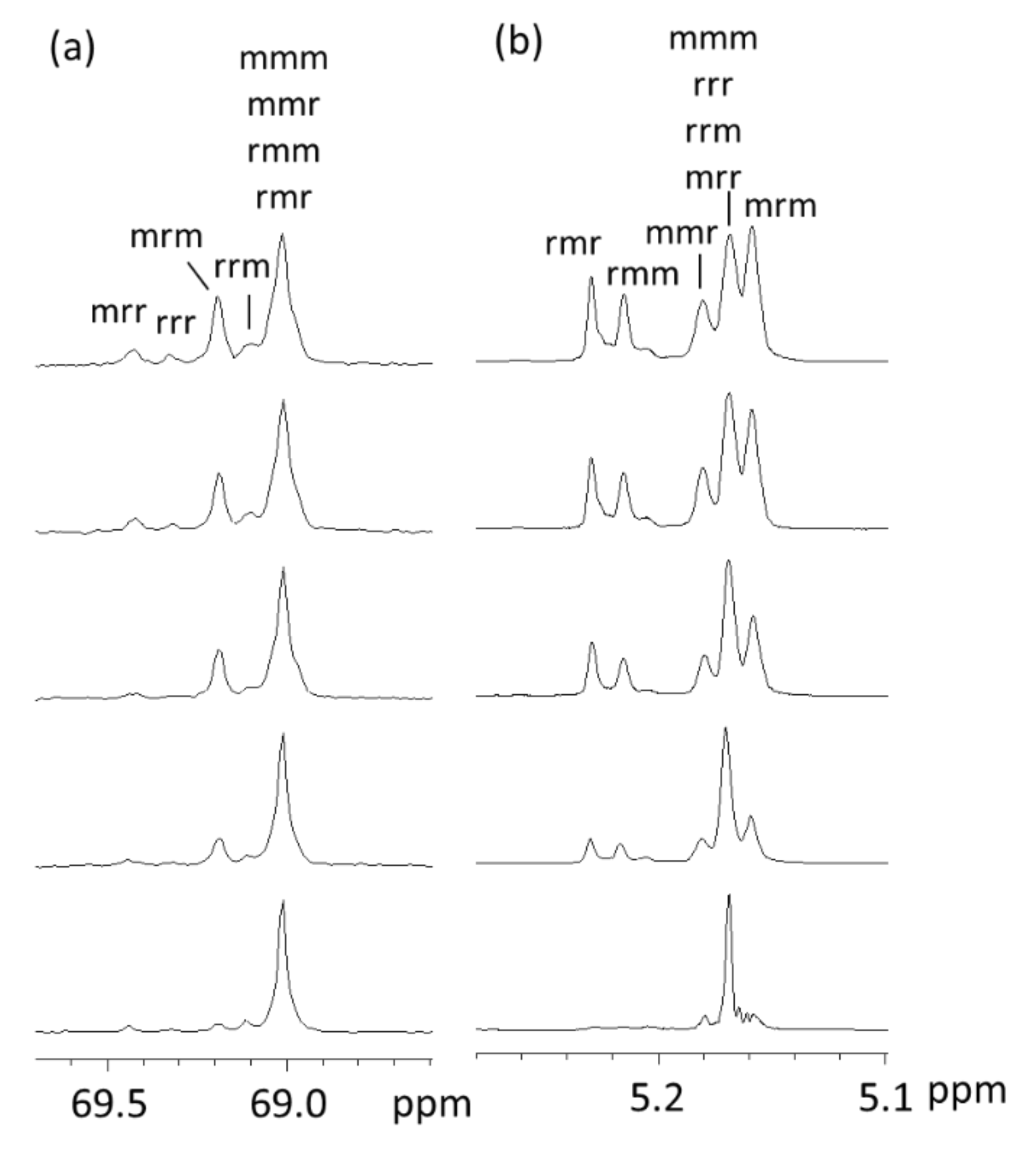
3.2. NMR Data and Assignments
3.3. Analysis of NMR Data
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Piemonte, V. Polylactic Acid Synthesis, Properties and Applications; Nova Science Publishers: Hauppauge, NY, USA, 2012. [Google Scholar]
- Auras, R.A.; Lim, L.Y.; Selke, S.E.M.; Tsuji, H. Poly(Lactic Acid): Synthesis, Structures, Properties, Processing, and Applications; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Gupta, A.P.; Kumar, V. New emerging trends in synthetic biodegradable polymers—Polylactide: A critique. Eur. Polym. J. 2007, 43, 4053–4074. [Google Scholar] [CrossRef]
- Lasprilla, A.J.R.; Martinez, G.A.R.; Lunelli, B.H.; Jardini, A.L.; Filho, R.M. Poly-lactic acid synthesis for application in biomedical devices—A review. Biotechnol. Adv. 2012, 30, 321–328. [Google Scholar] [CrossRef] [PubMed]
- Bergsma, J.E.; Bos, R.R.M.; Rozema, F.R.; Jong, W.D.; Boering, G.J. Biocompatibility of intraosseously implanted predegraded poly(lactide): An animal study. J. Mater. Sci. Mater. Med. 1996, 7, 1–7. [Google Scholar] [CrossRef]
- Fambri, L.; Pergoretti, A.; Fenner, R.; Incardona, S.D.; Migliarisi, C. Biodegradable fibres of poly(L-lactic acid) produced by melt spinning. Polymer 1997, 38, 79–85. [Google Scholar] [CrossRef]
- Masutani, K.; Kimura, Y. PLA synthesis, from the monomer to the polymer. In Poly(Lactic Acid) Science and Technology: Processing, Properties, Additives and Applications; Jiemenz, A., Peltzer, M., Ruseckeite, R., Eds.; RSC Publishing: Cambridge, UK, 2015; pp. 3–36. [Google Scholar]
- Fukushima, K.; Kimura, Y. A novel synthetic approach to stereo-block poly(lactic acid). Macromol. Symp. 2005, 224, 133–143. [Google Scholar] [CrossRef]
- Tonelli, A.E. NMR Spectroscopy and Polymer Microstructure: The Conformation Connection; VCH Publishers: New York, NY, USA, 1989. [Google Scholar]
- Matsuzaki, K.; Uryu, T.; Asakura, T. NMR Spectroscopy and Stereoregularity of Polymers; Japan Scientific Societies Press: Tokyo, Japan, 1996. [Google Scholar]
- Żółtowska, K.; Piotrowska, U.; Oledzka, E.; Sobczak, M. Efficient diethylzinc/gallic acid and diethylzinc/gallic acid ester catalytic systems for the ring-opening polymerization of rac-lactide. Molecules 2015, 20, 21909–21923. [Google Scholar] [CrossRef]
- Zell, M.T.; Padden, B.E.; Paterick, A.J.; Thakur, K.A.M.; Kean, R.T.; Hillmyer, M.A.; Munson, E.J. Unambiguous determination of the 13C and 1H NMR stereosequence assignments of polylactide using high resolution solution NMR spectroscopy. Macromolecules 2002, 35, 7700–7707. [Google Scholar] [CrossRef]
- Chisholm, M.H.; Iyer, S.S.; McCollum, D.G.; Pagel, M.; Werner-Zwanziger, U. Microstructure of poly(lactide). Phase-sensitive HETCOR spectra of poly(meso-lactide), poly(rac-lactide), and atactic poly(lactide). Macromolecules 1999, 32, 963–973. [Google Scholar] [CrossRef]
- Kasperczyk, J.E. HETCOR NMR study of poly(rac-lactide) and poly(meso-lactide). Polymer 1999, 40, 5455–5458. [Google Scholar] [CrossRef]
- Thakur, K.A.M.; Kean, R.T.; Hall, E.S.; Kolstad, J.J.; Lindgren, T.A.; Doscotch, M.A.; Siepmann, J.I.; Munson, E.J. High-resolution 13C and 1H solution NMR study of poly(lactide). Macromolecules 1997, 30, 2422–2428. [Google Scholar] [CrossRef]
- Wisniewski, M.; Borgne, A.L.; Spassky, N. Synthesis and properties of (D)- and (L)-lactide stereocopolymers using the system achiral Schiff’s base/aluminium methoxide as initiator. Macromol. Chem. Phys. 1997, 198, 1227–1238. [Google Scholar] [CrossRef]
- Bero, M.; Dobrzynski, P.; Kasperczyk, J.E. Synthesis of disyndiotactic polylactide. J. Polym. Sci. Part A Polym. Chem. 1999, 37, 4038–4042. [Google Scholar] [CrossRef]
- Kricheldorf, H.R.; Boettcher, C.; Tonnes, K. Polylactones: 23. Polymerization of racemic and meso d,l-lactide with various organotin catalysts-stereochemical aspects. Polymer 1992, 33, 2817–2824. [Google Scholar] [CrossRef]
- Chamberlain, B.M.; Cheng, M.; Moore, D.R.; Ovitt, T.M.; Lobkovsky, E.B.; Coates, G.W. Polymerization of lactide with zinc and magnesium β-diiminate complexes: Stereocontrol and mechanism. J. Am. Chem. Soc. 2001, 123, 3229–3238. [Google Scholar] [CrossRef] [PubMed]
- Coudane, J.; Ustariz-Peyret, C.; Schwach, G.; Vert, M. More about the stereodependence of DD and LL pair linkages during the ring-opening polymerization of racemic lactide. J. Polym. Sci. Part A Polym. Chem. 1997, 35, 1651–1658. [Google Scholar] [CrossRef]
- Kasperczyk, J.E. Microstructure analysis of poly (lactic acid) obtained by lithium tert-butoxide as initiator. Macromolecules 1995, 28, 3937–3939. [Google Scholar] [CrossRef]
- Bero, M.; Kasperczyk, J.; Jedlinski, J.Z. Coordination polymerization of lactides, 1. Structure determination of obtained polymers. Makromol. Chem. 1990, 191, 2287–2296. [Google Scholar] [CrossRef]
- Chabot, F.; Vert, M.; Chapelle, S.; Granger, P. Configurational structures of lactic acid stereocopolymers as determined by 13C-{1H} nmr. Polymer 1983, 24, 53–59. [Google Scholar] [CrossRef]
- Schindler, A.; Harper, D. Poly(lactic acid). I. stereosequence distribution in the polymerization of racemic dilactide. J. Polym. Sci. Polym. Lett. Ed. 1976, 14, 729–734. [Google Scholar] [CrossRef]
- Suganuma, K.; Horiuchi, K.; Matsuda, H.; Cheng, H.N.; Aoki, A.; Asakura, T. Stereoregularity of poly(lactic acid) and their model compounds as studied by NMR and quantum chemical calculations. Macromolecules 2011, 44, 9247–9253. [Google Scholar] [CrossRef]
- Suganuma, K.; Horiuchi, K.; Matsuda, H.; Cheng, H.N.; Aoki, A.; Asakura, T. NMR Analysis and chemical shift calculations of poly(lactic acid) dimer model compounds with different tacticities. Polym. J. 2012, 44, 838–844. [Google Scholar] [CrossRef]
- Suganuma, K.; Matsuda, H.; Cheng, H.N.; Iwai, M.; Nonokawa, R.; Asakura, T. Tacticity determination of 1H and 13C NMR spectra of poly(lactic acid) in C5D5N. Polym. Test. 2014, 38, 35–39. [Google Scholar] [CrossRef]
- Cheng, H.N. Polymerization and statistical models. In Encyclopedia of NMR; Grant, D.M., Harris, R.K., Eds.; Wiley: New York, NY, USA, 1996; pp. 3713–3721. [Google Scholar]
- Cheng, H.N. Structural Studies of Polymers by Solution NMR; RAPRA Review Reports; Rapra: Shrewsbury, UK, 2001; Volume 11, Number 5. [Google Scholar]
- Cheng, H.N.; Miri, M. Statistical models and NMR analysis of polymer microstructure. ACS Symp. Ser. 2011, 1077, 371–382. [Google Scholar]
- Cheng, H.N. 13C NMR sequence determination and modelling of polypropylene oil. Macromol. Symp. 1994, 86, 77–102. [Google Scholar] [CrossRef]
- Cheng, H.N. Computer-assisted NMR analysis of polymers in solution. Polym. News 2000, 25, 114–122. [Google Scholar]
- Cheng, H.N. 13C NMR sequence determination for multicomponent polymer mixtures. J. Appl. Polym. Sci. 1988, 35, 1639–1650. [Google Scholar] [CrossRef]
- Thakur, K.A.M.; Kean, R.T.; Hall, E.S.; Doscotch, M.A.; Munson, E.J. A quantitative method for determination of lactide composition in poly(lactide) using 1H NMR. Anal. Chem. 1997, 69, 4303–4309. [Google Scholar] [CrossRef] [PubMed]
- Price, F.P. Copolymerization mathematics and the description of stereoregular polymers. J. Chem. Phys. 1962, 36, 209. [Google Scholar] [CrossRef]
- Cheng, H.N. Stereochemistry of vinyl polymers and NMR characterization. J. Appl. Polym. Sci. 1988, 36, 229–241. [Google Scholar] [CrossRef]
| Sample Code | Lactide in Feed | Yield/% | Mn × 10−3 | Mw/Mn | |
|---|---|---|---|---|---|
| L,L | D,D | ||||
| 50/50 | 50 | 50 | 74 | 13.0 | 1.56 |
| 60/40 | 60 | 40 | 62 | 13.2 | 1.66 |
| 70/30 | 70 | 30 | 69 | 14.5 | 1.66 |
| 80/20 | 80 | 20 | 70 | 13.5 | 1.68 |
| 90/10 | 90 | 10 | 72 | 11.2 | 2.96 |
| Tetrad | mrr | rrr | mrm | rrm | mmm/mmr/rmm/rmr |
|---|---|---|---|---|---|
| 13C shift (ppm) | 69.42 | 69.32 | 69.19 | 69.09 | 69.02 |
| Tetrad | rmr | rmm | mmr | mmm/rrr/rrm/mrr | mrm |
| 1H shift (ppm) | 5.23 | 5.22 | 5.18 | 5.17 | 5.16 |
| Tetrad | Pair-Addition Bernoullian Model a | Single-Addition Bernoullian Model b | Two-State (Pair-Addition + Single-Addition Bernoullian) Model c |
|---|---|---|---|
| mmm | (p22 + q22 + p23 + q23)/2 | p14 + q14 | f2[(p22 + q22 + p23 + q23)/2] + f1[p14 + q14] |
| mrm | p2q2 | 2p12q12 | f2 p2q2 + f1 [2p12q12] |
| mmr | p2q2/2 | p13q1 + p1q13 | f2 p2q2/2 + f1 [p13q1 + p1q13] |
| rmm | p2q2/2 | p13q1 + p1q13 | f2 p2q2/2 + f1 [p13q1 + p1q13] |
| rmr | p2q2/2 | 2p12q12 | f2 p2q2/2 + f1 [2p12q12] |
| rrm | 0 | p13q1 + p1q13 | f1 [p13q1 + p1q13] |
| mrr | 0 | p13q1 + p1q13 | f1 [p13q1 + p1q13] |
| rrr | 0 | 2p12q12 | f1 [2p12q12] |
| Tetrad | Sample 50/50 | Sample 60/40 | Sample 70/30 | Sample 80/20 | Sample 90/10 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Iobsd | Icalc | Iobsd | Icalc1 | Icalc2 | Iobsd | Icalc1 | Icalc2 | Iobsd | Icalc1 | Icalc2 | Iobsd | Icalc1 | Icalc2 | |
| mmm | 26.3 | 37.5 | 30.0 | 40.0 | 38.0 | 39.9 | 47.5 | 40.1 | 49.4 | 60 | 57.7 | 71.5 | 77.5 | 71.5 |
| mrm | 22.3 | 25.0 | 20.7 | 24.0 | 24.8 | 21.4 | 21.0 | 24.0 | 13.5 | 16 | 16.9 | 5.2 | 9.0 | 11.4 |
| mmr | 13.4 | 12.5 | 13.6 | 12.0 | 12.4 | 11.3 | 10.5 | 12.0 | 7.4 | 8 | 8.5 | 6.9 | 4.5 | 5.7 |
| rmm | 13.0 | 12.5 | 12.5 | 12.0 | 12.4 | 10.9 | 10.5 | 12.0 | 7.7 | 8 | 8.5 | 3.5 | 4.5 | 5.7 |
| rmr | 12.9 | 12.5 | 12.3 | 12.0 | 12.4 | 12.0 | 10.5 | 12.0 | 7.8 | 8 | 8.5 | 2.5 | 4.5 | 5.7 |
| mrr | 6.5 | 0 | 6.0 | 0 | 0 | 2.5 | 0 | 0 | 3.9 | 0 | 0 | 3.9 | 0 | 0 |
| rrm | 3.6 | 0 | 2.7 | 0 | 0 | 1.5 | 0 | 0 | 9.1 | 0 | 0 | 4.7 | 0 | 0 |
| rrr | 2.0 | 0 | 2.4 | 0 | 0 | 0.7 | 0 | 0 | 1.2 | 0 | 0 | 1.8 | 0 | 0 |
| MD b | 3.5 | 3.4 | 3.1 | 1.9 | 1.2 | 3.6 | 3.5 | 3.2 | 2.9 | |||||
| p2 | 0.50 | 0.60 | 0.55 | 0.70 | 0.60 | 0.8 | 0.78 | 0.90 | 0.87 | |||||
| Tetrad | Sample 50/50 | Sample 60/40 | Sample 70/30 | Sample 80/20 | Sample 90/10 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Iobsd | Icalc | Iobsd | Icalc1 | Icalc2 | Iobsd | Icalc1 | Icalc2 | Iobsd | Icalc1 | Icalc2 | Iobsd | Icalc1 | Icalc2 | |
| mmm | 26.3 | 29.9 | 30.0 | 30.0 | 30.0 | 39.9 | 42.6 | 39.9 | 49.4 | 53.9 | 49.4 | 71.5 | 71.5 | 71.5 |
| mrm | 22.3 | 21.2 | 20.7 | 19.2 | 20.6 | 21.4 | 20.0 | 21.3 | 13.5 | 14.8 | 13.5 | 5.2 | 10.7 | 5.2 |
| mmr | 13.4 | 12.5 | 13.6 | 12.2 | 12.4 | 11.3 | 11.0 | 11.6 | 7.4 | 9.5 | 9.6 | 6.9 | 6.9 | 6.1 |
| rmm | 13.0 | 12.5 | 12.5 | 12.2 | 12.4 | 10.9 | 11.0 | 11.6 | 7.7 | 9.5 | 9.6 | 3.5 | 6.9 | 6.1 |
| rmr | 12.9 | 12.5 | 12.3 | 12.2 | 12.3 | 12.0 | 11.0 | 11.3 | 7.8 | 9.5 | 7.8 | 2.5 | 6.9 | 3.1 |
| mrr | 6.5 | 3.8 | 6.0 | 5.2 | 4.1 | 2.5 | 2.0 | 1.5 | 3.9 | 4.1 | 3.8 | 3.9 | 3.1 | 3.9 |
| rrm | 3.6 | 3.8 | 2.7 | 5.2 | 4.1 | 1.5 | 2.0 | 1.5 | 9.1 | 4.1 | 3.8 | 4.7 | 3.1 | 3.9 |
| rrr | 2.0 | 3.8 | 2.4 | 5.2 | 4.1 | 0.7 | 2.0 | 1.2 | 1.2 | 4.1 | 2.0 | 1.8 | 3.1 | 0.9 |
| MD b | 1.5 | 1.2 | 0.8 | 1.0 | 0.4 | 2.4 | 1.3 | 2.1 | 0.7 | |||||
| p2 | 0.50 | 0.60 | 0.55 | 0.69 | 0.65 | 0.80 | 0.77 | 0.89 | 0.90 | |||||
| f2 | 0.70 | 0.59 | 0.67 | 0.84 | 0.88 | 0.67 | 0.66 | 0.75 | 0.48 | |||||
| p1 | 0.50 | 0.51 | 0.55 | 0.50 | 0.66 | 0.50 | 0.78 | 0.50 | 0.9 | |||||
| f1 c | 0.30 | 0.41 | 0.33 | 0.16 | 0.12 | 0.33 | 0.34 | 0.25 | 0.52 | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suganuma, K.; Asakura, T.; Oshimura, M.; Hirano, T.; Ute, K.; Cheng, H.N. NMR Analysis of Poly(Lactic Acid) via Statistical Models. Polymers 2019, 11, 725. https://doi.org/10.3390/polym11040725
Suganuma K, Asakura T, Oshimura M, Hirano T, Ute K, Cheng HN. NMR Analysis of Poly(Lactic Acid) via Statistical Models. Polymers. 2019; 11(4):725. https://doi.org/10.3390/polym11040725
Chicago/Turabian StyleSuganuma, Koto, Tetsuo Asakura, Miyuki Oshimura, Tomohiro Hirano, Koichi Ute, and H. N. Cheng. 2019. "NMR Analysis of Poly(Lactic Acid) via Statistical Models" Polymers 11, no. 4: 725. https://doi.org/10.3390/polym11040725
APA StyleSuganuma, K., Asakura, T., Oshimura, M., Hirano, T., Ute, K., & Cheng, H. N. (2019). NMR Analysis of Poly(Lactic Acid) via Statistical Models. Polymers, 11(4), 725. https://doi.org/10.3390/polym11040725






