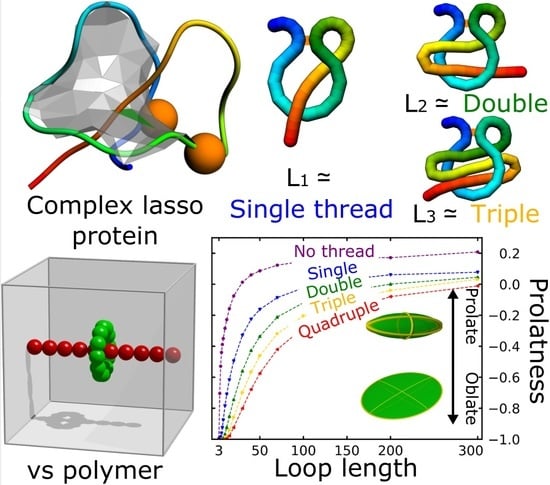
Statistical Properties of Lasso-Shape Polymers and Their Implications for Complex Lasso Proteins Function
Abstract
1. Introduction
2. Materials and Methods
2.1. Random Lassos Generation
2.2. Simulation Model
2.3. Data Analysis
2.4. Proteins Analyzed
2.5. Graphics
3. Results
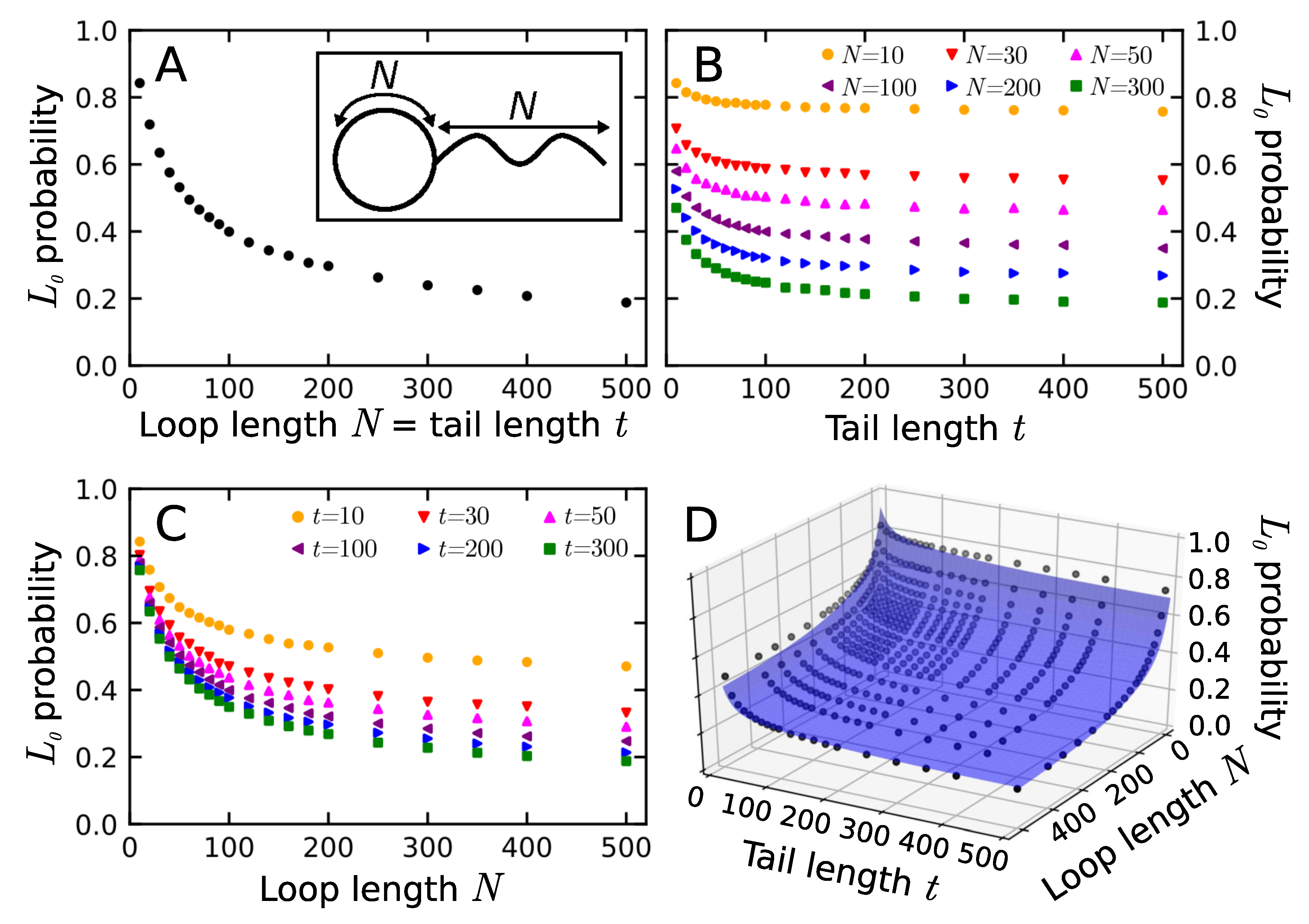
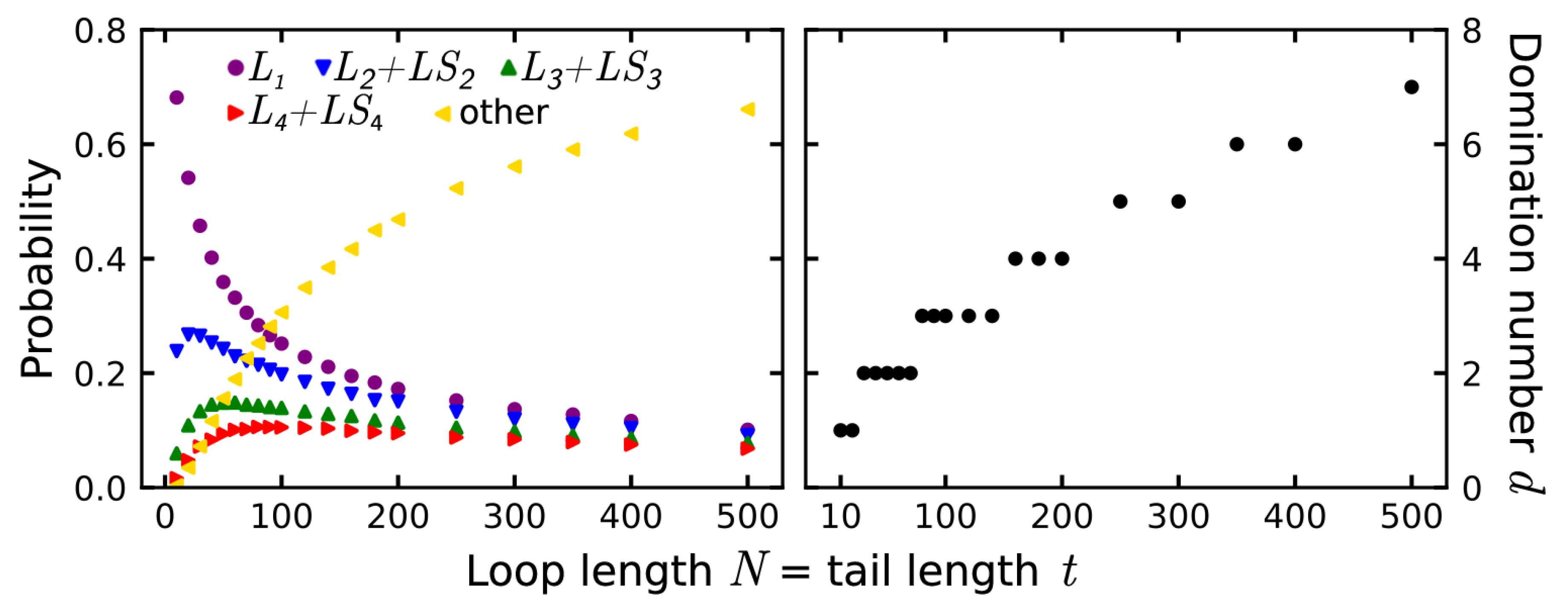
3.1. Probability That a Lasso Is Complex
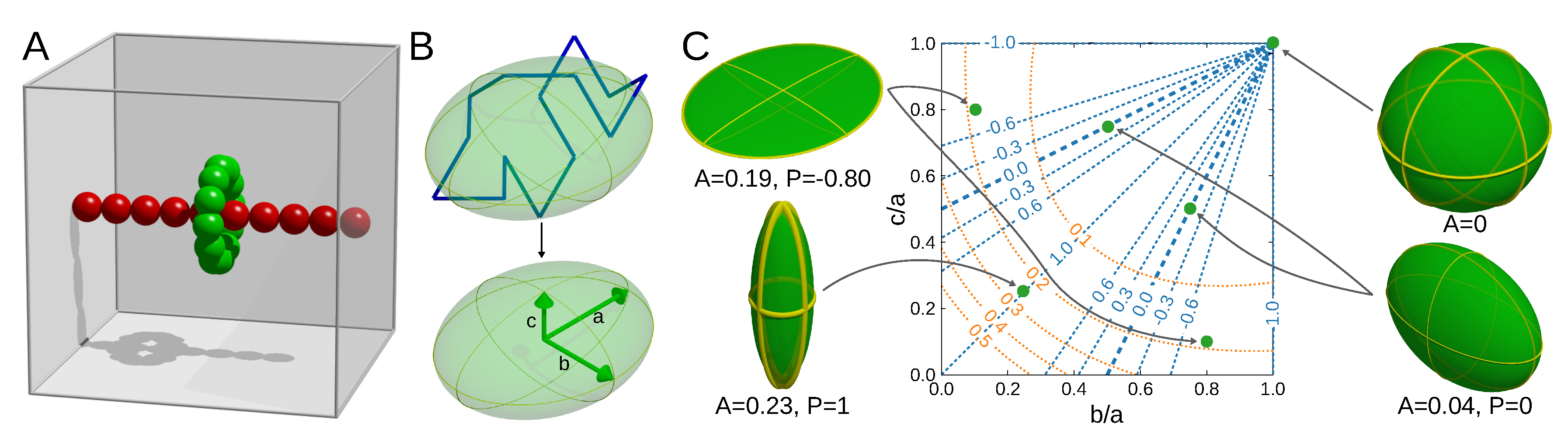
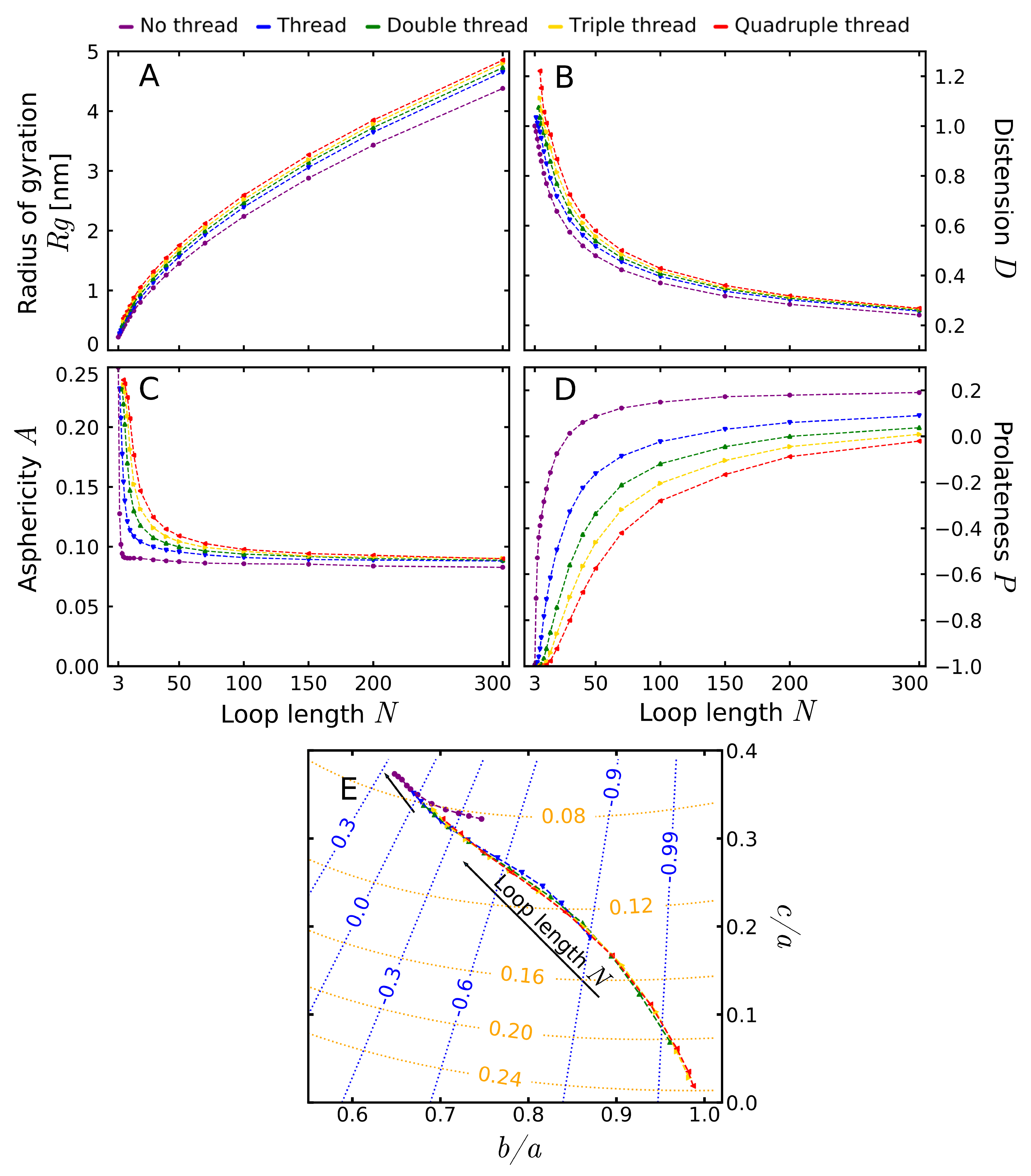
3.2. Shape Parameters of a Lasso Loop
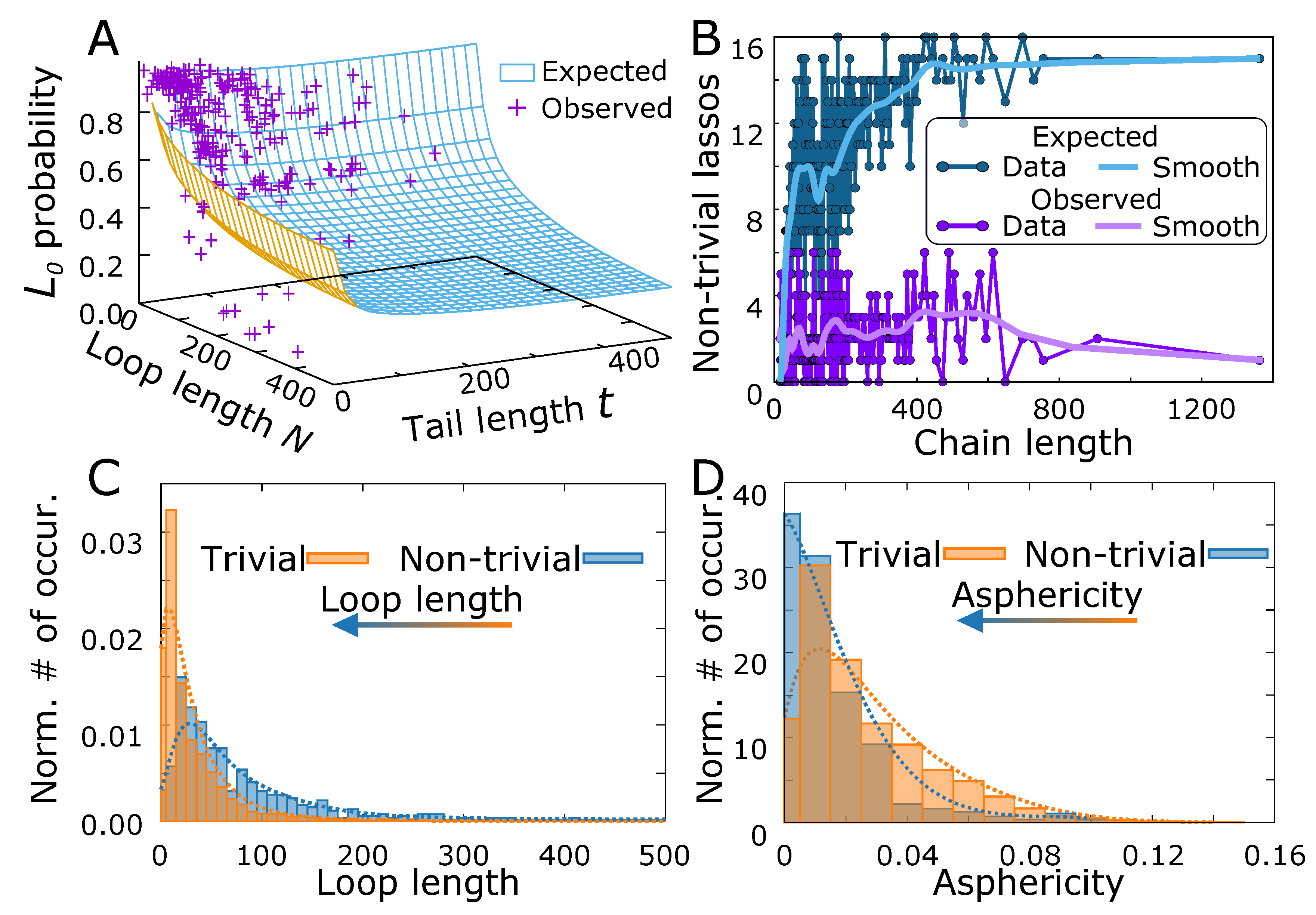
3.3. Comparison Of Simulated Polymers with Complex Lasso Proteins
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flory, P.J. Thermodynamics of high polymer solutions. J. Chem. Phys. 1942, 10, 51–61. [Google Scholar] [CrossRef]
- Flory, P.J. The configuration of real polymer chains. J. Chem. Phys. 1949, 17, 303–310. [Google Scholar] [CrossRef]
- de Gennes, P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Fukatsu, M.; Kurata, M. Hydrodynamic properties of flexible-ring macromolecules. J. Chem. Phys. 1966, 44, 4539–4545. [Google Scholar] [CrossRef]
- de Gennes, P. Conformations of polymers attached to an interface. Macromolecules 1980, 13, 1069–1075. [Google Scholar] [CrossRef]
- Deam, R.; Edwards, S.F. The theory of rubber elasticity. Philos. Trans. R. Soc. Lond. 1976, 280, 317–353. [Google Scholar] [CrossRef]
- Des Cloizeaux, J. Lagrangian theory for a self-avoiding random chain. Phys. Rev. 1974, 10, 1665. [Google Scholar] [CrossRef]
- Brás, A.R.; Pasquino, R.; Koukoulas, T.; Tsolou, G.; Holderer, O.; Radulescu, A.; Allgaier, J.; Mavrantzas, V.G.; Pyckhout-Hintzen, W.; Wischnewski, A.; et al. Structure and dynamics of polymer rings by neutron scattering: breakdown of the Rouse model. Soft Matter 2011, 7, 11169–11176. [Google Scholar] [CrossRef]
- Smrek, J.; Grosberg, A.Y. Understanding the dynamics of rings in the melt in terms of the annealed tree model. J. Phys. Condens. Matter 2015, 27, 064117. [Google Scholar] [CrossRef] [PubMed]
- Mirny, L.A. The fractal globule as a model of chromatin architecture in the cell. Chromosom. Res. 2011, 19, 37–51. [Google Scholar] [CrossRef]
- Obukhov, S.; Johner, A.; Baschnagel, J.; Meyer, H.; Wittmer, J. Melt of polymer rings: The decorated loop model. EPL (Europhys. Lett.) 2014, 105, 48005. [Google Scholar] [CrossRef]
- Grosberg, A.Y. Annealed lattice animal model and Flory theory for the melt of non-concatenated rings: Towards the physics of crumpling. Soft Matter 2014, 10, 560–565. [Google Scholar] [CrossRef] [PubMed]
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. I. Statics. J. Chem. Phys. 2011, 134, 204904. [Google Scholar] [CrossRef] [PubMed]
- Pasquino, R.; Vasilakopoulos, T.C.; Jeong, Y.C.; Lee, H.; Rogers, S.; Sakellariou, G.; Allgaier, J.; Takano, A.; Brás, A.R.; Chang, T.; et al. Viscosity of ring polymer melts. ACS Macro Lett. 2013, 2, 874–878. [Google Scholar] [CrossRef] [PubMed]
- Tsolou, G.; Stratikis, N.; Baig, C.; Stephanou, P.S.; Mavrantzas, V.G. Melt structure and dynamics of unentangled polyethylene rings: Rouse theory, atomistic molecular dynamics simulation, and comparison with the linear analogues. Macromolecules 2010, 43, 10692–10713. [Google Scholar] [CrossRef]
- Tsalikis, D.G.; Alatas, P.V.; Peristeras, L.D.; Mavrantzas, V.G. Scaling Laws for the Conformation and Viscosity of Ring Polymers in the Crossover Region around M e from Detailed Molecular Dynamics Simulations. ACS Macro Lett. 2018, 7, 916–920. [Google Scholar] [CrossRef]
- Alatas, P.V.; Tsalikis, D.G.; Mavrantzas, V.G. Detailed Molecular Dynamics Simulation of the Structure and Self-Diffusion of Linear and Cyclic n-Alkanes in Melt and Blends. Macromol. Theory Simul. 2017, 26, 1600049. [Google Scholar] [CrossRef]
- Papadopoulos, G.D.; Tsalikis, D.G.; Mavrantzas, V.G. Microscopic dynamics and topology of polymer rings immersed in a host matrix of longer linear polymers: Results from a detailed molecular dynamics simulation study and comparison with experimental data. Polymers 2016, 8, 283. [Google Scholar] [CrossRef]
- Witz, G.; Rechendorff, K.; Adamcik, J.; Dietler, G. Conformation of circular DNA in two dimensions. Phys. Rev. Lett. 2008, 101, 148103. [Google Scholar] [CrossRef]
- Grosberg, A.; Rabin, Y.; Havlin, S.; Neer, A. Crumpled globule model of the three-dimensional structure of DNA. EPL (Europhys. Lett.) 1993, 23, 373. [Google Scholar] [CrossRef]
- Halverson, J.D.; Smrek, J.; Kremer, K.; Grosberg, A.Y. From a melt of rings to chromosome territories: The role of topological constraints in genome folding. Rep. Prog. Phys. 2014, 77, 022601. [Google Scholar] [CrossRef]
- Lang, M.; Fischer, J.; Sommer, J.U. Effect of topology on the conformations of ring polymers. Macromolecules 2012, 45, 7642–7648. [Google Scholar] [CrossRef]
- Lang, M. Ring conformations in bidisperse blends of ring polymers. Macromolecules 2013, 46, 1158–1166. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Feigel, A.; Rabin, Y. Flory-type theory of a knotted ring polymer. Phys. Rev. E 1996, 54, 6618. [Google Scholar] [CrossRef]
- Micheletti, C.; Marenduzzo, D.; Orlandini, E.; Summers, D. Knotting of random ring polymers in confined spaces. J. Chem. Phys. 2006, 124, 064903. [Google Scholar] [CrossRef]
- Marcone, B.; Orlandini, E.; Stella, A.; Zonta, F. Size of knots in ring polymers. Phys. Rev. E 2007, 75, 041105. [Google Scholar] [CrossRef] [PubMed]
- Tubiana, L.; Orlandini, E.; Micheletti, C. Multiscale entanglement in ring polymers under spherical confinement. Phys. Rev. Lett. 2011, 107, 188302. [Google Scholar] [CrossRef] [PubMed]
- Rosa, A.; Orlandini, E.; Tubiana, L.; Micheletti, C. Structure and dynamics of ring polymers: Entanglement effects because of solution density and ring topology. Macromolecules 2011, 44, 8668–8680. [Google Scholar] [CrossRef]
- Smrek, J.; Grosberg, A.Y. Minimal surfaces on unconcatenated polymer rings in melt. ACS Macro Lett. 2016, 5, 750–754. [Google Scholar] [CrossRef]
- Michieletto, D.; Turner, M.S. A topologically driven glass in ring polymers. Proc. Natl. Acad. Sci. USA 2016, 113, 5195–5200. [Google Scholar] [CrossRef]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E.; Turner, M.S. Ring Polymers: Threadings, Knot Electrophoresis and Topological Glasses. Polymers 2017, 9, 349. [Google Scholar] [CrossRef]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E.; Alexander, G.P.; Turner, M.S. Threading dynamics of ring polymers in a gel. ACS Macro Lett. 2014, 3, 255–259. [Google Scholar] [CrossRef]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E.; Alexander, G.P.; Turner, M.S. Dynamics of self-threading ring polymers in a gel. Soft Matter 2014, 10, 5936–5944. [Google Scholar] [CrossRef] [PubMed]
- Uehara, E.; Deguchi, T. Statistical properties of multi-theta polymer chains. J. Phys. A Math. Theor. 2018, 51, 134001. [Google Scholar] [CrossRef]
- Uehara, E.; Deguchi, T. Mean-square radius of gyration and the hydrodynamic radius for topological polymers expressed with graphs evaluated by the method of quaternions revisited. React. Funct. Polym. 2018, 133, 92–102. [Google Scholar] [CrossRef]
- Deguchi, T.; Uehara, E. Statistical and dynamical properties of topological polymers with graphs and ring polymers with knots. Polymers 2017, 9, 252. [Google Scholar] [CrossRef] [PubMed]
- Caraglio, M.; Micheletti, C.; Orlandini, E. Mechanical Pulling of Linked Ring Polymers: Elastic Response and Link Localisation. Polymers 2017, 9, 327. [Google Scholar] [CrossRef] [PubMed]
- Tsalikis, D.G.; Mavrantzas, V.G.; Vlassopoulos, D. Analysis of slow modes in ring polymers: Threading of rings controls long-time relaxation. ACS Macro Lett. 2016, 5, 755–760. [Google Scholar] [CrossRef]
- Tsalikis, D.G.; Mavrantzas, V.G. Threading of ring poly (ethylene oxide) molecules by linear chains in the melt. ACS Macro Lett. 2014, 3, 763–766. [Google Scholar] [CrossRef]
- Harada, A.; Li, J.; Kamachi, M. The molecular necklace: A rotaxane containing many threaded α-cyclodextrins. Nature 1992, 356, 325–327. [Google Scholar] [CrossRef]
- Bruns, C.J.; Stoddart, J.F. Rotaxane-based molecular muscles. Acc. Chem. Res. 2014, 47, 2186–2199. [Google Scholar] [CrossRef] [PubMed]
- Valentina, S.; Ogawa, T.; Nakazono, K.; Aoki, D.; Takata, T. Efficient synthesis of cyclic block copolymers by rotaxane protocol by linear/cyclic topology transformation. Chem. Eur. J. 2016, 22, 8759–8762. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, T.; Usuki, N.; Nakazono, K.; Koyama, Y.; Takata, T. Linear—Cyclic polymer structural transformation and its reversible control using a rational rotaxane strategy. Chem. Commun. 2015, 51, 5606–5609. [Google Scholar] [CrossRef] [PubMed]
- Niemyska, W.; Dabrowski-Tumanski, P.; Kadlof, M.; Haglund, E.; Sułkowski, P.; Sulkowska, J.I. Complex lasso: New entangled motifs in proteins. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Niemyska, W.; Pasznik, P.; Sulkowska, J.I. LassoProt: Server to analyze biopolymers with lassos. Nucleic Acids Res. 2016, 44, W383–W389. [Google Scholar] [CrossRef]
- Haglund, E.; Pilko, A.; Wollman, R.; Jennings, P.A.; Onuchic, J.N. Pierced lasso topology controls function in leptin. J. Phys. Chem. B 2017, 121, 706–718. [Google Scholar] [CrossRef] [PubMed]
- Haglund, E.; Nguyen, L.; Schafer, N.P.; Lammert, H.; Jennings, P.A.; Onuchic, J.N. Uncovering the molecular mechanisms behind disease-associated leptin variants. J. Biol. Chem. 2018, 293, 12919–12933. [Google Scholar] [CrossRef] [PubMed]
- Rebuffat, S.; Blond, A.; Destoumieux-Garzón, D.; Goulard, C.; Peduzzi, J. Microcin J25, from the macrocyclic to the lasso structure: implications for biosynthetic, evolutionary and biotechnological perspectives. Curr. Protein Pept. Sci. 2004, 5, 383–391. [Google Scholar] [CrossRef]
- Pan, S.J.; Link, A.J. Sequence diversity in the lasso peptide framework: Discovery of functional microcin J25 variants with multiple amino acid substitutions. J. Am. Chem. Soc. 2011, 133, 5016–5023. [Google Scholar] [CrossRef] [PubMed]
- Ducasse, R.; Yan, K.P.; Goulard, C.; Blond, A.; Li, Y.; Lescop, E.; Guittet, E.; Rebuffat, S.; Zirah, S. Sequence determinants governing the topology and biological activity of a lasso peptide, microcin J25. ChemBioChem 2012, 13, 371–380. [Google Scholar] [CrossRef]
- Zimmermann, M.; Hegemann, J.D.; Xie, X.; Marahiel, M.A. The astexin-1 lasso peptides: Biosynthesis, stability, and structural studies. Chem. Biol. 2013, 20, 558–569. [Google Scholar] [CrossRef]
- Hegemann, J.D.; Zimmermann, M.; Xie, X.; Marahiel, M.A. Lasso peptides: An intriguing class of bacterial natural products. Acc. Chem. Res. 2015, 48, 1909–1919. [Google Scholar] [CrossRef]
- Braffman, N.R.; Piscotta, F.J.; Hauver, J.; Campbell, E.A.; Link, A.J.; Darst, S.A. Structural mechanism of transcription inhibition by lasso peptides microcin J25 and capistruin. Proc. Natl. Acad. Sci. USA 2019, 116, 1273–1278. [Google Scholar] [CrossRef]
- Allen, C.D.; Link, A.J. Self-assembly of catenanes from lasso peptides. J. Am. Chem. Soc. 2016, 138, 14214–14217. [Google Scholar] [CrossRef]
- Zong, C.; Maksimov, M.O.; Link, A.J. Construction of lasso peptide fusion proteins. ACS Chem. Biol. 2015, 11, 61–68. [Google Scholar] [CrossRef]
- Cantarella, J.; Duplantier, B.; Shonkwiler, C.; Uehara, E. A fast direct sampling algorithm for equilateral closed polygons. J. Phys. A Math. Theor. 2016, 49, 275202. [Google Scholar] [CrossRef]
- Clementi, C.; Nymeyer, H.; Onuchic, J.N. Topological and energetic factors: What determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? an investigation for small globular proteins1. J. Mol. Biol. 2000, 298, 937–953. [Google Scholar] [CrossRef]
- Weber, T.A.; Helfand, E. Time-correlation functions from computer simulations of polymers. J. Phys. Chem. 1983, 87, 2881–2889. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; Van Der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Topoly—A package to determine the topology of polymers. Under Construction. 2019.
- Ewing, B.; Millett, K.C. A load balanced algorithm for the calculation of the polynomial knot and link invariants. In The Mathematical Heritage of CF Gauss; World Scientific: Singapore, 1991; pp. 225–266. [Google Scholar]
- Gierut, A.M.; Niemyska, W.; Dabrowski-Tumanski, P.; Sułkowski, P.; Sulkowska, J.I. PyLasso: A PyMOL plugin to identify lassos. Bioinformatics 2017, 33, 3819–3821. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- Orlandini, E.; Van Rensburg, E.J.; Tesi, M.; Whittington, S. Random linking of lattice polygons. J. Phys. A Math. Gen. 1994, 27, 335. [Google Scholar] [CrossRef]
- Soteros, C.; Sumners, D.; Whittington, S. Linking of random p-spheres in Zd. J. Knot Theory Its Ramif. 1999, 8, 49–70. [Google Scholar] [CrossRef]
- Diao, Y. Unsplittability of random links. In Random Knotting and Linking; World Scientific: Singapore, 1994; pp. 147–157. [Google Scholar]
- Diao, Y.; van Rensburg, E.J. Percolation of linked circles. In Topology and Geometry in Polymer Science; Springer: Berlin/Heidelberg, Germany, 1998; pp. 79–88. [Google Scholar]
- Rawdon, E.J.; Kern, J.C.; Piatek, M.; Plunkett, P.; Stasiak, A.; Millett, K.C. Effect of knotting on the shape of polymers. Macromolecules 2008, 41, 8281–8287. [Google Scholar] [CrossRef]
- Tsurusaki, K.; Deguchi, T. Fractions of particular knots in Gaussian random polygons. J. Phys. Soc. Jpn. 1995, 64, 1506–1518. [Google Scholar] [CrossRef]
- Shimamura, M.K.; Deguchi, T. Knot complexity and the probability of random knotting. Phys. Rev. E 2002, 66, 040801. [Google Scholar] [CrossRef] [PubMed]
- Orlandini, E.; Tesi, M.; Van Rensburg, E.J.; Whittington, S.G. Asymptotics of knotted lattice polygons. J. Phys. A Math. Gen. 1998, 31, 5953. [Google Scholar] [CrossRef]
- Kuhn, W. The shape of fibrous molecules in solution. Kolloid-Zeitschrift 1934, 68, 2. [Google Scholar] [CrossRef]
- Drube, F.; Alim, K.; Witz, G.; Dietler, G.; Frey, E. Excluded volume effects on semiflexible ring polymers. Nano Lett. 2010, 10, 1445–1449. [Google Scholar] [CrossRef]
- Alim, K.; Frey, E. Shapes of semiflexible polymer rings. Phys. Rev. Lett. 2007, 99, 198102. [Google Scholar] [CrossRef]
- Bishop, M.; Michels, J. Scaling in two-dimensional linear and ring polymers. J. Chem. Phys. 1986, 85, 1074–1076. [Google Scholar] [CrossRef]
- Bishop, M.; Saltiel, C.J. Polymer shapes in two, four, and five dimensions. J. Chem. Phys. 1988, 88, 3976–3980. [Google Scholar] [CrossRef]
- Millett, K.C.; Plunkett, P.; Piatek, M.; Rawdon, E.J.; Stasiak, A. Effect of knotting on polymer shapes and their enveloping ellipsoids. J. Chem. Phys. 2009, 130, 04B623. [Google Scholar] [CrossRef]
- Diehl, H.; Eisenriegler, E. Universal shape ratios for open and closed random walks: Exact results for all d. J. Phys. A Math. Gen. 1989, 22, L87. [Google Scholar] [CrossRef]
- Jagodzinski, O.; Eisenriegler, E.; Kremer, K. Universal shape properties of open and closed polymer chains: Renormalization group analysis and Monte Carlo experiments. J. Phys. I 1992, 2, 2243–2279. [Google Scholar] [CrossRef]
- Jagodzinski, O. The asphericity of star polymers: A renormalization group study. J. Phys. A Math. Gen. 1994, 27, 1471. [Google Scholar] [CrossRef]
- Prellberg, T. Scaling of self-avoiding walks and self-avoiding trails in three dimensions. J. Phys. A Math. Gen. 2001, 34, L599. [Google Scholar] [CrossRef][Green Version]
- Lua, R.C.; Grosberg, A.Y. Statistics of knots, geometry of conformations, and evolution of proteins. PLoS Comput. Biol. 2006, 2, e45. [Google Scholar] [CrossRef]
- Ostermeir, K.; Alim, K.; Frey, E. Buckling of stiff polymer rings in weak spherical confinement. Phys. Rev. E 2010, 81, 061802. [Google Scholar] [CrossRef] [PubMed]
- Soler, M.A.; Rey, A.; Faísca, P.F. Steric confinement and enhanced local flexibility assist knotting in simple models of protein folding. Phys. Chem. Chem. Phys. 2016, 18, 26391–26403. [Google Scholar] [CrossRef] [PubMed]
- Niewieczerzal, S.; Sulkowska, J.I. Knotting and unknotting proteins in the chaperonin cage: Effects of the excluded volume. PLoS ONE 2017, 12, e0176744. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Dabrowski-Tumanski, P.; Niewieczerzal, S.; Sulkowska, J.I. The exclusive effects of chaperonin on the behavior of proteins with 52 knot. PLoS Comput. Biol. 2018, 14, e1005970. [Google Scholar] [CrossRef]
- Micheletti, C.; Orlandini, E. Knotting and unknotting dynamics of DNA strands in nanochannels. ACS Macro Lett. 2014, 3, 876–880. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Rubach, P.; Goundaroulis, D.; Dorier, J.; Sułkowski, P.; Millett, K.C.; Rawdon, E.J.; Stasiak, A.; Sulkowska, J.I. KnotProt 2.0: A database of proteins with knots and other entangled structures. Nucleic Acids Res. 2018, 47, D367–D375. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Stasiak, A.; Sulkowska, J.I. In search of functional advantages of knots in proteins. PLoS ONE 2016, 11, e0165986. [Google Scholar] [CrossRef] [PubMed]
- Allen, C.D.; Chen, M.Y.; Trick, A.Y.; Le, D.T.; Ferguson, A.L.; Link, A.J. Thermal unthreading of the lasso peptides astexin-2 and astexin-3. ACS Chem. Biol. 2016, 11, 3043–3051. [Google Scholar] [CrossRef]
| Thread | Radius of Gyration | Asphericity | Prolatness | |||||
|---|---|---|---|---|---|---|---|---|
| Thickness | ratio | |||||||
| 0 | 0.154 | −0.102 | 1.00 | 0.0342 | −0.186 | 0.0708 | −1.37 | 0.300 |
| 1 | 0.164 | −0.0825 | 1.06 | 0.188 | −0.753 | 0.0853 | −3.07 | 0.315 |
| 2 | 0.164 | −0.0162 | 1.06 | 0.353 | −0.822 | 0.0858 | −4.57 | 0.384 |
| 3 | 0.164 | 0.0376 | 1.06 | 0.845 | −0.993 | 0.0869 | −5.53 | 0.420 |
| 4 | 0.164 | 0.106 | 1.06 | 1.05 | −0.969 | 0.0856 | −6.10 | 0.413 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dabrowski-Tumanski, P.; Gren, B.; Sulkowska, J.I. Statistical Properties of Lasso-Shape Polymers and Their Implications for Complex Lasso Proteins Function. Polymers 2019, 11, 707. https://doi.org/10.3390/polym11040707
Dabrowski-Tumanski P, Gren B, Sulkowska JI. Statistical Properties of Lasso-Shape Polymers and Their Implications for Complex Lasso Proteins Function. Polymers. 2019; 11(4):707. https://doi.org/10.3390/polym11040707
Chicago/Turabian StyleDabrowski-Tumanski, Pawel, Bartosz Gren, and Joanna I. Sulkowska. 2019. "Statistical Properties of Lasso-Shape Polymers and Their Implications for Complex Lasso Proteins Function" Polymers 11, no. 4: 707. https://doi.org/10.3390/polym11040707
APA StyleDabrowski-Tumanski, P., Gren, B., & Sulkowska, J. I. (2019). Statistical Properties of Lasso-Shape Polymers and Their Implications for Complex Lasso Proteins Function. Polymers, 11(4), 707. https://doi.org/10.3390/polym11040707