Topological Methods for Polymeric Materials: Characterizing the Relationship Between Polymer Entanglement and Viscoelasticity
Abstract
1. Introduction
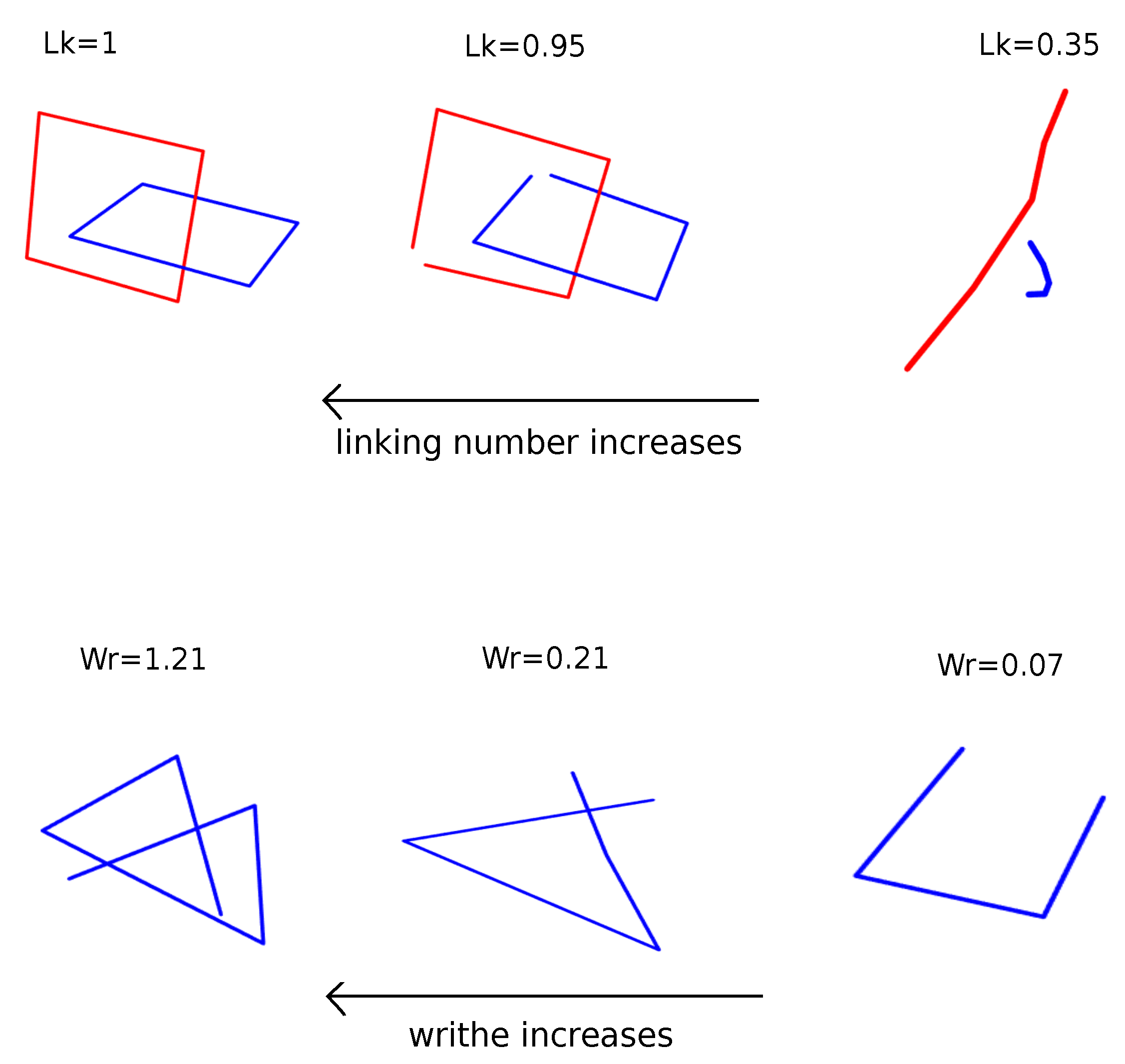
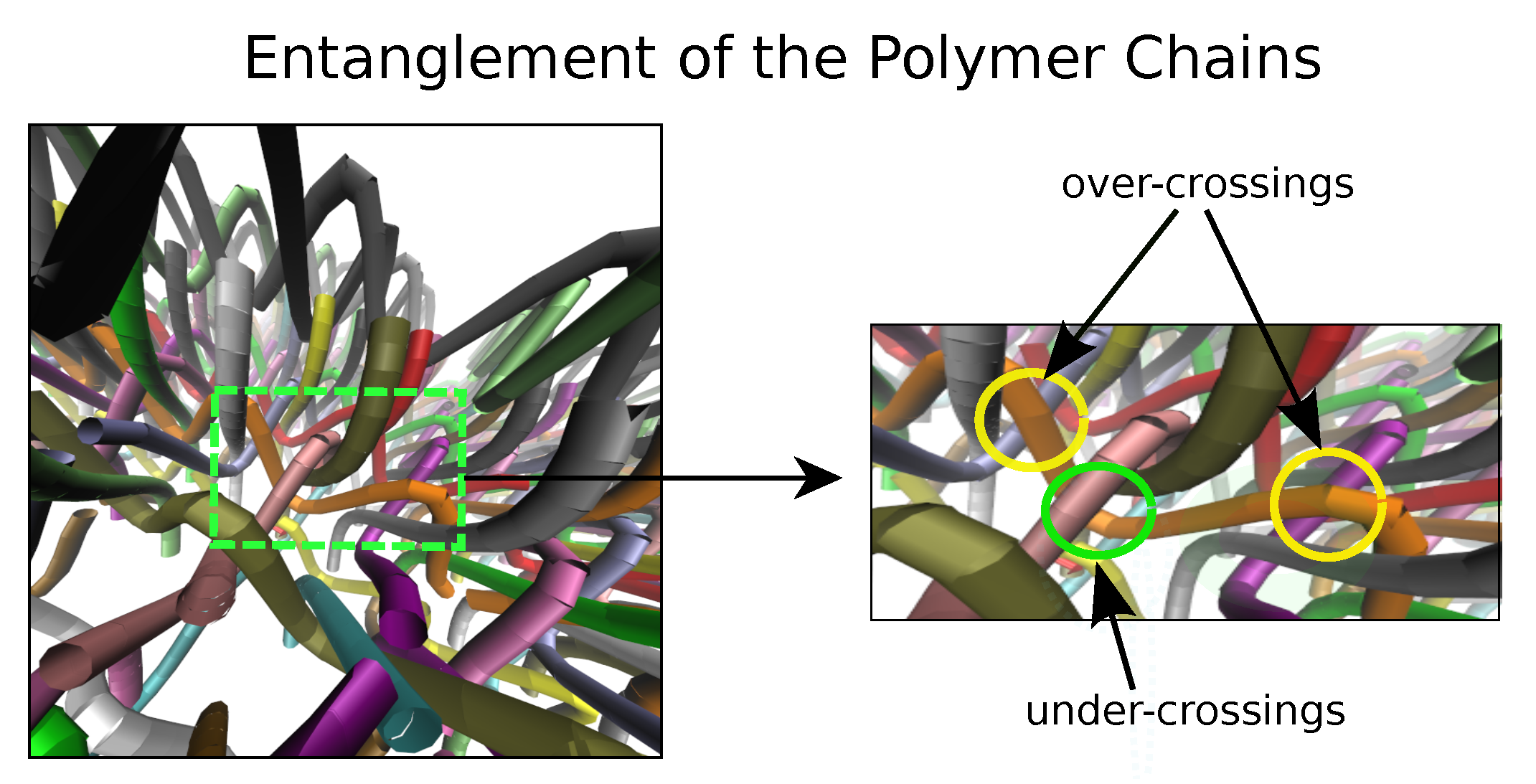
2. Characterizing Polymer Entanglement
3. Polymeric Materials with Weave-like Entanglements
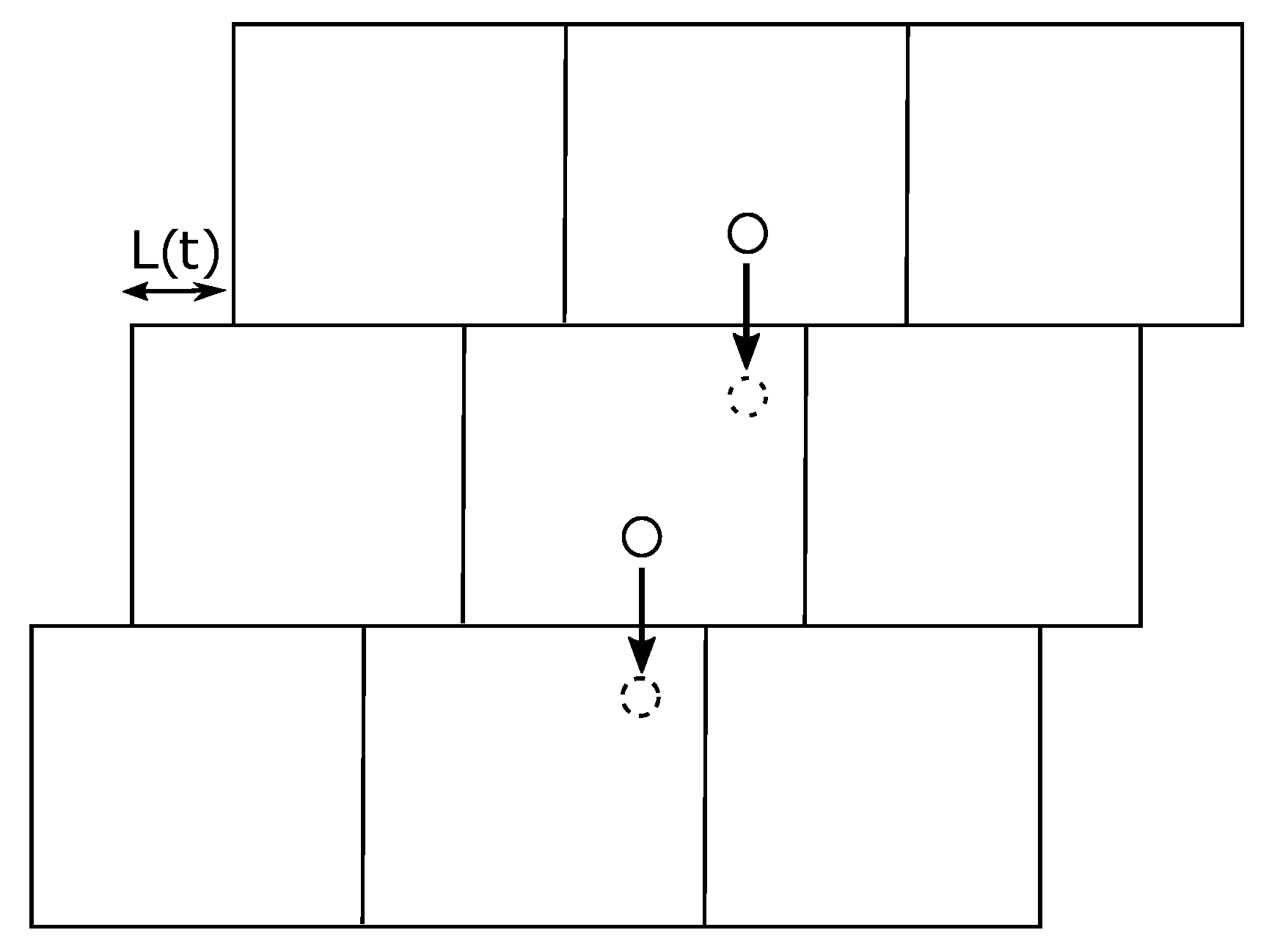
4. Simulation of the Polymers
5. Bulk Mechanical Responses
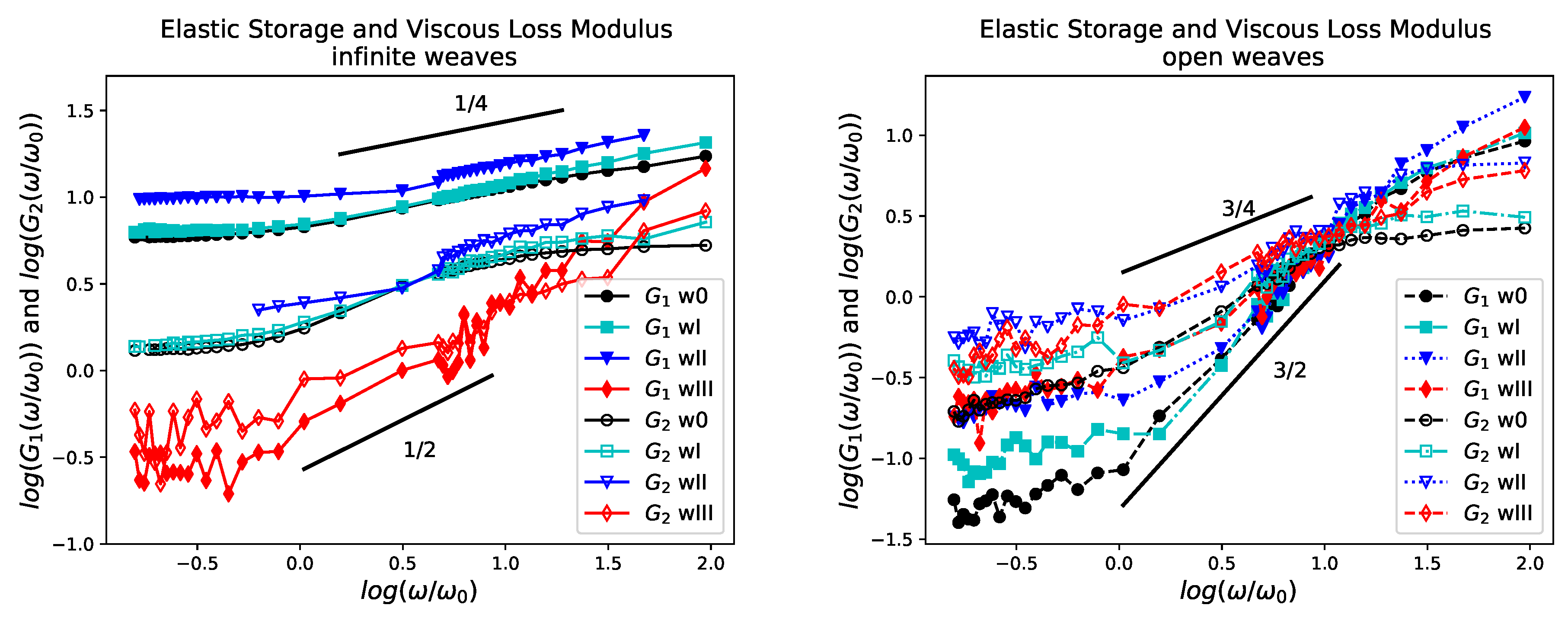
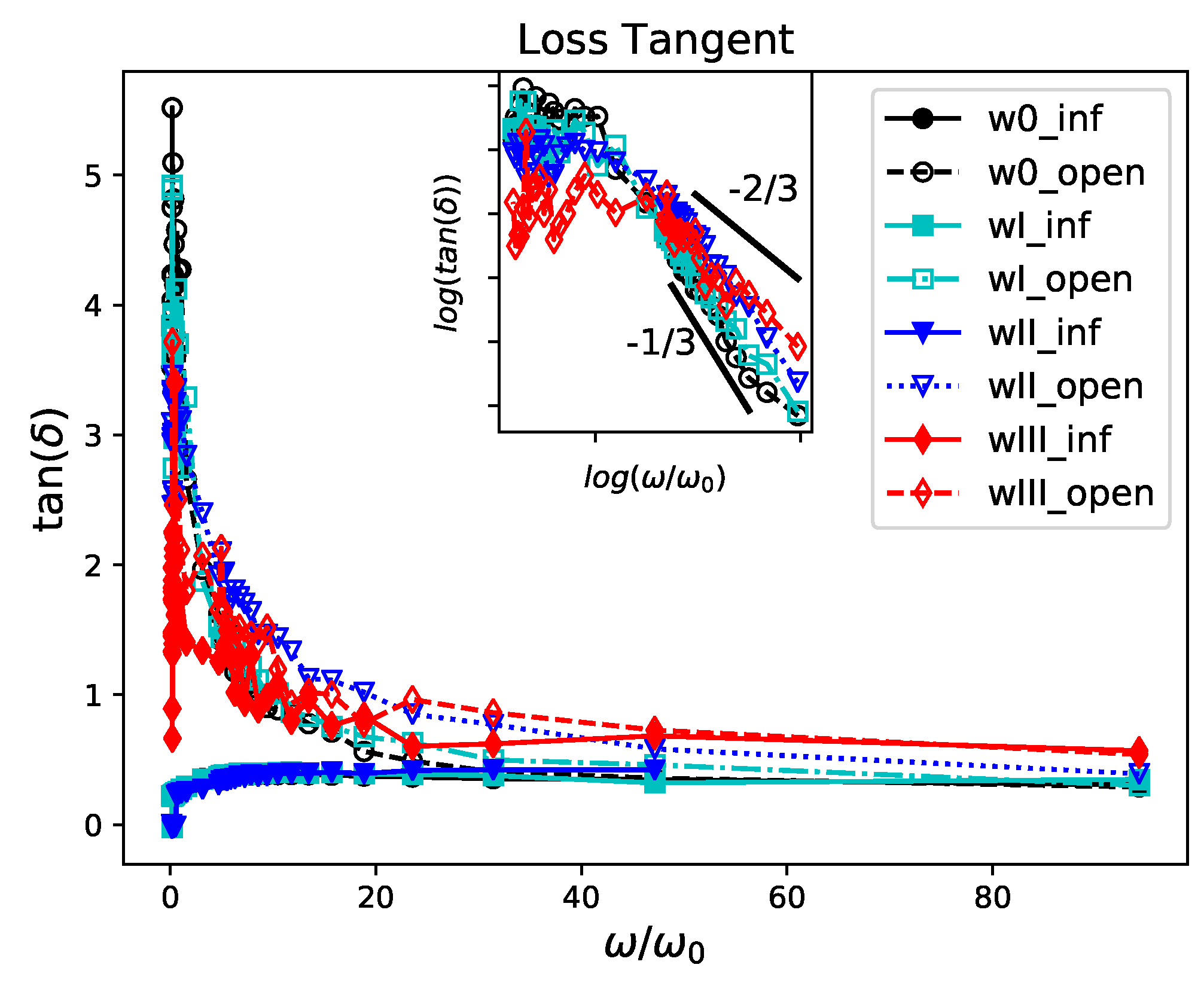
5.1. Complex Modulus
5.2. Conformational Analysis
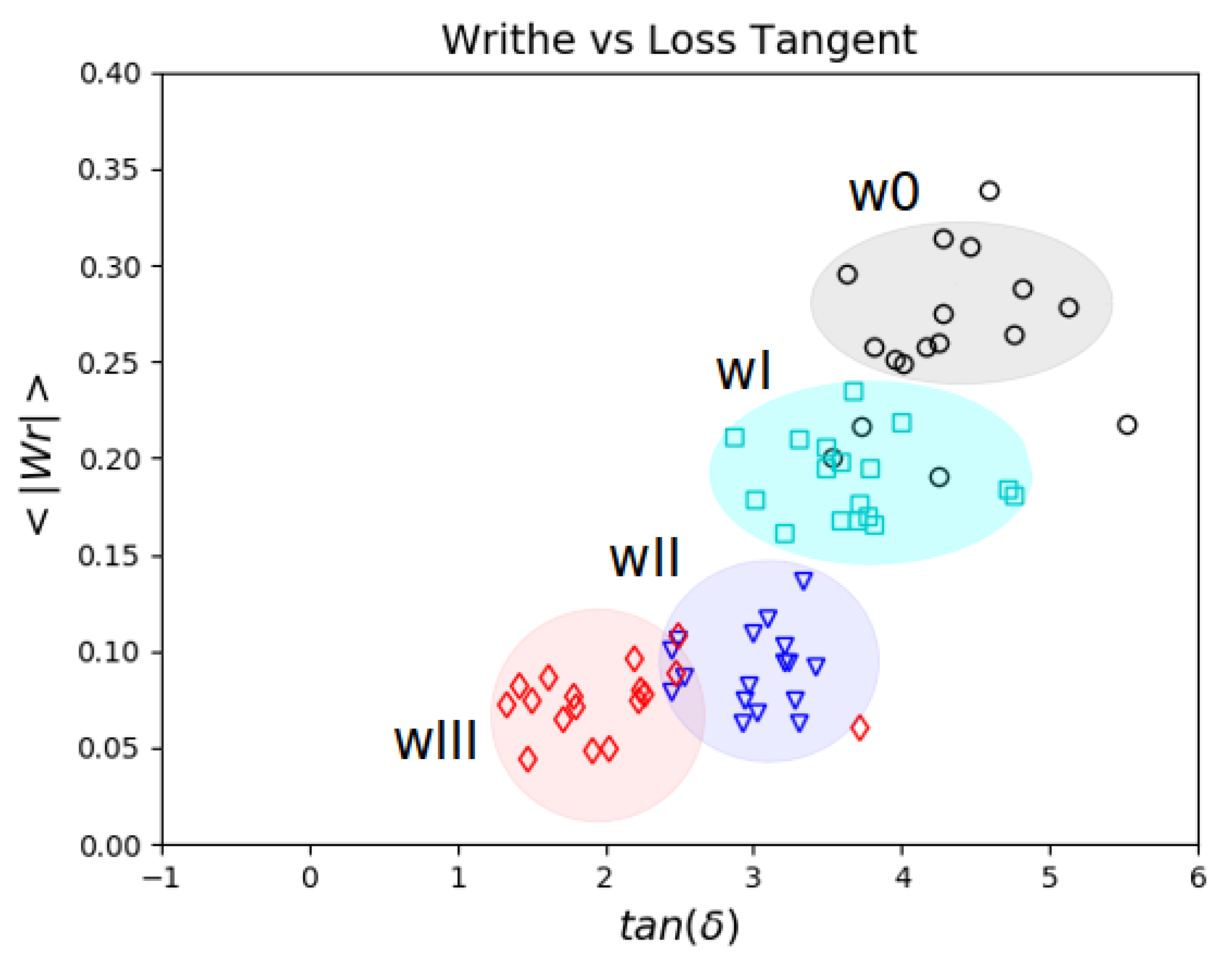
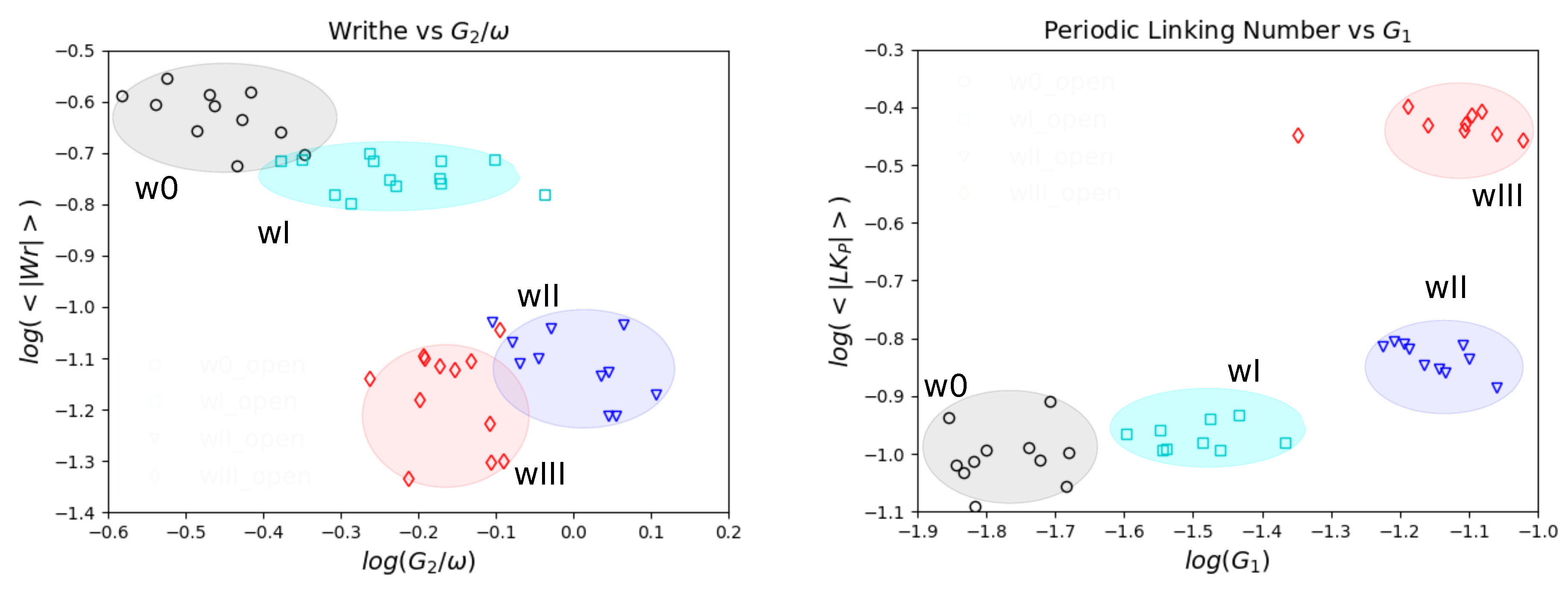
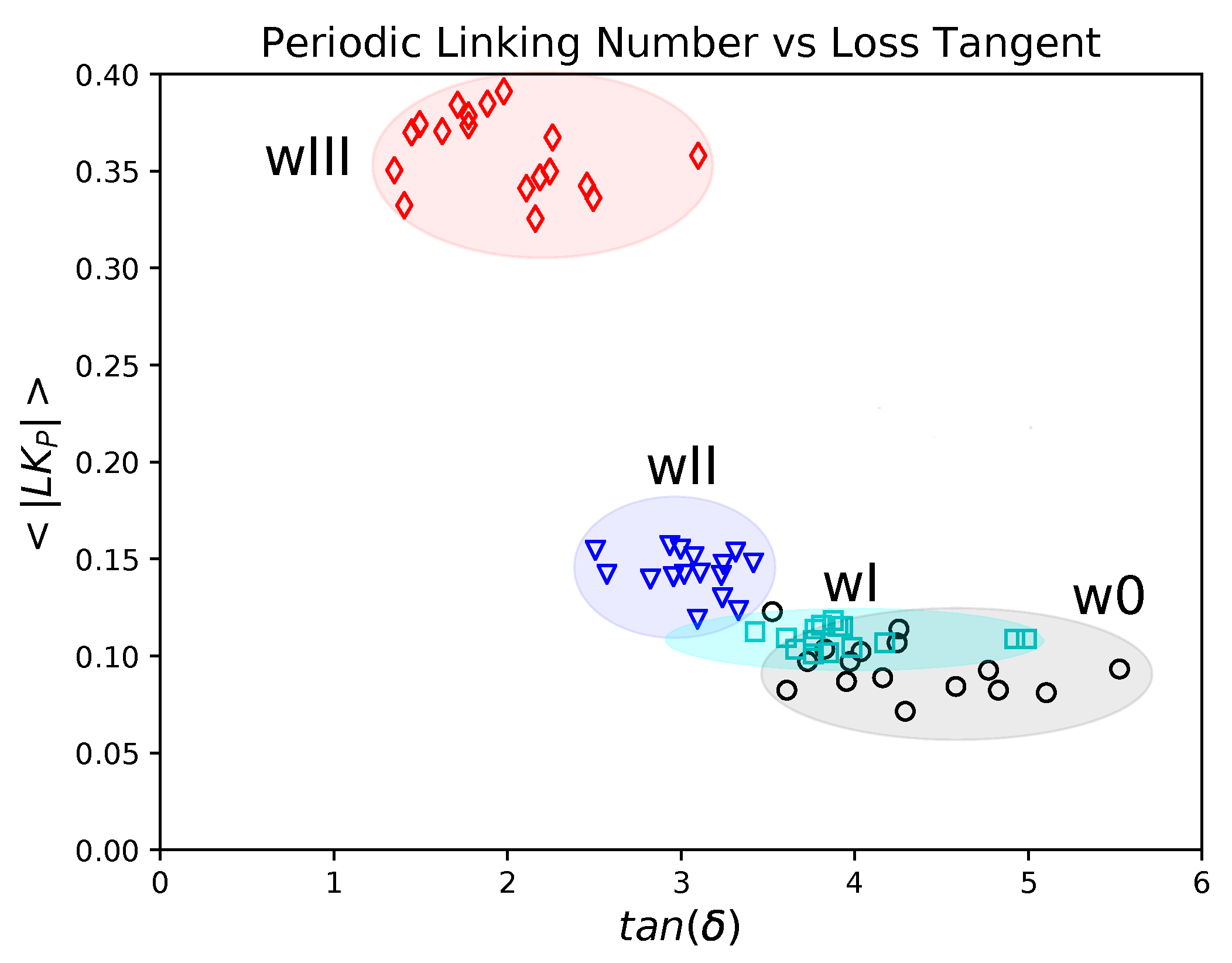
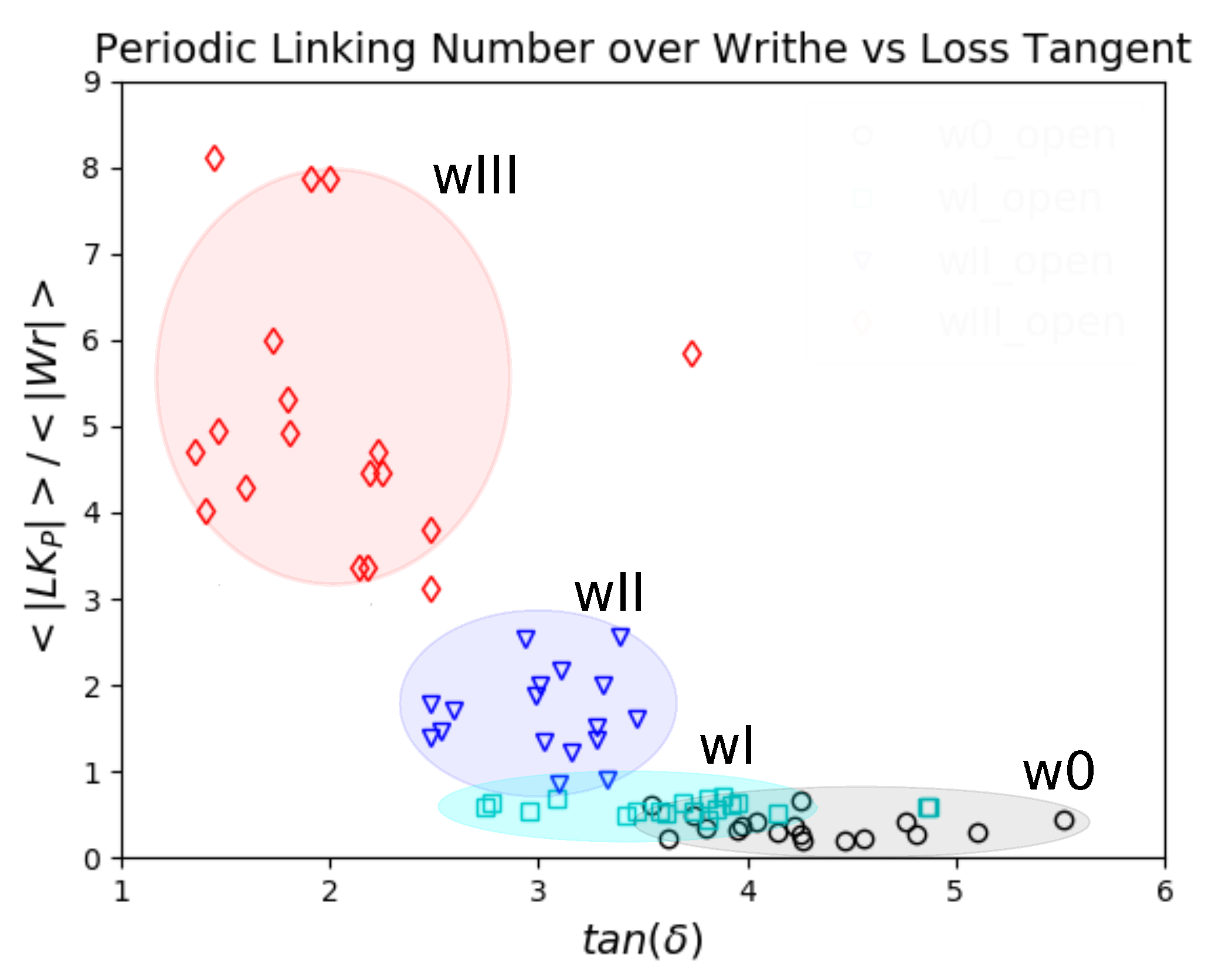
5.3. Topology and Mechanical Responses
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- de Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Rubinstein, M.; Colby, R. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Bird, R.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids: Volume I Fluid Mechanics; Wiley-Interscience: Hoboken, NJ, USA, 1987. [Google Scholar]
- Bird, R.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids: Volume II Kinetic Theory; Wiley-Interscience: Hoboken, NJ, USA, 1987. [Google Scholar]
- Edwards, F. Statistical mechanics with topological constraints: I. Proc. Phys. Soc. 1967, 91, 513–519. [Google Scholar] [CrossRef]
- Edwards, F. Statistical mechanics with topological constraints: II. J. Phys. A Gen. Phys. 1968, 1, 15–28. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Kim, J.M.; Keffer, D.J.; Edwards, B.J.; Kröger, M. Rheological and entanglement characterisitcs of linear-chain polyethylene liquids in planar Cuette and planar elongational flow. J. Non-Newotonian Fluid Mech. 2008, 152, 168–183. [Google Scholar] [CrossRef]
- Baig, C.; Mavrantzas, V.G.; Kröger, M. Flow effects on the melt structure and entanglement network of linear polymer melts: Results from a nonequilibrium molecular dynamics simulation study of a polyethylene melt in steady shear. Macromolecules 2010, 43, 6996. [Google Scholar]
- Hoy, R.S.; Foteinopoulou, K.; Kröger, M. Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length. Phys. Rev. E 2009, 80, 031803. [Google Scholar] [CrossRef] [PubMed]
- Shanbhag, S.; Kröger, M. Primitive path networks generated by annealing and geometrical methods: Insights into differences. Macromolecules 2007, 40, 2897. [Google Scholar] [CrossRef]
- Kröger, M.; Ramirez, J.; Öttinger, H.C. Projection from an atomistic chain contour to its primitive path. Polymer 2002, 43, 477–487. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Baig, C.; Tsolou, G.; Mavrantzas, V.G.; Kröger, M. Quantifying chain reptation in entangled polymer melts. J. Chem. Phys. 2010, 132, 124904. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; He, J.; Ruymbeke, E.; Keunings, R.; Bailly, C. Evaluation of different methods for the determination of the plateau modulus and the entanglement molecular weight. Polymer 2006, 47, 4461–4479. [Google Scholar] [CrossRef]
- Likhtman, A.E.; McLeish, T.C.B. Quantitative theory for linear dynamics of linear entangled polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar] [CrossRef]
- Everaers, R. Topological versus rheological entanglement length in primitive-path analysis protocols, tube models, and slip-link models. Phys. Rev. E 2012, 86, 022801. [Google Scholar] [CrossRef] [PubMed]
- Desai, P.S.; Kang, B.; Katzarova, M.; Hall, R.; Huang, Q.; Lee, S.; Shivokhnin, M.; Chang, T.; Venerus, D.C.; Mays, J.; et al. Challenging tube and slip-link models: predicting the linear rheology of blends of well-characterized star and linear 1,4-polybutadienes. Macromolecules 2016, 49, 4964–4977. [Google Scholar] [CrossRef]
- Snijkers, F.; Pasquino, R.; Olmsted, P.D.; Vlassopoulos, D. Perspectives on the viscoelasticity and flow behavior of entangled linear and branched polymers. J. Phys. Cpndens. Matter 2015, 27, 473002. [Google Scholar] [CrossRef] [PubMed]
- Unidad, H.J.; Goad, M.A.; Bras, A.R.; Zamponi, M.; Faust, R.; Allgaier, J.; Pyckhout-Hintzen, W.; Wischnewski, A.; Richter, D.; Fetters, L.J. Consequences of increasing packing length of the dynamics of polymer melts. Macromolecules 2015, 48, 6638–6645. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Milner, S.T.; Graessly, W.W. Packing length influence in linear polymer melts on the entanglement, critical, and reptation molecular weights. Macromolecules 1999, 32, 6847. [Google Scholar] [CrossRef]
- Sussman, D.M.; Schweizer, K.S. Microscopic theory of entangled polymer melt dynamics: flexible chains as primitive-path random walks and supercoarse grained needles. PRL 2012, 109, 168306. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Helfand, E.J. Statistics of Entanglements of Polymers: Concentration Effects. J. Chem. Phys. 1984, 82, 2477–2483. [Google Scholar] [CrossRef]
- Jain, A.; Dünweg, B.; Prakash, R. Dynamic crossover scaling in polymer solutions. PRL 2012, 109, 088302. [Google Scholar] [CrossRef] [PubMed]
- Everaers, R.; Sukumaran, S.K.; Grest, G.S.; Svaneborg, C.; Sivasubramanian, A.; Kremer, K. Rheology and microscopic topology of entangled polymeric liquids. Science 2004, 303, 823. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems. Comput. Phys. Commun. 2005, 168, 209–232. [Google Scholar] [CrossRef]
- Tzoumanekas, C.; Theodorou, D.N. Topological analysis of linear polymer melts: A statistical approach. Macromolecules 2006, 39, 4592–4604. [Google Scholar] [CrossRef]
- Bisbee, W.; Qin, J.; Milner, S.T. Finding the tube with isoconfigurational averaging. Macromolecules 2011, 44, 8972–8980. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M.; Kröger, M.; Mansfield, L. Universal scaling, entanglements and knots of model chain molecules. Phys. Rev. Lett. 2008, 101, 265702. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Milner, S.T. Counting polymer knots to find the entanglement length. Soft Matter 2011, 7, 10676–10693. [Google Scholar] [CrossRef]
- Kuei, S.; Slowicka, A.M.; Ekiel-Jezewska, M.L.; Wajnryb, E.; Stone, H.A. Dynamics and topology of a flexible chain: Knots in steady shear flow. New J. Phys. 2015, 17, 053009. [Google Scholar] [CrossRef]
- Everaers, R.; Kremer, K. Topological Interactions in Model Polymer Networks. Phys. Rev. E 1996, 53, R37–R40. [Google Scholar] [CrossRef]
- Millett, K.C.; Dobay, A.; Stasiak, A. Linear random knots and their scaling behavior. Macromolecules 2005, 38, 601–606. [Google Scholar] [CrossRef]
- Morton, H.R.; Grishanov, S. Doubly periodic textile structures. J. Knot Theory Ramif. 2009, 18, 1597–1622. [Google Scholar] [CrossRef]
- Panagiotou, E. The linking number in systems with periodic boundary conditions. J. Comput. Phys. 2015, 300, 533–573. [Google Scholar] [CrossRef]
- Panagiotou, E.; Kröger, M.; Millett, K.C. Writhe and mutual entanglement combine to give the entanglement length. Phys. Rev. E 2013, 88, 062604. [Google Scholar] [CrossRef] [PubMed]
- Panagiotou, E.; Kröger, M. Pulling-force-induced elongation and alignment effects on entanglement and knotting characteristics of linear polymers in a melt. Phys. Rev. E 2014, 90, 042602. [Google Scholar] [CrossRef] [PubMed]
- Panagiotou, E.; Tzoumanekas, C.; Lambropoulou, S.; Millett, K.C.; Theodorou, D.N. A Study of the Entanglement in Systems with Periodic Boundary Conditions. Prog. Theor. Phys. Suppl. 2011, 191, 172–181. [Google Scholar] [CrossRef]
- Panagiotou, E.; Plaxco, K.W. A topological study of protein folding kinetics. arXiv, 2018; arXiv:1812.08721. [Google Scholar]
- Lees, A.W.; Edwards, S. The computer study of transport processes under extreme conditions. J. Phys. C Solid State Phys. 1972, 5, 1921. [Google Scholar] [CrossRef]
- Gauss, K.F. Werke; Kgl. Gesellsch. Wiss.: Göttingen, Germany, 1877. [Google Scholar]
- Evans, M.E.; Robins, V.; Hyde, S.T. Periodic entanglement II: weavings from hyperbolic line patterns. Acta Chryst. 2013, A69, 262–275. [Google Scholar] [CrossRef]
- Liu, Y.; O’Keeffe, M.; Treacy, M.M.J.; Yaghi, O.M. The geometry of periodic knots, polycatenanes and weaving from a chemical perspective: A library for reticular chemistry. Chem. Soc. Rev. 2018, 47, 4642–4664. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, C.W. Handbook of Stochastic Methods; Series in Synergetics; Springer: Berlin, Germany, 1985. [Google Scholar]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Wang, Y.; Sigurdsson, J.K.; Atzberger, P.J. Fluctuating Hydrodynamics Methods for Dynamic Coarse-Grained Implicit-Solvent Simulations in LAMMPS. SIAM J. Sci. Comput. 2016, 38, S62–S77. [Google Scholar] [CrossRef]
- Vladkov, M.; Barrat, J. Linear and nonlinear viscoelasticity of a model unentangled polymer melt: Molecular dynamics and rouse modes analysis. Macromol. Theory Simul. 2006, 15, 252–262. [Google Scholar] [CrossRef]
- Irving, J.H.; Kirkwood, J.G. The statistical mechanical theory of transport processes. J. Chem. Phys. 1950, 18, 817–829. [Google Scholar] [CrossRef]
- Edwards, S.F.; Takano, H.; Terentjev, E.M. Dynamic mechanical response of polymer networks. J. Chem. Phys. 2000, 113, 5531. [Google Scholar] [CrossRef]
- Barlow, A.J.; Egrinsav, A.; Lamb, J. Viscoelastic relaxation in poly-1-butenes of low molecular weight. Proc. R. Soc. Lond. A 1967, 300, 356–372. [Google Scholar]
- Rosa, M.E.; Winter, H.H. The effect of entanglement on the rheological behavior of polybutadiene critical gels. Rheo. Acta 1994, 33, 220–237. [Google Scholar] [CrossRef]
- Hyun, K.; Kim, S.H.; Hyun Ahn, K.; Lee, S.J. Large amplitude oscillatory shear as a way to classify the complex fluids. J. Non Newtonian Fluid Mech. 2002, 107, 51–65. [Google Scholar] [CrossRef]
- Trappe, V.; Weitz, D.A. Scaling of the viscoelasticity of weakly attractive particles. Phys. Rev. Lett. 2000, 85, 449–452. [Google Scholar] [CrossRef] [PubMed]
- Lieu, C.; Durairaj, R.; Ramesh, S. Rheological studies of PMMA-PVC based polymer blend electrolytes with LiTFSI as doping salt. PLoS ONE 2014, 9, e102815. [Google Scholar]
- Ross-Murphy, S.B.; McEvoy, H. Fundamentals of hydrogels and gelatin. Br. Polym. J. 1986, 18, 2–7. [Google Scholar] [CrossRef]
- Clark, A.H.; Ross-Murphy, S.B. Structural and mechanical properties of biopolymer gels. Adv. Poly. Sci. 1987, 83, 57–192. [Google Scholar]
- Mortazavi, S.A. Extended rheology sweep: A more realistic rheological approach to investigate the process of mucoadhesive polymer-mucus gel chain interpenetration. Iran. Pol. J. 2003, 12, 413–420. [Google Scholar]
- Krajina, B.A.; Zhu, A.; Heilshort, S.C.; Spakowitz, A.J. Active DNA olympic hydrogels driven by topoisomerase activity. Phys. Rev. Lett. 2018, 121, 148001. [Google Scholar] [CrossRef] [PubMed]
- Lieleg, O.; Schmoller, K.M.; Claessens, M.M.A.E.; Bausch, A.R. Cytoskeletal polymer networks: Viscoelastic properties are determined by the microscopic interaction potential of cross-links. Biop. J. 2009, 96, 4725–4732. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Hwang, W.; Lee, H.; Kamm, R.D. Computational analysis of viscioelastic properties of crosslinked actin networks. PLoS Comput. Biol. 2009, 5, e1000439. [Google Scholar] [CrossRef] [PubMed]
- Mason, T.G.; Dhople, A.; Wirtz, D. Linear viscoelastic moduli of concentrated DNA solutions. Macromolecules 1998, 31, 3600–3603. [Google Scholar] [CrossRef]
- Wilson, M.; Rabinovitch, A.; Baljon, A.R.C. Computational study of the structure and rheological properties of self-associating polymer networks. Macromolecules 2015, 48, 6313–6320. [Google Scholar] [CrossRef]
- Szántó, L.; Vogt, R.; Meier, J.; Auhl, D.; Van Ruymbeke, E.; Friedrich, C. Entanglement relaxation time of polyethylene melts from high-frequency rheometry in the mega-hertz range. J. Rheol. 2017, 61, 1023. [Google Scholar]
- Saito, S.; Hashimoto, T.; Morfin, I.; Lindner, P.; Boué, F.; Pine, D.J. Phase separation in a polymer solution induced by theady and large amplitude oscillatory shear flow. Macromolecules 2003, 36, 3745–3748. [Google Scholar] [CrossRef]
- Shen, Z.; Röding, M.; Kröger, M.; Li, Y. Carbon nanotube length governs the viscoelasticity and permeability of buckypaper. Polymers 2017, 9, 9040115. [Google Scholar]
- Anogiannakis, S.; Tzoumanekas, C.; Theodorou, D.N. Microscopic description of entanglements in Polyethylene networks and melts. Macromolecules 2012, 45, 9475–9492. [Google Scholar] [CrossRef]
- Kapnistos, M.; Lang, M.; Vlassopoulos, D.; Pyckhout-Hintzen, W.; Richter, D.; Cho, D.; Chang, T.; Rubinstein, M. Unexpected power-law stress relaxation of entangled ring polymers. Nat. Mater. 2008, 7, 997–1002. [Google Scholar] [CrossRef] [PubMed]
- Tsalikis, D.G.; Mavrantzas, V.G. Threading of ring poly(ethylene oxide) molecules by linear chains in the melt. ACS Macro Lett. 2014, 3, 763–766. [Google Scholar] [CrossRef]
- Paturej, J.; Sheiko, S.S.; Panyukov, S.; Rubinstein, M. Molecular structure of bottlebrush polymers in melts. Sci. Adv. 2016, 2, e1601478. [Google Scholar] [CrossRef] [PubMed]
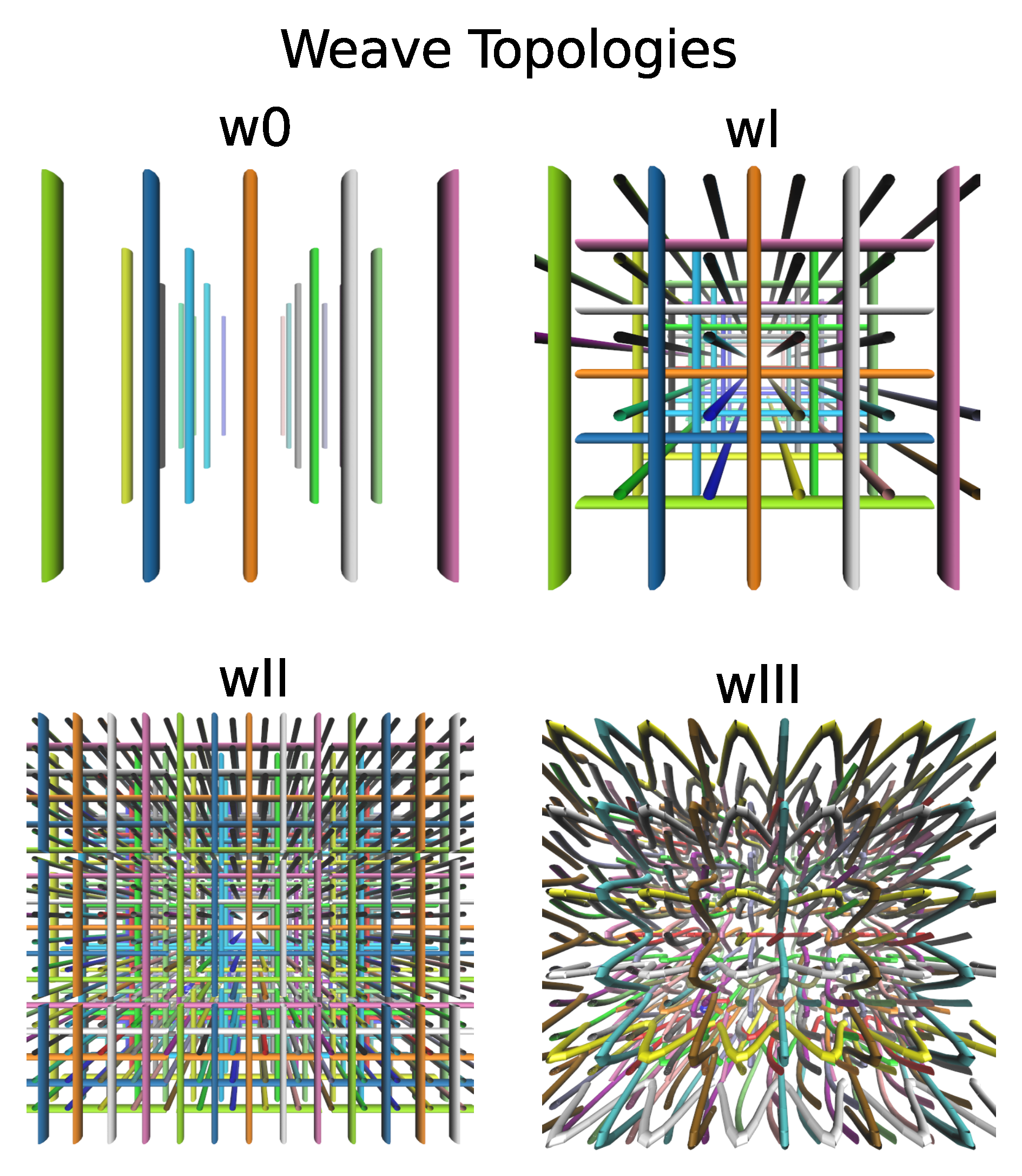
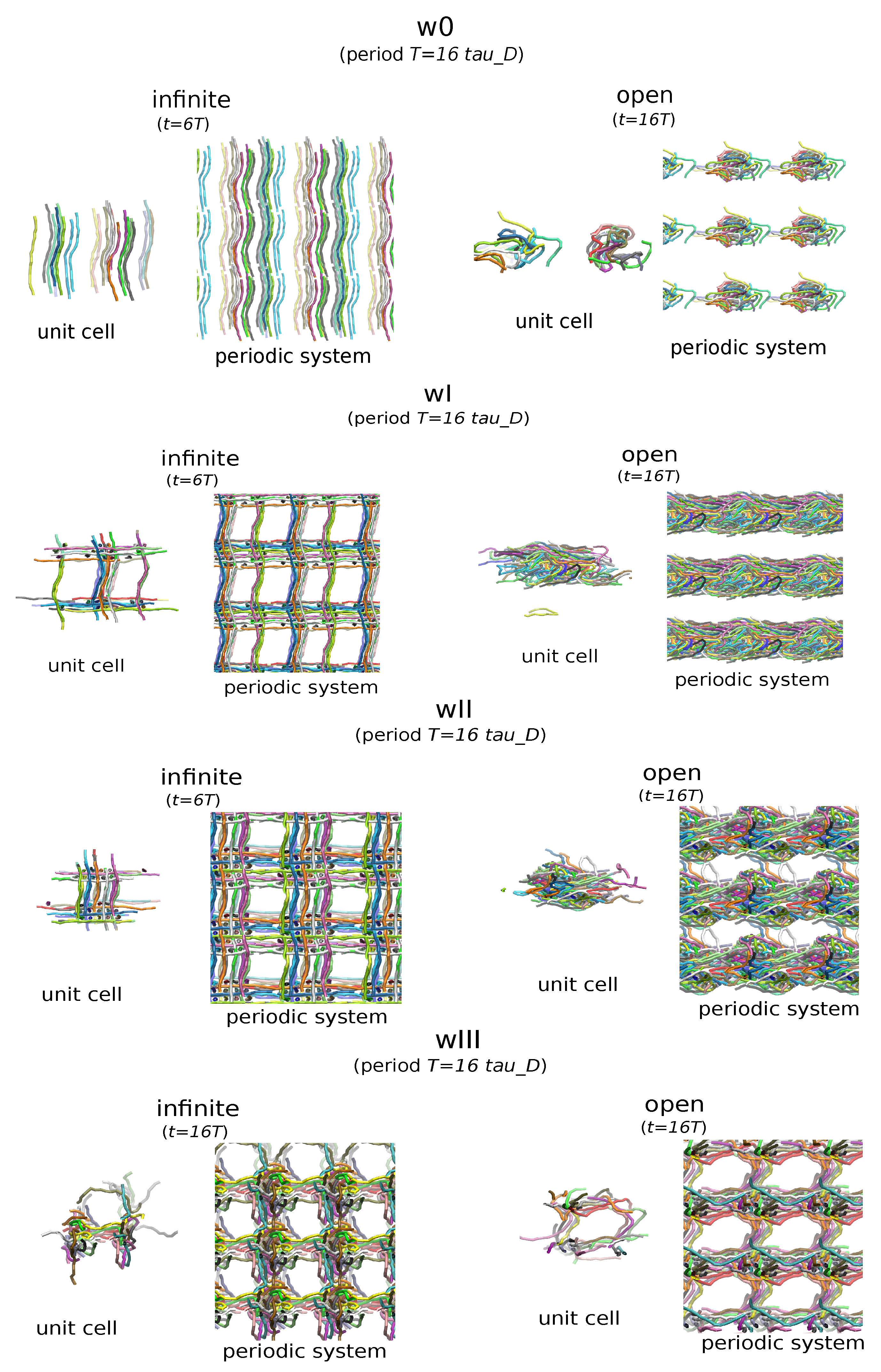
| Weave | Topology | Density | MW (open) |
|---|---|---|---|
| W0 | parallel, non-interlaced | 0.0625 (15 amu/nm) | 20 |
| WI | orthogonal (non interl.) | 0.1875 (45 amu/nm) | 20 |
| WII | orthogonal (non interl.) | 0.33 (80 amu/nm) | 15 |
| WIII | alternating interlaced | 0.35 (84 amu/nm) | 21–17 |
| Parameter | Description | Value |
|---|---|---|
| monomer radius | 1.0 nm | |
| energy scale | 2.5 amu·nm/ps | |
| reference mass | 1 amu | |
| energy potential width | ||
| m | monomer mass | 240 |
| LJ-time-scale | = 0.6 ps | |
| thermal energy | 1.0 | |
| solvent mass density | 39 | |
| solvent viscosity | 25 | |
| drag coefficient | 476 |
| Parameter | Description | Value |
|---|---|---|
| harmonic bonds potential constant | 619.5 amu/ps | |
| b | harmonic bonds rest length | 1.0 nm |
| harmonic angle potential constant | 19.8 amu·nm/ps | |
| harmonic angles’ rest length | 180 |
| Parameter | Description | value |
|---|---|---|
| advection time | propagation in fluid | 0.0013 ps |
| diffusion time | monomer moves a dist. | 302 ps |
| Rouse time | ideal chain | 6937 ps |
| critical time | cross-over reference time | 598 ps |
| T | period of oscillation | 6 ps < T < 3600 ps |
| t simulation time | longest simulation time | 150 ps < t < 90,000 ps |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panagiotou, E.; Millett, K.C.; Atzberger, P.J. Topological Methods for Polymeric Materials: Characterizing the Relationship Between Polymer Entanglement and Viscoelasticity. Polymers 2019, 11, 437. https://doi.org/10.3390/polym11030437
Panagiotou E, Millett KC, Atzberger PJ. Topological Methods for Polymeric Materials: Characterizing the Relationship Between Polymer Entanglement and Viscoelasticity. Polymers. 2019; 11(3):437. https://doi.org/10.3390/polym11030437
Chicago/Turabian StylePanagiotou, Eleni, Kenneth C. Millett, and Paul J. Atzberger. 2019. "Topological Methods for Polymeric Materials: Characterizing the Relationship Between Polymer Entanglement and Viscoelasticity" Polymers 11, no. 3: 437. https://doi.org/10.3390/polym11030437
APA StylePanagiotou, E., Millett, K. C., & Atzberger, P. J. (2019). Topological Methods for Polymeric Materials: Characterizing the Relationship Between Polymer Entanglement and Viscoelasticity. Polymers, 11(3), 437. https://doi.org/10.3390/polym11030437





