Physical Processes in Polymeric Filters Used for Dialysis †
Abstract
1. Introduction
2. Notes on the History of Dialysis
2.1. Hemodialysis
2.2. Peritoneal Dialysis
3. Transport of Water across Natural Membranes
3.1. Fluid Pathways in the Organism
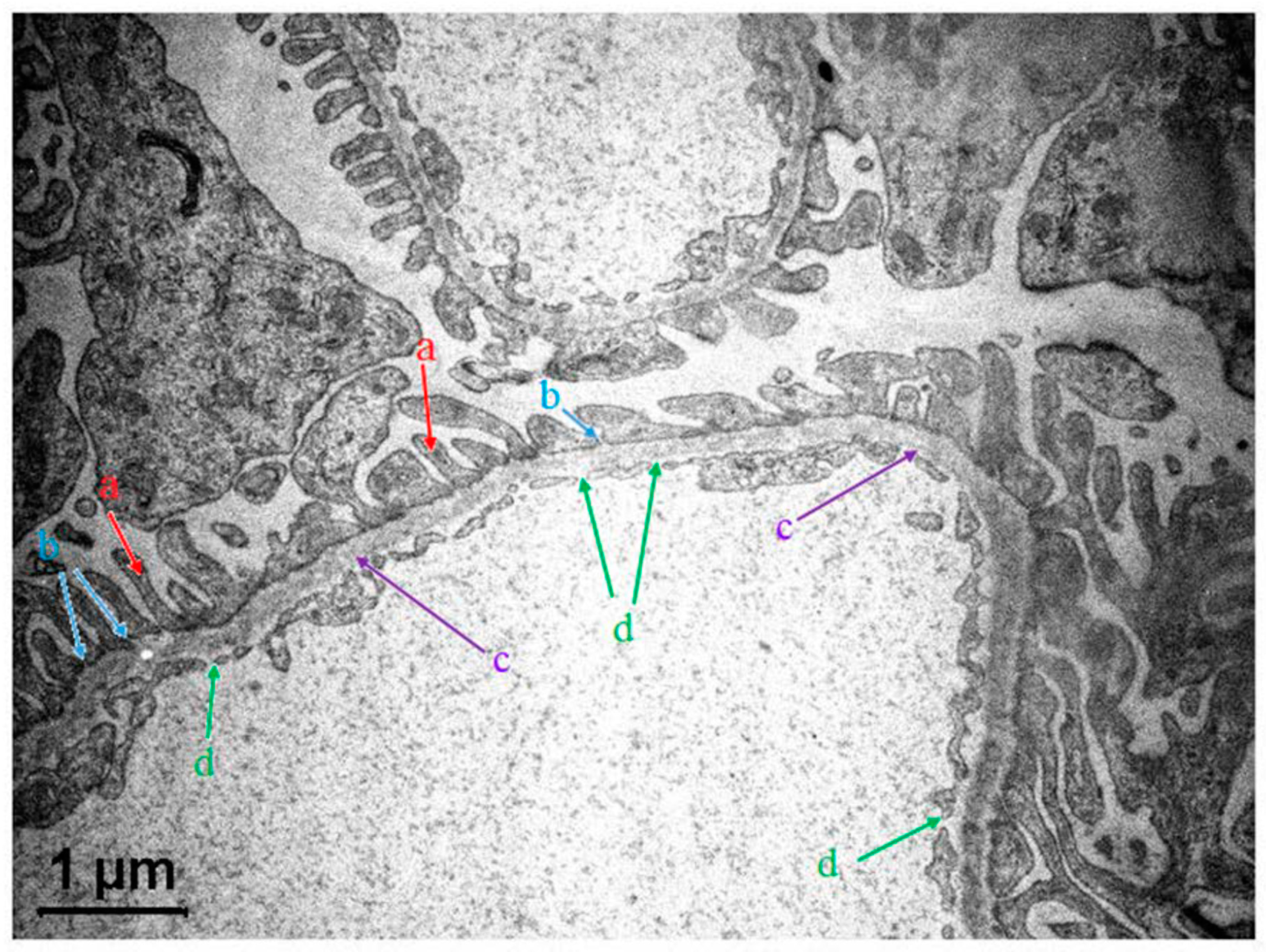
3.2. The Glomerular Filtration Barrier (GFB) in Kidneys
3.2.1. GFB Structure in a Nutshell
3.2.2. Modeling Glomerular Sieving
3.2.3. Debates on Albumin Sieving
3.3. Comparing Glomerular and Peritoneal Transport
3.4. Aquaporins
3.4.1. “Water-Only” Nanopores
3.4.2. Peritoneal Dialysis: Ultrafiltration, Osmotic Water Transport and AQP1s Involvement
3.4.3. Debates
4. Fundamental Thermodynamic Relations for the Transport of Fluid and Solutes in Dialysis
4.1. Nonequilibrium Thermodynamics of Irreversible Processes
Starling Equation
4.2. Thermodynamics of Membrane Transport
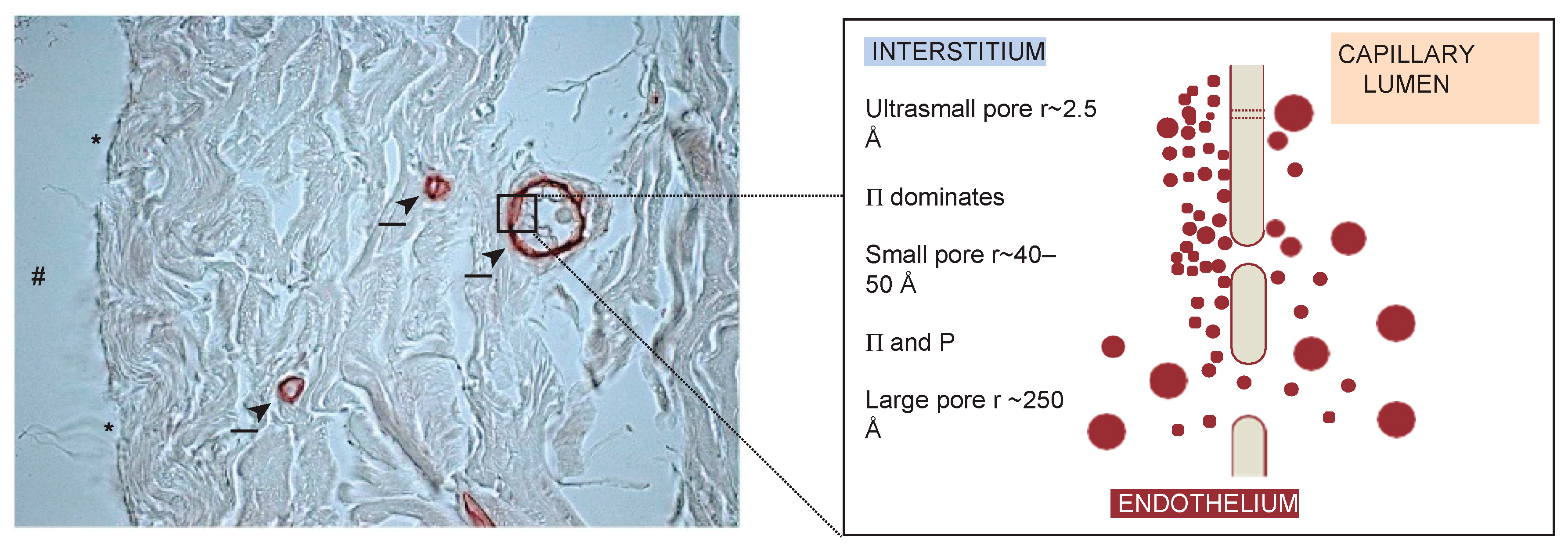
4.3. Two-Pore Membrane Model
4.3.1. Classical Two Pore–Model
4.3.2. Distributed Two–Pore Model
On the Choice of Log-Normal Distribution Function
4.4. Three Pore Model
4.4.1. Three Pore Model (TPM) of Peritoneal Membrane Transport
4.4.2. Extended TPM and Applications to the Automated Peritoneal Dialysis
4.5. Size-Selectivity of Synthetic Dialysis Membranes: Log-Normal Distributed + Shunt Model
New Developments
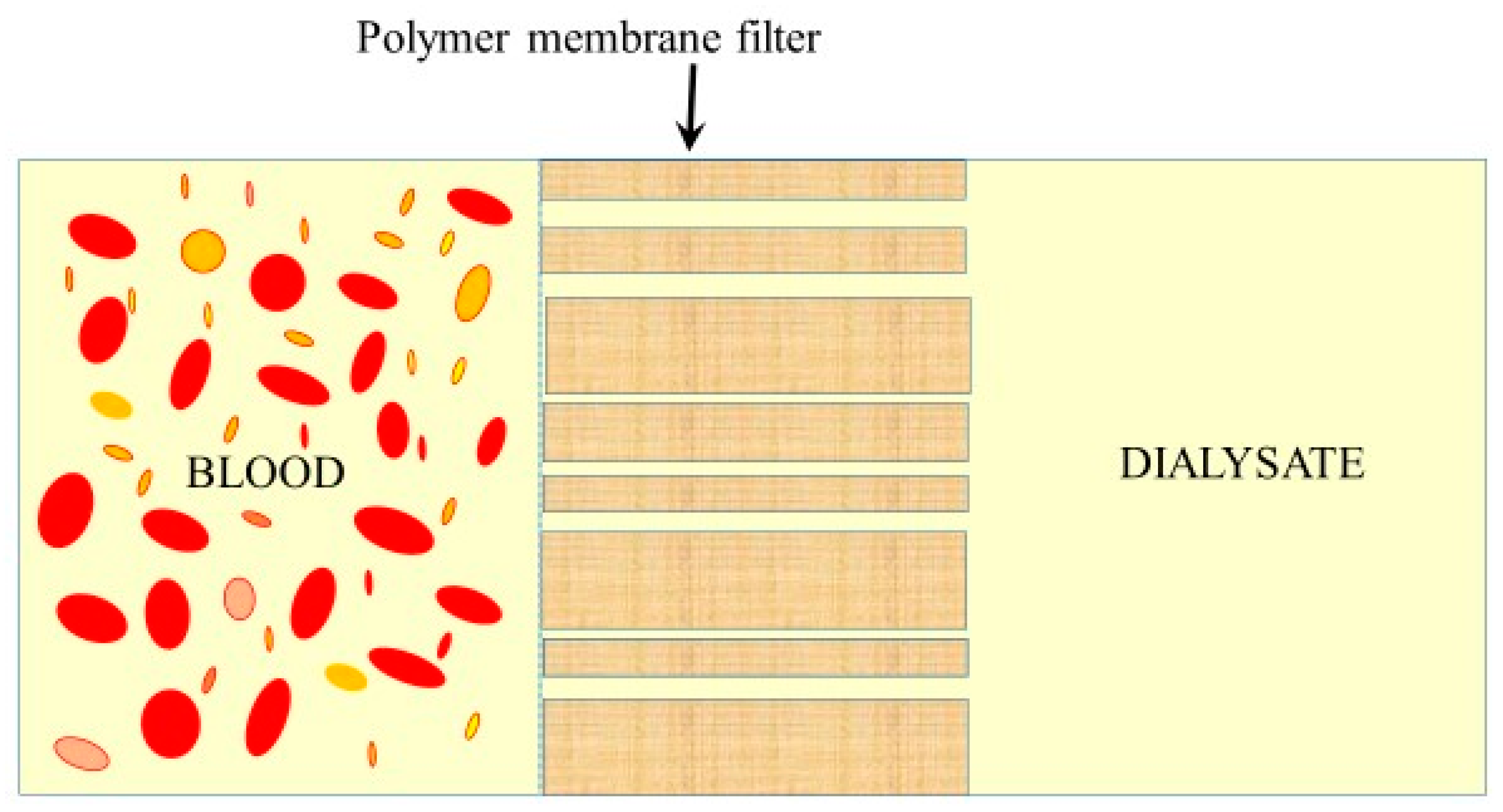
5. Water Transport across Artificial Dialysis Membranes
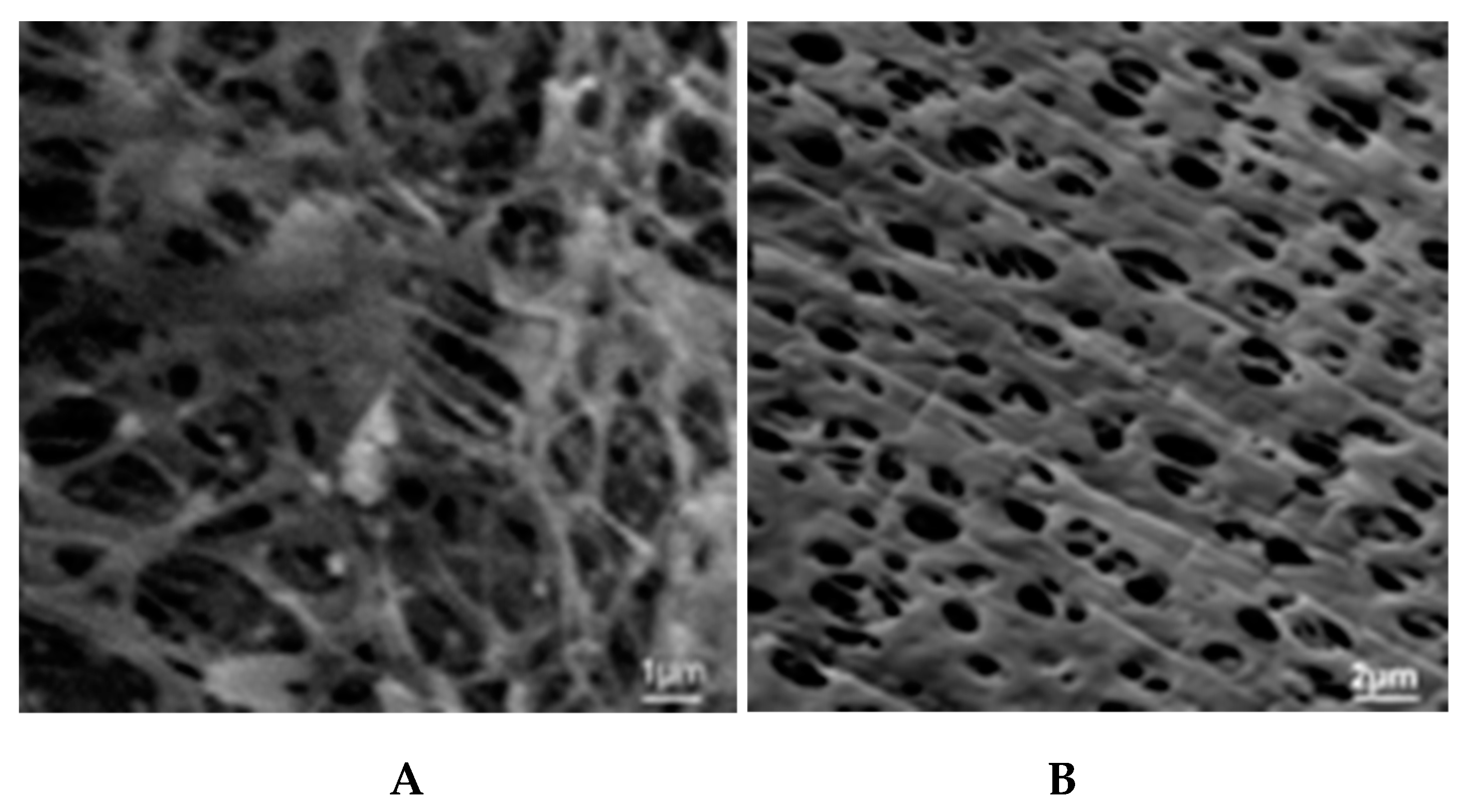
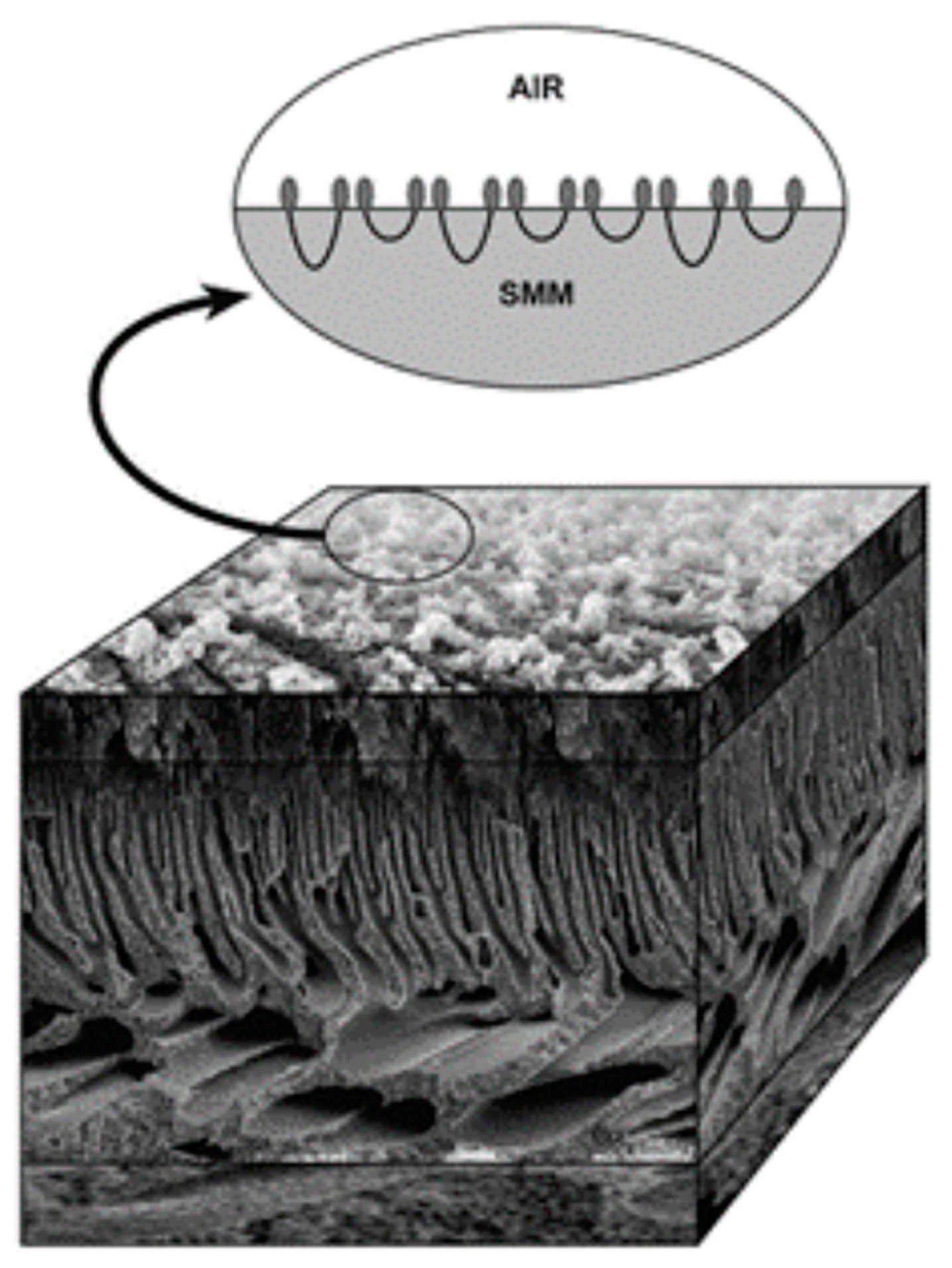
5.1. Microporous Membranes for Hemodialysis: Ultrastructure of Pores and Their Characteristics
5.2. Fouling of Dialysis Filters
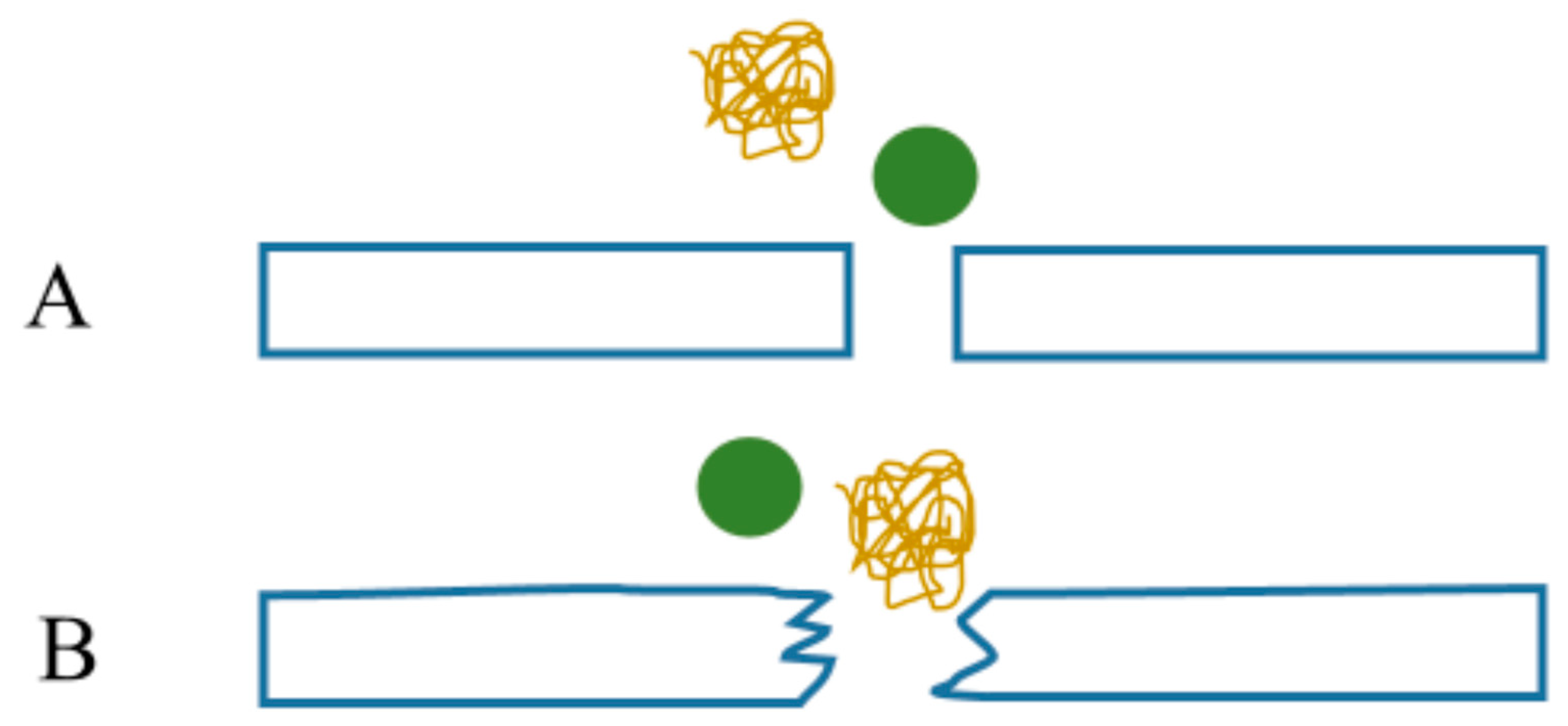
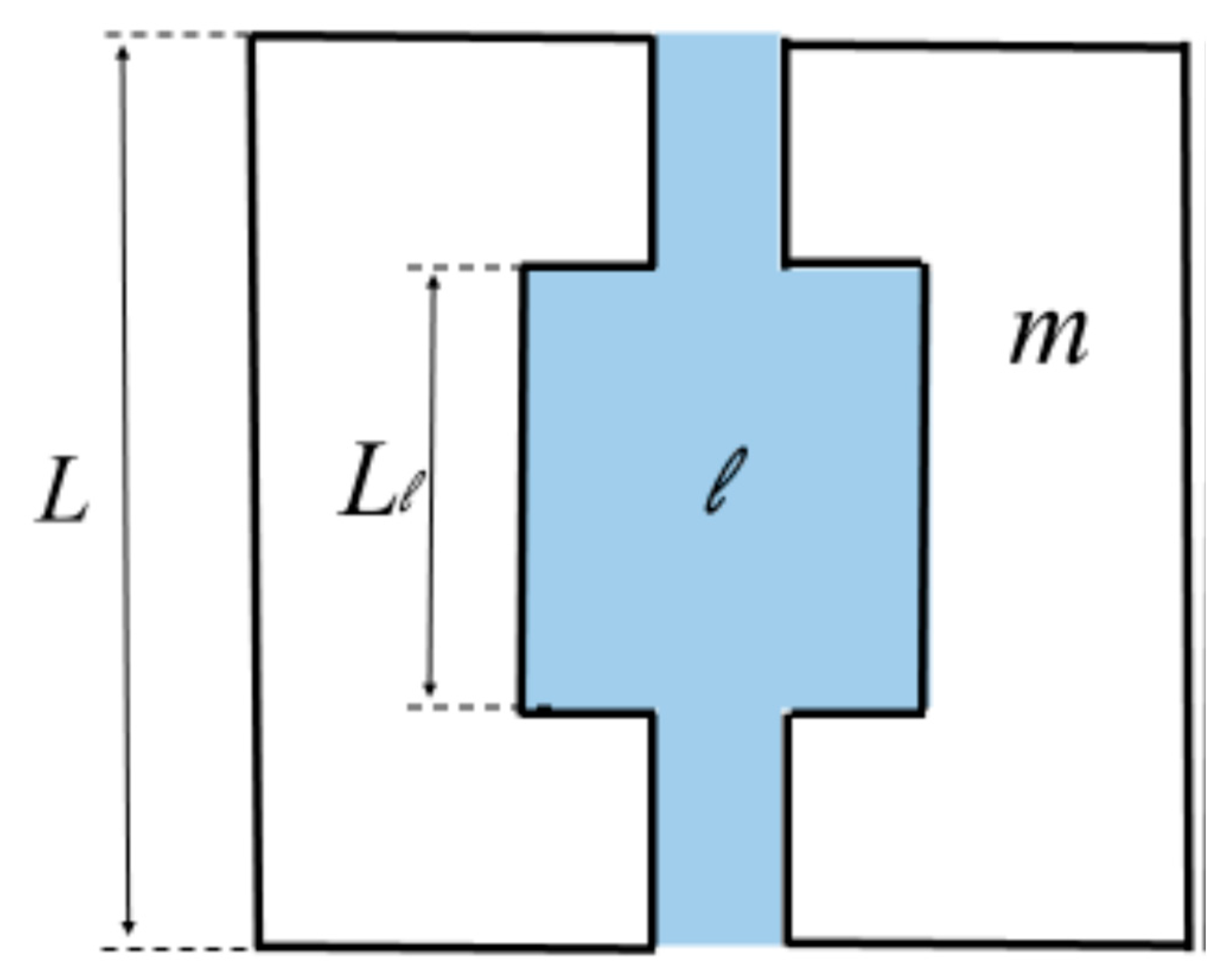
6. Mathematical Modeling of Molecular Transport in Tortuous Dialysis Membranes
6.1. Modeling Diffusion across the Tortuous Membrane Pathways
6.1.1. The “Hydraulic Tortuosity” Notion
6.1.2. Analogy between Electrical Conduction and Diffusion in Porous Media
6.1.3. Formation Resistivity Factor and Tortuosity
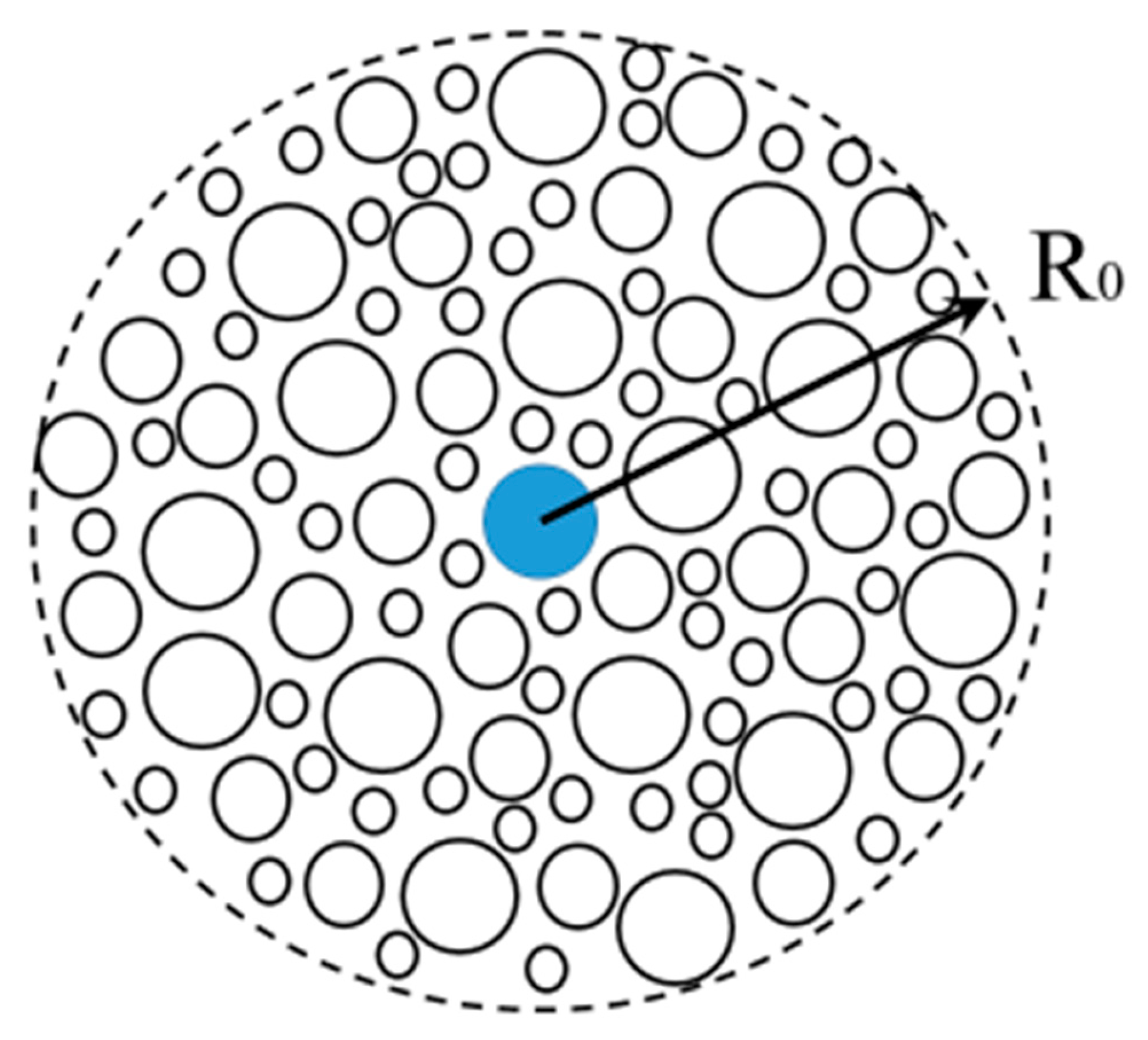
6.2. Geometrical Model of Hindered Diffusion in Fouling Layer Composed of Microspheres
6.3. Diffusive Tortuosity and Random Walks Simulations
7. Theoretical Modeling of Red Blood Cell–Polymeric Membrane Interaction
7.1. Cell Shape Modeling
7.1.1. Helfrich’s Curvature Elasticity Theory
7.1.2. Contact Potential
7.1.3. The Role of Membrane Tension
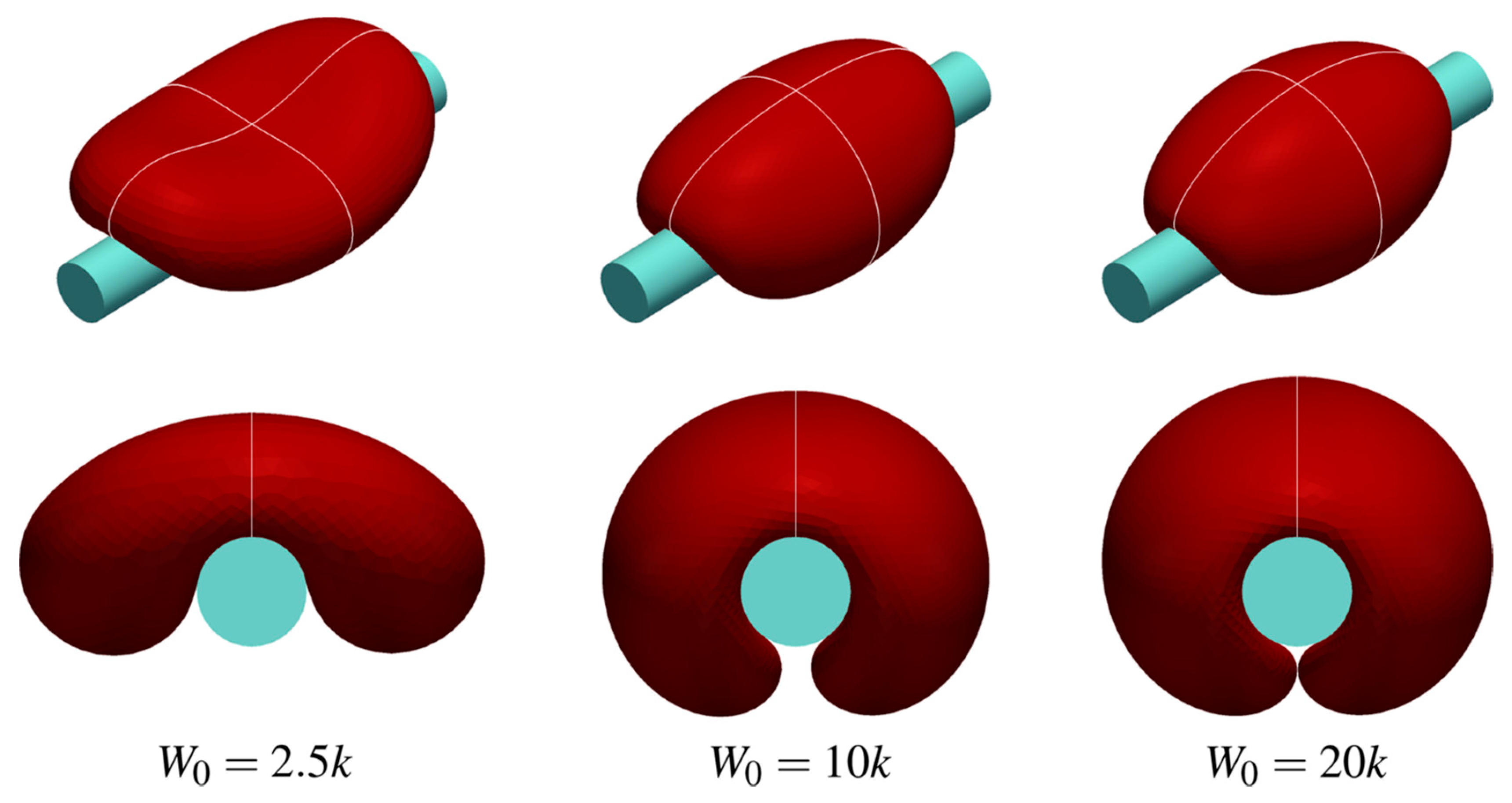
7.1.4. Altered RBC Shapes: Mechanics of the RBC Cytoskeleton
7.2. Morphology of RBCs in Contact with Polymer Surfaces of Dialysis Capillaries
8. Discussion and Outlook
9. Quantification of Dialysis: The Summary of Theoretical Concepts
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| APD | automated peritoneal dialysis |
| AQP | aquaporin |
| CA | cellulose acetate |
| CKD | chronical kidney disease |
| DFR | dialysate flow rate |
| FWT | free water transport |
| GFB | glomerular filtration barrier |
| GBM | glomerular basement membrane |
| HD | hemodialysis |
| HDF | hemodiafiltration |
| MRI | magnetic resonance imaging |
| PA | polyamide |
| PD | peritoneal dialysis |
| PET | peritoneal equilibration test |
| PES | polyethersulfone |
| PSf | polysulfone |
| RBC | red blood cell |
| RRT | renal replacement therapy |
| TPM | three-pore model |
| UF | ultrafiltration |
References
- Alexander, S.R.; Cochat, P. Notes on the history of dialysis therapy in children. In Pediatric Dialysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 3–16. [Google Scholar]
- Paskalev, D.N. Georg Haas (1886–1971): The Forgotten Hemodialysis Pioneer. Dial. Transplant. 2001, 30, 828–832. [Google Scholar]
- Schmaldienst, S.; Hörl, W.H. The biology of hemodialysis. In Replacement of Renal Function by Dialysis, 5th revised ed.; Hörl, W.H., Koch, K.M., Lindsay, R.M., Ronco, C., Winchester, J.F., Eds.; Springer-Science + Business Media: Berlin/Heidelberg, Germany, 2004; pp. 157–179. [Google Scholar]
- Pregl, F. Beitrage zur Methodik des Dialysierverfahrens von E.Abderhalden. Fermentforschung 1914, 1, 7–12. [Google Scholar]
- Shinaberger, J.H. Quantitation of dialysis: Historical perspective. Semin. Dial. 2001, 14, 238–245. [Google Scholar] [CrossRef] [PubMed]
- Abel, J.J.; Rowntree, L.G.; Turned, B.B. On the removal of diffusible substances from the circulation blood of living animals by dialysis. J. Pharmacol. Exp. Theor. 1914, 5, 275–316. [Google Scholar]
- Kolff, W.; Berk, H.; Welle, M.; van der Ley, A.J.W.; van Dijk, E.C.; van Noordwijk, J. The artificial kidney: A dialyser with a great area. Acta Med. Scand. 1944, 117, 121–134. [Google Scholar] [CrossRef]
- Haas, G. Uber die kunstliche Niere. Dt Med. Wochenschr. 1952, 77, 1640–1641. [Google Scholar] [CrossRef] [PubMed]
- Stegmayr, B. Utvecklingen av hemodialysis i Sverige. In Svensk Njurmedicinsk Förening 50 år. Berättelser om Dialys och Njursjukvård i Sverige; Under redaktion av Nils Grefberg: Stockholm, Sweden, 2016; Available online: https://njurmed.se/wp-content/uploads/2017/04/SNF-Jubileumsbok.pdf (accessed on 22 February 2019).
- Hakim, R.M.; Breillatt, J.; Lazarus, J.M.; Port, F.K. Complement activation and hypersensitivity reactions to dialysis membranes. N. Engl. J. Med. 1984, 311, 878–882. [Google Scholar] [CrossRef] [PubMed]
- Hakim, R.M.; Fearn, D.T.; Lazarus, J.M.; Perzanowski, C.S. Biocompatibility of dialysis membranes: Effects of chronic complement activation. Kidney Int. 1984, 26, 94–200. [Google Scholar] [CrossRef]
- Henderson, L.W.; Cheung, A.K.; Chenoweth, D.E. Choosing a Membrane. Am. J. Kid. Dis. 1983, 3, 5–20. [Google Scholar] [CrossRef]
- Yamashita, A.C.; Sakurai, K. Dialysis membranes–physico-chemical structures and features. In Updates in Hemodialysis; Suzuki, H., Ed.; INTECH: Vienna, Austria, 2015; Chapter 10; pp. 163–189. [Google Scholar]
- Babb, A.L.; Strand, M.J.; Uvelli, D.A.; Milutinovic, J.; Scribner, B.H. Quantitative description of dialysis treatment: A dialysis index. Kidney Int. Suppl. 1975, 2, 23–29. [Google Scholar]
- Tenckhoff, H.; Curtis, F.K. Experience with maintainance peritoneal dialysis in the home. Trans. Am. Soc Artif. Intern. Organs 1970, 16, 90–95. [Google Scholar] [PubMed]
- Arkill, K.P.; Qvortrup, K.; Starborg, T.; Mantell, J.M.; Knupp, C.; Michel, C.C.; Harper, S.J.; Salmon, A.H.J.; Squire, J.M.; Bates, D.O.; et al. Resolution of the three dimensional structure of components of the glomerular filtration barrier. BMC Nephrol. 2014, 15, 24–39. [Google Scholar] [CrossRef] [PubMed]
- Salmon, A.H.J.; Neal, C.R.; Harper, S.J. New aspects of glomerular filtration barrier structure and function: Five layers (at least) not three. Curr. Opin. Nephrol. Hypertens. 2009, 18, 197–205. [Google Scholar] [PubMed]
- Haraldsson, B.; Jeansson, M. Glomerular filter barrier. Curr. Opin. Nephrol. Hypertens. 2009, 18, 331–335. [Google Scholar] [CrossRef] [PubMed]
- Jarad, G.; Cunningham, J.; Shaw, A.S.; Miner, J.H. Proteinuria precedes podocytes abnormalities in Lamb mice, implicating the glomerular basement membrane as an albumin barrier. J. Clin. Investig. 2006, 166, 2272–2297. [Google Scholar] [CrossRef] [PubMed]
- Jarad, G.; Miner, J.H. Update on the glomerular filtration barrier. Curr. Opin. Nephrol. Hypertens. 2009, 18, 226–232. [Google Scholar] [CrossRef] [PubMed]
- Abrahamson, D.R.; Wang, R. Development of the glomerular capillary and its basement membrane. In The Kidney. From Normal Development to Congenital Disease; Vize, P.D., Woolf, A.S., Bard, J.B.L., Eds.; Academic Press: Cambridge, MA, USA, 2003; pp. 221–249. [Google Scholar]
- Leung, J.C.K.; La, K.N.; Tang, S.C.W. Crosstalk between podocytes and tubular epithelial cells. Podocytopathy. Contrib. Nephrol. 2014, 183, 54–63. [Google Scholar]
- Holthöfer, H. Molecular architecture of the glomerular slit diaphragm: Lessons learnt for a better understanding of disease pathogenesis. Nephrol. Dial. Transplant. 2007, 22, 2124–2128. [Google Scholar]
- Satchell, S.C.; Braet, F. Glomerular endothelial cell fenestrations: An integral component of the glomerular filtration barrier. Am. J. Physiol. Ren. Physiol. 2009, 296, F947–F956. [Google Scholar] [CrossRef] [PubMed]
- Sekulic, M.; Sekulic, S.P. A compendium of urinary biomarkers indicative of glomerular podocytopathy. Pathol. Res. Int. 2013, 2013, 782395. [Google Scholar] [CrossRef] [PubMed]
- Hackl, M.J.; Burford, J.L.; Villanueva, K.; Lam, L.; Suszták, K.; Schermer, B.; Benzing, T.; Peti-Peterdi, J. Tracking the fate of glomerular epithelial cells in vivo using serial multiphoton imaging in novel mouse models with fluorescent lineage tags. Nat. Med. 2013, 19, 1661–1666. [Google Scholar] [CrossRef] [PubMed]
- Peti-Peterdi, J.; Kidokoro, K.; Riquier-Brison, A. Novel in vivo techniques to visualize kidney anatomy and function. Kidney Int. 2015, 88, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Chagnac, A.; Herskovitz, P.; Weinstein, T.; Elyashiv, S.; Hirsh, J.; Hammel, I.; Gafter, U. The peritoneal membrane in peritoneal dialysis patients: Estimation of its functional surface area by applying stereologic methods to computerized tomography scans. J. Am. Soc. Nephrol. 1999, 10, 342–346. [Google Scholar] [PubMed]
- Heilmann, M.; Neudecker, S.; Wolf, I.; Gubhaju, L.; Sticht, C.; Schock-Kusch, D.; Kriz, W.; Bertram, J.F.; Schad, L.R.; Gretz, N. Quantification of glomerular number and size distribution in normal rat kidneys using magnetic resonance imaging. Nephrol. Dial. Transplant. 2011, 27, 100–107. [Google Scholar] [CrossRef] [PubMed]
- Layton, A.T. Mathematical modeling of kidney transport. WIREs Syst Biol Med. 2013, 5, 557–573. [Google Scholar] [CrossRef] [PubMed]
- Layton, A.T. Modeling transport and flow regulatory mechanisms of the kidney. Int. Sch. Res. Netw. ISRN Biomath. 2012, 170594. [Google Scholar] [CrossRef] [PubMed]
- Deen, W.M. Hindered transport of large molecules in liquid-filled pores. AIChE J. 1987, 33, 1409–1425. [Google Scholar] [CrossRef]
- Rippe, B.; Haraldsson, B. Transport of macromolecules across microvascular walls: The two-pore theory. Physiol. Rev. 1994, 74, 163–219. [Google Scholar] [CrossRef] [PubMed]
- Deen, W.M. What determines glomerular capillary permeability? J. Clin. Investig. 2004, 114, 1412–1414. [Google Scholar] [CrossRef] [PubMed]
- Deen, W.M.; Bohrer, M.P.; Epstein, N.B. Effects of molecular size and configuration on diffusion in microporous membranes. AIChE 1981, 27, 952–959. [Google Scholar] [CrossRef]
- Deen, W.M.; Bridges, C.R.; Brenner, B.M.; Myers, B.D. Heteroporous model of glomerular size selectivity: Application to normal and nephrotic humans. Am. J. Physiol. 1985, 249, F374–F389. [Google Scholar] [CrossRef] [PubMed]
- Deen, W.M.; Lazzara, M.J.; Myers, B.D. Structural determinants of glomerular permeability. Am. J. Physiol. Ren. Physiol. 2001, 281, F579–F596. [Google Scholar] [CrossRef] [PubMed]
- Edwards, A. Modeling transport in the kidney: Investigating function and dysfunction. Am. J. Physiol. Ren. Physiol. 2010, 298, F475–F484. [Google Scholar] [CrossRef] [PubMed]
- Edwards, A.; Daniels, B.S.; Deen, W.M. Ultrastructural model for size selectivity in glomerular filtration. Am. J. Physiol. Ren. Physiol. 1999, 276, F892–F902. [Google Scholar] [CrossRef] [PubMed]
- Comper, W.D.; Haraldsson, B.; Deen, W.M. Resolved: Normal glomeruli filter nephrotic levels of albumin. J. Am. Soc. Nephrol. 2008, 19, 427–432. [Google Scholar] [CrossRef] [PubMed]
- Haraldsson, B.; Nystrom, J.; Deen, W.M. Properties of the glomerular barrier and mechanisms of proteinuria. Physiol. Rev. 2008, 88, 451–487. [Google Scholar] [CrossRef] [PubMed]
- Russo, L.M.; Sandoval, R.M.; McKee, M.; Osicka, T.M.; Collins, A.B.; Brown, D.; Molitoris, B.A.; Comper, W.D. The normal kidney filters nephrotic levels of albumin retrieved by proximal tubule cells: Retrieval is disrupted in nephrotic states. Kidney Int. 2007, 71, 504–513. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Wassenhove-McCarthy, D.J.; Yamaguchi, Y.; Holzman, L.B.; van Kuppevelt, T.H.; Jenniskens, G.J.; Wijnhoven, T.J.; Woods, A.C.; McCarthy, K.J. Loss of heparan sulfate glycosaminoglycan assembly in podocytes does not lead to proteinuria. Kidney Int. 2008, 74, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Jeansson, M.; Haraldsson, B. Morphological and functional evidence for an important role of the endothelial cell glycocalyx in the glomerular barrier. Am. J. Physiol. Ren. Physiol. 2006, 290, F111–F116. [Google Scholar] [CrossRef] [PubMed]
- Harvey, S.J.; Miner, J.H. Revisiting the glomerular charge barrier in the molecular era. Curr. Opin. Nephrol. Hypertens. 2008, 17, 393–398. [Google Scholar] [CrossRef] [PubMed]
- Greive, K.A.; Nikolic-Paterson, D.J.; Guimaraes, M.A.; Nikolovski, J.; Pratt, L.M.; Mu, W.; Atkins, R.C.; Comper, W.D. Glomerular perselectivity factors are not responsible for the increase in fractional clearance of albumin in rat glomerulonephritis. Am. J. Pathol. 2001, 159, 1159–1170. [Google Scholar] [CrossRef]
- Asgeirsson, D.; Venturoli, D.; Fries, E.; Rippe, B.; Rippe, C. Glomerular sieving of three neutral polysaccharides, polyethylene oxide and bikunin in rat. Effects of molecular size and conformation. Acta Physiol. 2007, 196, 237–246. [Google Scholar] [CrossRef] [PubMed]
- Asgeirsson, D.; Axelsson, J.; Rippe, C.; Rippe, B. Similarity of permeabilities for Ficoll pullulan, charge-modified albumin and native albumin across the rat peritoneal membrane. Acta Physiol. 2009, 196, 427–433. [Google Scholar] [CrossRef] [PubMed]
- Slattery, C.; Lee, A.; Zhang, Y.; Kelly, D.J.; Thorn, P.; Nikolic-Paterson, D.J.; Tesch, G.H.; Poronnik, P. In vivo visualization of albumin degradation in the proximal tubule. Kidney Int. 2008, 74, 1480–1486. [Google Scholar] [CrossRef] [PubMed]
- Axelsson, J.; Sverrisson, K.; Rippe, A.; Fissell, W.; Rippe, B. Reduced diffusion of charge-modified, conformationally intact anionic Ficoll relative to neutral Ficoll across the rat glomerular filtration barrier. J. Membr. Sci. 2012, 301, F708–F712. [Google Scholar] [CrossRef] [PubMed]
- Axelsson, J.; Öberg, C.M.; Rippe, A.; Krause, B.; Rippe, B. Size-selectivity of a synthetic high-flux and a high cut-off dialyzing membrane compared to that of the rat glomerular filtration barrier. J. Membr. Sci. 2012, 413, 29–37. [Google Scholar] [CrossRef]
- Venturoli, D.; Rippe, B. Ficoll and dextran vs. globular proteins as probes for testing glomerular permselectivity: Effects of molecular size, shape, charge, and deformability. Am. J. Physiol. Ren. Physiol. 2005, 288, F605–F613. [Google Scholar] [CrossRef] [PubMed]
- Rippe, C.; Asgeirsson, D.; Venturoli, D.; Rippe, A.; Rippe, B. Effects of glomerular filtration rate on Ficoll sieving coefficients (θ) in rats. Kidney Int. 2006, 69, 1326–1332. [Google Scholar] [CrossRef] [PubMed]
- Öberg, C.M.; Rippe, B. Quantification of the electrostatic properties of the glomerular filtration barrier modeled as a charged fiber matrix separating anionic from neutral Ficoll. Am. J. Ren. Physiol. 2013, 304, F781–F787. [Google Scholar] [CrossRef] [PubMed]
- Öberg, C.M.; Rippe, B. A distributed two-pore model: Theoretical implications and practical application to the glomerular sieving of Ficoll. Am. J. Physiol. Ren. Physiol. 2014, 306, F844–F854. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Öberg, C.M. Counterpoint: Defending pore theory. Perit. Dial. Int. 2015, 35, 9–13. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Davies, S. Permeability of peritoneal and glomerular capillaries: What are the differences according to pore theory? Perit. Dial. Int. 2011, 31, 249–258. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B. A three-pore model of peritoneal transport. Perit. Dial. Int. 1993, 13, S35–S38. [Google Scholar] [PubMed]
- Devuyst, O.; Rippe, B. Water transport across the peritoneal membrane. Kidney Int. 2014, 85, 750–758. [Google Scholar] [CrossRef] [PubMed]
- Devuyst, O.; Ni, J. Aquaporin-1 in the peritoneal membrane: Implications for water transport across capillaries and peritoneal dialysis. Biochim. Biophys. Acta 2005, 1758, 1078–1084. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Freichel, M.; van der Hoeven, F.; Nawroth, P.P.; Katus, H.; Kälble, F.; Zitron, E.; Schwenger, V. Novel endothelial cell-specific AQP1 knockout mice confirm the crucial role of endothelial AQP1 in ultrafiltration during peritoneal dialysis. PLoS ONE 2016, 11, e0145513. [Google Scholar] [CrossRef] [PubMed]
- Agre, P.; Kozono, D. Aquaporin water channels: Molecular mechanisms for human diseases. FEBS Lett. 2003, 555, 72–78. [Google Scholar] [CrossRef]
- Endeward, V.; Musa-Aziz, R.; Cooper, G.J.; Chen, L.M.; Pelletier, M.F.; Virkki, L.V.; Supuran, C.T.; King, L.S.; Boron, W.F.; Gros, G. Evidence that aquaporin1 is a major pathway for CO2 transport across the human erythrocyte membrane. FASEB J. 2006, 20, 1974–1981. [Google Scholar] [CrossRef] [PubMed]
- Ripoche, P.; Goossens, D.; Devuyst, O.; Gane, P.; Colin, Y.; Verkman, A.S.; Cartron, J.P. Role of RhAG and AQP1 in NH3 and CO2 gas transport in red cell ghosts: A stopped-flow analysis. Transf. Clin. Biol. 2006, 13, 117–122. [Google Scholar] [CrossRef] [PubMed]
- Missner, A.; Kügler, P.; Saparov, S.M.; Sommer, K.; Mathai, J.C.; Zeidel, M.L.; Pohl, P. Carbon dioxide transport through membranes. J. Biol. Chem. 2008, 37, 25340–25347. [Google Scholar] [CrossRef] [PubMed]
- Hub, J.S.; Grubmüller, H.; de Groot, B.L. Dynamics and energetics of permeation through aquaporins. What do we learn from molecular dynamics simulations? Handb. Exp. Pharmacol. 2009, 190, 57–76. [Google Scholar]
- Verkman, A.C. Aquaporins at a glance. J. Cell. Sci. 2011, 124, 2107–2112. [Google Scholar] [CrossRef] [PubMed]
- Verkman, A.C. Dissecting the role of aquaporins in renal pathophysiology using transgenic mice. Semin. Nephrol. 2008, 28, 217–226. [Google Scholar] [CrossRef] [PubMed]
- Noda, Y.; Sohara, E.; Ohta, E.; Sasaki, S. Aquaporins in kidney pathophysiology. Nat. Rev. Nephrol. 2010, 6, 168–178. [Google Scholar] [CrossRef] [PubMed]
- Day, R.E.; Kitchen, P.; Owen, D.S.; Bland, C.; Marshall, L.; Conner, A.C.; Bill, R.M.; Conner, M.T. Human aquaporins: Regulators of transcellular water flow. Biochim. Biophys. Acta 2014, 1840, 1492–1506. [Google Scholar] [CrossRef] [PubMed]
- Agre, P. Aquaporin water channels (Nobel Lecture). Angew. Chem. Int. Ed. Engl. 2004, 43, 4278–4290. [Google Scholar] [CrossRef] [PubMed]
- Verkman, A.C. Roles of aquaporins in kidney revealed by transgenic mice. Semin. Nephrol. 2006, 26, 200–208. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, S.; Frøkiær, J.; Marples, D.; Kwon, T.H.; Agre, P.; Kneppe, M.A. Aquaporins in the kidney: From molecules to medicine. Physiol. Rev. 2002, 82, 205–244. [Google Scholar] [CrossRef] [PubMed]
- Ni, J.; Verbavatz, J.-M.; Rippe, A.; Boisdé, I.; Moulin, P.; Rippe, B.; Verkman, A.S.; Devuyst, O. Aquaporin-1 plays an essential role in water permeability and ultrafiltration during peritoneal dialysis. Kidney Int. 2006, 69, 1518–1525. [Google Scholar] [CrossRef] [PubMed]
- Devuyst, O.; Yool, A.J. Aquaporin-1: New developments and perspectives for peritoneal dialysis. Perit. Dial. 2010, 30, 135–141. [Google Scholar] [CrossRef] [PubMed]
- Denker, B.M.; Smith, B.L.; Kuhajda, F.P.; Agre, P. Identification, purification, and partial characterization of a novel Mr 28,000 integral membrane protein from erythrocytes and renal tubules. J. Biol. Chem. 1988, 263, 15634–15642. [Google Scholar] [PubMed]
- Brown, D. The discovery of water channels (aquaporins). Ann. Nutr. Metab. 2017, 70, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Morelle, J.; Devuyst, O. Water and solute transport across the peritoneal membrane. Curr. Opin. Nephrol. Hypertens. 2015, 24, 434–443. [Google Scholar] [CrossRef] [PubMed]
- Morelle, J.; Amadou Sow, A.; Vertommen, D.; Jamar, F.; Rippe, B.; Devuyst, O. Quantification of osmotic water transport in vivo using fluorescent albumin. Am. J. Physiol. Ren. Physiol. 2014, 307, F981–F989. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Folkesson, H.G.; Yang, J.; Matthay, M.A.; Verkman, A.S. Reduced osmotic water permeability of the peritoneal barrier in aquaporin-1 knockout mice. Am. J. Physiol. 1999, 276, C76–C81. [Google Scholar] [CrossRef] [PubMed]
- Flessner, M. Water-only pores and peritoneal dialysis. Kidney Int. 2006, 69, 1494–1495. [Google Scholar] [CrossRef] [PubMed]
- King, L.S.; Moon, C.; Agre, P. Aquaporin-1 water channel protein in lung: Ontogeny, steroid-induced expression, and distribution in rat. J. Clin. Investig. 1996, 97, 2183–2191. [Google Scholar] [CrossRef] [PubMed]
- Stoenoiu, M.S.; Ni, J.; Verkaeren, C.; Debaix, H.; Janas, J.C.; Lameire, N.; Varbavatz, J.-M.; Devuyst, O. Corticosteroids induce expression of aquaporin-1 and induce transcellular water transport in rat peritoneum. J. Am. Soc. Nephrol. 2003, 14, 555–565. [Google Scholar] [CrossRef] [PubMed]
- Zomot, E.; Bakan, A.; Shrivastava, I.H.; DeChancie, J.; Lezon, T.R.; Bahar, I. Sodium-coupled Secondary Transporters: Insights from Structure-based Computations. In Molecular Machines; Roux, B., Ed.; World Scientific Publishing Co. Pte. Ltd: Singapore, 2011; pp. 199–230. [Google Scholar]
- Umenishi, F.; Schrier, R.W. Hypertonicity-induced aquaporin-1 (AQP1) expression is mediated by the activation of MAPK pathways and hypertonicity-responsive element in the AQP1 gene. J. Biol. Chem. 2003, 278, 15765–15770. [Google Scholar] [CrossRef] [PubMed]
- Belkacemi, L.; Beall, M.H.; Magee, T.R.; Pourtemou, M.; Ross, M.G. AQP1 gene expression is upregulated by arginine vasopressin and cyclic AMP agonists in trophoblast cells. Life Sci. 2008, 82, 1272–1280. [Google Scholar] [CrossRef] [PubMed]
- Bouley, R.; Palomino, Z.; Tang, S.S.; Nunes, P.; Kobori, H.; Lu, H.A.; Shum, W.W.; Sabolic, I.; Brown, D.; Ingelfinger, J.R.; et al. Angiotensin II and hypertonicity and hypertonicity modulate proximal tubular aquaporin 1 expression. Am. J. Physiol. Ren. Physiol. 2009, 297, F1575–F1586. [Google Scholar] [CrossRef] [PubMed]
- Krediet, R.T. The physiology of peritoneal solute transport and ultrafiltration. In Textbook of Peritoneal Dialysis; Gokal, R., Khanna, R., Krediet, R.T., Nolph, K.D., Eds.; Kluwer: Dordrecht, The Netherlands, 2000; pp. 135–172. [Google Scholar]
- Cnossen, T.T.; Smit, W.; Konings, C.J.A.M.; Kooman, J.P.; Leunissen, K.M.; Krediet, R.T. Quantification of free water transport during the peritoneal equilibration test. Perit Dial. Int. 2009, 29, 523–527. [Google Scholar] [PubMed]
- Twardowski, Z.J.; Nolph, K.D.; Khanna, R.; Prowant, B.F.; Ryan, L.P.; Moore, H.L.; Nielsen, M.P. Peritoneal equilibration test. Perit. Dial. Bull. 1987, 7, 138–147. [Google Scholar]
- Twardowski, Z.I. Clinical value of standardized equilibration tests in CAPD patients. Blood Purif. 1989, 7, 95–108. [Google Scholar] [CrossRef] [PubMed]
- Krediet, R.T.; Lindholm, B.; Rippe, B. Pathophysiology of peritoneal membrane failure. Perit. Dial. Int. 2000, 20, S22–S42. [Google Scholar] [PubMed]
- LaMilia, V.; Di Filippo, S.; Crepaldi, M.; Del Vecchio, L.; Dell’oro, C.; Andrulli, S.; Locatelli, F. Mini-peritoneal equilibration test: A simple and fast method to assess free water and small solute transport across the peritoneal membrane. Kidney Int. 2005, 68, 840–846. [Google Scholar] [CrossRef] [PubMed]
- Parikova, A.; Watske, S.; Struijk, D.G.; Machteld, M.; Krediet, R.T. The contribution of free water transport and small pore transport to the total fluid removal in peritoneal dialysis. Kidney Int. 2005, 68, 1849–1856. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Stelin, G. Simulations of peritoneal solute transport during CAPD. Applications of two-pore formalism. Kidney Int. 1989, 35, 1234–1244. [Google Scholar] [CrossRef] [PubMed]
- Asghar, R.B.; Davies, S.J. Pathways of fluid transport and reabsorption across the peritoneal membrane. Kidney Int. 2008, 73, 1048–1053. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Venturoli, D. Fluid loss from the peritoneal cavity by back-filtration through the small pores of the three-pore model. Kidney Int. 2008, 73, 985–986. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, S.; DiGiovanni, S.R.; Christensen, E.I.; Knepper, M.A.; Harris, H.W. Cellular and subcellular immunolocalization of vasopressin regulated water channel in rat kidney. Proc. Natl. Acad. Sci. USA 1993, 90, 11663–11667. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, S.; Kwon, T.H.; Christensen, B.M.; Promeneur, D.; Frøkiær, J.; Marples, D. Physiology and pathophysiology of renal aquaporins. J. Am. Nephrol. 1999, 10, 647–663. [Google Scholar] [CrossRef]
- Kishore, B.K.; Mandon, B.; Oza, N.B.; DiGiovanni, S.R.; Coleman, R.A.; Ostrowski, N.L.; Wade, J.B.; Knepper, M.A. Rat renal arcade segment expresses vasopressin-regulated water channel and vasopressin V2 receptor. J. Clin. Investig. 1996, 97, 2763–2771. [Google Scholar] [CrossRef] [PubMed]
- Me, P.; Taylor, A. Effect of nocodazole on the water permeability response to vasopressin in rabbit collecting tubules perfused in vitro. J. Physiol. (Lond.) 1989, 411, 529–544. [Google Scholar]
- Knepper, M.A. Molecular physiology of urinary concentrating mechanism: Regulation of aquaporin water channels by vasopressin. Am. J. Physiol. Ren. Physiol. 1997, 272, F3–F12. [Google Scholar] [CrossRef] [PubMed]
- Loffing, J.; Loffing-Cueni, D.; Macher, A.; Hebert, S.C.; Olson, B.; Knepper, M.A.; Rossier, B.C.; Kaissling, B. Localization of epitheliasodium channel and aquaporin-2 in rabbit kidney cortex. Am. J. Physiol. Ren. Physiol. 2000, 278, F530–F539. [Google Scholar] [CrossRef] [PubMed]
- Aguirre, A.R.; Abensu, H. Physiology of fluid and solute transport across the peritoneal membrane. J. Bras. Nefrol. 2014, 36, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Katz, M.A.; Schaeffer, R.C.; Gratrix, M.; Mucha, D.; Cárbajal, J. The glomerular barrier fits a two –pore-and-fiber-matrix model: Derivation and physiologic test. Microvasc. Res. 1999, 57, 227–243. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B. Free water transport, small pore transport and the osmotic pressure gradient three-pore model of peritoneal transport. Nephrol. Dial. Transplant. 2008, 23, 2147–2153. [Google Scholar] [CrossRef] [PubMed]
- Fu, B.M.; Curry, F.E.; Weinbaum, S. A diffusion wake model for tracer ultrastructure-permeability studies in microvessels. Am. J. Physiol. 1995, 269, H2124–H2140. [Google Scholar] [CrossRef] [PubMed]
- Henry, C.B.S.; Duling, B.R. TNF-alpha increases entry of macromolecules into luminal endothelial cell glycocalyx. Am. J. Physiol. 2000, 279, H2815–H2823. [Google Scholar]
- Kedem, O.; Katchalsky, A. Thermodynamic analysis of the permeability of biological membranes to nonelectrolytes. Biochim. Biophys. Acta 1958, 27, 229–246. [Google Scholar] [CrossRef]
- Kedem, O.; Katchalsky, A. A physical interpretation of the phenomenological coefficients of membrane permeability. J. Gen. Physiol. 1961, 45, 143–179. [Google Scholar] [CrossRef] [PubMed]
- Kedem, O.; Katchalsky, A. Permeability of composite membranes. Trans. Faraday Soc. 1963, 59, 1918–1954. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. Part, I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Kotyk, A.; Janáček, K. Cell membrane Transport. Principles and Techniques, 2nd ed.; Plenum Press: New York, NY, USA, 1975. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical physics. In Course of Theoretical Physics, 3rd ed.; Elsevier: Oxford, UK, 2009; Volume 5. [Google Scholar]
- Garlick, D.G.; Renkin, E.M. Transport of large molecules from plasma to interstitial fluid and lymph in dogs. Am. J. Physiol. Scand. 1970, 104, 1595–1605. [Google Scholar] [CrossRef] [PubMed]
- Renkin, E.M. Transport of large molecules across capillary walls. Physiologist 1964, 7, 13–28. [Google Scholar]
- Renkin, E.M. Capillary transport of macromolecules: Pores and other endothelial pathways. J. Appl. Physiol. 1985, 58, 315–325. [Google Scholar] [CrossRef] [PubMed]
- Tencer, J.; Frick, I.M.; Öqvist, B.W.; Alm, P.; Rippe, B. Size-selectivity of the glomerular barrier to high molecular weight proteins: Upper size limitations of shunt pathways. Kidney Int. 1998, 53, 709–715. [Google Scholar] [CrossRef] [PubMed]
- Bark, B.P.; Öberg, C.M.; Grände, P.O. Plasma volume expansion by 0.9% NaCl during sepsis/SIRS, after hemorrhage, and during a normal state. Shock 2013, 40, 59–64. [Google Scholar] [CrossRef] [PubMed]
- Miller, N.E.; Michel, C.C.; Nanjee, M.N.; Olszewski, W.L.; Miller, I.P.; Hazell, M.; Olivecrona, G.; Sutton, P.; Humphreys, S.M.; Frayn, K.N. Secretion of adipokines by human adipose tissue in vivo: Partitioning between capillary and lymphatic transport. Am. J. Physiol. Endocrinol. Metab. 2011, 301, E659–E667. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.E.; Granger, D.N.; Brace, R.A. Analysis of lymphatic protein flux data. I. Estimation of the reflection coefficient and permeability surface area product for total protein. Microvasc. Res. 1977, 13, 297–313. [Google Scholar] [CrossRef]
- Ibrahim, R.; Nitsche, J.M.; Kasting, G.B. Dermal clearance model for epidermal bioavailability calculations. J. Pharm. Sci. 2012, 101, 2094–2108. [Google Scholar] [CrossRef] [PubMed]
- Arturson, G.; Groth, T.; Grotte, G. Human glomerular membrane porosity and filtration pressure: Dextrane clearance data analysed by theoretical models. Clin. Sci. 1971, 40, 137–158. [Google Scholar] [CrossRef] [PubMed]
- Blouch, K.; Deen, W.M.; Fauvel, J.P.; Bialek, J.; Derby, G.; Myers, B.D. Molecular configuration and glomerular size selectivity in healthy and nephrotic humans. Am. J. Physiol. Ren. Physiol. 1985, 249, F373–F389. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Haraldsson, B. Fluid and protein fluxes across small and large pores in the microvasculature. Application of two-pore equations. Acta Physiol. Scand. 1987, 131, 411–428. [Google Scholar] [CrossRef] [PubMed]
- Renkin, E.M. Relation of capillary morphology to transport of fluid and large molecules: A review. Acta Physiol. Scand. Suppl. 1979, 463, 81–91. [Google Scholar] [PubMed]
- Renkin, E.M. Some consequences of capillary permeability to macromolecules: Starling’s hypothesis reconsidered. Am. J. Physiol. 1986, 250, H705–H710. [Google Scholar] [CrossRef] [PubMed]
- Renkin, E.M.; Joyner, W.L.; Sloop, C.H.; Watson, P.D. Influence of venous pressure on plasma-lymph transport in the dog’s paw: Convective and dissipative mechanisms. Microvasc. Res. 1977, 14, 191–204. [Google Scholar] [CrossRef]
- Renkin, E.M.; Watson, P.D.; Sloop, W.M.; Curry, F.E. Transport pathways for fluid and large molecules in miscovascular endothelium of the dog’s paw. Microvasc. Res. 1977, 14, 205–214. [Google Scholar] [CrossRef]
- Perl, W. Convection and permeation of albumin between plasma and interstitium. Microvasc. Res. 1975, 10, 83–94. [Google Scholar] [CrossRef]
- Lund, U.; Rippe, A.; Venturoli, D.; Tenstad, O.; Grubb, A.; Rippe, B. Glomerular filtration rate dependence of sieving of albumin and some neutral proteins in rat kidneys. Am. J. Physiol. Ren. Physiol. 2003, 284, F1226–F1234. [Google Scholar] [CrossRef] [PubMed]
- Öberg, C.M.; Groszek, J.J.; Roy, S.; Fissell, W.H.; Rippe, B. A distributed solute model: An extended two-pore model with application to the glomerular sieving of Ficoll. Am. J. Physiol. Ren. Physiol. 2017, 3, F475–F484. [Google Scholar] [CrossRef] [PubMed]
- Zydney, A.L.; Aimar, P.; Meireles, M.; Pimbley, J.M.; Belfort, G. Use of the log-normal probability density function to analyze membrane pore size distributions: Functional forms and discrepancies. J. Membr. Sci. 1994, 9, 293–298. [Google Scholar] [CrossRef]
- Haraldsson, B. Assessing the peritoneal dialysis capacities of individual patients. Kidney Int. 1995, 47, 1187–1198. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Stelin, G.; Haraldsson, B. Computer simulations of peritoneal fluid transport in CAPD. Kidney Int. 1991, 40, 315–325. [Google Scholar] [CrossRef] [PubMed]
- Devuyst, O.; Goffin, E. Water and solute transport in peritoneal dialysis: Models and clinical applications. Nephrol. Dial. Transplant. 2008, 23, 2120–2123. [Google Scholar] [CrossRef] [PubMed]
- Vonesh, E.F.; Rippe, B. Net fluid absorption under membrane transport models of peritoneal dialysis. Blood Purif. 1992, 10, 209–226. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Venturoli, D.; Simonsen, O.; de Arteaga, J. Fluid and electrolyte transport across the peritoneal membrane during CAPD according to the three-pore model. Perit. Dial. Int. 2004, 24, 10–27. [Google Scholar] [PubMed]
- Freida, P.; Galach, M.; Divino Filho, J.C.; Werynski, A.; Lindholm, B. Combination of crystalloid (glucose) and colloid (icodextrin) osmotic agents markedly enhances peritoneal fluid and solute transport during the long PD dwell. Perit. Dial. Int. 2007, 27, 267–276. [Google Scholar] [PubMed]
- Rippe, B.; Levin, L. Computer simulations of ultrafiltration profiles for an icodextrin-based peritoneal fluid in CAPD. Kidney Int. 2000, 57, 2546–2556. [Google Scholar] [CrossRef] [PubMed]
- Öberg, C.M.; Rippe, B. Optimizing automated peritoneal dialysis using an extended 3-pore model. Kidney Int. Rep. 2017, 2, 943–951. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Stelin, G.; Ahlmen, J. Lymph flow from the peritoneal cavity in CAPD patients. In Frontiers in Peritoneal Dialysis; Maher, J.F., Winchester, J.F., Eds.; Springer: New York, NY, USA, 1986; pp. 24–30. [Google Scholar]
- Rippe, B.; Krediet, R.T. Peritoneal physiology-transport of solutes. In The Textbook of Peritoneal Dialysis; Springer: Berlin/Heidelberg, Germany, 1994; pp. 69–113. [Google Scholar]
- Polyakov, Y.S.; Zydney, A.L. Ultrafiltration membrane performance: Effects of pore blockage/constriction. J. Membr. Sci. 2013, 434, 106–120. [Google Scholar] [CrossRef]
- Hermia, J. Constant pressure blocking filtration laws–application to power-law non-Newtonian fluids. Trans. Inst. Chem. Eng.–Lond. 1982, 60, 183–187. [Google Scholar]
- Hermia, J. Blocking filtration. Application to Non-Newtonian fluids. In Mathematical Models and Design Methods in Solid-Liquid Separation; Rushton, A., Ed.; Martinus Nijhoff Publishers: Boston, MA, USA, 1985; pp. 83–89. [Google Scholar]
- Santos, A.; Bedrikovetsky, P. A stochastic model for particulate suspension flow in porous media. Transp. Porous Media 2006, 62, 25–53. [Google Scholar] [CrossRef]
- Santos, A.; Bedrikovetsky, P.; Fontoura, S. Analytical micro model for size exclusion: Pore blocking and permeability reduction. J. Membr. Sci. 2008, 308, 115–127. [Google Scholar] [CrossRef]
- Mehta, A.; Zydney, A.L. Permeability and selectivity analysis for ultrafiltration membranes. J. Membr. Sci. 2005, 249, 245–249. [Google Scholar] [CrossRef]
- Mehta, A.; Zydney, A.L. Effect of membrane charge on flow and protein transport during ultrafiltration. Biotechnol. Progr. 2006, 22, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Zydney, A.L. High performance ultrafiltration membranes: Pore geometry and charge effects, membrane science and technology. In Inorganic, Polymeric, and Composite Membranes: Structure, Function, and Other Correlations, Part of Membrane Science and Technology Series; Oyama, S.T., Stagg-Williams, S.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 14, pp. 333–352. [Google Scholar]
- Kanani, D.M.; Fissel, W.H.; Roy, S.; Dubnisheva, A.; Fleishman, A.; Zydney, A. Permeability–selectivity analysis for ultrafiltration: Effect of pore geometry. J. Membr. Sci. 2010, 349, 405–410. [Google Scholar] [CrossRef] [PubMed]
- Armatas, G.S.; Salmas, C.E.; Louloudi, M.; Androutsopoulos, G.P.; Pomonis, P.J. Relationships among pore size, connectivity, dimensionality of capillary condensation, and pore structure tortuosity of functionalized mesoporous silica. Langmuir 2003, 19, 3128–3136. [Google Scholar] [CrossRef]
- Armatas, G.S. Determination of the effects of the pore size distribution and pore connectivity distribution on the pore tortuosity and diffusive transport in model porous networks. Chem. Eng. Sci. 2006, 61, 4662–4675. [Google Scholar] [CrossRef]
- Ronco, C.; Ghezzi, P.M.; Bowry, S.R. Membranes for hemodialysis. In Replacement of Renal Function by Dialysis, 5th revised ed.; Hörl, W.H., Koch, K.M., Lindsay, R.M., Ronco, C., Winchester, J.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 301–323. [Google Scholar]
- Aoyagi, S.; Abe, K.; Yamagishi, T.; Iwai, H.; Yamaguchi, S.; Sunohara, T. Evaluation of blood adsorption onto dialysis membranes by time-of-flight secondary ion mass spectrometry and near-filed infrared microscopy. Anal. Bioanal. Chem. 2017, 409, 6387–6396. [Google Scholar] [CrossRef] [PubMed]
- Ochoa, N.A.; Prádanos, P.; Palacio, L.; Pagliero, C.; Marchese, J.; Hernández, A. Pore size distributions based on AFM imaging and retention of multidisperse polymer solutes: Characterisation of polyethersulfone UF membranes with dopes containing different PVP. J. Membr. Sci. 2001, 187, 227–237. [Google Scholar] [CrossRef]
- Feinberg, B.J.; Hsiao, J.C.; Park, J.; Zydney, A.L.; Fissell, W.H.; Roy, S. Slit pores preferred over cylindrical pores for high selectivity in biomolecular filtration. J. Colloid Interface Sci. 2018, 517, 176–181. [Google Scholar] [CrossRef] [PubMed]
- Ileri, N.; Létant, S.E.; Palazoglu, A.; Stroeve, P.; Tringe, J.W.; Faller, R. Mesoscale simulations of biomolecular transport through nanofilters with tapered and cylindrical geometries. Phys. Chem. Chem. Phys. 2012, 21, 15066–15077. [Google Scholar] [CrossRef] [PubMed]
- Hedayat, A.; Szpunar, J.; Kiran Kumar, N.A.P.; Peace, R.; Elmoselhi, H.; Shoker, A. Morphological characterization of the polyflux 210H hemodialysis filter pores. Int. J. Nephrol. 2012, 304135. [Google Scholar] [CrossRef] [PubMed]
- Ronco, C.; Clark, W.R. Haemodialysis membranes. Nat. Rev. Nephrol. 2018, 14, 394–410. [Google Scholar] [CrossRef] [PubMed]
- Kim, A.S.; Chen, H. Diffusive tortuosity factor of solid and soft cake layers: A random walk simulation approach. J. Membr. Sci. 2006, 279, 129–139. [Google Scholar] [CrossRef]
- Kokubo, K.-I.; Sakai, K. Evaluation of dialysis membranes using a tortuous pore model. AlChE J. 1998, 44, 2607–2620. [Google Scholar] [CrossRef]
- Kazuhiko, I.; Fukumoto, K.; Iwasaki, Y. Modification of polysulfone with phospholipid polymer for improvement of the blood compatibility. Part 1. Surface characterization. Biomaterials 1999, 20, 1545–1551. [Google Scholar]
- Xie, B.; Zhang, R.; Zhang, H.; Xu, A.; Deng, Y.; Ly, Y.; Deng, F.; Wei, S. Decoration of heparin and bovine serum albumin on polysulfone membrane assisted via polydopamine strategy for hemodialysis. J. Biomater. Sci. Polym. Ed. 2016, 27, 880–897. [Google Scholar] [CrossRef] [PubMed]
- Yua, H.; Caoa, Y.; Kanga, G.; Liua, J.; Lia, M.; Yuana, Q. Enhancing antifouling property of polysulfone ultrafiltration membrane by grafting zwitterionic copolymer via UV-initiated polymerization. J. Membr. Sci. 2009, 342, 6–13. [Google Scholar] [CrossRef]
- Wisniewski, N.; Moussy, F.; Reichert, W.M. Characterization of implantable biosensor membrane biofouling. Fresenius J. Anal. Chem. 2000, 366, 611–621. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; He, C.; Huiyuan, W.; Baihai, S.; Shudong, S.; Changsheng, Z. Improved antifouling property of polyethersulfone hollow fiber membranes using additive of poly(ethylene glycol) methyl ether-b-poly(styrene) copolymers. Ind. Eng. Chem. Res. 2011, 50, 3295–3303. [Google Scholar] [CrossRef]
- Zhao, W.; Huang, J.; Fang, B.; Nie, S.; Yi, N.; Su, B.; Li, H.; Zhao, C. Modification of polyethersulfone membrane by blending semi-interpenetrating network polymeric nanoparticles. J. Membr. Sci. 2011, 369, 258–266. [Google Scholar] [CrossRef]
- Yin, Z.; Cheng, C.; Qin, H.; Nie, C.; He, C.; Zhao, C. Hemocompatible polyethersulfone/polyurethane composite membrane for high-performance antifouling and antithrombotic dialyzer. J. Biomed. Mater. Res. Part B 2015, 103B, 97–105. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Song, H.; Wang, J.; Xue, L. Polysulfone hemodiafiltration membranes with enhanced antofouling and hemocompatibility modified by poly(vinyl pyrrolidone) via in situ cross-linked polymerization. Mater. Sci. Eng. C Mater. Biol. Appl. 2017, 74, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Rana, D.; Matsura, T. Surface modifications for antifouling membranes. Chem. Rev. 2010, 110, 2448–2471. [Google Scholar] [CrossRef] [PubMed]
- Hinrichs, W.L.J.; Ten Hoopen, H.W.M.; Engbers, G.H.M.; Feijen, J. In vitro evaluation of heparinized Cuprophan hemodialysis membranes. J. Biomed. Mater. Res. 1997, 35, 443–450. [Google Scholar] [CrossRef]
- Shen, J.I.; Winkelmayer, W.C. Use and safety of unfractionated heparin for anticoagulation during maintenance hemodialysis. Am. J. Kidney Dis. 2012, 60, 473–486. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.I.; Montez-Rath, M.E.; Mitani, A.A.; Erickson, K.F.; Winkelmayer, W.C. Correlates and variance decomposition analysis of heparin dosing for maintenance hemodialysis in older US patients. Pharmacoepidemiol. Drug Saf. 2014, 23, 515–525. [Google Scholar] [CrossRef] [PubMed]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Kozeny, J. Ueber kapillare Leitung des Wassers im Boden. Sitzungsberichte Wiener Akademie 1927, 136, 271–306. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. Lond. 1937, 15, 1–17. [Google Scholar] [CrossRef]
- Klinkenberg, L.J. Analogy between diffusion and electrical conductivity in porous rocks. Bull. Geol. Soc. Am. 1951, 62, 559–564. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 2nd ed.; Clarendon Press: Oxford, UK, 1881; Volume I. [Google Scholar]
- Landau, L.D.; Lishitz, E.M. Electrodynamics of Continuous Media, Course of Theoretical Physics; Pergamon: Oxford, UK, 1960; Volume 8. [Google Scholar]
- Neale, G.H.; Nader, W.K. Prediction of transport processes within porous media: Diffusive flow processes within a homogeneous swarm of spherical particles. AIChe J. 1973, 19, 112–119. [Google Scholar] [CrossRef]
- Rayleigh, L. On the influence of obstacles arranged in rectangular order upon the properties of a medium. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1892, 34, 481–502. [Google Scholar] [CrossRef]
- Wagner, K.W. Erklärung der dielektrischen Nachwirkungsvorgänge auf Grund Maxwellscher Vorstellungen. Arch. Electrotechn. 1914, 2, 371–387. [Google Scholar] [CrossRef]
- Hizi, U.; Bergman, D.J. Molecular diffusion in periodic porous media. J. Appl. Phys. 2000, 87, 1704–1711. [Google Scholar] [CrossRef]
- Mitra, P.P.; Sen, P.N.; Schwartz, L.M. Short-time behavior of the diffusion coefficient as a geometrical probe of porous media. Phys. Rev. B 1993, 47, 8565–8574. [Google Scholar] [CrossRef]
- Bessis, M. Living Blood Cells and Their Ultrastructure; Springer: New York, NY, USA, 1973. [Google Scholar]
- Lipowsky, R.; Sackmann, E. Structure and Dynamics of Membranes: From Cells to Vesicles; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Evans, E.; Skalak, R. Mechanics and Thermodynamics of Biomembranes; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Discher, D.E.; Mohandas, N.; Evans, E.A. Molecular maps of red-cell deformation—hidden elasticity and in-situ connectivity. Science 1994, 266, 1032–1035. [Google Scholar] [CrossRef] [PubMed]
- Grzhibovskis, R.; Krämer, E.; Bernhardt, I.; Kemper, B.; Zanden, C.; Repin, N.V.; Tkachuk, B.V.; Voinova, M.V. Shape of red blood cells in contact with artificial surfaces. Eur. Biophys J. 2017, 46, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Zandén, C.; Voinova, M.; Gold, J.; Mörsdorf, D.; Bernhardt, I.; Liu, J. Surface characterization of oxygen plasma treated electrospun polyurethane fibres and their interaction with red blood cells. Eur. Polymer J. 2012, 48, 472–482. [Google Scholar] [CrossRef]
- Bernhardt, I.; Ivanova, L.; Langehanenberg, P.; Kemper, B.; von Bally, G. Application of digital holographic microscopy to investigate the sedimentation of intact red blood cells and their interaction with artificial surfaces. Bioelectrochemistry 2008, 73, 92–96. [Google Scholar] [CrossRef] [PubMed]
- Canham, P.B. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 1970, 26, 61–81. [Google Scholar] [CrossRef]
- Deuling, H.J.; Helfrich, W. The curvature elasticity of fluid membranes: A catalogue of vesicle shapes. J. Phys. France 1976, 37, 1335–1345. [Google Scholar] [CrossRef]
- Deuling, H.J.; Helfrich, W. The theoretical explanation of the myelin shapes of red blood cells. Blood Cells 1977, 3, 713–720. [Google Scholar]
- Deuling, H.J.; Helfrich, W. Red blood cell shapes as explained on the basis of curvature elasticity. Biophys. J. 1976, 16, 861–868. [Google Scholar] [CrossRef]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforsch. 1973, 28C, 693–703. [Google Scholar] [CrossRef]
- Sheetz, M.P.; Singer, S.J. Biological membranes as bilayer couples: A molecular mechanism of drug-erythrocyte interactions. Proc. Natl. Acad. Sci. USA 1974, 71, 4457–4461. [Google Scholar] [CrossRef] [PubMed]
- Svetina, S.; Brumen, M.; Žeks, B. Lipid bilayer elasticity and the bilayer couple interpretation of red cell shape transformations and lysis. Stud. Biophys. 1985, 110, 177–184. [Google Scholar]
- Svetina, S.; Ziherl, P. Morphology of small aggregates of red blood cells. Bioelectrochemistry 2008, 73, 84–91. [Google Scholar] [CrossRef] [PubMed]
- Larkin, T.J.; Kuchel, P.W. Mathematical models of naturally “morphed” human erythrocytes: Stomatocytes and echinocytes. Bull. Math. Biol. 2010, 72, 1323–1333. [Google Scholar] [CrossRef] [PubMed]
- Diez-Silva, M.; Dao, M.; Han, J.; Lim, C.T.; Suresh, S. Shape and biomechanical characteristics of human red blood cells in health and disease. MRS Bull. 2010, 35, 382–388. [Google Scholar] [CrossRef] [PubMed]
- Rudenko, S.V. Erythrocyte morphological states, phases, transitions and trajectories. Biochim. Biophys. Acta 2010, 1798, 1767–1778. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Adhesion of vesicles in two dimensions. Phys. Rev. A 1991, 43, 6803. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Configurations of fluid membranes and vesicles. Adv. Phys. 1997, 46, 13–137. [Google Scholar] [CrossRef]
- Muñoz, S.; Sebastián, J.L.; Sancho, M.; Álvarez, G. Elastic energy of the discocyte–stomatocyte transformation. Biochim. Biophys. Acta 2014, 1838, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, R.; Seifert, U. Adhesion of vesicles and membranes. Mol. Cryst. Liq. Cryst. 1991, 202, 17–25. [Google Scholar] [CrossRef]
- Seifert, U.; Lipowsky, R. Adhesion of vesicles. Phys. Rev. A 1990, 42, 4768. [Google Scholar] [CrossRef] [PubMed]
- Hägerstrand, H.; Mrowczynska, L.; Salzer, U.; Prohaska, R.; Michelsen, K.A.; Kralj-Iglič, V.; Iglič, A. Curvature-dependent lateral distribution of raft markers in the human erythrocyte membrane. Mol. Membr. Biol. 2006, 23, 277–288. [Google Scholar] [CrossRef] [PubMed]
- Sackmann, E.; Bruinsma, R.F. Cell adhesion as wetting transition? ChemPhysChem. 2002, 3, 262–269. [Google Scholar] [CrossRef]
- Sackmann, E.; Smith, A.-S. Physics of cell adhesion: Some lessons from cell-mimetic systems. Soft Matter 2014, 10, 1644–1659. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, M.M.; Markin, V.S. A theory of osmotic lysis of lipid vesicles. J. Theor. Biol. 1984, 109, 17–39. [Google Scholar] [CrossRef]
- Voinova, M.V. Phase transitions in mesoscopic spherical membranes. In Statistical Mechanics of Biocomplexity; Proceedings, Sitges, Barcelona; Lecture in Physics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 38–45. [Google Scholar]
- Chabanon, M.; Ho, J.C.S.; Liedberg, B.; Parikh, A.N.; Rangamani, P. Pulsatile lipid vesicles under osmotic stress. Biophys. J. 2017, 112, 1682–1691. [Google Scholar] [CrossRef] [PubMed]
- Shibly, A.S.U.; Ghatak, C.; Karal, S.M.A.; Moniruzzaman, M.; Yamazaki, M. Experimental estimation of membrane tension induced by osmotic pressure. Biophys J. 2016, 111, 2190–2201. [Google Scholar]
- Diz-Munõz, A.; Fletcher, D.A.; Weiner, O.D. Use the force: Membrane tension as an organizer of cell shape and motility. Trends Cell. Biol. 2013, 23, 47–53. [Google Scholar]
- Sackmann, E.; Merkel, R. Lehrbuch der Biophysik; Wiley-VCH Verlag: Weinheim, Germany, 2010. [Google Scholar]
- Lipowsky, R. From membranes to membrane machines. In Statistical Mechanics of Biocomplexity; Proceedings, Sitges, Barcelona; Lecture in Physics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 1–23. [Google Scholar]
- Sukumaran, S.; Seifert, U. Influence of shear flow on vesicles near a wall: A numerical study. Phys. Rev. E 2001, 64, 011916. [Google Scholar] [CrossRef] [PubMed]
- Waugh, R.E. Elastic energy of curvature-driven bump formation on red blood cell membrane. Biophys. J. 1996, 70, 1027–1035. [Google Scholar] [CrossRef]
- Iglič, A.; Kralj-Iglič, V.; Hägerstrand, H. Stability of speculated red blood cells induced by intercalation of amphiphiles in cell membrane. Med. Biol. Eng. Comput. 1998, 36, 251–255. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, R.; Lim, G.H.W.; Wortis, M. Echinocyte shape: Bending, stretching, and shear determine spicule shape and spacing. Biophys. J. 2002, 82, 1756–1772. [Google Scholar] [CrossRef]
- Lim, G.H.W.; Wortis, M.; Mukhopadhyay, R. Stomatocyte discocyte-echinocyte sequence of the human red blood cell: Evidence for the bilayer-couple hypothesis from membrane mechanics. Proc. Natl. Acad. Sci. USA 2002, 99, 16766–16769. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, M.M.; Markin, V.S. Model of red blood cell membrane skeleton. In Contemporary Problems of Biomechanics; Chernyi, G.C., Regirer, S.A., Eds.; CRC Publications: Grand Rapids, MI, USA, 1990. [Google Scholar]
- Park, Y.K.; Best, C.A.; Badizadegan, K.; Dasari, R.R.; Feld, M.S.; Kuriabova, T.; Henle, M.L.; Levine, A.J.; Popescu, G. Measurement of red blood cell mechanics during morphological changes. Proc. Natl. Acad. Sci. USA 2010, 107, 6731–6736. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Dao, M.; Lim, C.T.; Suresh, S. Spectrin-level modeling of the cytoskeleton and optical tweezers stretching of the erythrocyte. Biophys. J. 2015, 88, 3707–3719. [Google Scholar] [CrossRef] [PubMed]
- Discher, D.E.; Boal, D.H.; Boey, S.K. Simulations of the erythrocyte cytoskeleton at large deformation. II. Micropipette aspiration. Biophys. J. 1998, 5, 1584–1597. [Google Scholar] [CrossRef]
- Lim, G.H.W.; Wortis, M.; Mukhopadhyay, R. Red Blood Cell Shapes and Shape Transformations: Newtonian Mechanics of a Composite Membrane: Sections 2.1–2.4. In Soft Matter: Lipid Bilayers and Red Blood Cells; Viley–VHC Verlag: Weinheim, Germany, 2008; Volume 4. [Google Scholar]
- Khairy, K.J.; Foo, J.J.; Howard, J. Shapes of red blood cells: Comparison of 3D confocal images with the bilayer-couple model. Cell. Mol. Bioeng. 2010, 1, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Albu, R.M.; Avram, E.; Stoica, I.; Ionid, E.G.; Popovici, D.; Ioan, S. Surface properties and compatibility with blood of new quaternized polysulfones. J. Biomater. Nanobiotechnol. 2011, 2, 114–123. [Google Scholar] [CrossRef]
- Reinhart, W.H.; Piety, N.Z.; Goede, J.S.; Shevkoplyas, S.S. Effect of osmolality on erythrocyte rheology and perfusion of an artificial microvascular network. Microvasc. Res. 2015, 98, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Burns, J.M.; Yang, X.; Forouzan, O.; Sosa, J.M.; Shevkoplyas, S.S. Artificial microvascular network: A new tool for measuring rheologic properties of stored red blood cells. Transfusion 2012, 52, 1010–1023. [Google Scholar] [CrossRef] [PubMed]
- Shevkoplyas, S.S.; Yoshida, T.; Gifforda, S.C.; Bitensky, M.W. Direct measurement of the impact of impaired erythrocyte deformability on microvascular network perfusion in a microfluidic device. Lab Chip 2006, 6, 914–920. [Google Scholar] [CrossRef] [PubMed]
- Bleilevens, C.; Lölsberg, J.; Cinar, A.; Knoben, M.; Grottke, O.; Rossaint, R.; Wessling, M. Microfluidic cell sorting: Towards improved biocompatibility of extracorporeal lung assist devices. Sci. Rep. 2018, 8, 8031. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.J.; Lee, S.-J. In vitro and ex vivo measurement of the biophysical properties of blood using microfluidic platforms and animal models. Analyst 2018, 143, 2723–2749. [Google Scholar] [CrossRef] [PubMed]
- Suwanpayak, N.; Jalil, M.A.; Aziz, M.S.; Ismail, F.D.; Ali, J.; Yupapin, P.P. Blood cleaner on-chip design for artificial human kidney manipulation. Int. J. Nanomed. 2011, 6, 957–964. [Google Scholar]
- Lange, J.R.; Metzner, C.; Richter, S.; Schneider, W.; Spermann, M.; Kolb, T.; Whyte, G.; Fabry, B. Unbiased high-precision cell mechanical measurements with microconstrictions. Biophys. J. 2017, 112, 1472–1480. [Google Scholar] [CrossRef] [PubMed]
- Antonova, N.; Riha, P.; Ivanov, I. Time dependent variation of human blood conductivity as a method for an estimation of RBC aggregation. Clin. Hemorheol. Microcirc. 2008, 39, 69–78. [Google Scholar] [PubMed]
- Zhang, W.; Zhang, Y.S.; Bakht, S.M.; Aleman, J.; Shin, S.R.; Yue, K.; Sica, M.; Ribas, J.; Duchamp, M.; Ju, J.; et al. Elastomeric free-form blood vessels for interconnecting organs on chip systems. Lab Chip 2016, 16, 1579–1586. [Google Scholar] [CrossRef] [PubMed]
- Ronco, C. Hemodiafiltration: Technical and clinical issues. Blood Purif. 2015, 40, 2–11. [Google Scholar] [CrossRef] [PubMed]
- Canaud, B.; Bosc, I.Y.; Cabrol, L.; Leray-Moragues, H.; Navino, C.; Verzetti, G.; Thomaseth, K. Urea as a marker of adequacy in hemodialysis. Lesson from in vivo urea dynamics monitoring. Kidney Int. Suppl. 2000, 76, S28–S40. [Google Scholar] [CrossRef] [PubMed]
- Ahlmen, J. Quality of life of the dialysis patient. In Replacement of Renal Function by Dialysis, 5th revised ed.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3, pp. 1315–1332. [Google Scholar]
- Pereira, B.J.G.; Cheung, A.K. Complications of biocompatibility of hemodialysis membranes. In Complications of Dialysis; Lameire, N., Mehta, R.L., Eds.; Marcel Dekker: New York, NY, USA, 2000; pp. 41–51. [Google Scholar]
- Voinova, M.V.; Gorelik, L.Y.; Sokol, E.I. Sensors and bioelectronics in the kidney replacement therapy applications. Chapter 2. In Advances in Biosensors: Reviews; Yurish, S.Y., Ed.; International Frequency Sensor Association (IFSA) Publishing, S.L.: Barcelona, Spain, 2018; Volume 2, pp. 65–132. [Google Scholar]
- Koda, Y. Clinical benefits of high-performance membrane dialyzers. In High-Performance Membrane Dialyzers; Saito, A., Kawanishi, H., Yamashita, A.C., Mineshima, M., Eds.; Karger AG: Basel, Switzerland, 2011; pp. 58–69. [Google Scholar]
- Fernández, E.A.; Valtuille, R.; Balzarini, M. Artificial Neural Networks Applications in Dialysis. In Modeling and Control of Dialysis Systems; Volume 1: Modeling Techniques of Hemodialysis Systems; Azar, A.T., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1145–1179. [Google Scholar]
- Hoenich, N.A.; Ghezzi, P.M.; Ronco, C. Hemodialyzers and related devices. In Replacement of Renal Function by Dialysis; Hörl, W.H., Koch, K.M., Lindsay, R.M., Ronco, C., Winchester, J.F., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; Volume 2, pp. 273–299. [Google Scholar]
- Humes, H.D.; Fissell, W.H.; Tiranathanagul, K. The future of hemodialysis membranes. Kidney Int. 2006, 69, 1115–1119. [Google Scholar] [CrossRef] [PubMed]
- Gambro Healthcare/Diaverum. Available online: https://www.baxter.com (accessed on 21 February 2019).
- Fresenius. Available online: https://www.fresenius.com (accessed on 21 February 2019).
- Asahi Kasei. Available online: https://www.asahi-kasei.co.jp/asahi/en/ (accessed on 21 February 2019).
- Nephros. Available online: https://www.nephros.com (accessed on 21 February 2019).
- Bouré, T.; Vanholder, R. Which dialyser membrane to choose? Nephrol. Dialys. Transplant. 2004, 19, 293–296. [Google Scholar] [CrossRef]
- Barzin, J.; Feng, C.; Khulbe, K.C.; Matssura, T.; Madaeni, S.S.; Mirzadeh, H. Characterization of polyethersulfone hemodialysis membrane by ultrafiltration and atomic force microscopy. J. Membr. Sci. 2004, 237, 77–85. [Google Scholar] [CrossRef]
- Eloot, S.; De Wachter, D.; Vienken, J.; Pohlmeier, R.; Verdonck, P. In vitro evaluation of the hydraulic permeability of polysulfone dialysers. Int. J. Artif. Organs 2002, 25, 210–216. [Google Scholar] [CrossRef] [PubMed]
- Kaysen, G.A.; Zhu, F.; Sarkar, S.; Heymsfield, S.B.; Wong, J.; Kaitwatcharachai, C.; Kuhlmann, M.K.; Levin, N.W. Estimation of total-body and limb muscle mass in hemodialysis patients by using multifrequency bioimpedance spectroscopy. Am. J. Clin. Nutr. 2005, 82, 988–995. [Google Scholar] [CrossRef] [PubMed]
- Sanchidrián, S.G.; Gómez, P.J.L.; Álvarez, J.P.M.; Herrero, M.C.J.; Cerviño, I.C.; Domínguez, S.G. Reacción a membranas sintéticas en hemodiálisis. Nefrologia 2016, 36, 707–709. [Google Scholar]
- Kim, J.Y.; Lee, H.K.; Kim, S.C. Surface structure and phase separation of polysulfone membrane by atomic force microscopy. J. Membr. Sci. 1999, 163, 159–166. [Google Scholar] [CrossRef]
- Álvarez-de Lara, M.A.; Martín-Malo, A. Hypersensitivity reactions to synthetic haemodialysis membranes—An emerging issue? Nefrologia 2014, 413, 698–702. [Google Scholar]
- Šefer, S.; Vidović, L. Allergic reactions to polysulfone dialysis membranes—An old problem taking a new dimension? Acta Med. Croatica 2017, 71, 141–143. [Google Scholar]
- Vienken, J. Membranes in hemodialysis. In Membrane Technology; Volume 1: Membranes for Life Sciences; Peinemann, K.-V., Nunes, S.P., Eds.; Wiley-VCH Verlag: Weinheim, Germany, 2008. [Google Scholar]
- Corbatón-Báguena, M.-J.; Álvarez-Blanco, S.; Vincent-Vela, M.-C. Fouling mechanisms of ultrafiltration membranes fouled with whey model solutions. Desalination 2015, 360, 87–96. [Google Scholar] [CrossRef]
- Koivu, V.; Decain, M.; Geindreau, C.; Mattila, K.; Bloch, J.F.; Kataja, M. Transport properties of heterogeneous materials. Combining computerised X-ray micro-tomography and direct numerical simulations. Int. J. Comput. Fluid Dyn. 2011, 23, 713–721. [Google Scholar] [CrossRef]
- Matsuda, T. Biological response at non-physiological interfaces and molecular design of biocompatible surfaces. Nephrol. Dial. Transplant. 1989, 4, 560–566. [Google Scholar]
- Chanard, J.; Lavaud, S.; Randoux, C.; Rieu, P. New insights in dialysis membrane biocompatibility: Relevance of adsorption properties and heparin binding. Nephrol. Dial. Transplant. 2003, 18, 252–257. [Google Scholar] [CrossRef] [PubMed]
- Namekawa, K.; Schreiber, M.T.; Aoyagi, T.; Ebara, M. Fabrication of zeolite-polymer composite nanofibers for removal of uremic toxins from kidney failure patients. Biomater. Sci. 2014, 2, 674–679. [Google Scholar] [CrossRef]
- Saito, A.; Foley, H.C. Curvature and parametric sensitivity in models for adsorption in micropores. AIChE J. 1991, 37, 429–436. [Google Scholar] [CrossRef]
- Qajar, A.; Daigle, H.; Prodanović, M. The effects of pore geometry on adsorption equilibrium in shale formations and coal-beds: Lattice density functional theory study. Fuel 2016, 163, 205–213. [Google Scholar] [CrossRef]
- Fang, A.; Kroenlein, K.; Riccardi, D.; Smolyanitsky, A. Highly mechanosensitive ion channels from graphene-embedded crown ethers. Nat. Mater. 2019, 18, 76–81. [Google Scholar] [CrossRef] [PubMed]
- Gotch, F.A.; Sargent, J.A. A mechanical analysis of the National Cooperative Dialysis Study (NCDS). Kidney Int. 1985, 28, 526–534. [Google Scholar] [CrossRef] [PubMed]
- Gotch, F.A. Kinetics of solute removal in hemodialysis. Adv. Exp. Med. Biol. 1987, 223, 227–237. [Google Scholar] [PubMed]
- Gotch, F.A. Recommendations for quantification of dialysis therapy in research protocols. Kidney Int. Suppl. 1975, 5, 246–248. [Google Scholar]
- Sargent, J.A. Control of dialysis by a single-pool urea model: The National Cooperative Dialysis Study. Kidney Int. Suppl. 1983, 13, S19–S25. [Google Scholar]
- Flanigan, M.J.; Fangman, J.; Lim, V.S. Quantitating hemodialysis: A comparison of three kinetic models [see comments]. Am. J. Kidney Dis. 1991, 17, 295–302. [Google Scholar] [CrossRef]
- Popovich, R.P.; Hlavinka, D.J.; Bomar, J.B.; Moncrief, J.W.; Decherd, J.F. The consequences of physiological resistance on metabolic removal from the patient-artificial kidney system. ASAIO 1975, 21, 108–116. [Google Scholar]
- Daugirdas, J.T.; Depner, T.A.; Greene, T.; Silisteanu, P. Solute-solver: A web-based tool for modeling urea kinetics for a broad range of hemodialysis schedules in multiple patients. Am. J. Kidney Dis. 2009, 54, 798–809. [Google Scholar] [CrossRef] [PubMed]
- Daugirdas, J.T.; Schneditz, D. Overestimation of hemodialysis dose depends on dialysis efficiency by regional blood flow but not by conventional two pool urea kinetic analysis. ASAIO 1995, 41, M719–M724. [Google Scholar] [CrossRef]
- Daugirdas, J.T.; Smye, S.W. Effect of a two compartment distribution on apparent urea distribution volume. Kidney Int. 1997, 51, 1270–1273. [Google Scholar] [CrossRef] [PubMed]
- Daugirdas, J.T.; Blake, G.; Ing, T.S. Handbook of Dialysis, 3rd ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2001. [Google Scholar]
- Waniewski, J. Mathematical models for peritoneal transport characteristics. Perit. Dial. Int. 1999, 19, 193–201. [Google Scholar]
- Waniewski, J. Mathematical modeling of fluid and solute transport in hemodialysis and peritoneal dialysis. J. Membr. Sci. 2006, 274, 24–37. [Google Scholar] [CrossRef]
- Waniewski, J.; Antosiewicz, S.; Baczynski, D.; Poleszczuk, J.; Pietribiasi, M.; Lindholm, B.; Wankowicz, Z. Peritoneal fluid transport rather than peritoneal solute transport associates with dialysis vintage and age of peritoneal dialysis patients. Comput. Math. Methods Med. 2016, 2016, 8204294. [Google Scholar] [CrossRef] [PubMed]
- Waniewski, J.; Debowska, M.; Lindholm, B. Can the diverse family of dialysis adequacy indices be understood as one integrated system? Blood Purif. 2010, 30, 257–265. [Google Scholar] [CrossRef] [PubMed]
- Waniewski, J.; Heimburger, O.; Werinski, A.; Lindholm, B. Simple models for fluid transport during peritoneal dialysis. Int J. Artif. Organs. 1996, 19, 455–466. [Google Scholar] [CrossRef] [PubMed]
- Waniewski, J.; Lucjanek, P.; Werynski, A. Impact of ultrafiltration on back-diffusion in hemodialyzer. Artif. Organs. 1994, 18, 933–936. [Google Scholar] [CrossRef] [PubMed]
- Waniewski, J.; Stachowska-Pietka, J.; Flessner, M.F. Distributed modeling of osmotically driven fluid transport in peritoneal dialysis: Theoretical and computational investigations. Am. J. Physiol. Heart Circ. Physiol. 2009, 296, H1960–H1968. [Google Scholar] [CrossRef] [PubMed]
- Waniewski, J.; Werynski, A.; Heimburger, O.; Lindholm, B. A comparative analysis of mass transport models in peritoneal dialysis. ASAIO Trans. 1991, 37, 65–75. [Google Scholar] [PubMed]
- Debowska, M.; Waniewski, J.; Lindholm, B. Dialysis adequacy indices for peritoneal dialysis and hemodialysis. Adv. Perit. Dial. 2005, 21, 94–97. [Google Scholar] [PubMed]
- Debowska, M.; Lindholm, B.; Waniewski, J. Kinetic modeling and adequacy of dialysis. In Progress in Hemodialysis—From Emergent Biotechnology to Clinical Practice; Carpi, A., Donadio, C., Tramonti, G., Eds.; INTECH: London, UK, 2011; pp. 3–26. [Google Scholar]
- Velasco, M. Flow modeling of hollow fiber dialyzers. In Modeling and Control of Dialysis Systems; Azar, A.T., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 1, pp. 563–626. [Google Scholar]
- Grzegorzewska, A.E.; Azar, A.T.; Roa, L.M.; Oliva, J.S.; Milán, J.A.; Palma, A. Single pool urea kinetic modeling. In Modeling and Control of Dialysis Systems; Azar, A.T., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 1, pp. 519–562. [Google Scholar]
- Azar, A.T.; Yashiro, M.; Schneditz, D.; Roa, L.M. Double pool urea kinetic modeling. In Modeling and Control of Dialysis Systems; Azar, A.T., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 1, pp. 627–688. [Google Scholar]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Annalen der Physik 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Hanai, T. Theory of the dielectric dispersion due to the interfacial polarization and its applications to emulsions. Kolloid Z. 1960, 171, 23–31. [Google Scholar] [CrossRef]
- Hanai, T.; Koizumi, N. Dielectric relaxation of W/O emulsions in particular reference to theories of interfacial polarization. Bull. Inst. Chem. Res. Kyoto Univ. 1975, 53, 153–160. [Google Scholar]
- Looyenga, H. Dielectric constants of heterogeneous mixture. Physica 1965, 31, 401–406. [Google Scholar] [CrossRef]
- De La Rue, R.E.; Tobias, C.W. On conductivity of dispersions. J. Electrochem. Soc. 1959, 106, 827–833. [Google Scholar]
- Fricke, H. The Maxwell-Wagner dispersion in a suspension of ellipsoids. J. Phys. Chem. 1953, 57, 934–937. [Google Scholar] [CrossRef]
- Varlet-Marie, E.; Brun, J.F. Prediction of RBC aggregability and deformability by whole body bioimpedance measurements analyzed according to Hanai’s mixture conductivity theory. Clin. Hemorheol. Microcirc. 2011, 47, 151–161. [Google Scholar] [PubMed]
- Ogston, A.G. The spaces in a uniform random suspension of fibres. Trans. Faraday Soc. 1958, 54, 1754–1757. [Google Scholar] [CrossRef]
- Lorenzo, A.D.; Andreoli, A.; Matthie, J.; Withers, P. Predicting body cell mass with bioimpedance by using theoretical methods: A technological review. J. Appl. Physiol. 1997, 82, 1542–1558. [Google Scholar] [CrossRef] [PubMed]
- Matthie, J.R. Second generation mixture theory equation for estimating intracellular water using bioimpedance spectroscopy. J. Appl. Physiol. 2005, 99, 780–781. [Google Scholar] [CrossRef] [PubMed]
- Matthie, J.R. Bioimpedance measurements of human body composition: Critical analysis and outlook. Expert Rev. Med. Devices. 2008, 5, 239–261. [Google Scholar] [CrossRef] [PubMed]
- Jaffrin, M.Y.; Morel, H. Body fluid volumes measurements by impedance: A review of bioimpedance spectroscopy (BIS) and bioimpedance analysis (BIA) methods. Med. Eng. Phys. 2008, 30, 1257–1269. [Google Scholar] [CrossRef] [PubMed]
- Jaffrin, M.Y.; Fenech, M.; Moreno, M.V.; Kieffer, R. Total body water measurement by a modification of the bioimpédance spectroscopy method. Med. Biol. Eng. Comput. 2006, 44, 873–882. [Google Scholar] [CrossRef] [PubMed]
- Starling, E.H. On the absorption of fluids from the connective tissue spaces. J. Physiol. 1896, 19, 312–326. [Google Scholar] [CrossRef] [PubMed]
- Staverman, A.J. The theory of measurement of osmotic pressure. Rac. Trav. Chim. 1951, 70, 344–352. [Google Scholar] [CrossRef]
- Hu, X.; Adamson, R.H.; Liu, B.; Curry, F.E.; Weinbaum, S. Starling forces that oppose filtration after tissue oncotic pressure is increased. Am. J. Physiol. Heart Circ. Physiol. 2000, 279, H1724–H1736. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity. In Course of Theoretical Physics, 3rd ed.; Pergamon Press: Oxford, UK, 1986; Volume 7. [Google Scholar]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voinova, M.; Repin, N.; Sokol, E.; Tkachuk, B.; Gorelik, L. Physical Processes in Polymeric Filters Used for Dialysis. Polymers 2019, 11, 389. https://doi.org/10.3390/polym11030389
Voinova M, Repin N, Sokol E, Tkachuk B, Gorelik L. Physical Processes in Polymeric Filters Used for Dialysis. Polymers. 2019; 11(3):389. https://doi.org/10.3390/polym11030389
Chicago/Turabian StyleVoinova, Marina, Nikolay Repin, Evgen Sokol, Bogdan Tkachuk, and Leonid Gorelik. 2019. "Physical Processes in Polymeric Filters Used for Dialysis" Polymers 11, no. 3: 389. https://doi.org/10.3390/polym11030389
APA StyleVoinova, M., Repin, N., Sokol, E., Tkachuk, B., & Gorelik, L. (2019). Physical Processes in Polymeric Filters Used for Dialysis. Polymers, 11(3), 389. https://doi.org/10.3390/polym11030389





