Design of Elastomer-CNT Film Photoactuators for Nanolithography
Abstract
1. Introduction
2. Materials and Methods
2.1. Fabrication of PDMS–CNT Composite Films
2.2. AFM Characterization
2.3. Finite Element Analysis
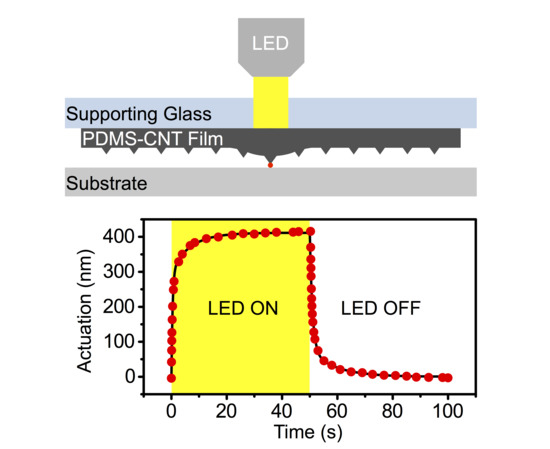
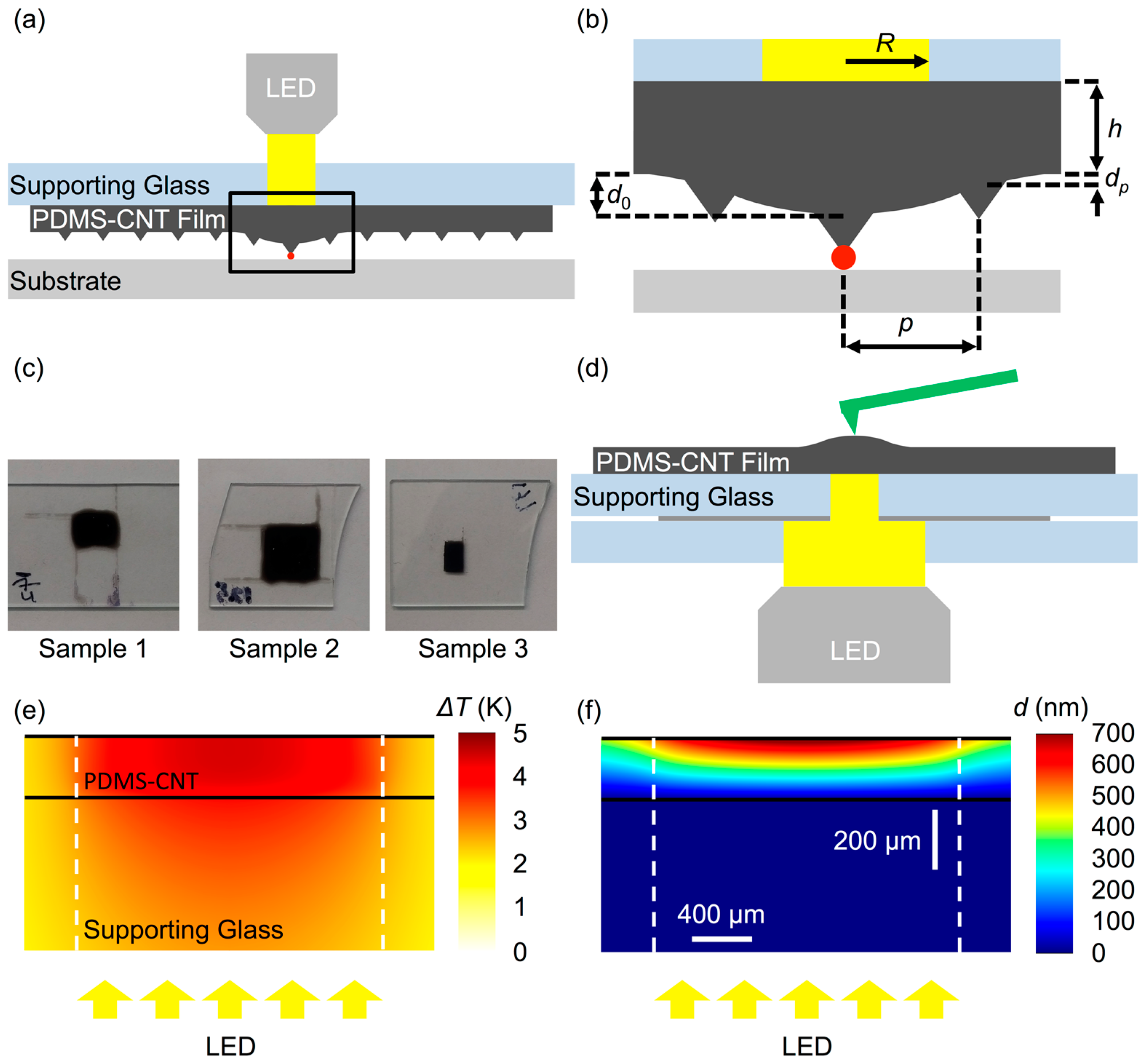
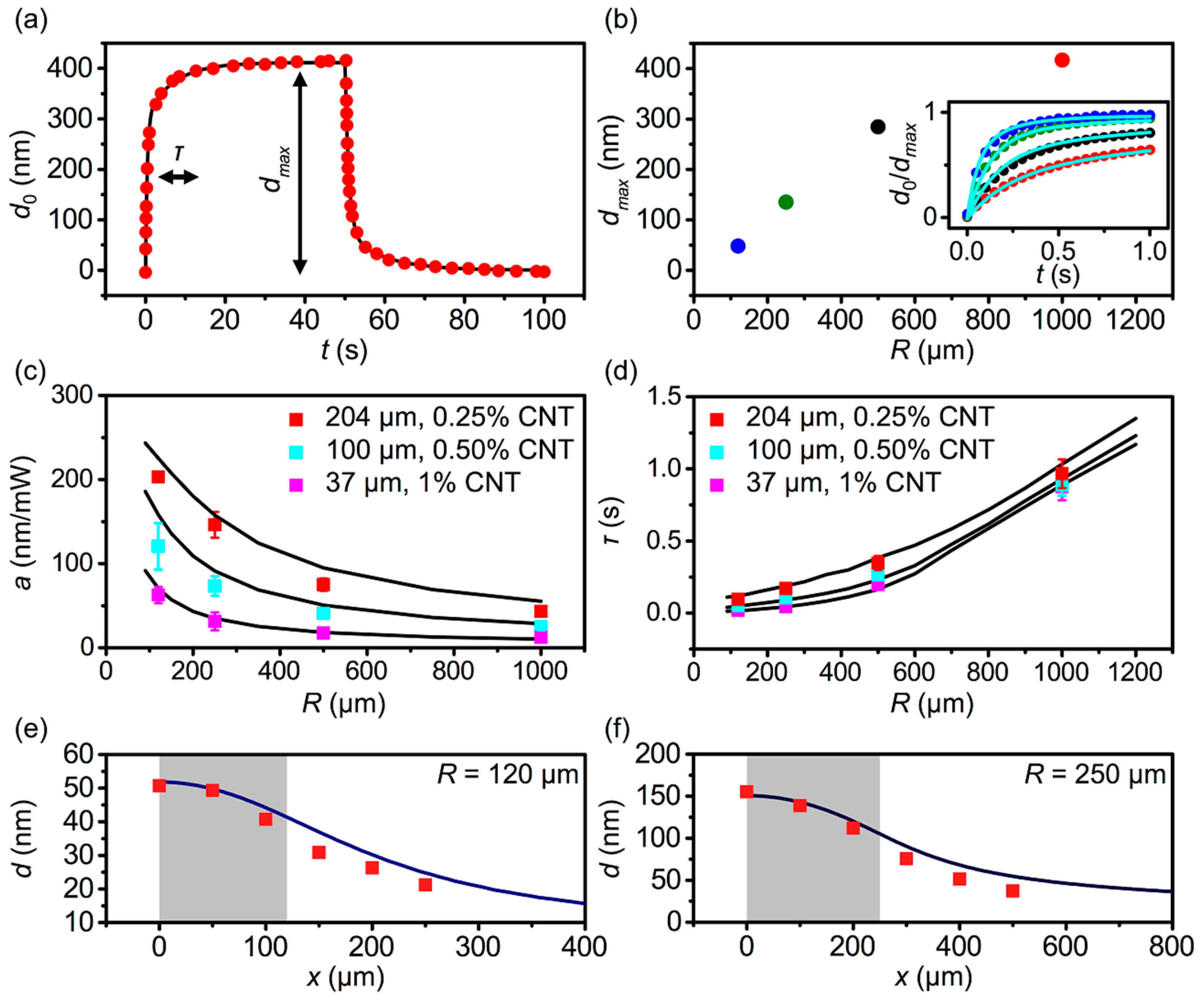
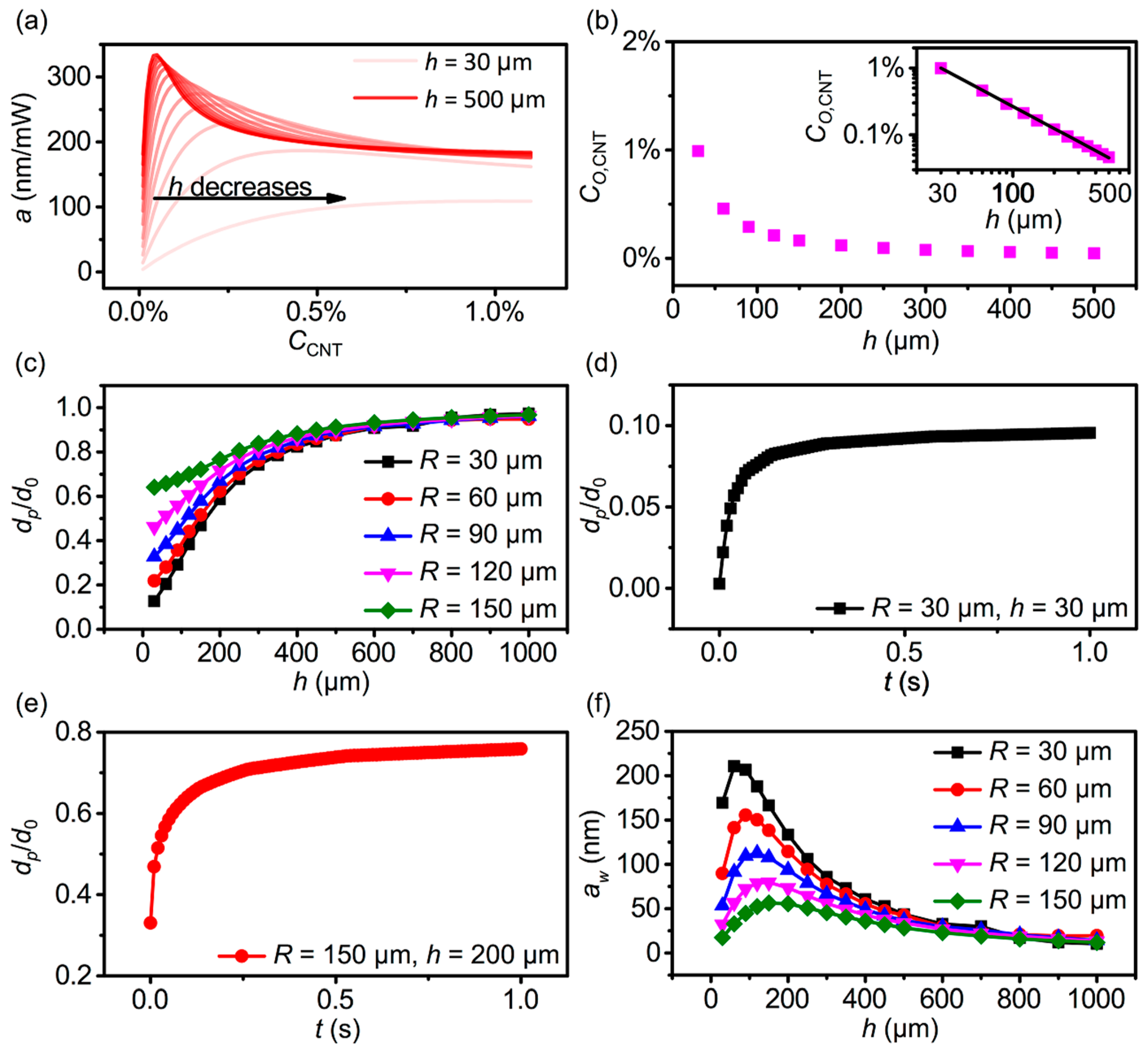
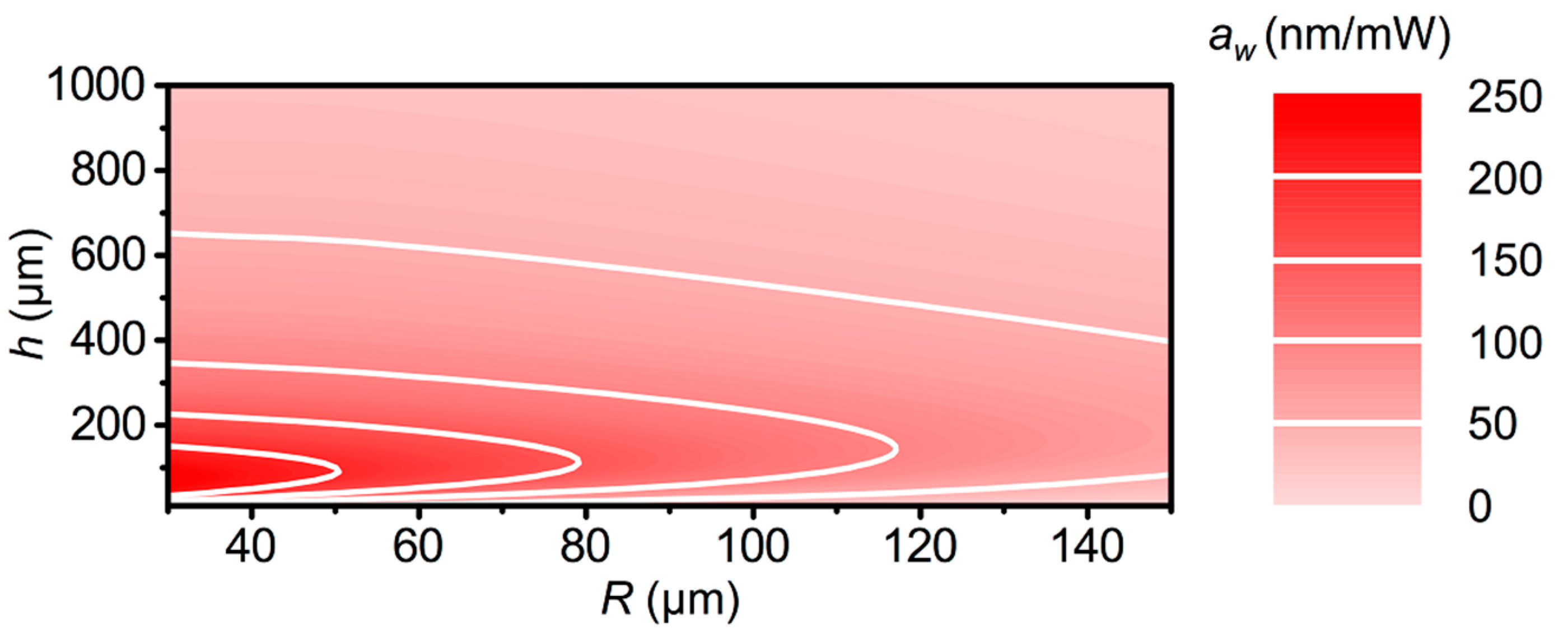
3. Results and discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chou, S.Y.; Krauss, P.R.; Renstrom, P.J. Imprint lithography with 25-nanometer resolution. Science 1996, 272, 85–87. [Google Scholar] [CrossRef]
- Tseng, A.A. Nanofabrication: Fundamentals and Applications; World Scientific: Singapore, 2008. [Google Scholar]
- Garcia, R.; Knoll, A.W.; Riedo, E. Advanced scanning probe lithography. Nature Nanotech. 2014, 9, 577–587. [Google Scholar] [CrossRef] [PubMed]
- Waldrop, M.M. The chips are down for moore’s law. Nature 2016, 530, 144–147. [Google Scholar] [CrossRef]
- Ryu, Y.K.; Garcia, R. Advanced oxidation scanning probe lithography. Nanotechnology 2017, 28, 142003. [Google Scholar] [CrossRef]
- van Assenbergh, P.; Meinders, E.; Geraedts, J.; Dodou, D. Nanostructure and microstructure fabrication: From desired properties to suitable processes. Small 2018, 14, 1703401. [Google Scholar] [CrossRef] [PubMed]
- Piner, R.D.; Zhu, J.; Xu, F.; Hong, S.; Mirkin, C.A. “Dip-pen” nanolithography. Science 1999, 283, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-B.; Park, S.-J.; Mirkin, C.A.; Smith, J.C.; Mrksich, M. Protein nanoarrays generated by dip-pen nanolithography. Science 2002, 295, 1702–1705. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Santana, A.; Irvine, E.; Faulds, K.; Graham, D. Rapid prototyping of poly (dimethoxysiloxane) dot arrays by dip-pen nanolithography. Chem. Sci. 2011, 2, 211–215. [Google Scholar] [CrossRef]
- Brown, K.A.; Eichelsdoerfer, D.J.; Liao, X.; He, S.; Mirkin, C.A. Material transport in dip-pen nanolithography. Front. Phys. 2014, 9, 385–397. [Google Scholar] [CrossRef]
- Huo, F.; Zheng, Z.; Zheng, G.; Giam, L.R.; Zhang, H.; Mirkin, C.A. Polymer pen lithography. Science 2008, 321, 1658–1660. [Google Scholar] [CrossRef]
- Zheng, Z.; Daniel, W.L.; Giam, L.R.; Huo, F.; Senesi, A.J.; Zheng, G.; Mirkin, C.A. Multiplexed protein arrays enabled by polymer pen lithography: Addressing the inking challenge. Angew. Chem. 2009, 121, 7762–7765. [Google Scholar] [CrossRef]
- Huang, L.; Braunschweig, A.B.; Shim, W.; Qin, L.; Lim, J.K.; Hurst, S.J.; Huo, F.; Xue, C.; Jang, J.-W.; Mirkin, C.A. Matrix-assisted dip-pen nanolithography and polymer pen lithography. Small 2010, 6, 1077–1081. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.; Huo, F.; Zheng, Z.; Giam, L.R.; Shim, W.; Mirkin, C.A. Scanning probe block copolymer lithography. Proc. Natl. Acad. Sci. USA 2010, 107, 20202–20206. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Shen, Y.; Zhou, X.; Yang, Y.; Tang, Q.; Miao, Q.; Su, J.; Wu, H.; Zheng, Z. Polymer pen lithography using dual-elastomer tip arrays. Small 2012, 8, 2664–2669. [Google Scholar] [CrossRef] [PubMed]
- Eichelsdoerfer, D.J.; Brown, K.A.; Boya, R.; Shim, W.; Mirkin, C.A. Tuning the spring constant of cantilever-free tip arrays. Nano Lett. 2013, 13, 664–667. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Chen, C.; Zhou, X.; Gao, T.; Liu, D.; Miao, Q.; Zheng, Z. Massively parallel patterning of complex 2d and 3d functional polymer brushes by polymer pen lithography. ACS Appl. Mater. Interfaces 2014, 6, 11955–11964. [Google Scholar] [CrossRef]
- Brown, K.A.; Hedrick, J.L.; Eichelsdoerfer, D.J.; Mirkin, C.A. Nanocombinatorics with cantilever-free scanning probe arrays. ACS Nano 2019, 13, 8–17. [Google Scholar] [CrossRef]
- Brown, K.A.; Eichelsdoerfer, D.J.; Shim, W.; Rasin, B.; Radha, B.; Liao, X.; Schmucker, A.L.; Liu, G.; Mirkin, C.A. A cantilever-free approach to dot-matrix nanoprinting. Proc. Natl. Acad. Sci. USA 2013, 110, 12921–12924. [Google Scholar] [CrossRef]
- Han, Y.; Liu, C. Pneumatically actuated active polymer pen lithography. Sens. Actuators A 2011, 167, 433–437. [Google Scholar] [CrossRef]
- Liao, X.; Brown, K.A.; Schmucker, A.L.; Liu, G.; He, S.; Shim, W.; Mirkin, C.A. Desktop nanofabrication with massively multiplexed beam pen lithography. Nat. Commun. 2013, 4, 2103. [Google Scholar] [CrossRef]
- Sun, X.; Wang, W.; Qiu, L.; Guo, W.; Yu, Y.; Peng, H. Unusual reversible photomechanical actuation in polymer/nanotube composites. Angew. Chem. Int. Ed. 2012, 51, 8520–8524. [Google Scholar] [CrossRef] [PubMed]
- Ahir, S.V.; Terentjev, E.M. Photomechanical actuation in polymer-nanotube composites. Nature Mater. 2005, 4, 491–495. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Li, L.; Zhang, X.A.; Alsharif, N.; Wu, X.; Peng, Z.; Cheng, X.; Wang, P.; Brown, K.A.; Wang, Y. Photoactuated pens for molecular printing. Adv. Mater. 2018, 30, 1705303. [Google Scholar] [CrossRef] [PubMed]
- Czaniková, K.; Krupa, I.; Ilcíková, M.; Kasák, P.; Chorvat, D.; Valentin, M.; Slouf, M.; Mosnácek, J.; Micušík, M.; Omastová, M. Photo-actuating materials based on elastomers and modified carbon nanotubes. J. Nanophotonics 2012, 6, 063522. [Google Scholar] [CrossRef]
- Deng, S.; Zhang, Y.; Brozena, A.H.; Mayes, M.L.; Banerjee, P.; Chiou, W.-A.; Rubloff, G.W.; Schatz, G.C.; Wang, Y. Confined propagation of covalent chemical reactions on single-walled carbon nanotubes. Nat. Commun. 2011, 2, 382. [Google Scholar] [CrossRef] [PubMed]
- Brown, K.A.; Eichelsdoerfer, D.J.; Mirkin, C.A. Cantilever-free thermal actuation. J. Vac. Sci. Technol. B 2013, 31, 06F201. [Google Scholar] [CrossRef]
- Jeong, S.H.; Kim, K.K.; Jeong, S.J.; An, K.H.; Lee, S.H.; Lee, Y.H. Optical absorption spectroscopy for determining carbon nanotube concentration in solution. Synt. Met. 2007, 157, 570–574. [Google Scholar] [CrossRef]
- Han, Z.; Fina, A. Thermal conductivity of carbon nanotubes and their polymer nanocomposites: A review. Prog. Polym. Sci. 2011, 36, 914–944. [Google Scholar] [CrossRef]
- Ilčíková, M.; Mrlík, M.; Sedláček, T.; Chorvát, D.; Krupa, I.; Šlouf, M.; Koynov, K.; Mosnáček, J. Viscoelastic and photo-actuation studies of composites based on polystyrene-grafted carbon nanotubes and styrene-b-isoprene-b-styrene block copolymer. Polymer 2014, 55, 211–218. [Google Scholar] [CrossRef]
- Ilievski, F.; Mazzeo, A.D.; Shepherd, R.F.; Chen, X.; Whitesides, G.M. Soft robotics for chemists. Angew. Chem. 2011, 123, 1930–1935. [Google Scholar] [CrossRef]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467. [Google Scholar] [CrossRef] [PubMed]
- Iamsaard, S.; Aßhoff, S.J.; Matt, B.; Kudernac, T.; Cornelissen, J.J.; Fletcher, S.P.; Katsonis, N. Conversion of light into macroscopic helical motion. Nature Chem. 2014, 6, 229. [Google Scholar] [CrossRef] [PubMed]
- Baigl, D. Photo-actuation of liquids for light-driven microfluidics: State of the art and perspectives. Lab Chip 2012, 12, 3637–3653. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Huang, Z.; Wang, Y.; Brown, K.A. Design of Elastomer-CNT Film Photoactuators for Nanolithography. Polymers 2019, 11, 314. https://doi.org/10.3390/polym11020314
Li L, Huang Z, Wang Y, Brown KA. Design of Elastomer-CNT Film Photoactuators for Nanolithography. Polymers. 2019; 11(2):314. https://doi.org/10.3390/polym11020314
Chicago/Turabian StyleLi, Le, Zhongjie Huang, YuHuang Wang, and Keith A. Brown. 2019. "Design of Elastomer-CNT Film Photoactuators for Nanolithography" Polymers 11, no. 2: 314. https://doi.org/10.3390/polym11020314
APA StyleLi, L., Huang, Z., Wang, Y., & Brown, K. A. (2019). Design of Elastomer-CNT Film Photoactuators for Nanolithography. Polymers, 11(2), 314. https://doi.org/10.3390/polym11020314