Enhanced Foamability with Shrinking Microfibers in Linear Polymer
Abstract
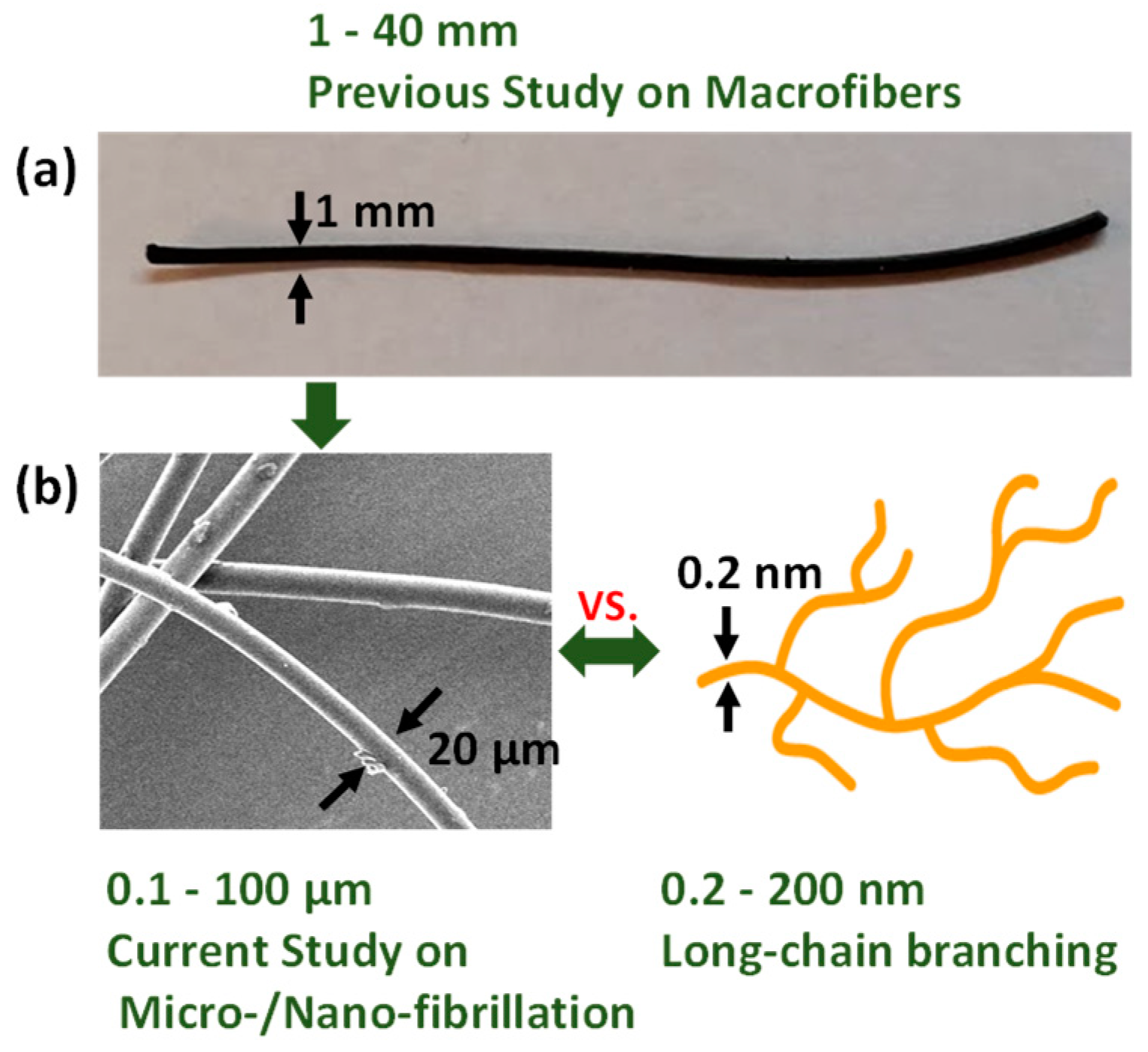
1. Introduction
2. Materials and Methods
2.1. Materials
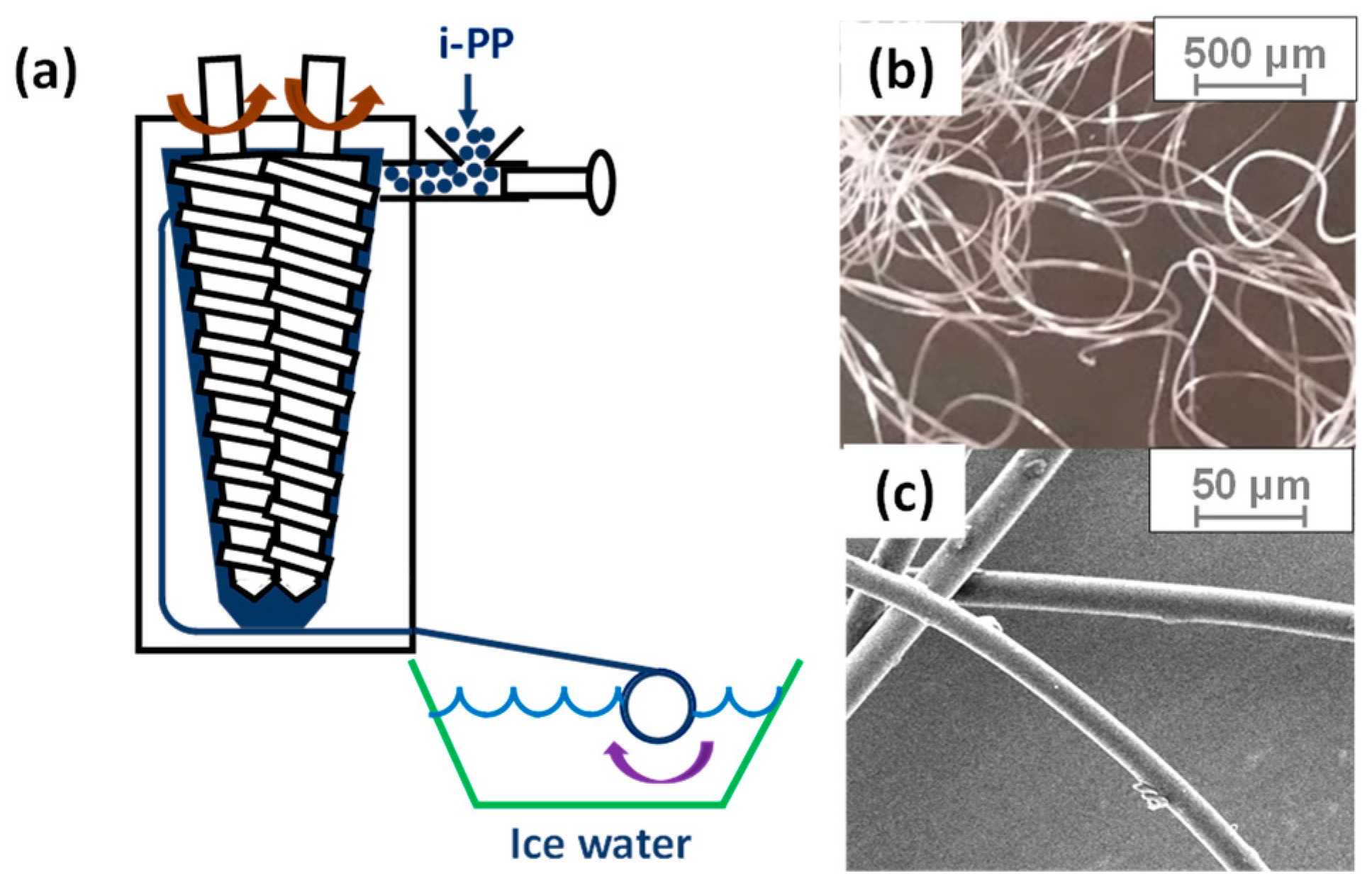
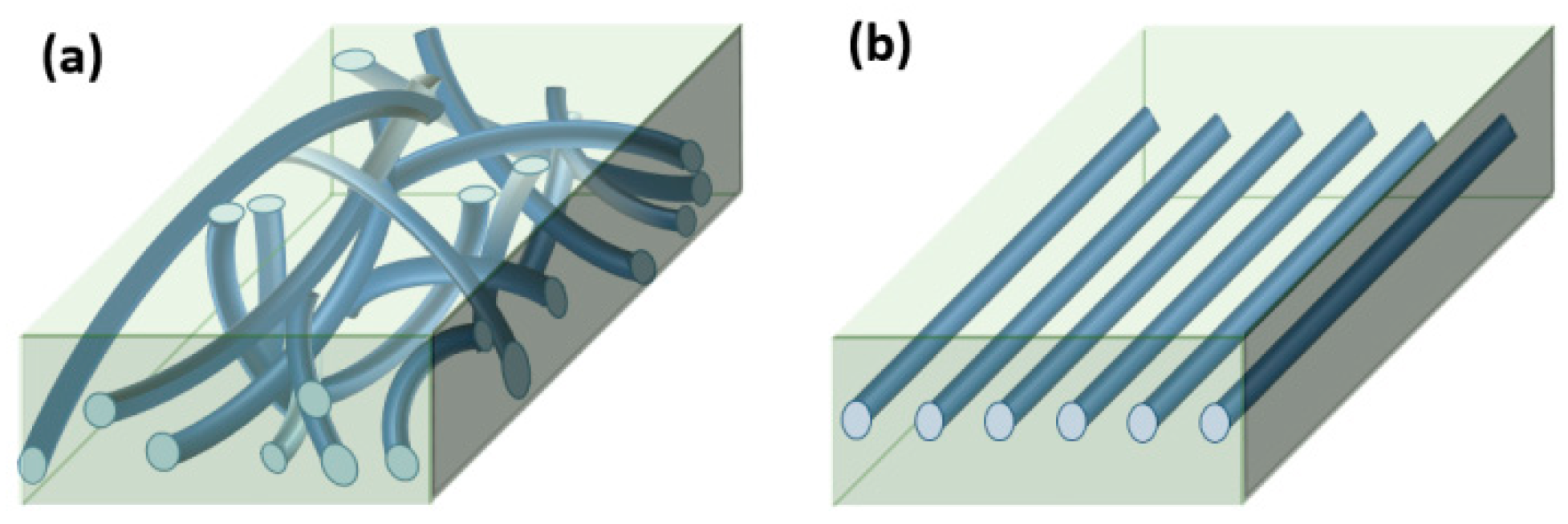
2.2. Sample Preparation
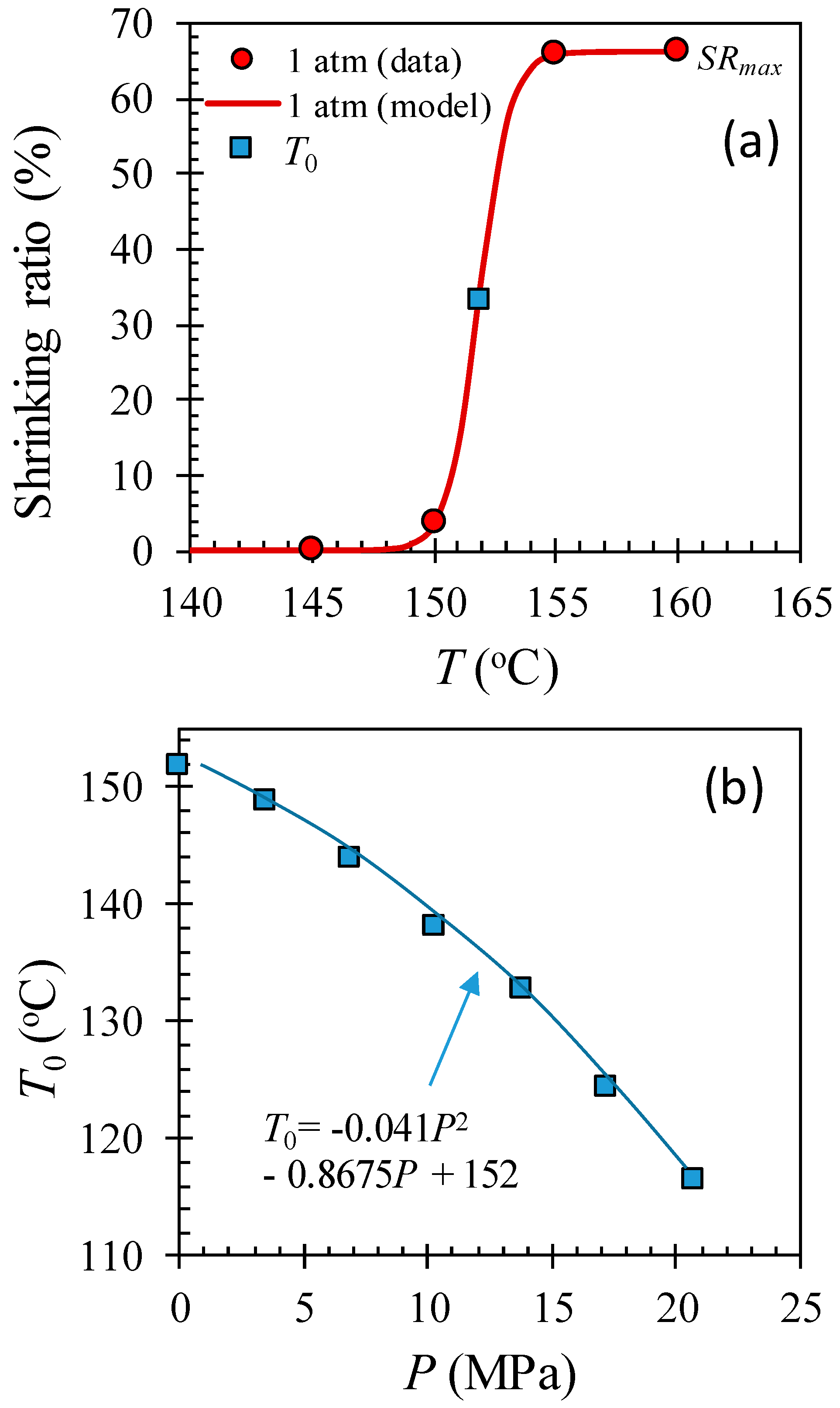
2.3. Microfiber Shrinkage Ratio
2.4. Shrinking Behavior of HAS Microfibers
2.5. Tensile Properties of Microfibers
2.6. Single Microfiber Pull-Out Test
2.7. Extensional Rheometry
2.8. Shear Rheometry
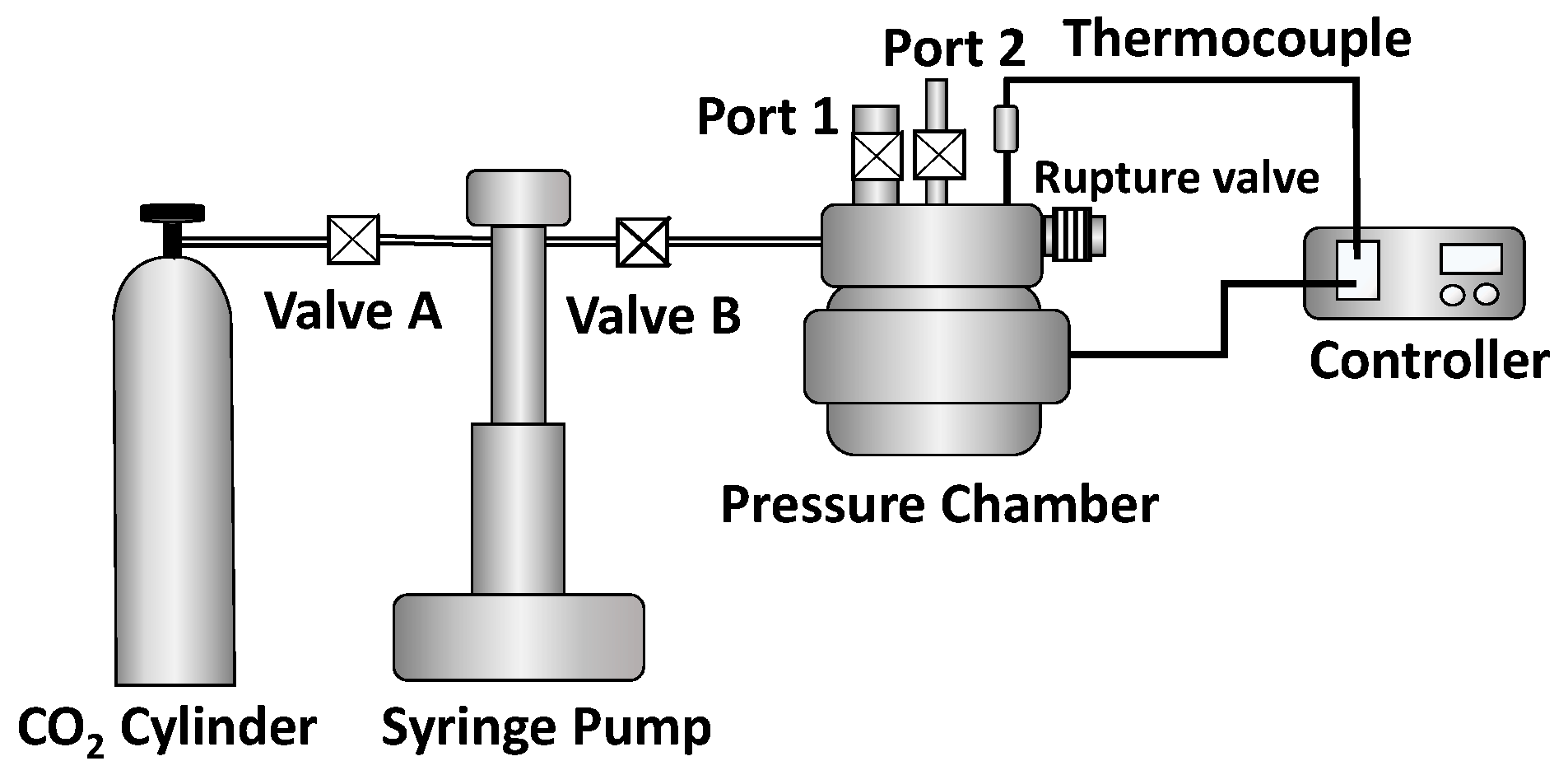
2.9. Batch Physical Foaming
3. Results
3.1. Polymer Characteristic Analysis
3.2. Tensile Test Properties of HAS and HP Microfibers
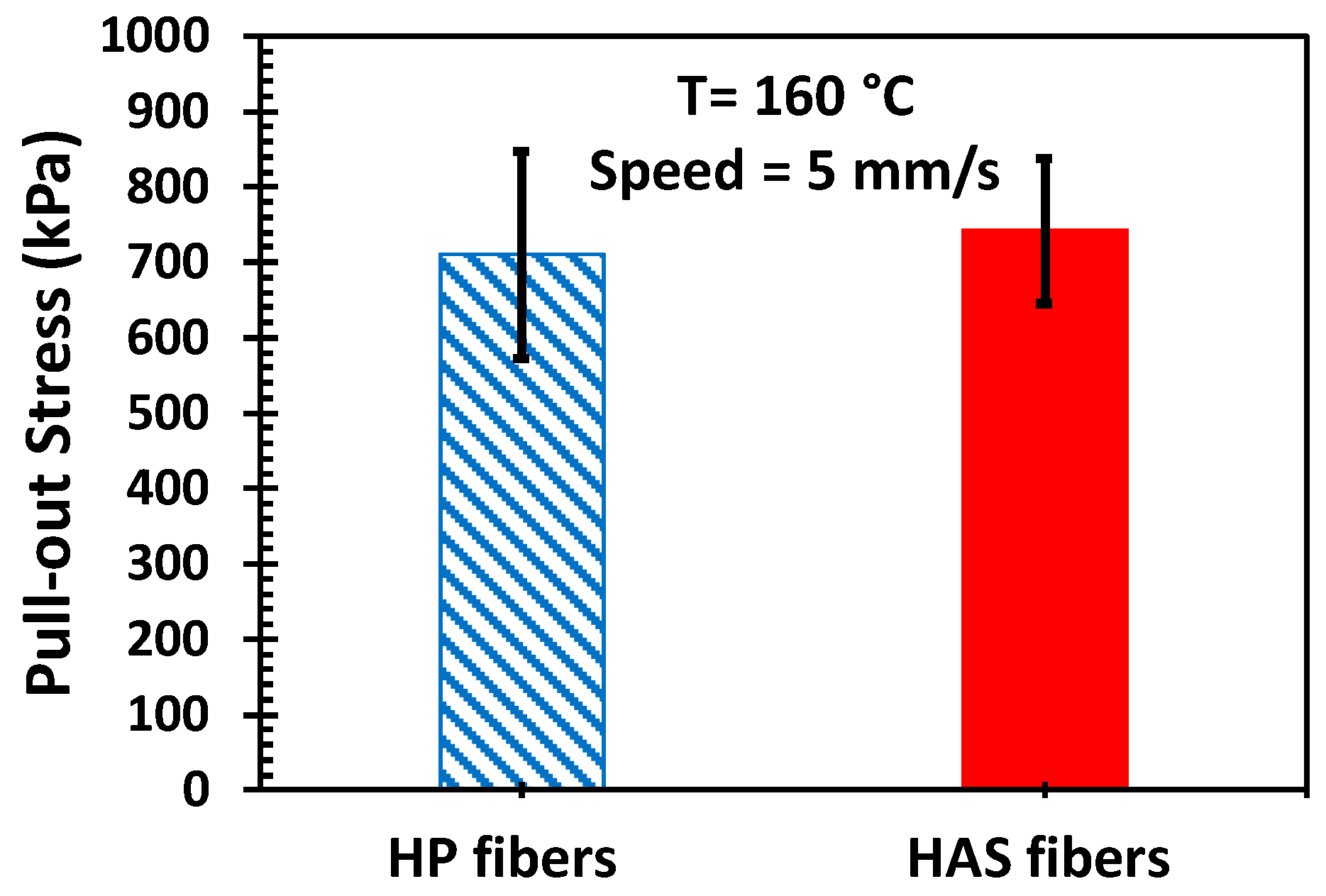
3.3. Microfiber Pull-Out Test
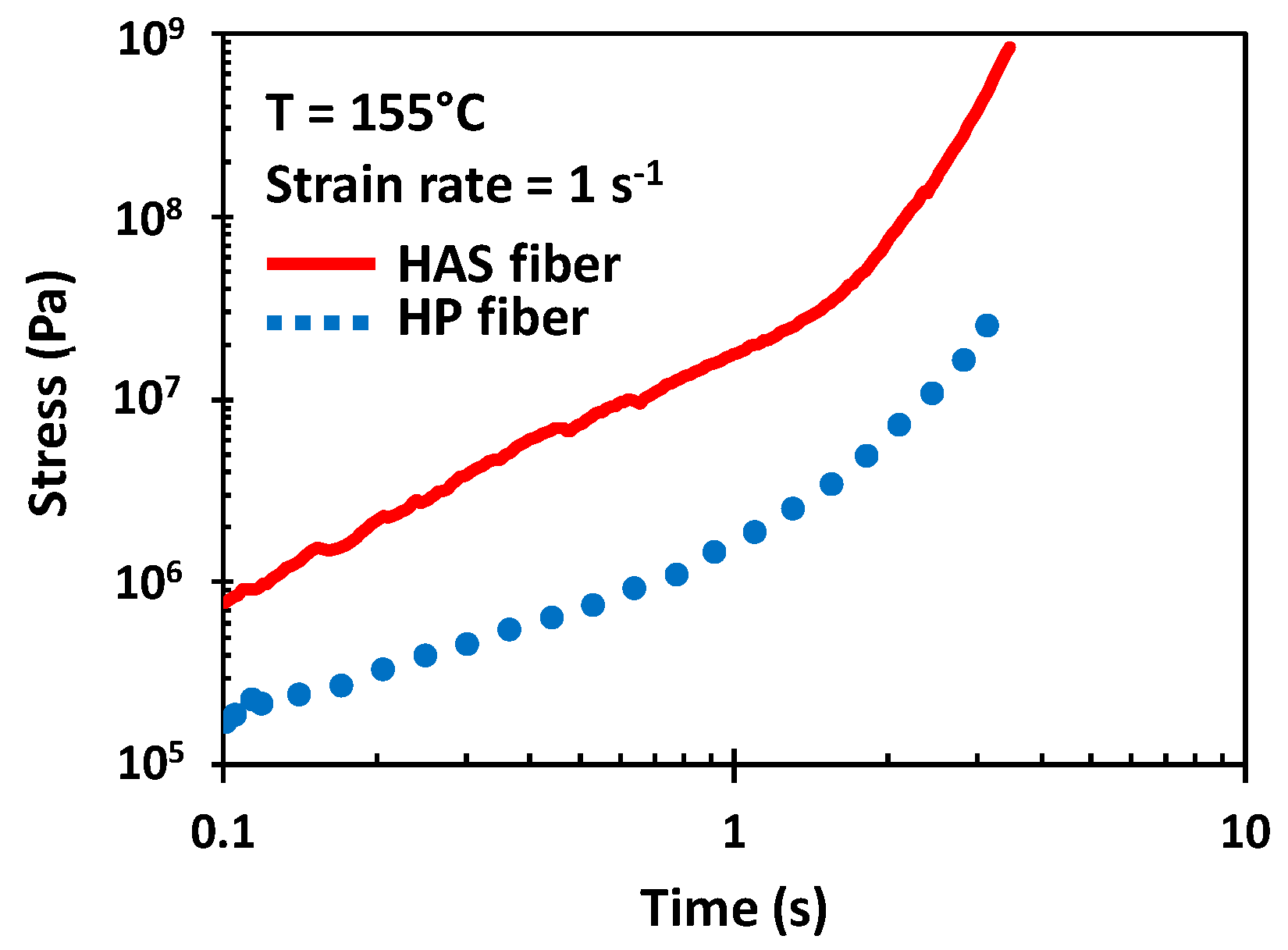
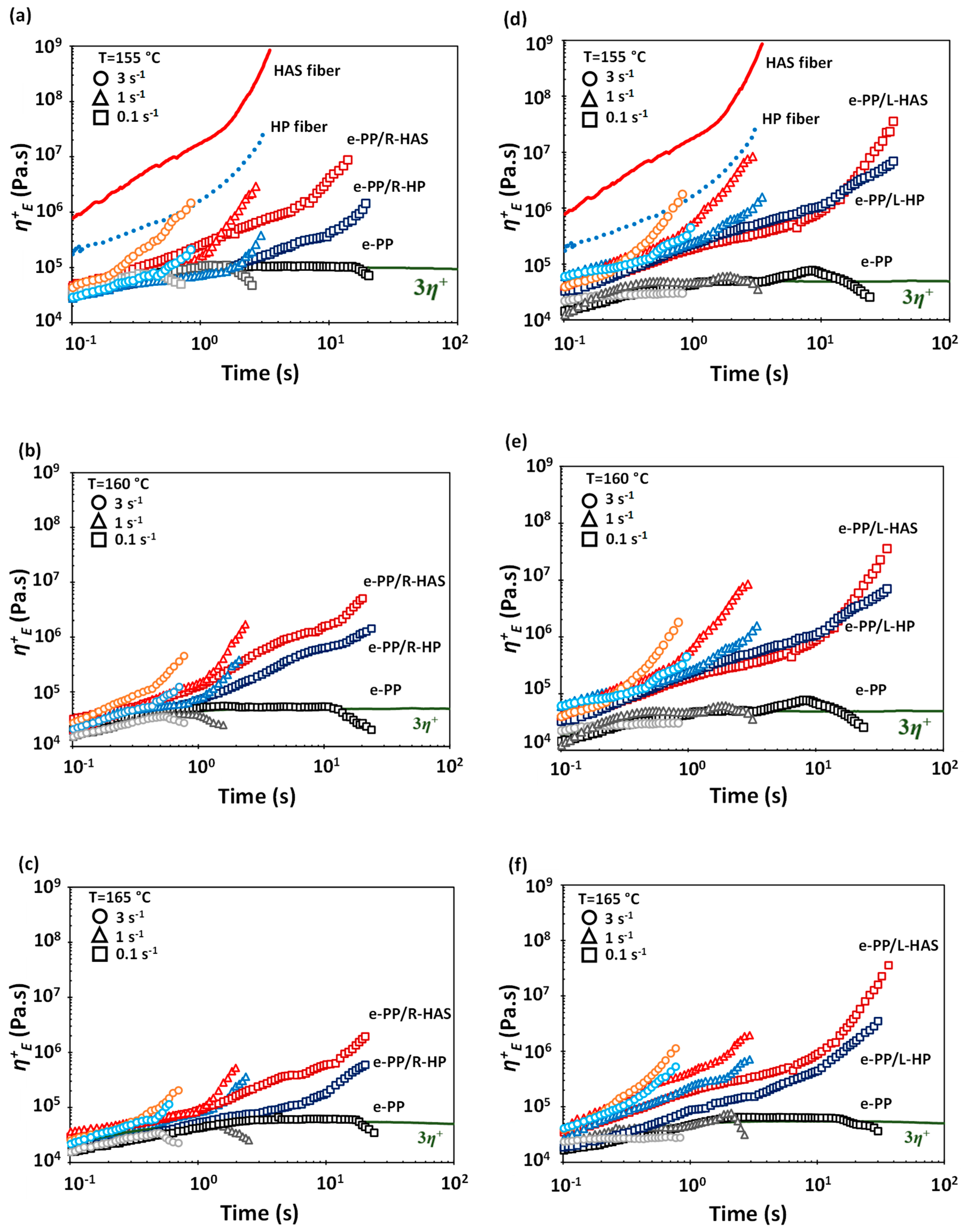
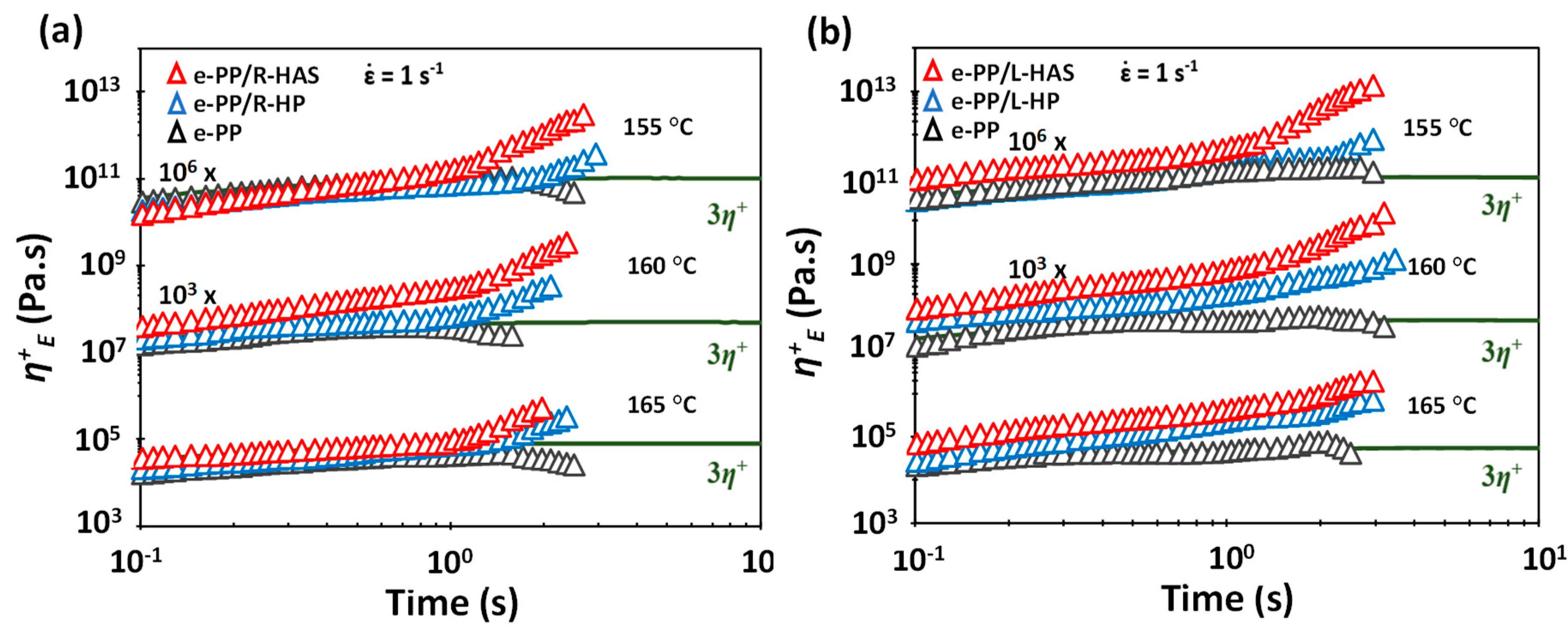
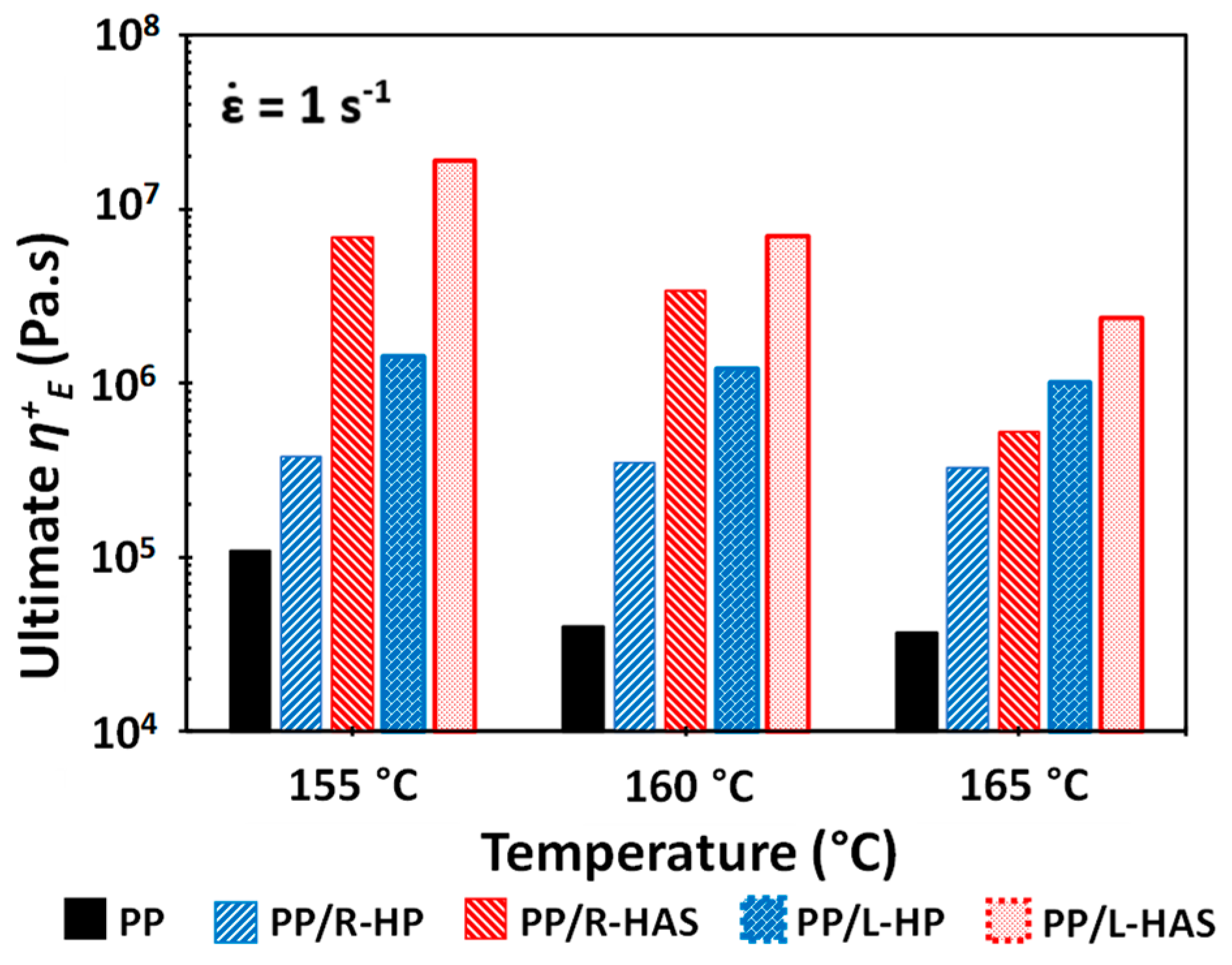
3.4. Extensional Rheometry
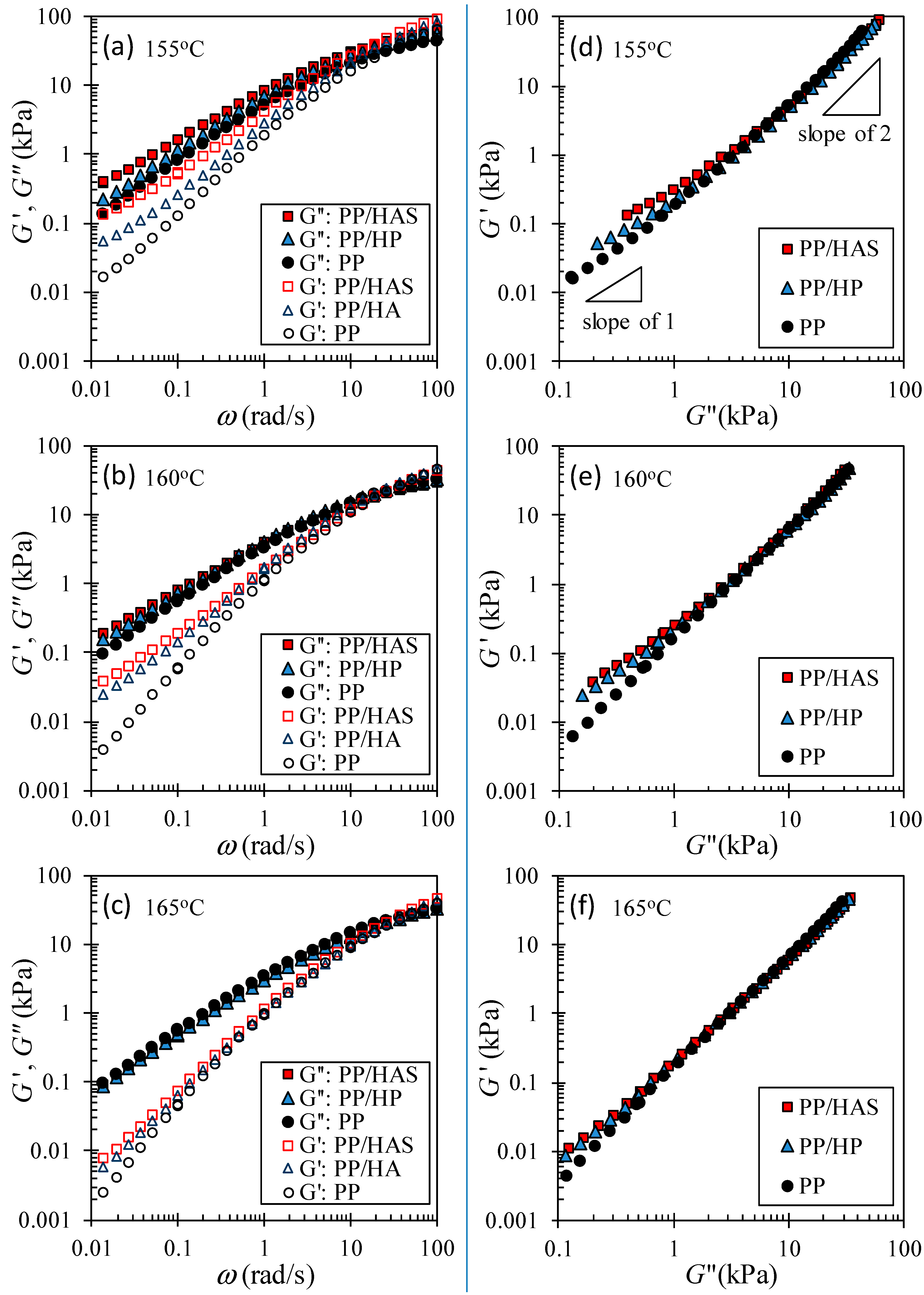
3.5. Linear Viscoelastic Shear Behavior
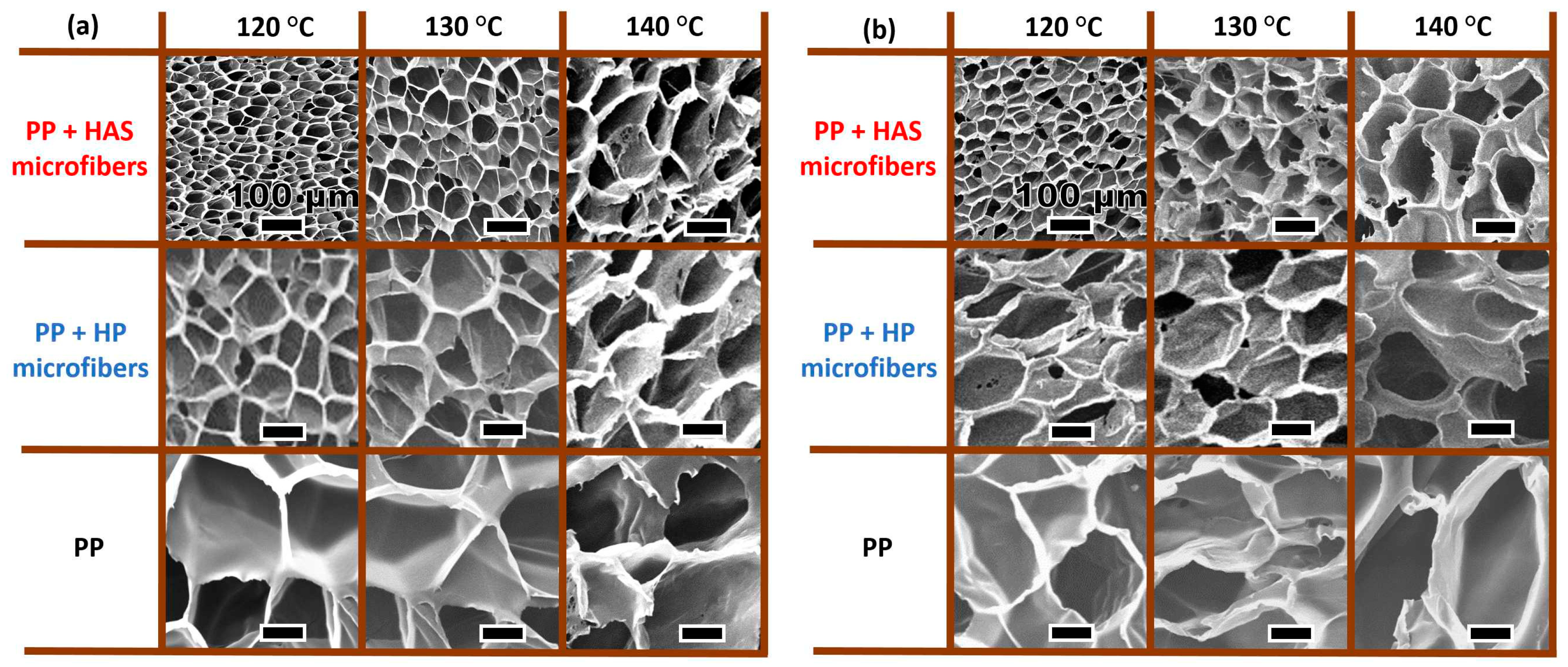
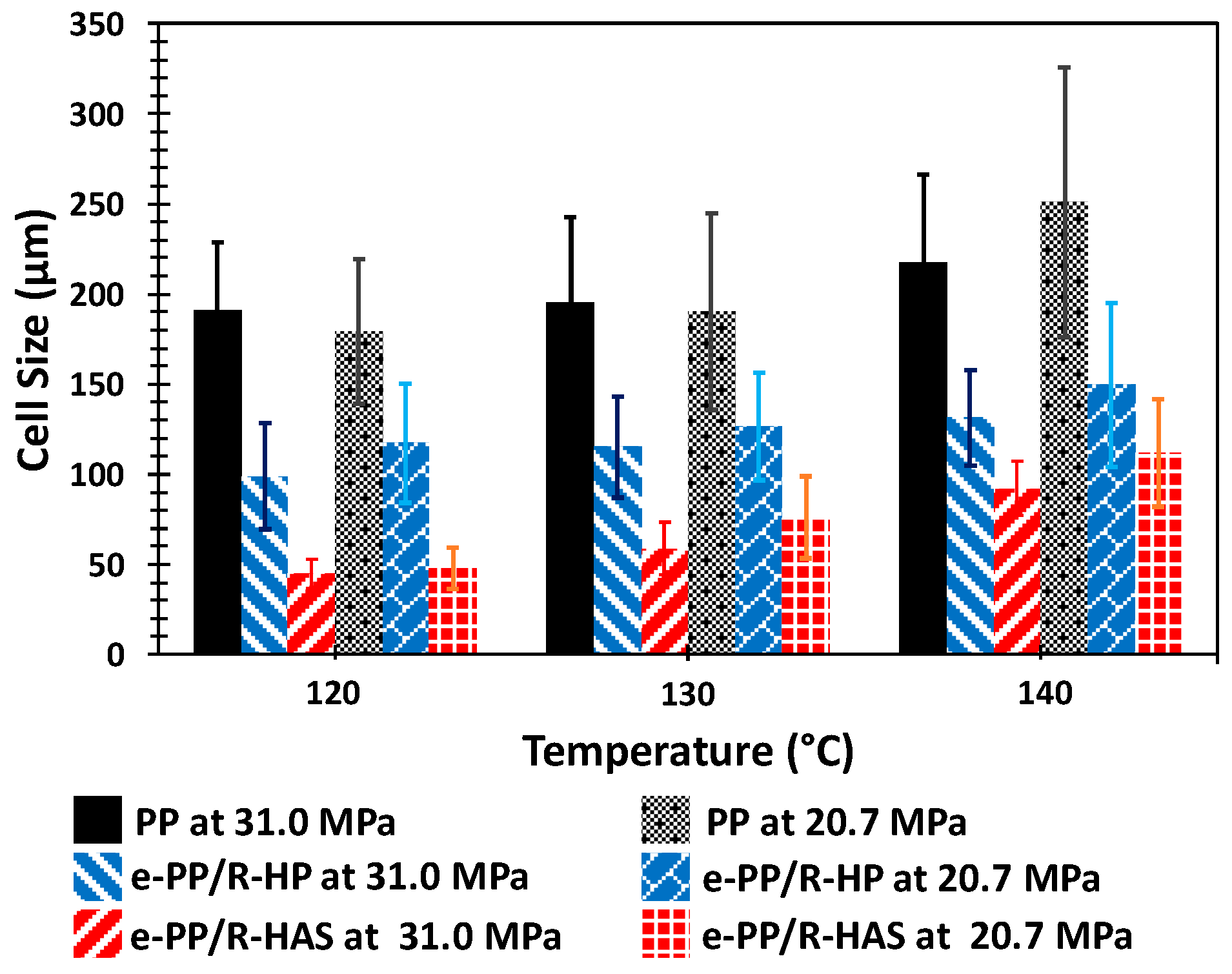
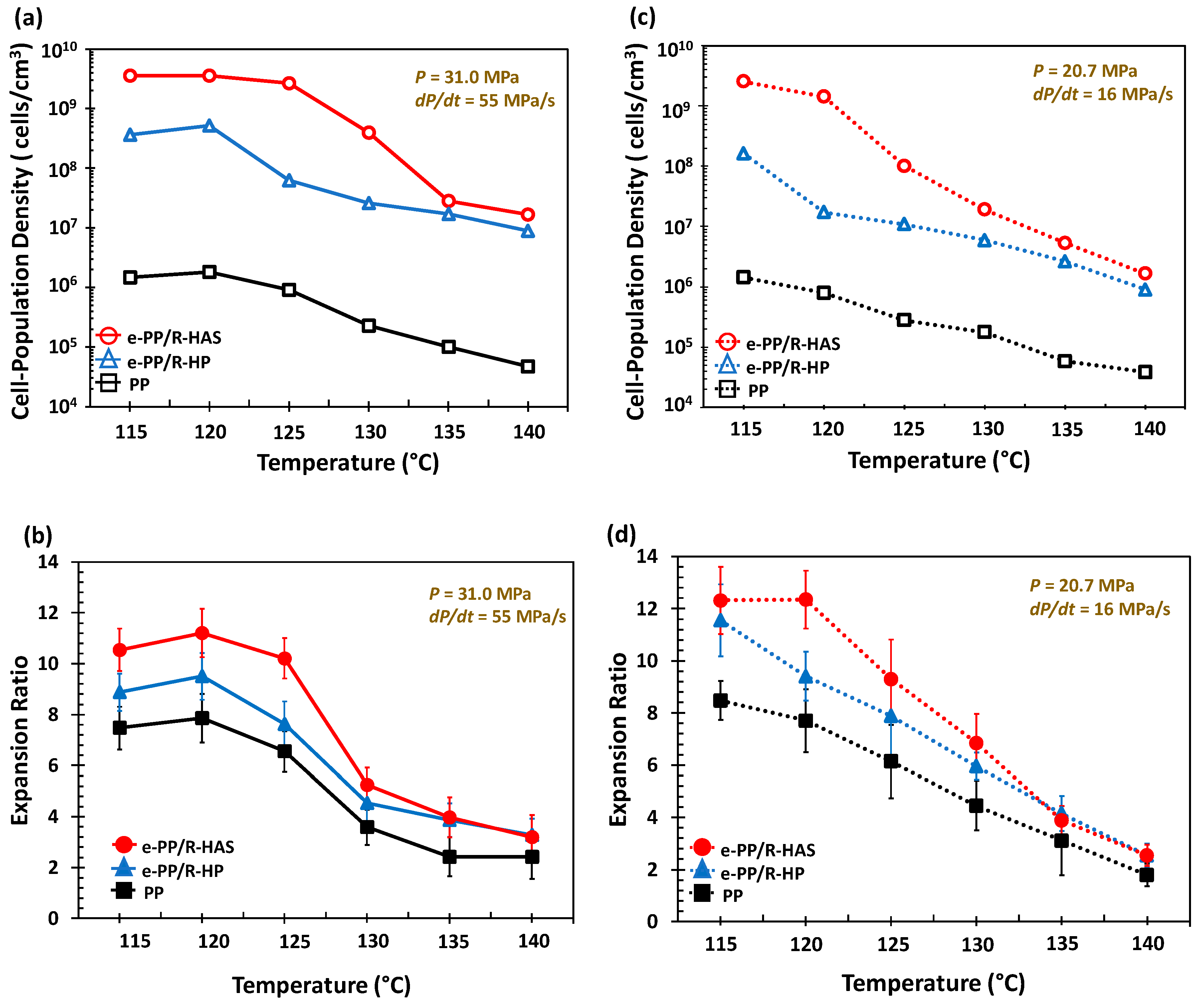
3.6. Batch Foaming
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gabriel, C.; Münstedt, H. Strain Hardening of Various Polyolefins in Uniaxial Elongational Flow. J. Rheol. 2003, 47, 619–630. [Google Scholar] [CrossRef]
- Rizivi, A.; Andalib, Z.K.M.; Park, C.B. Fiber-spun Polypropylene/Polyethylene Terephthalate Microfibrillar Composites with Enhanced Tensile and Rheological Properties and Foaming Ability. Polymer 2017, 110, 139–148. [Google Scholar] [CrossRef]
- Spitael, P.; Macosko, C.W. Strain Hardening in Polypropylenes and Its Role in Extrusion Foaming. Polym. Eng. Sci. 2004, 44, 2090–2100. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, Z.; Guan, Y.; Wei, D.; Zheng, A. Investigation of Extensional Rheological Behaviors of Polypropylene for Foaming. J. Cell. Plast. 2013, 49, 317–334. [Google Scholar] [CrossRef]
- Zhang, Y.; Parent, J.S.; Kontopoulou, M.; Park, C.B. Foaming of Reactively Modified Polypropylene: Effects of Rheology and Coagent Type. J. Cell. Plast. 2015, 51, 505–522. [Google Scholar] [CrossRef]
- Stange, J.; Münstedt, H. Effect of Long-chain Branching on the Foaming of Polypropylene with Azodicarbonamide. J. Cell. Plast. 2006, 42, 445–467. [Google Scholar] [CrossRef]
- Torres, E.; Li, S.; Costeux, S.; Dealy, J.M. Branching Structure and Strain Hardening of Branched Metallocene Polyethylenes. J. Rheol. 2015, 59, 1151–1172. [Google Scholar] [CrossRef]
- Tabatabaei, S.H.; Carreau, P.J.; Ajji, A. Rheological Properties of Blends of Linear and Long-chain Branched Polypropylenes. Polym. Eng. Sci. 2010, 50, 191–199. [Google Scholar] [CrossRef]
- Jahani, Y.; Ghetmiri, M.; Vaseghi, M.R. The Effects of Long Chain Branching of Polypropylene and Chain Extension of Poly(ethylene terephthalate) on the Thermal Behavior, Rheology and Morphology of Their Blends. RSC Adv. 2015, 5, 21620–21628. [Google Scholar] [CrossRef]
- Ameli, A.; Jung, P.U.; Park, C.B. Electrical Properties and Electromagnetic Interference Shielding Effectiveness of Polypropylene/carbon Fiber Composite Foams. Carbon 2013, 60, 379–391. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, W.; Zou, J.; Turng, L. Dual-scale Modeling and Simulation of Film Casting of Isotactic Polypropylene. J. Plast. Film. Sheet. 2016, 32, 239–271. [Google Scholar] [CrossRef]
- Kim, E.S.; Park, H.E.; Lee, P.C. In situ Shrinking Fibers Enhance Strain Hardening and Foamability of Linear Polymers. Polymer 2018, 136, 1–5. [Google Scholar] [CrossRef]
- Maddah, H.A. Polypropylene as a Promising Plastic: A review. Am. J. Polym. Sci. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Drabek, J.; Zatloukal, M. Evaluation of Thermally Induced Degradation of Branched Polypropylene by Using Rheology and Different Constitive Equations. Polymers 2016, 8, 317. [Google Scholar] [CrossRef]
- Mohebbi, A.; Mighri, F.; Ajji, A.; Rodrigue, D. Current Issues and Challenges in Polypropylene Foaming: A Review. Cell. Polym. 2015, 34, 229–338. [Google Scholar] [CrossRef]
- Yang, Y.; Boom, R.; Heerden, D.V.; Kuiper, P.; Wit, H.D. Recycling of Composite Materials. Chem. Eng. Process. 2012, 51, 53–68. [Google Scholar] [CrossRef]
- Münstedt, H. New Univeral Extensional Rheometer for Polymer Melts. Measurements on a Polystyrene Sample. J. Rheol. 1979, 23, 421–436. [Google Scholar] [CrossRef]
- Bach, A.; Rasmussen, H.K.; Hassager, O. Extensional Viscosity for Polymer Melts Measured in the Filament Stretching Rheometer. J. Rheol. 2003, 47, 429–441. [Google Scholar] [CrossRef]
- Meissner, J.; Hostettler, J. A New Elongational Rheometer for Polymer Melts and Other Highly Viscoelastic Liquids. Rheol. Acta. 1994, 33, 1–21. [Google Scholar] [CrossRef]
- Kim, J.; Mai, Y. Engineered Interfaces in Fiber Reinforced Composites, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1998; ISBN 9780080426952. [Google Scholar]
- Baired, D.G.; Collias, D.I. Polymer Processing: Principles and Design, 2nd ed.; Wiley: Hoboken, NJ, USA, 1993; ISBN 9780470930588. [Google Scholar]
- Dealy, J.M.; Morris, J.; Morrison, F.; Vlassopoulos, D. Official symbols and nomenclature of The Society of Rheology. J. Rheol. 2013, 57, 1047–1055. [Google Scholar] [CrossRef]
- Sato, Y.; Fujiwara, K.; Takikawa, T.; Takishima, S.; Masuoka, H. Solubilities and Diffusion Coefficients of Carbon Dioxide and Nitrogen in Polypropylene, High-density Polyethylene, and Polystyrene under Higher Pressures and Temperatures. Fluid Phase Equilibr. 1999, 162, 261–276. [Google Scholar] [CrossRef]
- Park, H.E. Effects of Pressure and Dissolved Carbon Dioxide on the Rheological Properties of Molten Polymers. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2005. [Google Scholar]
- Wang, L.; Lee, R.; Wang, G.; Chu, R.K.M.; Zhao, J.; Park, C.B. Use of Stereocomplex Crystallites for Fully-biobased Microcellular Low-density Poly(lactic acid) Foams for Green Packaging. Chem. Eng. J. 2017, 327, 1151–1162. [Google Scholar] [CrossRef]
- Tran, M.; Gong, P.; Detrembleur, C.; Thomassin, J.; Buahom, P.; Saniei, M.; Kenig, S.; Park, C.B.; Lee, S. Reducing Thermal Conductivity of Polymeric Foams with High Volume Expansion Made From Polystyrene/expanded Graphite. SPE ANTEC Indianap. 2016, 2016, 1870–1881. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1986; ISBN 9780198533689. [Google Scholar]
- Wunderlich, B. Macromolecular Physics. Vol. 3: Crystal Melting; Academic Press: New York, NY, USA, 1980; pp. 61–64. [Google Scholar]
- Han, C.D.; Baek, D.M.; Kim, J.K.; Ogawa, T.; Sakamoto, N.; Hashimoto, T. Effect of Volume Fraction on Order-Disorder Transition in Low Molecular Weight Polystyrene-block-Polyisoprene Copolymers. Macromolecules 1995, 28, 5043–5062. [Google Scholar] [CrossRef]
- Kossuth, M.B.; Morse, D.C.; Bates, F.S. Viscoelastic Behavior of Cubic Phases in Block Copolymer Melts. J. Rheol. 1999, 43, 167–196. [Google Scholar] [CrossRef]

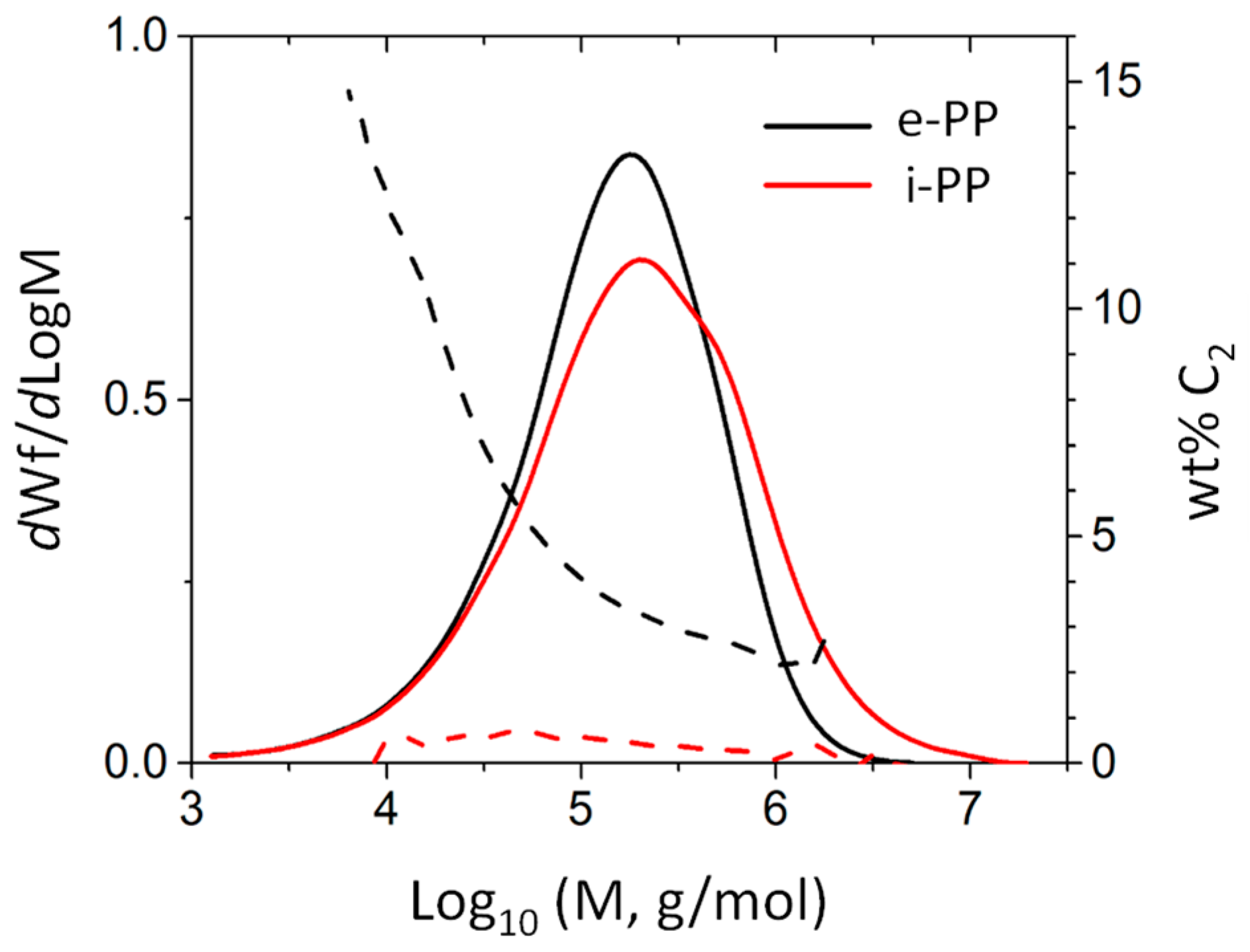
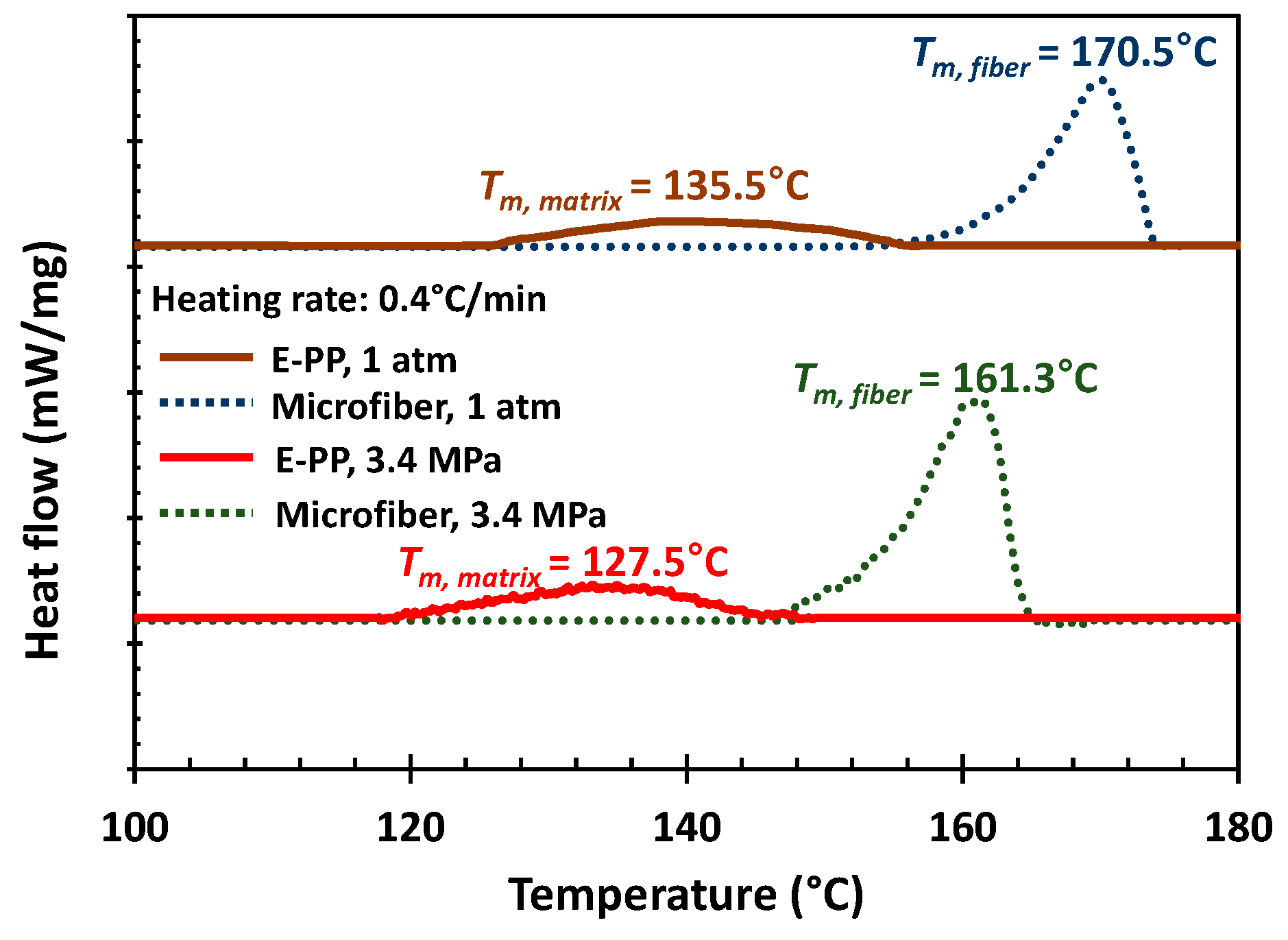
| Code | Function | Molecular Weights (kg/mol) | Mw/Mn | Tacticity (Triad mol %) | Comonomer Content | Peak Tm (°C) | Crystallinity (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mn | Mw | Mz | rr | mm | mr | mol % | mass % | 1 atm | 3.4 MPa with CO2 | ||||
| e-PP | matrix | 55 | 252 | 621 | 4.58 | a 84.7 | propylene (92) ethylene (8) | propylene (94.5) ethylene (5.5) | 135.5 | 127.5 | 14.5 | ||
| i-PP | micro- fiber | 60 | 451 | 2080 | 7.55 | 3 | 93 | 4 | b N.A. | b N.A. | 170.5 | 161.3 | c 62.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, E.S.; Park, H.E.; Lopez-Barron, C.R.; Lee, P.C. Enhanced Foamability with Shrinking Microfibers in Linear Polymer. Polymers 2019, 11, 211. https://doi.org/10.3390/polym11020211
Kim ES, Park HE, Lopez-Barron CR, Lee PC. Enhanced Foamability with Shrinking Microfibers in Linear Polymer. Polymers. 2019; 11(2):211. https://doi.org/10.3390/polym11020211
Chicago/Turabian StyleKim, Eric S., Heon E. Park, Carlos R. Lopez-Barron, and Patrick C. Lee. 2019. "Enhanced Foamability with Shrinking Microfibers in Linear Polymer" Polymers 11, no. 2: 211. https://doi.org/10.3390/polym11020211
APA StyleKim, E. S., Park, H. E., Lopez-Barron, C. R., & Lee, P. C. (2019). Enhanced Foamability with Shrinking Microfibers in Linear Polymer. Polymers, 11(2), 211. https://doi.org/10.3390/polym11020211








