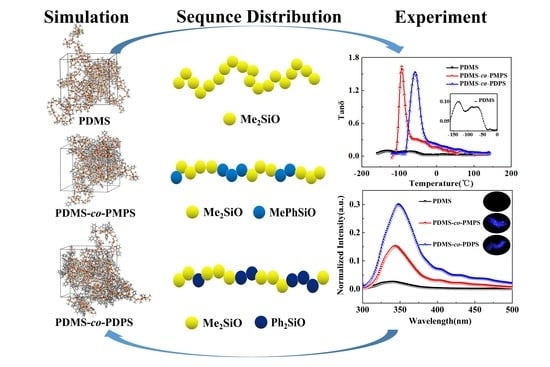
Molecular Insights into Sequence Distributions and Conformation-Dependent Properties of High-Phenyl Polysiloxanes
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Samples Preparation
2.2. Characterization
2.3. Simulation Methodology
3. Results and Discussion
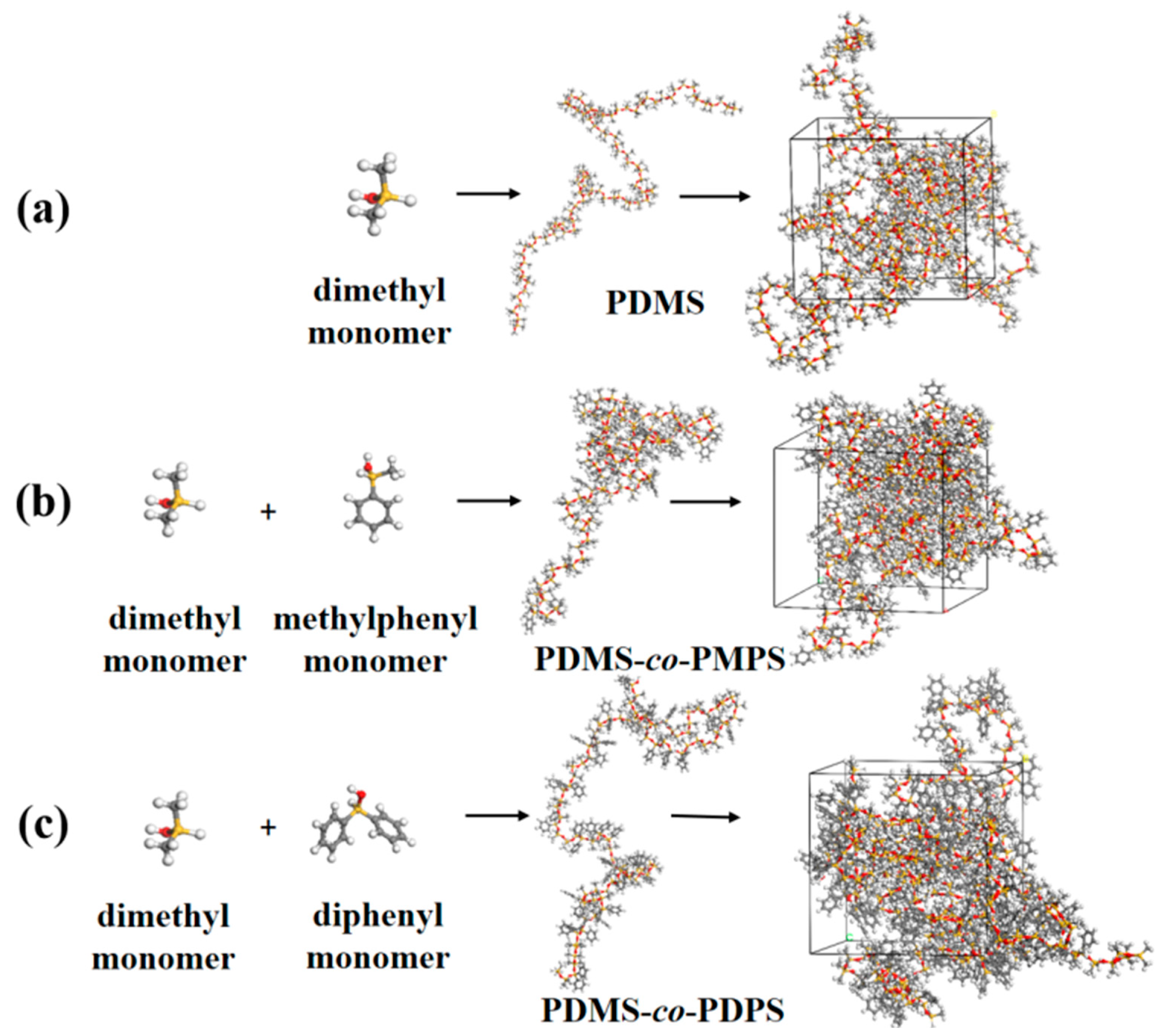
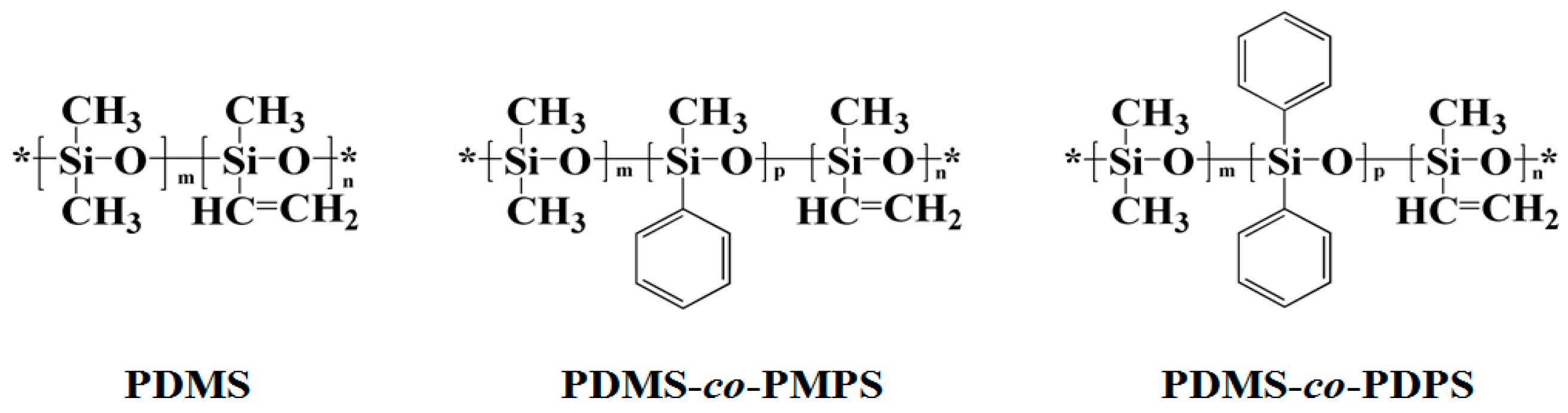
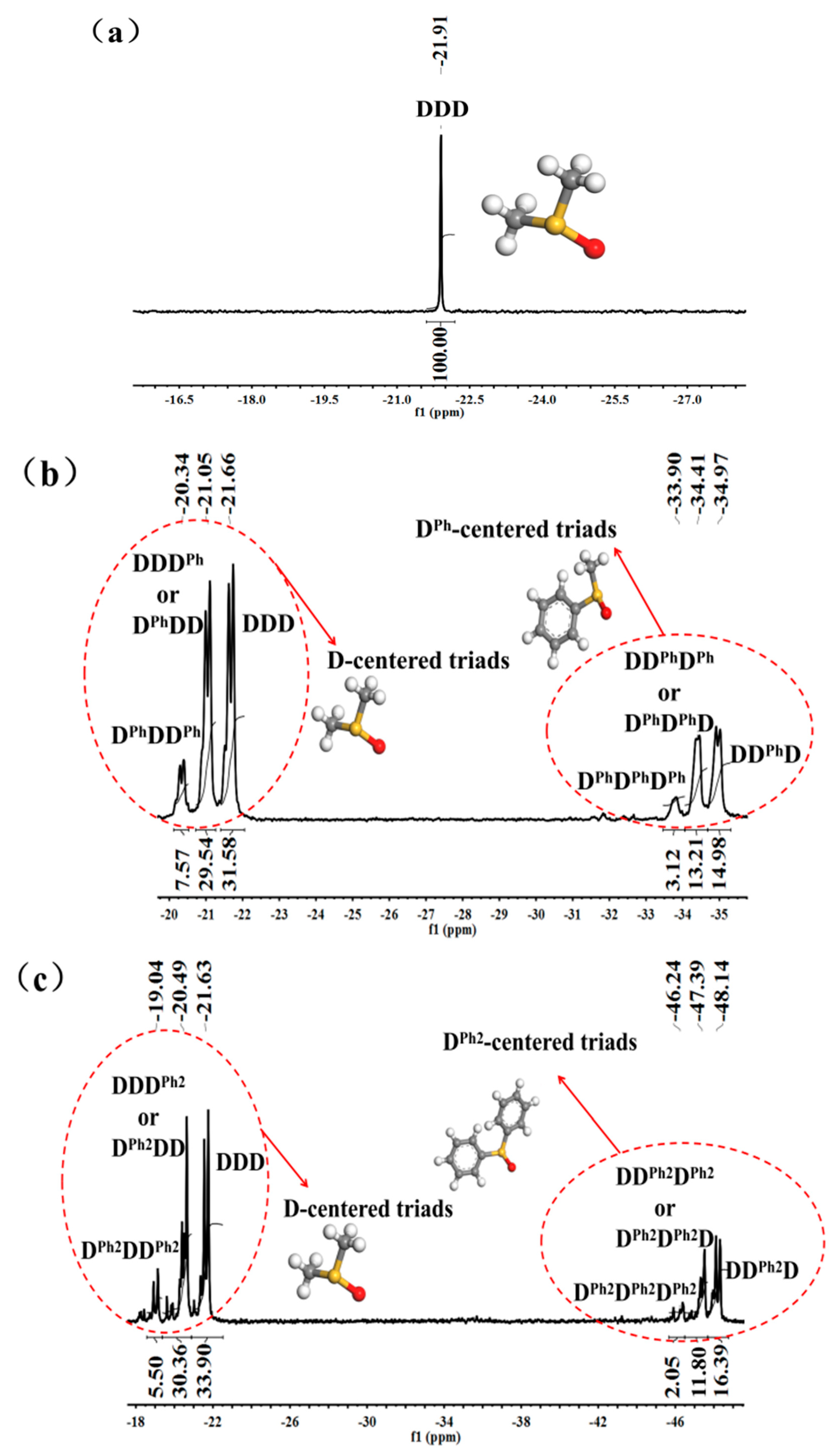
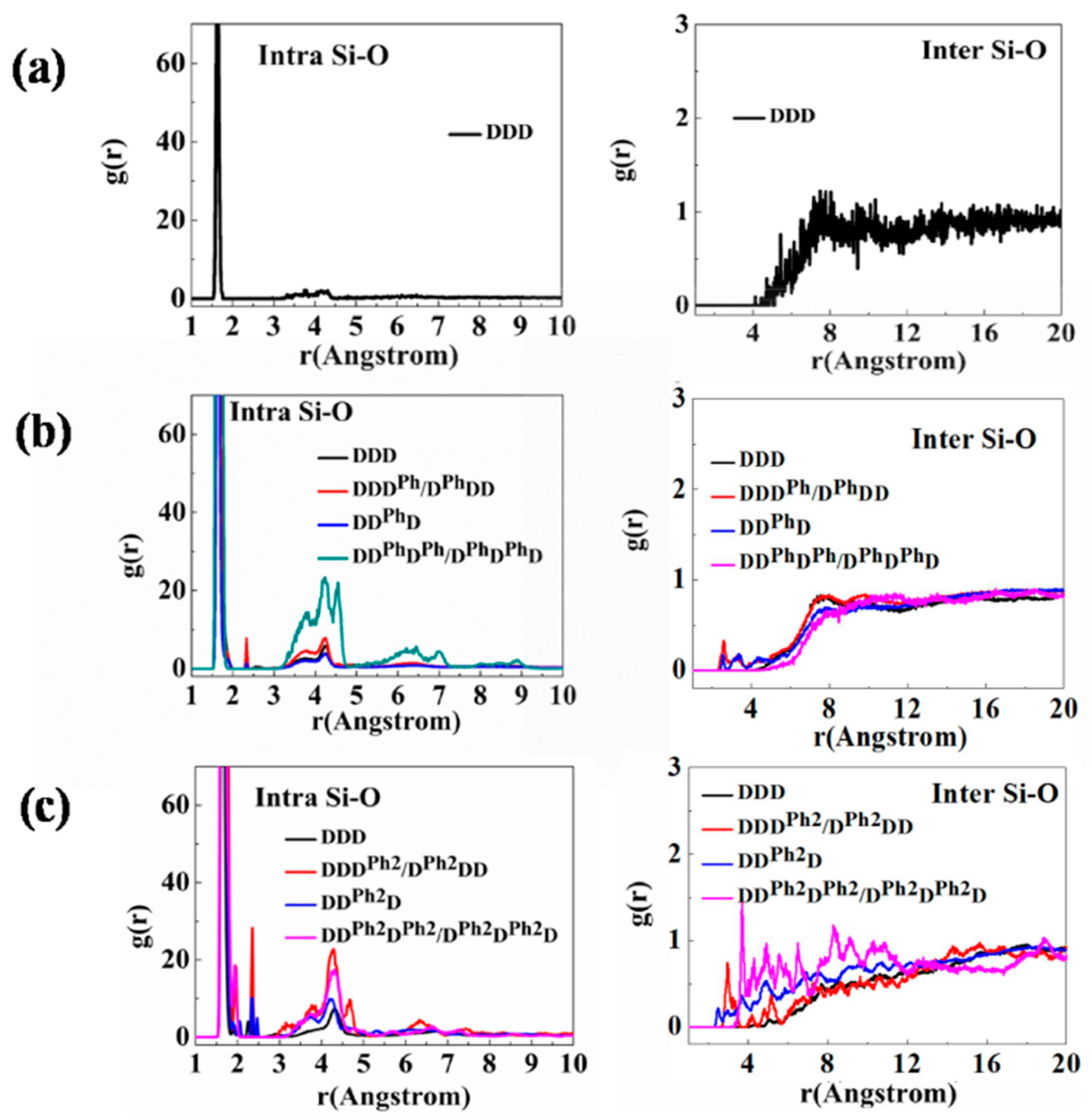
3.1. Structural Characterization and Sequence Analysis
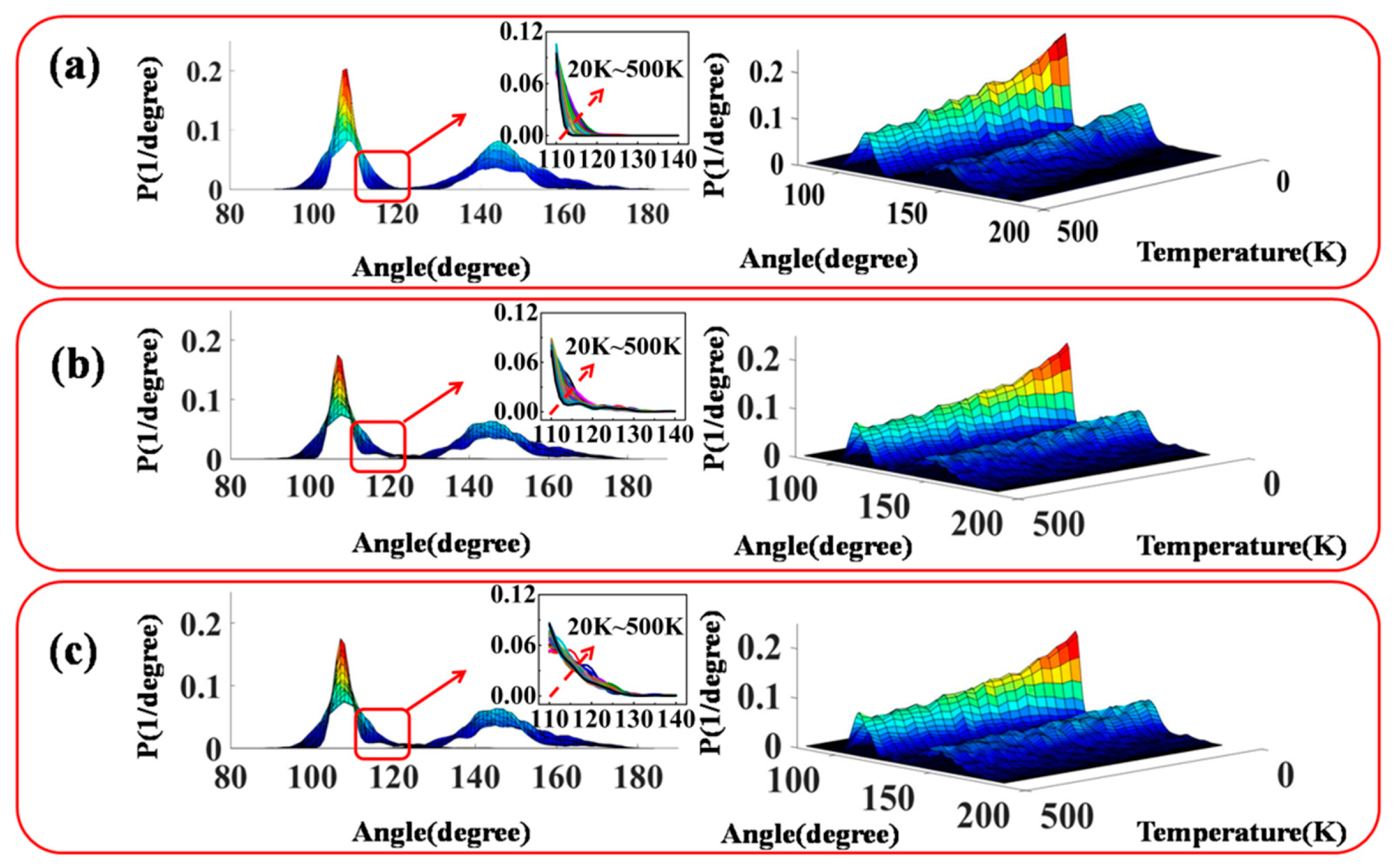
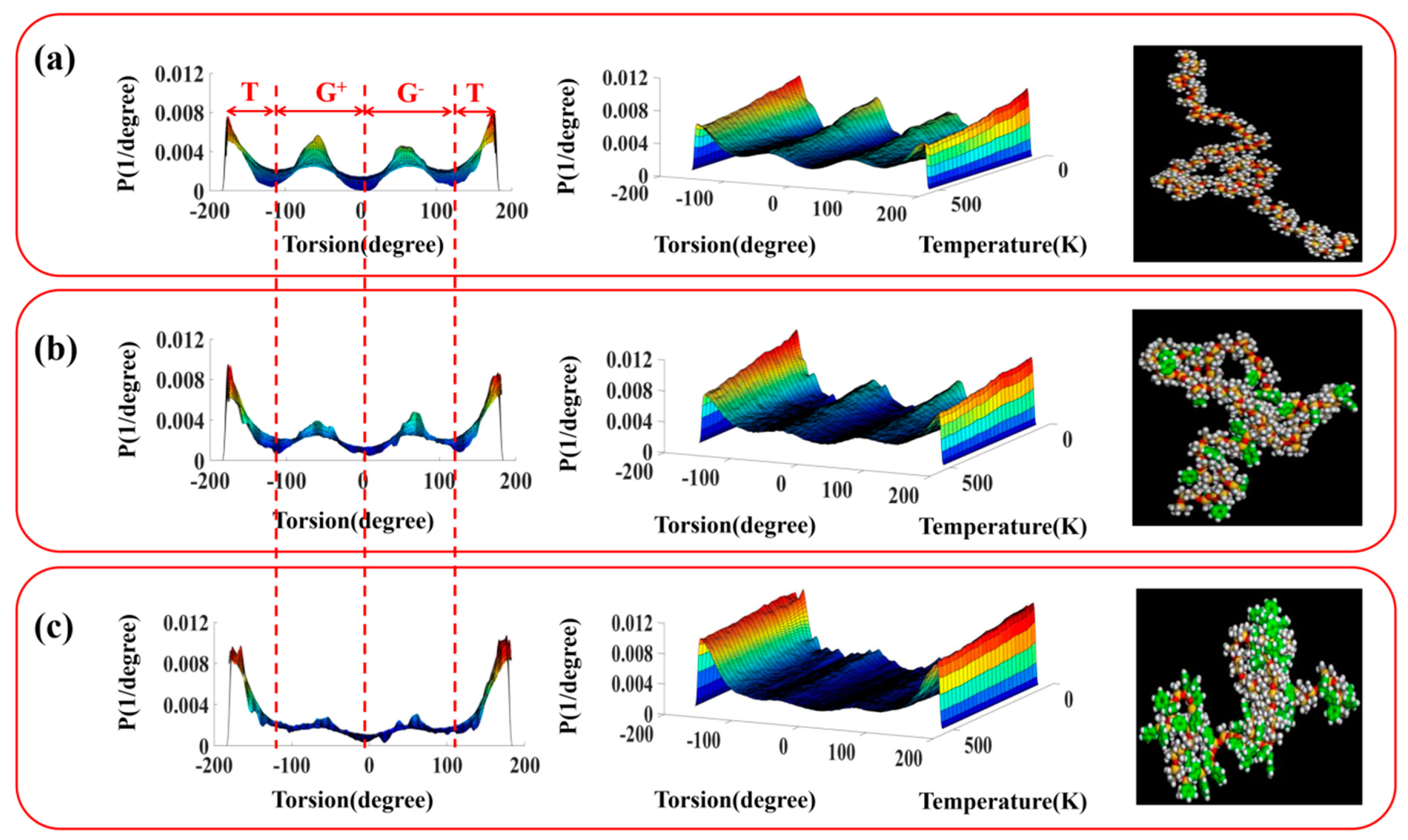
3.2. Configuration and Conformation of Polysiloxane Chains
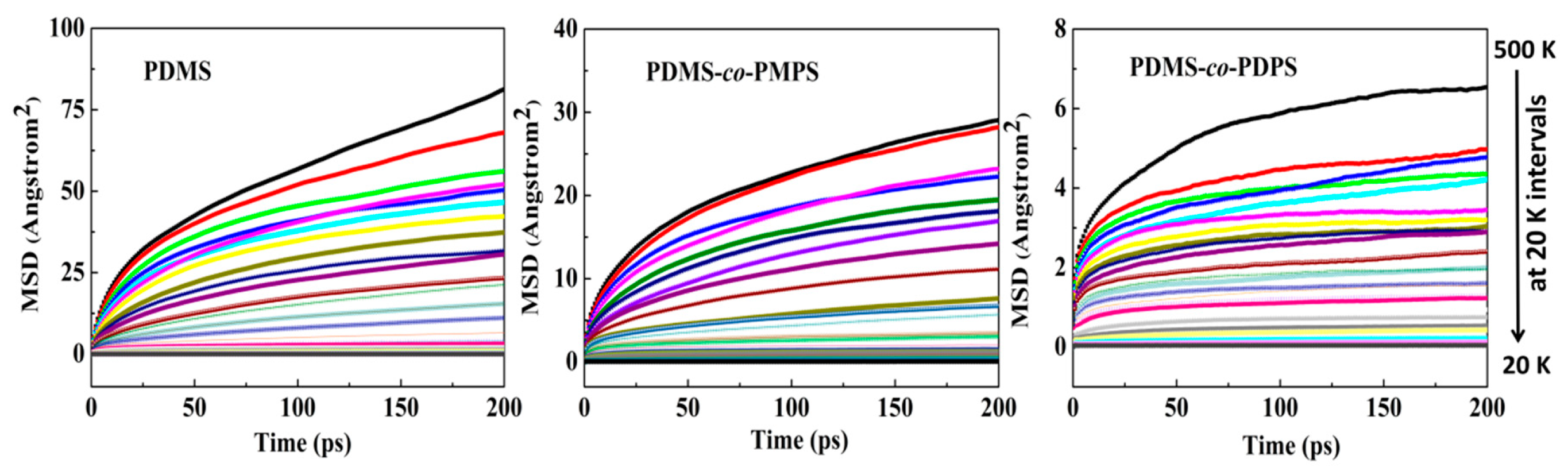
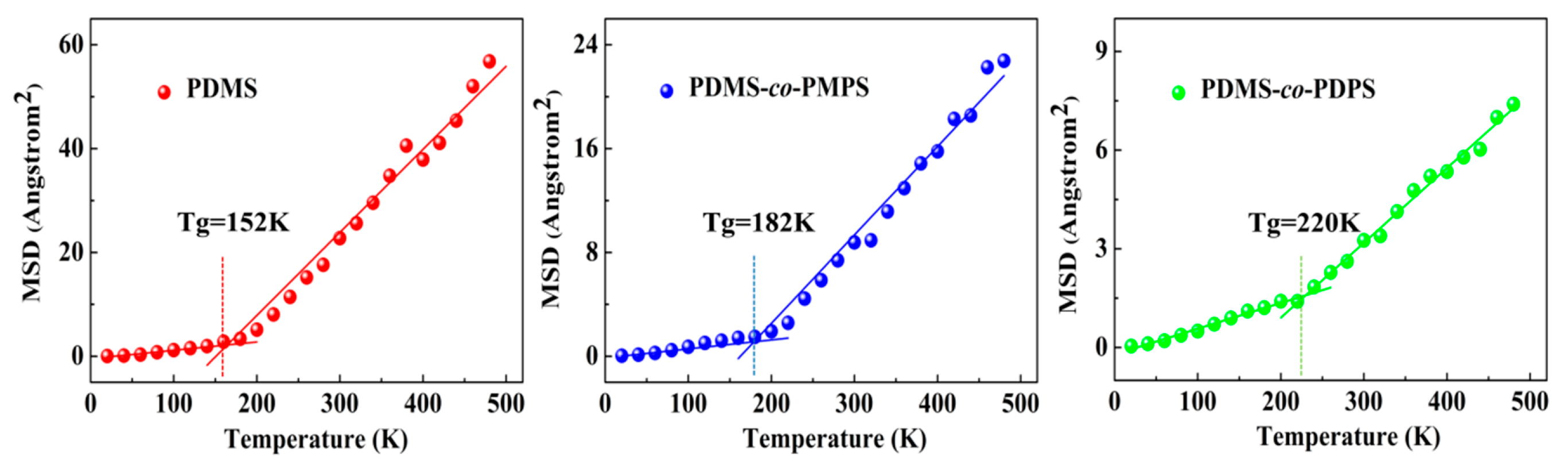
3.3. Thermodynamics Properties
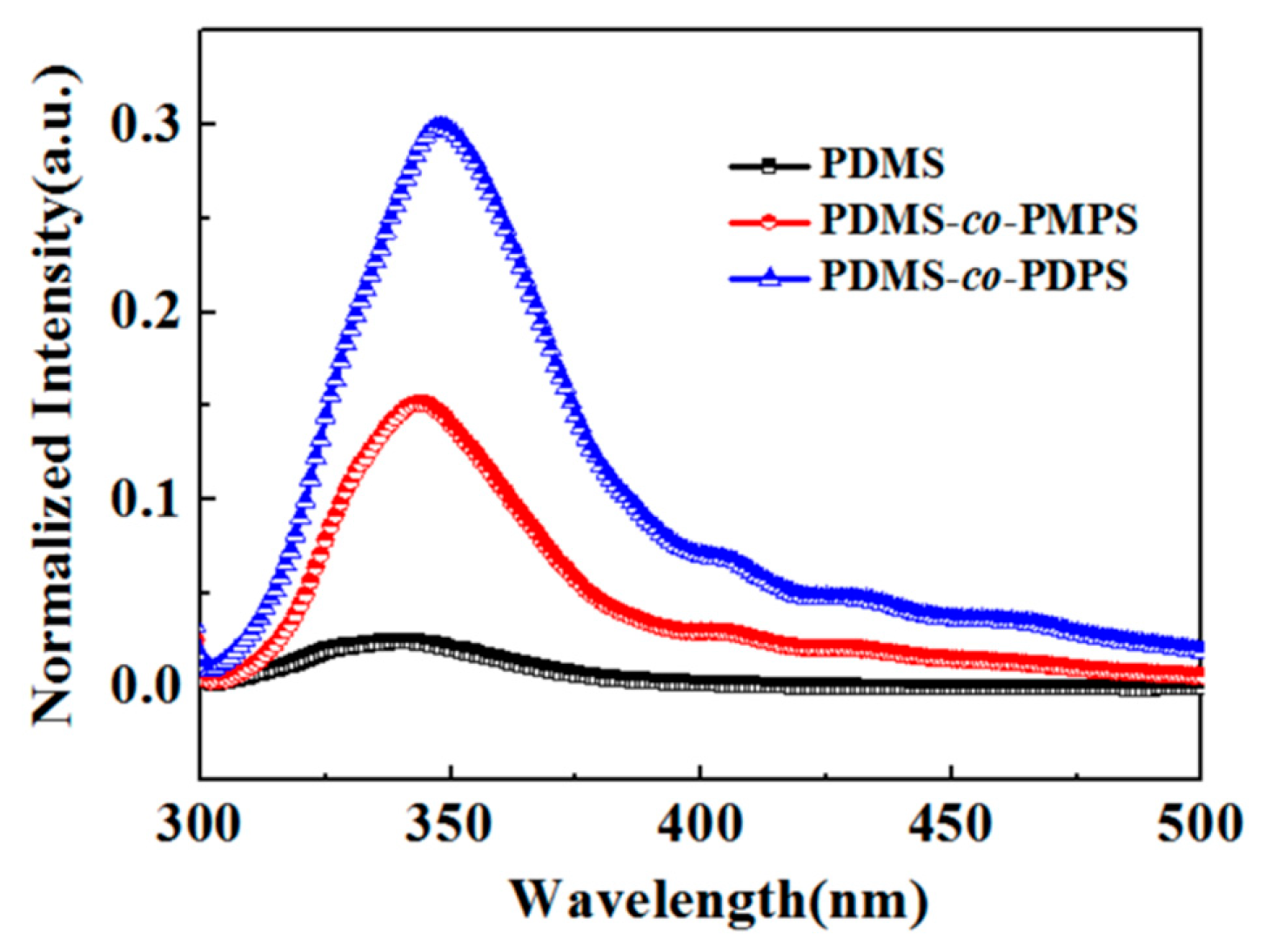
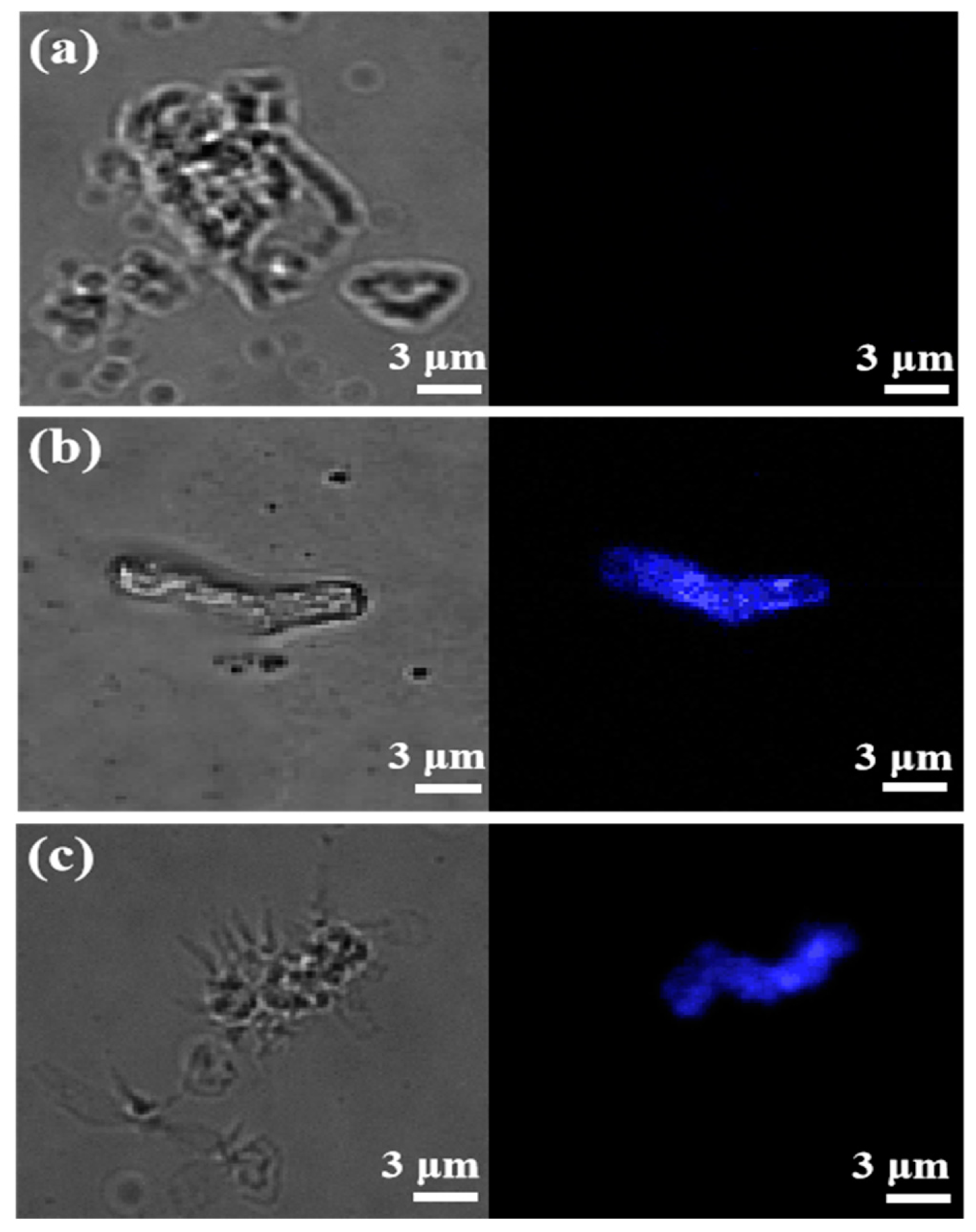
3.4. Photophysical Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
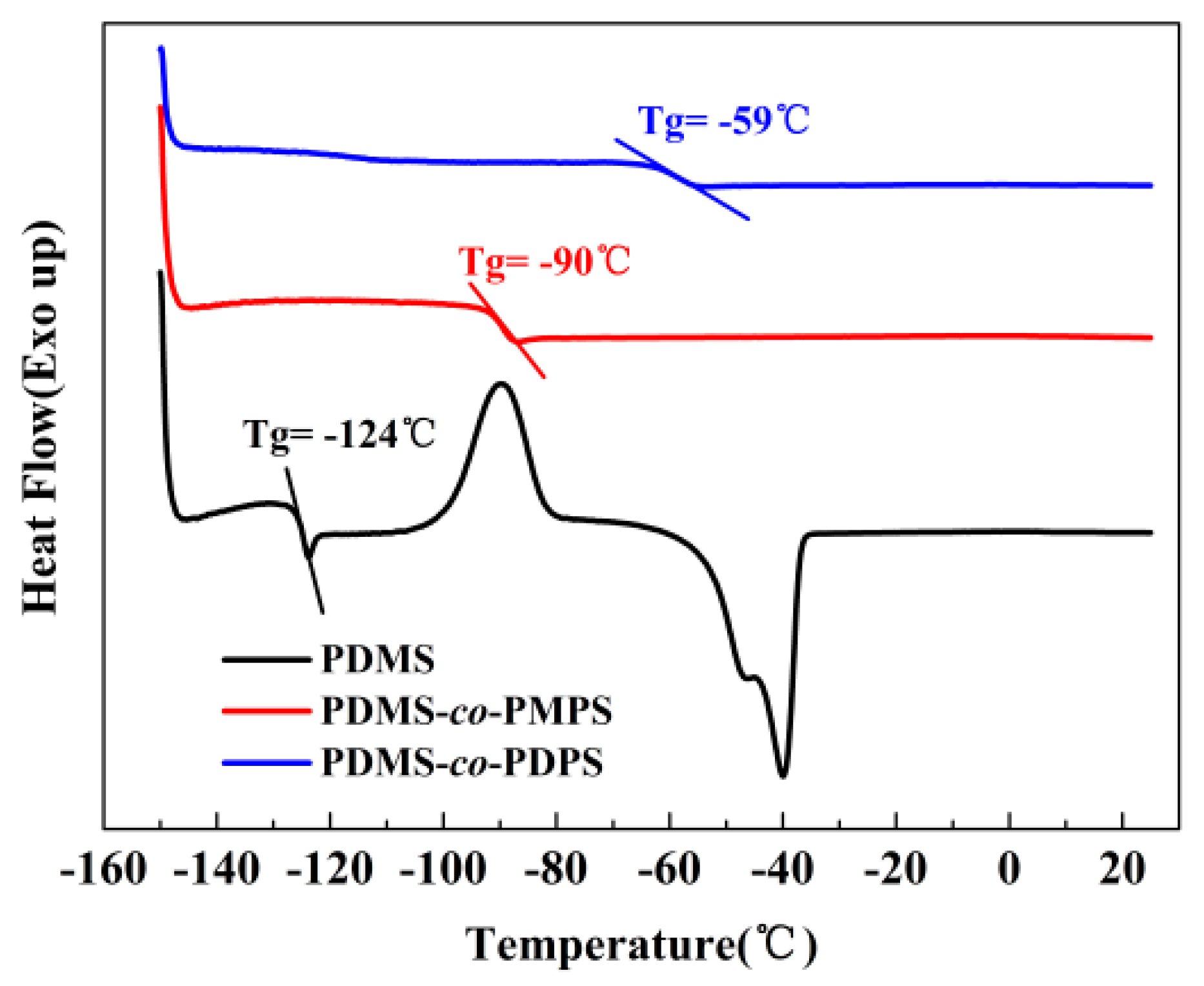
Appendix A.1. DSC of Polysiloxanes
Appendix A.2. GPC of Polysiloxanes
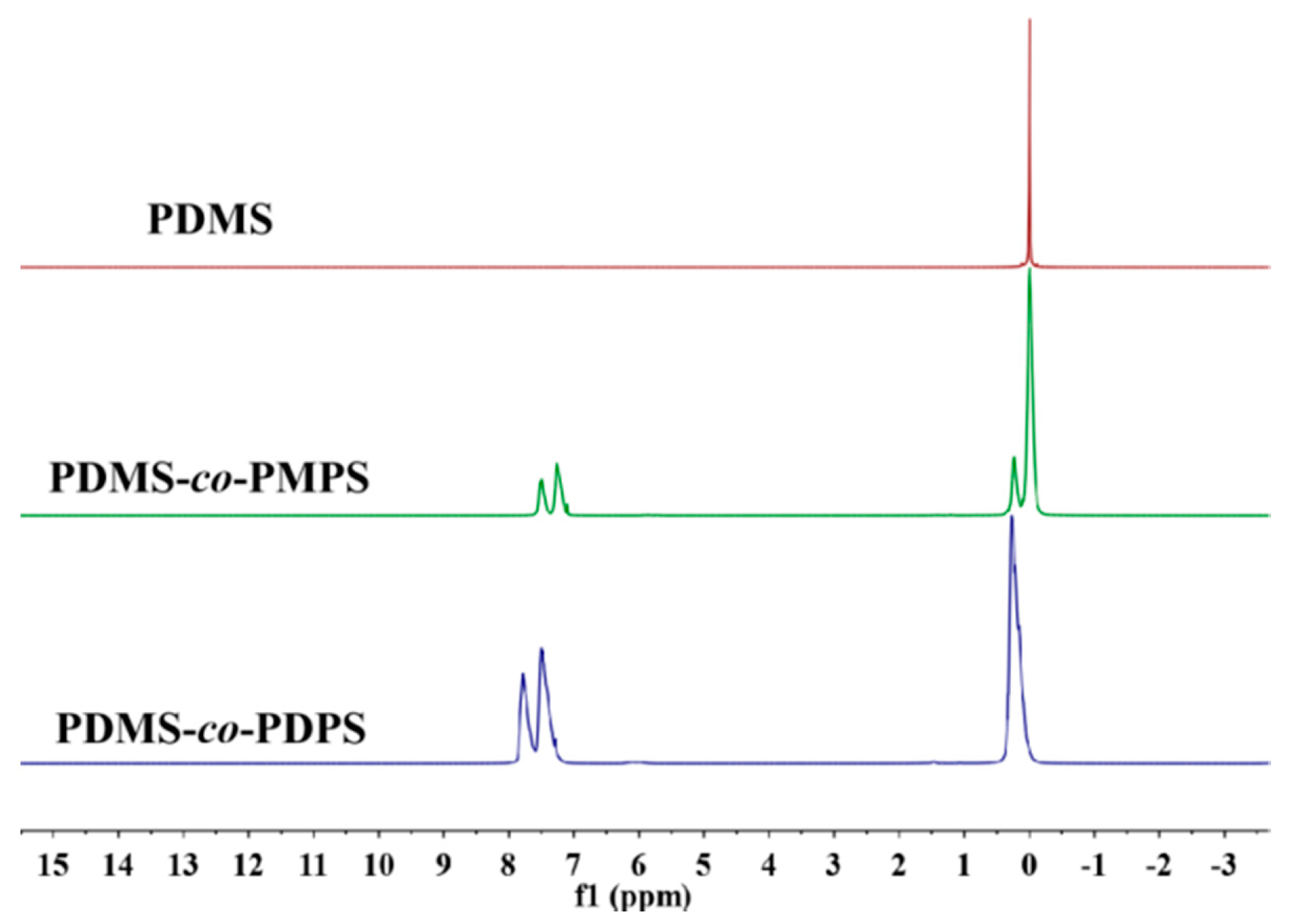
Appendix A.3. 1H NMR of Polysiloxanes
Appendix A.4. Construction Models of PDMS, PDMS–co–PMPS and PDMS–co–PDPS
References
- Ren, Z.J.; Yan, S. Polysiloxanes for optoelectronic applications. Prog. Mater. Sci. 2016, 83, 383–416. [Google Scholar] [CrossRef]
- Yilgör, E.; Yilgör, I. Silicone containing copolymers: Synthesis, properties and applications. Prog. Polym. Sci. 2014, 39, 1165–1195. [Google Scholar] [CrossRef]
- Shi, J.F.; Zhao, N.; Xia, S.; Liu, S.F.; Li, Z.B. Phosphazene superbase catalyzed ring-opening polymerization of cyclotetrasiloxane toward copolysiloxanes with high diphenyl siloxane content. Polym. Chem. 2019, 10, 2126–2133. [Google Scholar] [CrossRef]
- Qu, L.L.; Huang, G.S.; Wang, Q.; Xie, Z.J. Effect of diphenylsiloxane unit content on aggregation structure of poly(dimethylsiloxane-co-diphenylsiloxane). J. Polym. Sci. Polym. Phys. 2008, 46, 72–79. [Google Scholar] [CrossRef]
- Zlatanic, A.; Radojcic, D.; Wan, X.M.; Messman, J.M.; Dvornic, P.R. Suppression of crystallization in polydimethylsiloxanes and chain branching in their phenyl-containing copolymers. Macromolecules 2017, 50, 3532–3543. [Google Scholar] [CrossRef]
- Zlatanic, A.; Radojcic, D.; Wan, X.M.; Messman, J.M.; Bowen, D.E.; Dvornic, P.R. Dimethyl-methylphenyl copolysiloxanes by dimethylsilanolate-initiated ring opening polymerization. Evidence for linearity of the resulting polymer structures. J. Polym. Sci. Polym. Chem. 2019, 57, 1122–1129. [Google Scholar] [CrossRef]
- Chou, C.; Yang, M.H. Structural effects on the thermal properties of PDPS/PDM copolymers. J. Therm. Anal. Calorim. 1993, 40, 657–667. [Google Scholar] [CrossRef]
- Yu, F.M.; Lu, A.; Lu, J.L.; Wang, Z.Y.; Zhang, Q.; Geng, C.Z.; Li, Z.M. Effect of phenyl content, sample thickness and compression on damping performances of silicone rubber: A study by dynamic mechanical analysis and impact damping test. Polym. Test. 2019, 80, 106101. [Google Scholar] [CrossRef]
- Palma, M.D.; Marchi, T.; Carturan, S.; Checchia, C. Pulse shape discrimination in polysiloxane-based liquid scintillator. IEEE Trans. Nucl. Sci. 2016, 63, 1608–1615. [Google Scholar]
- Quaranta, A.; Carturan, S.M.; Marchi, T.; Kravchuk, V.L.; Gramegna, F.; Maggioni, G.; Degerlier, M. Optical and scintillation properties of polydimethyl-diphenylsiloxane based organic scintillators. IEEE Trans. Nucl. Sci. 2010, 57, 891–900. [Google Scholar] [CrossRef]
- Palma, M.D.; Carturan, S.M.; Degerlier, M.; Marchi, T.; Cinausero, M.; Gramegna, F.; Quaranta, A. Non-toxic liquid scintillators with high light output based on phenyl-substituted siloxanes. Opt. Mater. 2015, 42, 111–117. [Google Scholar] [CrossRef]
- Rubio, A.; Freire, J.J.; Piérda Inés, F. Excimer-Forming Sites of Poly(methylphenylsiloxane). Macromolecules 1989, 22, 4014–4019. [Google Scholar] [CrossRef]
- Horta, A.; Pie’rola, I.F.; Macanita, A.L. Molecular dynamics of methylphenylsiloxane chains. Macromolecules 2000, 33, 1213–1223. [Google Scholar] [CrossRef]
- Dias, F.B.; Lima, J.C.; Macanita, A.L.; Clarson, S.J.; Horta, A.; Pie’rola Ine´s, F. Anomalous fluorescence of linear poly(methylphenylsiloxane) in dilute solution at temperatures below −50°C. Macromolecules 2000, 33, 4772–4779. [Google Scholar] [CrossRef]
- Shang, Y.R.; Zhang, X.X.; Xu, H.; Li, J.Q.; Jiang, S.C. Microscopic study of structure/property interrelation of amorphous polymers during uniaxial deformation: A molecular dynamics approach. Polymer 2015, 77, 254–265. [Google Scholar] [CrossRef]
- Nam, K.H.; Choi, H.K.; Yeo, H.; You, N.H.; Ku, B.C.; Yu, J. Molecular design and property prediction of sterically confined polyimides for thermally stable and transparent materials. Polymers 2018, 10, 630. [Google Scholar] [CrossRef]
- Guseva, D.V.; Rudyak, V.Y.; Komarov, P.V.; Bulgakov, B.A.; Babkin, A.V.; Chertovich, A.V. Dynamic and static mechanical properties of crosslinked polymer matrices: Multiscale simulations and experiments. Polymers 2018, 10, 792. [Google Scholar] [CrossRef]
- Dalgakiran, E.; Tatlipinar, H. The role of hydrophobic hydration in the LCST behaviour of POEGMA300 by all-atom molecular dynamics simulations. Phys. Chem. Chem. Phys. 2018, 20, 15389–15399. [Google Scholar] [CrossRef]
- Fu, K.; Xie, Q.; LÜ, F.C.; Duan, Q.J.; Wang, X.J.; Zhu, Q.S.; Huang, Z.Y. Molecular dynamics simulation and experimental studies on the thermomechanical properties of epoxy resin with different anhydride curing agents. Polymers 2019, 11, 975. [Google Scholar] [CrossRef]
- Shen, J.X.; Lin, X.S.; Liu, J.; Li, X. Effects of cross-link density and distribution on static and dynamic properties of chemically cross-linked polymers. Macromolecules 2019, 52, 121–134. [Google Scholar] [CrossRef]
- DasSk, A.; Ali, M. Molecular dynamics simulation studies on structure, dynamics, and thermodynamics of uranyl nitrate solution at various acid concentrations. J. Phys. Chem. B 2019, 123, 4571–4586. [Google Scholar]
- Bahar, I.; Zuniga, I.; Dodge, R.; Mattice, W.L. Conformational statistics of poly(dimethylsiloxane). 1.Probability distribution of rotational isomers from molecular dynamics simulations. Macromolecules 1991, 24, 2986–2992. [Google Scholar] [CrossRef]
- Freire, J.J.; Pie´rola, I.F.; Horta, A. Conformational analysis of methyl-phenyl-siloxane chains. Macromolecules 1996, 29, 5143–5148. [Google Scholar] [CrossRef]
- Neuburger, N.; Bahar, I.; Mattice, W.L. Molecular dynamics simulations of poly(dialkylsi1oxanes).Conformational statistics and unperturbed chain dimensions. Macromolecules 1992, 25, 2447–2454. [Google Scholar] [CrossRef]
- Kurbatov, A.O.; Balabaev, N.K.; Mazo, M.A.; Kramarenko, E.Y. Molecular dynamics simulations of single siloxane dendrimers: Molecular structure and intramolecular mobility of terminal groups. J. Chem. Phys. 2018, 148, 014902. [Google Scholar] [CrossRef]
- Sethi, S.K.; Soni, L.; Manik, G. Component compatibility study of poly(dimethyl siloxane) with poly(vinyl acetate) of varying hydrolysis content: An atomistic and mesoscale simulation approach. J. Mol. Liq. 2018, 272, 73–83. [Google Scholar] [CrossRef]
- Klonos, P.; Bolbukh, Y.; Koutsiara, C.S.; Zafeiris, K.; Kalogeri, O.D.; Sternik, D.; Marczewska, A.D.; Tertykh, V.; Pissis, P. Morphology and molecular dynamics investigation of low molecular weight PDMS adsorbed onto Stöber, fumed, and sol-gel silica nanoparticles. Polymer 2018, 148, 1–13. [Google Scholar] [CrossRef]
- Trazkovich, A.J.; Wendt, M.F.; Hall, L.M. Effect of Copolymer Sequence on Local Viscoelastic Properties near a Nanoparticle. Macromolecules 2019, 52, 513–527. [Google Scholar] [CrossRef]
- Zlatanic, A.; Radojcic, D.; Wan, X.M.; Messman, J.M.; Dvornic, P.R. Monitoring of the Course of the Silanolate-Initiated Polymerization of Cyclic Siloxanes. A Mechanism for the Copolymerization of Dimethyl and Diphenyl Monomers. Macromolecules 2018, 51, 895–905. [Google Scholar] [CrossRef]
- Babu, G.N.; Christopher, S.S.; Newmark, R.A. poly(dimethylsiloxane-co-diphenylsiloxanes): Synthesis, characterization, and sequence analysis. Macromolecules 1987, 20, 2654–2659. [Google Scholar] [CrossRef]
- Brewer, J.R.; Tsuchihara, K.; Morita, R. Poly(diethylsiloxane-co-diphenylsiloxane) and poly(diethylsiloxane-co-3,3,3-trifluoropropylmethylsiloxane): Synthesis, characterization and low-temperature properties. Polymer 1994, 35, 5109–5117. [Google Scholar] [CrossRef]
- Brewer, J.R.; Tsuchihara, K.; Morita, R. Poly(diethylsiloxane-co-ethylphenylsiloxane) and poly(diethylsiloxane-co-methylphenylsiloxane): Synthesis and characterization. Polymer 1994, 35, 5118–5123. [Google Scholar] [CrossRef]
- Ziemelis, M.J.; Saam, J.C. Sequence distribution in poly(dimethylsiloxane-co-methylvinylsiloxanes). Macromolecules 1989, 22, 2111–2116. [Google Scholar] [CrossRef]
- Harwood, H.J.; Ritchey, W.M. The characterization of sequence distribution in copolymers. J. Polym. Sci. B Polym. Lett. 1964, 2, 601–607. [Google Scholar] [CrossRef]
- Jancke, H.; Engelhardt, G.; Kriegsmann, H. Quantitative Mikrostrukturanalyse von siloxankopolymeren mit hilfe der 29 Si-NMR-spectroskopie. Plaste Kautsch. 1979, 26, 612–613. [Google Scholar]
- Engelhardt, G.; Jancke, H. Structure investigation of organosilicon polymers by silicon-29 NMR. Polym. Bull. 1981, 5, 577–584. [Google Scholar] [CrossRef]
- Okada, O.; Oka, K.; Kuwajima, S.; Toyoda, S.; Tanabe, K. Molecular simulation of an amorphous poly(methyl methacrylate)-poly(tetrafluoroethylene) interface. Comput. Theor. Polym. Sci. 2000, 10, 371–381. [Google Scholar] [CrossRef]
- Luo, Z.L.; Jiang, J.W. Molecular dynamics and dissipative particle dynamics simulations for the miscibility of poly(ethylene oxide)/poly(vinyl chloride) blends. Polymer 2010, 51, 291–299. [Google Scholar] [CrossRef]
- Makrodimitri Zoi, A.; Dohrn, R.; Economou, I.G. Atomistic simulation of poly(dimethylsiloxane): Force field development, structure, and thermodynamic properties of polymer melt and solubility of n-alkanes, n-perfluoroalkanes, and noble and light Gases. Macromolecules 2007, 40, 1720–1729. [Google Scholar] [CrossRef]
- Smith, J.S.; Borodin, O.; Smith, G.D. A quantum chemistry based force field for poly(dimethylsiloxane). J. Phys. Chem. B 2004, 108, 20340–20350. [Google Scholar] [CrossRef]
- Choi, J.; Yu, S.; Yang, S.; Cho, M. The glass transition and thermoelastic behavior of epoxy-based nanocomposites: A molecular dynamics study. Polymer 2011, 52, 5197–5203. [Google Scholar] [CrossRef]
- Trady, S.; Mazroui, M.; Hasnaoui, A.; Saadouni, K. Molecular dynamics study of atomic-level structure in monatomic metallic glass. J. Non-Cryst. Solids 2016, 443, 136–142. [Google Scholar] [CrossRef]
- Mohammdi, M.; Fazli, H.; karevan, M.; Davoodi, J. The glass transition temperature of PMMA: A molecular dynamics study and comparison of various determination methods. Eur. Polym. J. 2017, 91, 121–133. [Google Scholar] [CrossRef]
- Klonos, P.A. Crystallization, glass transition, and molecular dynamics in PDMS of low molecular weights: A calorimetric and dielectric study. Polymer 2018, 159, 169–180. [Google Scholar] [CrossRef]
- Liu, B.Z.; Gao, X.Y.; Zhao, Y.F.; Dai, L.N.; Xie, Z.M.; Zhang, Z.J. 9,10-Dihydro-9-oxa-10-phosphaphenanthrene 10-oxide-based oligosiloxane as a promising damping additive for methyl vinyl silicone rubber (VMQ). J. Mater. Sci. 2017, 52, 8603–8617. [Google Scholar] [CrossRef]
- Cvek, M.; Mrlík, M.; Ilčíková, M.; Mosnáček, J.; Münster, L.; Pavlínek, V. Synthesis of silicone elastomers containing silyl-based polymer-grafted carbonyl iron particles: An efficient way to improve magnetorheological, damping, and sensing performances. Macromolecules 2017, 50, 52189–52200. [Google Scholar] [CrossRef]
- Cabanelas, J.C.; Serrano, B.; Gonzalez, M.G.; Baselga, J. Confocal microscopy study of phase morphology evolution in epoxy/polysiloxane thermosets. Polymer 2005, 46, 6633–6639. [Google Scholar] [CrossRef][Green Version]
- Han, T.; Gui, C.; Lam, J.W.Y.; Jiang, M.J.; Xie, N.; Kwok, R.T.K.; Tang, B.Z. High-contrast visualization and differentiation of microphase separation in polymer blends by fluorescent AIE probes. Macromolecules 2017, 50, 5807–5815. [Google Scholar] [CrossRef]

| Sample | Tg (°C) (a) | Mw(kg/mol) (b) | PDI (c) |
|---|---|---|---|
| PDMS | −124 | 342.1 | 1.71 |
| PDMS–co–PMPS | −90 | 426.4 | 2.20 |
| PDMS–co–PDPS | −59 | 305.9 | 1.88 |
| Polymers | Experimental Density (g/cm−3) | Simulated Density (g/cm−3) |
|---|---|---|
| PDMS | 0.97 | 0.99 |
| PDMS–co–PMPS | 1.06 | 1.10 |
| PDMS–co–PDPS | 1.10 | 1.16 |
| Sample | Me2SiO (mol %) | MePhSiO (mol %) | Ph2SiO (mol %) | MeViSiO (mol %) |
|---|---|---|---|---|
| PDMS | 99.80 | - | - | 0.20 |
| PDMS–co–PMPS | 68.02 | 31.57 | - | 0.41 |
| PDMS–co–PDPS | 68.47 | - | 30.63 | 0.90 |
| Triad | PDMS | PDMS–co–PMPS | PDMS–co–PDPS | |||
|---|---|---|---|---|---|---|
| δ (ppm) | Intensity (%) | δ (ppm) | Intensity (%) | δ (ppm) | Intensity (%) | |
| D centered | ||||||
| DDD | −21.91 | 100 | −21.66 | 31.58 | −21.63 | 33.90 |
| DDD’+D’DD | - | - | −21.05 | 29.54 | −20.49 | 30.36 |
| D’DD’ | - | - | −20.34 | 7.57 | −19.04 | 5.50 |
| D’ centered | ||||||
| DD’D | - | - | −34.97 | 14.98 | −48.14 | 16.39 |
| DD’D’+D’D’D | - | - | −34.41 | 13.21 | −47.39 | 11.80 |
| D’D’D’ | - | - | −33.90 | 3.12 | −46.24 | 2.05 |
| Polymer | fD | fD’ | RD | RD’ | Rrandom |
|---|---|---|---|---|---|
| PDMS–co–PMPS | 0.664 | 1.383 | 45.16 | 43.67 | 42.95 |
| PDMS–co–PDPS | 0.562 | 1.472 | 38.45 | 45.10 | 41.94 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Cheng, X.; Su, W.; Zhao, J.; Zhou, C. Molecular Insights into Sequence Distributions and Conformation-Dependent Properties of High-Phenyl Polysiloxanes. Polymers 2019, 11, 1989. https://doi.org/10.3390/polym11121989
Zhu L, Cheng X, Su W, Zhao J, Zhou C. Molecular Insights into Sequence Distributions and Conformation-Dependent Properties of High-Phenyl Polysiloxanes. Polymers. 2019; 11(12):1989. https://doi.org/10.3390/polym11121989
Chicago/Turabian StyleZhu, Lin, Xiao Cheng, Wenlu Su, Jiaxin Zhao, and Chuanjian Zhou. 2019. "Molecular Insights into Sequence Distributions and Conformation-Dependent Properties of High-Phenyl Polysiloxanes" Polymers 11, no. 12: 1989. https://doi.org/10.3390/polym11121989
APA StyleZhu, L., Cheng, X., Su, W., Zhao, J., & Zhou, C. (2019). Molecular Insights into Sequence Distributions and Conformation-Dependent Properties of High-Phenyl Polysiloxanes. Polymers, 11(12), 1989. https://doi.org/10.3390/polym11121989